简单的线性规划典型例题

例1：生产计划问题某工厂明年根据合同，每个季度末向销售公司提供产品，有关信息如下表。

若当季生产的产品过多，季末有积余，则一个季度每积压一吨产品需支付存贮费O.2万元。

现该厂考虑明年的最佳生产方案，使该厂在完成合同的情况下，全年的生产费用最低。

试建立模型。

解：法1 设每个季度分别生产x1,x2,x3,x4则要满足每个季度的需求x4≥26x1+ x2≥40x1+ x2+ x3≥70x1+ x2+ x3+ x4=80考虑到每个季度的生产能力 0≤x1≤300≤x2≤400≤x3≤200≤x4≤10每个季度的费用为：此季度生产费用+上季度储存费用第一季度15.0x1第二季度14 x2 0.2(x1-20)第三季度15.3x3+0.2(x1+ x2-40)第四季度14.8x4+0.2(x1+ x2+ x3-70)工厂一年的费用即为这四个季度费用之和,得目标函数；minf=15.6 x1+14.4 x2+15.5 x3+14.8 x4-26s.t．x1+ x2≥40x1+ x2+ x3≥70x1+ x2+ x3+ x4=8020≤x1≤30 0≤x2≤40 0≤x3≤20 0≤x4≤10。

法2：设第i季度生产而用于第j季度末交货的产品数量为xij吨根据合同要求有：xll=20x12+x22=20x13+x23+x33=30x14+x24+x34+x44=10又根据每季度的生产能力有：xll+x12+x13+x14≤30x22+x23+x24≤40x33+x34≤20x44≤10第i季度生产的用于第j季度交货的每吨产品的费用cij=dj+0.2(j-i)，于是，有线性规划模型。

minf=15.Oxll+15.2x12+15.4xl3+15.6xl4+14x22+14.2x23+14.4x24+15.3 x33+15.5x34+14.8x44s．t． xll=20，x12+x22=20，x13+x23+x13=30，x14+x24+x34+x44=10，x1l+x12+x13+x14≤30，x22+x23+x24≤40，x33+x34≤20，x44≤10，xij≥0， i=1，…，4;j=1，…，4，j≥i。

线性规划经典例题一、问题描述我们考虑一个典型的线性规划问题，假设有一个工厂需要生产两种产品：产品A和产品B。

工厂有两个生产车间：车间1和车间2。

生产产品A需要在车间1和车间2进行加工，而生产产品B只需要在车间2进行加工。

每一个车间的加工时间和加工费用都是不同的。

我们的目标是找到最佳的生产计划，使得总的加工时间和加工费用最小。

二、问题分析1. 定义变量：- x1：在车间1生产产品A的数量- x2：在车间2生产产品A的数量- y：在车间2生产产品B的数量2. 定义目标函数：目标函数是最小化总的加工时间和加工费用。

假设车间1生产产品A的加工时间为t1，车间2生产产品A的加工时间为t2，车间2生产产品B的加工时间为t3，车间1生产产品A的加工费用为c1，车间2生产产品A的加工费用为c2，车间2生产产品B的加工费用为c3，则目标函数可以表示为：Z = t1 * x1 + t2 * x2 + t3 * y + c1 * x1 + c2 * x2 + c3 * y3. 约束条件：- 车间1生产产品A的数量不能超过车间1的生产能力：x1 <= capacity1- 车间2生产产品A的数量不能超过车间2的生产能力：x2 <= capacity2- 车间2生产产品B的数量不能超过车间2的生产能力：y <= capacity2 - 产品A的总需求量必须满足：x1 + x2 >= demandA- 产品B的总需求量必须满足：y >= demandB4. 线性规划模型：综上所述，我们可以建立如下的线性规划模型：最小化 Z = t1 * x1 + t2 * x2 + t3 * y + c1 * x1 + c2 * x2 + c3 * y满足约束条件：- x1 <= capacity1- x2 <= capacity2- y <= capacity2- x1 + x2 >= demandA- y >= demandB- x1, x2, y >= 0三、数据和解决方案为了展示如何求解该线性规划问题，我们假设以下数据：- 车间1的生产能力为100个产品A- 车间2的生产能力为150个产品A和100个产品B- 产品A的总需求量为200个- 产品B的总需求量为80个- 车间1生产产品A的加工时间为2小时，加工费用为10元/个- 车间2生产产品A的加工时间为1小时，加工费用为8元/个- 车间2生产产品B的加工时间为3小时，加工费用为15元/个根据以上数据，我们可以得到线性规划模型如下：最小化 Z = 2 * x1 + 1 * x2 + 3 * y + 10 * x1 + 8 * x2 + 15 * y满足约束条件：- x1 <= 100- x2 <= 150- y <= 100- x1 + x2 >= 200- y >= 80- x1, x2, y >= 0接下来，我们可以使用线性规划求解器来求解该问题。

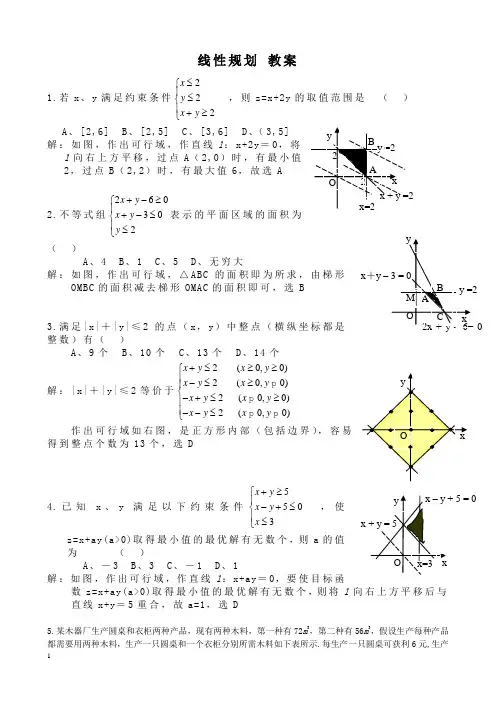
线性规划教案1.若x、y满足约束条件222xyx y≤⎧⎪≤⎨⎪+≥⎩，则z=x+2y的取值范围是（）A、[2,6]B、[2,5]C、[3,6]D、（3,5] 解：如图，作出可行域，作直线l：x+2y＝0，将l向右上方平移，过点A（2,0）时，有最小值2，过点B（2,2）时，有最大值6，故选 A2.不等式组260302x yx yy+-≥⎧⎪+-≤⎨⎪≤⎩表示的平面区域的面积为（）A、4B、1C、5D、无穷大解：如图，作出可行域，△ABC的面积即为所求，由梯形OMBC的面积减去梯形OMAC的面积即可，选 B3.满足|x|＋|y|≤2的点（x，y）中整点（横纵坐标都是整数）有（）A、9个B、10个C、13个D、14个解：|x|＋|y|≤2等价于2(0,0)2(0,0)2(0,0)2(0,0) x y x yx y x yx y x yx y x y+≤≥≥⎧⎪-≤≥⎪⎨-+≤≥⎪⎪--≤⎩ppp p作出可行域如右图，是正方形内部（包括边界），容易得到整点个数为13个，选 D4.已知x、y满足以下约束条件5503x yx yx+≥⎧⎪-+≤⎨⎪≤⎩，使z=x+ay(a>0)取得最小值的最优解有无数个，则a的值为（）A、－3B、3C、－1D、1解：如图，作出可行域，作直线l：x+ay＝0，要使目标函数z=x+ay(a>0)取得最小值的最优解有无数个，则将l向右上方平移后与直线x+y＝5重合，故a=1，选 D5.某木器厂生产圆桌和衣柜两种产品，现有两种木料，第一种有72m3，第二种有56m3，假设生产每种产品都需要用两种木料，生产一只圆桌和一个衣柜分别所需木料如下表所示.每生产一只圆桌可获利6元,生产一个衣柜可获利10元.木器厂在现有木料条件下,圆桌和衣柜各生产多少,才使获得利润最多?产 品 木料(单位m 3) 第 一 种第 二 种 圆 桌 0.18 0.08 衣 柜0.090.28解：设生产圆桌x 只,生产衣柜y 个,利润总额为z 元,那么⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+005628.008.07209.018.0y x y x y x 而z =6x +10y .如上图所示,作出以上不等式组所表示的平面区域,即可行域.作直线l :6x +10y =0,即l :3x +5y =0,把直线l 向右上方平移至l 1的位置时,直线经过可行域上点M,且与原点距离最大,此时z =6x +10y 取最大值解方程组⎩⎨⎧=+=+5628.008.07209.018.0y x y x ,得M 点坐标(350,100).答:应生产圆桌350只,生产衣柜100个,能使利润总额达到最大.指出:资源数量一定,如何安排使用它们,使得效益最好,这是线性规划中常见的问题之一6.某家俱公司生产甲、乙两种型号的组合柜，每种柜的制造白坯时间、油漆时间及有关数据如下：问该公司如何安排这两种产品的生产，才能获得最大的利润．最大利润是多少？解答提示：1．设x ，y 分别为甲、乙两种柜的日产量，目标函数z=200x＋240y，线性约束条件：作出可行域．z最大=200×4＋240×8=2720答：该公司安排甲、乙两种柜的日产量分别为4台和8台，可获最大利润2720元．。

专题简单(d e)线性规划含答案TPMK standardization office TPMK5AB- TPMK08- TPMK2C- TPMK18高考复习专题：简单(de)线性规划专题要点简单(de)线性规划：能从实际问题中抽象出二元一次不等式组. 理解二元一次不等式组表示平面(de)区域,能够准确(de)画出可行域.能够将实际问题抽象概括为线性规划问题,培养应用线性规划(de)知识解决实际问题(de)能力.线性规划等内容已成为高考(de)热点,在复习时要给于重视,另外,不等式(de)证明、繁琐(de)推理逐渐趋于淡化,在复习时也应是注意.考查主要有三种：一是求给定可行域(de)最优解；二是求给定可行域(de)面积；三是给出可行域(de)最优解,求目标函数（或者可行域）中参数(de)范围.多以选择填空题形式出现,不排除以解答题形式出现. 考纲要求了解二元一次不等式(de)几何意义,能用平面区域表示二元一次不等式组；了解线性规划(de)意义并会简单应用. 典例精析线性规划是高考热点之一,考查内容设计最优解,最值,区域面积与形状等,通常通过画可行域,移线,数形结合等方法解决问题. 考点1：求给定可行域(de)最优解例1.（2012广东文）已知变量x 、y 满足约束条件1110x y x y x +≤⎧⎪-≤⎨⎪+≥⎩,则2z x y =+(de)最小值为（ ）A ．3B ．1C ．5-D ．6- 解析:C.画出可行域,可知当代表直线过点A 时,取到最小值.联立11x y x =-⎧⎨=-⎩,解得12x y =-⎧⎨=-⎩,所以2z x y =+(de)最小值为5-. 例2.（2009天津）设变量x,y 满足约束条件：3123x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩.则目标函数z=2x+3y(de)最小值为（A ）6 （B ）7 （C ）8 （D ）23解析：画出不等式3123x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩表示(de)可行域,如右图,让目标函数表示直线332zx y +-=在可行域上平移,知在点B 自目标函数取到最小值,解方程组⎩⎨⎧=-=+323y x y x 得)1,2(,所以734min =+=z ,故选择B.发散思维：若将目标函数改为求x y z =(de)取值范围；或者改为求3+=x yz (de)取值范围；或者改为求22y x z +=(de)最大值；或者或者改为求()221y x z ++=(de)最大值.方法思路：解决线性规则问题首先要作出可行域,再注意目标函数所表示(de)几何意义,数形结合找出目标函数达到最值时可行域(de)顶点（或边界上(de)点）,但要注意作图一定要准确,整点问题要验证解决.练习1.（2012天津）设变量,x y 满足约束条件⎪⎩⎪⎨⎧≤-≥+-≥-+01042022x y x y x ,则目标函数32z x y =-(de)最小值为（ ）A ．5-B ．4-C ．2-D ．3 解析做出不等式对应(de)可行域如图,由y x z 23-=得223zx y -=,由图象可知当直线223z x y -=经过点)2,0(C 时,直线223zx y -=(de)截距最大,而此时y x z 23-=最小为423-=-=y x z ,选B.练习2．在约束条件⎩⎪⎨⎪⎧0≤x ≤10≤y ≤22y －x ≥1下,(x －1)2＋y 2(de)最小值为________．解析 在坐标平面内画出题中(de)不等式组表示(de)平面区域,注意到(x －1)2＋y 2可视为该区域内(de)点(x ,y )与点(1,0)之间距离,结合图形可知,该距离(de)最小值等于点(1,0)到直线2y －x ＝1(de)距离,即为|－1－1|5＝255. 答案 255练习3、（2011广东文、理数）已知平面直角坐标系xOy 上(de)区域D 由不等式组给定．若M （x,y ）为D 上(de)动点,点A(de)坐标为,则z=•(de)最大值为（ ） A 、3 B 、4 C 、3 D 、4 解答：解：首先做出可行域,如图所示： z=•=,即y=﹣x+z 做出l 0：y=﹣x,将此直线平行移动,当直线y=﹣x+z 经过点A 时,直线在y 轴上截距最大时,z 有最大值． 因为A （,2）,所以z(de)最大值为4故选B练习4.（2011福建）已知O 是坐标原点,点A(－1,1),若点M(x,y)为平面区域⎩⎪⎨⎪⎧x ＋y≥2x≤1y≤2上(de)一个动点,则OA →·OM →(de)取值范围是( )A ．[－1,0]B ．[0,1]C ．[0,2]D ．[－1,2] 分析 由于OA →·OM →＝－x ＋y,实际上就是在线性约束条件⎩⎪⎨⎪⎧x ＋y≥2x≤1y≤2下,求线性目标函数z ＝－x ＋y(de)最大值和最小值．解析 画出不等式组表示(de)平面区域(如图),又OA →·OM →＝－x ＋y,取目标函数z ＝－x ＋y,即y ＝x ＋z,作斜率为1(de)一组平行线．当它经过点C(1,1)时,z 有最小值,即zmin ＝－1＋1＝0；当它经过点B(0,2)时,z 有最大值,即zmax ＝－0＋2＝2.∴z(de)取值范围是[0,2],即OA →·OM →(de)取值范围是[0,2],故选C.考点2：求给定可行域(de)面积例3．在平面直角坐标系中,不等式组⎪⎩⎪⎨⎧≤+≥+≥43430y x y x x 表示(de)平面区域(de)面积为（ ）A ．23 B ．32 C ．34 D ．43 答案c考点3：给出最优解求目标函数（或者可行域）中参数例4．(2012广州一模文数)在平面直角坐标系中,若不等式组20,20,x y x y x t +-⎧⎪-+⎨⎪⎩≥≥≤表示(de)平面区域(de)面积为4,则实数t (de)值为A ．1B ．2C ．3D ．4 答案B练习5.（2009福建卷文）在平面直角坐标系中,若不等式组101010x y x ax y +-≥⎧⎪-≤⎨⎪-+≥⎩（α为常数）所表示(de)平面区域内(de)面积等于2,则a (de)值为A. -5B. 1C. 2D. 3 解析解析 如图可得黄色即为满足010101=+-≥-+≤-y ax y x x 的可行域，而与(de)直线恒过（0,1）,故看作直线绕点（0,1）旋转,当a=-5时,则可行域不是一个封闭区域,当a=1时,面积是1；a=2时,面积是23；当a=3时,面积恰好为2,故选D. 练习6. 设二元一次不等式组⎪⎩⎪⎨⎧≤-+≥+-≥-+0142,080192y x y x y x ，所表示(de)平面区域为M ,使函数y ＝a x (a ＞0,a ≠1)(de)图象过区域M (de)a (de)取值范围是c（A ）[1,3] (B)[2,10] (C)[2,9] (D)[10,9]练习7．设z ＝x ＋y ,其中x 、y 满足⎩⎪⎨⎪⎧x ＋2y ≥0x －y ≤00≤y ≤k ,若z (de)最大值为6,则z (de)最小值为A ．－3B ．3C ．2D ．－2解析 如图所示,作出不等式组所确定(de)可行域△OAB ,目标函数(de)几何意义是直线x ＋y －z ＝0在y 轴上(de)截距,由图可知,当目标函数经过点A时,取得最大值,由⎩⎨⎧x －y ＝0y ＝k解得A (k ,k ),故最大值为z ＝k ＋k ＝2k ,由题意,得2k ＝6,故k ＝3.当目标函数经过点B 时,取得最小值,由⎩⎨⎧x ＋2y ＝0y ＝3解得B (－6,3),故最小值为z ＝－6＋3＝－3.故选A.答案 A练习8.（2012课标文）已知正三角形ABC(de)顶点A(1,1),B(1,3),顶点C 在第一象限,若点(x ,y )在△ABC 内部,则z x y =-+(de)取值范围是 （ ）A ．(1-3,2)B ．(0,2)C ．(3-1,2)D ．(0,1+3)命题意图本题主要考查简单线性规划解法,是简单题.解析有题设知C(1+3,2),作出直线0l :0x y -+=,平移直线0l ,有图像知,直线:l z x y =-+过B 点时,max z =2,过C 时,min z =13-,∴z x y =-+取值范围为(1-3,2),故选A. 练习9.（2012福建文）若直线2y x =上存在点(,)x y 满足约束条件30230x y x y x m+-≤⎧⎪⎪--≤⎨⎪≥⎪⎩,则实数m (de)最大值为（ ）A ．-1B ．1C ．32D ．2答案B解析30x y +-=与2y x =(de)交点为(1,2),所以只有1m ≤才能符合条件,B 正确. 考点定位本题主要考查一元二次不等式表示平面区域,考查分析判断能力.逻辑推理能力和求解能力.练习10.（2012福建理）若函数2x y =图像上存在点(,)x y 满足约束条件30230x y x y x m+-≤⎧⎪⎪--≤⎨⎪≥⎪⎩,则实数m (de)最大值为（ ） A ．12 B ．1 C ．32D ．2答案B解析30x y +-=与2x y =(de)交点为(1,2),所以只有1m ≤才能符合条件,B 正确. 考点定位本题主要考查一元一次不等式组表示平面区域,考查分析判断能力、逻辑推理能力和求解计算能力 考点四：实际应用与大题例5（2009四川卷理）某企业生产甲、乙两种产品,已知生产每吨甲产品要用A 原料3吨、B 原料2吨；生产每吨乙产品要用A 原料1吨、B 原料3吨.销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A 原料不超过13吨,B 原料不超过18吨,那么该企业可获得最大利润是 A. 12万元 B. 20万元 C. 25万元 D. 27万元 解析：设甲、乙种两种产品各需生产x 、y 吨,可使利润z 最大,故本题即已知约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+001832133y x y x y x ,求目标函数y x z 35+=(de)最大值,可求出最优解为⎩⎨⎧==43y x ,故271215max =+=z ,故选择D. 练习11. （2012四川理）某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A 原料1千克、B 原料2千克;生产乙产品1桶需耗A 原料2千克,B 原料1千克.每桶甲产品(de)利润是300元,每桶乙产品(de)利润是400元.公司在生产这两种产品(de)计划中,要求每天消耗A 、B 原料都不超过12千克.通过合理安排生产计划,从每天生产(de)甲、乙两种产品中,公司共可获得(de)最大利润是 （ ） A ．1800元 B ．2400元C ．2800元D ．3100元 [答案]C[解析]设公司每天生产甲种产品X 桶,乙种产品Y 桶,公司共可获得 利润为Z 元/天,则由已知,得 Z=300X+400Y 且⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+00122122Y X Y X Y X 画可行域如图所示,目标函数Z=300X+400Y 可变形为Y=400z x 43+- 这是随Z 变化(de)一族平行直线解方程组⎩⎨⎧=+=+12y 2x 12y x 2 ⎩⎨⎧==∴4y 4x 即A(4,4) 280016001200max =+=∴Z[点评]解决线性规划题目(de)常规步骤:一列(列出约束条件)、二画(画出可行域)、三作(作目标函数变形式(de)平行线)、四求(求出最优解).练习12.(2012广州二模文数)甲、乙、丙三种食物(de)维生素含量及成本如下表所示：食物类型 甲 乙 丙 维生素C （单位/kg ） 300 500 300 维生素D （单位/kg ） 700 100 300成本（元/kg ） 5 4 3别为（1）试以,x y 表示混合食物(de)成本P ;（2）若混合食物至少需含35000单位维生素C 及40000单位维生素D ,问,,x y z 取什么值时,混合食物(de)成本最少(本小题主要考查线性规划等知识, 考查数据处理能力、运算求解能力和应用意识)（1）解：依题意得100,543.x y z P x y z ++=⎧⎨=++⎩ …………… 2分由100x y z ++=,得100z x y =--,代入543P x y z =++, 得3002P x y =++. …………… 3分(1) 解:依题意知x 、y 、z 要满足(de)条件为0,0,0,30050030035000,70010030040000.x y z x y z x y z ≥≥≥⎧⎪++≥⎨⎪++≥⎩……… 6分把100z x y =--代入方程组得0,0,1000,250,25.x y x y x y y ≥≥⎧⎪--≥⎪⎨-≥⎪⎪≥⎩……如图可行域（阴影部分）(de)一个顶点为A (让目标函数2300x y P ++=在可行域上移动,由此可知3002P x y =++在A ()37.5,25………∴当37.5x =(kg),25y =(kg),37.5z =(kg)时, 点评解答线性规划应用题(de)一般步骤可归纳为:(1)审题——仔细阅读,明确有哪些限制条件,(2)转化——设元.写出约束条件和目标函数;(3)求解——关键是明确目标函数所表示(de)直线与可行域边界直线斜率间(de)关系;(4)作答——就应用题提出(de)问题作出回答.体现考纲中要求会从实际问题中抽象出二元线性规划.来年需要注意简单(de)线性规划求最值问题。

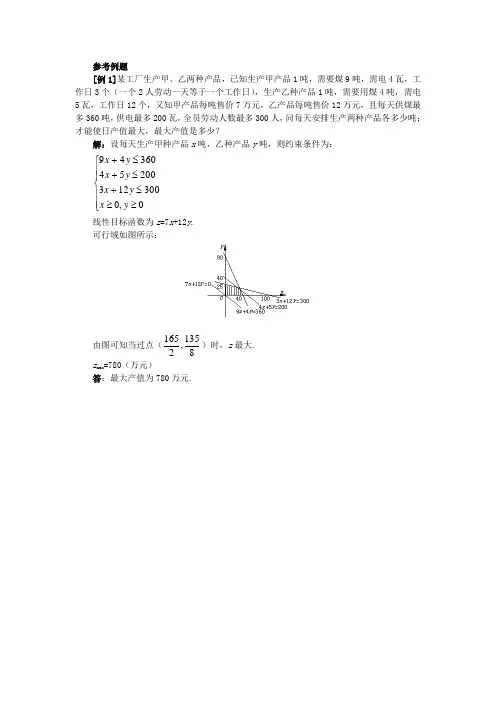
参考例题[例1]某工厂生产甲、乙两种产品，已知生产甲产品1吨，需要煤9吨，需电4瓦，工作日3个（一个2人劳动一天等于一个工作日），生产乙种产品1吨，需要用煤4吨，需电5瓦，工作日12个，又知甲产品每吨售价7万元，乙产品每吨售价12万元，且每天供煤最多360吨，供电最多200瓦，全员劳动人数最多300人，问每天安排生产两种产品各多少吨；才能使日产值最大，最大产值是多少？解：设每天生产甲种产品x 吨，乙种产品y 吨，则约束条件为：⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+≤+0,03001232005436049y x y x y x y x 线性目标函数为z =7x +12y .可行域如图所示：由图可知当过点（8135,2165）时，z 最大. z max =780（万元）答：最大产值为780万元.[例2]北京华欣公司计划在今年内同时出售“夜莺牌多功能”电子琴和“OK 智能型”洗衣机，由于这两种产品的市场需求量非常大，有多少就能销售多少，因此该公司要根据实际情况（如资金、劳动力）确定产品的月供应量，以使得总利润达到最大.己知对这两种产品有直接限制的因素是资金和劳动力，通过调查，得到关于这两种产品有关数据如下表：解：设月供应量临时性子琴x 架，洗衣机y 台，利润z 元，即⎪⎩⎪⎨⎧∈≥≥≤+≤++.,0,0,110105,3002030z x 、、y x y x y xz=6x+8y.作直线L ：6x+8y=0,即作直线L ：3x+4y=0.把直线L 向右上方平移至L ＇的位置时，直线L ＇过可行域上的M 点，且L ＇与原点距离最大.解方程组),,0,0(1101053002030+∈≥≥⎩⎨⎧=+=+Z x 、y x y x y x γ得⎩⎨⎧==,9,4y x得M 点坐标为（4，9）.将x=4,y=9代入z=6x+8y,得z=6×4+8×9=96（百元）为最大.所以，当月供应量为电子琴4架、洗衣机9台时，该店可获得最大利润为9600元.。

7.2简单的线性规划考点简单的线性规划1.(2018天津理,2文,2,5分)设变量x,y 满足约束条件+≤5,2t ≤4,-+≤1,≥0,则目标函数z=3x+5y 的最大值为()A.6B.19C.21D.45答案C 本题主要考查线性目标函数最值的求解.由变量x,y 满足的约束条件画出可行域(如图阴影部分所示).作出基本直线l 0:3x+5y=0,平移直线l 0,当经过点A(2,3)时,z 取最大值,z max =3×2+5×3=21,故选C.2.(2018北京理,8,5分)设集合A={(x,y)|x-y≥1,ax+y>4,x-ay≤2},则()A.对任意实数a,(2,1)∈AB.对任意实数a,(2,1)∉AC.当且仅当a<0时,(2,1)∉AD.当且仅当a≤32时,(2,1)∉A 答案D 本题主要考查不等式组的解法,元素与集合的关系.若(2,1)∈A,则有2−1≥1,2+1>4,2−≤2,解得a>32.结合四个选项,只有D 说法正确.故选D.易错警示注意区分集合条件中的“或”与“且”.本题容易把三个不等式的中间联结词认为是“或”而错选A.3.(2017课标Ⅲ文,5,5分)设x,y 满足约束条件3+2t6≤0,≥0,≥0,则z=x-y 的取值范围是()A.[-3,0]B.[-3,2]C.[0,2]D.[0,3]答案B 由题意,画出可行域(如图中阴影部分所示),易知A(0,3),B(2,0).由图可知,目标函数z=x-y 在点A,B 处分别取得最小值与最大值,z min =0-3=-3,z max =2-0=2,故z=x-y 的取值范围是[-3,2].故选B.4.(2017课标Ⅰ文,7,5分)设x,y 满足约束条件+3≤3,t ≥1,≥0,则z=x+y 的最大值为()A.0B.1C.2D.3答案D 本题考查简单的线性规划问题.作出约束条件表示的可行域如图:平移直线x+y=0,可得目标函数z=x+y 在A(3,0)处取得最大值,z max =3,故选D.一题多解由约束条件求出三个交点的坐标(3,0),(1,0),3212分别代入目标函数z=x+y,得到z max =3.5.(2016北京理,2,5分)若x,y 满足2t ≤0,+≤3,≥0,则2x+y 的最大值为()A.0B.3C.4D.5答案C 画出可行域,如图中阴影部分所示,令z=2x+y,则y=-2x+z,当直线y=-2x+z 过点A(1,2)时,z 最大,z max =4.故选C.思路分析先画出可行域,再令z=2x+y 并改写成斜截式,找到令z 取最大值时的点,代入求值.评析本题考查简单的线性规划,属容易题.6.(2016天津理,2,5分)设变量x,y 满足约束条件t +2≥0,2+3t6≥0,3+2t9≤0,则目标函数z=2x+5y 的最小值为()A.-4B.6C.10D.17答案B 由线性约束条件画出可行域(如图中阴影部分).当直线2x+5y-z=0过点A(3,0)时,z min =2×3+5×0=6,故选B.评析本题考查了简单的线性规划问题,正确画出可行域是求解的关键.7.(2016山东,4,5分)若变量x,y 满足+≤2,2t3≤9,≥0,则x 2+y 2的最大值是()A.4B.9C.10D.12答案C 作出不等式组所表示的平面区域,如图(阴影部分)所示,x 2+y 2表示平面区域内的点到原点的距离的平方,由图易知平面区域内的点A(3,-1)到原点的距离最大,所以x 2+y 2的最大值是10,故选C.评析本题考查了数形结合的思想方法.利用x 2+y 2的几何意义是求解的关键.8.(2016浙江,4,5分)若平面区域+t3≥0,2tt3≤0,t2+3≥0夹在两条斜率为1的平行直线之间,则这两条平行直线间的距离的最小值是()A.355 B.2C.322D.5答案B 作出可行域如图.由2tt3=0,+t3=0,得A(2,1),由+t3=0,t2+3=0,得B(1,2).斜率为1的平行直线l 1,l 2分别过A,B 两点时它们之间的距离最小.过A(2,1)的直线l 1:y=x-1,过B(1,2)的直线l 2:y=x+1,此时两平行直线间的距离=2.故选B.9.(2015重庆,10,5分)若不等式组+t2≤0,+2t2≥0,t +2≥0表示的平面区域为三角形,且其面积等于43,则m 的值为()A.-3 B.1C.43D.3答案B 如图,要使不等式组表示的平面区域为三角形,则-2m<2,即m>-1,所围成的区域为△ABC,S △ABC =S △ADC -S △BDC .点A 的纵坐标为1+m,点B 的纵坐标为23(1+m),C,D 两点的横坐标分别为2,-2m,所以S △ABC =12(2+2m)(1+m)-12(2+2m)·23(1+m)=13(1+m)2=43,解得m=-3(舍去)或m=1.故选B.10.(2015山东理,6,5分)已知x,y 满足约束条件t ≥0,+≤2,≥0.若z=ax+y 的最大值为4,则a=()A.3B.2C.-2D.-3答案B 作出可行域如图.①当a<0时,显然z=ax+y 的最大值不为4;②当a=0时,z=y 在B(1,1)处取得最大值,为1,不符合题意;③当0<a<1时,z=ax+y 在B(1,1)处取得最大值,z max =a+1=4,故a=3,舍去;④当a=1时,z=x+y 的最大值为2,不符合题意;⑤当a>1时,z=ax+y 在A(2,0)处取得最大值,z max =2a=4,得a=2,符合题意.综上,a=2.11.(2015福建文,10,5分)变量x,y 满足约束条件+≥0,t2+2≥0,B-≤0.若z=2x-y 的最大值为2,则实数m 等于()A.-2B.-1C.1D.2答案C 当m<0时,约束条件所表示的平面区域是开放的,目标函数z=2x-y 无最大值,排除A,B,当m=2时,目标函数z=2x-y 的最大值为0,于是排除D,故选C.12.(2014课标Ⅱ理,9,5分,0.798)设x,y 满足约束条件+t7≤0,t3+1≤0,3tt5≥0,则z=2x-y 的最大值为()A.10B.8C.3D.2答案B 由约束条件得可行域如图阴影部分所示.由+t7=0,t3+1=0得A(5,2).当直线2x-y=z 过点A 时,z=2x-y 取得最大值.其最大值为2×5-2=8.故选B.方法总结解决线性规划问题的一般步骤:①画出可行域;②根据目标函数的几何意义确定其取得最优解的点,并求出该点坐标;③求出目标函数的最大值或最小值.13.(2014课标Ⅱ文,9,5分,0.700)设x,y 满足约束条件+t1≥0,tt1≤0,t3+3≥0,则z=x+2y 的最大值为()A.8B.7C.2D.1答案B 约束条件表示的平面区域如图中阴影部分所示,由z=x+2y,得y=-12x+2,2为直线y=-12x+2在y 轴上的截距,要使z 最大,则需2最大,所以当直线y=-12x+2经过点B(3,2)时,z 最大,最大值为3+2×2=7,故选B.14.(2014课标Ⅰ文,11,5分,0.236)设x,y 满足约束条件+≥st≤−1,且z=x+ay 的最小值为7,则a=()A.-5B.3C.-5或3D.5或-3答案B 二元一次不等式组表示的平面区域如图所示,其中平移直线x+ay=0,可知在点,z 取得最值,因此t12+a×r12=7,化简得a 2+2a-15=0,解得a=3或a=-5,但a=-5时,z 取得最大值,故舍去,故选B.解后反思本题也可由排除法选出答案,当a=-5时,目标函数无最小值,当a=3时,可以判断出目标函数的最小值为7,所以选B.15.(2014北京理,6,5分)若x,y 满足+t2≥0,B-+2≥0,≥0,且z=y-x 的最小值为-4,则k 的值为()A.2B.-2C.12D.-12答案D 由t =−4,=0得A(4,0).由图推测直线kx-y+2=0必过A(4,0),得k=-12,经验证符合题目条件.故选D.16.(2014课标Ⅰ理,9,5分)不等式组+≥1,t2≤4的解集记为D.有下面四个命题:p 1:∀(x,y)∈D,x+2y≥-2,p 2:∃(x,y)∈D,x+2y≥2,p 3:∀(x,y)∈D,x+2y≤3,p 4:∃(x,y)∈D,x+2y≤-1.其中的真命题是()A.p 2,p 3B.p 1,p 2C.p 1,p 4D.p 1,p 3答案B 不等式组+≥1,t2≤4表示的平面区域D 如图阴影区域所示.设z=x+2y,作出基本直线l 0:x+2y=0,经平移可知直线l:z=x+2y 经过点A(2,-1)时z 取得最小值0,无最大值.对于命题p 1:由于z 的最小值为0,所以∀(x,y)∈D,x+2y≥0恒成立,故x+2y≥-2恒成立,因此命题p 1为真命题;由于∀(x,y)∈D,x+2y≥0,故∃(x,y)∈D,x+2y≥2,因此命题p 2为真命题;由于z=x+2y 的最小值为0,无最大值,故命题p 3与p 4错误,故选B.17.(2013课标Ⅱ文,3,5分,0.693)设x,y 满足约束条件t +1≥0,+t1≥0,≤3,则z=2x-3y 的最小值是()A.-7B.-6C.-5D.-3答案B 由约束条件得可行域(如图),当直线2x-3y-z=0过点A(3,4)时,z min =2×3-3×4=-6.故选B.18.(2013课标Ⅱ理,9,5分,0.788)已知a>0,x,y 满足约束条件≥1,+≤3,≥ot3).若z=2x+y 的最小值为1,则a=()A.14B.12C.1D.2答案B 由约束条件画出可行域(如图所示的△ABC 及其内部),由=1,=ot3)得A(1,-2a),当直线2x+y-z=0过点A 时,z=2x+y 取得最小值,所以1=2×1-2a,解得a=12,故选B.解题关键根据约束条件准确画出可行域,从而经过平移确定直线z=2x+y 过可行域内的点A 时z 取得最小值是解题的关键.19.(2013湖北文,9,5分)某旅行社租用A 、B 两种型号的客车安排900名客人旅行,A 、B 两种车辆的载客量分别为36人和60人,租金分别为1600元/辆和2400元/辆,旅行社要求租车总数不超过21辆,且B 型车不多于A 型车7辆.则租金最少为()A.31200元B.36000元C.36800元D.38400元答案C 设旅行社租用A 型客车x 辆,B 型客车y 辆,租金为z 元,则线性约束条件为+≤21,t ≤7,36+60≥900,≥0,≥0,目标函数为z=1600x+2400y.画出可行域:当目标函数z=1600x+2400y 经过点A(5,12)时,z min =1600×5+2400×12=36800.选C.20.(2012课标,5,5分)已知正三角形ABC 的顶点A(1,1),B(1,3),顶点C 在第一象限,若点(x,y)在△ABC 内部,则z=-x+y 的取值范围是()A.(1-3,2)B.(0,2)C.(3-1,2)D.(0,1+3)答案A 由题意知可行域为△ABC(不含边界).当直线-x+y-z=0过点C(1+3,2)时,z min =1-3;当过点B(1,3)时,z max =2.故选A.评析本题考查了简单的线性规划,考查了数形结合的思想.正确理解直线的斜率、截距的几何意义是求解的关键.21.(2016浙江,3,5分)在平面上,过点P 作直线l 的垂线所得的垂足称为点P 在直线l 上的投影.由区域t2≤0,+≥0,t3+4≥0中的点在直线x+y-2=0上的投影构成的线段记为AB,则|AB|=()A.22B.4C.32D.6答案C 由不等式组画出可行域,如图中的阴影部分所示.因为直线x+y-2=0与直线x+y=0平行,所以可行域内的点在直线x+y-2=0上的投影构成的线段的长|AB|即为|CD|.易得C(2,-2),D(-1,1),所以|AB|=|CD|=(2+1)2+(−2−1)2=32.故选C.22.(2022全国乙文,5,5分)若x ,y 满足约束条件+≥2,+2≤4,≥0,则z =2x -y 的最大值是()A.-2B.4C.8D.12答案C 由约束条件作出可行域如图中阴影部分所示,联立+2=4,=0,可得A (4,0),当直线z =2x -y 过点A 时,z =2x -y 取最大值,z max =2×4-0=8,故选C .23.(2021全国乙文,5,5分)若x ,y 满足约束条件+≥4,−≤2,≤3,则z =3x +y 的最小值为()A.18B.10C.6D.4答案C 解题指导:思路一:先画出可行域,然后移动直线3x +y =0,最后由z 与纵截距的关系得最优解,计算即可;思路二:先求出可行域顶点的坐标,然后分别求出各顶点处目标函数值,通过比较大小得到z 的最小值.解析解法一:作出不等式组表示的可行域,如图.作直线l :3x +y =0,平行移动直线l ,可知当平移后的直线过点(1,3)时,纵截距最小,即z 最小.故z min =3×1+3=6.故选C .解法二:根据线性约束条件得出可行域为△ABC 及其内部(如上图所示),其中A (3,1),B (1,3),C (5,3),经检验,知目标直线过点B (1,3)时,z 取最小值,即z min =3×1+3=6.解后反思:对于直线z =Ax +By ,若B >0,则当目标直线向上移动时,z 变大;若B <0,则当目标直线向下移动时,z 变大.24.(2020课标Ⅰ理,13,5分)若x ,y 满足约束条件2+−2≤0,−−1≥0,+1≥0,则z =x +7y 的最大值为.答案1审题指导:作出可行域移动直线x +7y =0过A (1,0)时有z max .解题思路:作出可行域如图,由z =x +7y 得y =-7+7,易知当直线y =-7+7经过点A (1,0)时,z 取得最大值,z max =1+7×0=1.方法总结:线性规划问题的最优解一般在可行域的边界或顶点处取得,所以可以通过平移目标函数所对应的直线判断最优解,还可以通过比较边界或顶点处的目标函数值进行判断.25.(2016江苏,12,5分)已知实数x,y 满足t2+4≥0,2+t2≥0,3tt3≤0,则x 2+y 2的取值范围是.答案,13解析画出不等式组t2+4≥0,2+t2≥0,3tt3≤0表示的可行域如图:由x-2y+4=0及3x-y-3=0得x 2+y 2表示可行域内的点(x,y)与点(0,0)的距离的平方可得22)max =22+32=13,(x 2+y 2)min =d 2=45,其中d 表示点(0,0)到直线2x+y-2=0的距离,所以x 2+y 2的取值范围,13.解后反思对于线性规划问题,要正确作出可行域,并理解目标函数的几何意义,分清常规的“距离型”“斜率型”与“截距型”是解题的关键.26.(2020课标Ⅱ文,15,5分)若x,y 满足约束条件+≥−1,t ≥−1,2t ≤1,则z=x+2y 的最大值是.答案8解析作出约束条件表示的可行域,如图所示.由图可知直线z=x+2y 过点A(2,3)时,z 取得最大值,最大值为2+2×3=8.27.(2019课标Ⅱ文,13,5分)若变量x,y 满足约束条件2+3t6≥0,+t3≤0,t2≤0,则z=3x-y 的最大值是.答案9解析本题考查简单的线性规划问题;以二元一次不等式组作为约束条件考查学生数形结合思想及运算求解能力;考查数学运算的核心素养.作出可行域(如图阴影部分所示).易得A(3,0),B(1,2),C(0,2).将z=3x-y 化为y=3x-z,由图知,当直线y=3x-z 经过点A(3,0)时,截距-z 取得最小值,从而z 取得最大值.z max =3×3=9.易错警示因为目标函数中y 的系数为负值,所以容易理解为在点C 处取得最大值,导致错误.28.(2018课标Ⅲ文,15,5分)若变量x,y 满足约束条件2++3≥0,t2+4≥0,t2≤0,则z=x+13y 的最大值是.答案3解析本题考查简单的线性规划.解法一:根据约束条件作出可行域,如图所示.z=x+13y 可化为y=-3x+3z.求z 的最大值可转化为求直线y=-3x+3z 纵截距的最大值,显然当直线y=-3x+3z 过A(2,3)时,纵截距最大,故z max =2+13×3=3.解法二:画出可行域(如上图),由图知可行域为三角形区域,易求得顶点坐标分别为(2,3),(2,-7),(-2,1),将三点坐标代入,可知z max =2+13×3=3.29.(2018浙江,12,6分)若x,y 满足约束条件t ≥0,2+≤6,+≥2,则z=x+3y 的最小值是,最大值是.答案-2;8解析本小题考查简单的线性规划.由约束条件得可行域是以A(1,1),B(2,2),C(4,-2)为顶点的三角形区域(含边界),如图.当直线y=-13x+3过点C(4,-2)时,z=x+3y 取得最小值-2,过点B(2,2)时,z=x+3y 取得最大值8.思路分析(1)作出可行域,并求出顶点坐标.(2)平移直线y=-13x,当在y 轴上的截距最小时,z=x+3y 取得最小值,当在y 轴上的截距最大时,z=x+3y 取得最大值.30.(2016课标Ⅲ,13,5分)设x,y 满足约束条件2t +1≥0,t2t1≤0,≤1,则z=2x+3y-5的最小值为.答案-10解析可行域如图所示(包括边界),直线2x-y+1=0与x-2y-1=0相交于点(-1,-1),当目标函数线过(-1,-1)时,z 取最小值,z min =-10.31.(2014安徽,13,5分)不等式组+t2≥0,+2t4≤0,+3t2≥0表示的平面区域的面积为.答案4解析不等式组表示的平面区域为如图所示的阴影部分.由+3t2=0,+2t4=0得=8,=−2.∴A(0,2),B(2,0),C(8,-2).直线x+2y-4=0与x 轴的交点D 的坐标为(4,0).因此S △ABC =S △ABD +S △BCD =12×2×2+12×2×2=4.故答案为4.32.(2013课标Ⅰ,14,5分,0.660)设x,y 满足约束条件1≤≤3,-1≤t ≤0,则z=2x-y 的最大值为.答案3解析可行域为如图所示的阴影部分,由z=2x-y,得y=2x-z.-z 的几何意义是直线y=2x-z 在y 轴上的截距,要使z 最大,则-z 最小,所以当直线y=2x-z 过点A(3,3)时,z 最大,最大值为2×3-3=3.33.(2012课标理,14,5分)设x,y满足约束条件t ≥−1,+≤3,≥0,≥0,则z=x-2y的取值范围为.答案[-3,3]解析由不等式组画出可行域(如图所示).当直线x-2y-z=0过点B(1,2)时,z min=-3;过点A(3,0)时,z max=3.∴z=x-2y的取值范围是[-3,3].评析本题考查了简单线性规划知识;考查了数形结合的思想方法.34.(2011课标文,14,5分)若变量x,y满足约束条件3≤2+≤9,6≤t≤9,则z=x+2y的最小值为.答案-6解析画出约束条件所表示的平面区域,如图阴影部分所示:当目标函数表示的直线经过点A(4,-5)时,z有最小值,z min=4+2×(-5)=-6.失分警示本题易将平面区域画错或者将目标函数表示的直线的斜率看成12而致错.评析本题考查线性规划问题,正确作图是得分的前提.。

线性规划经典例题一、问题描述某公司生产两种产品A和B，每种产品分别需要使用两种原材料X和Y。

已知每种产品的利润和原材料的用量，求解最大利润的生产方案。

二、数据分析1. 产品A的利润为每单位100元，产品B的利润为每单位150元。

2. 产品A每单位需要用2单位的原材料X和1单位的原材料Y；产品B每单位需要用1单位的原材料X和3单位的原材料Y。

3. 公司每天可用的原材料X和Y的数量分别为10单位和15单位。

三、数学建模设产品A的生产数量为x，产品B的生产数量为y。

目标函数：最大化利润，即最大化目标函数Z = 100x + 150y。

约束条件：1. 原材料X的用量约束：2x + y ≤ 10。

2. 原材料Y的用量约束：x + 3y ≤ 15。

3. 非负约束：x ≥ 0，y ≥ 0。

四、求解过程1. 构建线性规划模型：最大化目标函数 Z = 100x + 150y约束条件：2x + y ≤ 10x + 3y ≤ 15x ≥ 0，y ≥ 02. 使用线性规划求解方法（如单纯形法）求解最优解。

五、最优解分析经过计算，得到最优解为：x = 5，y = 3，Z = 100*5 + 150*3 = 950。

六、结论为了实现最大利润，公司应生产5个单位的产品A和3个单位的产品B，此时可以获得最大利润950元。

七、敏感性分析通过敏感性分析可以了解目标函数和约束条件的变化对最优解的影响程度。

1. 原材料X的用量增加1单位，最优解变化情况：- 目标函数值：增加100元。

- 产品A的生产数量：不变。

- 产品B的生产数量：不变。

2. 原材料Y的用量增加1单位，最优解变化情况：- 目标函数值：增加150元。

- 产品A的生产数量：不变。

- 产品B的生产数量：不变。

3. 公司每天可用的原材料X的数量增加1单位，最优解变化情况：- 目标函数值：不变。

- 产品A的生产数量：不变。

- 产品B的生产数量：不变。

4. 公司每天可用的原材料Y的数量增加1单位，最优解变化情况：- 目标函数值：不变。

线性规划经典例题一、问题描述某公司生产两种产品A和B，每个产品的生产需要消耗不同的资源。

现在公司希望通过线性规划来确定每种产品的生产数量，以最大化利润。

已知产品A每个单位的利润为10元，产品B每个单位的利润为15元。

同时，产品A每个单位需要消耗2个资源X和3个资源Y，产品B每个单位需要消耗4个资源X和1个资源Y。

公司总共有40个资源X和30个资源Y可供使用。

二、数学建模1. 假设产品A的生产数量为x，产品B的生产数量为y。

2. 目标函数：最大化利润。

利润可以表示为10x + 15y。

3. 约束条件：a) 资源X的约束条件：2x + 4y ≤ 40b) 资源Y的约束条件：3x + y ≤ 30c) 非负约束条件：x ≥ 0，y ≥ 0三、求解过程1. 根据数学建模中的目标函数和约束条件，可以得到如下线性规划模型：最大化：10x + 15y约束条件：2x + 4y ≤ 403x + y ≤ 30x ≥ 0，y ≥ 02. 使用线性规划求解方法，可以得到最优解。

通过计算，得到最优解为x = 6，y = 6，利润最大化为180元。

四、结果分析根据最优解，可以得知最大利润为180元，其中产品A的生产数量为6个，产品B的生产数量为6个。

同时，资源X还剩余28个，资源Y还剩余24个。

五、灵敏度分析对于线性规划问题，灵敏度分析可以帮助我们了解目标函数系数和约束条件右端项的变化对最优解的影响。

1. 目标函数系数的变化：a) 如果产品A的利润提高到12元，产品B的利润保持不变，重新求解线性规划模型可以得到新的最优解。

新的最优解为x = 8，y = 4，利润最大化为168元。

b) 如果产品A的利润保持不变，产品B的利润提高到20元，重新求解线性规划模型可以得到新的最优解。

新的最优解为x = 4，y = 7，利润最大化为190元。

2. 约束条件右端项的变化：a) 如果资源X的数量增加到50个，资源Y的数量保持不变，重新求解线性规划模型可以得到新的最优解。

线性规划经典例题一、问题描述：某公司生产两种产品A和B，每天的生产时间为8小时。

产品A每件需要1小时的加工时间，产品B每件需要2小时的加工时间。

公司每天的总加工时间不能超过8小时。

产品A的利润为100元/件，产品B的利润为200元/件。

公司希望最大化每天的利润。

二、数学建模：设公司每天生产的产品A的件数为x，产品B的件数为y。

则目标函数为最大化利润，即：Maximize Z = 100x + 200y约束条件：1. 生产时间约束：x + 2y ≤ 82. 非负约束：x ≥ 0, y ≥ 0三、线性规划模型：Maximize Z = 100x + 200ySubject to:x + 2y ≤ 8x ≥ 0y ≥ 0四、求解方法：可以使用线性规划求解器进行求解，例如使用单纯形法或内点法等。

以下是使用单纯形法求解的步骤：1. 将目标函数和约束条件转化为标准形式：目标函数：Maximize Z = 100x + 200y约束条件：x + 2y ≤ 8x ≥ 0y ≥ 02. 引入松弛变量将不等式约束转化为等式约束：x + 2y + s1 = 8x ≥ 0y ≥ 0s1 ≥ 03. 构建初始单纯形表：基变量 | x | y | s1 | 常数项-----------------------------Z | 0 | 0 | 0 | 0-----------------------------s1 | 1 | 2 | 1 | 84. 进行单纯形法迭代计算：a. 选择进入变量：选择目标函数系数最大的非基变量，即选择y进入基变量。

b. 选择离开变量：计算各个约束条件的最小比值，选择比值最小的非基变量对应的约束条件的基变量离开基变量。

在本例中，计算得到最小比值为4，对应的约束条件为x ≥ 0，所以x对应的基变量离开基变量。

c. 更新单纯形表：基变量 | x | y | s1 | 常数项-----------------------------Z | 0 | 0 | -2 | -400-----------------------------s1 | 1 | 2 | 1 | 8d. 继续迭代计算，直到目标函数系数均为负数或零，达到最优解。

简单的线性规划典型例题例1画出不等式组⎪⎩⎪⎨⎧≤+-≤-+≤-+-.0330402y x y x y x ，，表示的平面区域．分析：采用“图解法”确定不等式组每一不等式所表示的平面区域，然后求其公共部分．解：把0=x ，0=y 代入2-+-y x 中得0200<-+-∴ 不等式02≤-+-y x 表示直线02=-+-y x 下方的区域（包括边界），即位于原点的一侧，同理可画出其他两部分，不等式组所表示的区域如图所示．说明：“图解法”是判别二元一次不等式所表示的区域行之有效的一种方法．例2 画出332≤<-y x 表示的区域，并求所有的正整数解),(y x ．分析：原不等式等价于⎩⎨⎧≤->.3,32y x y 而求正整数解则意味着x ，y有限制条件，即求⎪⎪⎩⎪⎪⎨⎧≤->∈∈>>.3,32,,,0,0y x y z y z x y x ． 解：依照二元一次不等式表示的平面区域，知332≤<-y x 表示的区域如下图：对于332≤<-y x 的正整数解，先画出不等式组．⎪⎪⎩⎪⎪⎨⎧≤->∈∈>>.3,32,,,0,0y x y z y z x y x 所表示的平面区域，如图所示．容易求得，在其区域内的整数解为)1,1(、)2,1(、)3,1(、)2,2(、)3,2(．说明：这类题可以将平面直角坐标系用网络线画出来，然后在不等式组所表示的平面区域内找出符合题设要求的整数点来．例3求不等式组⎪⎩⎪⎨⎧+-≤-+≥111x y x y 所表示的平面区域的面积． 分析：本题的关键是能够将不等式组所表示的平面区域作出来，判断其形状进而求出其面积．而要将平面区域作出来的关键又是能够对不等式组中的两个不等式进行化简和变形，如何变形？需对绝对值加以讨论．解：不等式11-+≥x y 可化为)1(-≥≥x x y 或)1(2-<--≥x x y ； 不等式1+-≤x y 可化为)0(1≥+-≤x x y 或)0(1<+≤x x y ． 在平面直角坐标系内作出四条射线)1(-≥=x x y AB ：， )1(2-<--=x x y AC ： )0(1≥+-=x x y DE ：，)0(1<+=x x y DF ：则不等式组所表示的平面区域如图由于AB 与AC 、DE 与DF 互相垂直， 所以平面区域是一个矩形．根据两条平行线之间的距离公式可得矩形的两条边的长度分别为22和223．所以其面积为23．例4若x 、y 满足条件⎪⎩⎪⎨⎧≤+-≥+-≤-+.0104010230122y x y x y x ，，求y x z 2+=的最大值和最小值．分析：画出可行域，平移直线找最优解．解：作出约束条件所表示的平面区域，即可行域，如图所示． 作直线z y x l =+2:，即z x y 2121+-=，它表示斜率为21-，纵截距为2z 的平行直线系，当它在可行域内滑动时，由图可知，直线l 过点时，z 取得最大值，当l 过点B 时，z 取得最小值． ∴18822max =⨯+=z ∴2222min =⨯+-=z说明：解决线性规划问题，首先应明确可行域，再将线性目标函数作平移取得最值．例5 用不等式表示以)4,1(A ，)0,3(-B ，)2,2(--C 为顶点的三角形内部的平面区域．分析：首先要将三点中的任意两点所确定的直线方程写出来，然后结合图形考虑三角形内部区域应怎样表示。