九年级(上)培优讲义-第2讲解直角三角形

第2讲：解直角三角形一、建构新知1.已知，在Rt△ABC中，∠C＝90°，∠A=30°, BC=2, 则AB= , AC= ,∠B= °.2.阅读教材后回答。

（1）已知，在Rt△ABC中，∠C＝90°，∠A=α, BC=a, 则AB= , AC= , ∠B= °. （2）解直角三角形至少需要个条件，其中关于的条件必须有.（3）课本例题1中给出了一种解的直角三角形的方法，除此之外有没有其它的解法了，请你试着解一下，并且请你比较一下哪种解法更好，为什么？3.填写下表：在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别是a ,b , c.已知条件已知条件解法一边一角一条直角边和一个锐角（a, ∠A）斜边和一个锐角（c, ∠A）两边两条直角边（a,b）斜边和一条直角边（a ,c）4.阅读教材后回答.（1）如图，在斜坡AB上，坡角为, 坡度等于与的比（或叫坡比），其实质就是坡角的值，可用字母表示. （2）若∠B逐渐变大，坡度是如何变化的？BACABC北 北 二、经典例题例1. 将一副三角板按如图的方式摆放在一起，连接AD ,求∠ADB 的正弦值．例2．由下列条件解题：在Rt △ABC 中，∠C =90°：（1）已知a =4，b =8，求c ． （2）已知b =10，∠B =60°，求a ，c ．例3.台湾“华航”客机失事后，祖国大陆海上搜救中心立即通知位于A 、B 两处的上海救捞人局所属专业救助轮“华意”轮、“沪救12”轮前往出事地点协助搜索.接到通知后，“华意”轮测得出事地点C 在A 的南偏东60°、“沪救12”轮测得出事地点C 在B 的南偏东30°.已知B 在A 的正东方向，且相距100浬，分别求出两艘船到达出事地点C 的距离.ABD C A BDCQPCBA例4. 在Rt △ABC 中，∠C =90°，BC =8cm ，sinB =53. 一只蚂蚁从点B 开始沿BC 方向向点C 以2cm /s 的速度移动，另一只蚂蚁从C 点开始以1cm /s 的速度向点A 移动. 如果两只蚂蚁分别从B 、C 点同时出发各自运动到P 、Q （如图），问：第几秒时△PCQ 与△ABC 相似？例5. 如图，边长为1的正方形OABC 的顶点O 为坐标原点，点A 在x 轴的正半轴上，点C 在y 轴的正半轴上. 动点D 在线段BC 上移动（不与B ，C 重合），连接OD ，过点D 作DE ⊥OD ，交边AB 于点E ，连接OE ．记CD 的长为t ． （1） 当t ＝31时，求tan ∠EDB ；（2） 如果记梯形COEB 的面积为S ，那么是否存在S 的最大值？若存在，请求出这个最大值及此时∠EOA 的度数．（精确到1度）三、基础演练1. 在Rt △ABC 中，∠C ＝90°，则下列式子中必定成立的是（ ）.A . c =asinAB . c =acosAC . c =cos a A D . c =sin aA2. 在Rt △ABC 中，∠C ＝90°，∠A ，∠B ，∠C 的对边分别是a ,b , c .根据条件完成填空.c =10,∠A = 45°，则a = ,b = ，∠B = . a =5,b =15,则∠B = ，∠A = ，c = . c =3， sinA =63，则a = ,b = .3. 在Rt △ABC 中，∠A 的对边为a ，∠C ＝90°，cosA =25，a =12, 则斜边AB 上的中线长为 .4. 等腰△ABC 中，底边BC =20，sinC =35, 则AB = . 5. 在Rt △ABC 中，∠C ＝90°，∠A ，∠B ，∠C 的对边分别是a ,b , c .请根据已知条件解直角三角形.（角度精确到1°，长度精确到0.1）(1) ∠B =72°，c =14； （2）a = 26,b = 62； （3）sinB =45，a =126. 已知：如图，在菱形ABCD 中，DE ⊥AB 于E ，BE ＝16cm ，⋅=1312sin A 求此菱形的周长和面积．7. 如图所示，在△ABC 中，∠A ＝30°，∠B ＝45°，BC =4，求△ABC 的面积.ABC8. 如图，大坝的横断面为梯形ABCD ，迎水坡BC 的坡角B 为30°，背水坡AD 的坡度为1:1.2，坝顶宽DC =2.5m ，坝高4.5m .求：（1）迎水坡BC 的坡比；（2）坝底AB 的长.9. 为打击索马里海盗，保护各国商船的顺利通行，我海军某部奉命前往该海域执行护航任务．某天我护航舰正在某小岛A 北偏西45︒并距该岛20海里的B 处待命．位于该岛正西方向C 处的某外国商船遭到海盗袭击，船长发现在其北偏东60︒的方向有我军护航舰，便发出紧急求救信号．我护航舰接警后，立即沿BC 航线以每小时60海里的速度前去救援．问我护航舰需多少分钟可以到达该商船所在的位置C 处？（结果精确到个位．参考数据：2 1.43 1.7≈，≈）10.已知：如图在平面直角坐标系xOy 中，直线AB 分别与y x 、轴交于点B 、A ，与反比例函数的图象分别交于点C 、D ，CE ⊥x 轴于点E ，21tan =∠ABO ，OB =4，OE =2。

第2讲解直角三角形解直角三角形为中考必考内容，至少有一道是解答题，常是利用解直角三角形的相关知识来解决实际问题。

在解直角三角形的综合题中，常与非特殊角结合在一起考，这种题几乎是中考数学的必考题。

在教学中，一要注意强调书写格式问题；二是要给学生储备典型的直角三角形模型（如：背靠背型和母子型等）。

知识点一、解直角三角形在直角三角形中，由已知元素(直角除外)求未知元素的过程，叫做解直角三角形.在直角三角形中，除直角外，一共有5个元素，即三条边和两个锐角.设在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，则有：①三边之间的关系：a2+b2=c2(勾股定理).②锐角之间的关系：∠A+∠B=90°.③边角之间的关系：，，，，，.④，h为斜边上的高.要点诠释：(1)直角三角形中有一个元素为定值(直角为90°)，是已知值.(2)这里讲的直角三角形的边角关系指的是等式，没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形，可以更加清楚、直观地理解.二、解直角三角形的常见类型及解法已知条件解法步骤Rt△ABC两边两直角边(a，b)由求∠A，∠B=90°－∠A，斜边，一直角边(如c，a)由求∠A，∠B=90°－∠A，一边一直角边和一锐角锐角、邻边(如∠A，b)∠B=90°－∠A，，知识精讲目标导航一角锐角、对边(如∠A，a)∠B=90°－∠A，，斜边、锐角(如c，∠A)∠B=90°－∠A，，要点诠释：1．在遇到解直角三角形的实际问题时，最好是先画出一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的，然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2．若题中无特殊说明，“解直角三角形”即要求出所有的未知元素，已知条件中至少有一个条件为边.【知识拓展1】如图，已知一商场自动扶梯的长l为10米，该自动扶梯到达的高度h为6米，自动扶梯与地面所成的角为α，则tanα的值为（）。

三角函数解直角三角形知识点：一、锐角三角函数：在直角三角形ABC 中，∠C 是直角，如图5－11、正弦：把锐角A 的对边与斜边的比叫做∠A 的正弦，记作c a A =sin 2、余弦：把锐角A 的邻边与斜边的比叫做∠A 的余弦，记作c bA =cos3、正切：把锐角A 的对边与邻边的比叫做∠A 的正切，记作b aA =tan4、余切：把锐角A 的邻边与对边的比叫做∠A 的余切，记作abA =cot说明：由定义可以看出tanA ·cotA ＝l （或写成AA cot 1tan =）5、锐角三角函数：锐角A 的正弦、余弦、正切、余切都叫做∠A 的锐角三角函数 说明：锐角三角函数都不能取负值。

0＜ sinA ＜ l ； 0＜cosA ＜；l6、锐角的正弦和余弦之间的关系任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等于它的余角的正弦值。

即sinA ＝cos （90°一 A ）＝cosB ；cosA ＝sin （90°一A ）＝sinB7、锐角的正切和余切之间的关系任意锐角的正切值等于它的余角的余切值，任意锐角的余切值等于它的余角的正切值。

即tanA ＝cot （90°一 A ）＝cotB ；cotA ＝tan （90°－A ）＝ tanB 说明：式中的90°一A = B 。

8、三角函数值的变化规律（1）当角度在0°— 90°间变化时，正弦值（正切值随着角度的增大（或减小）而增大（或减小）（2）当角度在0°—90°间变化时，余弦值（余切值）随着角度的增大（或减小）而减小（或增大）。

9、同角三角函数关系公式（1）1cos sin 22=+B A ；（2）A A cot 1tan =；（3） tanA ＝AAcos sin 10．一些特殊角的三角函数值二、解直角三角形由直角三角形中，除直角外的已知元素，求出所有未知元素的过程，叫做解直角三角形。

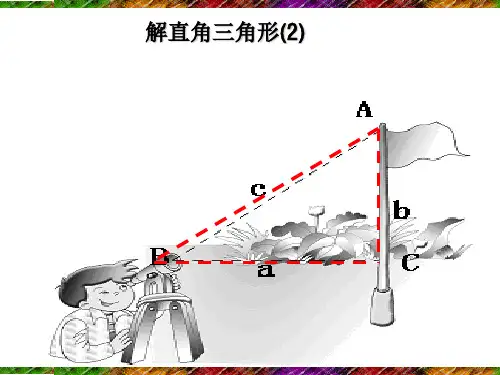
培优2学生版知识点巩固：1. 锐角三角函数定义：在Rt △ABC 中，∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c ，则∠A 的正弦可表示为：sinA= ，∠A 的余弦可表示为cosA= ∠A 的正切：tanA= ，它们称为∠A 的锐角三角函数提醒：1）sinA 、∠cosA 、tanA 表示的是一个整体，是两条线段的比，这些比值只与 有关，与直角三角形的 无关2）取值范围 <sinA< ， <cosA< ， tanA>2. 当 时，正弦和正切值随着角度的增大而 余弦值随着角度的增大而3.几个特殊关系：⑴sin 2A+cos 2A= ,tanA ∙ tanB =⑵若∠A+∠B=900，则sinA= ， cosA= ， tanB= 4. 坡面的__ _的比叫坡度i （也叫坡比），坡度越大，坡面越陡；坡面与___ _的夹角，用α表示，tan α=i=hl． 5. __ __ __ __ 称为仰角. 6. __ __ __ __ 称为俯角.7. __ __ __ __ 叫做解直角三角形..例题讲解：量了旗杆的高度．如图，某一时刻，旗杆AB 的影子一部分 落在平台上，另一部分落在斜坡上，测得落在平台上的影长 BC 为6米，落在斜坡上的影长CD 为4米，AB ⊥BC ，同一 时刻，光线与旗杆的夹角为37，斜坡的坡角为30，旗杆 的高度约为 米．（参考数据：sin370.6»，cos370.8»，tan370.75» 1.73）练习2．如图，在坡角为30的山坡FB 上有一座信号塔AB ，其右侧 有一堵防护墙CD ，测得BD 的长度是30米，当光线AC与水平地面 的夹角为53时，测得信号塔落在防护墙上的影子DE 的长为19米， 则信号塔AB 的高度约为（参考数据：sin370.60»，cos370.80»，tan370.75»1.73） 提升训练1. a 、b 、c 是△ABC 的∠A 、∠B 、∠C 的对边，且a ：b ：c=1 则cosB 的值为__2. 在Rt △ABC 中，∠C=90°，sinA=513, 则tanB 的值为__3. 如图，在Rt △ABC 中，∠C=90°，∠A=30°，E 为AB 上一点，并且AE ：EB=4：1，EF ⊥AB4. 如图，A 点的坐标为（-4，0），直线y=n +与坐标轴交于点B ，C ，连接AC ，如果∠ACD=90°，则n 的值为__5. 如图，在▱ABCD 中，点E 是AD 的中点，延长BC 到点F ，使CF ：BC=1：2， 连接DF ，EC ．若AB=5，AD=8，sinB=45, 则DF 的长等于__6. 如图，若△ABC 和△DEF 的面积分别为1S 、2S ，则（ ）A. 12S S =B. 1212S S =C. 1285S S =D. 1272S S = 7．如图，为测量一座山峰CF 的高度，将此山的某侧山坡划分为AB 和BC 两段，每一段山坡近似是“直”的，测得坡长AB=800米，BC=200米，斜坡AB 仰角050=∠CBE .则山峰的高度CF 约为_ 米. 可用的参考数据：sin 50°≈0.8，tan 50°≈1.2,24.25≈）8．某数学兴趣小组进行测量大楼BO 高度的综合实践活动. 如图，他们在点A 处测得大楼顶端B 点的仰角是37°，然后沿坡比i =1：2.4 的斜坡步行至C 点，测得大楼顶端B 点的仰角为45°，若斜坡AC 的长度为13米，那么建筑物BO 的高度约为_ 米（参考数据：tan 370.75≈，sin 370.60≈，cos370.80≈）B .21二、解答题：1.如图是某种自动卸货时的示意图，AC时水平汽车底盘，OB是液压举升杠杆，货车卸货时车厢AB与底盘AC夹角为30°，举升杠杆OB与底盘AC夹角为75°，已知举升杠杆上顶点B离火车支撑点A的距离为（2+2）米．试求货车卸货时举升杠杆OB的长．2.如图，在△ABC中，CD是边AB上的中线，∠B是锐角，且sinB=，tanA=，AC=3（1）求∠B的度数与AB的值；（2）求tan∠CDB．3.如图所示，山坡上有一棵与水平面垂直的大树，一场台风过后，大树被刮倾斜后折断倒在山坡上，树的顶部恰好接触到坡面．已知山坡的坡角∠AEF=23°，量得树干倾斜角∠BAC=38°，大树被折断部分和坡面所成的角∠ADC=60°，AD=8m．（1）求∠CAE的度数；（2）求这棵大树折断前的高度？（结果精确到个位，参考数据：=1.4，=1.7，=2.4）．4．如图，一次函数()0y ax b a =+≠的图象与反比例函数()0ky k x=≠的图象相交于A 、B 两点，以AB 为边，在直线AB 的左侧作菱形ABCD ，边BC ⊥y 轴于点E ．若点A 坐标为（m ，6），tan ∠BOE =163，OE =32．（1）求反比例函数和一次函数的解析式； （2）求点D 的坐标．5．如果把一个奇数位的自然数各数位上的数字从最高位到个位依次排列，与从个位到最高位依次排列出的一串数字完全相同，相邻两个数位上的数字之差的绝对值相等（不等于0），且该数正中间的数字与其余数字均不同，我们把这样的自然数称为“阶梯数”．例如自然数12321，从最高位到个位依次排出的一串数字是：1，2，3，2，1，从个位到最高是一个“阶梯数”，又如262，85258，……，都是“阶梯数”．若一个“阶梯数”t从左数到右，奇数位上的数字之和为M，偶数位上的数字之和为N，记()2=-，P t N M ()=+．Q t M N（1）已知一个三位“阶梯数”t，其中()P t=12，且()Q t为一个完全平方数，求这个三位数；Q t除以4余2，求该五位“阶梯数”t的最（2）已知一个五位“阶梯数”t能被4整除，且()大值与最小值．6．如图，在正方形ABCD 中，以CD 为底边作等腰CDE ∆，使得点E在正方形ABCD 内部，且CE DE =，连接BD 交CE 于点F ．过点C 作CG DE ⊥于点G ，过点G 作GH AD ⊥于点H ，连接HF ．若134CE =，54GE =，则四边形AEFH 的面积为____________．HGFE DCBA （第9题图）。