计量经济学第一次上机作业

计量经济学上机实验上机实验一：一元线性回归模型实验目的：EViews软件的基本操作实验内容：对线性回归模型进行参数估计并进行检验上机步骤：中国内地2011年中国各地区城镇居民每百户计算机拥有量和人均总收入一．建立工作文件：1.在主菜单上点击File\New\Workfile；2.选择时间频率，A3.键入起始期和终止期，然后点击OK；二．输入数据:1.键入命令：DATA Y X2.输入每个变量的统计数据；3.关闭数组窗口（回答Yes）;三．图形分析：1.趋势图：键入命令PLOT Y X2.相关图：键入命令 SCAT Y X 散点图：趋势图：上机结果：Yˆ11.958+0.003X=s (βˆ) 5.6228 0.0002t (βˆ) 2.1267 11.9826prob 0.0421 0.00002=0.831 R2=0.826 FR=143.584 prob(F)=0.0000上机实验二：多元线性回归模型实验目的：多元回归模型的建立、比较与筛选，掌握基本的操作要求并能根据理论对分析结果进行解释实验内容：对线性回归模型进行参数估计并进行检验上机步骤：商品的需求量与商品价格和消费者平均收入趋势图：散点图：上机结果:i Yˆ=132.5802-8.878007X1-0.038888X2s (βˆ) 57.118 4.291 0.419t (βˆ) 2.321 -2.069 -0.093prob 0.0533 0.0773 0.9286 R2=0.79 R2=0.73 F =13.14 prob(F)=0.00427三：非线性回归模型实验目的：EViews软件的基本操作实验内容：对线性回归模型进行参上机步骤：我国国有独立核算工业企业统计资料一．建立工作文件：1.在主菜单上点击File\New\Workfile；2.选择时间频率，A3.键入起始期和终止期，然后点击OK；二．输入数据:1.键入命令：DATA Y L K2.输入每个变量的统计数据；3.关闭数组窗口（回答Yes）;三．图形分析：1.趋势图：键入命令PLOT Y K L2.相关图：键入命令 SCAT Y K L四．估计回归模型：键入命令LS Y C K L上机结果：Y =4047.866K1.262204L-1.227157s (βˆ) 17694.18 0232593 0.759696t (βˆ) 0.228768 5.426669 -1.615325prob 0.8242 0.0004 0.1407R2=0.989758 R2=0.987482 F=434.8689 prob(F)=0.0000上机实验四：异方差实验目的：：掌握异方差的检验与调整方法的上机实现实验内容：我国制造工业利润函数行业销售销售行业销售销售实验步骤：一．检验异方差性1．图形分析检验：1) 观察Y、X相关图：SCAT Y X2) 残差分析:观察回归方程的残差图LS Y C X在方程窗口上点击Residual按钮；2． Goldfeld-Quant检验：SORT XSMPL 1 10LS Y C X（计算第一组残差平方和）SMPL 19 28LS Y C X（计算第二组残差平方和）计算F统计量，判断异方差性3．White检验：SMPL 1 28LS Y C X在方程窗口上点击：View\Residual\Test\White Heteroskedastcity 由概率值判断异方差性。

上机操作步骤：1、样本回归模型：data y x ls y c x2、Goldfeld-Quandt 法：Sort x （假设有60 个样本，去掉中间16个，则样本应是以下）Smpl 1 22Ls y c xRss1=Smpl 39 60Ls y c xRss2=F=rss2/rss1= >F 0.05(22,22) ≈2.05模型存在异方差。

3、White 方法检验模型：（解释变量只有x,就用no cross ,若是有x2 x3 x4等多个解释变量，就用cross ）Smpl 1 60Ls y c x在方程窗口点View/residual/white ………nR 2= ,> 205.0χ（2）=5.99,或P=0.0044 (n 是样本个数，R^2是可决系数) 4、加权最小二乘法（WLS ）法：ls y c xgenr w1=1/resid^2（建议采用此权重变量，也可以使用其他权重变量）ls(w=w1) y c x5、使用互相关分析命令，初步判断滞后期的长度：cross y x6、阿尔蒙法建立分布滞后模型：ls y c pdl(x,s,m) （s 代表滞后期长度，m 一般取2或者3.）7、模型的短期乘数就是x 的系数。

8、DW 检验法：DW=2，ρ=0，DW=0，一阶高度正相关，DW=4，一阶高度负相关。

dl DW ≤≤0，一阶正相关，44≤≤-DW dl ，一阶负相关。

9、BG 检验法：在方程窗口点击VIEW/RESIDUIAL TEST/ SERIAL CORRELATION LM TEST10、广义差分法：ident residls y c x ar(1)11、虚拟变量模型：（从1985-1998,1996为分界线）smpl 1985 1995genr d1 = 0smpl 1996 1998genr d1 = 1data d1genr xd = x*d1smpl 1985 1998ls y c x d1 xd12、多重共线性：1、简单相关系数检验COR X1 X2 X3 X42、某一解释变量(如X1)的VIFLS X1 C X2 X3 X4 VIF=1/(1-R2)3、某一解释变量(如X1)的TOL：TOL=1/VIF=1-R24、采用逐步回归法建立最终方程13、Glejser检验 (假定h=1时)Ls y c xGenr e1=abs(resid)Ls e1 c xF= ，或P=14、Park检验Ls y c xGenr lne2=log(resid^2)Genr lnx=log(x)Ls lne2 c lnxF= , 或P=15、偏相关系数检验LS Y C XIDENT RESID16：非线性回归模型1、可线性化(重点掌握)如：LNY=a + bLNX则 LS LOG(Y) C LOG(X)以及多项式模型、指数模型、幂函数等。

《计量经济学》上机实验参考答案实验一：计量经济学软件Eviews 的基本使用；一元线性回归模型的估计、检验和预测；多元线性回归模型的估计、检验和预测（3课时）；多元非线性回归模型的估计。

实验设备：个人计算机，计量经济学软件Eviews ，外围设备如U 盘。

实验目的：（1）熟悉Eviews 软件基本使用功能；（2）掌握一元线性回归模型的估计、检验和预测方法；正态性检验；（3）掌握多元线性回归模型的估计、检验和预测方法；（4）掌握多元非线性回归模型的估计方法。

实验方法与原理：Eviews 软件使用，普通最小二乘法（OLS ），拟合优度评价、t 检验、F 检验、J-B 检验、预测原理。

实验要求：（1）熟悉和掌握描述统计和线性回归分析；（2）选择方程进行一元线性回归；（3）选择方程进行多元线性回归；（4）进行经济意义检验、拟合优度评价、参数显著性检验和回归方程显著性检验；（5）掌握被解释变量的点预测和区间预测；（6）估计对数模型、半对数模型、倒数模型、多项式模型模型等非线性回归模型。

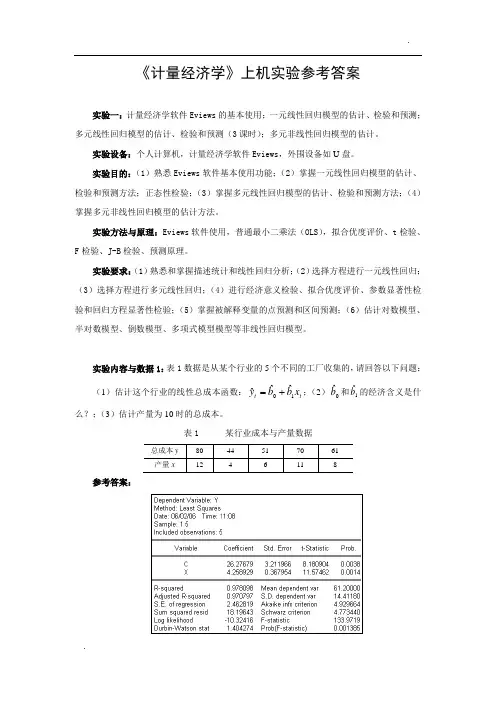
实验内容与数据1：表1数据是从某个行业的5个不同的工厂收集的，请回答以下问题：（1）估计这个行业的线性总成本函数：t t x b b y 10ˆˆˆ+=；（2）0ˆb 和1ˆb 的经济含义是什么？；（3）估计产量为10时的总成本。

表1 某行业成本与产量数据总成本y80 44 51 70 61 产量x 12 4 6 11 8参考答案：(1)总成本函数(标准格式)：t t x y25899.427679.26ˆ+= s = (3.211966) (0.367954)t = (8.180904) (11.57462)978098.02=R 462819.2.=E S 404274.1=DW 9719.133=F(2)0ˆb =26.27679为固定成本，即产量为0时的成本；1ˆb =4.25899为边际成本，即产量每增加1单位时，总成本增加了4.25899单位。

计量经济学第一次作业一、选择题1、在同一时间不同统计单位的相同统计指标组成的数据组合，是（ D ）A 、原始数据B 、时点数据C 、时间序列数据D 、截面数据2、同一统计指标按时间顺序记录的数据称为( B )。

A 、横截面数据B 、时间序列数据C 、修匀数据D 、原始数据3、下列模型中不属于线性模型的有（ C ）A 、u X Y ++=ln 10ββB 、u Z X Y +++=210βββC 、u X Y ++=10ββD 、Y=u X ++10ββ4、半对数模型μββ++=X Y ln 10中，参数1β的含义是（ C ）A ．X 的绝对量变化，引起Y 的绝对量变化B ．Y 关于X 的边际变化C ．X 的相对变化，引起Y 的期望值绝对量变化D ．Y 关于X 的弹性5、设OLS 法得到的样本回归直线为i i i e X Y ++=21ˆˆββ，以下说法不正确的是 ( )A ．0=∑i eB ．),(Y X 在回归直线上C ．Y Y =ˆD ．0),(≠i i e X COV6、根据样本资料估计得出人均消费支出Y 对人均收入X 的回归模型为i Y ∧ln =2.00+0.75lnXi ，这表明人均收入每增加1％，人均消费支出将增加（ B ）A 、0.2%B 、0.75%C 、2%D 、7.5%7、古典线性回归模型的普通最小二乘估计量的特性有A 、无偏性B 、线性性C.最小方差性 D 一致性 E. 有偏性8、利用普通最小二乘法求得的样本回归直线i i X Y 21ˆˆˆββ+=的特点（ ）A. 必然通过点),(Y XB. 可能通过点),(Y XC. 残差i e 的均值为常数D.i Y ˆ的平均值与i Y 的平均值相等 E. 残差i e 与解释变量i X 之间有一定的相关性二、判断正误(1) 随机误差项u i 与残差项e i 是一回事。

（×）1:Ui 为观察值Yi 围绕它的期望值E(Y|Xi)的离差（deviation ），是一个不可观测的随机变量.2:e 为残差，代表了其他影响Yi 的随机因素的集合，可看成Ui的估计量。

题目：第二题：下表中，Y代表新客车出售量，X1代表新车价格指数，X2代表消费者价格指数，X3代表个人可支配收入，X4代表利率，X5代表就业人数。

试建模并估计结果。

年度 1X2X3 X451971 10227 112 121.3 776.8 4.89 793671972 10872 111 125.3 839.6 4.55 821531973 11350 111.1 133.1 949.8 7.38 850641974 8775 117.5 147.7 1038.4 8.61 867941975 8539 127.6 161.2 1142.8 6.16 858461976 9994 135.7 170.5 1252.6 5.22 887521977 11046 142.9 181.5 1379.3 5.5 920171978 11164 153.8 195.3 1551.2 7.78 960481979 10559 166 217.7 1729.3 10.25 988241980 8979 179.3 247 1918 11.28 993031981 8535 190.2 272.3 2127.6 13.731982 7980 197.6 286.6 2261.4 11.2 995261983 9179 202.6 297.4 2428.1 8.691984 10394 208.5 307.6 2670.6 9.651985 11039 215.2 318.5 2841.1 7.751986 11450 224.4 323.4 3022.1 6.31第三题为了了解影响电信业务的发展情况，特收集了如下数据，请建模并估计合理的结果。

年电信业务总量邮政业务总量中国人口数市镇人口比重人均GDP人均消费水平1991 1.5163 0.5275 11.5823 0.2637 1.879 0.896 1992 2.2657 0.6367 11.7171 0.2763 2.287 1.070 1993 3.8245 0.8026 11.8517 0.2814 2.939 1.331 1994 5.9230 0.9589 11.9850 0.2862 3.923 1.746 1995 8.7551 1.1334 12.1121 0.2904 4.854 2.236 1996 12.0875 1.3329 12.2389 0.2937 5.576 2.641 1997 12.6895 1.4434 12.3626 0.2992 6.053 2.834 1998 22.6494 1.6628 12.4810 0.3040 6.307 2.972 1999 31.3238 1.9844 12.5909 0.3089 6.534 3.143第四题：X代表职工的工龄，Y代表薪水。

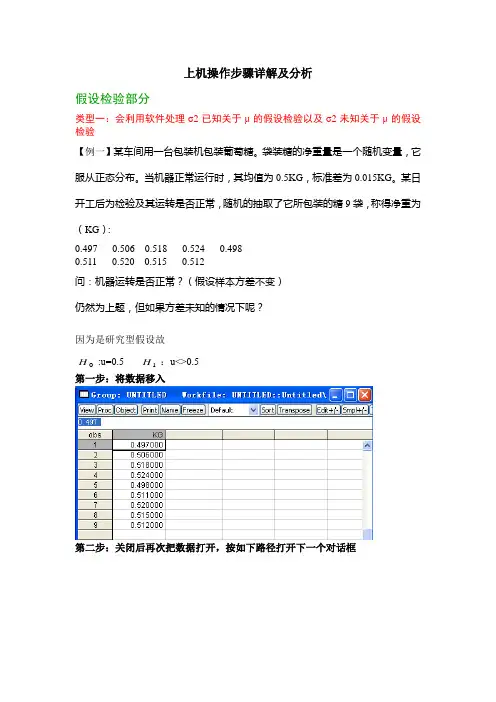
上机操作步骤详解及分析假设检验部分类型一：会利用软件处理σ2已知关于μ的假设检验以及σ2未知关于μ的假设检验【例一】某车间用一台包装机包装葡萄糖。

袋装糖的净重量是一个随机变量，它服从正态分布。

当机器正常运行时，其均值为0.5KG ，标准差为0.015KG 。

某日开工后为检验及其运转是否正常，随机的抽取了它所包装的糖9袋，称得净重为（KG ）：0.497 0.506 0.518 0.524 0.498 0.511 0.520 0.515 0.512问：机器运转是否正常？（假设样本方差不变） 仍然为上题，但如果方差未知的情况下呢？因为是研究型假设故0H :u=0.5 1H ：u<>0.5第一步：将数据移入第二步：关闭后再次把数据打开，按如下路径打开下一个对话框第三步：根据已知的均值和标准差输入下列对话框（注意：是标准差，如果题目告诉的是方差，则还要进一步转化成为标准差）第四步：点击OK后，得到如下结果，并分析该题的方差已知，故看Z-statistic的P值，因为0.0248<a/2=0.025，故拒绝原假设，结论为：在5%的显著性水平下，该机器运转不正常若该题的方差未知，则看t-statistic的P值，结论依然是：在5%的显著性水平下，该机器运转不正常类型二：会利用软件处理来自两个正态总体均值的假设检验：等方差和异方差【例2】用两种方法（A、B）测定冰从-0.72摄氏度变为0摄氏度的比热。

测得下列数据：两个样本独立且来自与方差相等的两个正态总体方法A 79.98 80.04 80.02 80.04 80.03 80.0380.04 79.97 80.05 80.03 80.02 80.00 80.02方法B 80.02 79.94 79.98 79.97 79.97 80.03 79.9579.971、两种方法是否具有显著性差异2、A方法是否比B方法测得的比热要大？解析：该题属于双样本的等方差检验，故在EXCEL背景下操作第一小问：第一步：移入数据，将原本的两行数据，分别调整为一行第二步：EXCEL的调试，“工具”——“加载宏”后选择如下选项：第三步：点击“工具”——“数据分析”——“t检验-双样本等方差检验”第四步：输入相应的数据第五步：分析相应结果解析：第一小问只需判断是否有显著性差异，也就是说只需要判断A U 与B U 是否相等,属于双侧检验，在统一用P(T<=t) 单尾分析的时候，与的是a/2比较0H ：AU-B U =0 1H ：A U -B U <>0如上图结果所示，P(T<=t) 单尾=0.001276<a/2=0.025，所以拒绝原假设，也就是说在5%的显著性水平下，方法A 和方法B 具有显著性差异第二小问：解析：第二小问不同于第一小问，判断的是A 与B 的大小，是研究型假设检验， 将认为研究结果是无效的说法或理论作为原假设H00H ：AU<=B U 1H ：A U >B U因为是单侧检验，故与a 相比，因为P(T<=t) 单尾=0.001276<a=0.05，所以拒绝原假设，结论是在5%的显著性水平下，A 方法测得的比热比B 方法的大【例3】下表给出两位文学家马克吐温的8篇小品文以及斯诺特格拉斯的10篇小品文中由3个字母组成的单字的比例 马克吐温0.225 0.262 0.217 0.240 0.2300.229 0.235 0.217 斯诺特格拉斯0.209 0.205 0.196 0.210 0.202 0.207 0.224 0.223 0.2200.201两组数据均来自正态总体，且方差相等。

计量经济学实验报告班级：数理金融1一元线性回归模型研究内容：研究全国各地区城市居民的消费是否有显著差异以及城市居民消费与人均收入之间的关系。

研究方法：最小二乘法（实验原理略）研究数据：详细数据见附录1.研究工具：Matlab2008研究过程：我们以城市居民的人均消费支出为被解释变量，以城市居民每人每年可支配收入为解释变量的一元回归分析模型。

21、散点图2、求解过程matlab代码：[n,k]=size(x);X=[ones(n,1),x];%构建结构阵X，A=X'*X; %求算信息阵A，C=inv(A); %求算信息阵的逆阵，b=X\y, % 求算回归统计数向量，其中第一行为回归截距a,RSS=y'*y-b'*X'*y, %求算离回归平方和，MSe=RSS/(n-k-1),%求算离回归方差，Up=b.*b./diag(C);%求算偏回归平方和，其中第一行是a与0差异的偏平方和，F=Up/MSe,%F测验，其中第一行为a与0差异的F值，34sb=sqrt(MSe*diag(C)); %求算回归统计数标准误，t=b./sb, % 回归统计数的 t 测验，其中第一行为a 与0差异的t 测验值。

[t, t.^2, F],%验证t^2=F SSy=var(y)*(n-1) R2=(SSy-RSS)/SSy3、回归方程Y =−554.5943+0.2484x4、回归曲线图5、指标分析估计值 t 值 F 值 b0 −554.5943 -16.8745 284.7 b 10.2484 35.46841258.0 R 20.9836分析：我们可以很清楚的看到，t值和F值都表明回归的截距项和系数都比较大，显然这一定落在拒绝域中，那么我们可以知道回归方程的截距项和斜率系数都是显著的。

上述的R^2=0.9836,已经很接近于1了，也就是说被解释变量有98.36%的变异可以被解释变量解释，那么这个比例已经很高了，这也从一定程度上说明回归的拟合效果比较好。

实验一 EViews软件的基本操作【实验目的】了解EViews软件的基本操作对象，掌握软件的基本操作。

【实验内容】一、EViews软件的安装；二、数据的输入、编辑与序列生成；三、图形分析与描述统计分析；四、数据文件的存贮、调用与转换。

实验内容中后三步以表1-1所列出的税收收入和国内生产总值的统计资料为例进行操作。

表1-1 我国税收与GDP统计资料单位：亿元年份税收 Y GDP X 年份税收 Y GDP X 1985 2041 8964 1992 3297 26638 1986 2091 10202 1993 4255 34634 1987 2140 11963 1994 5127 46759 1988 2391 14928 1995 6038 58478 1989 2727 16909 1996 6910 67885 1990 2822 18548 1997 8234 74463 1991 2990 21618 1998 9263 79396资料来源：《中国统计年鉴1999》【实验步骤】一、安装EViews软件㈠EViews对系统环境的要求⒈一台386、486奔腾或其他芯片的计算机，运行Windows3.1、Windows9X、Windows2000、WindowsNT或WindowsXP操作系统；⒉至少4MB内存；⒊VGA、Super VGA显示器；⒋鼠标、轨迹球或写字板；⒌至少10MB以上的硬盘空间。

㈡安装步骤⒈点击“网上邻居”，进入服务器；⒉在服务器上查找“计量经济软件”文件夹，双击其中的setup.exe，会出现如图1-1所示的安装界面，直接点击next按钮即可继续安装；⒊指定安装EViews软件的目录（默认为C:\EViews3，如图1-2所示），点击OK按钮后，一直点击next按钮即可；⒋安装完毕之后，将EViews的启动设置成桌面快捷方式。

图1-1 安装界面1图1-2 安装界面2二、数据的输入、编辑与序列生成㈠创建工作文件⒈菜单方式启动EViews软件之后，进入EViews主窗口（如图1-3所示）。

计量经济学（本科）第1次作业（任做其中两题）（1）：一元线性回归模型y = β0 + β1 x + u 中 β1 的最小二乘估计量用1ˆβ表示。

检验 β1 = 0的t 统计量定义为 t =)ˆ(ˆ11ββS ，其中S (1ˆβ)为1ˆβ的样本标准差。

试证明统计量F =)2/()12/(--T SSE SSR = t 2。

（2）：对于线性回归模型，用可决系数R 2表示F 统计量。

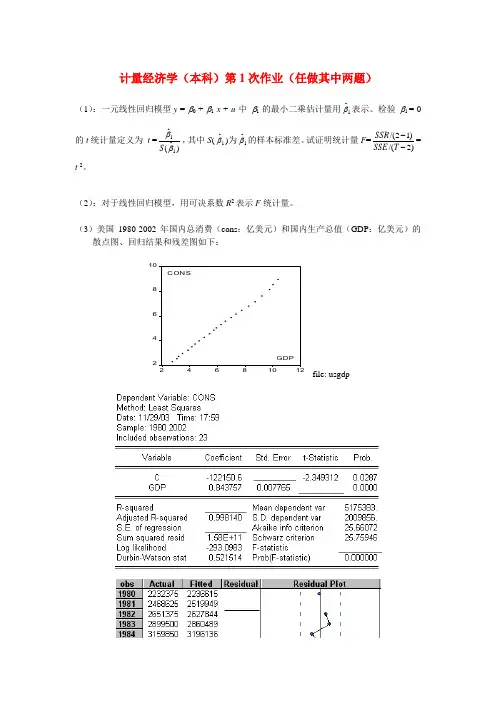
（3）美国1980-2002年国内总消费（cons ：亿美元）和国内生产总值（GDP ：亿美元）的散点图、回归结果和残差图如下：24681024681012GDP CONSfile: usgdp（1）在划线处填上相应数字（共6处）。

（2）把相对于1981年的残差点标在残差图的相应位置上并与相邻的残差点连线。

（3）根据计算机输出结果，写出一元回归模型表达式。

（4）给定检验水平α = 0.05，F检验的临界值F 0.05 ( , ) = ____ ____。

（5）给定检验水平α = 0.05，单个回归参数显著性的t检验临界值t 0.05 ( ) = __________。

（6）解释回归系数的经济意义。

（4）中国农村居民家庭对数的人均食品支出（Lnfood）与生活支出（Lnlive）数据（1978-1998）散点图、一元线性回归结果如下所示。

7.0LN F OOD6.56.05.55.04.5LN LIVE4.045678图1 Lnfood，Lnlive散点图（1）在划线处填上相应数字（共5处）（用保留4位小数运算。

）（2）根据以上计算机输出结果，写出估计的一元回归模型表达式。

（3）给定检验水平α = 0.05，检验上述回归模型显著性的临界值F0.05 ( , ) = __________。

（4）给定检验水平α = 0.05，检验上述模型回归参数显著性的临界值t0.05 ( ) = __________。

（5）解释回归系数0.951775的经济意义。

2009年秋季学期经济学院本科生计量经济学上机考试题姓名：王麻子（学号后四位：XXX ）考试成绩：注意：1.在规定时间内按照要求完成并提交：进行Eviews机上实例操作，将结果到WORD文档，进行判断，并作简要说明和分析。

2.题一为必做，题二鼓励做。

能做题二者可得加分，一二题全部做对者成绩评优秀。

题一：表1为1994-2004年我国出口贸易额与国内生产总值的两个时间序列。

试通过Eviews 建立随机计量模型：y t = β0 + β1 x t + u t来反映国内生产总值与出口额间的变化关系，并对估计结果进行讨论说明。

表1：历年出口贸易额与国内生产总值，（单位：亿元）年份EXP（Y）GDP（X）1994 46759.4 1210.11995 58478.1 1487.81996 67884.6 1510.51997 74462.6 1827.91998 78345.2 1837.11999 82067.5 1949.32000 89468.1 24922001 97314.8 26612002 105172.3 36562003 117390.2 4382.32004 136875.9 5933.2答：1.写出Eviews结果：那一张表Dependent Variable: YMethod: Least SquaresDate: 12/21/09 Time: 11:07Sample: 1994 2004C 41414.59 5118.481 8.091188 0.0000R-squared 0.917762 Mean dependent var 86747.15Adjusted R-squared 0.908625 S.D. dependent var 26282.71S.E. of regression 7944.830 Akaike info criterion 20.96140Sum squared resid 5.68E+08 Schwarz criterion 21.03374Log likelihood -113.2877 F-statistic 100.4388140000120000100000Y800006000040000100020003000400050006000X2.写出分析结果：那一个模型Y= 41414.59 + 17.22647XS.E. （5118.481）（1.718881）T (8.091188) (10.02191)R2=0.917762F=100.4388 DW=0.5533913.简要分析说明：从整体和局部给予评判其中括号里的为t检验值，R2 是可决系数，F与DW是有关两个检验统计量。

计量经济学上机操作
计量经济学上机操作是指利用计量经济学软件和数据进行实证研究的过程。

这一过程主要分为以下几个步骤：
一、数据清理和准备
在进行计量经济学实证研究之前，需要对收集到的数据进行清理和准备。

数据清理主要包括检查数据是否存在缺失值、异常值或重复值。

对于异常值和重复值，需要进行处理或剔除。

同时，还需要根据研究需要选择和转换变量。

二、建立模型
建立模型是计量经济学实证研究的重要步骤之一。

在这一阶段中，需要根据具体的研究问题选择适当的模型，例如线性回归模型、多元回归模型、时间序列模型等。

三、模型估计
模型估计是计量经济学实证研究的核心部分。

在这一阶段中，需要对建立的模型进行参数估计。

常用的方法有OLS（最小二乘法）估计、MLE（极大似然估计）估计等。

四、模型检验
模型检验是为了验证模型的适用性和准确性。

常用的检验方法有参数显著性检验、残差分析、多重共线性检验等。

五、模型应用
模型应用是将已建立、估计和检验的经济模型应用于实际政策分析、预测和决策制定中的环节。

例如，利用模型分析就业、通货膨胀、财政政策、货币政策等诸多问题。

六、结果解释与报告
将计量经济学实证研究的结果进行解释，并撰写研究报告是最后一个环节。

在这一阶段中，应该清晰地表达研究问题、研究方法、结果和结论。

在进行计量经济学上机操作时，需要熟练掌握各种计量经济学软件的使用，包括Stata、Eviews、SPSS等。

同时，还需要具备良好的数学、统计和计算机编程基础，有实证研究的经验更是必不可少。

千里之行，从认真完成每一次作业开始…… 第一、二章练习题：一、选择题：1.下面属于截面数据的是：（ ）A. 1991—2003年各年某地区20个乡镇的平均工业产值。

B. 1991—2003年各年某地区20个乡镇的各镇工业产值。

C. 某年某地区20个乡镇工业产值的合计数。

D. 某年某地区20个乡镇各镇的工业产值。

2.一个模型用于预测前必须经过的检验有：（ ） A. 经济准则检验。

B. 统计检验。

C. 计量经济学准则检验。

D. 模型预测检验。

E. 实践检验。

3.对计量经济模型的统计准则检验包括：（ ） A.估计标准误差评价。

B.拟合优度检验。

C.预测误差程度评价。

D.总体线性关系显著性检验。

E.单个回归系数的显著性检验。

4.对计量经济模型的计量经济学准则检验包括：（ ） A.误差程度检验。

B. 异方差检验。

C. 序列相关性检验。

D.超一直性检验 E.多重共线性检验。

5.计量经济分析工作的四个步骤是：（ ） A.理论研究。

B. 设定模型。

C. 估计参数。

D.检验模型. E.应用模型。

二、简答题：1.下面设计的计量经济模型是否合理，为什么？μ+⋅+=∑=i 31i i GDP b a GDP，其中，i GDP 是第一产业、第二产业和第三产业增加值。

μ为随机误差项。

第二章 练习题一、选择题：1.变量之间的关系可以分为两大类，它们是：（ ）A.函数关系和相关关系B.线性相关关系和非线性相关关系C.正相关关系和负相关关系D.简单相关关系和复杂相关关系 2.相关关系是指：（ ）A.变量间的非独立关系B.变量间的因果关系C.变量间的函数关系D.变量间的不确定的依存关系 3.进行相关分析时，假定相关的两个变量 （ ）A. 都是随机变量B.都不是随机变量C. 一个是随机变量，一个不是随机变量D. 随机的或非随机都可以4.参数β的估计量βˆ具有有效性是指 （ ） A. ()0var =βˆ B. ()βˆvar 为最小 C. ()0=-ββˆ D. ()ββ-ˆ为最小 5.对于ii 10ie X βˆβˆY ++=，以σˆ表示估计标准误差，iY ˆ表示回归值。

Date: 12/20/15 Time: 19:44Sample: 1 31In eluded observati ons: 31Variable Coefficie nt Std. Error t-Statistic Prob.C 246.8540 51.97500 4.749476 0.0001 X2 5.996865 1.406058 4.265020 0.0002 X3 -0.524027 0.179280 -2.922950 0.0069 X4 -2.265680 0.518837 -4.366842 0.0002 R-squared 0.666062 Mean depe ndent var 16.77355 Adjusted R-squared 0.628957 S.D.dependent var 8.252535 S.E. of regressi on 5.026889 Akaike info criteri on 6.187394 Sum squared resid 682.2795 Schwarz criteri on 6.372424 Log likelihood -91.90460 F-statistic 17.95108 Durbi n- Watson stat 1.147253 Prob(F-statistic) 0.000001 根据上图中数据，模型估计的结果为(51.9750) (1.4060) (0.1793) t=件7495) 件2650) (-2.9229)对模型进行检验: (0.5188) (-4.3668)R2= 0.6289 F=17.9511 n=31拟合优度检验: =0.6660, 接近于1，说明模型对样本拟合较好F检验：F=17.9511＞，这说明在显著性水平a=0.05下，回归方程是显著的。

检验：统计量分别为其绝对值均大于查表所得的（）Variable Coefficie nt Std. Error t-Statistic Prob.C 1148.758 228.2917 5.031974 0.0000X2 5.135670 1.010270 5.083465 0.0000LNX3 -22.81005 6.771820 -3.368378 0.0023LNX4 -230.8481 49.46791 -4.666624 0.0001R-squared 0.691952 Mean depe ndent var 16.77355S.E. of regressi on 0.117006 Akaike info criteri on -1.302176Sum squared resid 0.205355 Schwarz criteri on -1.153780Log likelihood 14.71958 F-statistic 542.8930Durbi n- Watson stat 0.684080 Prob(F-statistic) 0.000000 根据上图中数据，模型估计的结果为Method: Least SquaresDate: 12/21/15 Time: 13:14Sample: 1994 2011In eluded observati ons: 18Variable Coeffieie nt Std. Error t-Statistie Prob.C -13.77732 15.73366 -0.875659 0.3984X2 0.001382 0.001102 1.254330 0.2336X3 0.001942 0.003960 0.490501 0.6326X4 -3.579090 3.559949 -1.005377 0.3346X5 0.004791 0.005034 0.951671 0.3600X6 0.045542 0.095552 0.476621 0.6422R-squared 0.994869 Mean depe ndent var 12.76667 Adjusted R-squared 0.992731 S.D. dependent var 9.746631 S.E. of regressi on 0.830963 Akaike info eriteri on 2.728738 Sum squared resid 8.285993 Schwarz eriteri on 3.025529 Log likelihood -18.55865 F-statistie 465.3617 Durbi n- Watson stat 1.553294 Prob(F-statistie) 0.000000根据上表可得，回归模型估计结果为:模型参数估计结果与预期不相符，比现在X4与X5的符号与预期相反。