第八章 静电场中的导体和电介质(精)

第八章 静电场中的导体和电介质§8-1 静电场中的导体一、静电感应 导体的静电平衡条件 1、静电感应2、导体静电平衡条件（1）导体的静电平衡：当导体上没有电荷作定向运动时称这种状态为导体的静电平衡。

（2）静电平衡条件 从场强角度看：①导体内任一点，场强0=E；②导体表面上任一点E与表面垂直。

从电势角度也可以把上述结论说成：①⇒导体内各点电势相等；②⇒导体表面为等势面。

用一句话说：静电平衡时导体为等势体。

二、静电平衡时导体上的电荷分布 1、导体内无空腔时电荷分布如图所示，导体电荷为Q ，在其内作一高斯面S ，高斯定理为：∑⎰=∙内S Sq s d E 01ε导体静电平衡时其内0=E，∴ 0=∙⎰s d E S， 即0=∑内S q 。

S 面是任意的，∴导体内无净电荷存在。

结论：静电平衡时，净电荷都分布在导体外表面上。

2、导体内有空腔时电荷分布 （1）腔内无其它电荷情况如图所示，导体电量为Q ，在其内作一高斯面S ，高斯定理为：∑⎰=∙内S Sq s d E 01ε 静电平衡时，导体内0=E∴ 0=∑内S q ，即S 内净电荷为0，空腔内无其它电荷，静电平衡时，导体内又无净电荷∴空腔内表面上的净电荷为0。

但是，在空腔内表面上能否出现符号相反的电荷，等量的正负电荷？我们设想，假如有在这种可能，如图所示，在A 点附近出现+q ，B 点附近出现-q ，这样在腔内就分布始于正电荷上终于负电荷的电力线，由此可知，B A U U >,但静电平衡时，导体为等势体，即B A U U =，因此，假设不成立。

结论：静电平衡时，腔内表面无净电荷分布，净电荷都分布在外表面上，（腔内电势与导体电势相同）。

（2）空腔内有点电荷情况如图所示，导体电量为Q ，其内腔中有点 电荷+q ，在导体内作一高斯面S ，高斯定理为∑⎰=∙内S Sq s d E 01ε 静电平衡时0=E， ∴ 0=∑内S q 。

又因为此时导体内部无净电荷，而腔内有电荷+q ， ∴ 腔内表面必有感应电荷-q 。

取一体积元， dV 4πr 2 dr
2
R1
r
dr
Q R2 dWe wedV dr 2 8 π εr 2 2 R Q Q 1 1 2 dr We dWe ( ) 2 8 π ε R1 r 8 π ε R1 R2 9
8.5 静电场的能量
2
第8章 静电场中的导体和电介质
第8章 静电场中的导体和电介质
例：同轴电缆由内径为 R1、外径为 R2的两无限长金属圆柱 面构成，单位长度带电量分别为 +、 -，其间充有 r 电介 质。求： 1）两柱面间的场强 E；2）电势差 U；3）单位长 度电容 ；4）单位长度贮存能量。
介质中高斯定理： D dS q 0
5
8.5 静电场的能量
第8章 静电场中的导体和电介质
二、静电场的能量 能量密度 以平行板电容器为例，将电能用电场的量表示。
1 1 1 1 εS 2 2 2 2 ( Ed ) εE Sd εE V We CU 2 2 2 d 2
电场中单位体积的能量 称为电场能量密度：
d
S
εr
We we V
8.5 静电场的能量
第8章 静电场中的导体和电介质
静电场的能量 ( Electrostatic Energy ) 一个带电系统包含许多的电荷。电荷之间 存在着相互作用的电场力。 任何一个带电系统在形成的过程中，外力 必须克服电场力做功，即要消耗外界的能量。 外界对系统所做的功，应该等于系统能量 的增加。 因此，带电系统具有能量。
第8章 静电场中的导体和电介质
1 We QU 2

R1
1 λ R2 λh ln 2 2πε0 εr R1 2 λh R2 ln 4πε0 εr R1

第八章 静电场中的导体和电介质§8-1 静电场中的导体一、静电感应 导体的静电平衡条件 1、静电感应2、导体静电平衡条件（1）导体的静电平衡：当导体上没有电荷作定向运动时，称这种状态为导体的静电平衡。

（2）静电平衡条件从场强角度看：①导体内任一点，场强0=E；②导体表面上任一点E与表面垂直。

从电势角度也可以把上述结论说成： ①⇒导体内各点电势相等； ②⇒导体表面为等势面。

用一句话说：静电平衡时导体为等势体。

二、静电平衡时导体上的电荷分布 1、导体内无空腔时电荷分布如图所示，导体电荷为Q ，在其内作一高斯面S ，高斯定理为：∑⎰=•内S Sq s d E 01ε 导体静电平衡时其内0=E，∴ 0=•⎰s d E S， 即0=∑内S q 。

S 面是任意的，∴导体内无净电荷存在。

结论：静电平衡时，净电荷都分布在导体外表面上。

2、导体内有空腔时电荷分布（1）腔内无其它电荷情况如图所示，导体电量为Q ，在其内作一高斯面S ，高斯定理为：∑⎰=•内S Sq s d E 01ε 静电平衡时，导体内0=E∴ 0=∑内S q ，即S 内净电荷为0，空腔内无其它电荷，静电平衡时，导体内又无净电荷∴ 空腔内表面上的净电荷为0。

但是，在空腔内表面上能否出现符号相反的电荷，等量的正负电荷？我们设想，假如有在这种可能，如图所示，在A 点附近出现+q ，B 点附近出现-q ，这样在腔内就分布始于正电荷上终于负电荷的电力线，由此可知，B A U U >,但静电平衡时，导体为等势体，即BAU U =，因此，假设不成立。

结论：静电平衡时，腔内表面无净电荷分布，净电荷都分布在外表面上，（腔内电势与导体电势相同）。

（2）空腔内有点电荷情况如图所示，导体电量为Q ，其内腔中有点 电荷+q ，在导体内作一高斯面S ，高斯定理为∑⎰=•内S Sq s d E 01ε 静电平衡时0=E， ∴ 0=∑内S q 。

又因为此时导体内部无净电荷，而腔内有电荷+q ，∴ 腔内表面必有感应电荷-q ，。

静电场中的导体和电介质静电平衡时导体是个等势体，导体表面是等势面，大前提是整个导体都是一样的，不要因为单独说导体表面是个等势面就误以为导体表面和内部不是等势的。

（证明省略）由此公式得出：导体表面电荷密度大的地方场强大，面电荷密度小的地方场强小。

导体表面电荷分布规律①与导体形状有关②与附近有什么样的带电体有关。

定性分析来说，孤立导体面电荷密度与表面的曲率有关，但是并不是单一的函数关系。

拓展知识（尖端放电的原理以及应用；避雷针的原理）这是一个从带电体上吸取全部电荷的有效方法。

测量电量时，要在静电计上安装法拉第圆筒，并将带电体接触圆筒的内表面，就是为了吸取带电体的全部电量，使测量更准确。

库仑平方反比定律推出高斯定理，高斯定理推出静电平衡时电荷只能分布导体外表面。

所以可以由实验精确测定导体内部没有电荷，就证明了高斯定理的正确，进而就证明了库仑平方反比定律的正确。

所以说这是精确的，因为通过实验测定数据是一定会存在误差的，而通过实验测定导体内部没有电荷是不会存在误差的，所以是很精确的。

以上是库仑平方反比定律验证的发展历史。

见图2-1，导体壳内部没有电荷时，导体的电荷只是分布在外表面上，为了满足电荷守恒定理，见图2-1c，就要一边是正电荷，而另一边是负电荷，其实空腔内没有电场的说法是对于结果而言的，并不能看出本质，本质是外电场和感应电荷的电场在导体腔的内部总的场强为0。

使带电体不影响外界，则要求将带电体置于接地的金属壳或者金属网内，必须接地才能将金属壳或者金属网外表面感应电荷流入地下。

则外界不受带电体场强的作用，而本质上也是带电体的场强和内表面感应电荷的场强叠加作用使外界总场强为0。

孤立导体的电容：电容C与导体的尺寸和形状有关，与q，U无关，它的物理意义是使导体每升高单位电位所需要的电量。

电容器及其电容：对电容的理解要升高一个层次：电容是导体的一个基本属性，就好像水桶的容量一样，C=U/q。

然而导体A的附近有其他导体时，导体的电位不仅与自己的q 有关，还受到其他导体的影响。

Q + + + + ++ + + + + E= 0 S+ + + + + + + + ++
Q q + + + +++ + +-q + + - E= 0 S + 结论: 电荷分布在导体外表面, 导体 + q + + 内部和内表面没净电荷. + - - + + + + ++ 腔内有电荷q: E 0 q 0

i
结论: 电荷分布在导体内外两个表面,内表面感应电荷为-q. 外表面感应电荷为Q+q.
NIZQ
第 5页
大学物理学 静电场中的导体和电介质
结论: 在静电平衡下,导体所带的电荷只能分布在导体的 表面,导体内部没有净电荷. • 静电屏蔽 一个接地的空腔导体可以隔离内 外电场的影响. 1. 空腔导体, 腔内没有电荷 空腔导体起到屏蔽外电场的作用. 2. 空腔导体,腔内存在电荷 接地的空腔导 体可以屏蔽内、 外电场的影响.
NIZQ
第 3页
大学物理学 静电场中的导体和电介质
• 静电平衡时导体中的电场特性
E内 0
场强:
ΔVab
b
a
E dl 0
• 导体内部场强处处为零 E内 0 • 表面场强垂直于导体表面 E表面 // dS
• 导体为一等势体 V 常量 • 导体表面是一个等势面
S
0 E P dS qi

-
-
目录
静电场中的导体 和电介质
0
静电场中的导体和电介质
静电场中的导体和电介质
静电场是指在没有电流流动的情况下，电荷分布所产生的电场。在静电场中，导体和电介质 是两种不同的物质，它们的特性和作用也不同，本文将探讨导体和电介质在静电场中的性质 和应用 首先，我们需要了解导体和电介质的基本概念。导体是一种具有良好导电性能的物质，常见 的导体包括金属等。导体内的自由电子可以在外加电场的作用下移动，形成电流。而电介质 则是一种不良导电的物质，它的电导率远远低于导体。电介质在外加电场下无法形成连续的 电流，而是通过极化现象来响应电场的作用 在静电场中，导体和电介质的行为有很大的不同。对于导体来说，其特点是在静电平衡状态 下，内部电场为零。这是因为导体内的自由电子能够自由移动，它们会在外加电场的作用下 重新分布，直到达到平衡状态。这种现象被称为电荷运动的屏蔽效应。导体的另一个重要性 质是表面上的电荷分布是均匀的，这也是导体可以用来储存电荷的
与导体不同，电介质在静电场中的响应更加复杂。当外加电场作用于电介质时，电介 质分子会发生极化现象，即分子内部正、负电荷的分离。这种分离会导致电介质内部 产生电位移场，从而相应地改变电场分布。电介质的极化程度可以用极化强度来衡量 ，极化强度与外加电场的强度成正比。除了极化现象，电介质还可能发生击穿现象， 即在电场强度过高时，电介质内部的绝缘失效，导致电流的突然增加
0
静电场中的导体和电介质
导体在静电场中的一个重要应用 是电路中的导线。电路中的导线 由导体制成，它们能够有效地传 导电流。在电力系统中，导体连 接电源和电器设备，将电能传输 到目标地点。此外，在电子设备 制造中，导体用于制作电路板， 连接不同的电子元件，实现电信 号的传输和处理

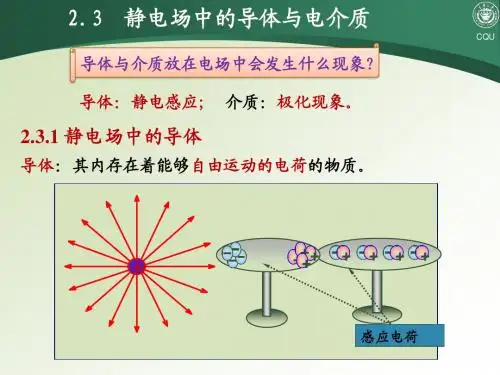
§2 静电场中的导体和电介质§2－1 静电场中的导体1. 导体的静电平衡条件当电荷静止不动时，电场散布不随转变，该体系就达到了静电平衡。

在导体中存在自由电荷，它们在电场的作用下可以移动，从而改变电荷的散布……导体内自由电荷无宏观运动的状态。

导体的静电平衡的必要条件是其体内图2－1导体的静电平衡场强处处为零。

从静电平衡的条件动身可以取得以下几点推论：推论1）导体是等位体，导体表面是等位面：2）导体表面周围的场强处处与它的表面垂直：因为电力线处处与等位面正交，所以导体外的场强必与它的表面垂直。

（注意：本章所用的方式与第一章不同，而是假定这种平衡以达图2－2导体对等位面的控制作用到，以平衡条件动身结合静电场的普遍规律分析问题。

）2．电荷散布1) 体内无电荷，电荷只散布在导体的表面上:当带电导体处于静电平衡时，导体内部不存在净电荷（即电荷的体密度）电荷仅散布在导体的表面。

可以用高斯定理来证明：设导体内有净电荷，则可在导体内部作一闭合的曲面，将包围起来，依静电条件知S面上处处, 即由高斯定理必有q=02） 面电荷密度与场强的关系:当导体静电平衡时，导体表面周围空间的 与该处导体表面的面电荷密度 有如下关系：论证： 在电荷面密度为 的点取面元设 点为导体表面之外周围空间的点，面元。

充分小，可以为 上的面电荷密度 是均匀的，以为横截面作扁圆柱形高斯面（S ）,上底面过P 点，把电荷q= 包围起来. 通太高斯面的电通量是：3） 表面曲率的影响、尖端放电导体电荷如何散布，定量分析研究较复杂，这不仅与这个导体的形状有关，还和它周围有何种带电体有关。

对孤立导体，电荷的散布有以下定性的规律：图2－3导体表面场强与电荷面密度曲率较大的地方（凸出而尖锐处），电荷密度e 较大；曲率较小的地方（较平坦处）电荷密度e 较小；曲率为负的地方（凹进去向）电荷密度e 更小。

1） 端放电的利和弊3 导体壳（腔内无带电体情况）大体性质：当导体壳内无带电体时，在静电平衡当导体壳内无 带电体时，在静电平衡下：导体壳内表面上处处无电荷，电荷仅散布在外 表面；空腔内无带电场，空腔内电位处处相等。

V 实验证明，对于绝大多数各向同性的介质，极化强度 P与电场强度E成正比，即P = 0 E
V 0
P
lim
p
式中称为介质的电极化率，它与场强E无关，取决于电介质。
2.5.3

束缚电荷
电介质处于极化状态时，在电介质的端面或内部上产生极化 电荷。这些电荷不能离开电介质表面，称为束缚电荷。 如果介质不均匀，在介质内部也会由于极化而出现束缚电荷。 设单位体积分子数为n，
这类分子在外电场的作用下，分子中的正负电荷中心
将发生相对位移，形成一个电偶极子，它们的等效电偶极 矩 P 的方向都沿着电场的方向，导致介质表面上出现了电
荷。这种情况称为介质的极化。
无极性分子电介质的这种极化方式称为位移极化。
有极性分子的极化
有极性分子的正负电荷中心即使在无外电场存在时也是不 重合的，例如水分子等。由于分子热运动的无规则性 , 在物理 小体积内的平均电偶极矩为零，宏观上也不显电性。 当介质受到外电场作用时，每个分子的电偶极矩都受到一 个力矩的作用，使分子电矩转向外电场方向，这样分子固有电 矩的矢量和就不等于零了。 但由于分子的热运动，这种转向并不完全。外电场越强， 分子电矩沿着电场方向排列得越整齐。
2.4
静电场中的导体
2.4.1 导体的静电平衡
金属导体中存在大量的自由电子，它们时刻作无规则的
微观运动（“热运动”）。当自由电子受到电场力作用时，
会在热运动的基础上附加一种有规则的宏观运动，形成电流。 当导体中自由电子不作宏观运动（没有电流）时，我们说导 体达到了静电平衡的状态。
2.4.1 导体的静电平衡
D＝E
2.5.5
静电场的边界条件
在两种介质的分界面上，电场强度矢量E的切线分量连续。

被积函数 代入原式
r r r r r r P(r ') ∇′ ⋅ P(r ')) 1 P(r ') ⋅∇′ = ∇′ ⋅ − R R R
r r r r P (r ') r 1 ∇′ ⋅ P (r ') ϕ p (r ) = ∇′ ⋅ dV ′ − ∫ dV ′ ∫V ′ V′ 4π ε0 R R
+
+++ +
+
+ + +
感应电荷
CQU
+ + + +
+ + + +
+ + + +
v E0
CQU
v E0
v E=0
v＇ E
+ + + + + + + +
v E0
v v v＇ E = E0 + E = 0
导体内电场强度 外电场强度 感应电荷电场强度
CQU
静电平衡条件: 静电平衡条件 （1）导体内部任何一点处的电场强度为零； ）导体内部任何一点处的电场强度为零； 都与导体表面垂直; （2）导体表面处的电场强度的方向 都与导体表面垂直 ）导体表面处的电场强度的方向,都与导体表面垂直 （3）导体为一等位体，导体表面为等位面； ）导体为一等位体，导体表面为等位面； （4）电荷（或感应电荷）分布在导体表面上，形成面电荷 ）电荷（或感应电荷）分布在导体表面上，形成面电荷. 导体表面是等势面
2.3 静电场中的导体与电介质
CQU
导体与介质放在电场中会发生什么现象？ 导体与介质放在电场中会发生什么现象？ 导体：静电感应； 介质：极化现象。 导体：静电感应； 介质：极化现象。

q2
EA
1 2 o
2 2 o
3 2 o
4 2 o
0
EB
1 2 O
2 2 O
3 2 o
4 2 o
0
1
23
4
由电荷守恒：
1S 2 S q1
A
B
3S 4S q2
1
4
q1 q2 2S
2
3
q1 q2 2S
20
1
4
q1 q2 2S
q1
2
3
q1 q2 2S
1
2
上述结果表明：平板相背的两面带电等
R3 R2
R3
RR11
qq1 1
RR33
问题：电势表
达式能直接写
R2 R1
q1
4 or
2
dr
R3
(q q1 )
4 or 2
dr
出来吗？
q1
4 o
1 R1
1 R2
q q1
4 o R3
V1 V2
同理，球壳的电势为：
V2
E dl
R3
R3
(q
4
q1 ) or 2
dr
q q1
2.内屏蔽
+
+
壳外表面上的电荷分布与腔内带电体的位置无关，只 取于导体外表面的形状。
若将空腔接地，则空腔外表面上的感应电荷被大地电荷 中和，腔外电场消失，腔内电荷不会对空腔外产生影响。即 接地空腔对内部电场起到了屏蔽作用，这是静电屏蔽的另外 一种——内屏蔽。
高压设备用金属导体壳接地做保护。 14
五、利用静电平衡条件和性质作定量计算
例1：半径为R和r的球形导体（R>r），用很长的细导线连 接起来，使两球带电Q、q，求两球表面的电荷面密度。

大学物理上册(机械工业出版社-许瑞珍-贾谊明编著)第8章--静电场中的导体与电介质第八章 静电场中的导体与电介质8－1 点电荷+q 处在导体球壳的中心，壳的内外半径分别为R l 和R 2，试求，电场强度和电势的分布。

解：静电平衡时，球壳的内球面带－q 、外球壳带q 电荷在r<R 1的区域内rrq ˆ4E 201πε=，)111(42101R R r qU+-=πε在R 1<r<R 2的区域内,02=E .,4202R q U πε=在r>R 2的区域内:.ˆ4E203r r πεq=.403rq U πε=8－2 把一厚度为d 的无限大金属板置于电场强度为E 0的匀强电场中，E 0与板面垂直，试求金属板两表面的电荷面密度。

解：静电平衡时，金属板内的电场为0， 金属板表面上电荷面密度与紧邻处的电场成正比R 2R 1习题 8－1图q -q0 E 0习题 8－2图σ1 σ2所以有,001E εσ-=.002E εσ=8－3 一无限长圆柱形导体，半径为a ，单位长度带有电荷量λ1，其外有一共轴的无限长导体圆简，内外半径分别为b 和c ，单位长度带有电荷量λ2，求（1）圆筒内外表面上每单位长度的电荷量；（2）求电场强度的分布。

解：（1）由静电平衡条件，圆筒内外表面上每单位长度的电荷量为;,21λλλ+-（2）在r<a 的区域内:E=0 在a<rb 的区域内:Er012πελ=e n在r>b 的区域内:E r212πελλ+=e n8－4 三个平行金属板A 、B 和C ，面积都是200cm 2，A 、B 相距4.0mm ，A 、C 相距2.0mm ，B 、C 两板都接地，如图所示。

如果A 板带正电3.0×10－7C ，略去边缘效应（1）求B 板和C 板上感应电荷各为多少?（2）以地为电势零点，求A 板的电势。

习题 8－3图解：（1）设A 板两侧的电荷为q 1、q 2，由电荷守恒 原理和静电平衡条件，有A q q q =+21（1）1q q B -=，2q qC-=（2） 依题意V AB =V AC ,即101d Sq ε＝22dS q ε112122q q d d q ==→代入（1）（2）式得q 1＝1.0×10-7C ，q 2＝2.0×10-7C ，q B ＝－1.0×10-7C ，q C =-q 2＝－2.0×10-7C ，（2）101d SqU A ε=＝202d Sq ε==⨯⨯⨯⨯⨯⨯----312471021085810200102. 2.3×103V8－5 半径为R 1=l.0cm 的导体球带电量为q=1.0×10－10C ，球外有一个内外半径分别为R 2=3.0cm 和R 3=4.0cm 的同心导体球壳，壳带有电量Q=11×10－10 C ，如图所示，求（1）两球的电势；（2）用导线将两球连接起来时两球的电势；（3）外球接地时，两球电势各为多少？（以地为电势零点）解：静电平衡时，球壳的内球面带－q 、外球壳带q+Q 电荷A B C 习题 8－4图d12（1）)(4132101R Q q R q R q U++-=πε代入数据)41113111(101085.814.34100.1212101++-⨯⨯⨯⨯⨯=---U＝3.3×102V2024R Q q U πε+=4)111(101085.814.34100.121210+⨯⨯⨯⨯⨯=---=2.7×102V（2）用导线将两球连接起来时两球的电势为2024R Q q U πε+=4)111(101085.814.34100.121210+⨯⨯⨯⨯⨯=---=2.7×102V（3）外球接地时，两球电势各为)(412101R q R q U -=πε)3111(101085.814.34100.1212101-⨯⨯⨯⨯⨯=---U ＝60V2=U8－6 证明:两平行放置的无限大带电的平行平面金属板A 和B 相向的两面上电荷面密度大小相等，符号相反，相背的两面上电荷面密度大小等，符号相同。

第八章静电场中的导体与电介质问题8-1 有人说：“某一高压输电线的电压有500kV，因此你不可与之接触”。

这句话是对还是不对？维修工人在高压输电线路上是如何工作的？解这种说法不正确，可以利用空腔导体的静电屏蔽原理，使维修工人穿上导电性能良好的屏蔽服，电场不会深入到人体，从而可以保证维修工人的安全。

8-2将一个带电小金属球与一个不带电的大金属球相接触，小球上的电荷会全部转移到大球上去吗？解不会。

带电小金属球与不带电的大金属球相接触后会达到静电平衡，内部电场强度为零。

若小球上的电荷全部转移到大球上去，则两球组成的整体内部电场强度不可能为零。

8-3 在高压电器设备周围，常围上一接地的金属栅网，以保证栅网外的人安全，试说明其道理。

解这是利用空腔导体的静电屏蔽作用。

金属栅网就是一个金属壳体，将栅网接地，栅网外部将不受栅网内部电场的影响。

8-4在绝缘支柱上放置一闭和的金属球壳，球壳内有一人，当球壳带电并且电荷越来越多时，他观察到的球壳表面的电荷面密度、球壳内的场强是怎样的？当一个带有跟球壳相异电荷的巨大带电体移近球壳时，此人又将观察到什么现象？此人处在球壳内是否安全？解带电金属球壳由于静电平衡，电荷分布于球壳表面，当电荷越多，球壳表面的电荷面密度增大，球壳内场强为零。

当带有异号电荷的巨大带电体移近球壳时，会发生放电现象，由于静电屏蔽作用，球壳空间电场不受外部空间场强的影响，所以人处于球壳内不会有危险。

8-5电介质的极化现象和导体的静电感应现象有些什么区别？解导体的静电感应现象是在外电场作用下导体中的自由电荷作定向运动而使自由电荷重新分布；电介质的极化现象是在外电场的作用下介质表面产生极化电荷。

二者有着实质的区别，静电感应所产生的电荷是导体内部的自由电荷，而极化现象中出现在介质表面上的电荷则是束缚电荷；而且它们形成的方式也不同，静电感应是导体内部自由电荷的运动，而极化实质是电介质内部电偶极矩的产生。

8-6 在下列情况下，平行平板电容器的电势差、电荷、电场强度和所贮的能量将如何变化。

静电场中的导体和电介质引言在物理学中，静电场是指当电荷处于静止状态时周围存在的电场。

导体和电介质是静电场中两种常见的物质类型。

理解导体和电介质在静电场中的行为对于理解静电现象和应用静电学原理具有重要意义。

本文将介绍导体和电介质在静电场中的特性和行为，包括导体的电荷分布和电场分布、导体内部电场为零的原因，以及电介质的电极化和电介质的介电常数。

导体导体的电荷分布在静电场中，导体具有特殊的电荷分布特性。

由于导体中的自由电子可以在导体内自由移动，一旦一个导体与其他带电体接触，自由电子将重新分布以达到平衡。

导体的外部表面电荷会分散在整个表面上，使得导体表面的电场强度为零。

这意味着在静电平衡条件下，导体表面任意一点的电势相等。

导体内部的电场分布特性在导体内部，电场强度为零。

这是由于自由电子可以在导体内自由移动，当导体中存在电场时，自由电子会沿着电场方向移动，直到达到平衡。

这种现象称为电荷迁移。

因此，导体内部的自由电子的运动将产生一个等量但相反方向的电场，导致导体内部的电场强度为零。

这也是为什么导体内部没有电场线存在的原因。

电介质电极化现象电介质是一种不易导电的物质，而其在静电场中的行为与导体有着显著不同。

当一个电介质暴露在静电场中时，电介质分子会发生电极化现象。

电极化是指电介质分子在电场作用下产生偶极矩。

在电场的作用下，电介质分子会发生形状变化，正负电荷分离，产生一个平均不为零的电偶极矩。

这种电极化现象可以分为两种类型：取向极化和感应极化。

取向极化是指电介质分子的取向方向在电场的作用下发生变化，而感应极化是指电场作用下导致电介质分子内部正负电荷的相对移动。

电介质的介电常数电介质的介电常数是描述电介质在电场中的响应特性的重要参数。

介电常数是一个比值，代表了电介质在电场力下的相对表现。

介电常数决定了电介质的极化程度和电场中的电场强度。

电介质的介电常数大于1，意味着电介质对电场的屏蔽效果更明显。

在实际应用中，通过选择合适的电介质和调整电场强度，可以改变静电场的分布和效果，用于电容器、绝缘材料等相关领域。

d O'
导 体 板

+
直线
O
x
E2 2 0
由总电场
E E E 0 O 1 2 得 2 d
(3)
二、 静电场中的电介质 1. D 的高斯定理 2. 电容器的电容 3.孤立导体球的电容 4. 电容器的能量 5. 静电场的能量
D d S q 0 内
电容:

(6)
2
2 r L 0 C ln( R 2/R 1)
(5)
例4:两个同心金属球壳，内球壳半径为R1，外球壳半径 为R2，中间充满相对介电常数为 r 的均匀介质，构成一 个球形电容器。 (1) 求该电容器的电容； (2)设内外球壳 上分别带有电荷+Q和-Q，求电容器储存的能量。 解: (1)设内外球壳上分别带电Q和-Q， 则两球壳中间的场强大小为
Q 20r rL
R2
R1 dr
r
在电场中取体积元 d V ( 2 rL ) d r 则在 dV 中的电场能量为：
L
r
+Q
–QLeabharlann d W0r2
2 E d V
2 R 1 Q d r 2 W W d R 1 r 2 2 L 0 r
2 1 Q R 1 Q ln 2 22 rL R 2 C 0 1
由导体内部场 强为零得
3. 有导体存在时静电场的分析与计算
1
2
3
4
1 2 3 4 0 2 0 2 0 2 0 2 0
S
P
(1)
例1: 同心导体球面，半径分别为R1和R2，电量分别为 Q1和Q2。当把内球接地时，内球带电多少？ 解：内球接地，其电势为零，设其电量为Q1

平行板电容器的电容，与极板的面积成正比，与极板 间的距离成反比。
圆柱形电容器的电容
两柱面间的场强大小 E Q 2 0 Lr 方向沿着径向 两柱面间的电势差
U A U B Edr Q 2 0 L ln R2 R1
R2
Q 2 0 Lr
R1
dr
柱形电容器的电容
dWe we dV
取半径为r，厚为dr的球壳， 电场总能量为： 其体积元为： 2
8r
2
dr
dV 4r dr
2
Q We dWe 8

R2
R1
dr 1 Q2 ( R2 R1 ) 2 r 2 4R2 R1
Q C U
4 0 R
★电量按半径比例进行重新分配
2 1 Q Q 2 Q 3 3 F 2 2 4π 0 R 18π 0 R
二. 电容器及其电容 常见的电容器： 平行板电容器----两块导体薄板； 圆柱形电容器----导体薄柱面； 球形电容器----导体薄球面； 当电容器的两极板分别带有等值异号电荷Q时，电荷Q与 两极板A、B间的电势差 (UA-UB) 的比值定义为电容器的 电容：
外 内
E内 ? S
★电荷只分布在外表面，内表面上处处无电荷
内表=0
E内=0
2、 若导体壳包围的空间（腔）有电荷：
内
q S ★内表面带电总量为-q,内表面上各处 电荷面密度取决于腔内电荷的分布
外
q内表 q
E内 0
3、静电屏蔽
S
A
Q
B
E内 0
在电子仪器中，用金属网罩把电路包起来，使其 不受外界带电体的干扰。 传送微弱电信号的导线，外表用金属丝编成的网 包起来，这种的导线叫屏蔽线。