天津南开中学小卷

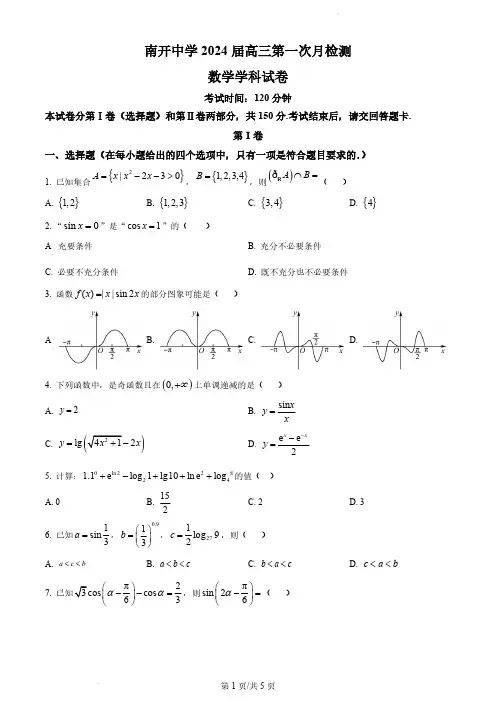
南开中学2024届高三第一次月检测数学学科试卷考试时间：120分钟本试卷分第Ⅰ卷（选择题）和第Ⅱ卷两部分，共150分.考试结束后，请交回答题卡.第Ｉ卷一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求的．）1. 已知集合{}2|230A x x x =-->，{}1,2,3,4B =，则()A B ⋂=Rð（）A. {}1,2 B. {}1,2,3 C. {}3,4 D. {}42. “sin 0x =”是“cos 1x =”的（ ）A 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件3. 函数()||sin 2f x x x =的部分图象可能是（ ）AB. C. D.4. 下列函数中，是奇函数且在()0,∞+上单调递减的是（ ）A. 2y = B. sin xy x=C. )lg2y x=- D. e e 2x xy --=5. 计算：0ln 228241.1e log 1lg10ln e log +-+++的值（ ）A. 0B.152C. 2D. 36. 已知1sin 3a =，0.913b ⎛⎫= ⎪⎝⎭，271log 92c =，则（ ）A. a c b<< B. a b c << C. b a c << D. c a b<<7.π2cos 63αα⎛⎫--= ⎪⎝⎭，则πsin 26α⎛⎫-= ⎪⎝⎭（ ）..A. 19-B.19C.13D.898. 将函数()π3sin 26f x x ⎛⎫=+ ⎪⎝⎭的图象向右平移π6个单位长度后，所得图象对应的函数为()y g x =，有下列命题：①函数()g x 的图象关于直线πx =对称 ②函数()g x 图象关于点π,012⎛⎫⎪⎝⎭对称③函数()g x 在π5π,2424⎡⎤-⎢⎥⎣⎦上单调递增 ④函数()g x 在[]0,2π上恰有5个极值点其中正确命题个数为（ ）A. 1B. 2C. 3D. 49. 设函数ln 2,0()π1sin ,π042x x x f x x x ω⎧+->⎪=⎨⎛⎫+--≤≤ ⎪⎪⎝⎭⎩有7个不同的零点，则正实数ω的取值范围为（ ）A. 131744⎡⎫⎪⎢⎣⎭，B. 174⎡⎢⎣C. 49121652⎡⎫⎪⎢⎣⎭， D. 65121732⎡⎫⎪⎢⎣⎭，第II 卷二、填空题（本大题共6小题，每小题5分，共30分．）10. 已知i 是虚数单位，化简32i12i-+的结果为____________．11.在代数式521x ⎫-⎪⎭的展开式中，常数项为_____________．12. 函数()()ππ2sin 0,22f x x ωϕωϕ⎛⎫=+>-<< ⎪⎝⎭的部分图象如图所示，则π=3f ⎛⎫⎪⎝⎭__________．的的13. 在亚运会女子十米跳台决赛颁奖礼上，五星红旗冉冉升起，在坡度15 的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60 和30 ，第一排A 点和最后一排E 点的距离为（如图所示），则旗杆的高度为____________米．14. 已知定义在[)0+∞，上的函数()f x ，当[0,2)x ∈时，()()1611f x x =--，且对任意的实数1[2222)n n x +∈--，（*2N n n ∈，≥），都有()1122x f x f ⎛⎫=- ⎪⎝⎭，若函数()()log a g x f x x =-有且仅有五个零点，则a 的取值范围__________.15. 记()ln f x x ax b =++（0a >）在区间[],2t t +（t 为正数）上的最大值为(),t M a b ，若{|(,)ln 3}R t b M a b a ≥+=，则实数t 的最大值为__________.三、解答题（本大题共5小题，共75分．解答应写出文字说明，证明过程或演算步骤．）16. 已知函数()()2π2sin πcos 2f x x x x ⎛⎫=+-+-⎪⎝⎭（1）求()f x 的最小正周期及对称轴方程；（2）当ππ,42x ⎡⎤∈⎢⎥⎣⎦时，求()f x 的最大值和最小值.17. 在ABC 中，角,,A B C 所对的边分别为,,a b c ，其中2C π≠，已知cos 2cos cos b c A a B C -=.（1）求角B 的大小；（2）若223125b c ac +=-，求ABC 面积的最大值.18. 如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，AD AB ⊥，//AB DC ，2AD DC AP ===，1AB =，E 为棱PC 的中点.（1）证明：//BE 平面PAD ；（2）求直线BE 与平面PBD 所成角的正弦值；（3）求点D 到平面PBC 的距离.19. 已知椭圆()2222:10x y C a b a b +=>>，短轴长为.（1）求C 的方程；（2）如图，经过椭圆左顶点A 且斜率为()0k k ≠的直线l 与C 交于A ，B 两点，交y 轴于点E ，点P 为线段AB 的中点，若点E 关于x 轴的对称点为H ，过点E 作OP （O 为坐标原点）垂直的直线交直线AH 于点M ，且APM △，求k 的值.20. 已知函数()11lnx aF x x x =--+.（Ⅰ）设函数()()()1h x x F x =-，当2a =时，证明：当1x >时，()0h x >；（Ⅱ）若()0F x >恒成立，求实数a 取值范围；（Ⅲ）若a 使()F x 有两个不同的零点12,x x，证明：21a a x x e e -<-<-.的南开中学2024届高三第一次月检测数学学科试卷考试时间：120分钟本试卷分第Ⅰ卷（选择题）和第Ⅱ卷两部分，共150分.考试结束后，请交回答题卡.第Ｉ卷一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求的．）1. 已知集合{}2|230A x x x =-->，{}1,2,3,4B =，则()A B ⋂=Rð（）A. {}1,2 B. {}1,2,3 C. {}3,4 D. {}4【答案】B 【解析】【分析】首先解一元二次不等式求出集合A ，再根据补集、交集的定义计算可得.【详解】由2230x x -->，即()()130x x +->，解得3x >或1x <-，所以{}2|230{|1A x x x x x =-->=<-或3}x >，所以{}|13A x x =-≤≤R ð，又{}1,2,3,4B =，所以(){}1,2,3A B ⋂=R ð.故选：B2. “sin 0x =”是“cos 1x =”的（ ）A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件【答案】C 【解析】【分析】根据充分性和必要性的定义结合同角三角函数的关系即可得出结论.【详解】解：因为sin 0x =，根据三角函数的基本关系式，可得cos 1x ==±，反之：若cos 1x =，根据三角函数的基本关系式，可得sin 0x ==，所以“sin 0x =”是“cos 1x =”的必要不充分条件.故选：C.3. 函数()||sin 2f x x x =的部分图象可能是（ ）A. B. C. D.【答案】C 【解析】【分析】根据()f x 是奇函数，排除B ，再取特殊值验证.【详解】因为()()||sin 2||sin 2()f x x x x x f x -=--=-=-所以()f x 是奇函数，排除B ，由02f ⎛⎫= ⎪⎝⎭π，排除A ，由44f ππ⎛⎫= ⎪⎝⎭，排除D ．故选：C ．【点睛】本题主要考查函数的图象和性质，还考查了数形结合的思想和理解辨析的能力，属于基础题.4. 下列函数中，是奇函数且在()0,∞+上单调递减的是（ ）A. 2y = B. sin x y x=C. )lg2y x=- D. e e 2x xy --=【答案】C 【解析】【分析】根据奇偶性定义、对数函数、指数函数单调性，结合复合函数的单调性依次判断各个选项即可.【详解】A 选项：()()2f x f x -==，不是奇函数，故A 选项错误；B 选项：()()()sin sin sin x x xf x f x x x x---====--，不是奇函数，故B 选项错误；C 选项：因为()f x 的定义域为R ，且()()))()22lg 2lg2lg 414lg10f x f x x x x x -+=++=+-==，∴()f x 是奇函数．设2t x ==因为t =()0,∞+上单调递减，lg y t =在()0,∞+上单调递增，由复合函数单调性知，()f x 在()0,∞+上单调递减，故C 选项正确；D 选项：()11e 2e x xf x ⎛⎫=- ⎪⎝⎭，因为1e e ,xxy y ==-在()0,∞+上都单调递增，所以()f x 在()0,∞+上单调递增，故D 选项错误，故选：C ．5. 计算：0ln 228241.1e log 1lg10ln e log +-+++的值（ ）A. 0B.152C. 2D. 3【答案】B 【解析】【分析】根据指数及对数的运算法则计算可得；【详解】0ln 222423151.1e log 1lg10ln e log 812012log 222+-+++=+-+++=.故选：B6. 已知1sin 3a =，0.913b ⎛⎫= ⎪⎝⎭，271log 92c =，则（ ）A. a c b <<B. a b c <<C. b a c <<D. c a b<<【答案】A 【解析】【分析】化简得13c =，构造函数()sin ,0,2πf x x x x ⎛⎫=-∈ ⎪⎝⎭，通过导数可证得sin ,0,2πx x x ⎛⎫<∈ ⎪⎝⎭，可得a c <，而0.91133b c ⎛⎫=>= ⎪⎝⎭，从而可得答案．【详解】2711lg 912lg 31log 922lg 2723lg 33c ==⨯=⨯=.设()sin ,0,2πf x x x x ⎛⎫=-∈ ⎪⎝⎭，则有()cos 10f x x '=-<，()f x 单调递减，从而()(0)0f x f <=，所以sin ,0,2πx x x ⎛⎫<∈ ⎪⎝⎭，故11sin 33<，即a c <，而0.91133b c ⎛⎫=>= ⎪⎝⎭，故有a c b <<．故选：A ．7.π2cos63αα⎛⎫--=⎪⎝⎭，则πsin26α⎛⎫-=⎪⎝⎭（）A.19- B.19C.13D.89【答案】A【解析】【分析】利用三角恒等变换化简已知条件，结合诱导公式、二倍角公式求得正确答案.π2cos63αα⎛⎫--=⎪⎝⎭，12sin cos23ααα⎫+-=⎪⎪⎭，1π2cos sin263ααα⎛⎫+=+=⎪⎝⎭.πππsin2cos2626αα⎡⎤⎛⎫⎛⎫-=--⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦2ππcos2cosπ233αα⎡⎤⎛⎫⎛⎫=-=-+⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦2ππcos22sin136αα⎛⎫⎛⎫=-+=+-⎪ ⎪⎝⎭⎝⎭2212139⎛⎫=⨯-=-⎪⎝⎭.故选：A8. 将函数()π3sin26f x x⎛⎫=+⎪⎝⎭的图象向右平移π6个单位长度后，所得图象对应的函数为()y g x=，有下列命题：①函数()g x的图象关于直线πx=对称②函数()g x的图象关于点π,012⎛⎫⎪⎝⎭对称③函数()g x在π5π,2424⎡⎤-⎢⎥⎣⎦上单调递增④函数()g x 在[]0,2π上恰有5个极值点其中正确的命题个数为（ ）A. 1 B. 2C. 3D. 4【答案】B 【解析】【分析】根据函数图象平移变换的特点，利用正弦弦函数的对称性、单调性、最值，结合函数的极值点定义逐项判断即可求解.【详解】函数()π3sin 26f x x ⎛⎫=+⎪⎝⎭的图象向右平移π6个单位长度后，所得图象对应的函数为()πππ3sin 23sin 2666y g x x x ⎡⎤⎛⎫⎛⎫==-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，对于①，当πx =时，()π3π3sin 2π62g ⎛⎫=-=- ⎪⎝⎭，不是函数()y g x =的最值，故①错误；对于②，当π12x =时，πππ3sin 2012126g ⎛⎫⎛⎫=⨯-= ⎪ ⎪⎝⎭⎝⎭，故②正确；对于③，当π5π,2424x ⎡⎤∈-⎢⎥⎣⎦时，πππ2,644x ⎡⎤-∈-⎢⎥⎣⎦，故函数在该区间上单调递增，故③正确；对于④，令(ππ2πZ 62x k k -=+∈，解得()ππZ 23k x k =+∈，当0,1,2,3k =时，π5π4π11π,,,3636x =，在[]0,2π上有4个极值点，故④错误．故选：B.9. 设函数ln 2,0()π1sin ,π042x x x f x x x ω⎧+->⎪=⎨⎛⎫+--≤≤ ⎪⎪⎝⎭⎩有7个不同的零点，则正实数ω的取值范围为（ ）A. 131744⎡⎫⎪⎢⎣⎭， B. 172144⎡⎫⎪⎢⎣⎭， C. 49121652⎡⎫⎪⎢⎣⎭， D. 65121732⎡⎫⎪⎢⎣⎭，【答案】C 【解析】【分析】分段函数分段处理，在1x >，01x <<各有1个零点，所以π0x -≤≤有5个零点，利用三角函数求出所有的零点，保证π0x -≤≤之间有5个零点即可.【详解】由题，当1x ≥时，()ln 2f x x x =+-，显然()f x 在()1,+∞上单调递增，且()110f =-<，()22ln 220f =+->，此时()f x 在()1,+∞在有一个零点；当01x <<时，()ln 2f x x x =--，1()10f x x'=-<，所以()f x 在()0,1上单调递减，2211()220e ef =+->，此时()f x 在()0,1上只有一个零点；所有当π0x -≤≤时，()π1sin 42f x x ω⎛⎫+- ⎪⎝⎭=有5个零点，令()0f x =，则π1sin 42x ω⎛⎫+= ⎪⎝⎭，即ππ2π46x k ω+=+，或π5π2π46x k ω+=+，k ∈Z ，解得π2π12k x ω-+=，或7π2π12k x ω-+=，k ∈Z ，当0k =时，12π7π1212,x x ωω--==；当1k =时，34π7π2π2π1212,x x ωω----==；当2k =时，56π7π4π4π1212,x x ωω----==；由题可得π0x -≤≤区间内的5个零点，即π4π12π7π4π12πωω⎧--⎪≥-⎪⎪⎨⎪--⎪<-⎪⎩，解得54912126ω≤<，即49651212ω⎡⎫∈⎪⎢⎣⎭，.故选：C.【点睛】分段函数的零点问题点睛：根据函数的特点分别考虑函数在每段区间上的单调性，结合零点存在性定理，得到每一段区间上的零点的个数，从而得出函数在定义域内的零点个数.第II 卷二、填空题（本大题共6小题，每小题5分，共30分．）10. 已知i 是虚数单位，化简32i12i-+的结果为____________．【答案】18i 55--【解析】分析】运用复数运算法则计算即可.【【详解】2232i (32i)(12i)36i 2i 4i 38i 418i 12i (12i)(12i)14i 1455-----+--====--++--+.故答案为：18i 55--.11.在代数式521x ⎫-⎪⎭的展开式中，常数项为_____________．【答案】-5【解析】【分析】写出二项式定理的通项，化简后，使得x 的指数幂为0，即可求得k 的值.【详解】521x ⎫-⎪⎭的展开式的通项为：()51552215521C C 1rrrr r r r T x x x --+⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭令5502r -=，解得1r =，所以()11215C 15T +=-=-，521x ⎫⎪⎭的展开式中的常数项为5-.故答案为：-512. 函数()()ππ2sin 0,22f x x ωϕωϕ⎛⎫=+>-<< ⎪⎝⎭的部分图象如图所示，则π=3f ⎛⎫⎪⎝⎭__________．【解析】【分析】根据函数()f x 的图象结合正弦函数的图象及性质，求得函数的解析式，再代入求值即可.【详解】由函数()f x 的图象可知，35ππ3π41234T ⎛⎫=--= ⎪⎝⎭，则2π=πT ω=，2ω=.把5π12x =代入()f x ，则5ππ22π122k ϕ⨯+=+，而ππ22ϕ-<<，所以π3ϕ=-，所以()π2sin 23f x x ⎛⎫=- ⎪⎝⎭，所以ππππ=2sin 22sin 3333f ⎛⎫⎛⎫⨯-==⎪ ⎪⎝⎭⎝⎭.13. 在亚运会女子十米跳台决赛颁奖礼上，五星红旗冉冉升起，在坡度15 的看台上，同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60 和30 ，第一排A 点和最后一排E 点的距离为（如图所示），则旗杆的高度为____________米．【答案】27【解析】【分析】根据已知可得30ECA ∠= ，在EAC 中由正弦定理可得AC ，再利用t ABC R 中计算可得答案.【详解】由图可得3609012012030∠=---= ECA ，在EAC sin 30= EA，即sin 452sin 30===EA AC ，在t ABC R 中，60CAB ∠= ，可得sin 6027=⨯== BC AC 米.故答案为：27.14. 已知定义在[)0+∞，上的函数()f x ，当[0,2)x ∈时，()()1611f x x =--，且对任意的实数1[2222)n n x +∈--，（*2N n n ∈，≥），都有()1122x f x f ⎛⎫=- ⎪⎝⎭，若函数()()log a g x f x x =-有且仅有五个零点，则a 的取值范围__________.【答案】1410⎛ ⎝【解析】【分析】写出()f x 的解析式并画出()f x 的图象，结合已知条件将问题转化为()y f x =图象与log a y x =图象在(0,)+∞上有且仅有5个交点，结合图象分析即可求得结果.【详解】当[0,2)x ∈，()16(1|1|)f x x =--，当2n =时，[2,6)x ∈，此时1[0,2)2x -∈，则11()(1)16(1|2|)8(1|2|)22222x x xf x f =-=⨯--=--，当3n =时，[6,14)x ∈，此时1[2,6)2x -∈，则1155()(1)8(1||)4(1||)2224242x x x f x f =-=⨯--=--，当4n =时，[14,30)x ∈，此时1[6,14)2x-∈，则111111()(1)4(1||)2(1||)2228484x x x f x f =-=⨯--=--，……因为()()log a g x f x x =-有且仅有5个零点，所以()y f x =图象与log a y x =图象在(0,)+∞上有且仅有5个交点，如图所示，由图可知，当log a y x =经过点(10,4)A 时，两函数图象有4个交点，经过点(22,2)B 时，两函数图象有6个交点，所以当()y f x =图象与log a y x =图象在(0,)+∞上有且仅有5个交点时，则1log 104log 222a aa >⎧⎪<⎨⎪>⎩，解得1410a <<.故答案为：1410（.15. 记()ln f x x ax b =++（0a >）在区间[],2t t +（t 为正数）上的最大值为(),t M a b ，若{|(,)ln 3}R t b M a b a ≥+=，则实数t 的最大值为__________.【答案】14##0.25【解析】【分析】由函数单调性性质及图象变换可画出()f x 的图象，进而可得(,)()t M a b f t ≥，结合已知条件可知只需()ln 3f t a ≥+，即(ln )ln 3t at b a -++≥+，由()(2)f t f t =+可得ln(2)ln 2(1)2t t a t b ++++=-，联立两者进而可求得结果.【详解】设()ln g x x ax b =++，（0a >），定义域为(0,)+∞，由单调性性质可知，()g x 在(0,)+∞上单调递增，当x 趋近于0时，()g x 趋近于-∞；当x 趋近于+∞时，()g x 趋近于+∞，设0()0g x =，则()g x 的图象如图所示，所以()f x 的图象如图所示，则由图象可知，{}max (),()(2)()(,)max (),(2)(2),()(2)t f t f t f t f x M a b f t f t f t f t f t ≥+⎧==+=⎨+<+⎩，所以(,)()t M a b f t ≥，如图所示，当()(2)f t f t =+时，有(ln )ln(2)(2)t at b t a t b -++=++++，则ln(2)ln 2(1)2t t a t b ++++=-，①又因为{|(,)ln 3}R t b M a b a ≥+=，所以()ln 3f t a ≥+，即(ln )ln 3t at b a -++≥+，所以ln ln 3b t at a ≤----，②由①②得ln(2)ln 2(1)ln ln 32t t a t t at a ++++≤-----，整理得ln(2)ln 2ln 3ln 9t t t +≥+=，即29t t +≥，所以14t ≤.故t 的最大值为14.故答案为：14【点睛】恒成立问题解题方法指导：方法1：分离参数法求最值.(1)分离变量．构造函数，直接把问题转化为函数的最值问题．(2)()a f x ≥恒成立⇔max ()a f x ≥；()a f x ≤恒成立⇔min ()a f x ≤；()a f x ≥能成立⇔min ()a f x ≥；()a f x ≤能成立⇔max ()a f x ≤.方法2：根据不等式恒成立构造函数转化成求函数的最值问题，一般需讨论参数范围，借助函数单调性求解．三、解答题（本大题共5小题，共75分．解答应写出文字说明，证明过程或演算步骤．）16. 已知函数()()2π2sin πcos 2f x x x x ⎛⎫=+-+-⎪⎝⎭（1）求()f x 的最小正周期及对称轴方程；（2）当ππ,42x ⎡⎤∈⎢⎥⎣⎦时，求()f x 的最大值和最小值.【答案】（1）πT =，()5ππ122k x k =+∈Z （2）min 1y =，max 2y =.【解析】【分析】（1）根据诱导公式以及二倍角公式化简，再根据周期公式、对称轴公式进行求解；（2）由x 的取值范围求出整体角的取值范围，再结合正弦型函数图像及性质得出结果.【小问1详解】()()2πcos 2sin πcos 2f x x x x ⎤⎛⎫=+-+⋅ ⎪⎥⎝⎭⎦)22sin cos 1cos2sin2x x x x x =+⋅=-+sin22sin 23x x x π⎛⎫=-=- ⎪⎝⎭，故周期为2ππ2T ==，令2π,32x k k ππ-=+∈Z ，解得()5ππ122k x k =+∈Z ，对称轴方程()5ππ122k x k =+∈Z ，【小问2详解】()2sin 23f x x π⎛⎫=- ⎪⎝⎭∵ππ42x ≤≤，∴ππ2π2,363t x ⎡⎤=-∈⎢⎥⎣⎦，当π6t =时，即π4x =时，()min π1sin sin 62t ==，此时min 1y =，当π2t =时，即5π12x =时，()max πsin sin 12t ==，此时max 2y =.17. 在ABC 中，角,,A B C 所对的边分别为,,a b c ，其中2C π≠，已知cos 2cos cos b c A a B C -=.（1）求角B 的大小；（2）若223125b c ac +=-，求ABC 面积的最大值.【答案】（1）3π（2【解析】【分析】（1）根据正弦定理边化角或余弦定理化简原式，根据2C π≠，所以cos 0C ≠或2222a b c b+-≠，化简即可得出1cos 2B =，即可得出答案；（1）根据余弦定理结合第一问得出的角B 的大小得出222a c b ac +-=，结合已知223125b c ac +=-，得出224412a ac c ++=，根据基本不等式得出22412422a c ac a c +=-≥⋅⋅即32ac ≤，即可由三角形面积公式得出答案；或将224412a ac c ++=化简为2(2)12a c +=，由三角形面积公式结合基本不等式得出ABC 的面积212sin 222a c S ac B c +⎫===⋅≤=⎪⎭，即可得出答案.【小问1详解】方法一：由cos 2cos cos b c A a B C -=根据正弦定理边化角得：sin sin cos 2sin cos cos B C A A B C -=，即()sin sin cos 2sin cos cos A C C A A B C +-=，所以sin cos 2sin cos cos A C A B C =，因为2C π≠，所以cos 0C ≠，又sin 0A >，所以1cos 2B =，又0πB <<，所以3B π=.方法二：由cos 2cos cos b c A a B C -=根据余弦定理：得2222222cos 22b c a a b c b c a B bc ab+-+--=⋅，即2222222cos 22b c a a b c B b b -++-=⋅，因为2C π≠，所以22202a b c b+-≠，所以1cos 2B =，又0πB <<，得3B π=.小问2详解】方法一：由（1）及余弦定理知2221cos 22a cb B ac +-==，所以222a c b ac +-=，因为223125b c ac +=-，所以()2221235a c c ac ac +---=，化简得224412a ac c ++=，因为0,0a c >>，所以22412422a c ac a c +=-≥⋅⋅，所以32ac ≤，当且仅当2a c ==a c ==时取等号，所以ABC的面积1sin 2S ac B ==≤，所以ABC方法二：由（1）及余弦定理知2221cos 22a cb B ac +-==，所以222a c b ac +-=.因为223125b c ac +=-，所以()2221235a c c ac ac +---=，化简得224412a ac c ++=，即2(2)12a c +=，所以ABC的面积212sin 222a c S ac B c +⎫===⋅≤=⎪⎭，【当且仅当2a c ==a c ==时取等号，所以ABC 18. 如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，AD AB ⊥，//AB DC ，2AD DC AP ===，1AB =，E 为棱PC 的中点.（1）证明：//BE 平面PAD ；（2）求直线BE 与平面PBD 所成角的正弦值；（3）求点D 到平面PBC 的距离.【答案】（1）证明见解析（2（3【解析】【分析】（1）以A 为原点建立空间直角坐标系，利用向量法证明线面平行；（2）求出平面PBD 的一个法向量，再由向量法求解；（3）求出平面PBC 的法向量()2111,,n x y z =，再由向量法求解.【小问1详解】解：以点A 为原点，AB ，AD ，AP 分别为x 轴，y 轴，z 轴，建立空间直角坐标系.可得()1,0,0B ，()2,2,0C ，()0,2,0D ，()002P ,,，由E 为棱PC 的中点，得()1,1,1E ，向量()0,1,1BE = ，()1,0,0AB =，故0BE AB ⋅= ，又AB为平面PAD 的一个法向量，又BE ⊄面PAD ，所以//BE 平面PAD .【小问2详解】向量()1,2,0BD =-，()1,0,2PB =- ，()0,1,1BE = 设(),,n x y z = 为平面PBD 的法向量，则0n BD n PB ⎧⋅=⎪⎨⋅=⎪⎩，即2020x y x z -+=⎧⎨-=⎩，令1y =，得()2,1,1n =为平面PBD 的一个法向量，所以cos ,n BE n BE n BE⋅===⋅所以直线BE 与平面PBD【小问3详解】向量()1,2,0BC = ，设平面PBC 的法向量()2111,,n x y z =，220n BC n PB ⎧⋅=⎪⎨⋅=⎪⎩，即11112020x y x z +=⎧⎨-=⎩，令11y =-，得()22,1,1n =- 为平面PBC 的一个法向量，则22BD n d n ⋅===.19. 已知椭圆()2222:10x y C a b a b +=>>，短轴长为..（1）求C 的方程；（2）如图，经过椭圆左顶点A 且斜率为()0k k ≠的直线l 与C 交于A ，B 两点，交y 轴于点E ，点P 为线段AB 的中点，若点E 关于x 轴的对称点为H ，过点E 作OP （O 为坐标原点）垂直的直线交直线AH 于点M ，且APM △，求k 的值.【答案】（1）22142x y += （2）【解析】【分析】（1）根据题意得出,a b 的值，进而可得结果；（2）设直线l 的方程为()2y k x =+，将其与椭圆方程联立，得出EM 斜率，联立方程组得出M 点的坐标，利用点到直线距离公式式，结合韦达定理以及三角形面积公式将面积表示为关于k 的方程，解出即可得结果.小问1详解】由题意可得2222c e a b a b c ⎧==⎪⎪⎪=⎨⎪=+⎪⎪⎩，解得2a =，b =，c =∴椭圆C 的方程为22142x y +=.【小问2详解】易知椭圆左顶点()2,0A -，设直线l 的方程为()2y k x =+，则()0,2E k ，()0,2H k -，由()222142y k x x y ⎧=+⎪⎨+=⎪⎩，消y 可得()2222128840k x k x k +++-=，设()11,A x y ，()22,B x y ，()00,P x y ，∴()()422644841216k k k ∆=--+=，【则有2122812k x x k +=-+，21228412k x x k-=+，∴()2012214212k x x x k =+=-+，()0022212=+=+k y k x k ，∴0012OP y k x k ==-，∴直线EM 的斜率2EM k k =，∴直线EM 的方程为22y kx k =+，直线AH 的方程为()2y k x =-+，∴点42,33M k ⎛⎫-- ⎪⎝⎭，∴点M 到直线:20l kx y k -+=的距离d =，∴AB ==∴1||2AP AB ==∴241132212APM k S AP d k =⋅=⨯==+△，解得k =.20. 已知函数()11lnx a F x x x =--+.（Ⅰ）设函数()()()1h x x F x =-，当2a =时，证明：当1x >时，()0h x >；（Ⅱ）若()0F x >恒成立，求实数a 的取值范围；（Ⅲ）若a 使()F x 有两个不同的零点12,x x ，证明：21a a x x e e -<-<-.【答案】（Ⅰ）证明见解析；（Ⅱ）2a ≤；（Ⅲ）证明见解析.【解析】分析】（Ⅰ）当2a =时对()h x 求导，证明1x >时，()0h x '>即可.（Ⅱ）设函数()()1ln 1a x f x x x -=-+，根据函数的单调性判断ln x 与()11a x x -+的关系，根据()0F x >恒成立，确定a 的取值范围；（Ⅲ）根据函数的单调性求出2121a a t t x x e e --<-<-，得到【21t t -==，证明结论成立即可.【详解】（Ⅰ）()()ln 111x a h x x x x ⎛⎫=--⎪-+⎝⎭当2a =时，()()()21ln 21ln 111x x h x x x x x x -⎛⎫=--=- ⎪-++⎝⎭()()()()()()()()2222221211111114x x x x h x x x x x x x x +---+-'=-==+++，当1x >时，()0h x '>，所以()h x 在()1,+∞上为单调递增函数，因为()10h =，所以()()10h x h >=，（Ⅱ）设函数()()1ln 1a x f x x x -=-+，则()()()222111x a x f x x x +-+'=+，令()()2211g x x a x =+-+，当1a ≤时，当0x >时，()0g x >，当12a <≤时，2480a a ∆=-≤，得()0g x ≥，所以当2a ≤时，()f x 在()0,∞+上为单调递增函数，且()10f =，所以有()101f x x >-，可得()0F x >．当2a >时，有2480a a ∆=->，此时()g x 有两个零点，设为12,t t ，且12t t <.又因为()12210t t a +=->，121t t =，所以1201t t <<<，在()21,t 上，()f x 为单调递减函数，所以此时有()0f x <，即()1ln 1a x x x -<+，得ln 011x a x x -<-+，此时()0F x >不恒成立，综上2a ≤．（Ⅲ）若()F x 有两个不同的零点12, x x ，不妨设12x x <，则12, x x 为()()1ln 1a x f x x x -=-+的两个零点，且11x ≠，21x ≠，由（Ⅱ）知此时2a >，并且()f x 在()10,t ，()2,t +∞为单调递增函数，在()12,t t 上为单调递减函数，且()10f =，所以()10f t >，()20f t <，因为()201a a a f e e -=-<+，()201aa a f e e =>+，1a a e e -<<，且()f x 图象连续不断，所以()11,a x e t -∈，()22,a x t e∈，所以2121a a t t x x e e--<-<-，因为21t t -==综上得:21||a a x x e e -<-<-.【点睛】方法点睛：求不等式恒成立问题的方法（1）分离参数法若不等式(),0f x λ≥()x D ∈（λ是实参数）恒成立，将(),0f x λ≥转化为()g x λ≥或()()g x x D λ≤∈恒成立，进而转化为()max g x λ≥或()()min g x x D λ≤∈，求()g x 的最值即可.（2）数形结合法结合函数图象将问题转化为函数图象的对称轴、区间端点的函数值或函数图象的位置关系（相对于x 轴）求解.此外，若涉及的不等式转化为一元二次不等式，可结合相应一元二次方程根的分布解决问题.（3）主参换位法把变元与参数变换位置，构造以参数为变量的函数，根据原变量的取值范围列式求解，一般情况下条件给出谁的范围，就看成关于谁的函数，利用函数的单调性求解.。

天津市南开中学创新人才早期培养实验班招生考试数学仿真模拟测试卷（2）同学们好! 答题前请注意:1.数学测试试卷共3页,考试时间为90分钟。

2.请用蓝色、黑色水笔或圆珠笔将答案写在答题纸的相应位置。

1.设a△2b a a b=⨯-⨯，那么，5△6=______，(5△2) △3=_____.2251251251251251 4881212162000200420042008+++++⨯⨯⨯⨯⨯=_______3.计算：2349899123 (9798)345991001239798357 (195197)34599100+++++=+++++．4.一个正方体容器，容器内部边长为24厘米，存有若干水，水深17.2厘米，现将一些碎铁块放入容器中，铁块沉入水底，水面上升2.5厘米，如果将这些铁块铸成一个和容器等高的实心圆柱，重新放入池中，则水面升高_______厘米.5.甲、乙、丙三个班的学生一起去郊外活动，他们租了一辆大巴，但大巴只够一个班的学生坐，于是他们计划先让甲班的学生步行，乙丙两班的学生步行，甲班学生搭乘大巴一段路后，下车步行，然后大巴车回头去接乙班学生，并追赶上步行的甲班学生，再回头载上丙班学生后一直驶到终点，此时甲、乙两班也恰好赶到终点，已知学生步行的速度为5千米/小时，大巴车的行驶速度为55千米/小时，出发地到终点之间的距离为8千米，这些学生到达终点一共所花的时间是_______小时.6.一个水箱有甲、乙、丙三根进水管，如果只打开甲、丙两管，甲管注入30吨水时，水箱已满；如果只打开乙、丙两管，乙管注入40吨水时，水箱才满．已知乙管每分钟注水量是甲管的1.5倍，则该水箱注满时可容纳吨水．7.一条单线铁路上有A ，B ，C ，D ，E 五个车站，它们之间的路程如下图所示（单位：千米）。

甲、乙两列火车分别从A ，E 两站相对开出，甲车先开4分，每时行60千米，乙车每时行50千米，两车只能在车站停车，互相让道错车。

南开中学试题及答案一、单项选择题（每题2分，共10分）1. 下列关于南开中学的描述，哪一项是不正确的？A. 南开中学是中国著名的中学之一B. 南开中学位于天津市C. 南开中学成立于20世纪初D. 南开中学的校训是“自强不息，厚德载物”答案：D2. 南开中学的创始人是：A. 张伯苓B. 蔡元培C. 梁启超D. 胡适答案：A3. 南开中学的校徽颜色是：A. 蓝色B. 绿色C. 红色D. 黄色答案：A4. 南开中学的校歌名称是：A. 《南开之歌》B. 《南开校歌》C. 《南开颂》D. 《南开精神》答案：B5. 南开中学的教育理念是：A. 德智体美劳全面发展B. 以学生为中心C. 培养创新精神和实践能力D. 以上都是答案：D二、填空题（每题2分，共10分）1. 南开中学的校训是“________”。

答案：允公允能，日新月异2. 南开中学的校庆日是每年的________月________日。

答案：10月17日3. 南开中学的校园内有一个著名的景点，名为________。

答案：南开园4. 南开中学的校旗颜色是________和________。

答案：蓝色和白色5. 南开中学的校歌由________作词，________作曲。

答案：张伯苓，萧友梅三、简答题（每题5分，共20分）1. 请简述南开中学的发展历程。

答案：南开中学始建于1904年，由张伯苓先生创办，是中国近代教育史上具有重要影响的中学之一。

学校秉承“允公允能，日新月异”的校训，培养了大批优秀人才。

2. 南开中学的教育理念是什么？答案：南开中学的教育理念是“德智体美劳全面发展”，强调学生在道德、智力、体育、美育和劳动教育方面的均衡发展。

3. 南开中学的校歌有什么特殊意义？答案：南开中学的校歌《南开校歌》由张伯苓作词，萧友梅作曲，歌词中体现了南开精神和教育理念，是学校文化的重要组成部分。

4. 南开中学的校园文化有哪些特色？答案：南开中学的校园文化特色包括丰富的历史传统、浓厚的学术氛围、多样的社团活动和积极的社会实践，这些都为学生提供了全面发展的平台。

选择题下列哪个数集是有限集？A. 所有正整数的集合B. 所有负偶数的集合C. 小于100的正质数的集合（正确答案）D. 所有实数的集合在平面直角坐标系中，点A(3,4)关于x轴对称的点的坐标是？A. (-3,4)B. (3,-4)（正确答案）C. (-3,-4)D. (4,3)已知等差数列{an}的首项为a1，公差为d，若a3 = 7，a5 = 11，则a7等于？A. 13B. 14C. 15（正确答案）D. 16函数f(x) = x2 - 4x + 5的最小值出现在x等于？A. -2B. 0C. 2（正确答案）D. 4下列哪个不等式组无解？A. { x > 2, x < 5 }B. { x ≤ -1, x ≥ 1 }（正确答案）C. { x < -3, x > -5 }D. { x ≥ 0, x ≤ 10 }已知三角形ABC的三边长为a, b, c，且满足a2 + b2 = c2 + 2ab，则三角形ABC是？A. 锐角三角形B. 直角三角形（正确答案）C. 钝角三角形D. 等边三角形若复数z = 2 + 3i，则z的共轭复数乘以z的模等于？A. 5 + 3iB. 3 - 2iC. √13(2 - 3i)（正确答案，模为√13，共轭复数为2 - 3i）D. 13i下列哪个函数是奇函数？A. f(x) = x2 + 1B. f(x) = sin(x)cos(x)C. f(x) = x3 - x（正确答案）D. f(x) = ex + e(-x)已知圆C的方程为(x - 2)2 + (y - 3)2 = 16，则圆心C到直线l: 3x - 4y + 5 = 0的距离为？A. 3B. 4（正确答案）C. 5D. 6。

2025届天津市南开区南开中学高三3月份第一次模拟考试数学试卷注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．等差数列{}n a 的前n 项和为n S ，若13a =，535S =，则数列{}n a 的公差为（ ） A ．-2B ．2C ．4D ．72．在一个数列中，如果*n N ∀∈，都有12n n n a a a k ++=（k 为常数），那么这个数列叫做等积数列，k 叫做这个数列的公积.已知数列{}n a 是等积数列，且11a =，22a =，公积为8，则122020a a a ++⋅⋅⋅+=（ ） A ．4711B ．4712C ．4713D ．47153．如图，圆锥底面半径为2，体积为223π，AB 、CD 是底面圆O 的两条互相垂直的直径，E 是母线PB 的中点，已知过CD 与E 的平面与圆锥侧面的交线是以E 为顶点的抛物线的一部分，则该抛物线的焦点到圆锥顶点P 的距离等于（ ）A ．12B ．1C ．104D 5 4．将函数()cos f x x =的图象先向右平移56π个单位长度，在把所得函数图象的横坐标变为原来的1ω(0)>ω倍，纵坐标不变，得到函数()g x 的图象，若函数()g x 在3(,)22ππ上没有零点，则ω的取值范围是（ ） A ．228(0,][,]939 B ．2(0,]9C ．28(0,][,1]99D ．(0,1]5．函数sin y x x =+在[]2,2x ππ∈-上的大致图象是（ ）A ．B ．C ．D ．6．在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测． 甲：我的成绩比乙高．乙：丙的成绩比我和甲的都高． 丙：我的成绩比乙高．成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为 A ．甲、乙、丙 B ．乙、甲、丙 C ．丙、乙、甲D ．甲、丙、乙7．已知函数3(1),1()ln ,1x x f x x x ⎧-≤=⎨>⎩，若()()f a f b >，则下列不等关系正确的是（ ）A ．221111a b <++ B ．33a b >C ．2a ab <D ．()()22ln 1ln 1a b +>+8．袋中装有标号为1，2，3，4，5，6且大小相同的6个小球，从袋子中一次性摸出两个球，记下号码并放回，如果两个号码的和是3的倍数，则获奖，若有5人参与摸球，则恰好2人获奖的概率是（ ） A ．40243B ．70243C ．80243D ．382439．已知函数()(N )k f x k x+=∈，ln 1()1x g x x +=-，若对任意的1c >，存在实数,a b 满足0a b c <<<，使得()()()g a f b g c ==，则k 的最大值是( )A ．3B ．2C ．4D ．510．如图，在中，点M 是边的中点，将沿着AM 翻折成，且点不在平面内，点是线段上一点.若二面角与二面角的平面角相等，则直线经过的（ ）A ．重心B ．垂心C ．内心D ．外心11．已知正方体1111ABCD A B C D -的棱长为2，点M 为棱1DD 的中点，则平面ACM 截该正方体的内切球所得截面面积为（ ） A ．3π B ．23π C ．πD ．43π 12．已知函数()f x 的导函数为()f x '，记()()1f x f x '=，()()21f x f x '=，…，()()1n n f x f x +'=(n ∈N *). 若()sin f x x x =，则()()20192021f x f x += （ ）A ．2cos x -B ．2sin x -C ．2cos xD ．2sin x二、填空题：本题共4小题，每小题5分，共20分。

专题六南开中学小卷2010年能力测试数学试卷1、有一位老师和两位学生，他们要去博物馆，老师只有一辆摩托车，一辆摩托车可承载一名学生。

全程33千米，摩托车载人时时速为20km/h，空载时为25km/h，步行速度为5km/h。

怎样才能到达博物馆不超过3小时？请设计一个方案。

2、有一个400米的环形跑道，甲乙分别从同一点出发，背向而行，甲速2m/s，乙速3m/s，6秒之后，一只小狗以6m/s的速度从任意一点出发向甲跑去，遇到乙返回迎甲，遇到甲返回迎乙，直到甲乙相遇。

问狗跑多少米？3、如图，E为A,D中点，AF=2FB，问阴影部分占总面积的多少？4、若干个大小相同的正五边形如图排成环状，图中所示的只是三个五边形。

那么要完成这一圈一共需要＿＿＿＿＿＿个五边形。

5、888、518、666三个吉利数除以一个数余数分别得a、a+7、a+10。

问除的数是＿＿＿＿＿6、有一批图书总数在1000本以内，若按24本书包成一捆，则最后一捆差2本；若按28本书包成一捆，则最后一捆还是差2本；若按32本书包一捆，则最后一捆是30本。

那么这批图书共有（）本。

7、十个同心圆，任意两个相邻的同心圆半径之差等于里面最小圆的半径。

如果射击时命中，那么最里面的小圆得10环，命中最外面的圆环得1环，得1环圆环的面积是10环圆面积的＿＿＿＿＿倍。

8、一些人在开讨论会，在会议开始后10分钟时大钟开始报时（1点报一下、2点报两下…），会议结束时，大钟共报14，且此时分针和时针成90度角。

会议在几点几分开始，几点几分结束。

9、学校买45个文具盒，每个9元。

文具店规定，凡购物满100元可优惠10元，满200元优惠20元，满300元优惠30元……以此类推。

学校买回的45个文具盒，每个可少花多少钱？（得数保留两位小数）10、汽车和自行车分别从A、B两地同时相向而行，汽车每小时行50千米，自行车每小时行10千米，两车相遇后，各自仍沿原方向行驶，当汽车到达B地后返回到两车相遇地时，自行车在前面10千米处正向A地行驶，求A、B两地距离。

天津南开中学中考小卷
天津南开中学中考小卷指的是南开中学针对中考的一种特殊考试形式。

通常来说，中考小卷的难度和要求相对于正式的中考来说更高，因为它旨在筛选出具有更高等级学科潜力和综合能力的考生。

在南开中学的中考小卷中，可能会出现一些特别有挑战性的题目，旨在测试学生的学科能力和思维水平。

以下是天津南开中学中考小卷试题示例：
1.阅读以下材料，然后回答问题：
材料：一项研究显示，在过去的十年中，全球气候变暖的速度正在加快。

科学家们认为，人类活动是导致气候变暖的主要原因。

问题：请简述全球气候变暖的主要原因是什么？
答案：人类活动是导致全球气候变暖的主要原因。

2.计算题：已知地球的半径为6371公里，现在我们要计算地球的表面积。

请
写出计算过程和结果。

答案：地球的表面积约为5100万平方公里。

一、听力（计25分）A）听对话，选择正确的答语（听两遍）（共10小题；每题1分，计10分）听第1段对话，回答第1-2小题。

()?听第2段对话，回答第3-4小题。

()?听第3段对话，回答第5-7小题。

()’sbook?,听第4段对话，回答第8-10小题。

()?,gototheendofthestreet.,walkonuntiltheendofthestreet.,gotothethirdcrossing.()?’）听句子，从A、B、C三个选项中选择一个与你所听到的句子意思最接近的选项，每个句子听两遍。

（共5小题；每小题1分，计5分）( ) ’saquarterpastone.’soneforty-five.( ) ’tinteresting..( ) ..( ) ..( ) ..C）听短文，从所给的选项中选出最佳答案（听三遍）。

（共10小题；每小题1分，计10分）听第1段材料，回答第16-20小题。

()?...()?,听第2段材料，回答第21-25小题。

()?..()?’二、单项选择（共15小题；每小题1分，计15分）在下列各题A、B、C、D四个选项中选择一个能填入题干空白处的最佳答案。

()’tthink_________rainthisafternoon.’’’’sgoingto().,,,,yet(),myfatherwasreading.三、完形填空（共10小题；每小题1分，计10分）,’(童子军),,andwhile__3__wentintotheirsleepingbagsforthenight,theywerenothappy tosnuggle(紧偎)insideadoublesleepingbagtheirmothermadeforthem.Atschooltheirclassmates____4____themBlackOneandBlackTwo,sopeoplecoul dn’tevenseetheirdifferenceaccordingtotheirinitials（第一个字母）身份).Beforehewenttocollege,duringhislastsecondaryschool____6____,hegotaj obonabuildingsite(地点).Histwinbrother,MikeBlack,didn’工头),“CanIhaveaweekoff?”“Certainly,”theforemansaid,“butyouwon’thav ethejobwhenyou____7____back.”,Martindidn’,MikewentdowninMartin’sjean s,.NowMartinisgrowingoldandhefeelsverydifferent___10__histwinbrother.()()()()()()()()()四、阅读理解（共15小题；每小题2分，计30分）阅读下列短文，从文后各题所给的四个选项中选出最佳答案。

天津市南开中学小卷考题1. 任务背景天津市南开中学是一所位于天津市南开区的知名中学，以其严谨的教学方法和优秀的教师队伍而闻名。

每年，该校都会组织小卷考试，以检验学生对各个学科知识的掌握情况。

2. 考试内容小卷考题通常涵盖以下几个学科：语文、数学、英语、物理、化学、生物、历史和地理。

每个科目都有若干道选择题和解答题。

2.1 语文语文部分主要测试学生对文字理解和写作能力的掌握。

选择题涉及诗词鉴赏、古代文言文阅读等方面。

解答题则要求学生根据所给材料进行文章写作或阅读理解。

2.2 数学数学部分主要测试学生对基本数学概念和计算方法的掌握。

选择题涉及代数、几何和概率等方面。

解答题则要求学生灵活运用所学知识解决实际问题。

2.3 英语英语部分主要测试学生对英语语法和词汇的理解能力。

选择题涉及单词拼写、语法填空等方面。

解答题则要求学生根据所给材料进行听力、阅读和写作。

2.4 物理物理部分主要测试学生对物理基本概念和实验方法的掌握。

选择题涉及力学、热学和光学等方面。

解答题则要求学生运用所学知识解决物理问题。

2.5 化学化学部分主要测试学生对化学元素和化合物的了解。

选择题涉及元素周期表、化合反应等方面。

解答题则要求学生分析实验数据或进行化学计算。

2.6 生物生物部分主要测试学生对生命科学的掌握情况。

选择题涉及细胞结构、遗传规律等方面。

解答题则要求学生根据所给材料进行实验设计或问题回答。

2.7 历史历史部分主要测试学生对历史事件和人物的了解。

选择题涉及中国历史和世界历史等方面。

解答题则要求学生根据所给材料进行历史事件分析或论述。

2.8 地理地理部分主要测试学生对地球表面和人文地理的认识。

选择题涉及地理知识和地图阅读等方面。

解答题则要求学生根据所给材料进行地理问题解答或分析。

3. 考试安排小卷考试一般在一个上午或下午进行，具体时间根据学校安排而定。

每个科目的考试时间为40分钟，其中选择题占30分钟，解答题占10分钟。

4. 考试评分考试结束后，老师会对学生的答卷进行评分。

天津市南开中学小升初数学期末试卷达标检测卷（Word版含解析）一、选择题1．一个长6cm、宽4cm、高12cm的牛奶盒装满牛奶，明明不小心洒了一些（图中空白部分），洒出（）mL牛奶。

（纸盒厚度忽略不计）A．36 B．72 C．1442．已知一个半圆的半径是r，计算它的周长，正确的算式为( )．A．r+2r B．2r+r C．r+r D．2r+2r3．在一个三角形中，三个内角的度数的比是1∶3∶5，这个三角形是（）。

A．锐角三角形B．直角三角形C．钝角三角形4．用5千克棉花的16和1千克铁的56相比较，结果是（）．A．5千克棉花的16重B．1千克铁的56重C．一样重D．无法比较5．从前面、右面和上面观察下面的三个物体，从（）看到的图形不同．A．前面B．右面C．上面6．一项工程，甲队单独做需要10天完成，乙队单独做需要12天完成。

下面说法有错误的是（）。

A．甲每天可以完成这项工程的110B．两队合作每天可以完成这项工程的11 1012C．甲的工作效率比乙的工作效率低D．甲乙两队合作一共需要60 11天7．圆锥和圆柱底面积相等，体积的比是1∶4，如果圆锥的高是2.4厘米，那么圆柱高是（）。

A．9.6厘米B．3.2厘米C．0.6厘米D．4.2厘米8．某地今年九月份有13是阴天，雨天不超过8天，剩下的是晴天，天数最多的是（）。

A．晴天B．阴天C．雨天D．无法计算9．观察下面的点阵图形，根据圆点的变化，探究其规律，则第8个图形中圆点的个数为（）．A．25 B．26 C．27 D．29二、填空题10．我国香港特别行政区的总面积是十一亿零六百三十四万平方米，横线上的数写作（________），省略亿位后面的尾数约是（________）亿。

11．（ ）÷（ ）＝0.6＝()15 ＝24∶（ ）＝（ ）%。

12．40吨比50吨少（________）%；（________）吨比50吨多20%。

13．如图，把一个圆转化成一个近似的长方形，周长增加了6厘米，这个圆的面积是（________）平方厘米。