当前位置：文档之家 › 第10章含有耦合电感的电路-邵阳学院

第10章含有耦合电感的电路-邵阳学院

  • 格式：doc
  • 大小：525.00 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

10章 含有耦合电感的电路

10章 含有耦合电感的电路

jω L2 (支路 支路3)L ± 同侧取 同侧取“ 支路 3=±M(同侧取“＋”,异 异
R2
侧取“ 侧取“－”) (支路 1’=L1 m M，M前所取符 支路1)L 支路 ， 前所取符 号与L 号与 3中的相反 (支路 2’=L2 m M，M前所取 支路2)L 支路 ， 前所取 符号与L 符号与 3中的相反
反相串联无互感等效电路
R1 u1 u M L1 R1 L1-M u1 R2 u2 L2 u R2 L2-M u2
Z = Z1 + Z 2 = R1 + R2 + jω ( L1 + L2 − 2 M )
R1
L1 u1
2、顺向串联 、 每一耦合电感支路的阻抗为： 每一耦合电感支路的阻抗为：
Z1 = R1 + jω ( L1 + M )
两个耦合线圈的磁通链可表示为： 两个耦合线圈的磁通链可表示为：
ψ 1 = ψ 11 ± ψ 12
= L1i1±Mi2
ψ 2 = ±ψ 21 + ψ 22
= ±Mi1+L2i2 上式表明， 上式表明 ， 耦合线圈中的磁通链与施感电流 线性关系 关系， 成 线性 关系 ， 是各施感电流独立产生的磁通链叠 加的结果。 加的结果。
di di u2 = R2i + ( L2 −M ) dt dt di = R2i + ( L2 − M ) dt
无互感等效电路
R1 u1 u M L1 R1 L1-M u1 R2 u2 L2 u R2 L2-M u2
di u = u1 + u 2 = ( R1 + R2 )i + ( L1 + L2 − 2 M ) dt
L1 N1 L2 N2

PP10 含有耦合电感的电路

PP10 含有耦合电感的电路

& & U = − jω M I 3 + [R1 + jω (L1 + M )] I1 & （去耦等效电路相量关系） & & & U = − jω M I 3 + [R2 + jω (L2 + M )] I 2
⇒ L1 = L1 + M , L2 = L2 + M , L3 = −M ′ ′
& & & U 2 = [R2 + jω (L2 + M )] I = Z 2 I , Z 2 = R2 + jω (L2 + M ) & & & U = [R1 + R2 + jω(L1 + L2 + 2M )] I = Z I , Z = (R1 + R2 ) + jω(L1 + L2 + 2M )
其中
Z1 = R1 + jω L1 , Z2 = R2 + jω L2 , ZM = jω M
& = Z2 + ZM U = 1+ ZM Y2 U, I = Z1 + ZM U = 1+ ZM Y1 U & & & & & I1 2 2 2 2 2 Z1Z2 − ZM Z1 − ZM Y2 Z1Z2 − ZM Z2 − ZM Y1 & = I + I = Z1 + Z2 + 2ZM U 式中 Y1 = 1 , Y2 = 1 & I3 &1 &2 2 Z1 Z2 Z1Z2 − ZM
③ 同名端：在两个耦合的线圈中各取一 同名端： 端子，并用“ ” 表示， 端子，并用“”或“*”表示，且当一对 同名端流进（ 施感电流 i1 和 i2 从 同名端流进（出） 各自的线圈时，互感起增助作用。 各自的线圈时，互感起增助作用。 多个线圈耦合时： ④ 多个线圈耦合时：

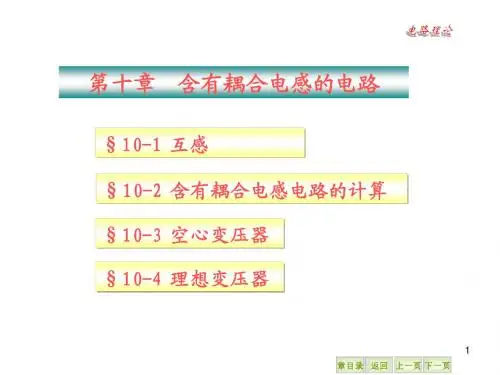
第10章含有耦合电感的电路37072共42页

第10章含有耦合电感的电路37072共42页

i1 +
i2 +
L1
L2
- - u1
M
di2 dt
+
–
-
+
M
di1 dt
–
u2
-
i2
注意受控电压源 （即互感电压）的 极性问题
12
相量模型：耦合电感的受控电源模型
i1
+
u 1 L1
-
M
L2
+ i2
+
•
U1
u2
-
-
•
I1
jωL1
•+
jM I2
-
•
I2
+
jω L2
•
U2
+
•
jM I1
-
-
•
•
•
U1 jωL1 I1 jωM I2
jωM
•
I
.
.
R1
+
jωL1
U1 -
jωL2 R2
a
b
16
• 解：1、求开路电压
•+
U1 -
•
I
.
jωM
.
R1
jωL1
jωL2 R2
•
•
•
U oc R2 I jωM I
•
( R2
jωM ) R1
U1 jωL1 R2
300V
a +
•
U oc
b-
17
• 2、求等效阻抗
Jω(L1-M) R1
+ uL11
*
L2
+ u2 u
-

电路PPT课件第10章含有耦合电感的电路

电路PPT课件第10章含有耦合电感的电路

由同名端及u、i参考方向确定互感线圈的特性方程
有了同名端，以后表示两个线圈相互作用，就不再考虑实际绕向，而只画 出同名端及参考方向即可。
M
*
*
i1
+ u21 –
M
*
*
i1
– u21 +
u21
M
di1 dt
u21
M
di1 dt
例
i1
M
i2
+*
*+
u1 L1 _
L2 u2 _
u1
L1
di1 dt
M
di2 dt
u
L1
L2
–
i1
M
i2
+
**
+
u
L1
L2
u
–
–
•
I
jM
j(L1－M)
•
•
I1 I2
j(L2－M)
•
I1
j(L1－M)
•
I2
j(L2－M)
jM
4. 受控源等效电路
i1
M
i2
+
**
+
u
L1
L2 u
–
–
•
I1
+
j L1
•
U1
+
•
jM
–
I–2
•
I2
+
j L2
•
+
U2
•
jMI 1
–
–
•
•
•
U 1 jL1 I 1 jM I 2
US
j (L1 L3 2M31)

(整理)含有耦合电感的电路(学生用).

(整理)含有耦合电感的电路(学生用).

精品文档第十章 含有耦合电感的电路§1. 耦合电感器与互感电压 一、耦合电感器──如果电感器L 1，L 2之间有公共磁通相交链，这两个电感器就构成一个耦合电感器。

有公共磁通交链 二、耦合电感器中的自感与互感 1、 自感与互感 11φ──自感磁通21φ──互感磁通（同时交链N 1，N 2） 1L φ──漏磁通)(211111111φφφψ+==L N N电感器1的自感：11111111i N i L φψ=∆=电感器2与1的互感（mutual inductance ）121212121i N i M φψ=∆注2，21φ的方向与电感器2导线的绕向无关。

1 1’2 2’1L 11’22’11精品文档22φ──自感磁通 12φ──互感磁通2L φ──漏磁通)(122222222φφφψ+==L N N电感器2的自感：22222222i N i L φψ=∆电感器1与2的互感212121212i N i M φψ=∆同样，12φ的方向与电感器1导线的绕向无关。

物理学中已证明。

M M M ∆=2112单位：亨利H 2. 耦合系数k──表明两个电感器之间磁耦合的紧密程度。

22211112ψψψψ⋅∆k21 L L M k =),,,(12121222221111Mi Mi i L i L ====ψψψψ1≤k1=k ──全耦合电感器（相当于021==L L φφ无漏磁通） 实际中：当双线并绕时，耦合最强，1→k 。

当两个耦合电感器相距甚远，或彼此垂直时，其间耦合较弱，0→k 。

11’22’⎩⎨⎧><称强耦合时称弱耦合时,5.0,5.0k k21112111Mi i L +=+=ψψψ 12221222Mi i L +=+=ψψψ表明：在该种绕线方式中，互感磁链与自感磁链方向一致，称为互感的“增助”作用。

改变电感器2的绕线方式：31113111Mi i L -=-=ψψψ 13331333Mi i L -=-=ψψψ表明：在这种绕线方式中，互感磁链与自感磁链方向相反，称为互感的“削弱”作用。

含有耦合电感的电路解读

含有耦合电感的电路解读

名端应当一对一对地加以标记，每一对
宜用不同符号。如每一电感都有电流时，则每一个电感中的 磁通链将等于自感磁通链与所有互感磁通链的代数和。凡 与自感磁通链同方向的互感磁通链(增助)，求和时该项前 面取“+”号，反之(削弱)则取“-”号。
第十章 含有耦合电感的电路
10-1 互 感
8
2020年3月11日星期 三
u1

d1 dt

L1
di1 dt

M
di2 dt
u2

d2 dt
M
di1 dt
L2
di2 dt
(10 1)
表示两耦合电感电压电流关系。
令自感电压
u11

L1
di1 dt
,
u22

L2
di2 dt
互感电压
u12

M
di2 dt
,
u21

M
di1 dt
u12是变动电流i2在L1中产生的互感电压，u21是变动电流i1
第十章 含有耦合电感的电路
2
2020年3月11日星期 三
10-1 互 感
• 载流线圈间通过彼此磁场相互联系的物理现象称磁耦 合。互感
• 图10-1(a)两个有耦合载流线圈(电感L1和L2)，其中电 流i1和i2称施感电流，线圈匝数分别为N1和N2。
• 根据两个线圈绕向、施感电流参考方向和两线圈相对 位置，按右螺旋法则确定施感电流产生磁通方向和彼
• 最后得(按右螺旋法则指定磁通链参考方向)：
Ψ1=L1i1+Mi2=[20+5cos(10t)] Wb Ψ2=Mi1+L2i2=[10+15cos(10t)] Wb

第10章 含有耦合电感的电路

•
–
相量形式
2
–
U1
+
2
•
•
+ –
U
j ωM I
j ωM I 1
–
–
–
还可以用电流控制电压源来表 示互感电压的作用。 示互感电压的作用。
9
控制源形式的互感模型
思考：三种不同形式的方程特点？ 思考：三种不同形式的方程特点？
章目录 返回 上一页 下一页
五、耦合系数 (coupling coefficient)k： ：
Φ
* 2 2'
1'
di > 0, dt
u22' = M di > 0 dt
R S 1 ♦ 1'
i *
电压表瞬时正偏。 电压表瞬时正偏。 思考：当开关 打开时 电压表？ 打开时， 思考：当开关S打开时，电压表？
*2 ♦ 2'
+ V –
12
章目录 返回 上一页 下一页
10--2 含有耦合电感电路的计算
在正弦交流电路中， 在正弦交流电路中，其相量形式的方程为
*
*
L2
△
L1
+ u2 _
时域形式
•
•
U 1 = j ω L1 I 1 + j ω M I 2
•
•
•
I1
jωM
•
I
2
+
•
U
2
•
= jω M I 1 + jω L2 I 2
•
•
•
j ω L1
*
*
+
j ω L2
•
U1
I

10 含有耦合电感的电路


M 21
21
i1

N 1 21
i1
M21：线圈2对线圈1的互感系数。
当线圈周围无铁磁物质(空心线圈)时，有 M12= M21= M。
互感系数 M 只与两个线圈的几何尺寸、匝数 、 相互位置 和周围的介质磁导率有关。
1= 11+ 12 2= 22+ 21
11=L1i1
22=L2i2
L反 L1 L2 2M
互感的测量方法：
* 顺接一次，反接一次，就可以测出互感：
M L顺 L反 4
二、互感线圈的并联
1、 两个线圈的同名端接在公共端(同侧并联)
I1 jM
I 2
1
••
2
jL1
jL2
I1
1
j(L1–M)
I 2
2
j(L2–M)
I
3
U 13 jL1 I1 jMI2
L2
_u2
0 1 2 t/s
解
u2 (t)

M
di1 dt

101V0V 0
0 t 1s 1 t 2s 2 t
10t 0 t 1s
i1 20 10t 1 t 2s
0
2 t
u(t)

R1i1

L
di1 dt

10100t0t 0

u2i2

u1i1

1 n u1
(ni1)

0
表明 a) 理想变压器既不储能，也不耗能，在电路中
只起传递信号和能量的作用。
b) 理想变压器的特性方程为代数关系，因此它 是无记忆的多端元件。
例1

第10章耦合电感电路201936856


u 2 L cd d 2 it L bd (id 1 i2 ) t L bd d 1 i( tL b L c )d d 2it
L1 La Lb L2 Lb Lc M Lb
La L1 M Lb M Lc L2 M
这种等效变换得出的T型电路已消除了两个线 圈的互感作用，称为互感消除法。这种等效电 路称为互感线圈的T型去耦等效电路。
(b)磁通相消
i1 11
a
u1
b
21
12
i2
c
u2
d
22
3、同名端的应用：
互感电压符号的确定：当两线圈电流均从同名
端流入（或流出）时，互感电压与该线圈中的
自感电压同号。当两线圈电流均从异名端流入
（或流出）时，互感电压与自感电压异号。
或：互感电压的参考极性与产生它的变化电流
的参考方向对同名端一致。
u1 L1 L2 u2
b
d
Fig-a
a i1 La
Lc i2 c
+
+
u1 Lb b
u2 d
Fig-b
Fig-a: u1 L1dd1itMddi2t
u2
L2
d2i Md1i dt dt
L1 La Lb L2 Lb Lc M Lb
Fig-bu :1 L ad d 1 it L bd (id 1 i2 ) t (L a L b )d d 1 it L bd d 2it
(b)
空心变压器电路


R 1j L 1I1j M I2U S


jM I1R 2jL 2 Z LI2 0I1 R1
I 2 R2

第十章--含有耦合电感的电路


正值表示自感磁链与互感磁链方向一致，互感起
增助作用，负值表示自感磁链与互感磁链方向相 反，互感起削弱作用。
2024年7月17日星期
11
三
3. 同名端的概念及其判断方法！
通过线圈的绕向、 位置和施感电流的
F12
参考方向，用右手
螺旋法则，就可以 F11 判定互感是“增助”
还是“削弱” 。
但实际的互感线圈 往往是封闭的，看 不出绕向；
三
§10-1 互感
1. 互感的概念 一个电感线圈的情况
L1 N1
i1产生的磁通为F11。
i1与F11的参考方向符 F11
合右手螺旋法则，为
关联的参考方向。
i1
1' -
u11
1 +
F11穿越自身线圈时，
产生的自感磁通链用
若u11与i1取关联参考方向
Y11表示：Y11= L1i1
当i1变化时，将产生 自感电压u11。
第十章 含有耦合电感的电路
学习要点 熟练掌握互感的概念； 具有耦合电感电路的计算方法：
①直接列写方程的支路法或回路法。 ②受控源替代法。 ③互感消去法。 掌握空心变压器和理想变压器的应用。
2024年7月17日星期
1
三
重点
互感和互感电压的概念及同名端的含义； 含有互感电路的计算； 空心变压器和理想变压器的电路模型。
名端要用不同的符号一对一对标记。
L2
M
L1 *
* L2
2'பைடு நூலகம்
1 i1
+
M
i2 2
+
M
L3 M
u1
-
L1
1'
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第10章 含有耦合电感的电路教研室：基础教研室 教师姓名：§10-1 互感 （复习第6章第2节）一、自感：一个线圈自身电流的变化引起自身线圈中产生感应电动势的现象。

P129 二、互感：邻近线圈中电流的变化引起另一个线圈产生感应电动势的现象。

1.磁耦合：载流线圈之间通过彼此的磁场相互联系的物理现象。

⎩⎨⎧=Φ=ψ→Φ→=Φ=ψ→Φ→12121221211111111111i M N i L N i 互感磁通链互感磁通自感磁通链自感磁通施感电流⎩⎨⎧=Φ=ψ→Φ→=Φ=ψ→Φ→21212112122222222222 i M N i L N i 互感磁通链互感磁通自感磁通链自感磁通施感电流 M M M ==2112 (两个线圈耦合时的互感系数) ，单位与电感一致。

2．磁通链 自感磁通链 互感磁通链12122212222121112111 i M i L ΨΨΨi M i L ΨΨΨ±=+=±=+=M 前“+”号表示互感磁通与自感磁通方向一致，称为互感的“增助”作用；“-”号则相反，表示互感的“削弱”作用。

注意：M 值与线圈的形状、几何位置、空间媒质有关，与线圈中的电流无关。

三、同名端1．定义：同名端：在两个耦合的线圈中各取一端子，用“·”或“*”表示，当两个电流 1i 和2i 从同名端流进（出）各自的线圈时，互感起增助作用。

异名端：在两个耦合的线圈中各取一端子，当两个电流 1i 和 2i 从异名端流进（出）各自的线圈时，互感起削弱作用。

注意：同名端必须两两确定。

2．判定方法 a , 根据实际的绕向；b , 利用实验方法，根据线圈相对位置变化时，电压的变化情况判断；c , 电流流同时从同名端流入，M 取正，磁场增加；同时从异名端流入，M 取负，磁场削弱；例10-1：互感耦合电路中()H M H L H L A t i A i 1 ,3 ,2 ,10cos 5 ,102121=====,求两耦合线圈中的磁通链。

解： 1i 、2i 都是从标记的同名端流进，互感“增助”，则 (); 10cos 15 ; 2022221111W b t i L ΨW b i L Ψ==== (); 10 ; 10cos 5121212W b Mi ΨW b t Mi Ψ====∴ ()Wb t ΨΨΨ10cos 52012111+=+=()Wb t ΨΨΨ10cos 151022212+=+=四、耦合系数用耦合系数k 表示两个线圈磁耦合的紧密程度121≤=L L M k d e fk=1时，全耦合； k=0时，无耦合五、耦合电感上电压电流的关系设 21,L L 中电压和电流 11,i u 和 22,i u 都取关联参考方向，有212212222121121111u u dt di M dt di L dt d u u u dtdi M dt di L dt d u ±=±=ψ=±=±=ψ=11u ，12u ——自感电压互感电压 dt diM u 212= 是 2i 在 1L 中产生的互感电压；互感电压 dt diM u 121= 是 1i 在 2L 中产生的互感电压。

耦合电感的电压是自感电压和互感电压的线性叠加；① 如果电感两端电流，电压为非关联参考方向，则自感电压取“-”； ② 如果互感电压的极性，由磁场的增减决定。

例10-2：求例10-1中两耦合电感的端电压 21 ,u u 。

解： ()V t dt di M dt di L u 10sin 502111-=+=; 互感电压 ()V t dtdiM dt di L u 10sin 1501222-=+=; 自感电压 六、耦合电感的等效受控源电路⎩⎨⎧+=+=⇒⎪⎪⎩⎪⎪⎨⎧+=+=1222211112222111 I M j I L j U I M j I L j U dt di M dt di L u dt di M dt di L u ωωωωM M j Z M ωω , = 为互感抗§10-2 含有耦合电感电路的计算含有耦合电感电路的正弦稳态分析可采用相量法。

在表达式中应计入互感作用引起的互感电压，要根据同名端和电流方向正确判断互感电压。

一、电感串联1．反串反向串联，同名端相接，磁场削弱a .()dt di M L i R dt di M dtdiL i R u -+=⎪⎭⎫ ⎝⎛-+=11111()dt di M L i R dt di M dtdiL i R u -+=⎪⎭⎫ ⎝⎛-+=22222()()dtdiM L L i R R u u u 2 212121-+++=+=0221≥-+=M L L L eqb .()[]()M L j R Z I Z I M L j R U -+==-+=1111111 , ωω ()[]()M L j R Z I Z I M L j R U -+==-+=2222222 , ωω ;()[]()()M L L j R R Z I Z I M L L j R R U 2 , 221212121-+++==-+++=ωω ; ()ZU M L L j R R U I =-+++=22121ω反接，类似于串联电容，常称为互感的“容性 ”效应，但整个电路仍呈感性。

2．顺串顺向串联，异名端相接，磁场增强a .()dt di M L i R dt di M dtdiL i R u ++=⎪⎭⎫ ⎝⎛++=11111()dt di M L i R dt di M dtdiL i R u ++=⎪⎭⎫ ⎝⎛++=22222()()dtdiM L L i R R u u u 2 212121++++=+=M L L L eq 221++=b .()[]()()M L L j R R Z I Z I M L L j R R U 2 , 221212121++++==++++=ωω 例10-3：反接耦合电路中 , 5.12 , 5, 5.7 , 3 , 502211Ω=Ω=Ω=Ω==L R L R V U ωωΩ=8 M ω, 求耦合系数k 和各支路的复功率 1S 和 2S 。

解：① 826.05.125.782121=⨯==L L M L L M def k ωωω② ()Ω︒-∠=-=-+= 46.904.35.03111j M L j R Z ω（容性）()Ω︒∠=+=-+= 4273.65.45222j M L j R Z ω（感性） Ω︒∠=+=+= 57.2694.84821j Z Z Z令 V U 050︒∠= , 电流 I 为 A Z U I 57.2659.557.2694.8050︒-∠=︒∠︒∠== ∴ ()VA j Z I S 63.1575.93121-== ()VA j Z I S 63.14025.156222+==电源发出的复功率 ()21* 125250 S S VA j I U S +=+== 二、 电感并联1．同侧并联（同名端连接在同一个结点上）()()⎪⎩⎪⎨⎧++=++=22212111 I L j R I M j U I M j I L j R U ωωωω (原电路相量关系)∴ ()[]()[]⎪⎩⎪⎨⎧-++=-++=22231113 I M L j R I M j U I M L j R I M j U ωωωω （去耦等效电路相量关系）⇒ M L M L L M L L =-='-='32211 , , (同侧并联替代电感) 2．异侧并联（异名端连接在同一个结点上）()()⎪⎩⎪⎨⎧+-=++-=-=-+=22122212112111 I Z I Z I L j R I M j U I Z I Z I M j I L j R U M M ωωωω (原电路相量关系)∴ ()[]()[]⎪⎩⎪⎨⎧+++-=+++-=22231113 I M L j R I M j U I M L j R I M j U ωωωω（去耦等效电路相量关系）⇒ M L M L L M L L -=+='+='32211 , , (异侧并联替代电感) 例10-4：见教材260页例10-4 3．总结如果耦合电感的两条支路各有一端与第3支路形成一个仅含3条支路的共同结点，则可用3条无耦合的电感支路等效替代：ML M L M L ==±=123)1()2()3(支路支路支路 例10-5：见教材260页例10-5§10-3 耦合电感的功率当耦合电感中的施感电流变化时，将出现变化的磁场，从而产生电场（互感电压），耦合电感通过变化的电磁场进行电磁能的转换和传输，电磁能从耦合电感一边传输到另一边。

互感电压耦合的复功率为虚部同号，而实部异号，这一特点是耦合电感本身的电磁特性所决定的；耦合功率中的有功功率相互异号，表明有功功率从一个端口进入，必从另一端口输出，这是互感M 非耗能特性的体现。

耦合功率中的无功功率同号，表明两个互感电压耦合功率中的无功功率对两个耦合线圈的影响、性质是相同的，即，当M 起同向耦合作用时，它的储能特性与电感相同，将使耦合电感中的磁能增加；当M 起反向耦合作用时，它的储能特性与电容相同，将使耦合电感的储能减少。

例10-6：见教材263页例10-6§10-4 变压器原理变压器由两个具有互感的线圈构成，一个线圈接向电源（一次回路，一次侧，原边回路，初级回路），另一线圈接向负载（二次回路，二次侧，副边回路，次级回路），变压器是利用耦合作用，传递能量。

1.变压器电路①正弦稳态法分析()()⎪⎩⎪⎨⎧=+=+⇒⎪⎩⎪⎨⎧=++++=++00 222112111222112111I Z I Z U I Z I Z I jX R L j R I M j U I M j I L j R M M L L ωωωω 其中 M j Z jX R L j R Z L j R Z M L L , , 22221111ωωω=+++=+=解得：2221112221111) ( Y M Z U Y Z Z U I M ω+=-= ②结果分析1) 原边输入阻抗()2221111 Y M Z I U Z i ω+== ← 次级回路在初级回路中的反映阻抗引入阻抗的性质与22Z 相反，即感性（容性）变容性（感性）。

2) 等效次级回路2212 Z I M j I ω-= ()Leq OC L L eq Z Z U jX R Z U Y M j Y M Z U Y M j I +=++-=+-= 111112221112 ) ( ωωω 其中， ()11222 Y M L j R Z eq ωω++= ← （初级在次级的反映阻抗）111 U Y M j U OC ω-= （次级开路电压）例：见教材267页例10-8§10-5 理想变压器1.理想变压器应当满足的3个条件1) 变压器本身无损耗 2) 全耦合，耦合系数 121==L L Mk 3) 1L ﹑2L 和M 均为无限大，但保持n L L =21不变，21N Nn =为匝数比 2.理想变压器的电压、电流变换。