2016年高考数学(文)备考之百强校大题狂练系列 08(第01期)(原卷版)

班级 姓名 学号 分数（测试时间：25分钟 满分：50分）一、选择题（共6小题，每题5分，共30分）1.【甘肃省河西五市部分普通高中2016届高三第一次联考数学（文）试题】已知:p m R ∀∈，210x mx --=有解， 0:q x N ∃∈，200210x x --≤则下列选项中是假命题的为（）A ．p q ∧B ．()p q ⌝∧C ． p q ∨D ．()p q ⌝∨ 【答案】B.【解析】2. 【新疆乌鲁木齐地区2016年高三年级第一次诊断性测试数学（文）试题】等差数列{}n a 中，365,S 36,a ==则9S =A. 17B. 19C. 81D. 100【答案】C .【解析】 试题解析：31125656362a a d d a =+=⎧⎪⎨⨯+=⎪⎩，得112a d =⎧⎨=⎩，∴91989812d S a ⨯=+=，故选C . 3. 【吉林省长春市普通高中2016届高三质量监测（二） 数学（文）试题】已知AB 为圆221x y +=的一条直径，点P 为直线20x y -+=上任意一点，则PA PB ⋅的最小值为A. 1C. 2D.A 【命题意图】本题考查直线与圆的位置关系以及向量的运算.【解题思路】 由题可知，从圆外一点指向圆直径的两个端点的向量数量积为定值，即为22d r -，其中d 为圆外点到圆心的距离，r 为半径，因此当d 取最小值时，PA PB ⋅的取值最小，由方程的图象可知d，故PA PB ⋅的最小值为1. 故选A.4. 【新疆乌鲁木齐地区2016年高三年级第一次诊断性测试数学（文）试题】设函数()f x 在R 上存在导函数()f x '，对任意x R ∈，都有2()()f x f x x +-=，且()0+x ∈∞，时，()f x x '>，若2(2-)()22f a f a a ≥-－，则实数a 的取值范围是（ ） A. [)1+∞，B. (],1-∞C. (],2-∞D. [)2+∞， 【答案】B【解析】5. 【辽宁省沈阳市2016届高三教学质量监测（一）数学（文）试题】从某小学随机抽取100名同学，现已将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．若要从身高在[120,130），[130，140）,[140,150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[140，150]内的学生中选取的人数应为（ ）A ．2B ．3C ．4D ．5【答案】B【解析】6. 【辽宁省沈阳市2016届高三教学质量监测（一）数学（文）试题】已知正四面体ABCD 的棱长为a ，其外接球表面积为1S ，内切球表面积为2S ，则12:S S 的值为（ ）A ．3B ．C ．9D ．494【答案】C【解析】 试题分析：如图所示，设点O 是内切球的球心，正四面体棱长为a ， 由图形的对称性知，点O 也是外接球的球心．设内切球半径为r ，外接球半径为R ．在Rt △BEO 中，222BO BE EO =+，即 ，可得3R r =，2212::9S S R r ==，故选C. (或由等体积法设内切球半径为r ，外接球半径为R ，正四面体的侧面积为S ，易有11()433S R r Sr +=⋅，有3R r =) 二、填空题（共2小题，每题5分，共10分）7.【辽宁省沈阳市2016届高三教学质量监测（一）数学（文）试题】已知正方形ABCD 的边长为2，E 为CD 的中点，则AC BE ⋅= ； 【答案】2【解析】8.【甘肃省河西五市部分普通高中2016届高三第一次联考数学（文）试题】已知sin 2cos αα=，则2015cos(2)2πα-的值为 【答案】45-. 【解析】试题分析：2220152sin cos cos(2)sin 22sin cos παααααα-=-=-+22tan 41tan 5αα=-=-+，故填：45-. 三、解答题（共1小题，每题10分，共10分）9.【吉林省长春市普通高中2016届高三质量监测（二） 数学（文）试题】已知函数2()2sin cos f x x x x =+.(1)求函数()f x 的最小正周期和单调减区间；(2) 已知ABC ∆的三个内角,,A B C 的对边分别为,,a b c ，其中7a =，若锐角A 满足()26A f π-=，且sin sinBC +=b c ⋅的值. 【命题意图】本题主要考查三角函数的化简运算，以及三角函数的性质，并借助正弦定理考查边角关系的运算.解：(1) 2()2sin cos sin 22f x x x x x x =+=+2sin(2)3x π=+，因此()f x 的最小正周期为22T ππ==. ()f x 的单调递减区间为3222232k x k πππππ+++≤≤， 即7[,]1212x k k ππππ∈++()k ∈Z . (6分)。

【百强校】一轮复习之小题精做8一、选择题（共12小题，每题5分，共60分）1.【2016辽宁鞍山中学四模】若集合{}|128x P x =≤<,{}1,2,3Q =,则PQ =( )A ．{}1,2B ．{}1C ．{}2,3D ．{}1,2,32.【2016云南玉溪中学月考】欧拉公式cos sin ix e x i x =+（i 为虚数单位）是由瑞士著名数学家欧拉发明的，它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”，根据欧拉公式可知，i e 2-表示的复数在复平面中位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3.【2016湖南省长沙市长郡中学调研】已知命题:p 0x ∀≥，21x ≥；命题:q 若x y >，则22x y >．则下列命题为真命题的是（ ）A ．p q ∧B ．p q ∧⌝C ．p q ⌝∧⌝D ．p q ⌝∨4.【2016湖南师大附中月考六】如图所示的程序框图运行的结果是（ ）A ．20142015B ．20152016C ．20142013D ．201520145.【2016辽宁鞍山中学二模】设,,αβγ为不同的平面，,m n 为不同的直线，则m β⊥的一个充分条件是（ ）A ．,,n m n αβαβ⊥=⊥B ．,,m αγαγβγ=⊥⊥C ．,,m αββγα⊥⊥⊥D ．,,n n m αβα⊥⊥⊥6.【2016河北邯郸一中调研七】已知函数()2211x x f x x ++=+，若()23f a =，则()f a -=（ ） A ．23 B ．23- C ．43 D ．43-7.【2016黑龙江省哈市六中开学考】已知y x ,满足约束条件34y xy x x y ≤⎧⎪≥⎨⎪+≤⎩，则下列目标函数中，在点(3,1)处取得最小值的是（ ）A.2z x y =-B.2z x y =-+C.y x z --=21 D.2z x y =+ 8.【2016湖北武汉师大附中八校联考】已知函数21()sin ()2f x x ω=-，(0)ω>的周期为π，若将其图象沿x 轴向右平移a 个单位(0)a >，所得图象关于原点对称，则实数a 的最小值为（ ）A ．πB ．34πC ．2πD ．4π 9.【2016海南文昌中学高三期末】一个棱锥的三视图如右图所示，则这个棱锥侧面中面积最大的是（ ）A ．29B ．6C ．26D ．1010.【2016吉林省吉林大学附中四模】若，，a b c 均为单位向量，且12⋅=-a b ，x y =+c a b ()x y ∈R ，，则x y +的最大值为（ ）（A ）1（B ）2 （C ）3 （D ）411.【2016湖南省长沙市长郡中学调研】已知三棱锥C S -AB 的所有顶点都在球O 的球面上，C ∆AB 是边长为1的正三角形，C S 为球O 的直径，且C 2S =，则此棱锥的体积为（ ）ABCD12.【2016吉林省东北师大附中等三校联考】已知函数)(x f 定义在R 上的奇函数，当0<x 时，()(1)x f x e x =+，给出下列命题：①当0>x 时，()(1)x f x e x =- ②函数)(x f 有2个零点 ③0)(>x f 的解集为),1()0,1(+∞- ④R x x ∈∀21,，都有2)()(21<-x f x f ，其中正确的命题是（ ）A ．①③B ．②③C ．③④D ．②④二、填空题（共4小题，每题5分，共20分）13.【2016湖南师大附中等四校联考】设函数2log (0)()()(0)x x f x g x x >⎧=⎨<⎩，若)(x f 为奇函数，则)41(-g 的值为_______.14.【2016吉林省松原实验中学联考】已知0θπ<<，1tan()47πθ+=，那么sin cos θθ+= . 15．【2016河北武邑中学期中】双曲线22221x y a b-=（0a >，0b >）的左、右焦点分别为1F 、2F ，渐近线分别为1l ，2l ，点P 在第一象限内且在1l 上，若21l PF ⊥，22l PF ，则该双曲线的离心率为 .16.【2016黑龙江省哈市六中开学考】正三角形ABC 的边长为2，F E D ,,分别在三边CA BC AB ,,上，D 为AB 的中点，DF DE ⊥，且DE DF 23=，则=∠BDE .：。

班级 姓名 学号 分数大题狂做测试卷3（测试时间：90分钟 满分：120分）1.已知函数x x x f -=3)(.（Ⅰ）求)(x f 在区间]0,2[-上的最大值；(Ⅱ)若过点),2(t P 存在3条直线与曲线)(x f y =相切，求t 的取值范围．2。

已知等差数列{}na 前三项的和为3-，前三项的积为8。

（Ⅰ)求等差数列{}na 的通项公式; (Ⅱ)若2a ,3a ,1a 成等比数列，求数列{||}n a 的前n 项和.3。

已知函数())cos cos f x x x x =-．(1)求函数()f x 的最小正周期和单调递减区间；⑵记ABC ∆的内角,,A B C 的对应边分别为,,a b c ，且()12f B =，1a c +=，求b 的取值范围．4。

在锐角ABC ∆中，222cos()sin cos b a c A C ac A A--+=．（I ）求角A ；（Ⅱ）若a =bc 的取值范围．5.在ABC ∆中，角A ，B ，C 的对边分别为a ,b ，c cos cos C A =。

（Ⅰ)求角A 的值； （Ⅱ）若角6B π=，BC 边上的中线AM =ABC ∆的面积。

6.已知函数()2cos()(05)63f x x x ππ=+≤≤，点B A ,分别是函数)(x f y =图象上的最高点和最低点．（1）求点B A ,的坐标以及OB OA ⋅的值；(2)设点B A ,分别在角])2,0[,(,πβαβα∈的终边上,求)22sin(βα-的值．7。

已知函数),()(R k m mx ex f k x ∈-=定义域为),0(+∞. （1）若1=k 时，)(x f 在),1(+∞上有最小值，求m 的取值范围； （2）若2=k 时，)(x f 的值域为),0[+∞,试求m 的值; （3）试证:对任意实数m ,k ，总存在0x ，使得当),(0+∞∈x x 时，恒有0)(>x f8.设数列{}n a 的前n 项和为n S ，对一切*N n ∈,点 ⎝⎛⎪⎭⎫n S n n ,都在函数xa x x f n2)(+=的图象上（1）求,,,321a a a 归纳数列{}n a 的通项公式(不必证明）； （2）将数列{}n a 依次按1项、2项、3项、4项循环地分为（1a ），(),32a a ，(),,654a a a , (),,,10987a a a a ;()11a ,()1312,a a ,(),,161514a a a ，(),,,20191817a a a a ；()21a ，…..,分别计算各个括号内各数之和，设由这些和按原来括号的前后顺序构成的数列为{}n b ，求1005b b +的值;(3）设n A 为数列⎭⎬⎫⎩⎨⎧-n na a 1的前n 项积，若不等式a a a f a A n n n 23)(1+-<+对一切 *N n ∈都成立，其中0>a ，求a 的取值范围9。

【百强校】一轮复习之小题精做6一、选择题（共12 小题，每题5 分，共60 分）1.【2015湖南省浏阳一中期末】设集合{}{}1,2,3,4,2,==|-2≤≤∈P Q x x x R ，则P Q 等于 （ ） A .{}1,2,0,1,2-- B.{}3,4 C.{}1 D.{}1,22.【2015河南南阳一中三模】已知集合{}lg(3),A x y x ==-，{}5B x x =≤，则A B ⋃=（ ）A ．{}35x x <≤B ．{}5x x ≥C ．{}3x x <D ．R3.【2015湖南浏阳一中期末】“21<-x 成立”是“0)3(<-x x 成立”的 （ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件4.【2015福建泉州一中5月模拟】已知函数21()cos 2f x x =-，则 A ．()f x 为偶函数且最小正周期为π B.()f x 为奇函数且最小正周期为πC. ()f x 为偶函数且最小正周期为2πD.()f x 为奇函数且最小正周期为2π5.【2015江西高安中学押题一】三个数20.310.3120.31,log ,2a b c ===之间的大小关系是（ ）A ．a c b <<B ．b a c <<C ．a b c <<D ．b c a << 6.【2015河南南阳中学三模】已知函数2()3f x ax bx a b =+++是定义在[1,2]a a -上的偶函数，则2cos[()]3y a b x π=+- 错误！未找到引用源。

的最小正周期是（ ） A. 6π B. 5π C.4π D.2π7.【2015湖北襄阳中学一模】设1311321,log 2,log 32a b c ⎛⎫=== ⎪⎝⎭，则（ ） A ．a>b>c B ．a>c>b C ．b>c>a D ．c>a>b8.【2015山东实验中学二模】已知函数 ()sin()f x A x ωϕ=+ (其中A>0, 2πϕ<)的部分图象如图所示，为了得到g(x)=sin 2x 的图象，则只需将f (x)的图象Ａ．向右平移6π个长度单位 Ｂ．向右平移 12π个长度单位 C ．向左平移 6π个长度单位 D ．向左平移 12π个长度单位 9.【2015天津市武清区杨村第一中学检测】函数)(x f 在定义域R 内可导，若)2()(x f x f -=,且当)1,(-∞∈x 时，0)()1(<'-x f x ,设)3(),21(),0(f c f b f a ===,则 ( ) A ．c b a << B ．b a c << C ．a b c << D ．a c b <<10.【2015山西太原五中5月月考】将函数)sin(ϕ+=x y 2的图象沿x 轴向左平移8π个单位后，得到一个偶函数的图象，则ϕ的一个可能取值为( ) A. 43π B. 4π C. 0 D. - 4π 11.【2015甘肃天水一中仿真模拟】设函数22,()ln )3(x x g x x x x f e +-=+-=. 若实数a , b 满足()0,()0f a g b ==, 则（ ）A ．()()0f b g a <<B ．()0()f b g a <<C ．0()()g a f b <<D ．()0()g a f b << 12.【2015湖北四校联考】已知集合M 是由具有如下性质的函数()f x 组成的集合：对于函数()f x ，在定义域内存在两个变量12,x x 且12x x <时有1212()()f x f x x x ->-．则下列函数①()(0)x f x e x => ②ln ()x f x x =③()f x =④()1sin f x x =+在集合M 中的个数是 A ．1个 B ．2个 C ．3个 D ．4个二、填空题（共4 小题，每题5 分，共20 分）13.【2015湖南浏阳中学期末】曲线y ＝xln x 在点(e ，e)处的切线与直线x ＋ay ＝1垂直，则实数a 的值为________14.【2015山东实验中学6月模拟】定义空间两个向量的一种运算sin ,⊗=⋅<>a b a b a b ，则关于空间向量上述运算的以下结论中，①⊗=⊗a b b a ，②()()λλ⊗=⊗a b a b ，③()()()+⊗=⊗+⊗a b c a c b c ， ④若1122(,),(,)x y x y ==a b ，则1221x y x y ⊗=-a b .恒成立的是 （写上所有正确的序号）.15.【2015陕西西工大附中一模】ABC ∆中,a,b,c 分别是角A 、B 、C 的对边,若C A B b c a sin cos 6sin ,222⋅==-且, 则b=16.【2015山西太原五中检测】已知函数ln ,1()1(2)(),1x x f x x x a x e≥⎧⎪=⎨+-<⎪⎩（a 为常数，e 为自然对数的底数）的图象在点(,1)A e 处的切线与该函数的图象恰好有三个公共点，则实数a 的取值范围是：。

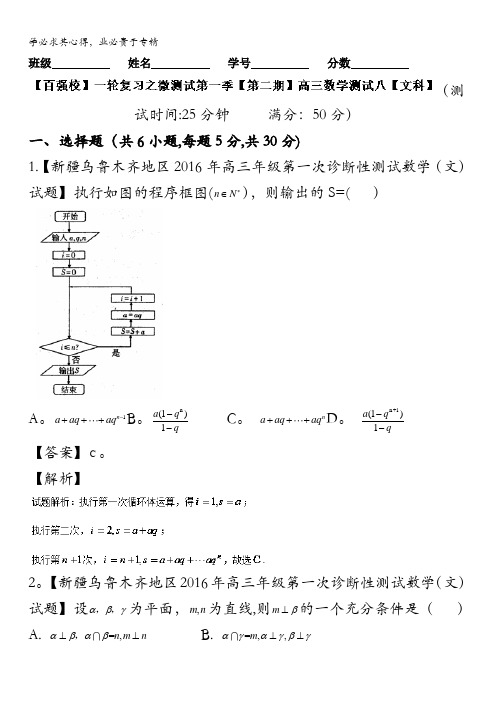
班级 姓名 学号 分数（测试时间:25分钟 满分：50分）一、选择题（共6小题,每题5分,共30分)1.【新疆乌鲁木齐地区2016年高三年级第一次诊断性测试数学（文）试题】执行如图的程序框图(n N *∈），则输出的S=( ）A 。

1n a aq aq -+++B 。

n (1)1a q q --C 。

n a aq aq +++D 。

n +1(1)1a q q-- 【答案】C 。

【解析】2。

【新疆乌鲁木齐地区2016年高三年级第一次诊断性测试数学（文）试题】设αβγ，，为平面，,m n 为直线,则m β⊥的一个充分条件是（ ）A. =,n m n αβαβ⊥⊥，B. =,,m αγαγβγ⊥⊥C. m αγβγα⊥⊥⊥，， D 。

n ,,n m αβα⊥⊥⊥【答案】D 。

【解析】试题解析：∵,n m αα⊥⊥，∴m ∥n ，又n β⊥，∴m β⊥，故选D 。

3。

【吉林省长春市普通高中2016届高三质量监测（二） 数学(文）试题】以正方形的一条边的两个端点为焦点,且过另外两个顶点的椭圆与双曲线的离心率之积为A 。

1B 。

22 C. 2 D. 2A 【命题意图】本题考查椭圆与双曲线离心率的概念。

【解题思路】 以正方形的一条边的两个端点为焦点，且过另外两个顶点的椭圆的离心率为11221t et t ==++,双曲线的离心率为21221t e t t ==--，故他们的积为1，故选A 。

4. 【甘肃省河西五市部分普通高中2016届高三第一次联考数学(文）试题】函数]),[()(cos ππ-∈=x xex f x 的图象大致是（ ）A 。

B 。

C 。

D 。

【答案】B 。

【解析】5.【吉林省长春市普通高中2016届高三质量监测（二) 数学（文)试题】已知直线21y x =+与圆224xy +=相交于A 、B 两点，设α、β分别是以,OA OB 为终边的角,则sin()αβ+= A. 35 B. 35- C. 45 D 。

班级 姓名 学号 分数大题狂做测试卷10（测试时间：90分钟 满分：120分）1.已知S n 为数列{a n }的前n 项和，且S n =2a n +n 2—3n —1，n=l ，2，3…（1）求证：数列{a n —2n}为等比数列：（2）设b n =a n ·cosn π，求数列{b n }的前n 项和T n 。

2. 在ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c ，面积为S ，已知b A c C a 232cos 2cos 22=+ （1）求证：c b a 、、成等差数列；（2）若，34,3==S B π求b . 3. f(x)=3sin(x+2ϕ)cos(x+2ϕ)+sin 2(x+2ϕ)(0<φ<2π)的图象经过点(3π,1) (1)求f(x). (2)在△ABC 中，A 、B 、C 的对边为a 、b 、c ，a=5，S △ABC =25，角C 为锐角且 f(2C -12π)=67，求c 边长 4.（本题满分12分）在数列{}n a 中， ,31=a 122(2,n n a a n n -=+-? 且*)n N Î（Ⅰ）求32,a a 的值；（Ⅱ）证明：数列{}n a n +是等比数列，并求{}n a 的通项公式； （Ⅲ）求数列{}n a 的前n 项和n S ．5.已知函数()()0b f x ax c a x=++>的图象在点()()1,1f 处的切线方程为1y x =-. （Ⅰ）用a 表示出b ，c ；（Ⅱ）若()x ln x f ≥在[)∞+,1上恒成立，求a 的取值范围．6.在锐角△ABC 中，角A,B,C 的对边分别为a,b,c,已知().3),sin(2C A m +=, ⎪⎭⎫ ⎝⎛-=12cos 2,2cos 2B B ,且m ∥n(1)求角B 的大小(2)若b=1，求△ABC 面积的最大值。

7.已知函数21()ln (0).2f x x a x a =-> (Ⅰ)若2,a =求()f x 在(1,(1))f 处的切线方程；(Ⅱ)求()f x 在区间[1,e]上的最小值；(Ⅲ)若()f x 在区间(1,e)上恰有两个零点,求a 的取值范围.8.已知函数2()26sin cos 2cos 41,f x x x x x x π⎛⎫=++- ⎪+⎝⎭∈R . (Ⅰ) 求()f x 的最小正周期；(Ⅱ)求()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值. 9.设,0>a 且1≠a ，已知函数11log )(--=x bx x f a是奇函数 （Ⅰ）求实数b 的值；（Ⅱ）求函数)(x f 的单调区间； （Ⅲ）当)2,1(-∈a x 时，函数)(x f 的值域为),1(+∞，求实数a 的值．10.已知实数0a >，函数()f x =+（1）当1a =时，求()f x 的最小值;（2）当1a =时,判断()f x 的单调性,并说明理由；（3）求实数a 的范围，使得对于区间⎡⎢⎣上的任意三个实数r s t 、、，都存在以()()()f r f s f t 、、为边长的三角形.：。

【百强校】一轮复习之小题精做8一、选择题（共 12 小题，每题 5 分，共 60 分）1.【2015江西高安中学押题一】已知{}}222,1,2x M y y x N x y ⎧⎪===+=⎨⎪⎩则M N ⋂=( )A ．{(1,1),(1,1)}-B ．{1}C ．D ． [0,1]【答案】C .【解析】由题意知，{}{}}22200,1x 2x M y y x y y N x y ⎧⎪==≥=≥=+==≤≤⎨⎪⎩所以M N ⋂=，故应选C .2.【2015海南嘉积中学检测】集合{1,2,3,4,5,6}U =，{1,4,5}S =,{2,3,4}T =，则()U S C T =（ ）A ．{1,4,5}B ．{1,5}C ．{4}D ．{1,2,3,4,5}【答案】B【解析】{}651，，=T C U ,{}51，=T C S U 3.【2015山东实验中学二模】若 ,R αβ∈， 则 90αβ+=是sin sin 1αβ+> 的A ．充分而不必要条件 B.必要而不充分条件 C ．充耍条件 D ．既不充分也不必要条件 【答案】D4.【2015黑龙江哈尔滨市九中三模】对于实数"0",,<<a b b a 是"11"ab >成立的 A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件 【答案】B【解析】若0<<a b ，则a b 11>；若ab 11>，则有可能是0,<>a o b 、0>>b a 、0<<a b ；所以应选B.5.【2015海南嘉积中学质检】函数f(x)＝x-11＋lg(1＋x)的定义域是( ) A ．(－∞，－1)B ．(1，＋∞)C ．(－1,1)∪(1，＋∞)D ．(－∞，＋∞)【答案】C 【解析】⎩⎨⎧>+≠-0101x x 解得()()∞+，11,1-6.【2015山东师大附中七模】设函数()sin(2)3f x x π=+，则下列结论正确的是（ ）①()f x 的图象关于直线3x π=对称； ②()f x 的图象关于点(,0)4π对称；③()f x 的图象向左平移12π个单位，得到一个偶函数的图象；④()f x 的最小正周期为π，且在[0,]6π上为增函数．A. ①③ B . ②④ C.①③④ D . ③ 【答案】D7【2015海南省嘉积中学五模】若定义域为R 的函数f(x)的周期为2，当x ∈(－1,1]时，f(x)＝|x|，则函数y ＝f(x)的图象与y ＝log 3|x|的图象的交点个数为( ) A ．8B ．6C ．4D ．2【答案】C 【解析】分别画出函数()x f y =，与函数x y 3log =的图像，由图像可得，共4个交点. 8.【2015海南海南中学5月月考】将函数()y f x =的图像向右平移2π单位得到函数cos 2y x =的图像，则将函()y f x =的横坐标伸长到原来的2倍，纵坐标不变，得到函数()y g x =的图像，则()g x =（ ） A ．sin 4x - B ．cos 4xC ．sin xD ．cos x -【答案】D9.【2015湖南长沙市雅礼中学月考】设非空集合{}S x m x n =≤≤满足：当x S ∈时，有2x S ∈，给出如下三个命题：①若1,m =则{}1S =；②若1,2m =-则114n ≤≤； ③若1,2n =则0m ≤≤． 其中正确命题的是（ ）A.①B.①②C.②③D.①②③ 【答案】D【解析】由题意可知函数2y x =在S 上的值域是定义域S 的子集，画图讨论. 10.【2015陕西西工大附中一模】将函数()x x f y cos =的图像向左平移4π个单位后,再做关于x 轴的对称变换得到函数1cos 22-=x y 的图像,则()x f 可以是 ( )A.x cos 2-B. x sin 2-C. x cos 2D. x sin 2 【答案】B【解析】 做22cos 1cos2y x x =-=的图像关于x 轴的对称变换,再向右平移4π个单位得cos 22y x π⎛⎫=-⎪⎝⎭的图像,而cos 2sin 22sin cos 2y x x x x π⎛⎫=-=-=- ⎪⎝⎭,所以()x f 可以是x sin 2-,故选B. 11.【2015山东师大附中九模】函数||ln 2sin )(x e x x f +=的图象的大致形状是( )【答案】B12.【2015东北师大附中四模】已知函数()xf x e ax =-有两个零点12x x <，则下列说法错误．．的是( ) A.a e >B.122x x +>C.121x x >D.有极小值点0x ，且1202x x x +<【答案】C【解析】由题意得：方程()0xf x e ax =-=有两个不等的根，即y a =与xey x=有两个不同的交点，因为2(1)x e x y x -'=，所以xe y x=在(,0)-∞上单调递减且0y <，在(0,1)上单调递减且y e >，在(1,)+∞上单调递增且y e >，因此a e >且1201x x <<<， A 正确；因为1212,x xe ax e ax ==，所以2121x x x ex -=，设21x t x =，则1(1)1ln 1,1t x t t et x t ->=⇒=-，因此12111142(1)2(ln 2)(ln 2)1111t t t x x t x t t t t t t +-++-=+-=-⨯=-+-+-+令4()ln 21g t t t =-++，则22214(1)()0(1)(1)t g t t t t t -'=-=>++，所以()(1)0g t g >=，因此121220, 2.x x x x +->+> B正确；2121111)1)x x tx t -=-==令()ln h t t=-1()0h t t '=-=<，所以()(1)0h t h <=，因此121210,1x x x x -<<，C 错；由()0x f x e a '=-=得ln 1x a =>，当ln x a >时，()0f x '>，当ln x a <时，()0f x '<，所以()x f x e ax =-有极小值点0ln x a =，由1212,x x e ax e ax ==得1122ln ln ,ln ln x a x x a x =+=+，因此12121212120+2ln ln ln +2ln ln 0+2ln 2.x x a x x x x a x x x x a x =++⇒-=<⇒<=D 正确二、填空题（共4 小题，每题5 分，共 20 分）13.【2015海南嘉积中学五模】已知曲线f (x )＝x sin x ＋1在点(2π，2π＋1)处的切线与直线ax －y ＋1＝0互相垂直，则a ＝________.【答案】1-14.【2015江西高安中学月考】已知函数)(x f 是R 上的奇函数，且)2(+x f 为偶函数．若1)1(=f ，则=+)9()8(f f __________【答案】1 【解析】试题分析：因为()2+x f 是偶函数，所以()()22+=+-x f x f ，所以函数关于2=x 对称，那么()()()x f x f x f -=+=-4，所以函数满足()()()x f x f x f =+-=++444，所以函数是8=T 的周期函数，所以()()()()11098=+=+f f f f15.【2015黑龙江哈市九中模拟】已知向量2(,1),(1,)a x x b x t =+=-，若函数()f x a b =⋅在区间(1,1)-上是增函数，则实数t 的取值范围是 ．【答案】[)∞+，516.【2015江西临川一中五月模拟】已知定义在R 上的函数()f x 的图象连续不断,若存在常数()R t t ∈,使得()()0f x t tf x ++=对任意的实数x 成立,则称f (x )是回旋函数,其回旋值为t ．给出下列四个命题：①函数()2f x =为回旋函数的充要条件是回旋值t ＝－1； ②若x y a =(a >0,且a ≠1)为回旋函数,则回旋值t ＞1；③若()sin (0)f x x ωω=≠为回旋函数,则其最小正周期不大于2； ④对任意一个回旋值为t (t ≥0)的回旋函数f (x ),方程()0f x =均有实数根．其中为真命题的是_____________(写出所有真命题的序号)． 【答案】①③④ 【解析】试题分析：①是真命题,因为当t ＝－1时()()220f x t tf x ++=-=,对于②,当t ＞1时恒有()()0x t x f x t tf x a ta +++=+>,故②错；对于③,()()()0sin sin 0f x t tf x x t t x ωω++=⇔++=,取0x =得sin 0t ω=,令π2x =,得cos t t ω=-,所以1t =± ,()k k ωπ=∈Z ,所以2π2T ω=≤,故③正确；对于④,若t =0,则f （x ）=0满足条件,若0t >,令()()00f t x f t=⇒=-,所以()()00f f t <,故函数()f x =0有实根,④正确.：。

班级 姓名 学号 分数大题狂做测试卷6(测试时间：90分钟 满分：120分)1。

【天津市武清区杨村第一中学2015届高三上学期第一次阶段性检测数学（理）】已知函数x xx f -=3)(.（Ⅰ）求)(x f 在区间]0,2[-上的最大值； (Ⅱ）若过点),2(t P 存在3条直线与曲线)(x f y =相切，求t 的取值范围．【答案】(Ⅰ）239；（Ⅱ）62<<-t 。

（Ⅱ）设切点为),(03x xx -，切线斜率1320-=x k从而切线方程为))(13()(02003x x x x x y --=-- …………7分又过点),2(t P ,所以)2)(13()(020030x x x x t --=--整理得0262203=++-t x x令262)(23++-=t x x x g ，则x x x g 126)(2/-=由0)(/=x g得0=x 或2=x当x 变化时，)(x g 与)(/x g的变化如下表:…………11分于是,⎩⎨⎧<-=>+=06)2(02)0(t g t g ，所以62<<-t …………12分 【考点】1。

导数与函数的单调性、极值;2.导数几何意义.2.【浙江省绍兴市第一中学2015届高三下学期回头考试数学（理）】已知正项数列{}na 的前n 项和为11,,2nS a=且满足1241()n nS S n N *+=+∈． （Ⅰ）求数列{}na 的通项公式；(Ⅱ)当1i n ≤≤，1j n ≤≤（,,i j n 均为正整数）时，求ia 和j a 的所有可能的乘积i ja a之和。

【答案】(Ⅰ）22n na-=；(Ⅱ）21(21)4n- .x )0,(-∞0 )2,0(2),2(+∞)(/x g+— 0 +)(x g↗极大值↘极小值↗【考点】1。

数列nS 与na 的关系；2。

等比数列的性质与求和.3。

【天津市南开中学2015届高三第四次月考数学(理）】设()4sin sin cos 63f x x x x ππ⎛⎫⎛⎫=++-+ ⎪ ⎪⎝⎭⎝⎭.（Ⅰ)求函数()f x 的最小正周期和单调递减区间； (Ⅱ）若锐角ABC ∆中，,,A B C 的对边分别为,,,a b c 且()2f A =，2a =,6b =求角C 及边c . 【答案】(Ⅰ)2T π=， ()f x 的单调递减区间是52,244k k ππππ⎡⎤++⎢⎥⎣⎦()k Z ∈ ；（Ⅱ) 512C π=，31c =+。

1。

【黑龙江省大庆第一中学2014届高三下学期第二次阶段考试数学（文）】在ABC ∆中，设内角,,A B C 的对边分别为,,a b c 向量(cos ,sin )m A A =,向量(2sin ,cos )n A A =-，若2m n +=(1）求角A 的大小 (2)若42b =，且2c a =，求ABC ∆的面积.1(1)4A π=； (2)16。

2. 【吉林省实验中学2015届高三上学期第五次模拟考试数学（文)】已知正项数列}{na 的首项11=a,前n 项和n S 满足)2(1≥+=-n S S a n n n ．（I ）求证：}{n S 为等差数列,并求数列}{n a 的通项公式；(II ）记数列}1{1+n n a a 的前n 项和为n T ,若对任意的*N n ∈,不等式a a T n -<24恒成立,求实数a 的取值范围． 2（I ）12-=n a n ；（2）)121121(21)12)(12(111+--=+-=+n n n n a a n n ，∴21)1211(21)1211215131311(21<+-=+--++-+-=n n n T n ,又 a a T n -<24，∴a a -≤22，解得1-≤a 或2≥a ，即所求实数a 的取值范围为1-≤a 或2≥a ．3. 【山东省枣庄市第八中学2015届高三4月模拟考试数学(文)】如图，在ABC ∆中,已知10,14,3AB AC B π===，D 是BC 边上的一点， 6.DC =(Ⅰ）求ADB ∠的值；（Ⅱ）求sin DAC ∠的值。

3法一：（Ⅰ）由余弦定理222cos 2AB BC AC B AB BC +-=⋅得2100196cos 3210BC BCπ+-=⨯⨯，166()BC BC ==-或舍去,210,33BD ABD ADB ADC ππ=∆∠=∠=等边三角形，， (Ⅱ）2221001963613cos 22101414AD AC CD DAC AD AC +-+-∠===⋅⨯⨯得33sin 14DAC ∠=法二:由正弦定理可得5311sin cos sin sin 1414AB AC C C C B =⇒=⇒=，222cos 102AC DC AD C AD AC DC+-=⇒=⋅,210,33BD ABD ADB ADC ππ=∆∠=∠=等边三角形，， 由正弦定理可得33sin sin sin 14AD DC DAC C DAC =⇒∠=∠4。

【百强校】一轮复习之小题精做9一、选择题（共12 小题，每题5 分，共60 分）1.【2015湖北荆州中学质检】已知集合，则( )A ．B ．C ．D ． 2.【2015福建泉州一中5月模拟】下列说法正确的是A ．“若3x π=，则sin x =”的逆命题为真 B ．,,a b c 为实数，若a b >，则22ac bc >C ．命题p ：x R ∃∈，使得210x x +-<，则p ⌝：x R ∀∈，使得210x x +->D ．若命题p q ⌝∧为真，则p 假q 真3.【2015江西临川一中检测】下列函数中，既是偶函数又在区间(－∞，0)上单调递增的是( )A. f(x)＝21xB. f(x)＝x 2＋1C. f(x)＝x 3D. f(x)＝2－x 4.【2015湖南长流宁市三县一中5月模拟】设{a n }是等比数列，则“a 1<a 2 <a 4”是“数列{a n }是递增数列”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件5.【2015甘肃天水一中五月仿真】设全集为R , 函数()f x =的定义域为M , 则C M R 为 （ ）A ．(-∞,1)B ．(1, + ∞)C ．(,1]-∞D ．[1,)+∞6.【2015湖北四校联考】设α为锐角，若cos ()6πα+＝45，则sin (2)3πα+的值为（ ） A ．2512 B ．2425 C ．2425- D ．1225- 7.【2015海南省海南中学5月月考】将函数()y f x =的图像向右平移2π单位得到函数cos 2y x =的图像，则将函()y f x =的横坐标伸长到原来的2倍，纵坐标不变，得到函数()y g x =的图像，则()g x =（ ）A ．sin 4x -B ．cos 4xC ．sin xD ．cos x -8.【2015湖南浏阳中学月考】函数x x x f 2)1ln()(-+=的零点所在的大致区间是 （ ） A ．（3，4） B ．（2，e ） C ．（1，2）D ．（0，1）9.【2015黑龙江哈尔滨市六中三模】函数)4sin 2cos 4cos2(sin log 21ππx x y -=的单调递减区间是（ ） A.Z k k k ∈++),85,8(ππππ B.Z k k k ∈++),83,8(ππππ C.Z k k k ∈+-),83,8(ππππ D.Z k k k ∈++),85,83(ππππ 10.【2015东北师大附中四模】函数1ln ||x x y e e -=-的部分图象大致为( )11.【2015山东省实验中学一模】函数)(x f 的定义域为A ，若1x ，A x ∈2且)()(21x f x f =时总有21x x =，则称)(x f 为单函数，则：①函数3)1()(-=x x f 是单函数；②函数⎩⎨⎧<-≥=2,22,log )(2x x x x x f 是单函数；③若)(x f 为单函数，1x ， A x ∈2且21x x ≠，则)()(21x f x f ≠；④若函数)(x f 在定义域内某个区间D 上具有单调性，则)(x f 一定是单函数；以上命题正确的是（ ）A ．①④B ．②③C ．①③D ．①③④12.【2015黑龙江省哈尔滨市九中三模】已知函数()()21ln ,2+==x x g e x f x ，对()+∞∈∃∈∀,0,b R a ，使得()()b g a f =，则a b -的最小值为A . 22ln 1+B ． 22ln 1- C ． 12-e D ．1-e 二、填空题（共 4 小题，每题5 分，共 20 分）13.【2015湖北荆州中学质检】若b a bx ax x f +++=3)(2是偶函数，其定义域是[]a a 2,1-，则)(x f 的最大值为 ．14.【2015福建泉州中学模拟】已知a 、b 、c 分别为ABC ∆三个内角A 、B 、C 的对边，sin cos a A a B =-则角B =__________.15.【2015湖南长沙雅礼中学月考】数列｛n a ｝中，1a ＝2a ＝1, 2＋n a ＝1＋n a ＋n a ，它的通项公式为n a ＝⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛n n 25125151＋12的最大整数为 . 16.【2015江西高安中学押题一】已知函数32()f x x ax bx c =+++有两个极值点12,x x ，若112()f x x x =<，则关于x 的方程22(())()033b f x af x ++=的不同实根个数为 .：。