北京理工大学624电磁学2012-2015真题

课程编号:INF05005 北京理工大学2013-2014学年第一学期2011级电子类电磁场理论基础期末试题B 卷班级________ 学号________ 姓名________ 成绩________一、简答题（12分）1．请写出无源媒质中瞬时麦克斯韦方程组积分形式的限定形式。

（4分） 答：媒质中无源，则0su J =，0ρ=()l s E H dl E ds t ∂εσ∂⎡⎤⋅=+⋅⎢⎥⎢⎥⎣⎦⎰⎰()lsH E dl ds t∂μ∂⋅=-⋅⎰⎰=0sE ds ε⋅⎰=0sH ds μ⋅⎰（评分标准：每式各1分）2．请写出理想导体表面外侧时变电磁场的边界条件。

（4分）答：⎩⎨⎧==⨯00ˆt E E n,⎩⎨⎧==⋅s nsD D n ρρˆ, ⎩⎨⎧==⋅00ˆnB B n, ⎩⎨⎧==⨯s t sJ H J H nˆ3．请利用动态矢量磁位A 和动态电位U 分别表示磁感应强度B 和电场E ；并简要叙述引入A 和U 的依据条件。

（4分）答：B A =∇⨯，AE U t∂=-∇-∂； 引入A 的依据为：0B ∇⋅=，也就是对无散场可以引入上述磁矢位；引入U 的依据为：0A E t ⎛⎫∂∇⨯+= ⎪∂⎝⎭，也就是对无旋场，可以引入势函数。

二、选择题（共20分）（4题）1. 以ˆz为正方向传播的电磁波为例，将其电场分解为x ，y 两个方向的分量：(,)cos()x xm x E z t E t kz ωφ=-+和(,)sin()y ym y E z t E t kz ωφ=-+。

判断以下各项中电磁波的极化形式：线极化波为（ B ）；右旋圆极化波为（ C ）。

（4分）A. x y φφπ-=,3ym xmE E = B. 2x y πφφ-=，3ym xmE E =C. 0x y φφ-=， xm ym E E =D. x y φφπ-=-， xm ym E E =2. 以下关于导电媒质中的均匀平面电磁波论述正确的是（ BC ）。

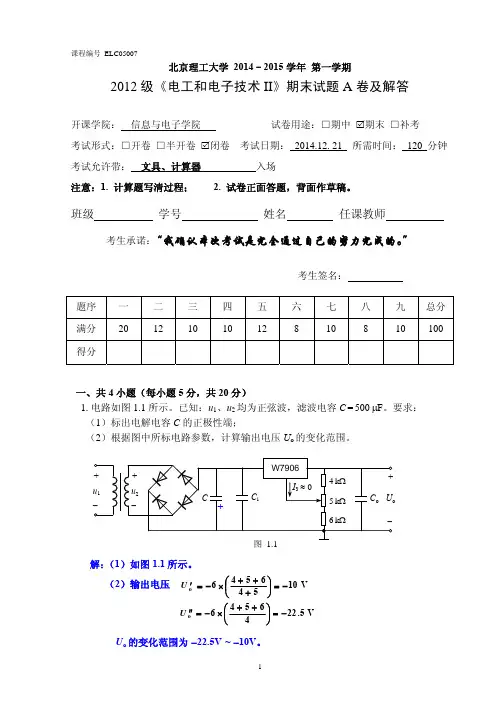
一、图示系统处于同一铅锤平面内，半径为R 1=3r 的圆盘在半径为R 2=33r 的固定凹圆面上做纯滚动，通过长为L=3r 的连杆BC 带动滑块C 沿倾角为60°的滑道滑动，且AB=r 。

在图示时刻（D 、A 两点连线为铅垂线，A 、B 两点连线与水平线夹角为90°并与BC 垂直，B 、C 处为铰接），圆盘角速度、角加速度分别为0W 、2023W ，转向如图所示，试求该瞬时滑块C 的速度和加速度。

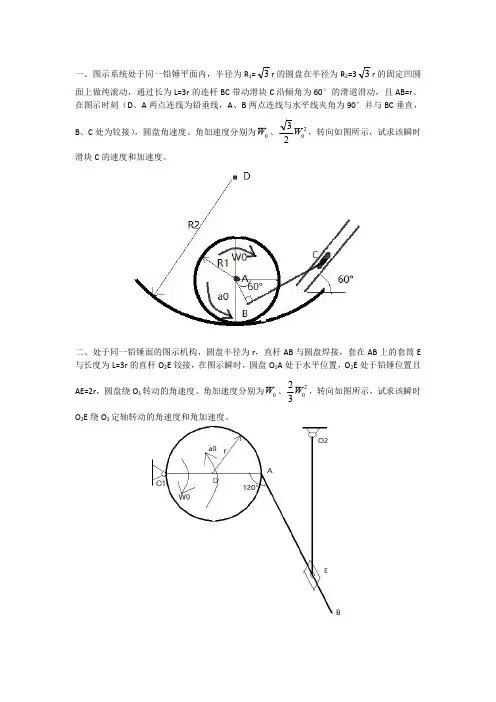
二、处于同一铅锤面的图示机构，圆盘半径为r ，直杆AB 与圆盘焊接，套在AB 上的套筒E 与长度为L=3r 的直杆O 2E 铰接，在图示瞬时，圆盘O 1A 处于水平位置，O 2E 处于铅锤位置且AE=2r ，圆盘绕O 1转动的角速度、角加速度分别为0W 、2032W ，转向如图所示，试求该瞬时O 2E 绕O 2定轴转动的角速度和角加速度。

三、图示系统处于同一铅锤面，均质圆盘半径为r ，重量为P,细杆0A 长度为L=23r ，自重不计，圆盘与墙面摩擦因数为23f s =D ，圆盘与直杆间123f s =B ,不计固定铰支座O 处摩擦，今在OA 的A 端作用一与杆成60°夹角的图示指向的主动力F ，大小为F=2P ，为使系统在图示位置保持平衡需在圆盘上作用一主动力偶，求力偶M 的取值范围。

四、图示平面机构由OA 、AB 、CD 和直角弯杆BEG 在接触处相互铰接而成，O 、G 为固定支座，几何尺寸由图所示M=2ql 2，不计各自重和摩擦，求CD 杆内力。

L 33L32五、同一铅锤面内，滑块A 和质心为D 的套筒质量都为m ，套筒对其定轴回转半径为AD=b,b 62=D ρ；与滑块A 铰接的可在套筒D 中滑动的均质细直杆AB 质量为m 1=2m ，长度为L=4b ，弹簧原长为L 0=2b ，刚度系数为mg =K ，不计摩擦，系统在图示位置无初速释放，求滑块沿铅锤滑道刚上升b 高度的瞬时杆AB 的角速度W AB ,并写出系统的动量和对点D 的动量矩。

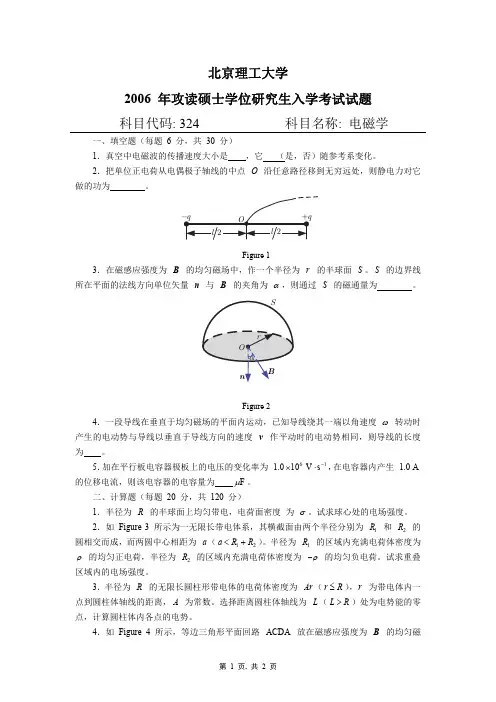
北京理工大学2006 年攻读硕士学位研究生入学考试试题 科目代码: 324科目名称: 电磁学一、填空题（每题 6 分，共 30 分）1．真空中电磁波的传播速度大小是 ，它 （是，否）随参考系变化。

2．把单位正电荷从电偶极子轴线的中点 O 沿任意路径移到无穷远处，则静电力对它做的功为 。

Figure 13．在磁感应强度为 B 的均匀磁场中，作一个半径为 r 的半球面 S 。

S 的边界线所在平面的法线方向单位矢量 n 与 B 的夹角为 α，则通过 S 的磁通量为。

Figure 24．一段导线在垂直于均匀磁场的平面内运动，已知导线绕其一端以角速度 ω 转动时产生的电动势与导线以垂直于导线方向的速度 v 作平动时的电动势相同，则导线的长度为 。

5．加在平行板电容器极板上的电压的变化率为 611.010 V s -⨯⋅，在电容器内产生 1.0 A 的位移电流，则该电容器的电容量为 F μ。

二、计算题（每题 20 分，共 120 分）1．半径为 R 的半球面上均匀带电，电荷面密度 为 σ。

试求球心处的电场强度。

2．如 Figure 3 所示为一无限长带电体系，其横截面由两个半径分别为 1R 和 2R 的圆相交而成，而两圆中心相距为 a （12a R R <+）。

半径为 1R 的区域内充满电荷体密度为 ρ 的均匀正电荷，半径为 2R 的区域内充满电荷体密度为 ρ- 的均匀负电荷。

试求重叠区域内的电场强度。

3．半径为 R 的无限长圆柱形带电体的电荷体密度为 Ar （r R ≤），r 为带电体内一点到圆柱体轴线的距离，A 为常数。

选择距离圆柱体轴线为 L （L R >）处为电势能的零点，计算圆柱体内各点的电势。

4．如 Figure 4 所示，等边三角形平面回路 ACDA 放在磁感应强度为 B 的均匀磁场中，磁场方向垂直于回路平面。

回路上的 CD 段为滑动导线，它以匀速 v 远离 A 端运动，并始终保持回路是等边三角形。

西安电子科技大学2012年攻读硕士学位研究生入学考试试题 考试科目代码及名称 822 电磁场与微波技术 A 考试时间 2012 年 1 月 8 日下午（ 3 小时）答题要求:所有答案（填空题按照标号写）必须写在答题纸上，写在试卷上一律作废，准考证号写在指定位置!一、（15 分）位于XOY 平面内的半径为a 、圆心在坐标原点的均匀带电圆盘，其面电荷密度为ρs ，如图所示，试求圆盘的电位。

二、（15 分）一个Z 方向无限长、横截面为axb 的矩形金属管，其三个边的电位为零，第四边与其它边绝缘，电位是10sin()xaπ，如图所不，试求管内的电位分布。

三、（15 分）已知无源自由空间中的电场强度矢量y m E E sin(t kz)êω=-（1）由麦克斯韦方程求磁场强度；（2）证明ω/k 等于光速；（3）试求坡印廷矢量的时间平均值。

四、（15分）均匀平面电磁波自空气入射到理想导体表面（z=0）。

己知入射波电场)5(j z i x E e e e -=+（V/m ）试求：（1）反射波电场和磁场；（2）理想导体表面的面电荷密度和面电流密度。

五、（25 分）（1）特性阻抗Z 0=500Ω，负载Z L =1000Ω，试求输入反射系数г和驻波比ρ。

（2）试给出导波波长λg 与波长λ的关系式。

如图a*b 矩形波导，试求TE 10截止波长λc 。

（3）什么是TEM 波？什么是TE 、TM 波？ （4）为什么柱形空心波导不能传输TEM 波？（5）带线传输线如图。

若带宽w 增加，特性阻抗如何变化？若高度b 增加，特性阻抗如何变化？为什么？六、（10 分）典型的微波衰减器网络如图所示，其中均表示归一化参数。

试求出输入端匹配时要求1R 和2R 满足的关系式（1R 和2R表示电阻）。

七、（10 分）半波长矩形波导（两端短路）谐振腔如图所示，若工作模式为TE 101，试画出电磁场分布图。

八、（10 分）若天线在最大辐射方向的辐射电场为 ˆˆ()()y x j j jkz xm ym E z xEe yE e e φφ-=+ ，则 （1）在 情况下，天线呈线极化特性；（2）在 情况下，天线呈圆极化特性； （3）左旋圆极化天线发射 极化波； （4）右旋圆极化天线接收 极化波。

2012年普通高等学校招生全国统一考试 数学 （理）（北京卷）第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项. 1.已知集合{}320A x R x =∈+>，{}(1)(3)0B x R x x =∈+->，则A B = ( ) A ．(,1)-∞- B ．2(1,)3-- C ．2(,3)3- D ．(3,)+∞2.设不等式组0202x y ≤≤⎧⎨≤≤⎩表示的平面区域为D.在区域D 内随机取一个点，则此点到坐标原点的距离大于2的概率是（ ） A ．4π B ．22π- C ．6π D ．44π- 3.设,a b R ∈, “0a =”是“复数a bi +是纯虚数”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分又不必要条件4. 执行如图所示的程序框图，输出的S 值为（ ） A ． 2 B ． 4 C ． 8 D ． 165.如图，∠ACB=90°，CD ⊥AB 于点D,以BD 为直径的圆与BC 交于点E ，则（） A ．CE ·CB=AD ·DB B ．CE ·CB=AD ·AB C ．AD ·AB= 2CD D ．CE ·EB= 2CD6.从0,2 中选一个数字，从1,3,5中选两个数字，组成无重复数字的三位数， 其中奇数的个数为（ ）A ． 24B ． 18C ． 12D ． 67. 某三棱锥的三视图如图所示，该三棱锥的表面积是（ ） A．28+ B．30+ C．56+．60+8. 某棵果树前n 年得总产量n S 与n 之间的关系如图所示，从目前记录的结果看，前m 年的年平均产量最高，m 的值为（ ）A ．5B ． 7C ． 9D ．11（第4题图）B第二部分（非选择题 共110分） 二、填空题：本大题共6小题，每小题5分，共30分. 9. 直线2,1x t y t =+⎧⎨=--⎩（t 为参数）与曲线3cos 3sin x y =α⎧⎨=α⎩（α为参数）的交点个数为 .10.已知{}n a 为等差数列，n S 为其前n 项和.若112a =，23S a =，则2a = . 11.在△ABC 中，若2a =，7bc +=，1cos 4B =-，则b = . 12.在直角坐标系xoy 中，直线l 过抛物线24y x =的焦点F,且与该抛物线相较于A 、B 两点，其中点A 在x 轴上方，若直线l 的倾斜角为60°，则△OAF 的面积为 .13.已知正方形ABCD 的边长为1，点E 是AB 边上的动点，则DE CB ⋅的值为 ； DE DC ⋅的最大值为 .14.已知()(2)(3)f x m x m x m =-++，()22x g x =-.若同时满足条件：①,()0x R f x ∀∈<或()0g x <；②(,4)x ∃∈-∞- ，()()0f x g x <. 则m 的取值范围是 . 三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15.（本小题13分） 已知函数(sin cos )sin 2()sin x x xf x x-=.（1）求()f x 的定义域及最小正周期； （2）求()f x 的单调递增区间.16. （本小题14分）如图1，在Rt △ABC 中，∠C=90°，BC=3，AC=6，D,E 分别是AC ，AB 上的点， 且DE ∥BC ，DE=2，将△ADE 沿DE 折起到△A 1DE 的位置，使A 1C ⊥CD ，如图2. （1）求证：A 1C ⊥平面BCDE;（2）若M 是A 1D 的中点，求CM 与平面A 1BE 所成角的大小；（3）线段BC 上是否存在点P,使平面A 1DP 与平面A 1BE 垂直？说明理由.17.（本小题13分）近年来，某市为促进生活垃圾的分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱，为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾，数据统计如下（单位：吨）：（1）试估计厨余垃圾投放正确的概率； （2）试估计生活垃圾投放错误的概率；（3）假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为,,a b c ，其中0a >，600a b c ++=.当数据,,a b c 的方差2S 最大时，写出,,a b c 的值（结论不要求证明），并求此时2S 的值. （注：方差2222121[()()()]n s x x x x x x n=-+-++- ，其中x 为12,,n x x x 的平均数）18.（本小题13分）已知函数2()1f x ax =+（0a >），3()g x x bx =+.（1）若曲线()y f x =与曲线()y g x =在它们的交点（1，c ）处具有公共切线，求,a b 的值； （2）当24a b =时，求函数()()f x g x +的单调区间，并求其在区间(,1]-∞-上的最大值.19.（本小题14分）已知曲线C: 22(5)(2)8()m x m y m R -+-=∈ (1)若曲线C 是焦点在x 轴的椭圆，求m 的范围；(2)设4m =，曲线C 与y 轴的交点为A,B （点A 位于点B 的上方），直线4y kx =+与曲线C 交于不同的两点M,N,直线1y =与直线BM 交于点G 求证：A,G,N 三点共线.20.（本小题13分）设A 是由m n ⨯个实数组成的m 行n 列的数表，满足：每个数的绝对值不大于1，且所有数的和为零.记(,)S m n 为所有这样的数表构成的集合.对于(,)A S m n ∈，记()i r A 为A 的第i 行各数之和1i m ≤≤，()j c A 为A 的第j 列各数之和1j n ≤≤； 记()k A 为1|()|r A ，2|()|r A ，…，|()|m r A ，1|()|c A ，2|()|c A ，…，|()|n c A 中的最小值. （1）对如下数表A,求()k A 的值；（2）设数表A=(2,3)S 形如求()k A 的最大值；（3）给定正整数t ，对于所有的A ∈S(2，21t +),求()k A 的最大值。

北京大学信息科学技术学院考试试卷考试科目： 电磁学 姓名： 学号： 考试时间： 2012 年 6 月 20 日 任课教师:以下为试题和答题纸，共 10 页。

题 号 一 二三 四 五 六 总分分 数 阅卷人一、（30分）填空、判断、简答1.（10分）判断题，请在每一小题前面的空格内写上“对”或者“错”解答 题号 题目错 （1） 某点的电场强度的方向就是点电荷在该点所受的电场力的方向。

错 （2） 电势为零处电场强度也为零。

对 （3） 有一个未接地的金属导体形成的闭合空腔。

如果只改变导体外表面以外的电荷量，则空腔内的电场不会发生改变；如果只改变空腔内表面以内的电荷量，则空腔外的电场会发生改变。

错 （4） 在外磁场中，圆形载流线圈整体受到的总的安培力必为零。

对 （5） 电场强度沿一闭合环路的环量可以不等于零。

2.（8分）选择题，请请从选项中选择正确的答案，将正确选项前的字母A、B 或C，填在小题前面的空格内。

解答题号 题目和选项A(1） 将一个空心的螺线管（其自身的电阻忽略不计），和一个电阻串联后连接到理想无内阻的稳压直流电源上，然后将一个原本未磁化的铁棒匀速插入螺线管中。

插入过程中，铁棒受磁场的作用力的情况是： A. 吸引力， B.排斥力， C.不受力；A（2） 如上（1）所述，与插入铁棒之前相比较，螺线管内的磁场能变化是：A.增加，B.减少，C.不变；A（3） 如上（1）所述，电源的输出功率：设插入铁棒之前为P 1，插入铁棒的过程中平均功率为P 2，插入铁棒之后为P 3；请问P 1和P 2之间的关系是：A. P 1 > P 2 ,B. P 1 = P 2 ,C. P 1 < P 2 ；B（4） 如上（3）所述，请问P 1和P 3之间的关系是： A. P 1 > P 3 , B. P 1 = P 3 , C. P 1 < P 3 ；3. （12分）填空题（1）假设有一电流元为Idx iˆ位于坐标原点处，其中，I 为电流强度，dx 为x 坐标的微分，i ˆ是x 方向单位矢量（分别以i ˆ，j ˆ，kˆ代表x，y，z 方向的单位矢量），某点P 1（a ，0，0），其中,a≠0,请问电流元在P 1点产生的磁感应强度B K=（ 0 ）（2）如上（1）所述，如果有某点P 2（0，0，c ）, 且c > 0, 请问电流元在P 2点产生的磁感应强度B K=（ j cIdx ˆ420πμ−）（3）理想电感L 和电阻R 串联构成闭合回路，初始时刻电路中的电流为I ，假设不考虑电磁辐射，请问经过很长时间后最终电阻R 上产生的焦耳热的总能量是：（ LI 2/2 ）（4）已知一个处于静电平衡的导体，电势为U ，带有电荷量为Q ，其静电能是：（ QU/2 ）二、(15分) 如图所示，一半径为R 的圆柱形无穷长直导线内通有均匀分布的稳恒电流I ，导线的相对磁导率为1。

892 力学与电磁学综合（2012版）请考生注意：1、《力学与电磁学综合》试题含力学和电磁学两部分的内容。

2、每部分试题满分75分。

一、基本内容与要求第一部分：力学(一)质点运动学；动量定理及动量守恒定律1、掌握伽利略变换和经典力学的速度变换关系。

理解伽利略变换蕴含的时空观。

理解物理量在时空坐标变换下具有协变性或对称性的问题。

掌握惯性定律及其涉及的时空观问题。

2、从动量定理和动量守恒观点重新认识牛顿第二、第三定律。

掌握非惯性系的动力学中平动惯性力、离心惯性力和科里奥利力的概念。

3、掌握冲量概念，质点组的动量定理，质心运动定理和用外力矢量和为零为条件表述的动量守恒定律。

4、通过动量守恒定律和牛顿定律对伽利略变换的不变性，初步理解物理规律对时空坐标变换的对称性。

（二）动能和势能；角动量.关于对称性；万有引力1、理解对力作功、元功、变力的功以及作用力反作用力之功的关系。

2、掌握质点和质点组动能定理并正确应用。

掌握势能概念。

对于各种力作功情况，正确运用动能定理和机械能守恒定律。

3、运用动量和能量研究碰撞和散射问题。

在质心系研究碰撞问题。

4．掌握质点和质点组的角动量定理的角动量守恒定律以及对质心的角动量定理和守恒律。

5、认识总能量对时空坐标变换的对称性和守恒律的关系。

6．理解万有引力定律的建立、内容、叠加原理以及定律在物理学、天文学的及星际航行中的意义。

在保守力概念基础上建立引力势能的概念。

7、研究与引力有关的一系列问题，如逃逸速度、潮汐和宇宙膨胀。

（三）刚体力学1、掌握在运动学方面可用描述质点运动的方法描述平动。

用微积分研究角位移、角速度和角加速度间的关系。

2、刚体定轴转动动力学。

掌握转动惯量概念，用积分法求简单形状物体的转动量，运用平行轴定理和垂直轴定理。

掌握从质点组角动量定理导出转动定理，从质点组动能定理推出转动的动能定理。

3、刚体平面运动。

质心运动定理和绕质心轴的转动定理。

讨论力沿作用线的滑移、力偶和力的平移等作用于刚体的力的性质，掌握克尼希定理在刚体上的应用，滚动摩擦力偶矩。

北京理工大学2017 年攻读硕士学位研究生入学考试试题 科目代码：624科目名称：电磁学1．厚度为 2d 的无限大带电平板的电荷体密度为 0x d ρρ=。

按如图 1 所示那样建立坐标系，求（1）在 0x > 区域的电场强度分布；（2）在 0x > 区域的电势分布。

2．如图 2 所示的螺旋线由载流 I 的长导线密绕而成，其内、外半径分别为 1R 、2R ，载流线圈共 N 匝。

求螺旋线中心 O 处的磁感应强度。

图 11R 2R图 23．一同轴圆柱形电容器，内圆柱的半径为 1R ，外圆柱的半径为 2R ，长为 L （21L R R −2），两圆柱之间充满相对介电常数为 r ε 的各项同性均匀电介质。

设内、外圆柱单位长度上的带电量（电荷线密度）分别为 λ+ 和 λ−。

求：（1）该电容器的电容； （2）电容器储存的能量。

4．（30 分）如图 3 图所示，一半径为 a 的小圆线圈，电阻为 R ，开始时与一个半径为 b （b a 2）的大线圈共面且同心，固定大线圈，并在其中维持恒定电流 I ，使小线圈绕其直径以匀角速度 ω 转动（忽略线圈的自感）。

求：（1）小线圈中的感应电流；（2）求大线圈和小线圈之间的互感系数； （3）大线圈中的感应电动势。

5．无限长直圆筒的电荷面密度为 σ，以角加速度为 β（β 为常数）绕其中心轴线转动，如图 4 所示。

（1）求空间磁场分布； （2）求空间电场分布；（3）在圆筒外部放置一根无限长的导线 AB ，求 AB 中的电动势的大小和方向。

图3A B图46．如图5 所示，平行板电容器的上下极板面积为均为S，板间距为d，板间电压为0U。

今用力F将高度为d的木板往电容里推。

（情形一）若电容器充满电后断开电源，求：（1）将木板完全推入电容器后，力F所做的功1A；（2）求将木板推进距离x后木板受到的力的大小和方向。

（情形二）若电容器一直与电源保持连接，求：（1）将木板完全推入电容器后，力F所做的功2A；（2）求将木板推进距离x后木板受到的力的大小和方向。

高考物理2024电磁学历年题目全解在高考物理中，电磁学是一个重要的考点。

了解历年的电磁学题目，并进行全面解析，可以帮助考生更好地熟悉相关知识点和解题技巧。

以下将对高考物理2024年的电磁学题目进行全解。

题目一：某电磁波的波长为600nm，频率为5.0×10^14Hz。

求该电磁波的速度。

解析：根据电磁波的性质，速度v=λf，其中λ为波长，f为频率。

代入已知数据可得：v = 600nm × 5.0×10^14Hz = 3.0×10^8 m/s题目二：一根长度为0.5m的导线在磁感应强度为0.4T的磁场中，以速度为2m/s做平行于磁感线的匀速运动。

求导线两端的感应电动势。

解析：根据法拉第电磁感应定律，感应电动势的大小为ε = Blv，其中B为磁感应强度，l为导线长度，v为导线的速度。

代入已知数据可得：ε = 0.4T × 0.5m × 2m/s = 0.4V题目三：一个长度为10cm的导线搁置在水平磁场中，磁感应强度B为2T，导线电阻为5Ω。

当导线两端加上电压为4V时，通过导线的电流大小为多少？解析：根据欧姆定律，电流I = U/R，其中U为电压，R为电阻。

代入数据可得：I = 4V / 5Ω = 0.8A题目四：一根长度为1m的直导线在磁感应强度为1T的均匀磁场中，与磁场中的感应矢量成60°的角。

求直导线两端的感应电动势大小。

解析：根据法拉第电磁感应定律，感应电动势的大小为ε = Bvlcosθ，其中B为磁感应强度，l为导线长度，v为导线的速度，θ为磁场感应矢量与导线的夹角。

代入数据可得：ε = 1T × 1m × v × cos60° = 0.5v V题目五：一个长度为0.6m的直导线，其两端的电势差为6V。

将这根导线匀速地沿着水平方向拉出磁感应强度为 1.2T的磁场。

求导线运动的速度。

解析：根据电动势的定义，电势差等于感应电动势。