人造卫星和卫星中的追击问题

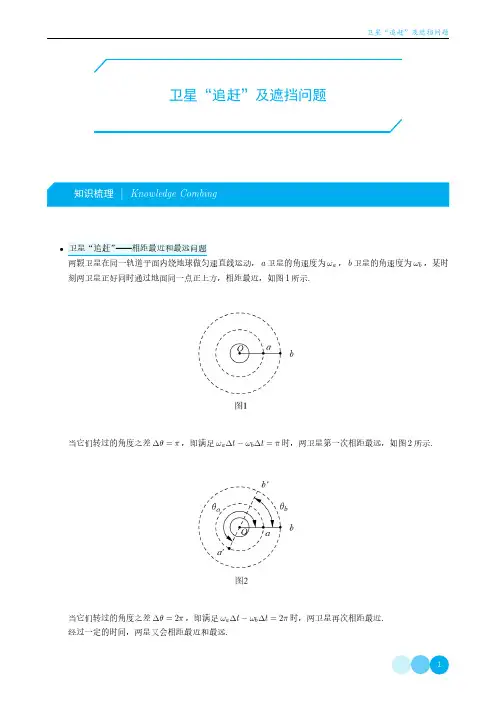
卫星“追赶”及遮挡问题•卫星“追赶”——相距最近和最远问题两颗卫星在同一轨道平面内绕地球做匀速直线运动，a卫星的角速度为ωa，b卫星的角速度为ωb，某时刻两卫星正好同时通过地面同一点正上方，相距最近，如图匱所示匮当它们转过的角度之差匁θ匽π，即满足ωa匁t−ωb匁t匽π时，两卫星第一次相距最远，如图匲所示匮当它们转过的角度之差匁θ匽匲π，即满足ωa匁t−ωb匁t匽匲π时，两卫星再次相距最近匮经过一定的时间，两星又会相距最近和最远匮匱.两星相距最远的条件ωa匁t−ωb匁t匽匨匲n匫匱匩π匨n匽匰,匱,匲,匳...匩匲.两星相距最近的条件ωa匁t−ωb匁t匽匲nπ匨n匽匰,匱,匲,匳...匩期分别为T A和T B，绕行方向与地同一直线上）时开始计时，则要经过•卫星遮挡问题如图匴所示，飞船绕地球做圆周运动，地球半径为R，宇航员在A点测出的张角为α，则飞船扫描地球的弧长为¯MN，若太阳光为平行光，则在A点状态下，宇航员可以观察到日全食匮根据几何关系有即卩卮α匲匽Rr进而可以求出飞船的运行轨道、速度、周期等匮若地球自转周期为T0，卫星绕地球运转周期为T，则一天内飞船经历“日全食”的次数为n匽T0 T若在A点发射信号，则处于地球上¯MN范围内可以接收到信号匮解决卫星遮挡问题，关键在于找对切线位置，进而根据几何关系进行求解匮卫星遮挡问题宇宙飞船以周期为T绕地球作圆周运动时，由于地球遮挡阳光，会经历“日全食”过程，如图所示。

已知地球的半径为R，地球质量为M，引力常量为G，地球自转周期为T0。

太阳光可看作平行光，宇航员在A点测出的张角为α，则则（）动的线速度为匲πR T即卩卮α匲历“日全食”的次数为T T0全食”过程的时间为αT0例题1（$$$）利用三颗位置适当的地球同步卫星，可使地球赤道上任意两点之间保持无线电通讯，目前地球同步卫星的轨道半径为地球半径的匶.匶倍，假设地球的自转周期变小，若仍仅用三颗同步卫星来实现上述目的，则地球自转周期的最小值约为（）匮十.匱卨卂.匴卨千.匸卨卄.匱匶卨O答案卂O解析设地球的半径为R，则地球同步卫星的轨道半径为r匽匶.匶R.已知地球的自转周期T匽匲匴卨，地球同步卫星的转动周期与地球的自转周期一致，若地球的自转周期变小，则同步卫星的转动周期变小.由GMm R2匽m匴π2RT2可知，做圆周运动的半径越小，则运动周期越小.由于需要三颗卫星使地球赤道上任意两点之间保持无线电通讯，所以由几何关系可知三颗同步卫星的连线构成等边三角形并且三边与地球相切，如图由几何关系可知地球同步卫星的轨道半径为r 匽匲R由开普勒第三定律r3T3匽k得T 匽Tr 3r3匽匲匴匨匲R匩3匨匶.匶R匩3≈匴卨故选：卂.O答案十O解析人造卫星绕地球做匀速圆周运动，根据万有引力提供向心力，设卫星的质量为m、轨道半径为r、地球质量为M，有F匽GMmr2匽mω2r解得ω匽…GMr3卫星再次经过某建筑物的上空，卫星多转动一圈，有匨ω−ω0匩t匽匲π地球表面的重力加速度为：g匽GM R2联立解得t匽匲π…gR2r3−ω0故选：十.为匲θ，求同步卫星的轨道半径r赤道上A，B之间的区域，∠AOB和θ表示）习题匲（$$$）我国自主研发的首颗高分辨率对地观测卫星“高分一号”，于匲匰匱匳年匴月匱匲日由长征二号丁运载火箭发射升空，匲匰匱匳年匱匲月正式投入使用，该卫星对地面拍摄的分辨率可达匲米，可对全球进行扫描拍摄，达到了世界的先进水平。

(1)网络结构(2)卫星在椭圆轨道上的远地点、近地点的加速度与对应圆轨道上的加速度关系应用a ＝GMr 2比较．(3)卫星在同一轨道上稳定运行过程中机械能守恒；在变轨过程中，轨道升高机械能增加，轨道降低机械能减少．规律方法卫星变轨问题的有关规律(1)卫星变轨时速度的变化，根据万有引力和所需向心力的大小关系判断；稳定在新轨道上的运行速度变化由v ＝GMr判断． (2)航天器在不同轨道上运行时机械能不同，轨道半径越大，机械能越大．(3)航天器经过不同轨道相交的同一点时加速度相等，外轨道的速度大于内轨道的速度． (4)同一轨道对接，应先减速到低轨再加速回高轨，实现与目标航天器对接． 典例分析【例1】 (多选)(2017年河南六市高三联考)2009年5月，航天飞机在完成对哈勃空间望远镜的维修任务后，由圆形轨道Ⅰ从A 点进入椭圆轨道Ⅱ，B 为轨道Ⅱ上的一点，如图所示．关于航天飞机的运动，下列说法中正确的是( )A ．在轨道Ⅱ上经过A 点的速度小于经过B 点的速度B ．在轨道Ⅱ上经过A 点的速度等于在轨道Ⅰ上经过A 点的速度C ．在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期D．在轨道Ⅱ上经过A点的加速度小于在轨道Ⅰ上经过A点的加速度【答案】AC【例2】(2017年广西四校调研)(多选)“嫦娥三号”发射取得圆满成功，这标志着我国的航空航天技术又迈进了一大步．“嫦娥三号”探月卫星沿地月转移轨道到达距月球表面200 km的P点进行第一次“刹车制动”后被月球捕获，进入椭圆轨道Ⅰ绕月飞行，再经过一次制动进入距月球表面15 km的圆形轨道Ⅱ上绕月球做匀速圆周运动．则下面说法正确的是()A．由于“刹车制动”，卫星沿轨道Ⅱ运动的周期将比沿轨道Ⅰ运动的周期长B．虽然“刹车制动”，但卫星沿轨道Ⅱ运动的周期比沿轨道Ⅰ运动的周期短C．卫星在到达月球附近时需进行第一次“刹车制动”，是因为卫星到达月球附近时的速度大于月球的第二宇宙速度D．卫星沿轨道Ⅱ运动的加速度小于沿轨道Ⅰ运动到P点时的加速度【答案】：BC【解析】：由开普勒第三定律k＝r3T2可知，TⅠ>TⅡ，A项错误，B项正确；由第二宇宙速度的含义可知，卫星到达月球附近并被月球捕获时的速度不能超过月球的第二宇宙速度，不然卫星将脱离月球，C项正确；由GMmr2Ⅱ＝maⅡ，得卫星在轨道Ⅱ上的加速度aⅡ＝GMr2Ⅱ，由GMmr2P＝ma P，得卫星在P点的加速度a P＝GMr2P，因r P>rⅡ，则a P<aⅡ，D项错误．天体相遇问题的解法围绕同一中心天体做圆周运动的运行天体，因在同一轨道上运行快慢相同不可能相遇(除非是同一轨道上绕行方向相反)，故天体的相遇定义为运行天体A 位于运行天体B 正上方时，即A 、B 与中心天体位于同一直线上且A 、B 在中心天体的同一侧时的状态．如图甲，当两运行天体A 、B 的轨道平面在同一平面内时，若运行方向相同，则内侧天体B 比A 每多运行一圈时相遇一次，在Δt 时间内相遇的次数n ＝Δt T B －Δt T A ＝ωB －ωA2πΔt .若运行方向相反时，则A 、B 每转过的圆心角之和等于2π时发生一次相遇，在Δt 时间内相遇的次数为：n ＝ωA Δt ＋ωB Δt 2π＝Δt T B ＋ΔtT A.如图乙，若两运行天体轨道平面不重合时，当A 、B 均运行至P 、Q 所在直线上，且A 、B 位于同侧时二者才相遇，因此从某次相遇到下次相遇，B 比A 一定多转1圈，而且A 、B 各自转的圈数都是半圈的奇数倍，即在Δt 时间内，Δt T A ＝(2k A ＋1)×12，Δt T B ＝(2k B ＋1)×12，且k B －k A ＝1.专题练习1.某行星和地球绕太阳公转的轨道均可视为圆．每过N 年，该行星会运行到日地连线的延长线上，如图所示．该行星与地球的公转半径之比为( )A.N ＋1N 23B.N N －123C.N ＋1N 32D.N N －132【答案】 B【解析】 由开普勒第三定律得r 31＝kT 21，r 32＝kT 22，所以有r 1r 1＝T 2T 123，由于每过N 年，该行星会运行到日地连线的延长线上，即“相遇”，亦即在相同时间内，地球比该行星多转一圈，于是有NT 1＝(N －1)T 2，联立解得r 1r 2＝N N －123.学科&网2．2017年10月19日“神舟十一号”飞船与“天宫二号”空间实验室自动交会对接成功．假设“天宫二号”与“神舟十一号”都围绕地球做匀速圆周运动，为了实现飞船与空间实验室的对接，下列措施可行的是()A．使飞船与空间实验室在同一轨道上运行，然后飞船加速追上空间实验室实现对接B．使飞船与空间实验室在同一轨道上运行，然后空间实验室减速等待飞船实现对接C．飞船先在比空间实验室半径小的轨道上加速，加速后飞船逐渐靠近空间实验室，两者速度接近时实现对接D．飞船先在比空间实验室半径小的轨道上减速，减速后飞船逐渐靠近空间实验室，两者速度接近时实现对接【答案】：C3．(多选)(2017年甘肃天水市联考)有a、b、c、d四颗地球卫星，a还未发射，在地球赤道上随地球表面一起转动，b是处于地面附近的近地轨道上正常运动的卫星，c是地球同步卫星，d是高空探测卫星，各卫星排列位置如图，则有()A．a的向心加速度等于地表重力加速度gB．c在4小时内转过的圆心角为60°C．b在相同时间内转过的弧长最短D．d的运动周期有可能是28小时【答案】：BD4．(多选)物体在万有引力场中具有的势能叫做引力势能，若取两物体相距无穷远时的引力势能为零，一个质量为m 0的质点距质量为M 0的引力中心r 0时，其万有引力势能E p ＝－GM 0m 0r 0(式中G 为引力常量)，一颗质量为m 的人造地球卫星以半径为r 1圆形轨道环绕地球飞行，已知地球的质量为M ，要使此卫星绕地球做匀速圆周运动的轨道半径增大为r 2，则在此过程中( )A ．卫星势能增加了GMm ⎝⎛⎭⎫1r 1－1r 2B ．卫星动能减少了GMm 3⎝⎛⎭⎫1r 1－1r 2 C ．卫星机械能增加了GMm 2⎝⎛⎭⎫1r 1－1r 2 D ．卫星上的发动机所消耗的最小能量为2GMm 3⎝⎛⎭⎫1r 1－1r 2 【答案】：AC【解析】：引力势能的增加量ΔE p ＝－GMm r 2－⎝⎛⎭⎫－GMm r 1＝GMm ⎝⎛⎭⎫1r 1－1r 2，故A 正确；根据万有引力提供向心力，由G Mm r 21＝m v 21r 1，解得v 1＝ hGM r 1，则E k1＝12mv 21＝GMm2r 1. 同理，E k2＝GMm2r 2.所以，动能的减少量为ΔE k ＝GMm 2r 1－GMm 2r 2＝GMm 2⎝⎛⎭⎫1r 1－1r 2，故B 错误； 根据能量守恒定律，卫星增加的机械能等于发动机消耗的能量，为E ＝ΔE p －ΔE k ＝GMm 2⎝⎛⎭⎫1r 1－1r 2，故C 正确，D 错误．5．(2017年河北石家庄模拟)如图所示，有A 、B 两颗卫星绕地心O 做圆周运动，绕行方向相同．A 卫星的周期为T 1，B 卫星的周期为T 2，在某一时刻两卫星相距最近，则(引力常量为G )( )A ．两卫星经过时间t ＝T 1＋T 2再次相距最近B ．两卫星的轨道半径之比为T 321∶T 232C ．若已知两卫星相距最近时的距离，可求出地球的密度D ．若已知两卫星相距最近时的距离，可求出地球表面的重力加速度 【答案】：B8．(多选)(2017年河南三市三模)中国月球探测卫星“嫦娥号”简化后的路线示意图如图所示，卫星由地面发射后，先经过地面发射轨道进入地球附近的停泊轨道做匀速圆周运动；然后从停泊轨道经过调控进入地月转移轨道；到达月球附近时，再次调控进入工作轨道做匀速圆周运动，这时卫星将开始对月球进行探测．已知地球与月球的质量之比为a ，卫星的停泊轨道与工作轨道的轨道半径之比为b ，则下列说法中正确的是 ()A ．卫星从停泊轨道调控进入到地月转移轨道的过程中，卫星的机械能不守恒B ．卫星在停泊轨道运行的速度大于地球的第一宇宙速度C ．卫星在停泊轨道和工作轨道运行的线速度大小之比为b ∶aD ．卫星在停泊轨道和工作轨道运行的周期之比为b b ∶a 【答案】：AD【解析】：卫星变轨需点火做功，故机械能增加，A 对；由v ＝ GMr，半径较大，线速度较小，故停泊轨道速度小于第一宇宙速度，B 错；卫星G Mm r 2＝mv 2r ＝m 4π2T2·r ，v ＝GMr，T ＝2π r 3GM，已知地球与月球质量比为a ，卫星停泊轨道与工作轨道比为b ，则速度比为a ∶b ，卫星停泊轨道与工作轨道周期比为b3∶a，C错D对．学科&网9.2013年5月2日凌晨0时06分，我国“中星11号”通信卫星发射成功．“中星11号”是一颗地球同步卫星，它主要用于为亚太地区等区域用户提供商业通信服务．图为发射过程的示意图，先将卫星发射至近地圆轨道1，然后经点火，使其沿椭圆轨道2运行，最后再一次点火，将卫星送入同步圆轨道3.轨道1、2相切于Q点，轨道2、3相切于P点，则当卫星分别在1、2、3轨道上正常运行时，以下说法正确的是()A．卫星在轨道3上的速率大于在轨道1上的速率B．卫星在轨道3上的角速度大于在轨道1上的角速度C．卫星在轨道1上经过Q点时的速度大于它在轨道2上经过Q点时的速度D．卫星在轨道2上经过P点时的速度小于它在轨道3上经过P点时的速度【答案】D10.发射地球同步卫星时，先将卫星发射至近地圆轨道1，然后点火，使其沿椭圆轨道2运行，最后再次点火，将卫星送入同步圆轨道3.轨道1、2相切于Q点，轨道2、3相切于P点，如图所示．当卫星分别在1、2、3轨道上正常运行时，设卫星在1轨道和3轨道正常运行的速度和加速度分别为v1、v3和a1、a3，在2轨道经过P点时的速度和加速度为v2和a2，且当卫星分别在1、2、3轨道上正常运行时周期分别为T1、T2、T3，以下说法正确的是()A． v1＞v2＞v3 B． v1＞v3＞v2C． a1＞a2＞a3 D． T1＞T2＞T3【答案】B11、如图所示.地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为R,运转周期为T.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角).已知该行星的最大视角为,当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.若某时刻该行星正处于最佳观察期,问该行星下一次处于最佳观察期至少需经历多长时间?【答案】【解析】:根据题意可得行星的轨道半径设行星绕太阳的转动周期为T'由开普勒第三定律有:设行星最初处于最佳观察时期前,其位置超前于地球,且经时间t地球转过角后,该行星再次处于最佳观察期,12、地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动.地球的轨道半径为,运转周期为.地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角(简称视角),如图甲或图乙所示.当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期.已知某行星的最大视角为.求该行星的轨道半径和运转周期.最终计算结果保留两位有效数字)【答案】该行星的轨道半径是,运转周期是.【解析】设行星的轨道半径为r',运行周期为T'当行星处于最大视角处时,地球和行星的连线应与行星轨道相切.由几何关系可以知道:地球与某行星围绕太阳做匀速圆周运动,根据万有引力提供向心力列出等式:。

高中物理：天体运动中的追及相遇问题，卫星的追及和相遇问题地面上的物体常常出现追及相遇问题，关键是找出它们的位移、速度和时间等关系，运动路线应该在同一轨道上。

天体运动中也有追及相遇问题，它与地面上的追及相遇问题在思维有上相似之处，即也是找出一些物理量的关系，但它也不同之处，有其自身特点。

根据万有引力提供向心力，即，所以当天体速度增加或减少时，对应的圆周轨道会发生相应的变化，所以天体不可能能在同一轨道上追及或相遇。

分析天体运动的追及相遇重点是角度、角速度和时间等关系的判断。

1、追及问题例1、如图1所示，有A 、B 两颗行星绕同一颗恒星M 做圆周运动，旋转方向相同，A 行星的周期为T 1，B 行星的周期为T 2，在某一时刻两行星相距最近，则①经过多长时间，两行星再次相距最近？②经过多长时间，两行星第一次相距最远？解析：A 、B 两颗行星做匀速圆周运动，由万有引力提供向心力，因此T 1<T 2。

可见当A 运动完一周时，B 还没有达到一周，但是要它们的相距最近，只有A 、B 行星和恒星M 的连线再次在一条直线上，且A 、B 在同侧，从角度看，在相同时间内，A 比B 多转了2π；如果A 、B在异侧，则它们相距最远，从角度看，在相同时间内，A 比B 多转了π。

所以再次相距最近的时间t1，由；第一次相距最远的时间t 2，由。

如果在问题中把“再次”或“第一次”这样的词去掉，那么结果如何？2、相遇问题1月14日高中物理例2、设地球质量为M，绕太阳做匀速圆周运动，有一质量为m的飞船由静止开始从P点沿PD方向做加速度为a的匀加速直线运动，1年后在D点飞船掠过地球上空，再过3个月又在Q处掠过地球上空，如图2所示（图中“S”表示太阳）。

根据以上条件，求地球与太阳之间的万有引力大小。

解析：飞船开始与地球相当于在D点相遇，经过3个月后，它们又在Q点相遇，因此在这段时间内，地球与太阳的连线转过的角度。

设地球的公转周期为T，飞船由静止开始做加速度为a的匀加速直线运动，则地球的公转半径为所以 地球与太阳之间的万有引力大小为例3、阅读下列信息，并结合该信息解题：（1）开普勒从1609年～1619年发表了著名的开普勒行星运动三定律，其中第一定律为：所有的行星分别在大小不同的椭圆轨道上围绕太阳运动，太阳在这个椭圆的一个焦点上。

微专题三宇宙航行的几种问题知识点一卫星的追及相遇问题1．“北斗"系统中两颗工作卫星1和2在同一轨道上绕地心O 沿顺时针方向做匀速圆周运动，轨道半径为r，某时刻它们分别位于轨道上的A、B两位置，如图所示,已知地球表面处的重力加速度为g，地球半径为R，不计卫星间的相互作用力，以下判断正确的是（）A．这两颗卫星的向心加速度大小为错误!gB ．这两颗卫星的角速度大小为R错误!C．卫星1由位置A运动至位置B所需时间为错误!错误!D．如果使卫星1加速，它就一定能追上卫星22．如图所示，A、B为地球的两个轨道共面的人造卫星，运行方向相同，A为地球同步卫星，A、B卫星的轨道半径的比值为k，地球自转周期为T0，某时刻A、B两卫星距离达到最近，从该时刻起到A、B间距离最远时所经历的最短时间为（) A。

错误! B.错误!C。

错误!D。

错误!3．两颗人造卫星绕地球逆时针运动，卫星1、卫星2分别沿圆轨道、椭圆轨道运动,圆的半径与椭圆的半长轴相等，两轨道相交于A、B两点，某时刻两卫星与地球在同一直线上，如图所示，下列说法中正确的是（)A．两卫星在图示位置的速度v2＝v1B．卫星2在A点的加速度较大C．两卫星在A或B点可能相遇D．两卫星永远不可能相遇知识点二多星问题4.（多选)2017年，人类第一次直接探测到来自双中子星合并的引力波，根据科学家们复原的过程,在两颗中子星合并前约100 s时，它们相距约400 km，绕二者连线上的某点每秒转动12圈,将两颗中子星都看做是质量均匀分布的球体，由这些数据、万有引力常量并利用牛顿力学知识，可以估算出这一时刻两颗中子星（)A．质量之积B．质量之和C．速率之和D．各自的自转角速度5．天文学家如果观察到一个星球独自做圆周运动，那么就想到在这个星球附近存在着一个看不见的黑洞．星球与黑洞由万有引力的作用组成双星，以两者连线上某点为圆心做匀速圆周运动，那么（)A．它们做圆周运动的角速度与其质量成反比B．它们做圆周运动的周期与其质量成反比C．它们做圆周运动的半径与其质量成反比D．它们所受的向心力与其质量成反比6。

卫星的变轨问题、天体追及相遇问题一、卫星的变轨、对接问题1．卫星发射及变轨过程概述人造卫星的发射过程要经过多次变轨方可到达预定轨道，如右图所示。

(1)为了节省能量，在赤道上顺着地球自转方向发射卫星到圆轨道 Ⅰ上。

(2)在A 点点火加速，由于速度变大，万有引力不足以提供向心力，卫星做离心运动进入椭圆轨道Ⅰ。

(3)在B 点(远地点)再次点火加速进入圆形轨道Ⅰ。

2．卫星的对接问题(1)低轨道飞船与高轨道空间站对接如图甲所示，低轨道飞船通过合理地加速，沿椭圆轨道(做离心运动)追上高轨道空间站与其完成对接.(2)同一轨道飞船与空间站对接如图乙所示，后面的飞船先减速降低高度，再加速提升高度，通过适当控制，使飞船追上空间站时恰好具有相同的速度.二、变轨前、后各物理量的比较1．航天器变轨问题的三点注意事项(1)航天器变轨时半径的变化，根据万有引力和所需向心力的大小关系判断；稳定在新圆轨道上的运行速度由v ＝GM r判断。

(2)航天器在不同轨道上运行时机械能不同，轨道半径越大，机械能越大。

(3)航天器经过不同轨道的相交点时，加速度相等，外轨道的速度大于内轨道的速度。

2．卫星变轨的实质 两类变轨离心运动 近心运动 变轨起因卫星速度突然增大 卫星速度突然减小 受力分析 G Mm r 2<m v 2rG Mm r 2>m v 2r 变轨结果变为椭圆轨道运动或在较大半径圆轨道上运动变为椭圆轨道运动或在较小半径圆轨道上运动 3.变轨过程各物理量分析(1)速度：设卫星在圆轨道Ⅰ和Ⅰ上运行时的速率分别为v 1、v 3，在轨道Ⅰ上过A 点和B 点时速率分别为v A、v B.在A点加速，则v A>v1，在B点加速，则v3>v B，又因v1>v3，故有v A>v1>v3>v B.(2)加速度：因为在A点，卫星只受到万有引力作用，故不论从轨道Ⅰ还是轨道Ⅰ上经过A点，卫星的加速度都相同，同理，经过B点加速度也相同．(3)周期：设卫星在Ⅰ、Ⅰ、Ⅰ轨道上的运行周期分别为T1、T2、T3，轨道半径分别为r1、r2(半长轴)、r3，由开普勒第三定律r3T2＝k可知T1<T2<T3.(4)机械能：在一个确定的圆(椭圆)轨道上机械能守恒．若卫星在Ⅰ、Ⅰ、Ⅰ轨道的机械能分别为E1、E2、E3，则E1<E2<E3.三、卫星的追及与相遇问题1．相距最近两卫星的运转方向相同，且位于和中心连线的半径上同侧时，两卫星相距最近，从运动关系上，两卫星运动关系应满足(ωA－ωB)t＝2nπ(n＝1，2，3，…)。

天体运动中的追击相遇问题练习题万有引力与航天题号一二三总分得分、单选题（本大题共9 小题，共36.0 分）1.如图所示，A，B 为地球两个同轨道面的人造卫星，运行方向相同，A为同步卫星，A，B卫星的轨道半径之比为=k，地球自转周期为T。

某时刻A，B 两卫星位于地球同侧直线上，从该时刻起至少经过多长时间A，B间距离最远（）2.天文上曾出现几个行星与太阳在同一直线上的现象，假设地球A. B. C. D.和火星绕太阳的运动看作是匀速圆周运动，周期分别是和，它们绕太阳运动的轨道基本上在同一平面上，若某时刻地球和火星都在太阳的一侧，三者在一条直线上，那么再经过多长的时间，将再次出现这种现象已知地球离太阳较近，火星较远）（）A. B. C. D.3.万有引力定律是科学史上最伟大的定律之一，利用它我们可以进行许多分析和预测。

2016年3月8日出现了“木星冲日”。

当地球位于太阳和木星之间且三者几乎排成一条直线时，天文学称之为“木星冲日”。

木星与地球几乎在同一平面内沿同一方向绕太阳近似做匀速圆周运动，木星到太阳的距离大约是地球到太阳距离的5 倍。

下列说法正确的是A.木星运行的加速度比地球的大B.木星运行的周期比地球的小C.下一次的“木星冲日”时间肯定在2017 年D.下一次的“木星冲日”时间肯定在2018 年4.如图，运行轨道在同一平面内的两颗人造卫星A、B，同方向绕地心做匀速圆周运动，此时刻A、B 连线与地心恰在同一直线上且相距最近，己知A 的周期为T，B的周期为．下列说法正确的是（）A.A 的线速度大于B的线速度B.A 的加速度大于B 的加速度C.A、B 与地心连线在相同时间内扫过的面积相等D.从此时刻到下一次A、B 相距最近的时间为T5.两颗行星、均在同一平面内沿相同的环绕方向围绕中心天体运动，经过观测发现每隔最短时间行星与行星相距最近一次。

两行星的运动均可看作匀速圆周运动，若行星的运行周期为，则行星的运行周期为（）二、多选题（本大题共 4 小题，共 16.0 分）10. 太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动， 当地球恰好运行到 某地外行星和太阳之间，且三者几乎排成一条直线的现象，天文学家称为 “行星冲 日”，据报道， 2014年各行星冲日时间分别为： 1月 6日木星冲日； 4月 9日火星冲日；5月 11日土星冲日； 8月 29日海王星冲日； 10月 8日天王星冲日．已知地球 及各地球火星 木星 土星 天王星 海王星 轨道半径（AU ） 1.0 1.5 5.2 9.5 19 30A. 各地外行星每年都会出现冲日现象6. A. B. C. D.2018年 7月 27日将发生火星冲日现象，我国整夜可见。

专题11 卫星的变轨问题和追及相遇问题一、卫星的变轨问题1．2018年5月21日5点28分，在我国西昌卫星发射中心，由中国航天科技集团有限公司抓总研制的嫦娥四号中继星“鹊桥”搭乘长征四号丙运载火箭升空。

卫星由火箭送入近地点约200公里、远地点约40万公里的地月转移轨道1。

在远地点40万公里处点火加速，由椭圆轨道变成高度为40万公里的圆轨道2，在此圆轨道上飞船运行周期等于月球公转周期。

下列判断正确的是（ ）A ．卫星在轨道1的运行周期大于在轨道2的运行周期B ．卫星在圆轨道2的P 点向心加速度小于轨道1上的P 点向心加速度C ．卫星在此圆轨道2上运动的角速度等于月球公转运动的角速度D ．卫星变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 【答案】C【解析】A ．由开普勒第三定律得33122212R R T T 轨道1的半长轴小于轨道2的半径，故卫星在轨道1的运行周期小于在轨道2的运行周期，A 错误；BD ．根据牛顿第二定律，万有引力提供向心力，提供卫星的向心加速度，同一位置，万有引力一定，向心加速度相等，卫星变轨前通过椭圆轨道远地点时的加速度等于变轨后沿圆轨道运动的加速度BD 错误；C ．圆轨道2上飞船运行周期等于月球公转周期，故卫星在此圆轨道2上运动的角速度等于月球公转运动的角速度，C 正确。

故选C 。

2．如图所示，“嫦娥一号”探月卫星进入月球轨道后，首先在椭圆轨道Ⅰ上运动，P 、Q 两点是轨道Ⅰ的近月点和远月点，Ⅰ是卫星绕月做圆周运动的轨道，轨道Ⅰ和Ⅰ在P 点相切，关于该探月卫星的运动，下列说法正确的是（ ）A ．卫星在轨道Ⅰ上运动周期大于在轨道Ⅰ上运动的周期B ．卫星由轨道Ⅰ进入轨道Ⅰ必须要在P 点加速C ．卫星在轨道Ⅰ上运动时，P 点的速度小于Q 点的速度D ．卫星在轨道Ⅰ上运动时，P 点的加速度小于Q 点的加速度 【答案】A【解析】A ．根据开普勒第三定律可知，卫星在轨道Ⅰ上运动周期大于在轨道Ⅰ上运动的周期，故A 正确；B ．卫星由轨道Ⅰ进入轨道Ⅰ必须要在P 点减速，做近心运动，故B 错误；C ．根据开普勒第二定律，卫星在轨道Ⅰ上运动时，近地点P 点的速度大于远地点Q 点的速度，故C 错误；D ．卫星在轨道Ⅰ上运动时，根据2MmG ma R ，P 点的加速度大于Q 点的加速度，故D 错误。

第2讲人造卫星宇宙速度目标要求1.会比较卫星运行的各物理量之间的关系.2.理解三种宇宙速度，并会求解第一宇宙速度的大小.3.会分析天体的“追及”问题．考点一卫星运行参量的分析1．基本公式(1)线速度：由G Mmr 2＝m v 2r得v ＝GMr .(2)角速度：由G Mmr2＝mω2r 得ω＝GMr 3.(3)周期：由GMm r 2＝m (2πT)2r 得T ＝2πr 3GM.(4)向心加速度：由GMm r 2＝ma 得a ＝GMr 2.结论：同一中心天体的不同卫星，轨道半径r 越大，v 、ω、a 越小，T 越大，即越高越慢．2．“黄金代换式”的应用忽略中心天体自转影响，则有mg ＝G MmR2，整理可得GM ＝gR 2.在引力常量G 和中心天体质量M 未知时，可用gR 2替换GM .3．人造卫星卫星运行的轨道平面一定通过地心，一般分为赤道轨道、极地轨道和其他轨道，同步卫星的轨道是赤道轨道．(1)极地卫星运行时每圈都经过南北两极，由于地球自转，极地卫星可以实现全球覆盖．(2)同步卫星①轨道平面与赤道平面共面，且与地球自转的方向相同．②周期与地球自转周期相等，T＝24h.③高度固定不变，h＝3.6×107m.④运行速率约为v＝3.1km/s.(3)近地卫星：轨道在地球表面附近的卫星，其轨道半径r＝R(地球半径)，运行速度等于第一宇宙速度v＝7.9km/s(人造地球卫星的最大圆轨道运行速度)，T＝85min(人造地球卫星的最小周期)．注意：近地卫星可能为极地卫星，也可能为赤道卫星．1．同一中心天体的两颗行星，公转半径越大，向心加速度越大．(×)2．同一中心天体质量不同的两颗行星，若轨道半径相同，速率不一定相等．(×) 3．近地卫星的周期最小．(√)4．极地卫星通过地球两极，且始终和地球某一经线平面重合．(×)5．不同的同步卫星的质量不一定相同，但离地面的高度是相同的．(√)1．公式中r指轨道半径，是卫星到中心天体球心的距离，R通常指中心天体的半径，有r＝R ＋h.2．同一中心天体，各行星v、ω、a、T等物理量只与r有关；不同中心天体，各行星v、ω、a、T等物理量与中心天体质量M和r有关．考向1卫星运行参量与轨道半径的关系例1(2022·广东卷·2)“祝融号”火星车需要“休眠”以度过火星寒冷的冬季．假设火星和地球的冬季是各自公转周期的四分之一，且火星的冬季时长约为地球的1.88倍．火星和地球绕太阳的公转均可视为匀速圆周运动．下列关于火星、地球公转的说法正确的是() A．火星公转的线速度比地球的大B．火星公转的角速度比地球的大C．火星公转的半径比地球的小D．火星公转的加速度比地球的小答案D解析由题意可知，火星的公转周期大于地球的公转周期，根据G Mmr2m4π2T2r，可得T＝2πr3GM，可知火星的公转半径大于地球的公转半径，故C 错误；根据G Mmr 2＝m v 2r，可得v ＝GMr ，结合C 选项解析，可知火星公转的线速度小于地球公转的线速度，故A 错误；根据ω＝2πT可知火星公转的角速度小于地球公转的角速度，故B 错误；根据G Mm r 2＝ma ，可得a ＝GMr 2，可知火星公转的加速度小于地球公转的加速度，故D 正确．例2(2020·浙江7月选考·7)火星探测任务“天问一号”的标识如图所示．若火星和地球绕太阳的运动均可视为匀速圆周运动，火星公转轨道半径与地球公转轨道半径之比为3∶2，则火星与地球绕太阳运动的()A ．轨道周长之比为2∶3B ．线速度大小之比为3∶2C ．角速度大小之比为22∶33D ．向心加速度大小之比为9∶4答案C解析轨道周长C ＝2πr ，与半径成正比，故轨道周长之比为3∶2，故A 错误；根据万有引力提供向心力有GMmr 2＝m v 2r，得v ＝GMr ，则v 火v 地＝r 地r 火＝23，故B 错误；由万有引力提供向心力有GMmr2＝mω2r ，得ω＝GMr 3，则ω火ω地＝r 地3r 火3＝2233，故C 正确；由GMm r 2＝ma ，得a ＝GMr 2，则a 火a 地＝r 地2r 火2＝49，故D 错误．考向2同步卫星例3关于地球同步卫星，下列说法错误的是()A ．它的周期与地球自转周期相同B ．它的周期、高度、速度大小都是一定的C ．我国发射的同步通信卫星可以定点在北京上空D ．我国发射的同步通信卫星必须定点在赤道上空答案C解析地球同步卫星的周期与地球自转周期相同，选项A 正确；根据G Mm r 2＝m v 2r＝m 4π2T 2r 可知，因地球同步卫星的周期一定，则高度、速度大小都是一定的，选项B 正确；同步卫星必须定点在赤道上空，不可以定点在北京上空，选项C 错误，D 正确．例4常用的通信卫星是地球同步卫星，它定位于地球赤道正上方，已知某同步卫星离地面的高度为h ，地球自转的角速度为ω，地球半径为R ，地球表面附近的重力加速度为g 0，该同步卫星运动的加速度的大小为()A ．g 0B ．(R R ＋h2g 0C ．ω2hD ．ω(R ＋h )答案B解析对同步卫星，角速度等于地球自转的角速度，则GMm (R ＋h )2＝ma ＝mω2(R ＋h )，又GMm 0R 2＝m 0g 0，解得a ＝(R R ＋h)2g 0＝ω2(R ＋h )，故选B.考向3同步卫星、近地卫星和赤道上物体比较例5(多选)如图所示，同步卫星与地心的距离为r ，运行速率为v 1，向心加速度为a 1，地球赤道上的物体随地球自转的向心加速度为a 2，第一宇宙速度为v 2，地球半径为R ，则下列比值正确的是()A.a 1a 2＝r RB.a 1a 2＝(R r)2C.v 1v 2＝r RD.v 1v 2＝R r答案AD解析根据万有引力提供向心力，有G Mmr 2＝m v 12r ，G Mm ′R 2＝m ′v 22R ，故v 1v 2＝Rr；对于同步卫星和地球赤道上的物体，其共同点是角速度相等，有a 1＝ω2r ，a 2＝ω2R ，故a 1a 2＝rR ，故选A 、D.例6有a 、b 、c 、d 四颗地球卫星，卫星a 还未发射，在地球赤道上随地球表面一起转动，卫星b 在地面附近近地轨道上正常运行，c 是地球同步卫星，d 是高空探测卫星，各卫星排列位置如图，重力加速度为g ，则有()A ．a 的向心加速度大小等于重力加速度大小gB ．b 在相同时间内转过的弧长最长C ．c 在4h 内转过的圆心角是π6D ．d 的运行周期有可能是20h 答案B解析赤道上随地球自转的卫星所需的向心力大小等于万有引力的一个分力，万有引力大小近似等于重力大小，则a 的向心加速度小于重力加速度g ，故A 错误；由G Mmr 2＝m v 2r ，解得v ＝GMr，卫星的轨道半径r 越大，速度v 越小，所以在b 、c 、d 中b 的速度最大，又由v ＝ωr 知a 的速度小于c 的速度，故在相同时间内b 转过的弧长最长，故B 正确；c 是地球同步卫星，周期是24h ，则c 在4h 内转过的圆心角是4h 24h ×2π＝π3，故C 错误；由开普勒第三定律可知，卫星的半径r 越大，周期T 越大，所以d 的运动周期大于c 的运动周期，即大于24h ，则不可能是20h ，故D 错误．同步卫星、近地卫星及赤道上物体的比较如图所示，a 为近地卫星，轨道半径为r 1；b 为地球同步卫星，轨道半径为r2；c 为赤道上随地球自转的物体，轨道半径为r 3.比较项目近地卫星(r 1、ω1、v 1、a 1)同步卫星(r 2、ω2、v 2、a 2)赤道上随地球自转的物体(r 3、ω3、v 3、a 3)向心力来源万有引力万有引力万有引力的一个分力轨道半径r 2>r 1＝r 3角速度ω1>ω2＝ω3线速度v 1>v 2>v 3向心加速度a 1>a 2>a 3考点二宇宙速度第一宇宙速度(环绕速度)v 1＝7.9km/s ，是物体在地球附近绕地球做匀速圆周运动的最大环绕速度，也是人造地球卫星的最小发射速度第二宇宙速度(逃逸速度)v 2＝11.2km/s ，是物体挣脱地球引力束缚的最小发射速度第三宇宙速度v 3＝16.7km/s ，是物体挣脱太阳引力束缚的最小发射速度1．地球的第一宇宙速度的大小与地球质量有关．(√)2．月球的第一宇宙速度也是7.9km/s.(×)3．同步卫星的运行速度一定小于地球第一宇宙速度．(√)4．若物体的发射速度大于第二宇宙速度而小于第三宇宙速度，则物体绕太阳运行．(√)1．第一宇宙速度的推导方法一：由G m 地mR 2＝m v 2R ，得v ＝Gm 地R ＝ 6.67×10－11×5.98×10246.4×106m/s ≈7.9×103m/s.方法二：由mg ＝m v 2R得v ＝gR ＝9.8×6.4×106m/s ≈7.9×103m/s.第一宇宙速度是发射人造卫星的最小速度，也是人造卫星的最大环绕速度，此时它的运行周期最短，T min ＝2πRg＝2π 6.4×1069.8s ≈5075s ≈85min.正是近地卫星的周期．2．宇宙速度与运动轨迹的关系(1)v 发＝7.9km/s 时，卫星绕地球表面做匀速圆周运动．(2)7.9km/s<v 发<11.2km/s ，卫星绕地球运动的轨迹为椭圆．(3)11.2km/s ≤v 发＜16.7km/s ，卫星绕太阳运动的轨迹为椭圆．(4)v 发≥16.7km/s ，卫星将挣脱太阳引力的束缚，飞到太阳系以外的空间．例7(2023·广东深圳市模拟)2020年12月17日凌晨，经过23天的太空之旅后，嫦娥五号返回器携带1731克月壤样品成功着陆，这标志着我国首次月球采样返回任务圆满完成．已知月球的质量为M＝7.3×1022kg.月球的半径为R＝1.7×103km，引力常量G＝6.67×10－11N·m2/kg2，则月球的第一宇宙速度约为()A．17m/s B．1.7×102m/sC．1.7×103m/s D．1.7×104m/s答案C解析近月球表面的卫星运行速度即第一宇宙速度，由万有引力提供向心力可得G MmR2＝mv2R，解得v＝GMR≈1.7×103m/s，故选C.例8(2023·广东广州市模拟)星球上的物体脱离星球引力所需的最小速度称为该星球的第二宇宙速度，第二宇宙速度v2与第一宇宙速度v1的关系是v2＝2v1；某星球的半径为r，表面的重力加速度为地球表面重力加速度g的18，不计其他星球的影响，则该星球的第二宇宙速度为()A.grB.2gr2C.gr2D.14gr答案C解析近地卫星的环绕速度即第一宇宙速度，由重力提供向心力可得mg＝m v12R，可得地球的第一宇宙速度为v1＝gR，同理可知，该星球的第一宇宙速度为v1′＝18gr，则该星球的第二宇宙速度为v2′＝2v1′＝gr2，C正确．考点三天体的“追及”问题例9(2023·广东中山市调研)小明站在地球赤道上某点，每经过T4时间，卫星A经过头顶上空一次，已知地球的自转周期为T，卫星A轨道平面与赤道平面重合，且运动方向与地球自转方向相同，则A卫星的运动周期为()A.T 4B.T5C.3T4D.T2答案B解析由题意可知，每经过一段时间，卫星A比地球多转一圈；设卫星的运动周期为T A，则T 4T A －T4T ＝1，解得T A ＝15T ，故选B.例10如图所示，A 、B 为地球的两个轨道共面的人造卫星，运行方向相同，A 为地球同步卫星，A 、B 两卫星的轨道半径的比值为k ，地球自转周期为T 0.某时刻A 、B 两卫星距离达到最近，从该时刻起到A 、B 间距离最远所经历的最短时间为()A.T 02(k 3＋1)B.T 0k 3－1C.T 02(k 3－1)D.T 0k 3＋1答案C解析由开普勒第三定律得r A 3T A 2＝r B 3T B 2，设两卫星至少经过时间t 距离最远，即B 比A 多转半圈，t T B －t T A ＝n B －n A ＝12，又由A 是地球同步卫星知T A ＝T 0，联立解得t ＝T 02(k 3－1)，故选C.天体“追及”问题的处理方法1．相距最近：两同心转动的卫星(r A <r B )同向转动时，位于同一直径上且在圆心的同侧时，相距最近．从相距最近到再次相距最近，两卫星的运动关系满足：(ωA －ωB )t ＝2π或t T A －tT B ＝1.2．相距最远：两同心转动的卫星(r A <r B )同向转动时，位于同一直径上且在圆心的异侧时，相距最远．从相距最近到第一次相距最远，两卫星的运动关系满足：(ωA －ωB )t ′＝π或t ′T A －t ′T B＝12.课时精练1.(2023·江苏海安市高三检测)神舟十三号飞船首次采用径向端口对接；飞船从空间站下方的停泊点进行俯仰调姿和滚动调姿后与天宫空间站完成对接，飞船在完成对接后与在停泊点时相比()A．线速度增大B．绕行周期增大C．所受万有引力增大D．向心加速度增大答案B解析飞船绕地球稳定运行时，万有引力提供向心力，有GMmr2＝mv2r＝m4π2T2r＝F万＝ma，解得v＝GMr，T＝4π2r3GM，a＝GMr2，依题意，飞船从停泊点到完成对接属于从低轨到高轨，即轨道半径增大，可知线速度减小，周期增大，所受万有引力减小，向心加速度减小，故A、C、D错误，B正确．2．我国首颗量子科学实验卫星“墨子”已于酒泉卫星发射中心成功发射．“墨子”由火箭发射至高度为500km的预定圆形轨道．此前在西昌卫星发射中心成功发射了第二十三颗北斗导航卫星G7，G7属于地球静止轨道卫星(高度约为36000km)，它将使北斗系统的可靠性进一步提高．关于卫星以下说法中正确的是()A．这两颗卫星的运行速度可能大于7.9km/sB．通过地面控制可以将北斗G7定点于西昌正上方C．量子科学实验卫星“墨子”的周期比北斗G7的周期小D．量子科学实验卫星“墨子”的向心加速度比北斗G7的小答案C解析根据G Mmr2＝mv2r，得v＝GMr，知轨道半径越大，线速度越小，北斗G7和量子科学实验卫星“墨子”的线速度均小于地球的第一宇宙速度，故A错误；北斗G7为同步卫星，只能定点于赤道正上方，故B错误；根据G Mmr2＝m4π2T2r，得T＝2πr3GM，所以量子科学实验卫星“墨子”的周期小，故C正确；卫星的向心加速度a＝GMr2，半径小的量子科学实验卫星“墨子”的向心加速度比北斗G7的大，故D错误．3．(2023·广东茂名市模拟)如图，“嫦娥五号”、“天问一号”探测器分别在近月、近火星轨道运行．已知火星的质量为月球质量的9倍、半径为月球半径的2倍．假设月球、火星均可视为质量均匀分布的球体，忽略其自转影响，则()A．月球表面重力加速度比火星表面重力加速度大B．月球的第一宇宙速度比火星的第一宇宙速度大C．质量相同的物体在月球、火星表面所受万有引力大小相等D．“嫦娥五号”绕月周期比“天问一号”绕火星周期大答案D解析由mg＝G Mmr2，可得g＝GMr2，结合题意可得g月＝49g火，A项错误；由mg＝mv2r可知v＝gr，所以v月＝23v火，B项错误；由F引＝G Mmr2，可知F月＝49F火，C项错误；由G Mmr2＝m(2πT )2r可知T＝2πr3GM，所以T月＝324T火，D项正确．4．(2022·河北卷·2)2008年，我国天文学家利用国家天文台兴隆观测基地的2.16米望远镜，发现了一颗绕恒星HD173416运动的系外行星HD173416b,2019年，该恒星和行星被国际天文学联合会分别命名为“羲和”和“望舒”，天文观测得到恒星羲和的质量是太阳质量的2倍，若将望舒与地球的公转均视为匀速圆周运动，且公转的轨道半径相等．则望舒与地球公转速度大小的比值为()A．22B．2 C.2 D.22答案C解析地球绕太阳公转和行星望舒绕恒星羲和公转都是由万有引力提供向心力，有G Mm r2＝m v2r，解得公转的线速度大小为v＝GMr，其中中心天体的质量之比为2∶1，公转的轨道半径相等，则望舒与地球公转速度大小的比值为2，故选C.5．(2023·广东珠海市模拟)2020年7月23日12时41分，火星探测器“天问一号”成功发射，标志着我国已经开启了探索火星之旅．“天问一号”首先进入圆轨道环绕火星做匀速圆周运动，然后调整姿态悬停在火星上空，再向下加速、减速，着陆火星表面并执行任务．已知地球与火星的质量比为a，地球与火星的半径比为b.则下列说法正确的是()A．地球与火星表面的重力加速度的比值为abB ．地球与火星的近地卫星周期的比值为b aC ．地球与火星的第一宇宙速度的比值为a bD ．“天问一号”在环绕火星运动、悬停、向下加速以及减速的过程中，始终处于失重状态答案C解析对于在星体表面的物体，万有引力与重力的关系为GMm R 2＝mg ，整理得g ＝GMR 2，则地球与火星表面的重力加速度的比值为g 地g 火＝a b2，A 错误；对于近地卫星，由G Mm R 2＝m 4π2T 2R ，整理得T ＝4π2R 3GM ，则地球与火星的近地卫星周期的比值为T 地T 火＝b baB 错误；星球的第一宇宙速度为v ＝gR ，则地球与火星的第一宇宙速度的比值为v 地v 火＝ab，C 正确；“天问一号”在环绕火星运动时处于完全失重状态，悬停时处于平衡状态，向下加速时处于失重状态，向下减速时处于超重状态，D 错误．6．如图所示，a 为地球赤道上的物体，b 为沿地球表面附近做匀速圆周运动的人造卫星，c 为地球同步卫星．关于a 、b 、c 做匀速圆周运动的说法中正确的是()A ．角速度关系为ωa ＝ωb >ωcB ．向心加速度的大小关系为a a >a b >a cC ．线速度的大小关系为v b >v c >v aD ．周期关系为T a ＝T b >T c 答案C解析卫星c 为地球同步卫星，所以T a ＝T c ，则ωa ＝ωc ；对于b 和c ，由万有引力提供向心力，有GMmr2＝mω2r ，得ω＝GMr 3，因为r b <r c ，可知ωc <ωb ，即ωb >ωc ＝ωa ，A 错误．因a 、c 有相同的角速度，由a ＝ω2r 得a a <a c ；对b 和c ，由万有引力提供向心力，有G Mmr 2＝ma ，得a ＝GMr 2，因为r b <r c ，可知a b >a c ，即a b >a c >a a ，B 错误．因a 、c 有相同的角速度，由v ＝ωr 可知v a <v c ；对b 和c ，由万有引力提供向心力，有G Mmr 2＝m v 2r，得v ＝GMr，因为r b <r c ，可知v b >v c ，即v b >v c >v a ，C 正确．对b 和c ，由万有引力提供向心力，有G Mm r 2＝m 4π2T 2r ，得T ＝2πr 3GM，因为r b <r c ，可知T c >T b ，即T a ＝T c >T b ，D 错误．7．(2023·广东汕头市模拟)早在2012年，某公司提出将人送上火星，展开星际移民的计划．已知地球质量大约是火星质量的10倍，地球半径大约是火星半径的2倍．不考虑地球、火星自转的影响，由以上数据可推算出(取5＝2.2)()A ．地球的平均密度小于火星的平均密度B ．地球表面重力加速度小于火星表面重力加速度C ．靠近地球表面的航天器的周期与靠近火星表面的航天器的运行周期之比约为10∶11D ．地球的第一宇宙速度与火星的第一宇宙速度之比约为11∶10答案C解析根据密度公式可知ρ＝M43πR 3，则ρ地＝54ρ火，地球的平均密度大于火星的平均密度，故A错误；根据物体在星球表面的重力等于万有引力可知GMmR 2＝mg ，解得星球表面的重力加速度g ＝GM R 2，所以g 地＝52g 火，地球表面的重力加速度大于火星表面的重力加速度，故B 错误；根据万有引力提供向心力可知GMm R 2＝m 4π2T 2R ，解得星球表面航天器的运行周期T ＝2πR 3GM，则靠近地球表面的航天器的周期与靠近火星表面的航天器的周期之比约为10∶11，故C 正确；根据万有引力提供向心力GMmR 2＝m v 2R，解得星球的第一宇宙速度v ＝GMR，则地球的第一宇宙速度与火星的第一宇宙速度之比约为11∶5，故D 错误．8.(多选)地月系统是双星模型，为了寻找航天器相对地球和月球不动的位置，科学家们做出了不懈努力．如图所示，欧拉推导出L 1、L 2、L 3三个位置，拉格朗日又推导出L 4、L 5两个位置．现在科学家把L 1、L 2、L 3、L 4、L 5统称地月系中的拉格朗日点．中国“嫦娥四号”探测器成功登陆月球背面，并通过处于拉格朗日区的“嫦娥四号”中继卫星“鹊桥”把信息返回地球，引起众多师生对拉格朗日点的热议．下列说法正确的是()A ．在拉格朗日点航天器的受力不再遵循万有引力定律B ．在不同的拉格朗日点航天器随地月系统运动的周期均相同C ．“嫦娥四号”中继卫星“鹊桥”应选择L 1点开展工程任务实验D ．“嫦娥四号”中继卫星“鹊桥”应选择L 2点开展工程任务实验答案BD解析在拉格朗日点的航天器仍然受万有引力，仍遵循万有引力定律，A 错误；因在拉格朗日点的航天器相对地球和月球的位置不变，说明它们的角速度一样，因此周期也一样，B 正确；“嫦娥四号”探测器登陆的是月球的背面，“鹊桥”要把探测器在月球背面采集的信息传回地球，L 2在月球的背面，因此应选在L 2点开展工程任务实验，C 错误，D 正确．9．(2023·辽宁丹东市月考)2021年10月16日，神舟十三号载人飞船顺利将翟志刚、王亚平、叶光富3名航天员送入太空，假设神舟十三号载人飞船在距地面高度为h 的轨道做圆周运动．已知地球的半径为R ，地球表面的重力加速度为g ，引力常量为G ，下列说法正确的是()A ．神舟十三号载人飞船运行的周期为T ＝2π(R ＋h )3gR 2B ．神舟十三号载人飞船的线速度大小为g (R ＋h )C ．神舟十三号载人飞船轨道处的重力加速度为0D ．地球的平均密度为3g 4πGR 2答案A解析根据万有引力提供向心力，可得G Mm r 2＝m v 2r ，G Mm r 2＝m 4π2r T 2，G Mmr 2＝ma ，且在地球表面满足GMmR2＝mg ，即GM ＝gR 2，由题意知神舟十三号载人飞船轨道半径为r ＝R ＋h ，解得周期为T ＝2π(R ＋h )3gR 2，线速度大小为v ＝gR 2R ＋h，向心加速度大小即重力加速度大小为a ＝gR 2(R ＋h )2，故A 正确，B 、C 错误；根据密度公式得地球的平均密度为ρ＝M V ＝3gR 24πGR 3＝3g 4πGR ，故D 错误．10．(2023·湖北省荆州中学模拟)设想在赤道上建造如图甲所示的“太空电梯”，站在太空舱里的宇航员可通过竖直的电梯缓慢直通太空站．图乙中r 为宇航员到地心的距离，R 为地球半径，曲线A 为地球引力对宇航员产生的加速度大小与r 的关系；直线B 为宇航员由于地球自转而产生的向心加速度大小与r 的关系．关于相对地面静止且在不同高度的宇航员，下列说法正确的有()A ．随着r 增大，宇航员的角速度增大B ．图中r 0为地球同步卫星的轨道半径C ．宇航员在r ＝R 处的线速度等于第一宇宙速度D ．随着r 增大，宇航员对太空舱的压力增大答案B解析宇航员站在“太空电梯”上，相对地面静止，故角速度与地球自转角速度相同，在不同高度角速度不变，故A 错误；当r ＝r 0时，引力加速度正好等于宇航员做圆周运动的向心加速度，即万有引力提供做圆周运动的向心力，若宇航员相当于卫星，此时宇航员的角速度跟地球的自转角速度一致，可以看作是地球的同步卫星，即r 0为地球同步卫星的轨道半径，故B 正确；宇航员在r ＝R 处时在地面上，除了受到万有引力还受到地面的支持力，线速度远小于第一宇宙速度，故C 错误；宇航员乘坐太空舱在“太空电梯”的某位置时，有GMmr 2－F N ＝mω2r ，其中F N 为太空舱对宇航员的支持力，大小等于宇航员对太空舱的压力，则F 压＝F N ＝GMmr2－mω2r ＝ma 引－ma 向＝m (a 引－a 向)，其中a 引为地球引力对宇航员产生的加速度大小，a 向为地球自转而产生的向心加速度大小，由题图可知，在R ≤r ≤r 0时，(a 引－a 向)随着r 增大而减小，宇航员对太空舱的压力随r 的增大而减小，故D 错误．11．(多选)(2023·广东惠州市模拟)2018年7月27日，天宇上演“火星冲日”天象，此时火星离地球最近，是发射火星探测器的最佳时段．为此，洞察号火星探测器于2018年5月5日发射升空，飞行205天，于11月27日成功着陆火星．已知火星质量约为地球质量的19，半径约为地球半径的12，公转周期约为地球公转周期的2倍．则()A ．火星公转轨道的半径约为地球公转轨道半径的2倍B ．火星表面的重力加速度约为地球表面重力加速度的49C ．洞察号绕火星做匀速圆周运动的最大运行速度约为地球第一宇宙速度的23D ．下一个火星探测器的最佳发射期最早出现在2020年答案BCD解析地球和火星绕太阳公转时，都是由太阳的万有引力提供向心力，即GM太mr2＝mr(2πT)2，可得r＝3GM太T24π2，故火星公转轨道的半径约为地球公转轨道半径的34倍，故A错误；星球表面，万有引力近似等于重力，即GMmR2＝mg，故g＝GMR2，代入数据可知火星表面的重力加速度约为地球表面重力加速度的49，故B正确；洞察号绕火星做匀速圆周运动的最大运行速度即为火星的第一宇宙速度，根据第一宇宙速度的定义式v＝GMR，代入数据可得洞察号绕火星做匀速圆周运动的最大运行速度约为地球第一宇宙速度的23，故C正确；设经时间t，地球公转周期为T0，火星和地球再次相距最近，则有(2πT0－2π2T0)t＝2π，解得t＝2T0，故下一个火星探测器的最佳发射期最早出现在2020年，故D正确．。