当前位置：文档之家 › 第7章 图论 -5二部图、平面图

第7章 图论 -5二部图、平面图

  • 格式：pdf
  • 大小：1.13 MB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

二部图与完全二部图精讲

二部图与完全二部图精讲

哈密尔顿图
与欧拉回路类似的是哈密尔顿回路问题。 它是1859年哈密尔顿首先提出的一个关于 12面体的数学游戏： 能否在下页图中找到 一个回路，使它含有图中所有结点一次且 仅一次？ 若把每个结点看成一座城市，连 接两个结点的边看成是交通线，那么这个 问题就变成能否找到一条旅行路线，使得 沿着该旅行路线经过每座城市恰好一次， 再回到原来的出发地呢？为此，这个问题 也被称作周游世界问题。
(1) G中无圈, 则G必有一个度数为1的顶点v, 删除v及它关 联的边, 记作G . G 连通, 有n-1个顶点, k条边和r个面. 由归 纳假设, (n-1)-k+r=2, 即n-(k+1)+r=2, 得证m=k+1时结论成立.
(2) 否则,删除一个圈上的一条边,记作G . G 连通, 有n个顶 点,k条边和r-1个面. 由归纳假设, n-k+(r-1)=2, 即n-(k+1)+r=2, 得证m=k+1时结论也成立. 证毕.
但我们继续考察(b)图可以发现， 该图中有一条路 v2v3v4v5v2v1v5， 它经过(b)图中的每条边一次且仅
一次， 我们把这样的路称为欧拉路。
7
定义2 通过图G的每条边一次且仅一次的 路称为图G的欧拉路。 对于欧拉路有下面
的判定方法。
定理2 连通图G具有一条连接结点vi和vj的 欧拉路当且仅当vi和vj是G中仅有的两个奇
s=|V2|.
注意: n 阶零图为二部图.
2
二部图的判别法
定理 无向图G=<V,E>是二部图当且仅当G中无奇圈 例 下述各图都是二部图
3
欧拉图
历史上的哥尼斯堡七桥问题是著名的图论问题。 问题是这样的： 18世纪的东普鲁士有个哥尼斯堡

图论期末考试整理复习资料

图论期末考试整理复习资料

目录第一章图的基本概念 (1)二路和连通性 (3)第二章树 (3)第三章图的连通度 (4)第四章欧拉图与哈密尔顿图 (5)一，欧拉图 (5)二．哈密尔顿图 (6)第五章匹配与因子分解 (9)一．匹配 (9)二．偶图的覆盖于匹配 (10)三．因子分解 (11)第六章平面图 (14)二．对偶图 (16)三．平面图的判定 (17)四．平面性算法 (20)第七章图的着色 (24)一．边着色 (24)二．顶点着色 (25)第九章有向图 (30)二有向树 (30)第一章图的基本概念1.点集与边集均为有限集合的图称为有限图。

2.只有一个顶点而无边的图称为平凡图。

3.边集为空的图称为空图。

4.既没有环也没有重边的图称为简单图。

5.其他所有的图都称为复合图。

6.具有二分类（X, Y）的偶图（或二部图）：是指该图的点集可以分解为两个（非空）子集X 和Y ，使得每条边的一个端点在X 中，另一个端点在Y 中。

7.完全偶图：是指具有二分类（X, Y）的简单偶图，其中X的每个顶点与Y 的每个顶点相连，若|X|=m，|Y|=n，则这样的偶图记为Km,n8. 定理1 若n 阶图G 是自补的（即），则n = 0, 1（mod 4）9. 图G 的顶点的最小度。

10. 图G 的顶点的最大度。

11. k-正则图: 每个点的度均为 k 的简单图。

例如,完全图和完全偶图Kn,n 均是正则图。

12. 推论1 任意图中，奇点的个数为偶数。

13.14. 频序列：定理4 一个简单图G 的n 个点的度数不能互不相同。

15. 定理5 一个n 阶图G 相和它的补图有相同的频序列。

16.17.18. 对称差：G1△G2 = (G1∪G2) - (G1∩G2) = (G1-G2)∪(G2-G1)19. 定义： 联图 在不相交的G1和G2的并图G1+G2中，把G1的每个顶点和G2的每个顶点连接起来所得到的图称为G1和G2的联图，记为G1∨G220. 积图：积图 设G1= (V1, E1)，G2 = (V2, E2)，对点集V = V1×V2中的任意两个点u =(u1,u2)和v = (v1,v2)，当(u1 = v1和 u2 adj v2) 或 (u2 = v2 和 u1 adj v1) 时就把 u 和 v 连接起来所得到的图G 称为G1和G2积图。

离散数学基础

离散数学基础
7
二、重点和难点
1、掌握元素与集合之间的关系，集合与集合之间的关系。 2、运用集合运算的基本定律去化简集合表达式或证明集合等 式。 3、掌握二元关系的五个性质和二元关系的运算。 4、等价关系的证明、等价类的求解，偏序关系的特定元素的 求解。 5、函数的性质，求复合函数和逆函数。
8
三、例题
1、 这两个关系是否正确？
(g°f)-1: RR，且(g°f)-1(x)=(((x+2)/3)^(1/3)-5)/3
11
第二部分 图论
一、内容提要
1、图的基本概念：无向图、有向图、简单图、结点的度数、 子图、补图、图的同构。 2、握手定理：所有结点的度数之和等于边数的2倍。 3、图的连通性：割边、割点、边割集、点割集。通路、回路、 连通分支。 4、图的矩阵表示：邻接矩阵、关联矩阵。 5、欧拉图和哈密尔顿图的定义和判定条件。 6、树的定义、性质、判定条件和遍历。 7、二部图和平面图的定义、性质和判定条件
《离散数学》总复习
1
概述
一、什么是离散数学？
离散数学是现代数学的一个重要分支，是计算机专业的一 门重要的专业基础课程。它是以研究离散量的结构和相互间的 关系为主要目标，其研究对象一般是有限个或可数个元素，因 此它充分描述了计算机科学离散性的特点。
2
二、为什么要学离散数学？
1、离散数学是计算机专业的一门核心基础课程，离散数学为计 算机专业的后继课程如数据结构、操作系统、数据库、编译原 理、网络和算法设计等课程提供必要的数学基础。
解： ((A∩B)∪A)⊕((B∩~B)⊕A⊕(B∪~B)) (吸收律和零律)
=A⊕⊕A⊕U (同一律)
= A⊕A⊕U (零律)
= ⊕U = U
9

数学建模-图论

数学建模-图论

图论导引
问题3:四色猜想 地图或地球仪上，最多用四种颜色就可把每一 国的版图染好，使得国界线两侧异色。
电子计算机问世以后，由于演算速度迅速提高，加 之人机对话的出现，大大加快了对四色猜想证明的进 程。美国伊利诺大学哈肯在1970年着手改进“放电过 程”，后与阿佩尔合作编制一个很好的程序。就在 1976年6月，他们在美国伊利诺斯大学的两台不同的电 子计算机上，用了1200个小时，作了100亿判断，终于 完成了四色定理的证明，轰动了世界。
有向图：
1, 若vi是ei的始点 aij 1, 若vi是ei的终点 0, 若v 与e 不关联 i i
无向图：
1, 若vi与v j 关联 aij 0, 若vi与v j 不关联
图的矩阵表示
例6：写出右图与其基本图 的关联矩阵 解：分别为：
图论的基本概念
几个基本定理：
1、对图G V，E ，有 d v 2 E .
vV
2、度为奇数的顶点有偶数个。
3、设G V，E 是有向图， 则 d v d v E .
vV vV
子图
定义 设图 G=(V,E, ),G1=(V1,E1, 1 )
(3)设 E1 E,且 E1 ,以 E1 为边集,E1 的端点集为顶点集的图 G 的子图, 称为 G 的由 E1 导出的子图,记为 G[E1].
G
G[{v1,v4,v5}]
G[{e1,e2,e3}]
基 本 概 念
定义１ 在无向图 G=(V,E)中： （１） 顶点与边相互交错的有限非空序列 w (v0 e1v1e2 vk 1ek vk ) 称为一条从 v 0 到 v k 的通路，记为 Wv0vk （２）边不重复但顶点可重复的通路称为道路，记为 Tv0vk （３）边与顶点均不重复的通路称为路径，记为 Pv 0 v k 始点和终点相同的路称为圈或回路.

优化建模与LINGO第07章

优化建模与LINGO第07章
Global optimal solution found at iteration: 6 Objective value: 161.0000 Variable Value Reduced Cost X( 1, 1) 2.000000 0.000000 X( 1, 2) 17.00000 0.000000 X( 1, 3) 1.000000 0.000000 X( 2, 1) 13.00000 0.000000 X( 2, 4) 12.00000 0.000000 X( 3, 3) 21.00000 0.000000 Row Slack or Surplus Dual Price OBJ 161.0000 -1.000000 SUP( 1) 10.00000 0.000000
MODEL: 1]! 3 Warehouse, 4 Customer Transportation Problem; 2]sets: 3] Warehouse /1..3/: a; 4] Customer /1..4/: b;
优化建模
5] Routes( Warehouse, Customer) : c, x; 6]endsets 7]! Here are the parameters; 8]data: 9] a = 30, 25, 21 10] b = 15, 17, 22, 12; 11] c = 6, 2, 6, 7, 12] 4, 9, 5, 3, 13] 8, 8, 1, 5; 14]enddata 15]! The objective; 16][OBJ] min = @sum( Routes: c * x);
优化建模
LINDO软件虽然给出最优解，但上述模型还存在 软件虽然给出最优解， 软件虽然给出最优解 着缺点，例如，上述方法不便于推广的一般情况， 着缺点，例如，上述方法不便于推广的一般情况，特 别是当产地和销地的个数较多时，情况更为突出. 别是当产地和销地的个数较多时，情况更为突出 下面写出求解该问题的LINGO程序，并在程序中 程序， 下面写出求解该问题的 程序 用到在第三章介绍的集与数据段， 用到在第三章介绍的集与数据段，以及相关的循环函 数. 写出相应的LINGO程序，程序名： exam0702.lg4 程序， 写出相应的 程序 程序名：

离散数学图论作业7-二部图匹配

离散数学图论作业7-二部图匹配

离散数学图论作业7-二部图匹配Problem1证明：一个无回路的简单连通图最多只有一个完美匹配。

（完美匹配指能饱和所有顶点的匹配）Problem2从下图G=(A,B,E)中，找出相对于匹配M(粗边的集合)的任意三条交错路径(alternating path)和至少两条增广路径(augmenting path)，然后利用增广路径扩大M来找到最大匹配。

a0 a1 a2 a3 a4 a5b0 b1 b2 b3 b4 b5Problem3对于哪些n值来说，下列图是存在完美匹配的二部图？a)K nb)C nc)Q n对于每一个二部图G=(A,B,E)，判断G是否有饱和A的匹配。

如果没有，请说明理由。

(1)(2)(3)(4)Problem5令k为一整数。

对于任意有限集合，证明对它的任意两个k划分都存在一个相同的代表集。

•集合的k划分指划分为大小相同的互不想交的k个子集，为简便起见，设集合的大小为k的整数倍从而每个子集均有相同个元素。

•一个划分的代表集指从每个子集中取出一个元素而构成的集合。

举例：集合{1,2,3,4}的一个2划分为A:{1,2}{3,4}。

此划分的代表集有{1,3},{2,3},{1,4},{2,4}，但{1,2}不是其代表集。

集合的另外一个划分为B:{2,3}{1,4}。

易见，A与B存在相同的代表集{1,3}。

Problem6假设某校计算机系学生选导师时出现了这样的情况：对于每一位学生，至少对k名导师感兴趣；对于每一位导师，至多有k名学生对他感兴趣。

假设每位导师只能指导1名学生，且每位学生也只能选择1名导师。

试证明：存在这样的匹配，使得每位学生都能选到自己感兴趣的导师。

证明一个6×6的方格纸板挖去左上角和右下角后不能用剪刀裁剪成若干1×2的小矩形。

图论-图的基本概念

图论-图的基本概念
若 i, j 中有奇数，比如 i 是奇数，则路 P 上 v0 到 vi 的一段与边 v0vi 构成一个偶圈； 若 i, j 都是偶数，则路 P 上 vi 到 v j 的一段与边 v0vi 及 v0v j 构成一个偶圈。证毕。 例 1.1.4 设 G 是简单图，若δ (G) ≥ 3 ,则 G 中各个圈长的最大公因数是 1 或 2。 证明：由上例知，G 中有长分别为 i + 1, j + 1和 j − i + 2 的圈。若 i + 1, j + 1， j − i + 2 三 数有公因数 m > 2 ，则 m | ( j − i) ，于是 m | 2 ，这是不可能的。因此 i + 1, j + 1， j − i + 2
证明：按每个顶点的度来计数边，每条边恰数了两次。 推论 1.1.1 任何图中，奇度顶点的个数总是偶数（包括 0）。 4. 子图
子图(subgraph)：如果 V (H ) ⊆ V (G) 且 E(H ) ⊆ E(G) ，则称图 H 是 G 的子图，记为 H ⊆G。
生成子图(spanning subgraph): 若 H 是 G 的子图且V (H ) = V (G) ，则称 H 是 G 的生成子图。
这便定义出一个图。
2. 图的图示
通常，图的顶点可用平面上的一个点来表示，边可用平面上的线段来表示（直的或曲的）。 这样画出的平面图形称为图的图示。
例如，例 1.1.1 中图的一个图示为
v1
v2
e1
e6 e5
e2
e4
v5
e7
v3
e3 v4
注：（1）由于表示顶点的平面点的位置的任意性，同一个图可以画出形状迥异的很多图示。

离散数学图论

离散数学图论

图的同构
对于两个图G和G,如果它们的顶点之间存在一一对应关系，而 且这种关系保持了两顶点间的邻接关系（在有向图中，还保 持了边的方向）和边的重数，则这两个图是同构的。
同构的图除了点和边的名称不同外，实际上代表同样的组织结 构。 由于图形的顶点位置和连线长度都可任意选择，同一个图可能 画出不同的形状来，因而引出图同构的概念。 如下面两个图同构:
32

Zhengjin,Central South University
33
8.3 图的矩阵表示
定义 1 设 G=<V,E> 是无向图，且无平行边，其中 V={v1,v2,…,vn}, 定义一个nn的矩阵A,其中各元素aij为：
1 如果<vi,vj>E aij=
0 如果<vi,vj>E
称这样的矩阵为图 G 的邻接矩阵。（即若两点间有边相连，则对应 的为1，无边相连，则对应的为0）
Zhengjin,Central South University
23
Zhengjin,Central South University
24
Zhengjin,Central South University
25
Zhengjin,Central South University
26
Zhengjin,Central South University
连通图
定义3 设G=<V,E>，且vi,vjV.如果存在从vi到vj的路径，则 称从vi可达vj. (因vi 可看作长度为 0的路径，即从vi可达vi, 即任何顶点都是自己可达)。
定义4 在无向图中，如果任何两个顶点都可达，则称之为连通图。 如果G的子图是连通图，称之为连通子图。 一个无向图如果不是连通图，就是由若干个连通子图构成。 定义5 在有向图G中，如果在任两个顶点中，存在从一个顶点到 另一个顶点的路径，则称图 G为单向连通的。如果在 G中，任 何两个顶点都互相可达，则称G为强连通的。如果它的基础图 （底图）是连通的，则称之为弱连通的。 显然，强连通的，也是单向连通的，也是弱连通的。

图论之二部图图形解析

图论之二部图图形解析

*7.5 二部图及匹配7.5.1二部图在许多实际问题中常用到二部图，本节先介绍二部图的基本概念和主要结论，然后介绍它的一个重要应用—匹配。

定义7.5.1 若无向图,G V E =的顶点集V 能分成两个子集1V 和2V ，满足（1）12V V V = ，12V V φ= ；（2）(,)e u v E ∀=∈，均有1u V ∈，2v V ∈。

则称G 为二部图或偶图(Bipartite Graph 或Bigraph)，1V 和2V 称为互补顶点子集，常记为12,,G V V E =。

如果1V 中每个顶点都与2V 中所有顶点邻接，则称G 为完全二部图或完全偶图(Complete Bipartite Graph)，并记为,r s K ，其中12,r V s V ==。

由定义可知，二部图是无自回路的图。

图7-55中，(),(),(),(),(a b c d e 都是二部图，其中(),(),(),(b c d e 是完全二部图1,32,32,43,3,,,K K K K 。

图7-55二部图示例显然，在完全二部图中,r s K 中，顶点数n r s =+，边数m rs =。

一个无向图如果能画成上面的样式，很容易判定它是二部图。

有些图虽然表面上不是上面的样式，但经过改画就能成为上面的样式，仍可判定它是一个二部图，如图7-56中()a 可改画成图()b ，图()c 可改画成图()d 。

可以看出，它们仍是二部图。

图7-56二部图示例定理7.5.1 无向图,G V E =为二部图的充分必要条件为G 中所有回路的长度均为偶数。

证明 先证必要性。

设G 是具有互补节点子集1V 和2V 的二部图。

121(,,,,)k v v v v 是G 中任一长度为k 的回路，不妨设11v V ∈，则211m v V +∈，22m v V ∈，所以k 必为偶数，不然，不存在边1(,)k v v 。

再证充分性。

设G 是连通图，否则对G 的每个连通分支进行证明。

图论复习

图论复习

图论复习题第一章图主要内容：1．图的基本概念和基本定理（重点是完全图、二部图、图的同构、握手定理等）2．轨道和圈（最长轨理论）练习题目：1．5阶无向完全图的边数为__10_____。

2．图G1和G2的结点和边分别存在一一对应关系是G1和G2同构的_充分必要条件______。

3．图G1和G2的结点和边分别存在一一对应关系是G1和G2同构的_充分必要条件______。

4．设无向简单图的顶点个数为n，则该图最多有_n(n-1)/2_ 条边。

5．一个有n个结点的图，最少有___1____个连通分支。

6．有三个顶点的所有互不同构的简单无向图有___4____个。

7．单连通无向图G有12条边，G中有2个1度结点，2个2度结点，3个4度结点，其余结点度数为3．求G中有多少个结点．试作一个满足该条件的简单无向图．解：设G中有x各结点，则3度的结点有x-7根据握手定理有，1x2+2x2+4x3+3x(x-7)=2x12解得x=9,故G中有9个结点。

满足条件的图如下：8．单连通无向图G有9条边，G中有4个3度结点，2个1度结点，其余结点度数为2．求G中有多少个结点．试作一个满足该条件的简单无向图．9．面上有n个点S＝{x1,x2,……,x n}，其中任两个点之间的距离至少是1，证明在这n个点中距离为1的点对数不超过3n。

（38题）10．若图G是简单图，且(1)(2)2p pq-->，则G连通。

（42题）11．如果G是具有m条边的n阶简单图，证明：若G的直径为2且△= n-2，则m≥2n-4。

（50题）12．证明：在任何图中，奇度点个数为偶数。

（推论1.1）13．证明：图G是二部图当且仅当G无奇圈。

（定理1.2）14．证明：每个顶点度数都大于等于2的简单图必有圈。

（例1.9）15．证明：每个顶点度数都大于等于3的简单图必有偶圈。

（例1.11）16．画出4个顶点的不同构的图（包括连通和不连通图）。

第二章 树主要内容：1．树的定义和简单性质； 2．树的几个等价条件；3．生成树的个数（Cayley 公式）练习题目：1．设树T 中有2个3度顶点和3个4度顶点，其余的顶点都是树叶，则T 中有____片树叶。

第7章 图论 -5二部图、平面图

第7章 图论 -5二部图、平面图

第9章 图论
2）在G中求最大匹配 把边 (a2,b2) 从 M 中去掉，而把 (a1,b2) 和 (a2,b4) 添加到 M 中， 得到新的匹配M′=(a1,b2),(a2,b4),(a3,b3), (a5,b5)，如下图所示。 对于匹配M′= (a1,b2),(a2,b4),(a3,b3), (a5,b5)重复上述过程， 已找不到M′可扩路。所以M′就是最大匹配。
第9章 图论
在子图H中，任一结点至多与M中的一条边关联且与M1中 一条边关联。因而任一结点的度数是1或2。故H的连通分支是 一条路，或者是一个回路。 如果 H的连通分支是一条路 P，则它是 M 交替路，也是 M1 交替路。如果P的两个端点均与M中的边关联，则P是M1可扩路。 由假设知， M1 是最大匹配，所以，不存在 M1 可扩路，得到矛 盾。如果P的两个端点均与M1的边关联，那么P是一条M可扩路 与题设矛盾。故 P 只能是一个端点与 M 中的边关联，另一个端 点与M1中的边关联，这样P中属于M的边数与属于M1的边数相 等。 如果 H的连通分支是一个回路，回路中的边交替地属于 M 和M1，因而属于M的边数与属于M1的边数相等。 从上面可以看到，H中属于M的边与属于M1的边的数目相 等。再加上既属于M又属于M1的边，可以得出：M中的边数与 M1中的边数相等。所以，M是最大匹配。
第9章 图论
由上述讨论可见：利用可扩路可以增加匹配所含的边数。 不断地寻求G的可扩路，直到再也找不到新的可扩路，就可得 到一个最大匹配。将这个结论写成下列的定理。 定理 7.5.2 设 G=V1,V2,E是二部图， M为G的最大匹配的充分 必要条件是G中不存在M可扩路。 证明：设M为G的最大匹配，下证G中不存在M可扩路。 如果G中存在一条M可扩路，则可以得到比M的边数多1的 匹配，所以M 不是最大匹配，矛盾。所以G 中不存在M 可扩路。 设G中不存在M可扩路，下证M为G的最大匹配。 设M1是最大匹配，证明|M|=|M1|。 考察属于M而不属于M1和属于M1而不属于M中的边，由这 些边连同它们的端点一起构成G的子图H。

图论模型

图论模型

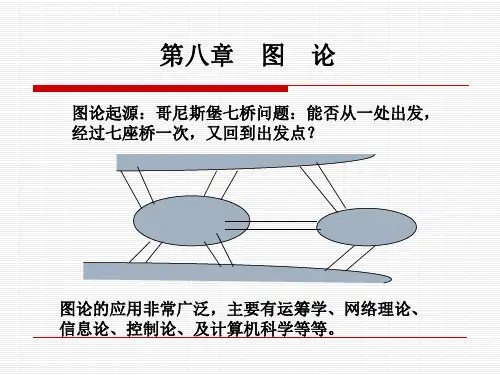
第七部分图论方法第十六章图论模型图论是应用数学的一个分支，它的概念和结果来源非常广泛，最早起源于一些数学游戏的难题研究，如欧拉所解决的哥尼斯堡七桥问题，以及在民间广泛流传的一些游戏难题，如迷宫问题、博弈问题、棋盘上马的行走路线问题等．这些古老的难题，当时吸引了很多学者的注意．在这些问题研究的基础上又继续提出了著名的四色猜想和汉米尔顿（环游世界）数学难题．1847年，图论应用于分析电路网络，这是它最早应用于工程科学，以后随着科学的发展，图论在解决运筹学，网络理论，信息论，控制论，博弈论以及计算机科学等各个领域的问题时，发挥出越来越大的作用．在实践中，图论已成为解决自然科学、工程技术、社会科学、军事等领域中许多问题的有力工具之一，图论模型属于离散类数学模型，是数学模型中比较容易为学生接受的一类模型，具有直观性、趣味性和简洁性，深得大学生的青睐。

另外，图论模型属于较为近代的前沿性数学知识，又具有强烈的，易于为学生接受的数学建模味道，对于培养学生通过建模解决实际问题的能力与学习兴趣都是不可多得的知识内容，因此越来越受到数学家和建模工作者的喜爱．我们所学的这一章只是介绍一些基本概念、原理以及一些典型的应用实例，目的是在今后的学习研究时，可以把图论的基本知识、方法作为工具．本章先介绍图论的基本概念，然后通过哥尼斯堡七桥问题、最短路径问题、中国邮递员问题、人员分派问题、稳定匹配问题、竞赛图等例子介绍图论的具体应用。

16.1 图的基本概念图是一个有序对<V，E>，V是结点集，E是边集，以表示结点数目，表示边的数目，则当∣V∣和∣E∣有限时，<V,E>称为有限图；否则称无限图.无向边, 与无序结点对(v, u)相关联的边；有向边，与有序结点对<v, u>相关联的边；无向图，每条边都是无向边的图，记作G＝<V,E>; 有向图，每条边都是有向边的图，记作D＝<V,E>.混合图，既有有向边，也有无向边的图.平凡图，仅有一个结点的图；零图，边集为空集的图<V, ∅>，即仅有结点的图.自回路(环)，关联于同一个结点的边.无向平行边，联结相同两个结点的多于1条的无向边；有向平行边，联结两个结点之间的多于1条且方向相同的有向边.简单图，不含平行边和自回路的图.在有向图D＝<V,E>中，以v(∈V)为起点的边之条数为出度deg＋(v)；以v(∈V)为终点的边之条数为入度deg－(v).在无向图G＝<V,E>中，与结点v(∈V)关联的边数，即为结点度数deg(v)或d(v).；在有向图中，结点v的出度和入度之和为度数.最大度数，∆(G)＝max{deg(v)∣v∈V}；最小度数，δ(G)=min{deg(v)∣v∈V}有n个结点的且每对结点都有边相连的无向简单图，称为无向完全图.此时有)1(21-=n n E ；有n 个结点的且每对结点之间都有两条方向相反的边相连的有向简单图为有向完全图. 此时有)1(-=n n E 。

二部图与完全二部图

二部图与完全二部图

6
定理 1 连通图 G是欧拉图的充要条件是 G的所 有结点的度数都是偶数。
下图中， (a) 图的每个结点的度数都为４， 所以它 是欧拉图；(b)图不是欧拉图。 但我们继续考察(b)图可以发现， 该图中有一条 路v2v3v4v5v2v1v5， 它经过(b)图中的每条边一次且仅 一次， 我们把这样的路称为欧拉路。
18

对右图 ， 图中粗 线给出了这样的回路。 定义4 给定图G， 若 有一条路通过G中每个结 点恰好一次， 则这样的 路称为哈密尔顿路；若 有一个圈， 通过G中每 个结点恰好一次(起点两 次)， 这样的圈称为哈 密尔顿回路（或哈密尔 顿圈）。 具有哈密尔顿回路 的图称为哈密尔 设G为n阶m条边r个面的连通平面图， 则 nm+r=2. 证 对边数m做归纳证明. m=0, G为平凡图, 结论为真. 设m=k(k0)结论为真, m=k+1时分情况讨论如下: (1) G中无圈, 则G必有一个度数为1的顶点v, 删除v及它关 联的边, 记作G . G 连通, 有n-1个顶点, k条边和r个面. 由归 纳假设, (n-1)-k+r=2, 即n-(k+1)+r=2, 得证m=k+1时结论成立. (2) 否则,删除一个圈上的一条边,记作G . G 连通, 有n个顶 点,k条边和r-1个面. 由归纳假设, n-k+(r-1)=2, 即n-(k+1)+r=2, 得证m=k+1时结论也成立. 证毕.
二部图?二部图?完全二部图1二部图定义图设无向图gve若能将v划分成v1和和v2v1v2vv1v2?使得g中的每条边的两个端点都一个属于中的每条边的两个端点都一个属于v1另一个属于v2则称g为为二部图记为v1v2e称v1和和v2为互补顶点子集

《图论》复习提纲

《图论》复习提纲

《图论》复习提纲1、 图（1） 图的概念：图的定义；空图；平凡图；简单图；完全图；二部图；完全二部图；星；轮；补图；正则图（k--正则图）；同构；图的分类。

（2） 子图：子图的概念；真子图；G 的生成子图；G 的导出子图；主子图；G 的边导出子图。

（3） 顶点的度：顶点v 的度；奇顶点；偶顶点；握手定理；握手定理的推论。

（4） 道路与连通性：途径；链；道路；圈；圈的分类；连通图；非连通图；测地线；u 与v 之间的距离；G 的围长；G 的周长；G 的直径；G 是二部图的充要条件。

（5） 图的运算： 图 和的并；交；差；环和。

2、 树（1） 树的特性：树的定义；树的六个等价命题。

（2） 割边与割点：割边；割点；圈和割边的关系；树和割边的关系；如何判断树中的割点；不可分图；割点的三个等价命题；割边的三个等价命题。

（3） 生成树：生成树的定义；图有生成树的充要条件；判断一棵生成树的充要条件；求生成树的两种方法。

3、 欧拉图和哈密顿图（1）环路：环路；环路中顶点的度满足什么条件；图G 是连通环路的充要条件；什么是开链；多个环路的环和。

（2） 欧拉图：欧拉图和欧拉链；闭链、环路和欧拉图的关系；图G 是连通欧拉图的充要条件；两个欧拉图的环和。

（3） 哈密顿图：哈密顿圈和哈密顿图；哈密顿图的必要条件；哈密顿图的充分条件；满足什么条件G 是哈密顿图的充要条件是G+uv 为哈密顿图；图G 的闭包；简单图的闭包和哈密顿图的关系。

4、 割集（1）割集与断集：割集；断集；设T 是连通图G 的一棵生成树，并且e 是任一树枝，则：连枝集中是否包含G 的割集，T e +包含G 的几个割集；割集和生成树之间的关系是什么？（2）关联集：关联集；任一断集和关联集的关系；任一顶点的关联集和其余顶点关联集的关系。

5、连通性（1）连通度和边连通度：顶点割；点连通度；边连通度；点连通度、边连通度和最小度之间有什么关系；点连通度和边连通度的范围是多少；在什么条件下，边连通度和最小度相等；（2）2-- 连通图：块；P 和Q 是内部不相交的；图G 是2—连通的充要条件；图是不可分的几个等价命题。

图论简介

图论简介

关于有 n 结点 m 边的(n,m)图度的定理
• 定理1-1 令 v1,…,vn为图的所有结点,则 i=1n deg(vi)=2m. (1) 定理1-2 任何图中度为奇数的结点必பைடு நூலகம்偶数个.
图的同构
定义:对给定两个图 G=V,E,G=V,E,若存在 双射 f:VV 使对任意a,bV, (a,b)E (f(a),f(b))E,并且(a,b)与 (f(a),f(b))有相同重数,则称 G 与 G同构,记 为 GG. 注:① 两图同构是相互的: GG GG. ② 两图同构时不仅结点之间要有一一对应关系, 而且要求这种对应关系保持结点间的邻接关系. 对有向图同构还要求保持边的方向. ③ 寻求判断图同构的简单有效方法仍是图论待 解决的重要问题.
无向图 G 能否一笔画的问题等价于 G 是 否有一条Euler路径(回路)的问题
a
1 b 2 3 9 6 4 5 8 7
若图只有两个奇结点,则任何Euler路径必 从其中一点开始到另一点结束.利用这条规律, 先在此2奇点之间加条边使之变成Euler图并画 出一条Euler回路,然后再去掉所加的边即得一 条Euler路径.
同构图举例
4 2 1 a c 3 1 2 3
G
4 a 5 d 6
H H’
b
G’
d b
f c e
G G’ 1a,2b,3c, 4d
H H’ 1a,2b,3c, 4d,5e,6f
非同构图举例
存在结点数及每个结点对应度都相等的两个图 仍然不同构的情况.; 如下:(注意:两个4度点 或邻接或不相邻接)
图的定义与记号
• 图G是一个二重组:G=V,E,其中V是非空有限集 合,它的元素称为结点或顶点, E 也是(可空)有 限集合,它的元素称为边. • 图G的边e是一个结点二重组:a,b,a,bV,e可 以是有序的,称为有向边,简称为弧,a称为弧e 的始点,b称为e的终点; e也可以是无序的,称 为无向边.e=a,b时,称e与a,b关联,或a,b与e 关联,或a与b相邻接;关联于同一顶点的一条边 称为自回路或环. • 每条边都是无向边的图称为无向图;每条边都 是有向边的图称为有向图;我们仅讨论无向图 和有向图.

总结-图论

总结-图论

生成树
设 T 为无向连通图 G 中一棵生成树，e 为 T 的任意一条弦，则 T ∪e 中含 G 中只含一条弦其余边均为树枝的圈，而且不同的弦对应的圈 也不同。
设 T 是连通图 G 的一棵生成树，e 为 T 的树枝，则G 中存在只含树 枝 e，其余边都是弦的割集，且不同的树枝对应的割集也不同。
r 叉完全正则树——树叶的层数均为树高的 r 叉正则树
r 叉完全正则有序树——r 叉完全正则树是有序的的
平面图
G 是可平面图或平面图——如果能将无向图 G 画在平面 上，使得除顶 点处外无边相交。
G 的平面嵌入——画出的无边相交的平面图。 非平面图——无平面嵌入的图。
K5 和 K3,3 都不是平面图。
平面图
(1)设 T 为根树，若将 T 中层数相同的顶点都标定次序，
则称 T 为有序树。 (2)分类：根据根树 T 中每个分支点儿子数以及是否有序 r 叉树——每个分支点至多有 r 个儿子
r 叉有序树——r 叉树是有序的
r 叉正则树——每个分支点恰有 r 个儿子 r 叉正则有序树——r 叉正则树是有序的
T 是 n (n≥2) 阶有向树， (1) T 为根树— T 中有一个顶点入度为 0， 其余顶点的入度均为 1
(2) 树根——入度为 0 的顶点
(3) 树叶——入度为 1，出度为 0 的顶点 (4) 内点——入度为 1，出度不为 0 的顶点 (5) 分支点——树根与内点的总称 (6) 顶点v的层数——从树根到v的通路长度 (7) 树高——T 中层数最大顶点的层数 (8) 根树——平凡树(规定)
d
i 1
n
i
0( mod 2)
图的基本概念
图同构、子图、生成子图、导出子图等。

图论简介

图论简介

图论简介图论属于拓扑学topology。

拓扑学分为一般拓扑学和代数拓扑学，前者来源于数学分析，最终研究一般的拓扑空间和一般的拓扑结构，而后者来源于几何，实际上是一种几何学的分支。

我们主要讨论后者，重点是利用图形的几何拓扑性质。

拓扑性质，就是几何图形在弯曲、变形、拉大、缩小下仍然保持的性质，只是这种变形要求原来不再一起的点不能粘在一起，原来一起的点也不能断开，也就是图形变换前后每点附近的点还是在附近。

这种变换和它的逆变换都是连续的一一对应，称为同胚。

一个图形和它同胚的图形称为拓扑等价。

拓扑学就是研究图形的拓扑性质。

也就是图形经过连续变换下，保持不变的性质。

图论以图为研究对象的数学分支。

图论中的图指的是一些点以及连接这些点的线的总体。

通常用点代表事物，用连接两点的线代表事物间的关系。

图论则是研究事物对象在上述表示法中具有的特征与性质的学科。

看一些例子：一、哥尼斯堡七桥问题。

当时的图论问题是盛行的迷宫问题和游戏问题。

最有代表性的工作是著名数学家L.Euler于1736年解决的哥尼斯堡七桥问题(Konigsberg Seven Bridges Problem)。

东普鲁士的哥尼斯堡城(现今是俄罗斯的加里宁格勒，在波罗的海南岸）位于普雷格尔(Pregel)河的两岸，河中有一个岛，于是城市被河的分支和岛分成了四个部分，各部分通过7座桥彼此相通。

如同德国其他城市的居民一样，该城的居民喜欢在星期日绕城散步。

于是产生了这样一个问题：从四部分陆地任一块出发，按什么样的路线能做到每座桥经过一次且仅一次返回出发点。

这就是有名的哥尼斯堡七桥问题。

哥尼斯堡七桥问题看起来不复杂，因此立刻吸引所有人的注意，但是实际上很难解决。

瑞士数学家(Leonhard Euler)在1736年发表的“哥尼斯堡七桥问题”的文章中解决了这个问题。

这篇论文被公认为是图论历史上的第一篇论文，Euler也因此被誉为图论之父。

欧拉把七桥问题抽象成数学问题---一笔画问题，并给出一笔画问题的判别准则，从而判定七桥问题不存在解。

离散数学_第7章 图论 -1-2图的基本概念、路和回路

离散数学_第7章 图论 -1-2图的基本概念、路和回路

第9章 图论
返回总目录
第9章 图论
第7章 图论
图论是一个重要的数学分支。数学家欧拉1736年发 表了关于图论的第一篇论文，解决了著名的哥尼斯堡七 桥问题。克希霍夫对电路网络的研究、凯来在有机化学 的计算中都应用了树和生成树的概念。随着科学技术的 发展，图论在运筹学、网络理论、信息论、控制论和计 算机科学等领域都得到广泛的应用。本章首先给出图、 简单图、完全图、子图、路和图的同构等概念，接着研 究了连通图性质和规律，给出了邻接矩阵、可达性矩阵、 连通矩阵和完全关联矩阵的定义。最后将介绍欧拉图与 哈密尔顿图、二部图、平面图和图的着色、树和根树。
v3
e7
a e6e3
e2
b e5
（本课程仅讨论无向图和有向图）
v4
c
9章 图论
【例7.1.1】无向图G=V(G),E(G),G
其中：V(G)=a,b,c,d
E(G)=e1,e2,e3,e4
G：G(e1)=(a,b) G(e2)=(b,c) G(e3)=(a,c) G(e4)=(a,a)
试画出G的图形。
即，deg(v)=deg－(v)+deg＋(v)，或简记为d(v)=d－(v)+d＋(v)
4）最大出度：+(G) =max deg＋(v) | vV
5）最小出度：+(G) = min deg＋(v) | vV
6）最大入度： (G) =max deg－(v) | vV
7）最小入度： (G) = min deg－(v) | vV
解：G的图形如图7.1.2所示。
图 7.1.2
由于在不引起混乱的情况下，图的边可以用有序对或无序 对直接表示。因此，图可以简单的表示为：
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

二部图
完全二部图K2,3
完全二部图K3,3
第9章 图论
二部图的判别定理
定理7.5.1 设G=V,E是无向图，G为二部图的充分必要条件是 G的所有回路的长均为偶数（即G中无奇长度的回路）。 证明：必要性 设G是二部图，下证G的所有回路的长均为偶数。
设G是二部图，则V可以分成两个互补的结点子集 V1和V2，每一 个边的两个端点分别在V1和V2中，令 C：v0v1v2„vl-1v0 是G中任一长度为l的回路。不失一般性，设v0V1，则v1V2，v2V1， 则 v3V2 ，„„。由此可知， v2iV1 ，v2i ＋ 1V2 。又因为 v0V1 ，所以 vl-1V2，l-1是奇数，l是偶数。 充分性 设G的所有回路的长均为偶数，下证G是二部图。 不妨设G是连通图，否则可对每一个连通分支进行讨论。v0V， 定义V的两个子集V1和V2为： V1=v | vV∧d(v0,v)为偶数 V2=v | vV∧d(v0,v)为奇数 因为G是连通图，任何结点与 v0 之间都有路，d(v0,v)不是偶数就 是奇数，所以V1∪V2=V，V1∩V2=。
第9章 图论
下面证明V1中任意两个结点不邻接，V2中任意两个结点也不邻接。 若存在viV1，vjV1，vi 和vj邻接，由于d(v0,vi)为偶数，v0到vi 有一条长为偶数的路。同样的道理，v0到vj也有一条长为偶数的路。 这两条路和边(vi,vj)构成一条回路，其长度为奇数。与条件矛盾。 所以 V1 中任意两个结点不邻接。类似的可证， V2 中任意两个结点 也不邻接。于是G为二部图。 根据此定理，下图中的(a)和(b)两个图是二部图。这比用定义 判断要方便得多。画二部图时，习惯将互补的结点子集V1和V2分 开画，画成类似左下图的形式。下图中的(a)，(b)两个二部图，一 定可以改画为互补的结点子集V1和V2分开的形式（请大家自己尝 试画画）。
非二部图
第9章 图论
匹配（对集）
定义7.5.3 (匹配) 设G=V1,V2,E是二部图，M是G中一些边 组成的集合，如果M中任意两条边都没有公共端点，则称M 为 G 的一个匹配或对集。设 v 是 G的结点，如果 v 是 M 中某条 边的端点，则称v为M的饱和点。否则，称v为M的非饱和点。 实例：下图中，边集M=(a1,b2), (a2,b3), (a4,b1)是一个匹配， a1, a2, a4和b1,b2,b3为M的饱和点。结点a3为M的非饱和点。
第9章 图论
在子图H中，任一结点至多与M中的一条边关联且与M1中 一条边关联。因而任一结点的度数是1或2。故H的连通分支是 一条路，或者是一个回路。 如果 H的连通分支是一条路 P，则它是 M 交替路，也是 M1 交替路。如果P的两个端点均与M中的边关联，则P是M1可扩路。 由假设知， M1 是最大匹配，所以，不存在 M1 可扩路，得到矛 盾。如果P的两个端点均与M1的边关联，那么P是一条M可扩路 与题设矛盾。故 P 只能是一个端点与 M 中的边关联，另一个端 点与M1中的边关联，这样P中属于M的边数与属于M1的边数相 等。 如果 H的连通分支是一个回路，回路中的边交替地属于 M 和M1，因而属于M的边数与属于M1的边数相等。 从上面可以看到，H中属于M的边与属于M1的边的数目相 等。再加上既属于M又属于M1的边，可以得出：M中的边数与 M1中的边数相等。所以，M是最大匹配。
第9章 图论
由上述讨论可见：利用可扩路可以增加匹配所含的边数。 不断地寻求G的可扩路，直到再也找不到新的可扩路，就可得 到一个最大匹配。将这个结论写成下列的定理。 定理 7.5.2 设 G=V1,V2,E是二部图， M为G的最大匹配的充分 必要条件是G中不存在M可扩路。 证明：设M为G的最大匹配，下证G中不存在M可扩路。 如果G中存在一条M可扩路，则可以得到比M的边数多1的 匹配，所以M 不是最大匹配，矛盾。所以G 中不存在M 可扩路。 设G中不存在M可扩路，下证M为G的最大匹配。 设M1是最大匹配，证明|M|=|M1|。 考察属于M而不属于M1和属于M1而不属于M中的边，由这 些边连下图中，匹配M=(a1,b2), (a2,b3), (a3,b5)， 路 L1：a1b2a2b3a3， L2：a2b3a3b5a4， L3：b1a3b5a4， L4：b1a1b2a2b3a3b5a4 都是M交替路，其中后两条交替路L3和L4的始点和终点都 是M的非饱和点，所以这两条路是M可扩路。
2）在G中求最大匹配 把 M 可 扩 路 a2b2a5b3 中 的 边 (a5,b2) 从 M 中 去 掉 ， 而 把 (a2,b2)和(a5,b3)添加到M中得到 新 的 匹 配 M′=(a3,b1), (a2,b2), (a5,b3)，如右图所示。
第9章 图论
对匹配M′= (a3,b1), (a2,b2), (a5,b3) 再用标记法： 用(*)标记V1中所有M′的非饱和点a1和 a4。 ①选V1的新标记过的结点a1，用(a1)标记不通过M′的边与 a1邻接且尚未标记过的V2的所有结点b1；再用(a4)标记b2。 ②选V2的新标记过的结点b1，用(b1)标记通过M′的边与b1 邻接且尚未标记过的V1的所有结点a3；再用(b2)标记a2。 ③选 V1 的新标记过的结点 a2 和 a3 ， V2 中已无可标记的结 点。 图中已不存在可扩路，所以M′就是最大匹配。
解：1）采用标记法寻找可扩路。 取该二部图的一个匹配： M= (a3,b1), (a5,b2) 用(*)标记V1中所有M的非饱 和点a1, a2, a4。 采用下述过程进行标记：
第9章 图论
①选V1的新标记过的结点a1，用(a1)标记不通过M的边与a1邻 接且尚未标记过的V2的结点b1；类似地用(a2)标记b2。 ②选V2的新标记过的结点b1，用(b1)标记通过 M的边与b1邻接 且尚未标记过的V1的结点a3；类似地用(b2)标记a5。 ③选V1的新标记过的结点a3，因为不存在不通过M的边与a3邻 接的V2的结点，所以不用(a3)标记V2的结点；用(a5)标记b3或 b4， 假定用(a5)标记b3。如上页图中所示。 b3是M的非饱和点，标记结束。 从 b3 倒 向 追踪 到 标 记 有 (*) 的 结 点， 就 得 到 了 M 可 扩 路 ： a4b2a5b3或a2b2a5b3，取后者。
第9章 图论
【例7.5.2】右下图是一个二部图，求其最大匹配。 解： 1) 用标记法寻找可扩路。 取该二部图的一个匹配 M=(a2,b2), (a3,b3), (a5,b5)。 用 (*) 标记 V1中所有 M 的非饱 和点a1, a4。 采用下述过程进行标记： ①选 V1 的新标记过的结点 a1 ， 用(a1)标记b2和b3。 ②选V2的新标记过的结点b2和b3，用(b2)标记a2，用(b3)标记a3。 ③选V1的新标记过的结点a2，用(a2)标记b1, b4和b5。 由于b1和b4都是M的非饱和点，说明找到了M可扩路。它 们是：a1b2a2b4和a1b2a2b1，选前者。
第9章 图论
设G=V1,V2,E是二部图，M 是G的一个匹配，P是G中的一 条M可扩路。把P中所有属于M的边从M中去掉，而把P中所有不 属于 M 的边添加到 M中，得到一个新的边集 M′ ，则 M′也是一个 匹配，其所含边数比匹配M所含的边数多1。 例如，在上页实例图中，把M可扩路L3：b1a3b5a4中属于M的 边(a3,b5) 从M中去掉，而把L3中不属于M的边(a3,b1)和(a4,b5) 添加 到M中，得到一个新的边集： M′=(a1,b2),(a2,b3),(a3,b1), (a4,b5)， 显然M′也是匹配且M′的边数比M的边数多l，即|M′|＝|M|+1。 如下图所示。
第9章 图论
7.5 二部图和平面图
• 7.5.1 二部图(Bipartite graph)及匹配(Matching) – 二部图的充要条件 – 二部图的匹配 • 7.5.2 平面图(Plane graph)
第9章 图论
7.5.1 二部图及匹配 二部图（亦称偶图）
定义7.5.1 (二部图)G=V,E是无向图，V1V，V2V，满足： ① V1∪V2= V，V1∩V2=。 ② G中每一条边的两端点，一个属于V1，另一个属于V2。 则称G为二部图或偶图，常记为G=V1,V2,E，V1和V2称为G的互 补的结点子集。 二部图的每一条边的两个端点位于两个互补的结点子集，所 以没有自回路。二部图是无自回路图。 定义7.5.2 (完全二部图)设G=V1,V2,E是二部图，|V1|=r, |V2|=s， 若V1的每个结点和V2的所有结点邻接, 则称G为完全二部图或完全 偶图，常记为Kr,s。
第9章 图论
2）在G中求最大匹配 将第一阶段寻找到的M可扩路中所有属于M的边从M中去掉， 而把M可扩路中所有不属于M的边添加到M中，得到一个新的匹 配M′且其所含边数比匹配M所含的边数多1。 对M′重复上述过程，„„，直到G中已不存在可扩路，此时 的匹配就是最大匹配。
【例7.5.1】右下图是一个二部图，求其最大匹配。
第9章 图论
实例
a b f e d
a
e
b c
d
非二部图 b
a g
c
d
c 二部图 V1={a,b,c}, V2={d,e} c b
二部图 V1={a,c,e}, V2={b,d,f}
a
f e
d
f e 二部图 V1={a,c,e},V2={b,d,f,g}
二部图 V1={a,c,e}, V2={b,d,f}
第9章 图论
最大匹配（最大对集）
在上页实例的图中，如果用 a1,a2,a3,a4 表示 4 位教师， b1,b2,b3 表示三门待开的课程。当某位教师能开某门课程时，则把它们的 对应结点用边连接起来。如果规定一个教师只能担任一门课程， 那么匹配M 就表示了一种排课方案。为了使排课方案能最大限度 地作到“各尽其能”，下面将引进最大匹配的概念。 定义7.5.4 设G=V1,V2,E是二部图，M是G的一个匹配，如果对G 的任意匹配M′，都有|M′|≤|M|，则称M为G的最大匹配或最大对集。 为寻求二部图的最大匹配，以下引进交替路和可扩路两个概念。 定义7.5.5 设G=V1,V2,E是二部图，M是G的匹配，P是G中的一 条路，如果P是由G中属于M的边和不属于M的边交替组成，则称 P为G的M交替路。如果交替路的始点和终点都是 M的非饱和点， 则称为G的M可扩路。