当前位置：文档之家 › 7弯曲变形

7弯曲变形

  • 格式：ppt
  • 大小：1.50 MB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

材料力学第七章课后题答案 弯曲变形

材料力学第七章课后题答案 弯曲变形
3．确定积分常数
(a) (b)
7
该梁的位移边界条件为：
在x 0处， w0 dw 在x 0处， 0 dx 将条件(c)与(d)分别代入式(b)和(a)，得 D 0，C 0 4．建立挠曲轴方程 将所得 C 与 D 值代入式(b)，得挠曲轴的通用方程为
1 Fa 2 F 3 3Fa [ x x xa EI 4 6 4 由此得 AC 段、 CD 段和 DB 段的挠曲轴方程依次为 w
5．计算 wC 和 θ B 将 x a 代入上述 w1或w2 的表达式中，得截面 C 的挠度为
41qa 4 ( ) 240EI 将以上所得 C 值和 x 2a 代入式(a)，得截面 B 的转角为 wC θB qa 3 7 4 16 1 187 203qa 3 [ ] EI 24 24 24 720 720 EI ()
(4)
D1 0 ， C1
由条件（4） 、式（a）与（c） ，得
qa 3 12 EI
C2
由条件（3） 、式（b）与（d） ，得
qa 3 3EI
D2
7qa 4 24 EI
3. 计算截面 C 的挠度与转角 将所得积分常数值代入式（c）与（d） ，得 CB 段的转角与挠度方程分别为
q 3 qa 3 x2 6 EI 3EI 3 q qa 7 qa 4 4 w2 x2 x2 24 EI 3EI 24 EI 将 x2=0 代入上述二式，即得截面 C 的转角与挠度分别为
5．计算 wC 和 θ B 将 x a 代入上述 w1 或 w2 的表达式中，得截面 C 的挠度为
Fa 3 ( ) 12 EI 将以上所得 C 值和 x 3a 代入式(a)，得截面 B 的转角为 wC

材料力学 第7章 弯曲变形

材料力学 第7章 弯曲变形

M
Fx 挠曲轴近似微分方程： w ' ' EI 3 2 Fx Fx w Cx D w' ( x) C 6 EI 2EI
梁的弯矩方程： M ( x ) Fx
2、确定积分常数
FAy
A x
F L
B
X=0, w=0 X=L, w=0
M
Me L C＝－ ，D＝0 6 EI
3、挠度方程、转角方程及B截面的转角
FAy
x
F L
B
M
3、挠度方程、转角方程及B截面的转角
Fx w' (x) 2EI 3 Fx w 6 EI
2
将 x=L 代入转角方程：
FL2 B 2 EI
例2：简支梁AB，弯曲刚 度 EI为常数，受力偶 M=FL作用，求w(x)，
FAy
A x
F L
B
θ(x)；
解：1、 建立挠曲轴微分方程并积分 A端约束反力 FAy=F
FA A a l
x
F D b
FB
B x
Fb 解：坐标系如图，求出反力。 FA l 分AD、DB两段分析：
y
Fa FB l
b AD段： 0 x a M x F x l b M x F x 则： EIw1 l
积分可得：
b M x F x EIw1 l
= 0
自由端：无位移边界条件。 位移连续与光滑条件 挠曲轴在B点连续且光滑 连续：wB左= wB右 光滑：左 = 右
F A B D
写出梁的挠曲轴方程的边界条件和连续条件。 例：
F A B C E D
思考： 1、 该梁可分几段积分？ 2、 各边界和内部分界点有多少位移边界与连续条件？ 分4段。 位移边界条件：A端：2个； C端：1个；D端：无。 位移连续条件：E：2个；B：1个；C：2个

第三章 弯 曲 (2)

第三章 弯 曲 (2)

ρ = r + xt
r：弯曲件内弯曲半径 t：材料厚度 x：中性层位移系数，查表。 弯曲件展开尺寸计算：
r/t < 0.5时,因为圆角区域发生了严重变薄，其相邻的直边也变薄，因 此需要采用经验公式计算。 对于复杂形状的弯曲件，在初步计算后，还需要反复试弯，不断修 正才能确定坯料尺寸。
3 回弹值的确定： 为了得到形状与尺寸精确的弯曲件，需要实现确定回弹值， 因为影响因素很多，理论计算方法往往不精确，而且很复杂，因此 一般是根据经验数值以及简单的计算来初步确定模具工作部分尺寸， 然后在试模时校正。
图3-21
产生偏移的原因： 1 弯曲坯料形状不对称； 2 弯曲件两边折弯个数 不相等； 3 弯曲凸凹模结构不对 称。
图3-22
控制偏移措施： 1 采用压料装置。
图3-23
2 利用工艺孔限制坯料移动。 3 对偏移量进行补偿。
4 对不对称零件，先成对弯曲，再切断。 5 尽量采用对称凸凹模结构
图3-24
0 .7 K B t σ b F自 = r+t
2
U型件：
]型件：
F = 2.4 Btσ b ac 自
上式中： F自：自由弯曲在冲压行程结束时的弯曲力； B：弯曲件的宽度； r：弯曲件的内弯曲半径； t：弯曲件材料厚度； σb：材料抗拉强度； K：安全系数，一般取1.3 a、c：系数； 校正弯曲时的弯曲力： 校正弯曲时的弯曲力一般按照下式计算：
2 应力状态 长度方向：弯曲内区受压，外区受拉，切向应力是绝对值最大的主应 力； 厚度方向：在变形区内存在径向压应力，在板料表面为0，由表及里 逐渐增加，到达中性层时达到最大值； 宽度方向：对于窄板，由于可以自由变形，因此内外区都为0，对于 宽板，内区为压应力，外区为拉应力

弯曲变形的过程及

弯曲变形的过程及
弯曲变形的过程及变形特点
肖永茂
弯曲变形的过程
弯曲变形过程： 如图3.1.2所示V形件的弯曲， 随着凸模进入凹模深度的增大，凹模与板料
的接触处位置发生变化，支点B沿凹模斜面 不断下移，弯曲力臂l 逐渐减小，接近行程 终了，弯曲半径r继续减小，而直边部分反 而向凹模方向变形，直至板料与凸、凹模 完全贴合。
中性层。应变中性层长度的确定是今后进行弯曲件毛坯展
开尺寸计算的重要依据。当弯曲变形程度很小时，应变中 性层位置基本上处于材料厚度的中心，但当弯曲变形程度 很大时，可以 发现应变中性层位置向材料内侧移动，变 形量愈大，内移量愈大。
3. 变形区材料厚度变薄的现象
弯曲变形程度愈大，变形区外侧材料受 拉伸长，使得材料厚度方向的材料减薄； 变形区内侧材料受到压缩，使得材料厚度 方向的材料增厚。应变中性层位置向材料 内侧移动，外侧的减薄区域随之扩大，内 侧的增厚区域随之缩小，外侧的减薄量大 于内侧的增厚量，因此使弯曲变形区的材 料厚度。变薄程度愈大，料的相对宽度B/t（B是板料的宽度，t是板料的厚度） 对变形区的材料变形有很大影响。一般将相对宽度B/t大于 3的板料称为宽板，相对宽度B/t小于等于3的板料称为窄板 。 窄板弯曲时，宽度方向的变形不受约束。由于弯曲变形区外 侧材料受拉引起宽度方向收缩，内侧材料受压引起宽度方 向增厚，其横断面形状变成了外窄内宽的扇形，变形区横 断面尺寸发生改变称为畸变。 宽板弯曲时，在宽度方向的变形会受到相邻部分材料的制约 ，材料不易流动，因此其横断面形状变化较小，仅在两端 会出现少量变形。
2.弯曲变形区存在应变中性层
比较变形区内前后相应位置的网格线长度可知，板料的外区 （靠 凹模一侧） ，纵向纤维受拉而伸长；内区（靠 凸模 一侧） ，横向纤维受压缩而缩短。内、外区至板料的中 心，其缩短和伸长的程度逐渐变小。由于材料的连续性， 在缩短和伸长两个变形区域之间。其中必定有一层金属纤 维材料的长度在弯曲前后保持不变，这一金属层称为应变

弯曲变形——精选推荐

弯曲变形——精选推荐

第六章弯曲变形判断弯曲变形1、“平面弯曲梁的挠曲线必定是一条与外力作用面重合或平行的平面曲线”2、“由于挠曲线的曲率与弯矩成正比，因此横截面的挠度与转角也与横截面的弯矩成正比”3、“只要满足线弹性条件，就可以应用挠曲线的近似微分方程”4、“两梁的抗弯刚度相同、弯矩方程相同，则两梁的挠曲线形状相同”5、“梁的挠曲线方程随弯矩方程的分段而分段，只要梁不具有中间铰，梁的挠曲线仍然是一条光滑、连续的曲线。

”6、“最大挠度处的截面转角一定为0”7、“最大弯矩处的挠度也一定是最大”8、“梁的最大挠度不一定是发生在梁的最大弯矩处。

”9、“只要材料服从虎克定律，则构件弯曲时其弯矩、转角、挠度都可以用叠加方法来求”10、“两根几何尺寸、支撑条件完全相同的静定梁，只要所受的载荷相同，则两梁所对应的截面的挠度和转角相同，而与梁的材料是否相同无关”11、“一铸铁简支梁在均布载荷的作用下，当其横截面相同且分别按图示两种情况放置时，梁同一截面的应力和变形均相同”选择弯曲变形1、圆截面的悬臂梁在自由端受集中力的作用，当梁的直径减少一半而其他条件不变时，最大正应力是原来的倍；最大挠度是原来的倍。

若梁的长度增大一倍，其他条件不变，最大弯曲正应力是原来的倍，最大挠度是原来的倍。

A：2； B：16 C：8 D：4；2、y’’=M(x)/EI在条件下成立。

A：小变形； B：材料服从虎克定律；C：挠曲线在xoy面内； D：同时满足A、B、C；3、等直梁在弯曲变形时，挠曲线最大曲率发生在处。

A：挠度最大； B：转角最大 C：剪力最大； D：弯矩最大；4、在简支梁中，对于减少弯曲变形效果最明显。

A：减小集中力P； B：减小梁的跨度；C：采用优质钢； D：提高截面的惯性矩5、板条弯成1/4圆，设梁始终处于线弹性范围内：①σ=My/I Z,②y’’=M(x)/EI Z哪一个会得到正确的计算结果？A：①正确、②正确；B：①正确、②错误； C:①错误、②正确； D：①错误、②错误；6、应用叠加原理求横截面的挠度、转角时，需要满足的条件是。

第七章 弯曲变形

第七章 弯曲变形

材料力学
弯曲变形/挠曲线的近似微分方程
二、挠曲线的近似微分方程
1 M ( x) 力学公式 ( x) EI z d2y 1 dx2 数学公式 3 ( x) dy 2 2 [1 ( ) ] dx 1

，得：
以上两式消去
材料力学
d2y M ( x) dx2 3 EI z dy 2 2 [1 ( ) ] dx
材料力学
x 0, y A 0
x a时，C左 C右 x a时，yC左 yC右
x L, yB lBD
FBy h EA
FBy k
弯曲变形/用积分法求梁的变形
讨论：
（1）凡载荷有突变处（包括中间支座），应作为分段点；
（2）凡截面有变化处，或材料有变化处，应作为分段点； （3）中间铰视为两个梁段间的联系，此种联系体现为两 部分之间的相互作用力，故应作为分段点；
B L x
A
x L时，yB 0.
材料力学
弯曲变形/用积分法求梁的变形 若B支座改为弹簧支撑，则： y A a
L
若B支座改为拉杆支撑，则： D B kx A a
L
F
C
b
F C b
EA
h
x 0, y A 0
B
x a时，C左 C右 x a时，yC左 yC右
x L, y B
弯曲变形/用积分法求梁的变形 AC段 (0 x a) BC段 (a x L) Fb 2 Fb 2 F EI y1 EI 1 x C1 , EI y2 EI 2 x ( x a ) 2 C2 , 2L 2L 2 Fb 3 Fb 3 F EIy 1 x C1 x D1 , EIy 2 x ( x a ) 3 C2 x D2 , 6L 6L 6 3、确定常数 由边界条件：

梁弯曲变形的计算

梁弯曲变形的计算

yC 2
A MA FA A F C
(a)
Fl 3 24 EI Z
B FB B FB
求得有无顶尖作用时，在刀 尖处变形比为：
yC 7 yC 2 32
结论：可见用顶尖可有效地 减小工件的变形，因而，在 细长轴加工中要设置顶尖， 甚至使用跟刀架。
材料力学
+ A C F B
(b)
F MA A 2a (a)
2
x
d y 2 dx
d y M ( x) 所以 2 dx EI z
2
O
1
2
M (x ) < 0
dy dx 2 < 0
2
x
材料力学
由弯矩的正负号规定可得，弯矩的符号与挠曲 线的二阶导数符号一致，所以挠曲线的近似微分方 程为：
d w M ( x) 2 dx EI z
由上式进行积分，就可以求出梁横截面的转角 和挠度。
1 M ρ EI z

忽略剪力对变形的影响
1 M ( x) ( x) EI z
材料力学
由数学知识可知：
d y 2 1 dx dy 2 3 [1 ( ) ] dx 略去高阶小量，得
2
y M (x ) > 0 M (x ) > 0
dy dx 2 > 0 O
y M (x ) < 0
3
11ql 3 ( ) 48EI
材料力学
wC
例4 已知：悬臂梁受力如图 示，q、l、EI均为已知。求C 截面的挠度wC和转角C 解 1）首先，将梁上的载荷变成 有表可查的情形
为了利用梁全长承受均 布载荷的已知结果，先将均 布载荷延长至梁的全长，为 了不改变原来载荷作用的效 果，在AB 段还需再加上集 度相同、方向相反的均布载 荷。

材料力学教程-7.弯曲变形

材料力学教程-7.弯曲变形
数据处理
根据需要，对数据进行计算、 绘图等处理，以便更好地理解 和分析实验结果。
结果分析
结合实验数据和理论分析，评 估材料的弯曲性能，并探讨影 响材料弯曲性能的因素。
结论总结
总结实验结果，得出结论，并 提出改进和优化材料弯曲性能
的建议。
04
弯曲变形的工程应用实例
桥梁的弯曲变形分析
总结词
桥梁的弯曲变形分析是确保桥梁安全的重要环节，通过分析桥梁在不同载荷下的弯曲变形程度，可以评估桥梁的 承载能力和安全性。
转角
梁在弯曲变形后，其横截 面绕其中性轴旋转的角度 称为转角。转角是衡量梁 横截面旋转程度的量。
弯曲变形的物理关系
弯矩
由于外力作用在梁上，使梁产生弯曲变形的力矩 称为弯矩。弯矩是引起梁弯曲变形的力。
剪力
在梁弯曲变形过程中，垂直于轴线的横向剪切力 称为剪力。剪力使梁产生剪切变形。
扭矩
当外力作用在梁的某一侧时，会使梁产生扭转变 形，这种使梁产生扭转变形的力矩称为扭矩。
详细描述
高层建筑由于其高度和规模，对风载和地震等外部载荷非常敏感。因此，在高层建筑设 计阶段，需要进行详细的弯曲变形分析。这包括对建筑物的整体结构和各个楼层在不同 载荷下的弯曲变形进行模拟和分析，以确保建筑物在各种外部载荷下的安全性和稳定性。
机械零件的弯曲变形分析
要点一
总结词
机械零件的弯曲变形分析是确保机械系统正常运行的关键 环节。通过对机械零件在不同工作载荷下的弯曲变形进行 分析，可以优化零件的设计和加工工艺，提高其工作性能 和寿命。
通过实例分析和习题练习，学生可以加深对弯曲 变形的理解，提高解决实际问题的能力。
弯曲变形的未来研究方向
弯曲变形的非线性行为

材料力学 第七章 弯曲变形

材料力学 第七章 弯曲变形

，
FA
3FP 4
(↑)
3FP
FP
FC
FP 4
(↑)
4
4
明德行远 交通天下
材料力学
（2）分段列梁的弯矩方程
AB段：
M1(x)
3 4
FP x
0x l 4
3
l
BC段：
M 2 ( x)
4
FP x
-
FP (x
-
) 4
l xl 4
（3）积分法求梁的挠曲线
挠曲线近似微分方程
EI
d 2w1 dx2
=
-
M1(x)
-
wC- wC
P
A （b）
图（b）： wA 0 A 0
或写成w C
左
wC右
光滑条件
C- C
或写成 C 左 C 右
明德行远 交通天下
材料力学
讨论： ①适用于小变形、线弹性材料、细长构件的平面弯曲。 ②可求解各种载荷作用下等截面或变截面梁上任意位置处的位移。 ③积分常数由挠曲线变形的几何相容条件（边界条件、光滑连续条件）确定。 ④优点：使用范围广，直接求出较精确； 缺点：计算较繁。
（2）
EIzw=EIz = -
q(x)dx3
1 2
C1x2
C2
x
C3
（3）
明德行远 交通天下
材料力学
例题7-1如图所示，受集中荷载的简支梁AC。已知EI、l、FP。试写出梁的挠 度方程和转角方程，并求截面A和C处的转角及B截面处的挠度。
明德行远 交通天下
y
FP
A
B
θA wB
l 4
EI
3l 4
C
θC

第7章 梁的弯曲变形与刚度(2)

第7章 梁的弯曲变形与刚度(2)

7.7 梁的刚度7.7.1 梁的刚度条件计算梁的变形的主要目的是为了判别梁的刚度是否足够以及进行梁的设计。

工程中梁的刚度主要由梁的最大挠度和最大转角来限定，因此，梁的刚度条件可写为：⎩⎨⎧≤≤][][maxmax θθw w （7-10） 其中，m a x)(m a x x w w =，max)(max x θθ=分别是梁中的最大挠度和最大转角，][w ，][θ分别是许可挠度和许可转角，它们由工程实际情况确定。

工程中][θ通常以度（）表示，而许可挠度通常表示为：mlw =][ 是大的自然数）是梁长，m l ( 上述两个刚度条件中，挠度的刚度条件是主要的刚度条件，而转角的刚度条件是次要的刚度条件。

7.7.2 刚度条件的应用与拉伸压缩及扭转类似，梁的刚度条件有下面三个方面的应用。

（1）校核刚度给定了梁的载荷，约束，材料，长度以及截面的几何尺寸等，还给定了梁的许可挠度和许可转角。

计算梁的最大挠度和最大转角，判断其是否满足梁的刚度条件式（7-15）和式（7-16），满足则梁在刚度方面是安全的，不满足则不安全。

很多时候工程中的梁只要求满足挠度刚度条件式（7-15）即可，而梁的最大转角由于很小，一般情况下不需要校核。

（2）计算许可载荷给定了梁的约束，材料，长度以及截面的几何尺寸等，根据梁的挠度刚度条件式（7-15）可确定梁的载荷的上限值。

如果还要求转角刚度条件满足的话，可由式（7-16）确定出梁的另一个载荷的上限值，两个载荷上限值中最小的那个就是梁的许可载荷。

（3）计算许可截面尺寸给定了梁的载荷，约束，材料以及长度等，根据梁的挠度刚度条件式（7-15）可确定梁的截面尺寸的下限值。

如果还要求转角刚度条件满足的话，可由式（7-16）确定出梁的另一个截面尺寸的下限值，两个截面尺寸下限值中最大的那个就是梁的许可截面尺寸。

例7-21 如图7-41（a ）所示的梁，其长度为m 1=L ，抗弯刚度为25Nm 109.4⨯=EI ，当梁的最大挠度不超过梁长的300/1时，试确定梁的许可载荷。

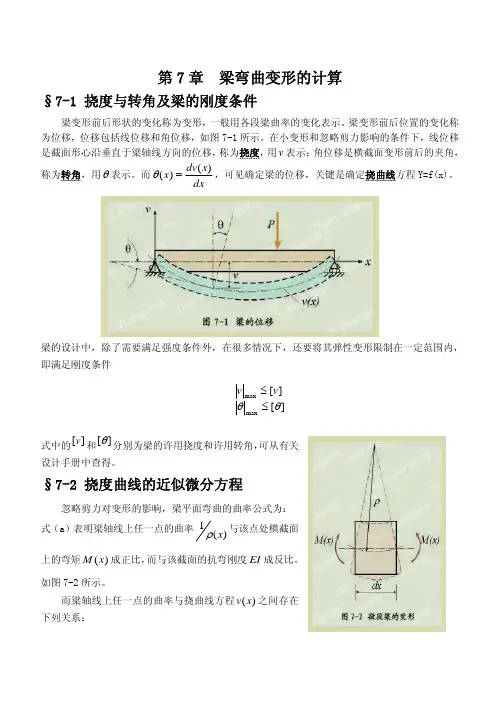
梁弯曲变形的计算

梁弯曲变形的计算

第7章 梁弯曲变形的计算§7-1 挠度与转角及梁的刚度条件梁变形前后形状的变化称为变形，一般用各段梁曲率的变化表示。

梁变形前后位置的变化称为位移，位移包括线位移和角位移，如图7-1所示。

在小变形和忽略剪力影响的条件下，线位移是截面形心沿垂直于梁轴线方向的位移，称为挠度，用v 表示；角位移是横截面变形前后的夹角，称为转角，用θ表示。

而dxx dv x )()(=θ，可见确定梁的位移，关键是确定挠曲线方程Y=f(x)。

梁的设计中，除了需要满足强度条件外，在很多情况下，还要将其弹性变形限制在一定范围内，即满足刚度条件][][max max θθ≤≤v v式中的和][v ][θ分别为梁的许用挠度和许用转角，可从有关设计手册中查得。

§7-2 挠度曲线的近似微分方程忽略剪力对变形的影响，梁平面弯曲的曲率公式为： 式（a）表明梁轴线上任一点的曲率)(1x ρ与该点处横截面上的弯矩成正比，而与该截面的抗弯刚度)(x M EI 成反比。

如图7-2所示。

而梁轴线上任一点的曲率与挠曲线方程v 之间存在下列关系：)(xEIx M x )()(1=ρ （a） 232221)(1⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛+±dx dv dx vd x ρ （b）将上式代入式（a），得到EIx M dx dv dx v d )(12322=⎥⎥⎦⎤⎢⎢⎣⎡⎟⎠⎞⎜⎝⎛+±（c） 小挠度条件下，1<<=θdxdv，式（c）可简化为： EI x M dxv d )(22=±（d）在图7-3所示的坐标系中，正弯矩对应着22dx vd 的正值（图7-3a），负弯矩对应着22dxvd 的负值（图7-3b），故式（d）左边的符号取正值EI x M dx v d )(22= （8-1）式（7-1）称为小挠度曲线微分方程，简称小挠度微分方程。

显然，小挠度微分方程仅适用于线弹性范围内的平面弯曲问题。

材料力学第7章

材料力学第7章

积分一次： Fb 2 EIw1 x C1 2l 积分二次： Fb 3 EIw1 x C1 x D1 6l
11
CB段（a x l）: 弯矩方程：
Fb M 2 x x F x a l
挠曲线近似微分方程：
Fb EIw2 x F x a l Fb 2 F 2 x x a C2 积分一次： EIw2 2l 2
ቤተ መጻሕፍቲ ባይዱ 1 x 0
Fab l b , B 2 6lEI
Fab l a B = 6lEI
Fl 3 Fl 3 Fl 3 2 EI 6 EI 3EI
7
wmax w x l
例题7.2：图示弯曲刚度为EI的简支梁，受集度为q的均布 荷载作用，试求梁的挠曲线方程和转角方程，并确定其最 大挠度和最大转角。 解：由平衡方程得支座反力 ql FA FB 2 建立坐标系，得梁的弯矩方程为 1 1 2 M x qlx qx 2 2 梁挠曲线近似微分方程
1 3 C ql ， D 0 24
9
梁的转角方程
q w (4 x3 6lx 2 l 3 ) 24 EI
梁的挠曲线方程
(5)
qx w ( x3 2lx 2 l 3 ) 24 EI
最大转角
(6)
max
ql 3 A B 24 EI
2
最大挠度
M ( x) F l x
1
挠曲线近似微分方程
EIw M x F l x 2 两次积分，得 1 2 EIw Flx Fx C 2 1 1 3 2 EIw Flx Fx Cx D 2 6

材料力学填空与判断题解

材料力学填空与判断题解

F122-题132-题第 2 章 轴向拉伸与压缩二、填空题2-6 承受轴向拉压的杆件，只有在（加力端一定距离外）长度范围内变形才是均匀的。

2-7 根据强度条件][σσ≤可以进行（强度校核、设计截面、确定许可载荷）三方面的强度计算。

2-8 低碳钢材料由于冷作硬化，会使（比例极限）提高，而使（塑性）降低。

2-9 铸铁试件的压缩破坏和（切）应力有关。

2-10 构件由于截面的（形状、尺寸的突变）会发生应力集中现象。

三、选择题2-11 应用拉压正应力公式AN=σ的条件是（ B ） （A ）应力小于比极限；（B ）外力的合力沿杆轴线； （C ）应力小于弹性极限；（D ）应力小于屈服极限。

2-12 图示拉杆的外表面上有一斜线，当拉杆变形时，斜线将（ D ） （A ）平动；（B ）转动；（C ）不动；（D ）平动加转动。

2-13 图示四种材料的应力-应变曲线中，强度最大的是材料（A ），塑性最好的是材料（D ）。

2-14 图示三杆结构，欲使杆3的内力减小，应该（ B ）σ（A ）增大杆3的横截面积； （B ）减小杆3的横截面积； （C ）减小杆1的横截面积； （D ）减小杆2的横截面积。

2-15 图示有缺陷的脆性材料拉杆中，应力集中最严重的是杆（ D ）二、填空题3-6 圆杆扭转时，根据（切应力互等定理），其纵向截面上也存在切应力。

3-7 铸铁圆杆发生扭转破坏的破断线如图所示，试画出圆杆所受外力偶的方向。

3-8 画出圆杆扭转时，两种截面的切应力分布图。

3-9 在计算圆柱形密围螺旋弹簧簧丝切应力时,考虑到(剪力引起的切应力及簧丝曲率的影响 ),而加以校正系数。

3-10 开口薄壁杆扭转时，截面上最大切应力发生在(最厚的矩形长边 )处；闭口薄壁杆扭转时,截面上最大切应力发生在( 最小厚度)处.题24（A （B （C ）（D第3章 扭转三,选择题3-11阶梯圆轴的最大切应力发生在( D ) (A) 扭矩最大的截面; (B)直径最小的截面; (C) 单位长度扭转角最大的截面; (D)不能确定.3-12 空心圆轴的外径为 D ，内径为 d ，D d /=α。

第七章弯曲变形案例

第七章弯曲变形案例

二、工程实例
实例一：起重机大梁
实例二、机床摇臂
7.2
梁的挠曲线近似微分方程
一、挠度和转角
梁在平面内弯曲时，梁轴线从原来沿 x 轴方向的直线变 成一条在 xy 平面内的曲线，该曲线称为挠曲线。
y
q
C’
挠曲线 B’
转角
wB B x
某截面的竖向位移，称为 该截面的挠度。 某截面的法线方向与x轴 的夹角称为该截面的转角。
EI zq EIw M ( x)dx C
EI z w ( M ( x)dx)dx Cx D
其中， C 和 D 是积分常数，需要通过边界条件或者连续条件来确 定其大小。
一、边界条件
在约束处的转角或挠度可以确定
F
EI z w ( M ( x)dx)dx Cx D
q
B
w
A
x
C
挠度和转角的大小和截面所处的 x 方向的位 置有关，可以表示为关于 x 的函数。 w f1 ( x) 挠度方程（挠曲线方程）
挠度
转角方程
q f 2 ( x)
y
q
B’ C’
挠度和转角的正负号规定
q
B w wB x
A
x
C
在图示的坐标系中， 挠度 w 向上为正，向下为负。转 角规定截面法线与 x 轴夹角，逆时针为正，顺时针为负, 即在图示坐标系中挠曲线具有正斜率时转角 q 为正。
挠度和转角的关系
y
q
B’ C’
q
B
w
wB x
dy 件下
A
x
C
tan q q
挠曲线的斜率（一阶导数）近似等于截面的转角
dy w tan q q dx

梁弯曲变形的计算

梁弯曲变形的计算
材料力学
3） 应用叠加法，将简单载荷 作用时的结果求和
5ql 4 ql 4 ql 4 wC wCi 384 EI 48EI 16 EI i 1
3
wC1
11ql 4 ( ) 384 EI
wC2 wC3
ql 3 ql 3 ql 3 B Bi 24 EI 16 EI 3EI i 1
材料力学
积分常数C、D 由梁的位移边界条件和光滑连续 条件确定。 光滑连续条件 位移边界条件
~
~
~
~
A
A
~ ~
~
~
~
~
~
~
~
A A
A
A
~
~
wA 0
wA 0
wA
－弹簧变形
wAL wAR
~
wAL wAR
A 0
AL AR
材料力学

~
A
~
~
A A AA
A
A
A AA
超静定次数：多余约束或多余支反力的数目。 相当系统：用多余约束力代替多余约束的静定系统。 2.求解方法： 解除多余约束，建立相当系统——比较变形，列变 形协调条件——由物理关系建立补充方程——利用 静力平衡条件求其他约束反力。
材料力学
材料力学
例5：试分析细长轴车削过程中顶尖的作用，已知：工件的抗弯刚度 为EIZ，切削力为F，且作用在零件的中间位置，零件长度为l。
2
x
d y 2 dx
d y M ( x) 所以 2 dx EI z
2
O
1
2
M (x ) < 0
dy dx 2 < 0

材料力学第2版 课后习题答案 第7章 弯曲变形

材料力学第2版 课后习题答案 第7章 弯曲变形

解：查自重得：
q = 587.02 N / m
J = 15760cm4 Pl 3 5ql 4 f =− − 48EJ 384EJ −176 × 103 × 113 = 48 × 210 × 109 × 15760 × 10−8 × 4 −587.02 × 5 × 114 + 385 × 210 × 109 × 15760 × 10−8 × 4 = 0.0377 m = 3.77cm
(d) 解：
D A P P E
' yC = y E + θ B ia + y C
C B P
− P ( 2a ) − Pa 3 − Pa3 = − − 3EJ 3EJ 3EJ 3 −10 Pa = 3EJ
3
252
7-5 门式起重机横梁由4根36a工字钢组成如图所示， 梁的两端均可视为铰支， 钢的弹 性模量E=210Gpa。试计算当集中载荷P＝176 kN作用在跨中并考虑钢梁自重时，跨中截面 C的挠度yC。
x=l
∴y =−
'
∴D = 0
y=0
∴C =
− M 0l 6
M 0l 2 ⎛ x x 3 ⎞ ⎜ − ⎟ 6 EJ ⎝ l l 3 ⎠
M 0l 2 ⎛ 1 3 x 2 ⎞ ∴θ = y = − ⎜ − ⎟ 6 EJ ⎝ l l 3 ⎠
− M 0l 2 l ；此时挠度最大 f = 3 9 3EJ 2 ⎛ l ⎞ − M 0l 中点挠度 y ⎜ ⎟ = ⎝ 2 ⎠ 16 EJ − M 0l Ml θA = θB = 0 6 EJ 3EJ （b）解： 设中点为C点，则分析CB段
''
C2 = −
D2 = −
a4 24
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

q l36 lx 24x3 2E 4I
22
q
qxl32lx 2x3
A
2E 4 I
B x
(5) 求最大值
l
x 0 或 x l: m a x A B 2 q E 3 4 l I
xl: 2
0;m a x l23 5q8 E 4l4I
弯曲变形的对称点：θ＝0。
边界条件： x 0 : 0 或
0l./52L
表7-1第8栏 d F C (d F )l(x )4 3 (lE 2 8 4 I(lx )2)
qCdFC
q0(lx)2(3l24(lx)2)dx 2l4EI
0 l.5 lq 0 (l x )2 ( 2 3 ll2 4 E 4 (lI x )2 )d x 2 q4 E 4 l0 I
q
解：① 简单载荷引起的变形
表7-1第7栏
FCF4(28E a)3I6 FEa3I
表7-1第9栏
qC 53q(82E a4)4I25q4Ea4I
② 叠加
C(25q4Ea4I6 FEa3I)
[例7-7] 用叠加法求C点挠度。
q0
解:积分法
A
C
B d Fq(x)dx 2q0(lx)d x
l
0.l5/2L
(2) 分段建立挠曲线近似微分方程，并积分
EI 1 F x1 a
EI 1
F 2
x1
a 2
C1
EI 1
F 6
x1
a 3
C1x1 a D1
EI 2
Fa l
x2 l
EI 2
Fa 2l
x2
l 2
C2
EI 2
Fa 6l
x2
l 3
C2x2 l D2
EI1 Fx1 a
EI1
F 2
所引起的该参量的代数和。
F
2a
F
q
=+
q
d2
EI dx2
M
MM FM q
EIdd2x2F
Ed d I2 x 2Ed d I2 x2FEd d I2x 2q
MF
d2 EI
Fq
dx2
EIdd2x2q Mq
Fq
* 表7-1
[例7-6] 荷载F作用在梁的中点，用叠加法求C点挠度。
F
2a
F
q
+
=
EIM (x) M(x)6Fx
6F
+
FS(x)dM dx(x)6F
q(x)dFS(x)0
l
6F
6Fl
dx
边界 x0 ， 0
6Fl
条件
ቤተ መጻሕፍቲ ባይዱ
x
l，
Pl3
EI
6F
故可确定其为悬臂梁。
§7-3 用积分法求挠度和转角
dd2x2
M(x) EI
d d xE Md IxC 转角方程
E Md IxdxC xD挠度方程
A
l
l
解:① 建立坐标系并
x
作弯矩图
C
EIM (x)
AB段: M 0 ， 0
m
MA
B
∴ 上凸
C BC段: M 0 ， 0
边界条件: C0，C0
B
C
A
∴ =0
同时B处须满足连续光滑条件， 即曲线与直线在B点相切。
[例7-2] 画出下列的挠曲线大致形状。
解:① 建立坐标系并
A
BF C
F x
作弯矩图
D
tan d
dx
dfx
小变形：tan
dx
§7-2 挠曲线近似微分方程
一、挠曲线近似微分方程
1 M(x)
(x) EI
M0
d 2
O
M0
0
0
x
1
(x)
1
dx 2
d
2
3
2
d 2 dx2
dx
d2
dx2
M(x) EI
dd2x2
M(x) EI
[例7-1] 画出下列的挠曲线大致形状。
m
Bm
xl2:0
x l: 0
xl2:0
[例7-5] 用积分法求C截面的转角和挠度，EI为常量。
F
A
B 解：(1) 分段写弯矩方程
C
x
RaA
l
RB
R A F a l l R B F l a
C 段 M 1 A F x 1 ： a － a x 1 0
M
Fa
A 段 B M 2 ： F lx a 2 l0 x 2 l
x1
a2
C1
F EI1
F 6
x1
a3
C1x1
a
EI2 Flax2 l EI2 F2lax2 l2 C2 EI2 F6lax2 l3 C2x2
D1
l
D2
(3) 确定积分常数 C A
B
边界条件 xl: 20 D20
x
连续性条件
x0:12
F22aC1F2alC2
x 0 : 1 2 0 F 63a C 1aD 1F 62 a C l2l0
C、D ——积分常数；由边界条件和连续性条件确定。
边界条件: 固定端： ＝0；＝0；
铰支座： ＝0；
弯曲变形的对称点： ＝0。
连续性条件: 在挠曲线的任意点上，有唯一确定的挠
度和转角。
[例7-4]用积分法求挠度方程和转角方程，并确定绝对
值最大的转角和最大的挠度。设EI为常量。
q
A
x
RA
l
B 解：(1) 写弯矩方程
x
RB
M (x )qx l qx 2 0x l
22
(2) 建立挠曲线近似微分方程，并积分
E I qx l qx 2 0xl
22
EIqlx2qx3C
46
EIqx l3-qx4C xD
12 24
(3) 利用边界条件确定积分常数
x 0 : 0 D0 x l: 0 C ql3
24
(4) 求转角方程、挠度方程 E I qx l qx 2 0xl
材料力学
第七章 弯曲变形
§7-1 概述
§7–2 挠曲线近似微分方程
§7-3 用积分法求挠度和转角
§7-4 用叠加法求挠度和转角 §7-5 梁的刚度计算
§7-6
§7-7 §7-8
简单超静定梁 梁的弯曲应变能 提高弯曲刚度的措施 本章习题
§7-1 概述
一、工程中的弯曲变形问题
二、弯曲变形的量度——挠度和转角
C2
Fal 6
C1
FalFa2 32
D1
Fa2al
3
(4) C截面的挠度和转角
x a : C 6 F E 2 a lI 3 a C 3 F E 2 a a Il
§7-4 用叠加法求挠度和转角
叠加原理：当梁上同时作用几个载荷时，梁的某一参量
（反力、内力、应力、变形）等于每个载荷单独作用时
EIM (x)
2a
aa
AB段: M 0 ， 0
边界条件: A0， A0
M
Fa
∴ =0
A
B CD
BD段: M 0 ， 0
A
BC
∴ 上凸且 C＝0
同时B处须满足连续条件。
[例7-3] 等截面直梁，其挠曲线 Px 3 ，长度为l，
确定梁的载荷、支撑情况。
EI
M FS
6F
解:① 作弯矩图、剪力图
6Fl
P
挠 度 (deflection) ： 横 截
A
B
面形心在垂直于轴线方向
x
挠曲线 x 的位移。向上为正。
(deflection curve) fx
转角(slope of cross section )：横截面绕中性轴转过的
角度，即 y 轴与挠曲线法线的夹角，或 x 轴
与挠曲线切线的夹角。逆时针方向为正。