第05章 热力学一般关系式
- 格式:ppt
- 大小:453.50 KB
- 文档页数:27




习题提示与答案 第五章 热力学第二定律5-1 蒸汽机中所用新蒸汽的温度为227 ℃,排出乏汽的温度为100 ℃,如按卡诺循环计算,试求其热效率。
提示:新蒸汽与乏汽的温度分别看做卡诺循环的高、低温热源温度。
答案: 254.0t =η。
5-2 海水表面温度为10 ℃,而深处的温度为4 ℃。
若设计一热机利用海水的表面和深处作为高温热源及低温热源并按卡诺循环工作,试求该热机的热效率。
提示:略。
答案: 2021.0t =η。
5-3 一卡诺热机的热效率为40%,若它从高温热源吸热4 000 kJ/h ,而向25 ℃的低温热源放热,试求高温热源的温度及热机的功率。
提示:略。
答案: 4971r =T K ,44.0=P kW 。
5-4 某内燃机每作出1 kW h 的功需消耗汽油514.8 g 。
已知每千克汽油燃烧时可放出41 868 kJ 的热量,试求该内燃机的实际热效率。
提示:热机的吸热量等于燃料的放热量。
答案:167.0t =η。
5-5 有报告宣称某热机自160 ℃的热源吸热,向5 ℃的低温环境放热,而在吸热1 000 kJ/h 时可发出功率0.12 kW 。
试分析该报告的正确性。
提示:热机热效率不可能大于在相同温度范围内工作的卡诺热机的热效率。
答案:报告不正确,不可能实现。
5-6 有A 、B 两个卡诺热机,A 从温度为700 ℃的热源吸热,向温度为t 的热源放热。
B 则从温度为t 的热源取得A 排出的热量并向温度为100 ℃的热源放热。
试求:当两热机的循环净功相同或两热机的热效率相同时温度t 的数值。
提示:卡诺循环热效率121211T T Q Q tc -=-=η。
答案:两热机循环净功相同时='t 400 ℃,两热机热效率相同时="t 329.4 ℃。
5-7 以氮气作为工质进行一个卡诺循环,其高温热源的温度为1 000 K 、低温热源的温度为300 K ;在定温压缩过程中,氮气的压力由0.1 MPa 升高到0.4 MPa 。
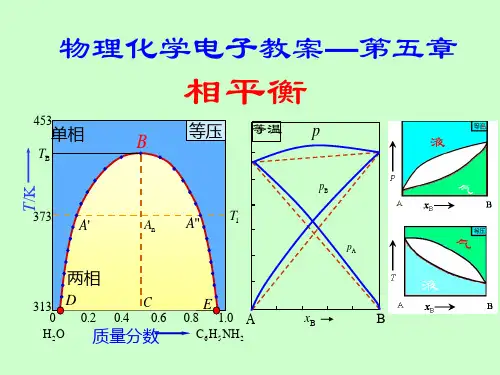

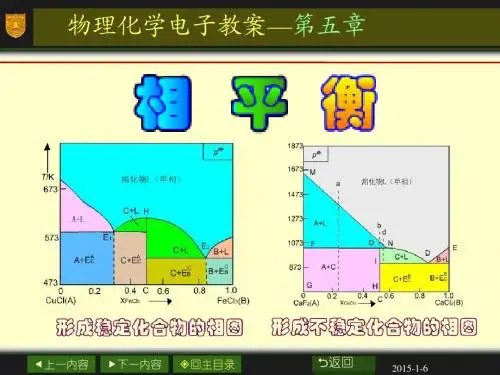

第五讲化学中能量的变化第一节热力学第一定律[知识概要]一、几个重要的基本概念1、热力学专门研究能量相互转换过程中所遵循的法则的一门科学。
它以两个定律为基础,通过热力学函数的变化来判断反应的方向与限度,是一种纯宏观的方法。
2、化学热力学把热力学的定律、原理、方法用来研究化学过程以及伴随这些化学过程而发生的物理变化,就形成了化学热力学。
它是有关化学过程的热力学,主要解决化学变化的方向、限度和能量的变化关系。
3、体系和环境体系被研究的物质或空间系统称为体系。
环境体系以外的、与体系有联系的其他部分称为环境。
体系和环境之间可以有明显的界面即真实的界面,也可以是假想的界面。
热力学体系可分为三种:(1)敞开体系体系与环境之间既有物质交换,又有能量交换。
(2)封闭体系体系与环境之间有能量交换但没有物质交换。
在热力学中主要研究封闭体系。
(3)孤立体系体系与环境之间既无能量交换,又无物质交换。
4、状态和状态函数状态由一系列表征体系性质的物理量所确定下来的体系的存在形式称为体系的状态。
状态函数借以确定体系状态的物理量。
例如:某理想气体是研究的体系,其物质的量n=1mol,压强p=1.013×105Pa,体积V=22.4L,温度T=273.2K,则体系处于标准状态。
这里的p、V、T就是体系的状态函数。
状态函数的特征体系状态一定,则状态函数有一定的值。
体系的状态函数发生改变,则体系的状态发生改变。
体系的始态和终态一经确定,各状态函数的改变量也就确定了。
或者说状态函数的增量只决定于体系变化的起始和终了状态,而与变化的途径无关。
5过程和途径过程体系从始态到终态的变化经过。
途径体系经历一个过程,由始态变化到终态,可以采取许多种不同的方式,每一种具体方式称为一种途径。
6、热力学能(原称为内能)体系内一切能量的总和叫做体系的热力学能,通常用U表示。
它是体系自身的性质,是状态的单值函数,其改变值只决定于体系的始终态,而与变化的途径无关,且绝对值无法确定。

热力学公式总结
一、热力学第一定律
热力学第一定律,也被称为能量守恒定律,表明在一个封闭系统中,能量不能被创造或毁灭,只能从一种形式转化为另一种形式。
公式如下:
ΔU = Q + W
其中,ΔU表示系统内能的改变,Q表示系统吸收或释放的热量,W表示系统对外界所做的功。
二、热力学第二定律
热力学第二定律表明,热量不能自发地从低温物体传递到高温物体,而不引起其他变化。
公式如下:
dS/dt ≥ 0
其中,S表示系统的熵,dS/dt表示熵的变化率。
如果dS/dt大于0,则表
示熵增加,如果dS/dt等于0,则表示熵不变。
三、理想气体状态方程
理想气体状态方程表示理想气体的压力、体积和温度之间的关系。
公式如下:PV = nRT
其中,P表示气体的压力,V表示气体的体积,n表示气体的摩尔数,R表
示气体常数,T表示气体的温度(以开尔文为单位)。
四、热力学第三定律
热力学第三定律表明,绝对零度不能通过有限的降温过程达到。
公式如下:ΔS(T→0) = 0
其中,ΔS表示系统熵的变化,T表示温度。
这个公式表明在绝对零度时,
系统的熵为零。

