当前位置：文档之家 › 13.11用图乘法计算悬臂梁的位移

13.11用图乘法计算悬臂梁的位移

  • 格式：ppt
  • 大小：160.50 KB
  • 文档页数：1

下载文档原格式

  / 1

合集下载

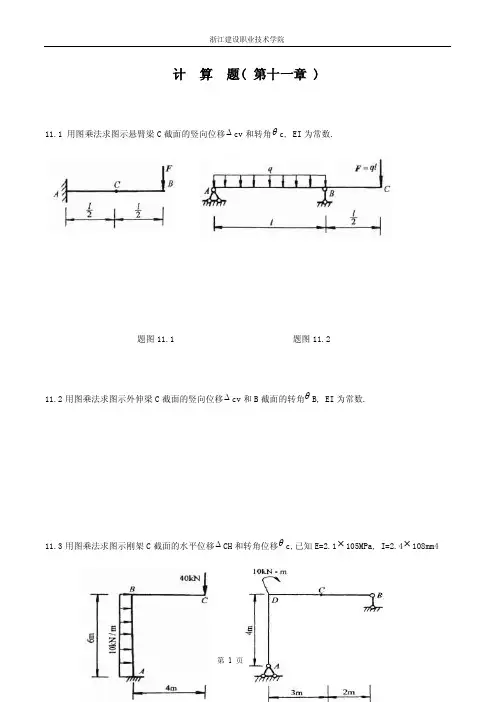
《建筑力学》第11章计算题解析

《建筑力学》第11章计算题解析

计算题( 第十一章 )11.1 用图乘法求图示悬臂梁C截面的竖向位移∆cv和转角θc, EI为常数.题图11.1 题图11.211.2用图乘法求图示外伸梁C截面的竖向位移∆cv和B截面的转角θB, EI为常数.11.3用图乘法求图示刚架C截面的水平位移∆CH和转角位移θc,已知E=2.1×105MPa, I=2.4×108mm4题图11.3 题图11.411.4 用图乘法求图示刚架C截面的竖向位移∆cv和B截面的水平位移∆BH,已知各杆EI为常数.11.5用图乘法求图示刚架铰C截面的竖向位移∆cv和转角θc, EI为常数.题图11.5 题图11.611.6 用图乘法求图示刚架B 截面的水平位移∆BH 和A 截面的转角θA,各杆EI 为常数.11.7 简支梁用No22a 号工字刚制成,已知=4KN,q=1.5KN/m,l=8m,E=200GPa,4001]lf [= 校核梁的刚度？题图11.7 题图11.811.8 图示桁架中,其支座B 有竖向沉陷C,试求BC 杆的转角BC ϕ.11.9 图示刚架中,其支座B 有竖向沉陷b , 试求C 点的水平位移CH ∆题图11.9 题图11.1011.10 求图示桁架结点C的水平位移 CH,设各杆,EA相等.11.11图示桁架各杆截面均为A=20cm2,E=2.1x104KN/cm2,P=40KN,d=2m,试求：（ａ）Ｃ点的竖向位移（ｂ）角ＡＤＣ的改变（ｃ）已知桁架的最大挠度为［ｆ］＝０．５ｃｍ，该校核桁架的刚度题图11.1111.12用积分法求图示悬臂梁A端的竖向位移VA∆和转角Aϕ（忽略剪切变形的影响）。

题图11.1211.13试用积分法求图示刚架的B点水平位移HB∆。

已知各杆EI＝常数。

题图11.13 题图11.1411.14图示桁架，各杆EA ＝常数。

求C 点的水平位移H C ∆。

11.15 求所示桁架D 点的竖向位移V D ∆和水平位移H D ∆。

图乘法

图乘法
§4.5 图乘法
(Graphic Multiplication Method)
刚架与梁的位移计算公式为： 刚架与梁的位移计算公式为：
∆ iP = ∑ ∫ MM P ds EI
在杆件数量多的情况下,不方便 下面介绍 在杆件数量多的情况下 不方便. 不方便 计算位移的图乘法. 计算位移的图乘法
一、图乘法 MM P ds ∫ EI 1 对于等 = ∫ M M P ds (对于等 截面杆) 截面杆 EI
ωyc
五、应用举例
图示梁EI 为常数， 点竖向位移。 例 3(a). 图示梁 为常数，求C点竖向位移。 点竖向位移
ql 2 / 2
MP
q ql 2 / 8
A
∆c = ∑
ωyc
l/2 C
1
C
l/2
B
1 1 ql 2 1 l = ⋅l ⋅ ⋅ ⋅ EI EI 3 2 2 2
l/2
Mi
1 ql 3 = ⋅ (↓) 24 EI
EI
试求图示结构B点竖向位移 点竖向位移. 例. 试求图示结构 点竖向位移
Pl EI l EI
MP
P B
l
Mi
=1
l
解: ∆ By = ∑
=∑
MM P ∫ EI ds
ωy c
EI 1 1 2 ( ⋅ Pl ⋅ l ⋅ l + Pl ⋅ l ⋅ l ) = EI 2 3 4 Pl 3 = ⋅ (↓) 3 EI
=1 1/ 2
1 1 Pl 1 Pl 2 ϕB = − ( ⋅ l ⋅ ⋅ ) = − ( EI 2 4 2 16EI
)
取 yc的图形必 须是直线,不能是曲 须是直线 不能是曲 线或折线. 线或折线

图乘法及其应用

图乘法及其应用

1 1 3ql 2 l 3 l l ql 2 l ∆C = ∑ = ⋅ × ⋅ + ⋅ ⋅ ) ( ⋅ EI EI 3 8 2 4 2 2 8 4 5 ql 3 = ( ↓) 128 EI
ωyc
三、应用举例
为常数， 例 4. 图示梁 EI 为常数，求C点竖向位移 。 点竖向位移
ql 2 / 2
MP
三、应用举例
为常数，求铰C两侧截面相对转角 例 2. 已知 EI 为常数，求铰 两侧截面相对转角 ϕ C 。 l q
A C =1 =1
B
Mi
1
l
ql / 4
2
l
ql 2 / 4
1/ l 0 解：作荷载弯矩图和单位荷载弯矩图
q
MP
ql / 4
1 2 ql 2 1 ∆ CD = ∑ =− × × × 8 2 EI EI 3 ql 3 ql / 4 =− ( ) 24 EI
ωyc
注意:各杆刚度 注意 各杆刚度 可能不同
1 1 2 1 ∆B = ∑ = ⋅ ⋅ Pl ⋅ l ⋅ ⋅ l × 2 + ⋅ Pl ⋅ l ⋅ l 3 4 EI EI EI 2 5 Pl 3 = (→ ) 8 EI
为常数， 并画出变形图。 已知 EI 为常数，求C、D两点相对水平位移 ∆CD,并画出变形图。 、 两点相对水平位移 并画出变形图
=1
1 1 2 × ( ×10 × 60 × − 3 EI 2 1 100 20 ×10 × ) = ( ) 2 EI
40
Mi
1 1 2 ϕB = ⋅ ×10 ×1× (60 × − 20) EI 2 3 100 = ( ) EI
20
ϕB =
1 1 2 × ( ×10 × 60 × − EI 2 3 1 100 20 ×10 × ) = ( ) 2 EI

悬臂梁计算公式一览表

悬臂梁计算公式一览表

悬臂梁计算公式一览表悬臂梁是一种常见的工程结构，常用于吊车起重、桥梁和建筑物中。

在设计和分析悬臂梁时，我们需要使用一系列的计算公式来确定其受力和变形情况。

下面是悬臂梁计算中常用的公式一览表：1. 弯矩公式（弯矩与力的关系）弯矩是悬臂梁受到外力作用产生的抗弯形变的指示。

对于集中力的悬臂梁，弯矩公式为：M = F * L其中，M为弯矩，F为作用在悬臂梁上的力，L为悬臂梁的长度。

2. 最大弯矩公式在悬臂梁上不同位置的弯矩大小不同。

最大弯矩是指悬臂梁上弯矩大小最大的位置。

对于集中力的悬臂梁，最大弯矩公式为：M_max = F * L其中，M_max为最大弯矩，F为作用在悬臂梁上的力，L为悬臂梁的长度。

3. 剪力公式（剪力与力的关系）剪力是指作用在悬臂梁上截面两侧的力的大小。

对于集中力的悬臂梁，剪力公式为：V = F其中，V为剪力，F为作用在悬臂梁上的力。

4. 获取剪力和弯矩图的公式剪力和弯矩图是对悬臂梁受力情况的图形表示。

对于集中力的悬臂梁，剪力和弯矩图的公式为：V = V0 - FM = M0 - F * x其中，V为截面处的剪力大小，M为截面处的弯矩大小，V0和M0为截面处离开力作用点时的剪力和弯矩大小，F为作用在悬臂梁上的力，x为距离力作用点的距离。

5. 变形公式（变形与力的关系）变形是悬臂梁在受力作用下产生的长度、角度或形状的改变。

对于悬臂梁的弹性变形，变形公式为：δ = (F * L^3) / (3 * E * I)其中，δ为悬臂梁在力作用下的弹性变形，F为作用在悬臂梁上的力，L为悬臂梁的长度，E为材料的弹性模量，I为悬臂梁的截面惯性矩。

这些公式是悬臂梁设计和分析中的基本工具。

通过使用这些公式，工程师可以计算悬臂梁的弯矩、剪力、变形等参数，以确保悬臂梁在使用中安全可靠。

同时，这些公式也可以帮助工程师优化设计，减少材料使用量，提高工程效率。

需要注意的是，上述公式适用于一些简化情况下的悬臂梁设计和分析。

第四章位移计算

第四章位移计算

M = −x
三 求A端的竖向位移
FQ = −1
FQ FQP MMP ∆ = ∑∫ ds + ∑ ∫ k ds = ∆ M + ∆ Q EI GA 3 l l qx 0.6ql 2 ql 4 qx ∆M = ∫ dx = ∆ Q = ∫ 1.2 dx = 0 2 EI 0 8 EI GA GA
qx 3 ql 4 ∆M = ∫ dx = 0 2 EI 8 EI l qx 0.6ql 2 ∆ Q = ∫ 1.2 dx = 0 GA GA
这就是图形相乘法的计算位移的方法简称为图乘法1必须符合上述三个条件顶点3l85l8顶点二次抛物线例例446用图乘法求例用图乘法求例4422悬臂梁悬臂梁aa端的竖向位移端的竖向位移bbaallqq取虚力状态如图aabbffpp作单位弯矩图及荷载弯矩图bbaallqqqlaabbffpp求a端的竖向位移eieiayeiql图乘分段和叠加当各杆段的截面不相等时应分段图乘再进行叠加eiay所属图形不是一段直线而是若干段直线组成时应分段图乘再进行叠加eieiay图乘分段例例447用图乘法求图示简支梁用图乘法求图示简支梁cc点竖向位移点竖向位移取虚力状态如图ffpp求c点竖向位移eieiaycyeiqleiqleieiaycy48复杂的图形分解成几个简单的图形然后将分解得简单图形分别与另一图形相乘再叠加eieiay图乘叠加均布荷载作用下的任何直杆段ab其弯矩图均可看成一个梯形与一个标准抛物线图形的叠加为负值eiay为正值eiay例例448用图乘法求图示梁用图乘法求图示梁cc点竖向位移点竖向位移ffppeiayeiql例例449用图乘法求图示刚架用图乘法求图示刚架cc点竖向位移点竖向位移eieiffppffppeiayffppeiayei32eiayffpp128811281564eiqleiqleiqleiqlds假定温度沿截面高度按直线规律变化一计算公式一般情况下各杆均为等截面tth沿每一杆为常量ds杆轴线温度变化值t杆上下边缘温度变化差值单位力与温度变化引起的杆件变形方向相同时取正号例441010图示刚架内侧温度升高图示刚架内侧温度升高101000cc求求cc端竖向位移端竖向位移各杆截面为矩形截面高度为各杆截面为矩形截面高度为h600mmh600mm000001000001取虚力状态如图106m6m10000016m6m47线性变形体系的互等定理dseidsgadsea1212dseidsgadsea12121状态在线性变形体系中第一种状态的外力在第二种状态的位移上所作虚功等于第二种状态的外力在第一种状态的位移上所作虚功2112位移互等定理21122112在线性变形体系中由第二个单位力引起的第一个单位力作用点沿其作用方向上的相应位移等于由第一个单位力引起的第二个单位力作用点沿其作用方向上的相应位移21不仅数值相等量纲也相同在线性变形体系中支座2由于支座1发生单位位移c起的反力等于支座1由于支座2沿r21方向发生单位位移反

悬臂梁计算公式一览表

悬臂梁计算公式一览表

悬臂梁计算公式一览表
以下是悬臂梁计算中常用的公式一览表：
1. 悬臂梁的弯矩公式：
弯矩(M) = (载荷(F) × 距离(L)) / (支点到载荷的距离)。

2. 悬臂梁的最大弯矩公式：
最大弯矩(Mmax) = (载荷(F) × 距离(L))。

3. 悬臂梁的挠度公式：
挠度(d) = (5 × 载荷(F) × 距离(L)^4) / (384 × 弹性
模量(E) × 惯性矩(I))。

4. 悬臂梁的最大挠度公式：
最大挠度(dmax) = (F × L^3) / (48 × E × I)。

5. 悬臂梁的剪力公式：
剪力(V) = 载荷(F)。

6. 悬臂梁的最大剪力公式：
最大剪力(Vmax) = 载荷(F)。

7. 悬臂梁的应力公式：
应力(σ) = (M × 距离到中性轴的距离(y)) / 惯性矩(I)。

8. 悬臂梁的最大应力公式：
最大应力(σmax)= (Mmax × y) / I.
9. 悬臂梁的挠度与载荷关系公式：
挠度(d) = (F × L^3) / (3 × E × I)。

10. 悬臂梁的自振频率公式：
自振频率(f) = (1 / (2π)) × √(弹性模量(E) / (质量(m) × 惯性矩(I))))。

这些公式可以用于计算悬臂梁在不同载荷和条件下的弯曲、挠度、剪力和应力等参数。

请注意，在实际应用中，还需要考虑材料的性质、几何形状和边界条件等因素，以获得更准确的计算结果。

静定梁与静定刚架位移计算的图乘法

工程力学
静定梁与静定刚架位移计算的图乘法
1.1
图乘法的计算公式
建筑结构多为梁和刚架,从上述例题中可以看到,直 接应用位移公式
进行积分运算是很麻烦的,但如果结构和荷载满足 以下条件,则此积分运算可以变得相对简单些：①EI沿 杆长度不变,即EI为常数；②杆件为直杆；③M图和MP 图中至少有一个为直线图形。
静定梁与静定刚架位移计算的图乘法
1.2
图乘法公式的应用
应用图乘法公式计算时应注意以下几点。 (1)必须满足前述的三个条件,若EI为分段常 数,应分段计算。 (2)面积ω与yC在杆的同侧时,ωyC的乘积取 正号；反之,ωyC的乘积取负号。 (3)yC必须取自直线图中,而ω则为另一图形 面积。 (4)如果某一个图形是由几段直线组成的折 线,则应分段计算。例如,对图14-9所示的情形, 计算式应为
图14-10
静定梁与静定刚架位移计算的图乘法
若直线图形具有正、负号两部分,如图14-11所示,则 可将MP图分解为两个三角形,采用上述方法可得
图14-11
静定梁与静定刚架位移计算的图乘法
（6）对于图14-12所示的均 布荷载作用的部分,其MP图可视为 同一简支梁两端受力偶作用下的 弯矩图(图中梯形ABDC部分)与均 布荷载作用下的弯矩图(图中虚线 与抛物线间部分)的叠加结果。计 算时可将 M 图分别与上述两部分 图乘,再求出其代数和。
静定梁与静定刚架位移计算的图乘法
在图14-8中,AB为直 杆,M图为一段直线,而MP 图为任意形状。现取AB杆 轴线为x轴,M图直线段的延 长线与x轴的交点为坐标原 点,建立坐标系,设杆截面的 抗弯刚度EI为常数,则
图14-8
静定梁与静定刚架位移计算的图乘法
静定梁与静定刚架位移计算的图乘法

梁位移计算公式

梁位移计算公式梁的位移计算公式基于梁的受力平衡和材料力学的基本原理。

在这里，我们将讨论一维梁的位移计算方法，即假设梁只在一个平面内受力，并且假设梁的截面尺寸和材料性质均为均匀的。

我们需要确定梁的边界条件。

常见的边界条件有两种：固定边界条件和自由边界条件。

在固定边界条件下，梁的两端被固定，不允许有任何位移和旋转；而在自由边界条件下，梁的两端可以自由位移。

接下来，我们需要确定梁的受力情况。

通常，梁在两端受到外部荷载作用，这些荷载可以是集中力、均布力或者集中力和均布力的组合。

此外，梁还可能受到自重的影响。

在计算位移时，我们需要将这些荷载转化为梁上的内力分布。

针对不同的受力情况，我们可以使用不同的位移计算方法。

在本文中，我们将重点介绍三种常见的位移计算方法：拉梁法、剪梁法和挠梁法。

拉梁法是一种基于受力平衡的位移计算方法。

它假设梁的变形是由拉伸和压缩引起的，而不考虑剪切变形。

根据拉梁法，我们可以通过梁上任意一点的变形位移和受力来计算梁的位移。

剪梁法是一种基于受力平衡和材料切变变形的位移计算方法。

它假设梁的变形是由剪切引起的，并考虑了横截面的形状和材料的性质。

根据剪梁法，我们可以通过梁上任意一点的切变位移和受力来计算梁的位移。

挠梁法是一种基于弯曲变形的位移计算方法。

它假设梁的变形是由弯曲引起的，并考虑了横截面的形状和材料的性质。

根据挠梁法，我们可以通过梁上任意一点的弯曲位移和受力来计算梁的位移。

在实际应用中，我们可以将以上三种方法结合起来，综合考虑拉伸、压缩、剪切和弯曲等因素，来计算梁的位移。

此外，我们还可以使用计算机辅助工具，如有限元分析软件，来进行更精确和复杂的梁位移计算。

需要注意的是，梁的位移计算是一个复杂的过程，需要综合考虑各种因素和假设。

在实际工程中，我们应该根据具体情况选择适当的位移计算方法，并进行合理的假设和简化，以确保计算结果的准确性和可靠性。

通过以上的讨论，我们可以看到，梁的位移计算是一个重要且复杂的问题。

第13讲 第六章 6-6.6图乘法求梁的位移计算


图乘法-梁的位移计算 § 6-6 图乘法 梁的位移计算
A m B m A
MP图
求: ϕB
Structural Mechanics
1
B
Mi图
1
A m
m B
MP图
求: ϕA
A
1 1
B
Mi图
图乘法-梁的位移计算 § 6-6 图乘法 梁的位移计算
2.直角三角形与直角梯形 直角三角形与直角梯形
ω⋅ y
1 2 1 = al ⋅ ( b + c) EI EI 2 3 3
顶点
l/4
三次抛物线
图乘法-梁的位移计算 § 6-6 图乘法 梁的位移计算
四、常见图乘公式 1.直角三角形与直角三角形 直角三角形与直角三角形
ω⋅ y
abl = EI 3EI
l
ω a
Structural Mechanics
MP图
ω a MP图
l
y
b Mi图
y
b Mi图
A
P
l
Pl
MP图
ωy
1 2 abl =− = − al b EI EI 2 3 3EI
方法三:面积取之于梯形。面积分为两个三角形。 方法三 面积取之于梯形。面积分为两个三角形。 面积取之于梯形
图乘法-梁的位移计算 § 6-6 图乘法 梁的位移计算
3.直角梯形与直角梯形 直角梯形与直角梯形 方法一:面积分为 两个三角形
c
方法二:面积分为矩形 和三角形
c
ω⋅ y
Structural Mechanics
方法三:把 方法三 把 面积补成 矩形。 矩形。
Structural Mechanics

建筑力学梁和结构的位移欢迎下载课件.ppt


A
B
C
A
MP
B
C
M

＝
CV
1 EI
1 2

2
20
2 3

2

1 2

4
20
2 3

2

2 3

4
0.5
2
4
CV
=
208 3EI
精选
【例11-13】求图中所示刚架在支座B处的转角 。
2EI EI EI
A LB
PL PL
P
A
B
MP图
1
2EI EI EI
A
B
M=1图
P
L/2
B
A
l
PL/2
PL
MP图
x
L/2
∑ L/2 = 1 yc
M图
EI
P=1 x
= 1 ×[（PL×L/4)×(2/3)×L/2+(PL×L/8)×(L/2)×1/3]
EI
= 5PL3
48EI
精选
例．求图示外伸梁C端的竖向位移 CV ，EI=常数。
精选
解：
1 ql 2 = 4
20
8
2
P=1
( = 1 1 1 ql 2 l 2 l 1 1 ql 2 l 2 l 2 1 ql 2 l l = 3ql 4
EI 2 2
3 22
3 38
2 8EI
精选
例 试求图示三铰刚架c铰处左右两截面的相对角位移，EI=常c 数。
解：1）作实际状态的弯矩图
x
___
M1 = x
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。