下载文档原格式
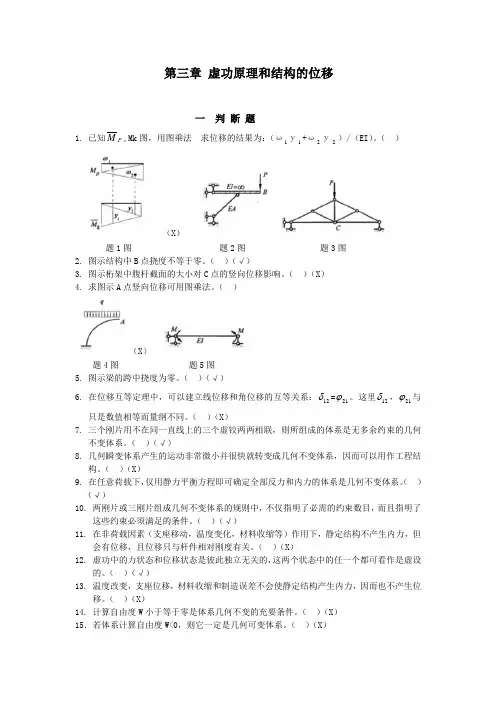
第三章 虚功原理和结构的位移一 判 断 题1. 已知P M ,Mk 图，用图乘法 求位移的结果为：（ω1у1+ω2у2）/（EI ）。
（ ） （X ） 题1图 题2图 题3图2. 图示结构中B 点挠度不等于零。
（ ）（√）3. 图示桁架中腹杆截面的大小对C 点的竖向位移影响。
（ ）（X ）4. 求图示A 点竖向位移可用图乘法。
（ ）（X ）题4图 题5图5. 图示梁的跨中挠度为零。
（ ）（√）6. 在位移互等定理中，可以建立线位移和角位移的互等关系：12δ=21ϕ。
这里12δ，21ϕ与只是数值相等而量纲不同。
（ ）（X ）7. 三个刚片用不在同一直线上的三个虚铰两两相联，则所组成的体系是无多余约束的几何不变体系。
（ ）（√）8. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系，因而可以用作工程结构。
（ ）（X ）9. 在任意荷载下，仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
（ ）（√）10. 两刚片或三刚片组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必须满足的条件。
（ ）（√）11. 在非荷载因素（支座移动，温度变化，材料收缩等）作用下，静定结构不产生内力，但会有位移，且位移只与杆件相对刚度有关。
（ ）（X ）12. 虚功中的力状态和位移状态是彼此独立无关的，这两个状态中的任一个都可看作是虚设的。
（ ）（√）13. 温度改变，支座位移，材料收缩和制造误差不会使静定结构产生内力，因而也不产生位移。
（ ）（X ）14. 计算自由度W 小于等于零是体系几何不变的充要条件。
（ ）（X ）15．若体系计算自由度W<0，则它一定是几何可变体系。
（ ）（X ）16．平面几何不变体系的三个基本组成规则是可以相互沟通的。
（ ）（√）17．三刚片由三个单铰或任意六根链杆两两相联，体系必为几何不变。
（ ）（X ）18．图示三铰刚架，EI 为常数，A 铰无竖向位移。
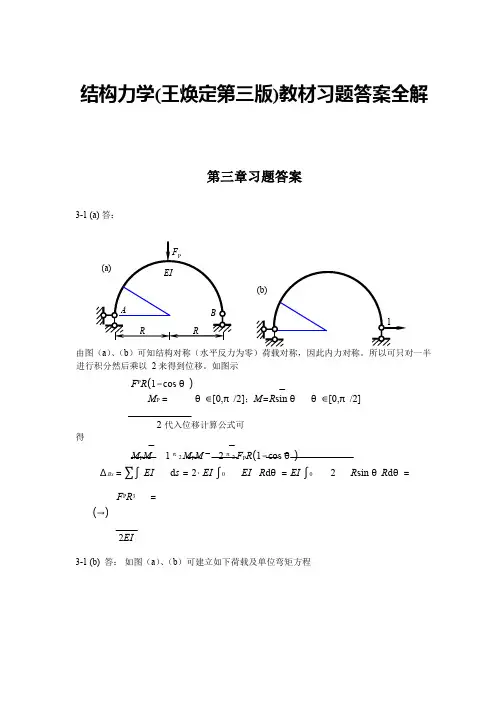
结构力学(王焕定第三版)教材习题答案全解第三章习题答案3-1 (a) 答：由图（a ）、（b ）可知结构对称（水平反力为零）荷载对称，因此内力对称。
所以可只对一半进行积分然后乘以 2 来得到位移。
如图示F P R (1−cos θ)M P = θ∈[0,π/2]；M =R sin θ θ∈[0,π/2]2 代入位移计算公式可得M P M1 π2 M P M2 π2 F P R (1−cos θ)∆Bx = ∑∫ EId s = 2⋅ EI ∫0EI R d θ= EI ∫02 R sin θR d θ=F P R 3 =(→)2EI3-1 (b) 答： 如图（a ）、（b ）可建立如下荷载及单位弯矩方程EIBARRF P( a )1pR ∆Bx =∑∫ MEIM d s =∫0π2 MEI P M R d θ= q EI 4∫0π2(1−2cos θ+cos 2 θ)R d θqR 4 ⎡ θ 1⎤3π⎞ qR 4= EI ×⎢θ−2sin θ+ 2 + 4sin2θ⎥⎦0 =⎝⎜ 4 − 2⎠⎟ 2EI (→)2 ⎣3-2 答：作M P 图和单位力弯矩图如下图： 由此可得内力方程根据题意EI (x ) = EI (l + x )代入位移公式积分可得 2 2 P 0s i n ( ) d (1 c o s ) (1 c o s ) q M R q R M R θθ α α θθ − = = − = − ∫AqRBα θ1( a ) θ( b )ABlq 03 0 p 6 x q M M xl = = xP M 图2 0 6q l1lM 图 x5 83 82l 代入位移公式并积分（查积分表）可得M P M l 2 q0x4∆Bx =∑∫ EI d x =∫0 6EI(l + x) d x7q0l40.07 ql4= (ln 2−)× = (→)123EI EI3-3 答：分别作出荷载引起的轴力和单位力引起的轴力如下图所示：由此可得C 点的竖向为移为：F NP F N1F NP F N1 ∆Cy =∑∫EA d s=∑ EA l =65112.5 kN× ×6 m+2×(62.5 kN× ×5 m+125 kN× ×5 m+75 kN× ×6 m)= 88EA=8.485×10−4 m当求CD 和CE 杆之间的夹角改变使：施加如图所示单位广义力并求作出F N2 图，则F∆=∑∫ F NP EA F N2 ds =∑ NP EAF N2 l2×62.5 kN ×(−0.15)×5 m +(−112.5 kN)×0.25×6 m =EA=−1.4×10−4 rad( 夹角减小）3-4 （a）答：先作出M p和M 如右图所示。
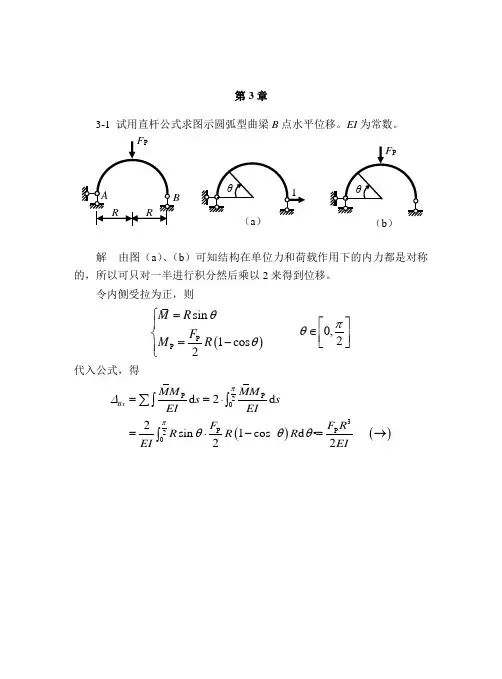
结构位移计算中复杂图形图乘法技巧探析摘要：以结构力学位移计算中复杂图形图乘法为背景，分析了图乘法的三个应用条件，总结了复杂图乘法的常用方法。
以线荷载作用下悬臂梁中点竖向位移和变刚度悬臂梁端点竖向位移的两个计算实例，分析了构造标准抛物线图形的技巧，总结了图乘法分段图乘、加减相伴的图乘原则，对复杂图形图乘法的计算效率大大提高。
关键词：结构力学；位移计算；图乘法；技巧探析1图乘法的基本公式结构力学单位荷载法计算位移的一般公式中，由积分法计算梁或刚架杆件的结点或截面位移。
若积分法满足如下三个条件：其一，杆件是直杆；其二，截面抗弯刚度EI为常数；其三，两个图形中至少有一个是直线图形时，可以采用图乘法求解结点或截面位移［1-2］。
图乘法的应用简化了位移计算求解过程，减少了计算量。
图乘法的发明是由当时为莫斯科铁路运输学院的学生V ereshchagin于1925年提出，该方法后以他的名字被命名为韦列夏金规则。
位移积分法简化为图乘法的公式如式（1），具体推导过程参见文献［3-4］。
∫BAMiMkEIds=1EIωy0（1）式中，Mi,Mk中至少有一个图形是直线的弯矩图，EI是截面抗弯刚度且为常数，A,B是杆件积分区间，ds是截面微段，ω是曲线弯矩的面积（若两弯矩图均为直线，可任取），y0是曲线弯矩图的形心位置对应直线弯矩图的纵坐标。
2复杂图乘法分析结构力学教材中给出一般图乘法总结如下：式中括号内a,b,c,d同侧为正，异侧为负。
特殊情况一个梯形为三角形，式（2）的a,b,c,d中一项为0，问题得以简化。
除文献4介绍的两种方法外，还可以采用延长1弯矩图形的方法。
图2中Mp弯矩图分解为ω1和ω2，ω1沿整个l长度为标准二次抛物线，对应形心位置为y1；同样ω2沿右端l/2长度为标准二次抛物线，对应形心位置为y2；两者所得位移相减，即为ΔC的竖向位移，如式（3）。
Δc=ω1·y1－ω2·y2＝1EI［13·12ql2·l·l4－(－13·18ql2·l2·l8)］=17ql4384EI(↓)（3）实例二，求解图3（a）B点竖向位移，（沿杆件各段EI不同）由于沿直杆EI不同，常用方法必须采用分段图乘。
