初三数学抛物线练习题

抛物线的练习题抛物线的练习题在数学学科中，抛物线是一个经常出现的图形，它具有许多有趣的性质和应用。

通过解决抛物线的练习题，我们不仅可以加深对抛物线的理解，还可以提高我们的数学思维能力和解决问题的能力。

下面，我们来看一些关于抛物线的练习题。

练习题一：求顶点坐标已知抛物线的标准方程为 y = ax^2 + bx + c，其中a ≠ 0。

求抛物线的顶点坐标。

解答：顶点是抛物线的最高点或最低点，它的 x 坐标可以通过公式 x = -b/2a求得。

将 x = -b/2a 代入抛物线的方程，即可求得顶点的 y 坐标。

练习题二：求焦点坐标已知抛物线的焦点坐标为 F(x1, y1)，顶点坐标为 V(xv, yv)，且焦距为 p。

求抛物线的方程。

解答：根据抛物线的定义可知，焦点到抛物线上任意一点的距离等于该点到直线的距离。

利用这个性质，我们可以得到焦点坐标与顶点坐标之间的关系。

根据焦点到顶点的距离等于焦距 p，可以得到以下关系式：√((x1 - xv)^2 + (y1 - yv)^2) = p将抛物线的标准方程 y = ax^2 + bx + c 代入上述关系式，再利用顶点坐标的求解方法，可以得到抛物线的方程。

练习题三：求抛物线与直线的交点已知抛物线的方程为 y = ax^2 + bx + c，直线的方程为 y = mx + n。

求抛物线与直线的交点坐标。

解答：将直线的方程代入抛物线的方程，可以得到一个关于 x 的二次方程。

解这个二次方程，即可求得交点的 x 坐标。

将求得的 x 坐标代入直线的方程，即可求得交点的 y 坐标。

练习题四：求两条抛物线的交点已知两条抛物线的方程分别为 y1 = a1x^2 + b1x + c1 和 y2 = a2x^2 + b2x + c2，其中a1 ≠ 0，a2 ≠ 0。

求两条抛物线的交点坐标。

解答：将两条抛物线的方程相减，可以得到一个关于 x 的二次方程。

解这个二次方程，即可求得交点的x 坐标。

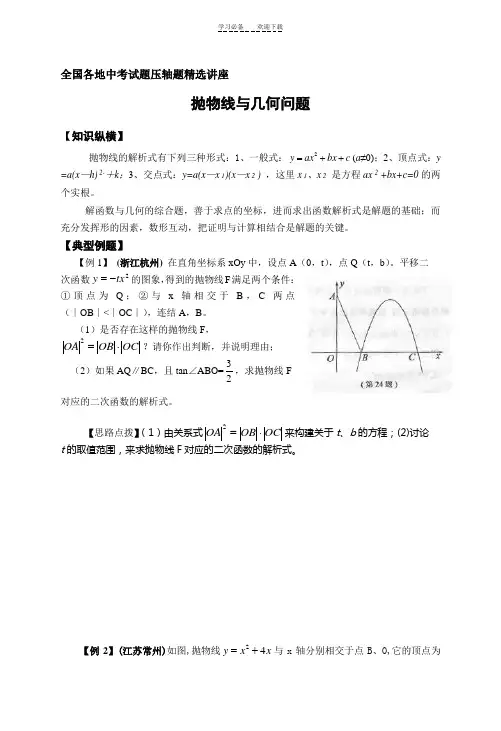
全国各地中考试题压轴题精选讲座抛物线与几何问题【知识纵横】抛物线的解析式有下列三种形式：1、一般式：2y ax bx c =++(a ≠0)；2、顶点式：y=a(x —h) 2-＋k ；3、交点式：y=a(x —x 1)(x —x 2 ) ，这里x 1、x 2 是方程ax 2 +bx+c=0的两个实根。

解函数与几何的综合题，善于求点的坐标，进而求出函数解析式是解题的基础；而充分发挥形的因素，数形互动，把证明与计算相结合是解题的关键。

【典型例题】【例1】 (浙江杭州) 在直角坐标系xOy 中，设点A （0，t ），点Q （t ，b ）。

平移二 次函数2tx y -=的图象，得到的抛物线F 满足两个条件：①顶点为Q ；②与x 轴相交于B ，C 两点（∣OB ∣<∣OC ∣），连结A ，B 。

（1）是否存在这样的抛物线F ，OC OB OA ⋅=2？请你作出判断，并说明理由；（2）如果AQ ∥BC ，且tan ∠ABO=23，求抛物线F 对应的二次函数的解析式。

【思路点拨】（1）由关系式OC OB OA ⋅=2来构建关于t 、b 的方程；(2)讨论t 的取值范围，来求抛物线F 对应的二次函数的解析式。

【例2】(江苏常州)如图,抛物线24y x x =+与x 轴分别相交于点B 、O,它的顶点为A,连接AB,把AB 所的直线沿y 轴向上平移,使它经过原点O,得到直线l,设P 是直线l 上一动点.（1）求点A 的坐标;（2）以点A 、B 、O 、P 为顶点的四边形中,有菱形、等 腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P 的坐标;（3）设以点A 、B 、O 、P 为顶点的四边形的面积为S, 点P 的横坐标为x,当46S +≤≤+,求x 的取值范围.【思路点拨】（3）可求得直线l 的函数关系式是y=-2x ，所以应讨论①当点P 在第二象限时，x<0、 ②当点P 在第四象限是，x>0这二种情况。

初中数学抛物线经典试题集锦编著】黄勇权第一组题型】1、已知二次函数y=x2+bx+c过点A（2,0），C（0, -8）（1）求此二次函数的解析式，（2）在抛物线上存在一点p 使△ ABP的面积为15，请直接写出p 点的坐标。

2、在平面直角坐标系xOy中，抛物线y=2x2+mx+n 经过点A（5，0 ），B（2，-6）．（1）求抛物线的表达式及对称轴2）设点 B 关于原点的对称点为C，写出过A、C两点直线的表达式3、在平面直角坐标系xOy 中，已知抛物线的顶点 C 为（2，4），并在x 轴上截得的长度为 6 。

（1）写出抛物线与x 轴交点 A 、B 的坐标（2）求该抛物线的表达式（3）写出抛物线与y 轴交点P 的坐标4、直线的解析式为y=2x+4 ，交x 轴于点 A ，交y 轴于点B，若以 A 为顶点,，且开口向下作抛物线，交直线AB 于点D，交y 轴负半轴于点 C ，（1）若△ ABC 的面积为20，求此时抛物线的解析式（2）若△ BDO 的面积为8，求此时抛物线的解析式答案】1、已知二次函数y=x2+bx+c过点A（2,0），C（0, -8）（1）求此二次函数的解析式，（2）在抛物线上存在一点p 使△ ABP的面积为15，请直接写出p 点的坐标解：【第一问】因为函数y=x2+bx+c过点A（2,0），C（0, -8）分别将x=2，y=0 代入y=x2+bx+c，得0=4+2b+c -①将x=0，y=-8 代入y=x2+bx+c，得-8=c -------- ②将②代入①，解得：b=2 ------------------------------------ ③此时，将② ③代入y=x2+bx+c，所以：二次函数的解析式y=x2+ 2x -8 【第二问】1△ABP的面积= 2│AB│*│y p│------------- ④因为A、B 两点在x 轴上，令x2+ 2x -8=0 （x-2）（x+4）=0 解得：x1=2，x2= -4所以：│ AB│=│X1- X2│=│2-（- 4）│ =6 ---- ⑤又△ ABP的面积=15 --------------------------------- ⑥1由④ ⑤ ⑥，得：2 *6* │y p│=15y p =5故有：y p= ± 5即：p 点的纵坐标为 5 或-5.把y=5 代入y=x2+ 2x -8 ，即：5=x2+ 2x -8x2+ 2x -13=0解得：x= -1 ± 14那么，此时p 点坐标（-1+ 14，5），（-1- 14，5）---- ⑦把y=-5 代入y=x2+ 2x -8，即：-5=x2+ 2x -8x2+ 2x -3=0 （x-1）（x+3）=0 解得：x= 1 或x= -3 那么，此时p 点坐标（1，-5），（-3，-5）⑧由⑦ ⑧得，使△ ABP的面积为15，p 点坐标是：（-1+ 14，5），（-1- 14，5），（1，-5），（-3，-5）2、在平面直角坐标系xOy中，抛物线y=2x2+mx+n 经过点A（5，0 ），B（2，-6）．（1）求抛物线的表达式及对称轴（2）设点 B 关于原点的对称点为C，写出过A、C两点直线的表达式。

抛物线试题及答案初三
一、选择题
1. 抛物线y=ax^2+bx+c的顶点坐标是（）
A. (-b/2a, f(-b/2a))
B. (-b/2a, f(-b/2a))
C. (-b/2a, f(-b/2a))
D. (-b/2a, f(-b/2a))
答案：A
2. 抛物线y=x^2-4x+3与x轴的交点坐标是（）
A. (1,0)和(3,0)
B. (-1,0)和(3,0)
C. (1,0)和(-3,0)
D. (-1,0)和(-3,0)
答案：A
二、填空题
3. 若抛物线y=ax^2+bx+c的对称轴为直线x=2，则b的值为______。

答案：-4a
4. 抛物线y=-2x^2+4x+1的顶点坐标为（1,3），则a=______。

答案：-2
三、解答题
5. 已知抛物线y=x^2-6x+9，求抛物线的顶点坐标。

答案：顶点坐标为(3,0)。

6. 抛物线y=2x^2-4x+1与直线y=x+2相交于A、B两点，求A、B两点
的坐标。

答案：A(1,3)，B(2,4)。

四、综合题
7. 抛物线y=x^2-2x-3与x轴相交于点C、D，与y轴相交于点E，求
三角形CDE的面积。

答案：三角形CDE的面积为9。

8. 已知抛物线y=ax^2+bx+c经过点(1,0)和(-1,0)，且顶点在x轴上，求抛物线的解析式。

答案：抛物线的解析式为y=x^2。

抛物线的练习题抛物线是数学中一个重要的曲线，它具有很多应用和性质。

在学习和掌握抛物线这一曲线的过程中，解决一些练习题是非常有效的。

下面，我将为大家提供一些关于抛物线的练习题，并帮助大家解答这些题目。

练习题1：已知抛物线的顶点为(2,-3)，过点(4,5)的直线与该抛物线有两个交点，求直线的方程以及交点坐标。

解答1：我们知道，抛物线的一般方程为 y = ax^2 + bx + c。

由于顶点为(2,-3)，所以可以得到 c = -3。

将过点(4,5)的直线与抛物线相交的坐标代入方程中，可以得到方程组：5 = a(4)^2 + b(4) + (-3)5 = 16a + 4b - 3同时，直线与抛物线有两个交点，即方程组有两个解。

解方程组可以得到直线的方程和交点坐标。

练习题2：已知抛物线的焦点为(1,2)，准线方程为 x = -1，求抛物线的方程。

解答2：我们知道，抛物线的一般方程为 y = ax^2 + bx + c。

由于焦点为(1,2)，所以可以得到 c = -4a。

再根据准线的方程 x = -1，将 x = -1 代入抛物线方程中得到 y = a((-1)^2) + b(-1) + c，即 y = a - b + c。

将抛物线对称性的性质应用于焦点和准线，可以得到焦点关于准线的对称点也在抛物线上。

因此，可以得到焦点关于准线的对称点为（-3,2）。

由于焦点关于准线的对称点也在抛物线上，将其代入抛物线方程中，有 2 = 9a - 3b + c。

结合 c = -4a，可以得到 2 = 9a - 3b - 4a。

由上述两个方程联立解得 a = 1，代入 c = -4a，可以得到 c = -4。

再结合 y = ax^2 + bx + c，所以抛物线的方程为 y = x^2 + x - 4。

练习题3：已知抛物线的焦点为(0,2)，与x 轴相切于点(4,0)，求抛物线的方程。

解答3：我们知道，抛物线的一般方程为 y = ax^2 + bx + c。

初三抛物线试题及答案一、选择题1. 抛物线y = ax^2 + bx + c的顶点坐标是什么？A. (-b, c)B. (-b/2a, c - b^2/4a)C. (-b/2a, c + b^2/4a)D. (-b/a, c)答案：B2. 如果抛物线y = x^2 + 2x + 1的对称轴是直线x = -1，那么a的值是多少？A. 1B. -1C. 0D. 2答案：A3. 抛物线y = 2x^2 - 4x + 3的开口方向是：A. 向上B. 向下C. 水平D. 无法确定答案：A二、填空题4. 已知抛物线y = 3x^2 - 6x + 5，求抛物线的顶点坐标。

答案：顶点坐标为(1, 2)5. 抛物线y = -x^2 + 4x - 3的焦点坐标是什么？答案：焦点坐标为(2, -2)三、解答题6. 已知抛物线y = 2x^2 - 8x + 7，求其与x轴的交点。

答案：首先将方程化为标准形式：y = 2(x - 2)^2 - 1。

抛物线与x轴的交点即为y = 0时的x值。

解方程2(x - 2)^2 - 1 = 0，得到x= 2 ± √(1/2)，即x = 2 ± √2/2。

7. 已知抛物线y = ax^2 + bx + c经过点(1, 3)和(-1, 1)，求a和b 的值。

答案：将点(1, 3)和(-1, 1)代入方程，得到两个方程：3 = a(1)^2 + b(1) + c1 = a(-1)^2 + b(-1) + c解这两个方程，得到a + b + c = 3和a - b + c = 1。

相减消去c，得到2b = 2，即b = 1。

将b的值代入任一方程，得到a + 1 + c = 3，即a + c = 2。

由于c = 3 - a - b = 3 - a - 1 = 2 - a，代入得到a + 2 - a = 2，这是一个恒等式，说明a可以是任意实数。

四、应用题8. 一个物体从地面向上抛，其高度h（米）与时间t（秒）的关系为h = -5t^2 + 20t。

初中抛物线试题及答案
一、选择题
1. 抛物线y = x^2 - 2x + 1的顶点坐标是（）。

A. (1, 0)
B. (1, -1)
C. (0, 1)
D. (0, -1)
答案：A
2. 如果抛物线y = ax^2 + bx + c的对称轴是直线x = -2，那么b的值是（）。

A. 4a
B. -4a
C. 2a
D. -2a
答案：B
二、填空题
1. 抛物线y = 2x^2 + 4x + 3的顶点坐标是（）。

答案：(-1, 1)
2. 抛物线y = -3x^2 + 6x - 2的对称轴方程是（）。

答案：x = 1
三、解答题
1. 已知抛物线y = x^2 - 6x + 9，求抛物线与x轴的交点坐标。

答案：抛物线与x轴的交点坐标为(3, 0)。

2. 抛物线y = 2x^2 - 4x + 3，求抛物线的顶点坐标和对称轴。

答案：抛物线的顶点坐标为(1, 1)，对称轴为直线x = 1。

四、应用题
1. 一个抛物线形的桥拱，其方程为y = -0.5x^2 + 4x + 1，桥拱的最高点离水面的高度是5米。

求桥拱的跨度。

答案：桥拱的跨度为8米。

2. 一个物体从地面以一定的初速度向上抛，其运动轨迹可以用抛物线y = -5x^2 + 20x + 2描述，其中x表示时间（秒），y表示高度（米）。

求物体达到最高点时的时间。

答案：物体达到最高点时的时间是2秒。

抛物线练习题一、选择题1．在直角坐标平面内，到点(1,1)和直线 x＋ 2y＝ 3 距离相等的点的轨迹是 ()A ．直线B．抛物线C．圆D．双曲线2．抛物线 y2＝ x 上一点 P 到焦点的距离是 2，则 P 点坐标为 ()3，± 67，± 79，± 35，± 10A. 22B. 42C. 42D. 223．抛物线 y＝ ax2的准线方程是y＝ 2，则 a 的值为 ()11A. 8 B ．－8C． 8D．－ 84．设抛物线 y2＝ 8x 上一点 P 到 y 轴的距离是4，则点 P 到该抛物线焦点的距离是 ()A ．4B ． 6C． 8D． 125．设过抛物线的焦点 F 的弦为 AB，则以 AB 为直径的圆与抛物线的准线的地址关系是()A ．订交B ．相切C．相离D．以上答案都有可能6．过点 F(0,3)且和直线 y＋ 3＝0 相切的动圆圆心的轨迹方程为 ()A ．y2＝ 12xB ．y2＝－ 12x C． x2＝ 12y D ．x2＝－ 12y7．抛物线 y2＝ 8x 上一点 P 到 x 轴距离为12，则点 P 到抛物线焦点 F 的距离为 ()A ．20B ．8C． 22D． 248．抛物线的极点在坐标原点，焦点是椭圆4x2＋ y2＝ 1 的一个焦点，则此抛物线的焦点到准线的距离为 ()11A． 2 3 B. 3 C.2 3 D.4 39．设抛物线的极点在原点，其焦点F 在 y 轴上，又抛物线上的点(k，－ 2)与 F 点的距离为4，则 k 的值是 ()A． 4 B ． 4 或－ 4C．－ 2 D ．2 或－ 212的焦点坐标是 ()10．抛物线 y＝m x (m<0)A.0，mB. 0，－mC. 0，1D. 0，－1 444m4m11．抛物线的极点在原点，对称轴是x 轴，抛物线上的点(－5,2 5) 到焦点的距离是6，则抛物线的方程为 ()A． y2＝－ 2x B ．y2＝－ 4x C． y2＝ 2x D． y2＝－ 4x 或 y2＝－ 36x12．已知抛物线y2＝2px(p>0) 的准线与圆 (x－ 3)2＋ y2＝ 16 相切，则p 的值为 () 1A. 2 B ． 1C．2 D ．4二、填空题13．过抛物线焦点 F 的直线与抛物线订交于A 、B 两点，若A 、B 在抛物线准线上的射影是A 1、B 1，则∠ A 1FB 1=。

完整版)抛物线基础练习题抛物线基础练习题1.抛物线方程及性质1.1 抛物线的标准方程为 $y = ax^2 + bx + c$，其中 $a$、$b$、$c$ 是实数常数。

a 的值决定了抛物线的开口方向。

当 $a。

0$ 时，抛物线开口向上。

当 $a < 0$ 时，抛物线开口向下。

1.2 抛物线的对称轴是垂直于 x-轴的直线，可以通过以下公式求得：x = -\frac{b}{2a}$$2.抛物线图像绘制2.1 绘制抛物线图像的步骤：确定抛物线的方程。

找出对称轴的 x 坐标。

绘制对称轴，并确定对称轴上的一点。

根据对称轴上的点，绘制抛物线的图像。

2.2 使用上述步骤绘制以下抛物线的图像：2.2.1 $y = x^2$，开口向上的抛物线。

首先，我们可以得知对称轴的 x 坐标为 $x = 0$。

确定对称轴上的一点 P(0,0)，然后根据 P 点的坐标起始绘制抛物线图像。

绘制结果如下图所示：抛物线图像](image.png)3.练习题请计算并回答下列问题：1.当抛物线方程为 $y = -2x^2 + 3x + 1$ 时，求其对称轴的 x 坐标。

2.给定抛物线方程 $y = 4x^2 + 2x + 1$，求其开口方向。

4.答案解析解答上述练习题：1.根据公式 $x = -\frac{b}{2a}$，代入 $a=-2$ 和 $b=3$，我们可以计算得到对称轴的 x 坐标为 $x = -\frac{3}{2}$。

2.根据抛物线方程 $y = 4x^2 + 2x + 1$，我们可以得知 $a = 4.0$，所以抛物线的开口方向是向上。

希望以上内容能够帮助你理解抛物线的基本概念和绘制方法。

如果还有其他问题，请随时提问。

初三数学抛物线线段最值压轴题在初三数学学习中，抛物线是一个非常重要的概念。

抛物线线段最值问题，则是抛物线的一个经典题型，这也是初三数学学习的一个难点。

今天我们就来深入探讨初三数学抛物线线段最值压轴题，希望通过本文的学习，能够让大家更深入地理解这个问题。

我们来了解一下什么是抛物线线段最值。

在数学中，抛物线是一种二次曲线，具有很多重要的性质。

在抛物线上取一段线段，我们希望找到这段线段的最值，即这段线段的最大值或最小值。

这就是抛物线线段最值问题。

接下来，我们来看一道经典的抛物线线段最值压轴题：题目：已知抛物线y = ax² + bx + c(a ≠ 0) 的顶点为 (-2, 3)，且经过点 (1, 2)，求抛物线上线段 [1, 3] 的最小值。

这道题目涉及到了抛物线的顶点、经过特定点和线段最值的求解。

我们可以利用一些数学知识来进行解题。

我们可以利用顶点坐标的性质，得到抛物线的一般式方程 y = a(x - h)² + k，其中顶点为 (h, k)。

代入题目给出的顶点坐标 (-2, 3)，得到抛物线一般式方程 y = a(x + 2)² + 3。

由题目给出的条件，抛物线经过点 (1, 2)，代入得到方程 2 = a(1 + 2)² + 3，解得 a = -1。

再次，利用所求线段 [1, 3] 的长度为 3-1 = 2，可以得到线段所对应的抛物线上的点为 (1, 2)，代入抛物线方程，得到纵坐标 y = -1。

经过以上计算，得知抛物线上线段 [1, 3] 的最小值为 y = -1。

通过以上题目的解析，我们可以清晰地看到抛物线线段最值问题的解题思路。

首先要利用抛物线的基本性质和条件，得到抛物线的一般式方程，并根据具体条件解出抛物线的参数。

然后结合线段的特点，求出所对应抛物线上的点和其纵坐标，最终得出线段的最值。

接下来，我们来总结一下抛物线线段最值问题的解题思路。

首先要得到抛物线的一般式方程，然后根据题目给定的条件，解出抛物线的参数。

抛物线练习题一、选择题1．在直角坐标平面内，到点(1,1)和直线x ＋2y ＝3距离相等的点的轨迹是( )A ．直线B ．抛物线C ．圆D ．双曲线2．抛物线y 2＝x 上一点P 到焦点的距离是2，则P 点坐标为( )A.⎝⎛⎭⎫32，±62B.⎝⎛⎭⎫74，±72C.⎝⎛⎭⎫94，±32D.⎝⎛⎭⎫52，±102 3．抛物线y ＝ax 2的准线方程是y ＝2，则a 的值为( )A.18 B ．－18C ．8D ．－8 4．设抛物线y 2＝8x 上一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是( )A ．4B ．6C ．8D ．125．设过抛物线的焦点F 的弦为AB ，则以AB 为直径的圆与抛物线的准线的位置关系是( )A ．相交B ．相切C ．相离D ．以上答案都有可能6．过点F (0,3)且和直线y ＋3＝0相切的动圆圆心的轨迹方程为( )A ．y 2＝12xB ．y 2＝－12xC ．x 2＝12yD ．x 2＝－12y7．抛物线y 2＝8x 上一点P 到x 轴距离为12，则点P 到抛物线焦点F 的距离为( )A ．20B ．8C ．22D ．248．抛物线的顶点在坐标原点，焦点是椭圆4x 2＋y 2＝1的一个焦点，则此抛物线的焦点到准线的距离为( )A ．2 3 B. 3 C.12 3 D.143 9．设抛物线的顶点在原点，其焦点F 在y 轴上，又抛物线上的点(k ，－2)与F 点的距离为4，则k 的值是( )A ．4B ．4或－4C ．－2D ．2或－210．抛物线y ＝1mx 2(m <0)的焦点坐标是( ) A.⎝⎛⎭⎫0，m 4 B.⎝⎛⎭⎫0，－m 4 C.⎝⎛⎭⎫0，14m D.⎝⎛⎭⎫0，－14m 11．抛物线的顶点在原点，对称轴是x 轴，抛物线上的点(－5,25)到焦点的距离是6，则抛物线的方程为( )A ．y 2＝－2xB ．y 2＝－4xC ．y 2＝2xD ．y 2＝－4x 或y 2＝－36x12．已知抛物线y 2＝2px (p >0)的准线与圆(x －3)2＋y 2＝16相切，则p 的值为( )A.12 B ．1 C ．2 D ．4二、填空题13．过抛物线焦点F的直线与抛物线相交于A、B两点，若A、B在抛物线准线上的射影是A1、B1，则∠A1FB1= 。

抛物线试题及答案初三抛物线试题及答案（初三）一、选择题1. 抛物线y=ax^2+bx+c（a≠0）的对称轴是直线x=-1，那么a+b+c的值是（）A. 0B. 1C. 2D. -1答案：D解析：抛物线的对称轴为x=-1，根据对称轴公式x=-b/2a，可得-b/2a=-1，即b=2a。

又因为抛物线过原点，所以c=0。

将b和c 的值代入a+b+c，得到a+2a+0=3a。

由于a≠0，所以a+b+c=-1。

2. 抛物线y=-2x^2+4x+1的顶点坐标是（）A. (1, 3)B. (2, 3)C. (1, 1)D. (2, 1)答案：B解析：抛物线的顶点坐标可以通过公式x=-b/2a求得，其中a=-2，b=4。

代入公式得到x=-4/(2*-2)=1。

将x=1代入抛物线方程求得y值，得到y=-2*1^2+4*1+1=3。

所以顶点坐标为(1, 3)。

3. 抛物线y=x^2-6x+9的开口方向是（）A. 向上B. 向下C. 向左D. 向右答案：A解析：抛物线的开口方向由二次项系数a决定。

在这个例子中，a=1，因为a>0，所以抛物线开口向上。

二、填空题4. 抛物线y=x^2-4x+c的顶点坐标是（）。

答案：(2, c-4)解析：抛物线的顶点坐标可以通过公式x=-b/2a求得，其中a=1，b=-4。

代入公式得到x=-(-4)/2*1=2。

将x=2代入抛物线方程求得y 值，得到y=2^2-4*2+c=c-4。

所以顶点坐标为(2, c-4)。

5. 抛物线y=2x^2-8x+5与x轴的交点坐标是（）。

答案：(1, 0) 和 (5/2, 0)解析：抛物线与x轴的交点即为抛物线方程的根。

将y=0代入抛物线方程得到2x^2-8x+5=0。

解这个二次方程，得到x1=1和x2=5/2。

所以与x轴的交点坐标是(1, 0)和(5/2, 0)。

三、解答题6. 已知抛物线y=x^2-2x-3，求证抛物线与x轴有两个交点。

答案：证明：将y=0代入抛物线方程得到x^2-2x-3=0。

初三抛物线试题及答案一、选择题1. 抛物线y=ax^2+bx+c（a≠0）的对称轴是直线x=-b/2a，那么下列抛物线中，对称轴是直线x=1的是（）。

A. y=x^2-2x+1B. y=x^2+2x+1C. y=-x^2+2x+1D. y=-x^2-2x+1答案：B解析：对于抛物线y=ax^2+bx+c，其对称轴为x=-b/2a。

将x=1代入，得到-b/2a=1，解得b=-2a。

因此，只有选项B满足条件。

2. 抛物线y=ax^2+bx+c（a≠0）与x轴有两个交点，那么下列说法正确的是（）。

A. b^2-4ac>0B. b^2-4ac=0C. b^2-4ac<0D. b^2-4ac≥0答案：A解析：抛物线与x轴有两个交点，说明方程ax^2+bx+c=0有两个不相等的实根。

根据判别式的性质，当b^2-4ac>0时，方程有两个不相等的实根。

因此，选项A正确。

二、填空题3. 已知抛物线y=x^2-4x+c与x轴有一个交点，求c的值。

答案：c=4解析：抛物线与x轴有一个交点，说明方程x^2-4x+c=0有两个相等的实根。

根据判别式的性质，当b^2-4ac=0时，方程有两个相等的实根。

将方程x^2-4x+c=0的系数代入，得到(-4)^2-4c=0，解得c=4。

4. 已知抛物线y=-2x^2+4x+m与y轴交于点（0，3），求m的值。

答案：m=3解析：将点（0，3）代入抛物线方程y=-2x^2+4x+m，得到3=-2(0)^2+4(0)+m，解得m=3。

三、解答题5. 已知抛物线y=-x^2+2x+3，求抛物线与x轴的交点坐标。

答案：交点坐标为（-1，0）和（3，0）。

解析：令y=0，得到方程-x^2+2x+3=0。

解这个二次方程，得到x=-1和x=3。

因此，抛物线与x轴的交点坐标为（-1，0）和（3，0）。

6. 已知抛物线y=x^2-6x+8，求抛物线的顶点坐标。

答案：顶点坐标为（3，-1）。

初中数学抛物线经典试题集锦【编著】黄勇权【第一组题型】1、已知二次函数y=x²+bx+c过点A（2,0），C（0, -8）（1）求此二次函数的解析式，（2）在抛物线上存在一点p使△ABP的面积为15，请直接写出p点的坐标。

2、在平面直角坐标系xOy中，抛物线y=2x²+mx+n经过点A（5，0），B（2，-6）．（1）求抛物线的表达式及对称轴（2）设点B关于原点的对称点为C，写出过A、C两点直线的表达式。

3、在平面直角坐标系xOy中，已知抛物线的顶点C为（2，4），并在x轴上截得的长度为6。

（1）写出抛物线与x轴交点A、B的坐标（2）求该抛物线的表达式（3）写出抛物线与y轴交点P的坐标4、直线的解析式为y=2x+4，交x轴于点A，交y轴于点B，若以A 为顶点,，且开口向下作抛物线，交直线AB于点D，交y轴负半轴于点C，（1）若△ABC的面积为20，求此时抛物线的解析式（2）若△BDO的面积为8，求此时抛物线的解析式【答案】1、已知二次函数y=x²+bx+c过点A（2,0），C（0, -8）（1）求此二次函数的解析式，（2）在抛物线上存在一点p使△ABP的面积为15，请直接写出p点的坐标。

解：【第一问】因为函数y=x²+bx+c过点A（2,0），C（0, -8）分别将x=2，y=0代入y=x²+bx+c，得0=4+2b+c-----①将x=0，y=-8代入y=x²+bx+c，得-8=c-------------②将②代入①，解得：b=2--------------------------------------③此时，将②③代入y=x²+bx+c，所以：二次函数的解析式y=x²+ 2x -8【第二问】△ABP的面积= 12│AB│*│y p│----------------------④因为A、B两点在x轴上，令x²+ 2x -8=0（x-2）（x+4）=0解得：x1=2，x2= -4所以：│AB│=│X1- X2│=│2-（- 4）│=6------⑤又△ABP的面积=15-------------------------------------⑥由④⑤⑥，得：12*6*│y p│=15│y p│=5故有：y p= ±5即：p点的纵坐标为5或-5.把y=5代入y=x²+ 2x -8，即：5=x²+ 2x -8x²+ 2x -13=0解得：x= -1± 14那么，此时p点坐标（-1+ 14，5），（-1- 14，5）-------⑦把y=-5代入y=x²+ 2x -8，即：-5=x²+ 2x -8x²+ 2x -3=0（x-1）（x+3）=0解得：x= 1或x= -3那么，此时p点坐标（1，-5），（-3，-5）------------------⑧由⑦⑧得，使△ABP的面积为15，p点坐标是：（-1+ 14，5），（-1- 14，5），（1，-5），（-3，-5）2、在平面直角坐标系xOy中，抛物线y=2x²+mx+n经过点A（5，0），B（2，-6）．（1）求抛物线的表达式及对称轴（2）设点B关于原点的对称点为C，写出过A、C两点直线的表达式。

【编著】 黄勇权【第一组题型】1、已知二次函数y=x ²+bx+c 过点A （2,0），C （0, -8）（1）求此二次函数的解析式，（2）在抛物线上存在一点p 使△ABP 的面积为15，请直接写出p 点的坐标。

2、在平面直角坐标系xOy 中，抛物线y=2x ²+mx+n 经过点A （5，0），B （2，-6）．（1）求抛物线的表达式及对称轴（2）设点B 关于原点的对称点为C ，写出过A 、C 两点直线的表达式。

初中数学抛物线 经典试题集锦3、在平面直角坐标系xOy中，已知抛物线的顶点C为（2，4），并在x轴上截得的长度为6。

（1）写出抛物线与x轴交点A、B的坐标（2）求该抛物线的表达式（3）写出抛物线与y轴交点P的坐标4、直线的解析式为y=2x+4，交x轴于点A，交y轴于点B，若以A为顶点,，且开口向下作抛物线，交直线AB于点D，交y轴负半轴于点C，（1）若△ABC的面积为20，求此时抛物线的解析式（2）若△BDO的面积为8，求此时抛物线的解析式【答案】1、已知二次函数y=x²+bx+c过点A（2,0），C（0, -8）（1）求此二次函数的解析式，（2）在抛物线上存在一点p使△ABP的面积为15，请直接写出p点的坐标。

解：【第一问】因为函数y=x ²+bx+c 过点A （2,0），C （0, -8）分别将x=2，y=0代入y=x ²+bx+c ， 得 0=4+2b+c-----①将x=0，y=-8代入y=x ²+bx+c ，得-8=c-------------②将②代入①，解得：b=2--------------------------------------③此时，将② ③代入y=x ²+bx+c ，所以：二次函数的解析式 y=x ²+ 2x -8【第二问】△ABP 的面积= 12│AB │*│y p │----------------------④ 因为A 、B 两点在x 轴上，令x ²+ 2x -8=0（x-2）（x+4）=0解得：x 1=2，x 2= -4所以：│AB │=│X 1- X 2│=│2-（- 4）│=6------⑤又△ABP 的面积=--------------------------⑥由 ④ ⑤ ⑥，得 ： 12*6*│y p │=15│y p│=5故有：y p= ±5即：p点的纵坐标为5或-5.把y=5代入 y=x²+ 2x -8，即：5=x²+ 2x -8x²+ 2x -13=0解得：x= -1± 14那么，此时p点坐标（-1+ 14，5），（-1- 14，5）-------⑦把y=-5代入 y=x²+ 2x -8，即：-5=x²+ 2x -8x²+ 2x -3=0（x-1）（x+3）=0解得：x= 1或x= -3那么，此时p点坐标（1，-5），（-3，-5）------------------⑧由⑦⑧得，使△ABP的面积为15，p点坐标是：（-1+ 14，5），（-1- 14，5），（1，-5），（-3，-5）2、在平面直角坐标系xOy中，抛物线y=2x²+mx+n经过点A（5，0），B（2，-6）．（1）求抛物线的表达式及对称轴（2）设点B关于原点的对称点为C，写出过A、C两点直线的表达式。

已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D. 求该抛物线的解析式；若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；△AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22）如图，抛物线21:23L y x x =--+交x 轴于A 、B 两点，交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ，2L 交x 轴于C 、D 两点.（1）求抛物线2L 对应的函数表达式； （2）抛物线1L 或2L 在轴上x 方的部分是否存在点N ，使以A ，C ，M ，N 为顶点的四边形是平行四边形.若存在，求出点N 的坐标；若不存在，请说明理由；（3）若点P 是抛物线1L 上的一个动点（P 不与点A 、B 重合），那么点P 关于原点的对称点Q 是否在抛物线2L 上，请说明理由.如图16，在平面直角坐标系中，直线y =-x 轴交于点A ，与y 轴交于点C，抛物线2(0)3y ax x c a =-+≠经过AB C ，，三点． （1）求过AB C ，，三点抛物线的解析式并求出顶点F 的坐标； （2）在抛物线上是否存在点P ，使ABP △为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明理由；（3）试探究在直线AC 上是否存在一点M ，使得MBF △的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在y 轴的正半轴上，且1AB =，OB =，矩形ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD ．点A 的对应点为点E ，点B 的对应点为点F ，点C 的对应点为点D ，抛物线2y ax bx c =++过点A E D ，，． （1）判断点E 是否在y 轴上，并说明理由；（2）求抛物线的函数表达式；（3）在x 轴的上方是否存在点P ，点Q ，使以点O B P Q ，，，为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．x已知：如图14，抛物线2334y x =-+与x 轴交于点A ，点B ，与直线34y x b =-+相交于点B ，点C ，直线34y x b =-+与y 轴交于点E ．（1）写出直线BC 的解析式．（2）求ABC △的面积．（3）若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A B ，重合），同时，点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB △的面积S 与t 的函数关系式，并求出点M 运动多少时间时，MNB △的面积最大，最大面积是多少？yOD EC F AB。

初三抛物线的平移练习题平移是几何变换中常见且重要的一种方式，它可以通过改变图形中各个点的位置来实现。

在初三数学学习中，平移也是一个重要的知识点。

本文将介绍初三抛物线的平移练习题，通过解题示例来帮助读者更好地理解和应用这一知识。

抛物线是一个二次函数的图像，具有特定的形状和性质。

平移是指将一个图像沿着横轴或纵轴方向上的某个向量进行移动，而不改变其形状和大小。

在解题之前，首先了解一下平移的基本概念和表示方法：1. 平移的基本概念：平移是指将一个图形沿着指定的向量方向进行移动，移动的距离由向量的大小确定。

2. 平移的表示方法：平移可以使用向量表示法，其中向量的大小和方向决定了平移的距离和方向。

水平方向上的平移可以用 (a, 0) 表示，其中 a 为横向平移的距离；垂直方向上的平移可以用 (0, b) 表示，其中 b 为纵向平移的距离。

了解了平移的基本概念和表示方法后，我们来看几道初三抛物线的平移练习题。

【例题一】已知函数 f(x) = x^2 的图像在坐标平面上的顶点为 A(0, 0)，将该抛物线沿 x 轴方向平移 2 个单位，请问平移后的抛物线方程是什么？解答：平移前抛物线的顶点为 A(0, 0)，那么平移后的顶点为 A'(2, 0)。

由于水平方向平移 2 个单位，所以平移后的抛物线方程为 g(x) = (x-2)^2。

【例题二】已知函数 g(x) = x^2 的图像在坐标平面上的顶点为 B(1, 1)，将该抛物线沿 y 轴方向平移 3 个单位，请问平移后的抛物线方程是什么？解答：平移前抛物线的顶点为 B(1, 1)，那么平移后的顶点为 B'(1, 4)。

由于垂直方向平移 3 个单位，所以平移后的抛物线方程为 h(x) = (x-1)^2 + 3。

【例题三】已知函数 h(x) = x^2 的图像在坐标平面上的顶点为 C(2, 4)，将该抛物线沿 x 轴和 y 轴方向分别平移 3 个单位，请问平移后的抛物线方程是什么？解答：先进行 x 轴方向的平移，平移后的顶点为 C'(5, 4)。

一、选择题：1、已知抛物线m x m x y +-+=)1(52与x 轴两交点在y 轴同侧，它们的距离的平方等于2549，则m 的值为（）A 、－2 B 、12 C 、24 D 、－2或24 2、已知二次函数c bx ax y ++=21（a ≠0）与一次函数m kx y +=2（k ≠0）的图像交于点A （－2，4），B （8，2），如图所示，则能使21y y >成立的x 的取值范围是（）A 、2-<x B 、8>x C 、82<<-x D 、2-<x 或8>x yx 第2题图BAOyx第3题图EBAO yx第4题图BAO3、如图，抛物线c bx ax y ++=2与两坐标轴的交点分别是A 、B 、E ，且△ABE 是等腰直角三角形，AE ＝BE ，则下列关系：①0=+c a ；②0=b ；③1-=ac ；④2c S A B E =D 其中正确的有（）A 、4个B 、3个C 、2个D 、1个4、设函数1)1(22++-+-=m x m x y 的图像如图所示，它与x 轴交于A 、B 两点，线段OA 与OB 的比为1∶3，则m 的值为（）A 、31或2 B 、31C 、1 D 、2 二、填空题：1、已知抛物线23)1(2----=k x k x y 与x 轴交于两点A （a ，0），B （b ，0），且1722=+b a ，则k ＝。

2、抛物线m x m x y 2)12(2---=与x 轴的两交点坐标分别是A （1x ，0），B （2x ，0），且121=x x ，则m 的值为。

3、若抛物线1212-++-=m mx x y 交x 轴于A 、B 两点，两点，交交y 轴于点C ，且∠ACB ＝900，则m ＝。

4、已知二次函数1)12(2--+=x k kx y 与x 轴交点的横坐标为1x 、2x )(21x x <，则对于下列结论：①当2-=x 时，1=y ；②当2x x >时，0>y ；③方程1)12(2--+x k kx ＝0有两个不相等的实数根1x 、2x ；④11-<x ，12->x ；⑤kkx x 21241+=-，其中所有正确的结论是所有正确的结论是 （只填写顺号）。

初三抛物线练习题1. 题目描述：某初三数学老师在课堂上给学生出了一道抛物线练习题，题目如下：已知二次函数 y = ax^2 + bx + c 的图像过点（1, 3），且对称轴为 x = 2，请你根据给出的信息完成以下任务。

任务一：求解二次函数的表达式。

任务二：求解 a、b、c 的值。

任务三：求解抛物线的焦点坐标。

2. 解题过程：根据题目给出的条件，我们需要求解出二次函数的表达式、a、b、c 的值以及抛物线的焦点坐标。

任务一：求解二次函数的表达式。

已知对称轴为 x = 2，可以得知顶点的横坐标为 2。

又由于抛物线过点（1, 3），可以带入顶点的横坐标和纵坐标，得到一个方程：3 = a * (1^2) + b * 1 + c化简后可得：a +b +c = 3 ----(1)现在我们还需要求解另外两个方程。

任务二：求解 a、b、c 的值。

由于已知对称轴为 x = 2，可以得知顶点的横坐标为 2。

根据顶点公式，顶点的横坐标为 -b / (2a)。

代入已知条件可得：2 = -b / (2a)化简可得：b = -4a ----(2)又由于顶点的横坐标为 2，根据顶点公式，顶点的纵坐标为 f(2) = a * (2^2) + b * 2 + c。

代入已知条件可得：f(2) = a * 4 + b * 2 + c化简可得：4a + 2b + c = f(2) ----(3)将方程（2）和方程（3）带入方程（1）中，可得：a + (-4a) + c = 3化简可得：-3a + c = 3 ----(4)现在我们有三个方程（2）、（3）、（4），需要求解 a、b、c 的值。

通过方程（2）可以将 b 表示为 -4a。

将 b = -4a 代入方程（3）中，可以得到：4a + 2(-4a) + c = f(2)化简可得：-6a + c = f(2) ----(5)通过方程（4）和方程（5）可以得到一个方程组：-3a + c = 3-6a + c = f(2)解方程组可以得到 a 和 c 的值，进而求解出 b 的值。