初三数学抛物线常考题型

初三数学二次函数经典题型二次函数单元检测 (A) 姓名___ ____一、填空题： 1、函数21(1)21my m x mx +=--+是抛物线，则m ＝ .2、抛物线223y x x =--+与x 轴交点为 ，与y 轴交点为 . 3、二次函数2y ax =的图象过点（－1，2），则它的解析式是 ， 当x 时，y 随x 的增大而增大.4．抛物线2)1(62-+=x y 可由抛物线262-=x y 向 平移 个单位得到．5．抛物线342++=x x y 在x 轴上截得的线段长度是 ．6．抛物线()4222-++=m x x y 的图象经过原点，则=m ． 7．抛物线m x x y +-=2，若其顶点在x 轴上，则=m ．8. 如果抛物线c bx ax y ++=2的对称轴是x ＝－2，且开口方向与形状与抛物线相同，又过原点，那么a ＝ ，b ＝ ，c ＝ .9、二次函数2y x bx c =++的图象如下左图所示，则对称轴是 ，当函数值0y <时， 对应x 的取值范围是 .10、已知二次函数21(0)y ax bx c a =++≠与一次函数2(0)y kx m k =+≠的图象相交于点A （－2，4）和B （8，2），如上右图所示，则能使1y 2y >成立的x 的取值范围 . 二、选择题：11.下列各式中,y 是x 的二次函数的是 ( )A ．21xy x += B ． 220x y +-= C ． 22y ax -=- D ．2210x y -+=223x y -=12．在同一坐标系中，作22y x =、22y x =-、212y x =的图象，它们共同特点是 ( ) A ． 都是关于x 轴对称，抛物线开口向上 B ．都是关于y 轴对称，抛物线开口向下 B ． 都是关于原点对称，顶点都是原点 D ．都是关于y 轴对称，顶点都是原点13．抛物线122+--=m mx x y 的图象过原点，则m 为（ ）A ．0B ．1C ．－1D ．±114．把二次函数122--=x x y 配方成为（ ）A ．2)1(-=x y B ． 2)1(2--=x y C ．1)1(2++=x yD ．2)1(2-+=x y15．已知原点是抛物线2(1)y m x =+的最高点，则m 的范围是( )A ． 1-<mB ． 1<mC ． 1->mD ． 2->m 16、函数221y x x =--的图象经过点( )A 、（－1，1）B 、（1 ，1）C 、（0 , 1）D 、(1 , 0 )17、抛物线23y x =向右平移1个单位，再向下平移2个单位，所得到的抛物线是( )A 、23(1)2y x =-- B 、23(1)2y x =+-C 、23(1)2y x =++ D 、23(1)2y x =-+18、已知h 关于t 的函数关系式212h gt =（ g 为正常数，t 为时间）如图，则函数图象为 ( )19、下列四个函数中, 图象的顶点在y 轴上的函数是（ ）A 、232y x x =-+ B 、25y x =- C 、22y x x =-+D 、244y x x =-+20、已知二次函数2y ax bx c =++，若0a <，0c >，那么它的图象大致是（ ）21、根据所给条件求抛物线的解析式：（1）、抛物线过点（0，2）、（1，1）、（3，5） （2）、抛物线关于y 轴对称，且过点（1，－2）和（－2，0）22．已知二次函数c bx x y ++=2的图像经过A （0，1），B （2，－1）两点.(1)求b 和c 的值； (2）试判断点P （－1，2）是否在此函数图像上？23、某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米1000元，设矩形一边长为x 米，面积为S 平方米.（1） 求出S 与x 之间的函数关系式，并确定自变量x 的取值范围； （2） 请你设计一个方案，使获得的设计费最多，并求出这个费用.24、某工厂现有80台机器，每台机器平均每天生产384•件产品，现准备增加一批同类机器以提高生产总量，在试生产中发现，•由于其他生产条件没变，因此每增加一台机器，每台机器平均每天将少生产4件产品．（1）如果增加x 台机器，每天的生产总量为y 件，请你写出y 与x 之间的关系式； （2）增加多少台机器，可以使每天的生产总量最大？最大生产总量是多少？25、如图，有一个抛物线的拱形立交桥，•这个桥拱的最大高度为16m ，跨度为40m ，现把它放在如图所示的直角坐标系里，•若要在离跨度中心点M5m 处垂直竖一根铁柱支撑这个拱顶，铁柱应取多长？24、如图，抛物线n x x y ++-=52经过点A(1，0)，与y 轴交于点B.⑴求抛物线的解析式；⑵P 是y 轴正半轴上一点，且△PAB 是以AB 为腰的等腰三角形，试求P 点坐标.二次函数单元检测 （B ） 姓名_______一、新课标基础训练1．下列二次函数的图象的开口大小，从大到小排列依次是（ ） ①y=13x 2；②y=23x 2+3；③y=-12（x-3）2-2；④y=-32x 2+5x-1． A ．④②③① B ．①③②④ C ．④②①③ D ．②③①④2．将二次函数y=3（x+2）2-4的图象向右平移3个单位，再向上平移1个单位，所得的图象的函数关系式（ ）A ．y=3（x+5）2-5；B ．y=3（x-1）2-5；C ．y=3（x-1）2-3；D ．y=3（x+5）2-33．将进货单价为70元的某种商品按零售价100元一个售出时，每天能卖出20个，•若这种商品的零售价在一定范围内每降价1元，其日销量就增加1个，为了获取最大利润，则应降价（ ） A ．5元 B ．10元 C ．15元 D ．20元4．若直线y=ax+b （ab ≠0）不过第三象限，则抛物线y=ax 2+bx 的顶点所在的象限是（ ） A ．一 B ．二 C ．三 D ．四5．已知二次函数y=x 2+x+m ，当x 取任意实数时，都有y>0，则m 的取值范围是（ ） A ．m ≥14 B ．m>14 C ．m ≤14 D ．m<146．二次函数y=mx 2-4x+1有最小值-3，则m 等于（ ） A ．1 B ．-1 C ．±1 D ．±12二、新课标能力训练7．如图，用2m 长的木条，做一个有横档的矩形窗子，为使透进的光线最多，那么这个窗子的面积应为_______m 2．8．如图，有一个抛物线型拱桥，其最大高度为16m ， •跨度为•40m ，• 现把它的示意图放在平面直角坐标系 中••，••则此抛物线的函数关系式为__________．9、已知函数4m m2x )2m (y -++=是关于x 的二次函数，求：(1)满足条件的m 值；(2)m 为何值时，抛物线有最低点?求出这个最低点．这时当x 为何值时，y 随x 的增大而增大? （3）m 为何值时，函数有最大值?最大值是什么?这时当x 为何值时，y 随x 的增大而减小?10、观察表格：23（1）求a ，b ，c 的值，并在表内空格处填入正确的数．（2）画出函数y=ax 2+bx+c 的图象，由图象确定，当x 取什么实数时，ax 2+bx+c>0．11、如图(2)，已知平行四边形ABCD 的周长为8cm ，∠B ＝30。

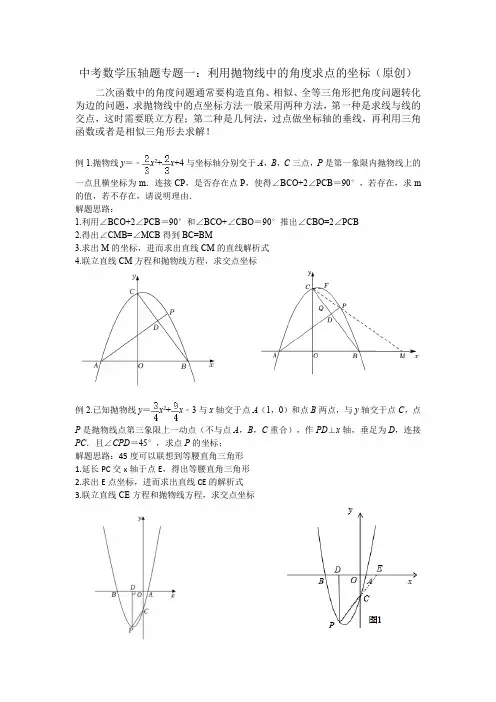
中考数学压轴题专题一：利用抛物线中的角度求点的坐标（原创）二次函数中的角度问题通常要构造直角、相似、全等三角形把角度问题转化为边的问题，求抛物线中的点坐标方法一般采用两种方法，第一种是求线与线的交点，这时需要联立方程；第二种是几何法，过点做坐标轴的垂线，再利用三角函数或者是相似三角形去求解！例1.抛物线y＝﹣x2+x+4与坐标轴分别交于A，B，C三点，P是第一象限内抛物线上的一点且横坐标为m．连接CP，是否存在点P，使得∠BCO+2∠PCB＝90°，若存在，求m 的值，若不存在，请说明理由．解题思路：1.利用∠BCO+2∠PCB＝90°和∠BCO+∠CBO＝90°推出∠CBO=2∠PCB2.得出∠CMB=∠MCB得到BC=BM3.求出M的坐标，进而求出直线CM的直线解析式4.联立直线CM方程和抛物线方程，求交点坐标例2.已知抛物线y＝x2+x﹣3与x轴交于点A（1，0）和点B两点，与y轴交于点C，点P是抛物线点第三象限上一动点（不与点A，B，C重合），作PD⊥x轴，垂足为D，连接PC．且∠CPD＝45°，求点P的坐标；解题思路：45度可以联想到等腰直角三角形1.延长PC交x轴于点E，得出等腰直角三角形2.求出E点坐标，进而求出直线CE的解析式3.联立直线CE方程和抛物线方程，求交点坐标例3.抛物线y＝x2﹣4x与直线y＝x交于原点O和点B，与x轴交于另一点A，顶点为D．连接OD，P为x轴上的动点，当tan∠PDO＝时，求点P的坐标；解题思路1.分情况讨论，分P在原点的左右侧进行讨论2.P在原点右侧比较简单3.P在原点左侧要结合P在原点右侧的情况，可以得出等腰△OGD，求出G点坐标4.利用GD的直线直线方程或相似三角形求出P点坐标例4.已知抛物线y＝﹣x2﹣6x﹣5与x轴交于点A（﹣1，0）和B（﹣5，0），与y轴交于点C，顶点为P，点N在抛物线对称轴上且位于x轴下方，连AN交抛物线于M，连AC、CM．tan ∠ACM＝2时，求M点的横坐标；解题思路：1.构造一线三垂直利用相似求出点F坐标2.求出直线CF的解析式3.联立直线CF方程和抛物线方程，求交点坐标（求交点可以利用韦达定理）例5.在平面直角坐标系中，抛物线y＝x2﹣2x﹣3与x轴交于点A（﹣1，0）和点B，与y轴交于点C，顶点D的坐标为（1，﹣4）．点P在抛物线上且满足∠PCB＝∠CBD，求点P 的坐标；解题思路：1.分情况讨论，P在直线BC的上方和下方2.P在直线BC上方，利用∠PCB＝∠CBD得出PC平行BD，利用斜率相等求出直线PC解析式联立PC方程和抛物线方程，求交点坐标3.P在直线BC的下方，∠PCB＝∠CBD得出等腰三角形CFB，4.可以得出△BCD为直角三角形，，推出F为BD的中点5.求出直线CF的方程，再联立抛物线方程求出交点坐标例6.如图，在平面直角坐标系中，直线y＝﹣x+2与x轴交于点A，与y轴交于点B，抛物线经过A，B两点且与x轴的负半轴交于点C．点D为直线AB上方抛物线上的一个动点，当∠ABD＝2∠BAC时，求点D的坐标；解题思路：1.过点B做OA平行线2.∠ABD＝2∠BAC得出∠ABD=2∠EBA，得出∠FBD=∠BAC3.利用tan∠FBD=tan∠BAC求出D点做坐标例7.已知抛物线y＝（x﹣1）2，D为抛物线的顶点，直线y＝kx+4﹣k与抛物线交于P、Q两点．求证：∠PDQ＝90°；解题思路思路1.构造一线三垂直思路2.证明直线PD和直线DQ斜率之积为-1思路3.利用勾股定理逆定理证明例8.如图，抛物线y＝x2﹣2x﹣6与x轴交于A、B两点，与y轴交于点C，其对称轴交抛物线于点D，交x轴于点E，已知OB＝OC＝6．连接BD，F为抛物线上一动点，当∠F AB ＝∠EDB时，求点F的坐标；解题思路：1.分点F在x轴下方时和上方时进行分类讨论2.AB在x轴上，利用tan∠FAB＝tan∠EDB去求最简便例9.如图，已知抛物线C1：交x轴于点A，B，交y轴于点C．在抛物线上存在点D，使，求点D的坐标．解题思路：1.分D在BC上方和下方讨论2.找到特殊点发现tan∠OBC=3.利用角平分线的性质去求F坐标4.求联立直线BF和抛物线方程求D点坐标例10，平面直角坐标系中，已知抛物线y＝﹣x2+5x﹣4与x轴交于点A，B两点（点A在点B左边），与y轴交于点C．D为抛物线x轴上方一点，连接BD，若∠DBA+∠ACB＝90°，求点D的坐标；解题思路：利用tan∠ACB=tan∠FDB去求解例11.已知抛物线y＝﹣x2﹣x+2，BC平分∠PCO时，求点P的横坐标．解题思路：1.角平分线联想到角平分线＋平行线得到等腰三角形2.利用PE=PC去求解（两点之间的距离公式）例12.抛物线y＝x2﹣1，M（﹣4，3），N是抛物线上两点，N在对称轴右侧，且tan∠OMN ＝，求N点坐标；解题思路：构造一线三垂直课后练习1.在平面直角坐标系中，已知抛物线y＝ax2+4ax+4a﹣6（a＞0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为点D．直线DC交x轴于点E，tan∠AED＝，求a的值和CE的长；2.已知抛物线y＝（x+1）2+1，点A（﹣1，2）在抛物线的对称轴上。

抛物线试题及答案初三
一、选择题
1. 抛物线y=ax^2+bx+c的顶点坐标是（）
A. (-b/2a, f(-b/2a))
B. (-b/2a, f(-b/2a))
C. (-b/2a, f(-b/2a))
D. (-b/2a, f(-b/2a))
答案：A
2. 抛物线y=x^2-4x+3与x轴的交点坐标是（）
A. (1,0)和(3,0)
B. (-1,0)和(3,0)
C. (1,0)和(-3,0)
D. (-1,0)和(-3,0)
答案：A
二、填空题
3. 若抛物线y=ax^2+bx+c的对称轴为直线x=2，则b的值为______。

答案：-4a
4. 抛物线y=-2x^2+4x+1的顶点坐标为（1,3），则a=______。

答案：-2
三、解答题
5. 已知抛物线y=x^2-6x+9，求抛物线的顶点坐标。

答案：顶点坐标为(3,0)。

6. 抛物线y=2x^2-4x+1与直线y=x+2相交于A、B两点，求A、B两点
的坐标。

答案：A(1,3)，B(2,4)。

四、综合题
7. 抛物线y=x^2-2x-3与x轴相交于点C、D，与y轴相交于点E，求
三角形CDE的面积。

答案：三角形CDE的面积为9。

8. 已知抛物线y=ax^2+bx+c经过点(1,0)和(-1,0)，且顶点在x轴上，求抛物线的解析式。

答案：抛物线的解析式为y=x^2。

在中考数学中，抛物线是一个常见的考点，经常以压轴题的形式出现。

以下是一个关于抛物线的中考压轴题的示例：题目：已知抛物线y=ax^2+bx+c(a,b,c是常数，a≠0)经过点(-1,-1)，(0,1)，当x=-2时，与其对应的函数值y>1。

1. 请你求出abc的值，并判断抛物线的开口方向。

2. 设直线y=kx+d(k≠0)经过点(1,-1)，且与抛物线的对称轴平行。

请你求出该直线的解析式。

3. 设E(m,n)是抛物线y=ax^2+bx+c上的一个动点，且满足∠APE=90°，请你求出m的值。

解析：1. 根据题目条件，抛物线经过点(-1,-1)，(0,1)，可得到方程：$a-b+c=-1$ ①$c=1$ ②将x=-2，y>1代入解析式得：$4a-2b+1>1$化简得：$2a-b>0$ ③由①②③解得：$a>0$$b>0$$c=1$所以，abc=1。

由于a>0，抛物线开口向上。

2. 由题意知：直线y=kx+d经过点(1,-1)，则有：k+d=-1 ④又因为直线与对称轴平行，所以其斜率等于对称轴的斜率，即：k=-b/2a=-1/2 ⑤由④⑤解得：d=-3/2所以，直线的解析式为：y=-x/2-3/2。

3. 根据题意知：E(m,n)在抛物线上，则有：$n=am^2+bm+c$ ⑥由于∠APE=90°，所以AE与PE垂直。

根据两直线垂直的条件：斜率之积等于-1。

即：$(m-1)/(n+1)=-1$ ⑦由⑥⑦解得：m=0或m=-2综上所述，m的值为0或-2。

中考压轴题专项训练1——抛物线专题考点分析：命题预测：函数是数形结合的重要体现，是每年中考的必考内容，函数的概念主要用选择、填空的形式考查自变量的取值范围，及自变量与因变量的变化图像、平面直角坐标系等，一般占2%左右．一次函数与一次方程有紧密地联系，是中考必考内容，一般以填空、选择、解答题及综合题的形式考查，占5%左右．反比例函数的图像和性质的考查常以客观题形式出现，要关注反比例函数与实际问题的联系，突出应用价值，3—6分；二次函数是初中数学的一个十分重要的内容，是中考的热点，多以压轴题出现在试卷中．要求：能通过对实际问题情景分析确定二次函数的表达式，并体会二次函数的意义；会用描点法画二次函数图像，能丛图像上分析二次函数的性质；会根据公式确定图像的顶点、开口方向和对称轴，并能解决复杂的图形综合问题。

二次函数常考点汇总：1. 两点间的距离公式：22)()(AB B A B A x x y y -+-=2. 中点坐标公式：已知A ),(A A y x ，B ),(B B y x ，则线段AB 的中点C 的坐标为⎪⎭⎫⎝⎛++2,2B A B A y y x x 。

3. 在平面直角坐标系中求面积的方法：公式法、割补法（做铅垂高或水平宽） 4. 几何分析法：特别是构造“平行四边形”、“梯形”、“相似三角形”、“直角三角形”、“等腰三角形”等图形时，利用几何分析法能给解题带来方便。

例题精讲：1.如图，直线y＝﹣x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y＝﹣x2+bx+c 经过点A，B．（1）求点B的坐标和抛物线的解析式；（2）M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点”．请直接写出使得M，P，N三点成为“共谐点”的m的值．2．如图①，抛物线y＝﹣x2+（a+1）x﹣a与x轴交于A，B两点（点A位于点B的左侧），与y轴交于点C．已知△ABC的面积是6．（1）求a的值；（2）求△ABC外接圆圆心的坐标；（3）如图②，P是抛物线上一点，Q为射线CA上一点，且P、Q两点均在第三象限内，Q、A是位于直线BP同侧的不同两点，若点P到x轴的距离为d，△QPB的面积为2d，且∠P AQ＝∠AQB，求点Q的坐标．3.已知，在平面直角坐标系xoy 中，点A 的坐标为（0，2），点P （m ，n ）是抛物线2114y x =+上的一个动点．（1）①如图1，过动点P 作PB ⊥x 轴，垂足为B ，连接PA ，求证：PA=PB ； ②如图2，设C 的坐标为（2，5），连接PC ，AP+PC 是否存在最小值？如果存在，求点P 的坐标；如果不存在，请说明理由；（2）如图3，过动点P 和原点O 作直线交抛物线于另一点D ，若AP=2AD ，求直线OP 的解析式．4.【变式】在平面直角坐标系xOy 中，抛物线21124y x =+的顶点为M ，直线2y x =，点()0P n ，为x 轴上的一个动点，过点P 作x 轴的垂线分别交抛物线21124y x =+和直线2y x =于点A ，点B.（1）直接写出A ，B 两点的坐标（用含n 的代数式表示）；⑵设线段AB 的长为d ，求d 关于n 的函数关系式及d 的最小值，并直接写出此时线段OB 与线段PM 的位置关系和数量关系；(3) 已知二次函数2y ax bx c =++（a ，b ，c 为整数且0a ≠），对一切实数x 恒有x ≤y ≤2124x +，求a ，b ，c 的值.5．如图，已知二次函数()21y x m x m =+--（其中0＜m ＜1）的图像与x 轴交于A 、B 两点（点A在点B 的左侧），与y 轴交于点C ，对称轴为直线l ．设P 为对称轴l 上的点，连接P A 、PC ，P A =PC ． （1）∠ABC 的度数为 °；（2）求P 点坐标（用含m 的代数式表示）；（3）在坐标轴上是否存在点Q （与原点O 不重合），使得以Q 、B 、C 为顶点的三角形与△P AC 相似，且线段PQ 的长度最小？如果存在，求出所有满足条件的点Q 的坐标；如果不存在，请说明理由．6.（本题满分10分）如图，二次函数2y x bx c =++的图像与x 轴交于A 、B 两点，与y 轴交于点C ，C OB =O ．点D 在函数图像上，CD//x 轴，且CD 2=，直线l 是抛物线的对称轴，E 是抛物线的顶点．（1）求b 、c 的值；（2）如图①，连接BE ，线段C O 上的点F 关于直线l 的对称点F '恰好在线段BE 上，求点F 的坐标； （3）如图②，动点P 在线段OB 上，过点P 作x 轴的垂线分别与C B 交于点M ，与抛物线交于点N ．试问：抛物线上是否存在点Q ，使得Q ∆P N 与∆APM 的面积相等，且线段Q N 的长度最小？如果存在，求出点Q 的坐标；如果不存在，说明理由．7．（8分）如图，已知抛物线y=x2﹣4与x轴交于点A，B（点A位于点B的左侧），C 为顶点，直线y=x+m经过点A，与y轴交于点D．（1）求线段AD的长；（2）平移该抛物线得到一条新拋物线，设新抛物线的顶点为C′．若新抛物线经过点D，并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD，求新抛物线对应的函数表达式．答案解析1.【解答】解：（1）∵y＝﹣x+c与x轴交于点A（3，0），与y轴交于点B，∴0＝﹣2+c，解得c＝2，∴B（0，2），∵抛物线y＝﹣x2+bx+c经过点A，B，∴，解得，∴抛物线解析式为y＝﹣x2+x+2；（2）①由（1）可知直线解析式为y＝﹣x+2，∵M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N，∴P（m，﹣m+2），N（m，﹣m2+m+2），∴PM＝﹣m+2，AM＝3﹣m，PN＝﹣m2+m+2﹣（﹣m+2）＝﹣m2+4m，∵△BPN和△APM相似，且∠BPN＝∠APM，∴∠BNP＝∠AMP＝90°或∠NBP＝∠AMP＝90°，当∠BNP＝90°时，则有BN⊥MN，∴N点的纵坐标为2，∴﹣m2+m+2＝2，解得m＝0（舍去）或m＝2.5，∴M（2.5，0）；当∠NBP＝90°时，过点N作NC⊥y轴于点C，则∠NBC+∠BNC＝90°，NC＝m，BC＝﹣m2+m+2﹣2＝﹣m2+m，∵∠NBP＝90°，∴∠NBC+∠ABO＝90°，∴∠ABO＝∠BNC，∴Rt△NCB∽Rt△BOA，∴＝，∴＝，解得m＝0（舍去）或m＝，∴M（，0）；综上可知当以B，P，N为顶点的三角形与△APM相似时，点M的坐标为（2.5，0）或（，0）；②由①可知M（m，0），P（m，﹣m+2），N（m，﹣m2+m+2），∵M，P，N三点为“共谐点”，∴有P为线段MN的中点、M为线段PN的中点或N为线段PM的中点，当P为线段MN的中点时，则有2（﹣m+2）＝﹣m2+m+2，解得m＝3（三点重合，舍去）或m＝；当M为线段PN的中点时，则有﹣m+2+（﹣m2+m+2）＝0，解得m＝3（舍去）或m＝﹣1；当N为线段PM的中点时，则有﹣m+2＝2（﹣m2+m+2），解得m＝3（舍去）或m＝﹣；综上可知当M，P，N三点成为“共谐点”时m的值为或﹣1或﹣．2．【解答】解：（1）∵y＝﹣x2+（a+1）x﹣a令y＝0，即﹣x2+（a+1）x﹣a＝0解得x1＝a，x2＝1由图象知：a＜0∴A（a，0），B（1，0）∵s△ABC＝6∴解得：a＝﹣3，（a＝4舍去）（2）设直线AC：y＝kx+b，由A（﹣3，0），C（0，3），可得﹣3k+b＝0，且b＝3∴k＝1即直线AC：y＝x+3，A、C的中点D坐标为（﹣，）∴线段AC的垂直平分线解析式为：y＝﹣x，线段AB的垂直平分线为x＝﹣1代入y＝﹣x，解得：y＝1∴△ABC外接圆圆心的坐标（﹣1，1）（3）作PM⊥x轴，则＝∵∴A、Q到PB的距离相等，∴AQ∥PB设直线PB解析式为：y＝x+b∵直线经过点B（1，0）所以：直线PB的解析式为y＝x﹣1联立解得：∴点P坐标为（﹣4，﹣5）又∵∠P AQ＝∠AQB可得：△PBQ≌△ABP（AAS）∴PQ＝AB＝4设Q（m，m+3）由PQ＝4得：解得：m＝﹣4，m＝﹣8（当m＝﹣8时，∠P AQ≠∠AQB，故应舍去）∴Q坐标为（﹣4，﹣1）3.【解答】解：（1）①设P（m，n）∴n=m2+1，∵PB⊥x 轴，∴PB=m2+1，∵A（0，2）∴AP==m2+1，∴PB=PA；②过点P作PB⊥x轴于B，由（1）得PA=PB，所以要使AP+CP最小，只需当BP+CP最小，因此当C，P，B共线时取得，此时点P的横坐标等于点C（2，5）的横坐标，所以点P的坐标为（2，2），（2）如图，作DE⊥x轴于E，作PF⊥x轴于F，由（1）得：DA=DE，PA=PF∵PA=2DA，∴PF=2DE，∵△ODE∽△OPF，∴==，设P（m，m2+1），则D（m，m2+）∵点D在抛物线y=x2+1上，∴m2+=（m）2+1，解得m=±2，∴P 1（，3），直线OP 的解析式为y=x ， P 2（﹣，3）直线OP 的解析式为y=﹣x ， 综上所求，所求直线OP 的解析式为y=x 或y=﹣x ．4.【解答】解：(1)21(2)4A n n +，，()B n n ，. (2) d =AB=A B y y -=2124n n -+.∴ d =2112()48n -+=2112()48n -+.∴ 当14n =时，d 取得最小值18. 当d 取最小值时，线段OB 与线段PM 的位置 关系和数量关系是OB ⊥PM 且OB=PM. (如图)(3) ∵对一切实数x 恒有 x ≤y ≤2124x +， ∴对一切实数x ，x ≤2ax bx c ++≤2124x +都成立. (0a ≠) ①当0x =时，①式化为 0≤c ≤14.xy111APBMO∴整数c 的值为0.此时，对一切实数x ，x ≤2ax bx +≤2124x +都成立.(0a ≠) 即 222,12.4x ax bx ax bx x ⎧≤+⎪⎨+≤+⎪⎩ 对一切实数x 均成立. 由②得 ()21ax b x +-≥0 (0a ≠) 对一切实数x 均成立.∴()210,10.a b >⎧⎪⎨∆=-≤⎪⎩ 由⑤得整数b 的值为1.此时由③式得，2ax x +≤2124x +对一切实数x 均成立. (0a ≠) 即21(2)4a x x --+≥0对一切实数x 均成立. (0a ≠) 当a=2时，此不等式化为14x -+≥0，不满足对一切实数x 均成立.当a≠2时，∵ 21(2)4a x x --+≥0对一切实数x 均成立，(0a ≠)∴2220,1(1)4(2)0.4a a ->⎧⎪⎨∆=--⨯-⨯≤⎪⎩∴由④，⑥，⑦得 0 <a ≤1.∴整数a 的值为1.∴整数a ，b ，c 的值分别为1a =，1b =，0c =.5．【解答】解：（1）45．理由如下：令x =0，则y =-m ，C 点坐标为（0，-m ）．令y =0，则()210x m x m +--=，解得11x =-，2x m =． ∵0＜m ＜1，点A 在点B 的左侧，∴B 点坐标为（m ，0）．∴OB =OC =m ．∵∠BOC ＝90°，∴△BOC 是等腰直角三角形，∠OBC ＝45°． （2）如图①，作PD ⊥y 轴，垂足为D ，设l 与x 轴交于点E ，由题意得，抛物线的对称轴为12mx -+=． 设点P 坐标为（12m-+，n ）． ∵P A = PC ， ∴P A 2= PC 2，即AE 2+ PE 2=CD 2+ PD 2．∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭．解得12m n -=．∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭． ④⑤② ③ ⑥ ⑦图①图②（3）存在点Q 满足题意．∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭， ∴P A 2+ PC 2=AE 2+ PE 2+CD 2+ PD 2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． ∵AC 2=21m +，∴P A 2+ PC 2=AC 2．∴∠APC ＝90°． ∴△P AC 是等腰直角三角形．∵以Q 、B 、C 为顶点的三角形与△P AC 相似， ∴△QBC 是等腰直角三角形．∴由题意知满足条件的点Q 的坐标为（-m ，0）或（0，m ）． ①如图①，当Q 点的坐标为（-m ，0）时，若PQ 与x 轴垂直，则12m m -+=-，解得13m =，PQ =13． 若PQ 与x 轴不垂直， 则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭． ∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ ．＜13， ∴当25m =，即Q 点的坐标为（25-，0）时， PQ 的长度最小．②如图②，当Q 点的坐标为（0，m ）时，若PQ 与y 轴垂直，则12m m -=，解得13m =，PQ =13． 若PQ 与y 轴不垂直， 则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭． ∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ ．＜13， ∴当25m =，即Q 点的坐标为（0，25）时， PQ 的长度最小．综上：当Q 点坐标为（25-，0）或（0，25）时，PQ 的长度最小．6. 【解答】解：（1）.3)(03,20.0,c -),,0(,.2,12.1x 2CD x //2-=∴=-=++=∴∴=-==-∴=∴=c c c c c c B c C OC OB b bl CD ，舍去或解得）点坐标为（：抛物线对称轴为直线，轴，（2）设点F 坐标为（0，m ）.∵对称轴是直线,1:=x l ∴点F 关于直线l 的对称点’F 的坐标为（2，m ）. ∵直线BE 经过点B （3,0），E （1，-4），∴利用待定系数法可得直线BE 的表达式为y=2x-6. ∵点’F 在BE 上，∴m=2⨯2-6=-2,即点F 的坐标为（0，-2）. （3）存在点Q 满足题意。

初三抛物线试题及答案一、选择题1. 抛物线y = ax^2 + bx + c的顶点坐标是什么？A. (-b, c)B. (-b/2a, c - b^2/4a)C. (-b/2a, c + b^2/4a)D. (-b/a, c)答案：B2. 如果抛物线y = x^2 + 2x + 1的对称轴是直线x = -1，那么a的值是多少？A. 1B. -1C. 0D. 2答案：A3. 抛物线y = 2x^2 - 4x + 3的开口方向是：A. 向上B. 向下C. 水平D. 无法确定答案：A二、填空题4. 已知抛物线y = 3x^2 - 6x + 5，求抛物线的顶点坐标。

答案：顶点坐标为(1, 2)5. 抛物线y = -x^2 + 4x - 3的焦点坐标是什么？答案：焦点坐标为(2, -2)三、解答题6. 已知抛物线y = 2x^2 - 8x + 7，求其与x轴的交点。

答案：首先将方程化为标准形式：y = 2(x - 2)^2 - 1。

抛物线与x轴的交点即为y = 0时的x值。

解方程2(x - 2)^2 - 1 = 0，得到x= 2 ± √(1/2)，即x = 2 ± √2/2。

7. 已知抛物线y = ax^2 + bx + c经过点(1, 3)和(-1, 1)，求a和b 的值。

答案：将点(1, 3)和(-1, 1)代入方程，得到两个方程：3 = a(1)^2 + b(1) + c1 = a(-1)^2 + b(-1) + c解这两个方程，得到a + b + c = 3和a - b + c = 1。

相减消去c，得到2b = 2，即b = 1。

将b的值代入任一方程，得到a + 1 + c = 3，即a + c = 2。

由于c = 3 - a - b = 3 - a - 1 = 2 - a，代入得到a + 2 - a = 2，这是一个恒等式，说明a可以是任意实数。

四、应用题8. 一个物体从地面向上抛，其高度h（米）与时间t（秒）的关系为h = -5t^2 + 20t。

初三数学二次函数综合练习卷一、填空题：1、函数21(1)21my m x mx +=--+是抛物线，则m ＝ .2、抛物线223y x x =--+与x 轴交点为 ，与y 轴交点为 . 3、二次函数2y ax =的图象过点（－1，2），则它的解析式是 ， 当x 时，y 随x 的增大而增大.4．抛物线2)1(62-+=x y 可由抛物线262-=x y 向 平移 个单位得到．5．抛物线342++=x x y 在x 轴上截得的线段长度是 ．6．抛物线()4222-++=m x x y 的图象经过原点，则=m ． 7．抛物线m x x y +-=2，若其顶点在x 轴上，则=m ．8. 如果抛物线c bx ax y ++=2的对称轴是x ＝－2，且开口方向与形状与抛物线相同，又过原点，那么a ＝ ，b ＝ ，c ＝ .9、二次函数2y x bx c =++的图象如下左图所示，则对称轴是 ，当函数值0y <时， 对应x 的取值范围是 .10、已知二次函数21(0)y ax bx c a =++≠与一次函数2(0)y kx m k =+≠的图象相交于点A （－2，4）和B （8，2），如上右图所示，则能使1y 2y >成立的x 的取值范围 . 二、选择题：11.下列各式中,y 是x 的二次函数的是 ( )A ．21xy x +=B ． 220x y +-= C ． 22y ax -=- D ．2210x y -+=12．在同一坐标系中，作22y x =、22y x =-、212y x =的图象，它们共同特点是 ( ) A ． 都是关于x 轴对称，抛物线开口向上 B ．都是关于y 轴对称，抛物线开口向下223x y -=B ． 都是关于原点对称，顶点都是原点 D ．都是关于y 轴对称，顶点都是原点 13．抛物线122+--=m mx x y 的图象过原点，则m 为（ ）A ．0B ．1C ．－1D ．±114．把二次函数122--=x x y 配方成为（ ）A ．2)1(-=x y B ． 2)1(2--=x y C ．1)1(2++=x yD ．2)1(2-+=x y15．已知原点是抛物线2(1)y m x =+的最高点，则m 的范围是( )A ． 1-<mB ． 1<mC ． 1->mD ． 2->m 16、函数221y x x =--的图象经过点( )A 、（－1，1）B 、（1 ，1）C 、（0 , 1）D 、(1 , 0 )17、抛物线23y x =向右平移1个单位，再向下平移2个单位，所得到的抛物线是( ) A 、23(1)2y x =-- B 、23(1)2y x =+-C 、23(1)2y x =++ D 、23(1)2y x =-+ 18、已知h 关于t 的函数关系式212h gt =（ g 为正常数，t 为时间）如图，则函数图象为 ( )19、下列四个函数中, 图象的顶点在y 轴上的函数是（ ）A 、232y x x =-+ B 、25y x =- C 、22y x x=-+ D 、244y x x =-+20、已知二次函数2y ax bx c =++，若0a <，0c >，那么它的图象大致是（ ）21、根据所给条件求抛物线的解析式：（1）、抛物线过点（0，2）、（1，1）、（3，5） （2）、抛物线关于y 轴对称，且过点（1，－2）和（－2，0）22．已知二次函数c bx x y ++=2的图像经过A （0，1），B （2，－1）两点.(1)求b 和c 的值； (2）试判断点P （－1，2）是否在此函数图像上？23、某工厂现有80台机器，每台机器平均每天生产384•件产品，现准备增加一批同类机器以提高生产总量，在试生产中发现，•由于其他生产条件没变，因此每增加一台机器，每台机器平均每天将少生产4件产品．（1）如果增加x 台机器，每天的生产总量为y 件，请你写出y 与x 之间的关系式； （2）增加多少台机器，可以使每天的生产总量最大？最大生产总量是多少？25、如图，有一个抛物线的拱形立交桥，•这个桥拱的最大高度为16m ，跨度为40m ，现把它放在如图所示的直角坐标系里，•若要在离跨度中心点M5m 处垂直竖一根铁柱支撑这个拱顶，铁柱应取多长？24、如图，抛物线n x x y ++-=52经过点A(1，0)，与y 轴交于点B.⑴求抛物线的解析式；⑵P 是y 轴正半轴上一点，且△PAB 是以AB 为腰的等腰三角形，试求P 点坐标.二次函数单元检测 （B ） ___ ____一、新课标基础训练1．下列二次函数的图象的开口大小，从大到小排列依次是（ ） ①y=13x 2；②y=23x 2+3；③y=-12（x-3）2-2；④y=-32x 2+5x-1． A ．④②③① B ．①③②④ C ．④②①③ D ．②③①④2．将二次函数y=3（x+2）2-4的图象向右平移3个单位，再向上平移1个单位，所得的图象的函数关系式（ ）A ．y=3（x+5）2-5；B ．y=3（x-1）2-5；C ．y=3（x-1）2-3；D ．y=3（x+5）2-33．将进货单价为70元的某种商品按零售价100元一个售出时，每天能卖出20个，•若这种商品的零售价在一定范围内每降价1元，其日销量就增加1个，为了获取最大利润，则应降价（ ） A ．5元 B ．10元 C ．15元 D ．20元4．若直线y=ax+b （ab ≠0）不过第三象限，则抛物线y=ax 2+bx 的顶点所在的象限是（ ） A ．一 B ．二 C ．三 D ．四5．已知二次函数y=x 2+x+m ，当x 取任意实数时，都有y>0，则m 的取值范围是（ ） A ．m ≥14 B ．m>14 C ．m ≤14 D ．m<146．二次函数y=mx 2-4x+1有最小值-3，则m 等于（ ） A ．1 B ．-1 C ．±1 D ．±12二、新课标能力训练7．如图，用2m 长的木条，做一个有横档的矩形窗子，为使透进的光线最多，那么这个窗子的面积应为_______m 2．8．如图，有一个抛物线型拱桥，其最大高度为16m ， •跨度为•40m ，• 现把它的示意图放在平面直角坐标系 中••，••则此抛物线的函数关系式为__________．9、已知函数4m m2x )2m (y -++=是关于x 的二次函数，求：(1)满足条件的m 值；(2)m 为何值时，抛物线有最低点?求出这个最低点．这时当x 为何值时，y 随x 的增大而增大? （3）m 为何值时，函数有最大值?最大值是什么?这时当x 为何值时，y 随x 的增大而减小?10、观察表格：2（1）求a ，b ，c 的值，并在表内空格处填入正确的数．（2）画出函数y=ax 2+bx+c 的图象，由图象确定，当x 取什么实数时，ax 2+bx+c>0．11、如图(2)，已知平行四边形ABCD 的周长为8cm ，∠B ＝30。

初中抛物线试题及答案
一、选择题
1. 抛物线y = x^2 - 2x + 1的顶点坐标是（）。

A. (1, 0)
B. (1, -1)
C. (0, 1)
D. (0, -1)
答案：A
2. 如果抛物线y = ax^2 + bx + c的对称轴是直线x = -2，那么b的值是（）。

A. 4a
B. -4a
C. 2a
D. -2a
答案：B
二、填空题
1. 抛物线y = 2x^2 + 4x + 3的顶点坐标是（）。

答案：(-1, 1)
2. 抛物线y = -3x^2 + 6x - 2的对称轴方程是（）。

答案：x = 1
三、解答题
1. 已知抛物线y = x^2 - 6x + 9，求抛物线与x轴的交点坐标。

答案：抛物线与x轴的交点坐标为(3, 0)。

2. 抛物线y = 2x^2 - 4x + 3，求抛物线的顶点坐标和对称轴。

答案：抛物线的顶点坐标为(1, 1)，对称轴为直线x = 1。

四、应用题
1. 一个抛物线形的桥拱，其方程为y = -0.5x^2 + 4x + 1，桥拱的最高点离水面的高度是5米。

求桥拱的跨度。

答案：桥拱的跨度为8米。

2. 一个物体从地面以一定的初速度向上抛，其运动轨迹可以用抛物线y = -5x^2 + 20x + 2描述，其中x表示时间（秒），y表示高度（米）。

求物体达到最高点时的时间。

答案：物体达到最高点时的时间是2秒。

如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90，AC=BC，OA=1，OC=4，抛物线y=x2+bx+c 经过A，B两点，抛物线的顶点为D．（1）求b，c的值；（2）点E是直角三角形ABC斜边AB上一动点（点A、B除外），过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；（3）在（2）的条件下：①求以点E、B、F、D为顶点的四边形的面积；②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，说明理由．在平面直角坐标系中，已知抛物线经过A（-4，0），B（0，-4），C（2，0）三点．（1）求抛物线的解析式；（2）若点M为第三象限抛物线上一动点，点M的横坐标为m，△AMB的面积为S、求S关于m的函数关系式，并求出S的最大值．（3）若点P是抛物线上的动点，点Q是直线y=-x上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．(4)补充：在（3）的条件下，点P、Q、B、O为顶点的四边形能否成为梯形，若能，求出相应Q的坐标。

41直角坐标系XOY中，将直线y=kx沿y轴下移3个单位长度后恰好经点B（-3,0）及y 轴上的C点。

若抛物y=-x2+bx+c与x轴交于A点B点，（点A在点B的右侧），且过点C 。

（1）求直线BC及抛物线解析式（2）设抛物线的顶点为D，点P在抛物线的对称轴上，且∠APD=∠ACB，求p点坐标如图，已知抛物线y=x2+bx+c与x轴交于A，B两点（A点在B点左侧），与y轴交于点C（0，-3），对称轴是直线x=1，直线BC交抛物线对称轴交于点D.（1）求抛物线的函数表达式；（2）求直线BC的函数表达式；（3）点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P，Q两点，且点P在第三象限.①当线段PQ=3AB/4时，求tan∠CED的值；②当以点C，D，E为顶点的三角形是直角三角形时，请直接写出点P的坐标.温馨提示：考生可以根据第（3）问的题意，在图中补出图形，以便作答.第25题图第25题备用图直角坐标系XOY中，半径2√5的⊙C与x轴交于A（-1，0），B（3，0）且点C在X轴上方。

初三中考数学函数综合题含答案一、单选题1．已知点A （1，y 1），B （2，y 2）在抛物线y =（x +1）2+2上，则下列结论正确的是（ ）． A ．122y y >> B ．212y y >> C ．122y y >>D ．212y y >>2．抛物线y ＝14（x ﹣6）2+3的顶点坐标是（ ）A ．（6，﹣3）B ．（6，3）C ．（﹣6，3）D ．（﹣6，﹣3） 3．抛物线y =2（x -1）2-3的顶点坐标是（ ） A ．()1,3-- B ．()1,3- C ．()1,3- D ．()1,3 4．一次函数y ＝－2x ＋5的图像不经过的象限是（ ）A ．一B ．二C ．三D ．四 5．将函数y ＝2x 的图象向上平移4个单位后，下列各点在平移后的图象上的是（ ） A ．()1,5 B ．()0,4 C ．()1,3- D ．()2,3- 6．在直角坐标系的x 轴的负半轴上，则点P 坐标为（ ）A ．()4,0-B ．()0,4C ．()0,3-D ．()1,0 7．直线7y x =--一定不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限8．下列各点中，在反比例函数2y x=-图象上的是-（ ）A ．(21)，B ．233⎛⎫⎪⎝⎭， C ．(21)--， D ．(12)-，9．已知点()11,A x y ，()22,B x y 在直线()0y kx b k =+≠上，当12x x <时，12y y >，且0kb <，则直线()0y kx b k =+≠在平面直角坐标系中的图象大致是（ ）A ．B ．C ．D ．10．下列一次函数中，y 随x 的增大而减小的是（ ） A ．y ＝x ﹣3 B ．y ＝1﹣x C ．y ＝2x D ．y ＝3x +2 11．下列二次函数中，对称轴是直线1x =的是（ ）A ．21y x =+B ．()221y x =+C ．()21y x =-+D ．()231y x =--12．反比例函数y ＝2x的图象位于（ ）A ．第一、三象限B ．第二、三象限C ．第一、二象限D ．第二、四象限13．如图，△ABC 中，点B ，C 是x 轴上的点，且A （3，2），以原点O 为位似中心，作△ABC 的位似图形△A ′B ′C ′，且△ABC 与A ′B ′C ′的相似比是1：2，则点A ′的坐标是（ ）A ．（﹣6，﹣4）B ．（﹣1.5，﹣1）C ．（1.5，1）或（﹣1.5，﹣1）D ．（6，4）或（﹣6，﹣4）14．已知点P （a ，a ﹣1）在平面直角坐标系的第四象限，则a 的取值范围在数轴上可表示为（ ） A ．B ．C ．D ．15．要得到抛物线()2321y x =-++可以将抛物线232y x =-+（ ） A ．先向右平移2个单位，再向上平移1个单位 B ．先向右平移2个单位，再向下平移1个单位C ．先向左平移2个单位，再向上平移1个单位D ．先向左平移2个单位，再向下平移1个单位二、填空题16．已知点(),P m n 在一次函数1y x =+的图象上，则n m -=______．17．已知某函数图像过点（－1，1），写出一个符合条件的函数表达式：______．18．将一次函数123=+y x 向上平移5个单位长度后得到直线AB ，则平移后直线AB 对应的函数表达式为______．19．将抛物线22(3)y x m =-+向右平移3个单位，再向上平移1个单位后恰好经过点(2,3)，则m 值是 __．20．若抛物线y =x 2+bx +经过点A （0，5），B （4，5），则其对称轴是直线______三、解答题21．已知抛物线y ＝－（x －m ）2＋1与x 轴的交点为A ，B （B 在A 的右边），与y 轴的交点为C ．(1)写出m ＝1时与抛物线有关的三个正确结论．(2)当点B 在原点的右边，点C 在原点的下方时，是否存在△BOC 为等腰三角形的情形？若存在，求出m 的值；若不存在，请说明理由． (3)请你提出两个对任意的m 值都能成立的正确命题．22．在平面直角坐标系xOy 中，点()11,A x y ，()22,B x y 在抛物线()2210y ax ax a =-+>上，其中12x x < (1)求抛物线的对称轴；(2)若122x x a +=-，比较1y 与2y 的大小关系，并说明理由．23．如图，在平面直角坐标系中，二次函数243y ax x =+-图象的顶点是A ，与x 轴交于B ，C 两点，与y 轴交于点D ．点B 的坐标是()1,0．(1)求A ，C 两点的坐标，并根据图象直接写出当0y >时x 的取值范围；(2)将图象向上平移m 个单位后，二次函数图象与x 轴交于E ，F 两点，若6EF =，求m 的值．24．一抛物线以()1,9-为顶点，且经过x 轴上一点()4,0-，求该抛物线解析式及抛物线与y 轴交点坐标．25．已知抛物线y ＝（x ﹣1）2+k 与y 轴相交于点A (0，﹣3)，点P 为抛物线上的一点． (1)求此抛物线的解析式；(2)若点P 的横坐标为2，则点P 到x 轴的距离为 ．【参考答案】一、单选题 1．D 2．B 3．C 4．C 5．B 6．A 7．A 8．D 9．C 10．B 11．D 12．A 13．D 14．C 15．D 二、填空题 16．117．y ＝-x （答案不唯一） 18．y =13x +719．-3020．2x = 三、解答题21．(1)抛物线的对称轴为直线x =1，抛物线与x 轴的两个交点为（0，0），（2，0），抛物线开口向下 (2)存在，2(3)无论m 为何值，函数的始终有最大值1；无论m 为何值，函数始终与x 轴有两个不同的交点 【解析】 【分析】（1）当m =1时，y =-（x -1）2+1，根据()2y a x h k =-+的性质写出三个结论即可； （2）求得C （0，1-m 2），根据点B 在原点的右边，点C 在原点的下方，可得m ＞1，根据等腰三角形的性质可得1+m =m 2-1，解方程求解即可；（3）根据()2y a x h k =-+的性质，可知无论m 为何值，函数的始终有最大值1；无论m为何值，函数始终与x 轴有两个不同的交点． (1)解：当m =1时，y =-（x -1）2+1， ∴抛物线的对称轴为直线x =1， 令0y =，-（x -1）2+1=0， 解得120,2x x ==，抛物线与x 轴的两个交点为（0，0），（2，0）， 抛物线开口向下； (2)存在，理由如下： 令x =0，则y =1-m 2， ∴C （0，1-m 2），令y =0，则x =1+m 或x =m -1， ∴B （1+m ，0），∵点B 在原点的右边，点C 在原点的下方， ∴1+m ＞0，1-m 2＜0， ∴m ＞1，∵△BOC 为等腰三角形， ∴1+m =m 2-1，解得m =2或m =-1（舍）， ∴m =2； (3)无论m 为何值，函数始终有最大值1；无论m 为何值，函数始终与x 轴有两个不同的交点． 【点睛】本题考查了()2y a x h k =-+的性质，等腰三角形的性质，解一元二次方程，二次函数与坐标轴交点问题，掌握()2y a x h k =-+的性质是解题的关键． 22．(1)直线1x = (2)12y y >，见解析 【解析】 【分析】（1）将解析式整理成顶点式，直接写出对称轴；（2）方法一：利用作差法，将12y y -表示出来，再进行判断正负，据此判断大小即可；方法二：判断12,y y 距离对称轴的大小，根据函数增减性判断． (1)解：∵()222111y ax ax a x a =-+=--+， ∴抛物线的对称轴为直线1x = (2)方法一：()()221211222121y y ax ax ax ax -=-+--+，()()22122122ax ax ax ax =-+-，()()12122a x x x x =-+-， ()212a x x =--，∵0a >，12x x <， ∴120y y ->， 即12y y >，方法二：∵0a >，122x x a +=-， ∴122x x +<， ∴1212x x +<， 又∵抛物线对称轴是直线1x =，开口向上，且12x x <， ∴1211x x ->-， ∴12y y >． 【点睛】本题主要考查二次函数中系数的运用，以及比较函数值的大小，熟练掌握二次函数的基础运算是解题的关键．23．(1)(2,1)A ，(3,0)C ，当0y >时，13x <<． (2)8m = 【解析】 【分析】（1）利用待定系数法求出a ，再求出点C 的坐标即可解决问题．（2）由题意得抛物线的解析式为243y x x m =-+-+，设二次函数图象与x 轴交于1(E x ，0)，2(F x ，0)两点，则124x x +=，123x x m =-，由12|6|x x -=可得出答案．(1)解：把(1,0)B 代入243y ax x =+-，得043a =+-，解得1a =-，2243(2)1y x x x ∴=-+-=--+，)1(2,A ∴，对称轴为直线2x =，B ，C 关于2x =对称，(3,0)C ∴，∴当0y >时，13x <<．(2)解：抛物线向上平移m 个单位，可得抛物线的解析式为243y x x m =-+-+，设二次函数图象与x 轴交于1(E x ，0)，2(F x ，0)两点，则124x x +=，123x x m =-，12||6x x ∴-=，212()36x x ∴-=，21212()436x x x x ∴+-=，164(3)36m ∴-⨯-=，8m ∴=．【点睛】本题考查了抛物线与x 轴的交点，二次函数的性质和二次函数图象上点的坐标特征，解决问题的关键是能够把二次函数的一般形式化为顶点式． 24．y =﹣x 2-2x ＋8；抛物线与y 轴交点为()0,8 【解析】 【分析】知道顶点和抛物线上一点，可以用抛物线的顶点式求答； 【详解】解：设抛物线解析式为()2y a x h k =-+，依题意1h =-，9k =，将()4,0-代入()219y a x =++中，得099a =+，解得1a =-，∴抛物线解析式为()219y x =-++，即y =﹣x 2-2x ＋8； 令0x =，则8y =，∴抛物线与y 轴交点为()0,8． 【点睛】本题考查待定系数法求二次函数的解析式；在知道顶点坐标的时候，利用顶点式求二次函数解析式十分方便． 25．(1)223y x x =-- (2)3 【解析】 【分析】（1）把点A (0，﹣3)，代入抛物线解析式，即可求解；（2）根据抛物线()214y x =--的对称轴为直线1x =，可得点P 和点A (0，﹣3)关于直线1x =对称，从而得到点的纵坐标为-3，即可求解．(1)解：∵抛物线y ＝（x ﹣1）2+k 与y 轴相交于点A (0，﹣3)， ∴()2301k -=-+， 解得：4k =-，∴此抛物线的解析式为()221423y x x x =--=--； (2)解：∵抛物线()214y x =--的对称轴为直线1x =， ∴点P 和点A (0，﹣3)关于直线1x =对称， ∴点的纵坐标为-3， ∴点P 到x 轴的距离为3． 【点睛】本题主要考查了求二次函数的解析式，利用抛物线的对称性求函数值，熟练掌握利用待定系数法求函数解析式的步骤是解题的关键．。

抛物线习题精选精讲（1）抛物线——二次曲线的和谐线椭圆与双曲线都有两种定义方法，可抛物线只有一种：到一个定点和一条定直线的距离相等的所有点的集合.其离心率e=1，这使它既与椭圆、双曲线相依相伴，又鼎立在圆锥曲线之中.由于这个美好的1，既使它享尽和谐之美，又生出多少华丽的篇章.【例1】P 为抛物线px y 22=上任一点，F 为焦点，则以PF 为直径的圆与y 轴（ ）.A 相交 .B 相切 .C 相离 .D 位置由P 确定【解析】如图，抛物线的焦点为,02p F ⎛⎫⎪⎝⎭，准线是 :2pl x =-.作PH ⊥l 于H ，交y 轴于Q ，那么PF PH =， 且2pQH OF ==.作MN ⊥y 轴于N 则MN 是梯形PQOF 的中位线，()111222MN OF PQ PH PF =+==.故以PF 为直径的圆与y 轴相切，选B.【评注】相似的问题对于椭圆和双曲线来说，其结论则 分别是相离或相交的.（2）焦点弦——常考常新的亮点弦有关抛物线的试题，许多都与它的焦点弦有关.理解并掌握这个焦点弦的性质，对破解这些试题是大有帮助的.【例2】 过抛物线()022 p px y =的焦点F 作直线交抛物线于()()1122,,,A x y B x y 两点，求证： （1）12AB x x p =++ （2）pBF AF 211=+ 【证明】（1）如图设抛物线的准线为l ，作1AA l ⊥11111,2pA BB l B AA x ⊥==+于，则AF ， 122pBF BB x ==+.两式相加即得：12AB x x p =++（2）当AB ⊥x 轴时，有AF BF p ==，112AF BF p∴+=成立； 当AB 与x 轴不垂直时，设焦点弦AB 的方程为：2p y k x ⎛⎫=- ⎪⎝⎭.代入抛物线方程：l XY FA(x,y)11B(x,y)22A 1B 1l2222p k x px ⎛⎫-= ⎪⎝⎭.化简得：()()222222014p k x p k x k -++=∵方程（1）之二根为x 1，x 2，∴1224k x x ⋅=.()122111212121111112224x x p p pp p AF BF AA BB x x x x x x +++=+=+=+++++ ()()121222121222424x x p x x p p p p pp x x p x x ++++===+++++. 故不论弦AB 与x 轴是否垂直，恒有pBF AF 211=+成立.（3）切线——抛物线与函数有缘有关抛物线的许多试题，又与它的切线有关.理解并掌握抛物线的切线方程，是解题者不可或缺的基本功.【例3】证明：过抛物线22y px =上一点M （x 0，y 0）的切线方程是：y 0y=p （x+x 0）【证明】对方程22y px =两边取导数：22.py y p y y''⋅=∴=，切线的斜率 00x x p k y y ='==.由点斜式方程：()()20000001p y y x x y y px px y y -=-⇒=-+20021y px =，代入（）即得： y 0y=p （x+x 0）（4）定点与定值——抛物线埋在深处的宝藏抛物线中存在许多不不易发现，却容易为人疏忽的定点和定值.掌握它们，在解题中常会有意想不到的收获.例如：1.一动圆的圆心在抛物线x y 82=上，且动圆恒与直线02=+x 相切，则此动圆必过定点（ ）()()()().4,0.2,0.0,2.0,2A B C D -显然.本题是例1的翻版，该圆必过抛物线的焦点，选B. 2.抛物线22y px =的通径长为2p ；3.设抛物线22y px =过焦点的弦两端分别为()()1122,,,A x y B x y ，那么：212y y p =-以下再举一例【例4】设抛物线22y px =的焦点弦AB 在其准线上的射影是A 1B 1，证明：以A 1B 1为直径的圆必过一定点【分析】假定这条焦点弦就是抛物线的通径，那么A 1B 1=AB=2p ，而A 1B 1与AB 的距离为p ，可知该圆必过抛物线的焦点.由此我们猜想：一切这样的圆都过抛物线的焦点.以下我们对AB 的一般情形给于证明.【证明】如图设焦点两端分别为()()1122,,,A x y B x y ，那么：22121112.y y p CA CB y y p =-⇒⋅==设抛物线的准线交x 轴于C ，那么.CF p =2111111.90A FB CF CA CB A FB ∴∆=⋅∠=︒中故.这就说明：以A 1B 1为直径的圆必过该抛物线的焦点.● 通法 特法 妙法（1）解析法——为对称问题解困排难 解析几何是用代数的方法去研究几何，所以它能解决纯几何方法不易解决的几何问题（如对称问题等）. 【例5】（07.四川文科卷.10题）已知抛物线y=-x 2+3上存在关于直线x+y=0对称的相异两点A 、B ，则|AB|等于（ ）A.3B.4C.32D.42【分析】直线AB 必与直线x+y=0垂直，且线段 AB 的中点必在直线x+y=0上，因得解法如下.【解析】∵点A 、B 关于直线x+y=0对称，∴设直线AB的方程为：y x m =+. 由()223013y x mx x m y x =+⎧⇒++-=⎨=-+⎩设方程（1）之两根为x 1，x 2，则121x x +=-. 设AB 的中点为M （x 0，y 0），则120122x x x +==-.代入x+y=0：y 0=12.故有11,22M ⎛⎫- ⎪⎝⎭. 从而1m y x =-=.直线AB 的方程为：1y x =+.方程（1）成为：220x x +-=.解得：2,1x =-，从而1,2y =-，故得：A （-2，-1），B （1，2）.AB ∴=，选C.（2）几何法——为解析法添彩扬威虽然解析法使几何学得到长足的发展，但伴之而来的却是难以避免的繁杂计算，这又使得许多考生对解析几何习题望而生畏.针对这种现状，人们研究出多种使计算量大幅度减少的优秀方法，其中最有成效的就是几何法.【例6】（07.全国1卷.11题）抛物线24y x =的焦点为F ，准线为l ，经过FXYAB FA 1B 11M C XOY ABMl x y +=ÿ物线在x 轴上方的部分相交于点A ，AK l ⊥，垂足为K ，则AKF △的面积（ ）A ．4 B． C． D ．8 【解析】如图直线AFAFX=60°. △AFK 为正三角形.设准线l 交x 轴于M ，则2,FM p ==且∠KFM=60°，∴24,44AKFKF S ∆===选C. 【评注】（1）平面几何知识：边长为a 的正三角形的面积用公式2S ∆=计算. （2）本题如果用解析法，需先列方程组求点A 的坐标，，再计算正三角形的边长和面积.虽不是很难，但决没有如上的几何法简单.（3）定义法——追本求真的简单一着许多解析几何习题咋看起来很难.但如果返朴归真，用最原始的定义去做，反而特别简单. 【例7】（07.湖北卷.7题）双曲线22122:1(00)x y C a b a b-=>>，的左准线为l ，左焦点和右焦点分别为1F 和2F ；抛物线2C 的线为l ，焦点为21F C ；与2C 的一个交点为M ，则12112F F MF MF MF -等于（ ）A ．1-B ．1C ．12-D ．12【分析】 这道题如果用解析法去做，计算会特别繁杂，而平面几何知识又一时用不上，那么就从最原始的定义方面去寻找出路吧.如图，我们先做必要的准备工作：设双曲线的半 焦距c ，离心率为e ，作 MH l H ⊥于，令1122,MF r MF r ==.∵点M 在抛物线上，1112222,MF MF rMH MF r e MH MF r ∴=====故，这就是说：12||||MF MF 的实质是离心率e.其次，121||||F F MF 与离心率e 有什么关系？注意到： ()1212111122111F F e r r c e a e e MF r r r e +⋅⎛⎫====-=- ⎪⎝⎭. XY O F(1,0)AK60°Y2=2px L:x=-1M这样，最后的答案就自然浮出水面了：由于()12112||||11||||F F MF e e MF MF -=-+=-.∴选 A..（4）三角法——本身也是一种解析三角学蕴藏着丰富的解题资源.利用三角手段，可以比较容易地将异名异角的三角函数转化为同名同角的三角函数，然后根据各种三角关系实施“九九归一”——达到解题目的.因此，在解析几何解题中，恰当地引入三角资源，常可以摆脱困境，简化计算.【例8】（07.重庆文科.21题）如图，倾斜角为a 的直线经过抛物线x y 82=的焦点F ，且与抛物线交于A 、B 两点。

初三数学中考必考题1.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.（1） 求该抛物线的解析式；（2） 若该抛物线与x 轴的另一个交点为E.求四边形ABDE 的面积；（3） △AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛−−abac a b 44,22）2.如图，在Rt ABC △中，90A ∠=，6AB =，8AC =，D E ，分别是边AB AC ，的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ BC ⊥于Q ，过点Q 作QR BA ∥交AC 于R ，当点Q 与点C 重合时，点P 停止运动．设BQ x =，QR y =．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使PQR △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．3在△ABC 中，∠A ＝90°，AB ＝4，AC ＝3，M 是AB 上的动点（不与A ，B 重合），过M 点作MN ∥BC 交AC 于点N ．以MN 为直径作⊙O ，并在⊙O 内作内接矩形AMPN ．令AMABC D ER P H Q＝x ．（1）用含x 的代数式表示△ＭNP 的面积S ； （2）当x 为何值时，⊙O 与直线BC 相切？（3）在动点M 的运动过程中，记△ＭNP 与梯形BCNM 重合的面积为y ，试求y 关于x 的函数表达式，并求x 为何值时，y 的值最大，最大值是多少？4.如图1，在平面直角坐标系中，己知ΔAOB 是等边三角形，点A 的坐标是(0，4)，点B 在第一象限，点P 是x 轴上的一个动点，连结AP ，并把ΔAOP 绕着点A 按逆时针方向旋转.使边AO 与AB 重合.得到ΔABD.（1）求直线AB 的解析式；（2）当点P 运动到点（3，0）时，求此时DP 的长及点D 的坐标；（3）是否存在点P ，使ΔOPD 的面积等于43，若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由.5如图，菱形ABCD 的边长为2，BD=2，E 、F 分别是边AD ，CD 上的两个动点，且满足AE+CF=2.（1）求证：△BDE ≌△BCF ；（2）判断△BEF 的形状，并说明理由；（3）设△BEF 的面积为S ，求S 的取值范围.ABC MN图 3OABC MND 图 2OABMNP图 1O6如图，抛物线21:23L y x x =−−+交x 轴于A 、B 两点，交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ，2L 交x 轴于C 、D 两点. （1）求抛物线2L 对应的函数表达式；（2）抛物线1L 或2L 在x 轴上方的部分是否存在点N ，使以A ，C ，M ，N 为顶点的四边形是平行四边形.若存在，求出点N 的坐标；若不存在，请说明理由；（3）若点P 是抛物线1L 上的一个动点（P 不与点A 、B 重合），那么点P 关于原点的对称点Q 是否在抛物线2L 上，请说明理由.7.如图，在梯形ABCD 中，AB ∥CD ，AB ＝7，CD ＝1，AD ＝BC ＝5．点M ，N 分别在边AD ，BC 上运动，并保持MN ∥AB ，ME ⊥AB ，NF ⊥AB ，垂足分别为E ，F ．（1）求梯形ABCD 的面积；（2）求四边形MEFN 面积的最大值．（3）试判断四边形MEFN 能否为正方形，若能， 求出正方形MEFN 的面积；若不能，请说明理由．8.如图，点A （m ，m ＋1），B （m ＋3，m －1）都在反比例函数xky =的图象上． C D A BE F NM（1）求m ，k 的值； （2）如果M 为x 轴上一点，N 为y 轴上一点， 以点A ，B ，M ，N 为顶点的四边形是平行四边形，试求直线MN 的函数表达式．（3）选做题：在平面直角坐标系中，点P 的坐标 为（5，0），点Q 的坐标为（0，3），把线段PQ 向右平 移4个单位，然后再向上平移2个单位，得到线段P 1Q 1， 则点P 1的坐标为 ，点Q 1的坐标为．9.如图16，在平面直角坐标系中，直线y =−x 轴交于点A ，与y 轴交于点C ，抛物线2(0)3y ax x c a =−+≠经过A B C ，，三点． （1）求过A B C ，，三点抛物线的解析式并求出顶点F 的坐标；（2）在抛物线上是否存在点P ，使ABP △为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明理由； （3）试探究在直线AC 上是否存在一点M ，使得MBF △的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．10.如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在y 轴的正半轴上，且1AB =，OB =，矩形ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD ．点A 的对应点为点E ，点B 的对应点为点F ，点C 的对应点为点D ，抛物x友情提示：本大题第（1）小题4分，第（2）小题7分．对完成第（2）小题有困难的同学可以做下面的（3）选做题．选做题2分，所得分数计入总分．但第（2）、（3）小题都做的，第（3）小题的得分不重复计入总分．线2y ax bx c =++过点A E D ，，． （1）判断点E 是否在y 轴上，并说明理由； （2）求抛物线的函数表达式；（3）在x 轴的上方是否存在点P ，点Q ，使以点O B P Q ，，，为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．11.已知：如图14，抛物线2334y x =−+与x 轴交于点A ，点B ，与直线34y x b =−+相交于点B ，点C ，直线34y x b =−+与y 轴交于点E ． （1）写出直线BC 的解析式． （2）求ABC △的面积．（3）若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A B ，重合），同时，点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB △的面积S 与t 的函数关系式，并求出点M 运动多少时间时，MNB △的面积最大，最大面积是多少？12.在平面直角坐标系中△ABC 的边AB 在x 轴上，且OA>OB,以AB 为直径的圆过点C 若yxODEC FA BC 的坐标为(0,2),AB=5,A,B 两点的横坐标X A ,X B 是关于X 的方程2(2)10x m x n −++−=的两根:(1) 求m ，n 的值(2) 若∠ACB 的平分线所在的直线l 交x 轴于点D ，试求直线l 对应的一次函数的解析式 (3) 过点D 任作一直线`l 分别交射线CA ，CB （点C 除外）于点M ，N ，则11CMCN+的值是否为定值，若是，求出定值，若不是，请说明理由13.已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.(1)求该抛物线的解析式；(2)若该抛物线与x 轴的另一个交点为E.求四边形ABDE 的面积；(3)△AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛−−abac a b 44,22）14.已知抛物线c bx ax y ++=232，ACO BNDML`（Ⅰ）若1==b a ，1−=c ，求该抛物线与x 轴公共点的坐标；（Ⅱ）若1==b a ，且当11<<−x 时，抛物线与x 轴有且只有一个公共点，求c 的取值范围；（Ⅲ）若0=++c b a ，且01=x 时，对应的01>y ；12=x 时，对应的02>y ，试判断当10<<x 时，抛物线与x 轴是否有公共点？若有，请证明你的结论；若没有，阐述理由．15.已知：如图①，在Rt △ACB 中，∠C ＝90°，AC ＝4cm ，BC ＝3cm ，点P 由B 出发沿BA 方向向点A 匀速运动，速度为1cm/s ；点Q 由A 出发沿AC 方向向点C 匀速运动，速度为2cm/s ；连接PQ ．若设运动的时间为t （s ）（0＜t ＜2），解答下列问题： （1）当t 为何值时，PQ ∥BC ？（2）设△AQP 的面积为y （2cm ），求y 与t 之间的函数关系式；（3）是否存在某一时刻t ，使线段PQ 恰好把Rt △ACB 的周长和面积同时平分？若存在，求出此时t 的值；若不存在，说明理由；（4）如图②，连接PC ，并把△PQC 沿QC 翻折，得到四边形PQP ′C ，那么是否存在某一时刻t ，使四边形PQP ′C 为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．16.已知双曲线k y x =与直线14y x =相交于A 、B 两点.第一象限上的点M （m ，n ）（在A 点左侧）是双曲线ky x=上的动点.过点B 作BD ∥y 轴于点D.过N （0，－n ）作NC ∥x 轴交双曲线ky x=于点E ，交BD 于点C.（1）若点D 坐标是（－8，0），求A 、B 两点坐标及k 的值.（2）若B 是CD 的中点，四边形OBCE 的面积为4，求直线CM 的解析式.（3）设直线AM 、BM 分别与y 轴相交于P 、Q 两点，且MA ＝pMP ，MB ＝qMQ ，求p －q 的值.P图①压轴题答案1.解：（1）由已知得：310c b c =⎧⎨−−+=⎩解得 c=3,b =2∴抛物线的线的解析式为223y x x =−++ (2)由顶点坐标公式得顶点坐标为（1，4）所以对称轴为x=1,A,E 关于x=1对称，所以设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO BOFD S S S ∆++梯形=111()222AO BO BO DF OF EF DF ⋅++⋅+⋅=11113(34)124222⨯⨯++⨯+⨯⨯ =9（3）相似如图，======所以2220BD BE +=,220DE =即：222BD BE DE +=,所以BDE ∆是直角三角形 所以90AOB DBE ∠=∠=︒,且2AO BO BD BE ==,所以AOB DBE ∆∆.2解：（1）Rt A ∠=∠，6AB =，8AC =，10BC ∴=．点D 为AB 中点，132BD AB ∴==．90DHB A ∠=∠=，B B ∠=∠．BHD BAC ∴△∽△， DH BD AC BC ∴=，3128105BD DH AC BC ∴==⨯=．（2）QR AB ∥，90QRC A ∴∠=∠=．C C ∠=∠，RQC ABC ∴△∽△，RQ QC AB BC ∴=，10610y x−∴=， 即y 关于x 的函数关系式为：365y x =−+． （3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠=，290C ∠+∠=，1C ∴∠=∠．84cos 1cos 105C ∴∠===，45QM QP ∴=， 1364251255x ⎛⎫−+ ⎪⎝⎭∴=，185x ∴=． ②当PQ RQ =时，312655x −+=， 6x ∴=．③当PR QR =时，则R 为PQ 中垂线上的点， 于是点R 为EC 的中点，11224CR CE AC ∴===．tan QR BAC CR CA ==， 366528x −+∴=，152x ∴=．ABCD ERP H QM21 HA BCD E R PHQ综上所述，当x 为185或6或152时，PQR △为等腰三角形． 3解：（1）∵MN ∥BC ，∴∠AMN =∠B ，∠ANM ＝∠C ．∴△AMN ∽△ABC ．∴AM AN AB AC=，即43x AN=．∴AN ＝43x ．……………2分∴S =2133248MNP AMN S S x x x ∆∆==⋅⋅=．（0＜x ＜4）……………3分 （2）如图2，设直线BC 与⊙O 相切于点D ，连结AO ，OD ，则AO =OD =21MN ． 在Rt △ABC 中，BC． 由（1）知△AMN ∽△ABC ．∴AM MN AB BC=，即45x MN=．∴54MN x =， ∴58OD x =．…………………5分过M 点作MQ ⊥BC 于Q ，则58MQ OD x ==． 在Rt △BMQ 与Rt △BCA 中，∠B 是公共角， ∴△BMQ ∽△BCA ． ∴BM QM BC AC=． ∴55258324xBM x ⨯==，25424AB BM MA x x =+=+=． ∴x ＝4996． ∴当x ＝4996时，⊙O 与直线B C 相切．…………………………………7分（3）随点M 的运动，当P 点落在直线BC 上时，连结AP ，则O 点为AP 的中点．∵MN ∥BC ，∴∠AMN =∠B ，∠AOM ＝∠APC∴△AMO ∽△ABP ．∴12AM AO AB AP ==．AM ＝MB ＝2． 故以下分两种情况讨论：①当0＜x ≤2时，2Δ83x S y PMN ==．∴当x ＝2时，2332.82y =⨯=最大……………………………………8分 ②当2＜x ＜4时，设PM ，PN 分别交BC 于E ，F ．BD 图 2P 图 3∵四边形AMPN 是矩形， ∴PN ∥AM ，PN ＝AM ＝x ． 又∵MN ∥BC ，∴四边形MBFN 是平行四边形． ∴FN ＝BM ＝4－x ．∴()424PF x x x =−−=−． 又△PEF ∽△ACB ．∴2PEF ABCS PF AB S ∆∆⎛⎫= ⎪⎝⎭． ∴()2322PEF S x ∆=−．………………………………………………9分 MNP PEF y S S ∆∆=−＝()222339266828x x x x −−=−+−．……………………10分当2＜x ＜4时，29668y x x =−+−298283x ⎛⎫=−−+ ⎪⎝⎭．∴当83x =时，满足2＜x ＜4，2y =最大．……………………11分 综上所述，当83x =时，y 值最大，最大值是2．…………………………12分4解：（1）作BE ⊥OA ，∴ΔAOB 是等边三角形∴BE=OB ·sin60o=B(∵A(0,4),设AB 的解析式为4y kx =+,所以42+=,解得k =, 以直线AB的解析式为43y x =−+ （2）由旋转知，AP=AD,∠PAD=60o, ∴ΔAPD 是等边三角形，=如图，作B E ⊥AO,DH ⊥OA,GB ⊥DH,显然ΔGBD 中∠GBD=30°∴GD=12BD=, ∴GB=2BD=32,OH=OE+HE=OE+BG=37222+=∴D(532,72)(3)设OP=x,则由（2）可得D(323,2x x++)若ΔOPD的面积为：133(2)2x x+=解得：2321x−±=所以P(2321−±,0)567解：（1）分别过D ，C 两点作DG ⊥AB 于点G ，CH ⊥AB 于点H ．……………1分 ∵AB ∥CD ，∴DG ＝CH ，DG ∥CH ．∴四边形DGHC 为矩形，GH ＝CD ＝1．∵DG ＝CH ，AD ＝BC ，∠AGD ＝∠BHC ＝90°，∴△AGD ≌△BHC （HL ）．∴AG ＝BH ＝2172−=−GH AB ＝3．………2分 ∵在Rt △AGD 中，AG ＝3，AD ＝5， ∴DG ＝4．∴()174162ABCD S +⨯==梯形．………………………………………………3分（2）∵MN ∥AB ，ME ⊥AB ，NF ⊥AB ，∴ME ＝NF ，ME ∥NF ．∴四边形MEFN 为矩形． ∵AB ∥CD ，AD ＝BC ， ∴∠A ＝∠B ．∵ME ＝NF ，∠MEA ＝∠NFB ＝90°， ∴△MEA ≌△NFB （AAS ）．∴AE ＝BF ．……………………4分设AE ＝x ，则EF ＝7－2x ．……………5分C DA B E FN M G H C DA B E F NM G H∵∠A ＝∠A ，∠MEA ＝∠DGA ＝90°， ∴△MEA ∽△DGA ． ∴DGME AG AE =． ∴ME ＝x 34．…………………………………………………………6分∴6494738)2(7342+⎪⎭⎫ ⎝⎛−−=−=⋅=x x x EF ME S MEFN 矩形．……………………8分当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．……………9分（3）能．……………………………………………………………………10分由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34．若四边形MEFN 为正方形，则ME ＝EF ． 即=34x 7－2x ．解，得1021=x ．……………………………………………11分∴EF ＝21147272105x −=−⨯=＜4． ∴四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫ ⎝⎛=MEFN S 正方形．8解：（1）由题意可知，()()()131−+=+m m m m ．解，得m ＝3．………………………………3分∴A （3，4），B （6，2）； ∴k ＝4×3=12．……………………………4分 （2）存在两种情况，如图：①当M 点在x 轴的正半轴上，N 点在y 轴的正半轴上时，设M 1点坐标为（x 1，0），N 1点坐标为（0，y 1）．∵四边形AN 1M 1B 为平行四边形，∴线段N 1M 1可看作由线段AB 向左平移3个单位， 再向下平移2个单位得到的（也可看作向下平移2由（1）知A 点坐标为（3，4），B 点坐标为（6，2），∴N 1点坐标为（0，4－2），即N 1（0，2）；………………………………5分 M 1点坐标为（6－3，0），即M 1（3，0）．………………………………6分设直线M 1N 1的函数表达式为21+=x k y ，把x ＝3，y ＝0代入，解得321−=k ．∴直线M 1N 1的函数表达式为232+−=x y ．……………………………………8分②当M 点在x 轴的负半轴上，N 点在y 轴的负半轴上时，设M 2点坐标为（x 2，0），N 2点坐标为（0，y 2）．∵AB ∥N 1M 1，AB ∥M 2N 2，AB ＝N 1M 1，AB ＝M 2N 2， ∴N 1M 1∥M 2N 2，N 1M 1＝M 2N 2．∴线段M 2N 2与线段N 1M 1关于原点O 成中心对称．∴M 2点坐标为（-3，0），N 2点坐标为（0，-2）．………………………9分设直线M 2N 2的函数表达式为22−=x k y ，把x ＝-3，y ＝0代入，解得322−=k ，∴直线M 2N 2的函数表达式为232−−=x y ．所以，直线MN 的函数表达式为232+−=x y 或232−−=x y ．………………11分（3）选做题：（9，2），（4，5）．………………………………………………2分9解：（1）直线y =−x 轴交于点A ，与y 轴交于点C ．(10)A ∴−，，(0C ，·················································································· 1分 点A C ，都在抛物线上，0a c c ⎧=⎪∴⎨⎪=⎩a c ⎧=⎪∴⎨⎪=⎩∴抛物线的解析式为2y x x =− ······················································ 3分 ∴顶点13F ⎛⎫− ⎪ ⎪⎝⎭， ······················································································· 4分 （2）存在 ····································································································· 5分1(0P ··································································································· 7分2(2P ··································································································· 9分 （3）存在 ··································································································· 10分理由： 解法一：延长BC 到点B '，使B C BC '=，连接B F '交直线AC 于点M ，则点M 就是所求的点． ················································································································· 11分 过点B '作B H AB '⊥于点H ．B点在抛物线233y x x =−(30)B ∴， 在Rt BOC △中，tan OBC ∠=，30OBC ∴∠=，BC =，在Rt BB H '△中，12B H BB ''==6BH H '==，3OH ∴=，(3B '∴−−， ············································· 12分设直线B F '的解析式为y kx b =+x3k bk b⎧−=−+⎪∴⎨=+⎪⎩解得6kb=⎪⎪⎨⎪=⎪⎩62y x∴=− ······················································································· 13分yy x⎧=−⎪∴⎨=−⎪⎩377xy⎧=⎪⎪⎨⎪=−⎪⎩37M⎛∴⎝⎭，∴在直线AC上存在点M，使得MBF△的周长最小，此时377M⎛⎫−⎪⎪⎝⎭，． ······· 14分解法二：过点F作AC的垂线交y轴于点H，则点H为点F关于直线AC的对称点．连接BH交AC于点M，则点M即为所求． ································ 11分过点F作FG y⊥轴于点G，则OB FG∥，BC FH∥．90BOC FGH∴∠=∠=，BCO FHG∠=∠HFG CBO∴∠=∠同方法一可求得(30)B，．在Rt BOC△中，tan3OBC∠=，30OBC∴∠=，可求得3GH GC==，GF∴为线段CH的垂直平分线，可证得CFH△为等边三角形，AC∴垂直平分FH．即点H为点F关于AC的对称点．0H⎛∴−⎝⎭， ··········································· 12分设直线BH的解析式为y kx b=+，由题意得03k bb=+⎧⎪⎨=⎪⎩kb⎧=⎪⎪⎨⎪=⎪⎩y∴=······················································································ 13分xy y ⎧=⎪∴⎨⎪=⎩77x y =⎪⎪⎨⎪=−⎪⎩377M ⎛∴− ⎝⎭， ∴在直线AC 上存在点M ，使得MBF △的周长最小，此时377M ⎛⎫− ⎪ ⎪⎝⎭，． 1 10解：（1）点E 在y 轴上 ··············································································· 1分 理由如下：连接AO ，如图所示，在Rt ABO △中，1AB =，BO =，2AO ∴=1sin 2AOB ∴∠=，30AOB ∴∠= 由题意可知：60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上，∴点E 在y 轴上． ································································· 3分 （2）过点D 作DM x ⊥轴于点M1OD =，30DOM ∠=∴在Rt DOM △中，12DM =，2OM = 点D 在第一象限，∴点D的坐标为122⎛⎫ ⎪ ⎪⎝⎭， ················································································ 5分 由（1）知2EO AO ==，点E 在y 轴的正半轴上∴点E 的坐标为(02)，∴点A的坐标为( ·················································································· 6分 抛物线2y ax bx c =++经过点E ，2c ∴=由题意，将(A，122D ⎛⎫ ⎪ ⎪⎝⎭，代入22y ax bx =++中得32131242a a ⎧+=⎪⎨++=⎪⎩解得99a b =−⎪⎪⎨⎪=−⎪⎩∴所求抛物线表达式为：28299y x x =−−+ ·················································· 9分 （3）存在符合条件的点P ，点Q ． ································································· 10分 理由如下：矩形ABOC 的面积3AB BO ==∴以O B P Q ，，，为顶点的平行四边形面积为由题意可知OB 为此平行四边形一边， 又3OB =OB ∴边上的高为2 ······················································································· 11分 依题意设点P 的坐标为(2)m ，点P在抛物线28299y x x =−−+上28229m ∴−+=解得，10m =，2m = 1(02)P ∴，，22P ⎛⎫ ⎪ ⎪⎝⎭以O B P Q ，，，为顶点的四边形是平行四边形，PQ OB ∴∥，PQ OB ==， ∴当点1P 的坐标为(02)，时， 点Q 的坐标分别为1(Q，22)Q ； 当点2P 的坐标为28⎛⎫−⎪ ⎪⎝⎭时，点Q的坐标分别为328Q ⎛⎫−⎪ ⎪⎝⎭，428Q ⎛⎫⎪ ⎪⎝⎭． ··········································· 14分 （以上答案仅供参考，如有其它做法，可参照给分） 11解：（1）在2334y x =−+中，令0y = 23304x ∴−+=12x ∴=，22x =−(20)A ∴−，，(20)B ， (1)又点B 在34y x b =−+上 302b ∴=−+32b =BC ∴的解析式为3342y x =−+ ········································································ 2分 （2）由23343342y x y x ⎧=−+⎪⎪⎨⎪=−+⎪⎩，得11194x y =−⎧⎪⎨=⎪⎩2220x y =⎧⎨=⎩ ····················································· 4分 914C ⎛⎫∴− ⎪⎝⎭，，(20)B ，4AB ∴=，94CD =······················································································· 5分 1994242ABC S ∴=⨯⨯=△ ·················································································· 6分 （3）过点N 作NP MB ⊥于点P EO MB ⊥ NP EO ∴∥BNP BEO ∴△∽△ ······················································································· 7分 BN NPBE EO∴=································································································· 8分 由直线3342y x =−+可得：302E ⎛⎫ ⎪⎝⎭， ∴在BEO △中，2BO =，32EO =，则52BE =25322t NP ∴=，65NP t ∴= ················································································ 9分 16(4)25S t t ∴=−2312(04)55S t t t =−+<< ············································································· 10分 2312(2)55S t =−−+ ····················································································· 11分 此抛物线开口向下，∴当2t =时，125S =最大∴当点M 运动2秒时，MNB △的面积达到最大，最大为125．12解：(1)m=-5,n=-3 (2)y=43x+2 (3)是定值.因为点D 为∠ACB 的平分线，所以可设点D 到边AC,BC 的距离均为h ， 设△ABCAB 边上的高为H, 则利用面积法可得：222CM h CN h MN H⋅⋅⋅+=（CM+CN ）h=MN ﹒HCM CN MNH h +=又H=CM CN MN⋅化简可得(CM+CN)﹒1MN CM CN h=⋅故111CM CN h+=13解：（1）由已知得：310c b c =⎧⎨−−+=⎩解得c=3,b =2∴抛物线的线的解析式为223y x x =−++ (2)由顶点坐标公式得顶点坐标为（1，4）所以对称轴为x=1,A,E 关于x=1对称，所以E(3,0) 设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形=111()222AO BO BO DF OF EF DF ⋅++⋅+⋅ =11113(34)124222⨯⨯++⨯+⨯⨯ =9（3）相似如图，======所以2220BD BE +=,220DE =即：222BD BE DE +=,所以BDE ∆是直角三角形所以90AOB DBE ∠=∠=︒,且2AO BO BD BE ==, 所以AOBDBE ∆∆.14解（Ⅰ）当1==b a ，1−=c 时，抛物线为1232−+=x x y ， 方程01232=−+x x 的两个根为11−=x ，312=x ． ∴该抛物线与x 轴公共点的坐标是()10−，和103⎛⎫ ⎪⎝⎭，． ············································ 2分 （Ⅱ）当1==b a 时，抛物线为c x x y ++=232，且与x 轴有公共点．对于方程0232=++c x x ，判别式c 124−=∆≥0，有c ≤31． ···································· 3分①当31=c 时，由方程031232=++x x ，解得3121−==x x ． 此时抛物线为31232++=x x y 与x 轴只有一个公共点103⎛⎫− ⎪⎝⎭，． ······························ 4分 ②当31<c 时， 11−=x 时，c c y +=+−=1231， 12=x 时，c c y +=++=5232．由已知11<<−x 时，该抛物线与x 轴有且只有一个公共点，考虑其对称轴为31−=x ，。

二次函数常考题型与解析一．选择题（共12小题）1．若二次函数y=x2+mx的对称轴是x=3，则关于x的方程x2+mx=7的解为（）A．x1=0，x2=6 B．x1=1，x2=7 C．x1=1，x2=﹣7 D．x1=﹣1，x2=72．点P1（﹣1，y1），P2（3，y2），P3（5，y3）均在二次函数y=﹣x2+2x+c的图象上，则y1，y2，y3的大小关系是（）A．y3＞y2＞y1B．y3＞y1=y2C．y1＞y2＞y3D．y1=y2＞y33．抛物线y=ax2+bx+c的图象如图所示，则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为（）A．B．C．D．4．二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：下列说法正确的是（）A．抛物线的开口向下B．当x＞﹣3时，y随x的增大而增大C．二次函数的最小值是﹣2D．抛物线的对称轴是x=﹣5．已知函数y=ax2﹣2ax﹣1（a是常数，a≠0），下列结论正确的是（）A．当a=1时，函数图象过点（﹣1，1）B．当a=﹣2时，函数图象与x轴没有交点C．若a＞0，则当x≥1时，y随x的增大而减小D．若a＜0，则当x≤1时，y随x的增大而增大6．如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0②4a+2b+c＞0③4ac﹣b2＜8a④＜a＜⑤b＞c．其中含所有正确结论的选项是（）A．①③B．①③④C．②④⑤D．①③④⑤7．抛物线y=x2+bx+c（其中b，c是常数）过点A（2，6），且抛物线的对称轴与线段y=0（1≤x≤3）有交点，则c的值不可能是（）A．4 B．6 C．8 D．108．已知二次函数y=ax2﹣bx﹣2（a≠0）的图象的顶点在第四象限，且过点（﹣1，0），当a﹣b为整数时，ab的值为（）A．或1 B．或1 C．或D．或9．已知二次函数y=ax2+bx+c（a＞0）的图象经过点A（﹣1，2），B（2，5），顶点坐标为（m，n），则下列说法错误的是（）A．c＜3 B．m≤C．n≤2 D．b＜110．已知抛物线y=ax2+bx+c（a＞0）过（﹣2，0），（2，3）两点，那么抛物线的对称轴（）A．只能是x=﹣1B．可能是y轴C．可能在y轴右侧且在直线x=2的左侧D．可能在y轴左侧且在直线x=﹣2的右侧11．如图，某厂有许多形状为直角梯形的铁皮边角料，为节约资源，现要按图中所示的方法从这些边角料上截取矩形（阴影部分）片备用，当截取的矩形面积最大时，矩形两边长x、y应分别为（）A．x=10，y=14 B．x=14，y=10 C．x=12，y=15 D．x=15，y=1212．如图，反比例函数y=的图象经过二次函数y=ax2+bx图象的顶点（﹣，m）（m＞0），则有（）A．a=b+2k B．a=b﹣2k C．k＜b＜0 D．a＜k＜0二．填空题（共9小题）13．已知点P（m，n）在抛物线y=ax2﹣x﹣a上，当m≥﹣1时，总有n≤1成立，则a的取值范围是．14．a、b、c是实数，点A（a+1、b）、B（a+2，c）在二次函数y=x2﹣2ax+3的图象上，则b、c的大小关系是b c（用“＞”或“＜”号填空）15．二次函数y=ax2+bx+c的图象如图所示，且P=|2a+b|+|3b﹣2c|，Q=|2a﹣b|﹣|3b+2c|，则P，Q的大小关系是．16．如图，抛物线y=﹣x2+2x+3与y轴交于点C，点D（0，1），点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为．17．如图，P是抛物线y=﹣x2+x+2在第一象限上的点，过点P分别向x轴和y轴引垂线，垂足分别为A，B，则四边形OAPB周长的最大值为．18．二次函数y=x2﹣2x﹣3的图象如图所示，若线段AB在x轴上，且AB为2个单位长度，以AB为边作等边△ABC，使点C落在该函数y轴右侧的图象上，则点C的坐标为．19．直线y=kx+b与抛物线y=x2交于A（x1，y1）、B（x2，y2）两点，当OA⊥OB 时，直线AB恒过一个定点，该定点坐标为．20．如图，在平面直角坐标系中，菱形OABC的顶点A在x轴正半轴上，顶点C 的坐标为（4，3），D是抛物线y=﹣x2+6x上一点，且在x轴上方，则△BCD面积的最大值为．21．抛物线y=﹣x2+4ax+b（a＞0）与x轴相交于O、A两点（其中O为坐标原点），过点P（2，2a）作直线PM⊥x轴于点M，交抛物线于点B，点B关于抛物线对称轴的对称点为C（其中B、C不重合），连接AP交y轴于点N，连接BC和PC．（1）a=时，求抛物线的解析式和BC的长；（2）如图a＞1时，若AP⊥PC，求a的值．三．解答题（共12小题）22．已知二次函数y=x2+bx+c的图象与y轴交于点C（0，﹣6），与x轴的一个交点坐标是A（﹣2，0）．（1）求二次函数的解析式，并写出顶点D的坐标；（2）将二次函数的图象沿x轴向左平移个单位长度，当y＜0时，求x的取值范围．23．已知二次函数y=ax2﹣2ax+c（a＞0）的图象与x轴的负半轴和正半轴分别交于A、B两点，与y轴交于点C，它的顶点为P，直线CP与过点B且垂直于x轴的直线交于点D，且CP：PD=2：3（1）求A、B两点的坐标；（2）若tan∠PDB=，求这个二次函数的关系式．24．已知，点M是二次函数y=ax2（a＞0）图象上的一点，点F的坐标为（0，），直角坐标系中的坐标原点O与点M，F在同一个圆上，圆心Q的纵坐标为．（1）求a的值；（2）当O，Q，M三点在同一条直线上时，求点M和点Q的坐标；（3）当点M在第一象限时，过点M作MN⊥x轴，垂足为点N，求证：MF=MN+OF．25．如图，已知点A（0，2），B（2，2），C（﹣1，﹣2），抛物线F：y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P．（1）当抛物线F经过点C时，求它的表达式；（2）设点P的纵坐标为y P，求y P的最小值，此时抛物线F上有两点（x1，y1），（x2，y2），且x1＜x2≤﹣2，比较y1与y2的大小；（3）当抛物线F与线段AB有公共点时，直接写出m的取值范围．26．如图，二次函数y=ax2+bx的图象经过点A（2，4）与B（6，0）．（1）求a，b的值；（2）点C是该二次函数图象上A，B两点之间的一动点，横坐标为x（2＜x＜6），写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．27．在平面直角坐标系xOy中，抛物线y=ax2+bx+2过B（﹣2，6），C（2，2）两点．（1）试求抛物线的解析式；（2）记抛物线顶点为D，求△BCD的面积；（3）若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC（包括端点B、C）部分有两个交点，求b的取值范围．28．如图，顶点为A（，1）的抛物线经过坐标原点O，与x轴交于点B．（1）求抛物线对应的二次函数的表达式；（2）过B作OA的平行线交y轴于点C，交抛物线于点D，求证：△OCD≌△OAB；（3）在x轴上找一点P，使得△PCD的周长最小，求出P点的坐标．29．如图1（注：与图2完全相同），二次函数y=x2+bx+c的图象与x轴交于A （3，0），B（﹣1，0）两点，与y轴交于点C．（1）求该二次函数的解析式；（2）设该抛物线的顶点为D，求△ACD的面积（请在图1中探索）；（3）若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC 边运动，其中一点到达端点时，另一点也随之停止运动，当P，Q运动到t秒时，△APQ沿PQ所在的直线翻折，点A恰好落在抛物线上E点处，请直接判定此时四边形APEQ的形状，并求出E点坐标（请在图2中探索）．30．已知抛物线y=ax2+bx﹣3经过（﹣1，0），（3，0）两点，与y轴交于点C，直线y=kx与抛物线交于A，B两点．（1）写出点C的坐标并求出此抛物线的解析式；（2）当原点O为线段AB的中点时，求k的值及A，B两点的坐标；（3）是否存在实数k使得△ABC的面积为？若存在，求出k的值；若不存在，请说明理由．31．在平面直角坐标系中，点O为原点，平行于x轴的直线与抛物线L：y=ax2相交于A，B两点（点B在第一象限），点D在AB的延长线上．（1）已知a=1，点B的纵坐标为2．①如图1，向右平移抛物线L使该抛物线过点B，与AB的延长线交于点C，求AC的长．②如图2，若BD=AB，过点B，D的抛物线L2，其顶点M在x轴上，求该抛物线的函数表达式．（2）如图3，若BD=AB，过O，B，D三点的抛物线L3，顶点为P，对应函数的二次项系数为a3，过点P作PE∥x轴，交抛物线L于E，F两点，求的值，并直接写出的值．32．小明的爸爸和妈妈分别驾车从家同时出发去上班，爸爸行驶到甲处时，看到前面路口时红灯，他立即刹车减速并在乙处停车等待，爸爸驾车从家到乙处的过程中，速度v（m/s）与时间t（s）的关系如图1中的实线所示，行驶路程s（m）与时间t（s）的关系如图2所示，在加速过程中，s与t满足表达式s=at2（1）根据图中的信息，写出小明家到乙处的路程，并求a的值；（2）求图2中A点的纵坐标h，并说明它的实际意义；（3）爸爸在乙处等待7秒后绿灯亮起继续前行，为了节约能源，减少刹车，妈妈驾车从家出发的行驶过程中，速度v（m/s）与时间t（s）的关系如图1中的折线O﹣B﹣C所示，加速过程中行驶路程s（m）与时间t（s）的关系也满足s=at2，当她行驶到甲处时，前方的绿灯刚好亮起，求此时妈妈驾车的行驶速度．33．科技馆是少年儿童节假日游玩的乐园．如图所示，图中点的横坐标x表示科技馆从8：30开门后经过的时间（分钟），纵坐标y表示到达科技馆的总人数．图中曲线对应的函数解析式为y=，10：00之后来的游客较少可忽略不计．（1）请写出图中曲线对应的函数解析式；（2）为保证科技馆内游客的游玩质量，馆内人数不超过684人，后来的人在馆外休息区等待．从10：30开始到12：00馆内陆续有人离馆，平均每分钟离馆4人，直到馆内人数减少到624人时，馆外等待的游客可全部进入．请问馆外游客最多等待多少分钟？2017年03月20日初中数学3的初中数学组卷参考答案与试题解析一．选择题（共12小题）1．（2016•荆门）若二次函数y=x2+mx的对称轴是x=3，则关于x的方程x2+mx=7的解为（）A．x1=0，x2=6 B．x1=1，x2=7 C．x1=1，x2=﹣7 D．x1=﹣1，x2=7【分析】先根据二次函数y=x2+mx的对称轴是x=3求出m的值，再把m的值代入方程x2+mx=7，求出x的值即可．【解答】解：∵二次函数y=x2+mx的对称轴是x=3，∴﹣=3，解得m=﹣6，∴关于x的方程x2+mx=7可化为x2﹣6x﹣7=0，即（x+1）（x﹣7）=0，解得x1=﹣1，x2=7．故选D．【点评】本题考查的是二次函数的性质，熟知二次函数的对称轴方程是解答此题的关键．2．（2016•兰州）点P1（﹣1，y1），P2（3，y2），P3（5，y3）均在二次函数y=﹣x2+2x+c的图象上，则y1，y2，y3的大小关系是（）A．y3＞y2＞y1B．y3＞y1=y2C．y1＞y2＞y3D．y1=y2＞y3【分析】根据函数解析式的特点，其对称轴为x=1，图象开口向下，在对称轴的右侧，y随x的增大而减小，据二次函数图象的对称性可知，P1（﹣1，y1）与（3，y1）关于对称轴对称，可判断y1=y2＞y3．【解答】解：∵y=﹣x2+2x+c，∴对称轴为x=1，P2（3，y2），P3（5，y3）在对称轴的右侧，y随x的增大而减小，∵3＜5，∴y2＞y3，根据二次函数图象的对称性可知，P1（﹣1，y1）与（3，y1）关于对称轴对称，故y1=y2＞y3，故选D．【点评】本题考查了函数图象上的点的坐标与函数解析式的关系，同时考查了函数的对称性及增减性．3．（2016•贺州）抛物线y=ax2+bx+c的图象如图所示，则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为（）A．B．C．D．【分析】根据二次函数图象与系数的关系确定a＞0，b＜0，c＜0，根据一次函数和反比例函数的性质确定答案．【解答】解：由抛物线可知，a＞0，b＜0，c＜0，∴一次函数y=ax+b的图象经过第一、三、四象限，反比例函数y=的图象在第二、四象限，故选：B．【点评】本题考查的是二次函数、一次函数和反比例函数的图象与系数的关系，掌握二次函数、一次函数和反比例函数的性质是解题的关键．4．（2016•临沂）二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：下列说法正确的是（）A．抛物线的开口向下B．当x＞﹣3时，y随x的增大而增大C．二次函数的最小值是﹣2D．抛物线的对称轴是x=﹣【分析】选出3点的坐标，利用待定系数法求出函数的解析式，再根据二次函数的性质逐项分析四个选项即可得出结论．【解答】解：将点（﹣4，0）、（﹣1，0）、（0，4）代入到二次函数y=ax2+bx+c 中，得：，解得：，∴二次函数的解析式为y=x2+5x+4．A、a=1＞0，抛物线开口向上，A不正确；B、﹣=﹣，当x≥﹣时，y随x的增大而增大，B不正确；C、y=x2+5x+4=﹣，二次函数的最小值是﹣，C不正确；D、﹣=﹣，抛物线的对称轴是x=﹣，D正确．故选D．【点评】本题考查了待定系数求函数解析式以及二次函数的性质，解题的关键是利用待定系数法求出函数解析式．本题属于基础题，难度不大，解决该题型题目时，结合点的坐标利用待定系数法求出函数解析式是关键．5．（2016•宁波）已知函数y=ax2﹣2ax﹣1（a是常数，a≠0），下列结论正确的是（）A．当a=1时，函数图象过点（﹣1，1）B．当a=﹣2时，函数图象与x轴没有交点C．若a＞0，则当x≥1时，y随x的增大而减小D．若a＜0，则当x≤1时，y随x的增大而增大【分析】把a=1，x=﹣1代入y=ax2﹣2ax﹣1，于是得到函数图象不经过点（﹣1，1），根据△=8＞0，得到函数图象与x轴有两个交点，根据抛物线的对称轴为直线x=﹣=1判断二次函数的增减性．【解答】解：A、∵当a=1，x=﹣1时，y=1+2﹣1=2，∴函数图象不经过点（﹣1，1），故错误；B、当a=﹣2时，∵△=42﹣4×（﹣2）×（﹣1）=8＞0，∴函数图象与x轴有两个交点，故错误；C、∵抛物线的对称轴为直线x=﹣=1，∴若a＞0，则当x≥1时，y随x的增大而增大，故错误；D、∵抛物线的对称轴为直线x=﹣=1，∴若a＜0，则当x≤1时，y随x的增大而增大，故正确；故选D．【点评】本题考查的是二次函数的性质，熟练掌握二次函数的性质是解题的关键．6．（2016•达州）如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A （﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0②4a+2b+c＞0③4ac﹣b2＜8a④＜a＜⑤b＞c．其中含所有正确结论的选项是（）A．①③B．①③④C．②④⑤D．①③④⑤【分析】根据对称轴为直线x=1及图象开口向下可判断出a、b、c的符号，从而判断①；根据对称轴得到函数图象经过（3，0），则得②的判断；根据图象经过（﹣1，0）可得到a、b、c之间的关系，从而对②⑤作判断；从图象与y轴的交点B在（0，﹣2）和（0，﹣1）之间可以判断c的大小得出④的正误．【解答】解：①∵函数开口方向向上，∴a＞0；∵对称轴在y轴右侧∴ab异号，∵抛物线与y轴交点在y轴负半轴，∴c＜0，∴abc＞0，故①正确；②∵图象与x轴交于点A（﹣1，0），对称轴为直线x=1，∴图象与x轴的另一个交点为（3，0），∴当x=2时，y＜0，∴4a+2b+c＜0，故②错误；③∵图象与x轴交于点A（﹣1，0），∴当x=﹣1时，y=（﹣1）2a+b×（﹣1）+c=0，∴a﹣b+c=0，即a=b﹣c，c=b﹣a，∵对称轴为直线x=1∴=1，即b=﹣2a，∴c=b﹣a=（﹣2a）﹣a=﹣3a，∴4ac﹣b2=4•a•（﹣3a）﹣（﹣2a）2=﹣16a2＜0∵8a＞0∴4ac﹣b2＜8a故③正确④∵图象与y轴的交点B在（0，﹣2）和（0，﹣1）之间，∴﹣2＜c＜﹣1∴﹣2＜﹣3a＜﹣1，∴＞a＞；故④正确⑤∵a＞0，∴b﹣c＞0，即b＞c；故⑤正确；故选：D．【点评】主要考查图象与二次函数系数之间的关系．解题关键是注意掌握数形结合思想的应用．7．（2016•绍兴）抛物线y=x2+bx+c（其中b，c是常数）过点A（2，6），且抛物线的对称轴与线段y=0（1≤x≤3）有交点，则c的值不可能是（）A．4 B．6 C．8 D．10【分析】根据抛物线y=x2+bx+c（其中b，c是常数）过点A（2，6），且抛物线的对称轴与线段y=0（1≤x≤3）有交点，可以得到c的取值范围，从而可以解答本题．【解答】解：∵抛物线y=x2+bx+c（其中b，c是常数）过点A（2，6），且抛物线的对称轴与线段y=0（1≤x≤3）有交点，∴解得6≤c≤14，故选A．【点评】本题考查二次函数的性质、解不等式，解题关键是明确题意，列出相应的关系式．8．（2016•泸州）已知二次函数y=ax2﹣bx﹣2（a≠0）的图象的顶点在第四象限，且过点（﹣1，0），当a﹣b为整数时，ab的值为（）A．或1 B．或1 C．或D．或【分析】首先根据题意确定a、b的符号，然后进一步确定a的取值范围，根据a﹣b为整数确定a、b的值，从而确定答案．【解答】解：依题意知a＞0，＞0，a+b﹣2=0，故b＞0，且b=2﹣a，a﹣b=a﹣（2﹣a）=2a﹣2，于是0＜a＜2，∴﹣2＜2a﹣2＜2，又a﹣b为整数，∴2a﹣2=﹣1，0，1，故a=，1，，b=，1，，∴ab=或1，故选A．【点评】本题考查了二次函数的性质，解题的关键是能够根据图象经过的点确定a+b+c的值和a、b的符号，难度中等．9．（2016•株洲）已知二次函数y=ax2+bx+c（a＞0）的图象经过点A（﹣1，2），B（2，5），顶点坐标为（m，n），则下列说法错误的是（）A．c＜3 B．m≤C．n≤2 D．b＜1【分析】根据已知条件得到，解方程组得到c=3﹣2a＜3，b=1﹣a＜1，求得二次函数的对称轴为x=﹣=﹣=﹣＜，根据二次函数的顶点坐标即可得到结论．【解答】解：由已知可知：，消去b得：c=3﹣2a＜3，消去c得：b=1﹣a＜1，对称轴：m=x=﹣=﹣=﹣＜，∵A（﹣1，2），a＞0，那么顶点的纵坐标为函数的最小值，∴n≤2，故B错．【点评】本题考查了二次函数的性质，二次函数图象上点的坐标特征，熟记二次函数的性质是解题的关键．10．（2015•南昌）已知抛物线y=ax2+bx+c（a＞0）过（﹣2，0），（2，3）两点，那么抛物线的对称轴（）A．只能是x=﹣1B．可能是y轴C．可能在y轴右侧且在直线x=2的左侧D．可能在y轴左侧且在直线x=﹣2的右侧【分析】根据题意判定点（﹣2，0）关于对称轴的对称点横坐标x2满足：﹣2＜x2＜2，从而得出﹣2＜＜0，即可判定抛物线对称轴的位置．【解答】解：∵抛物线y=ax2+bx+c（a＞0）过（﹣2，0），（2，3）两点，∴点（﹣2，0）关于对称轴的对称点横坐标x2满足：﹣2＜x2＜2，∴﹣2＜＜0，∴抛物线的对称轴可能在y轴左侧且在直线x=﹣2的右侧．故选：D．【点评】本题考查了二次函数的性质，根据点坐标判断出另一个点的位置是解题的关键．11．（2007•临沂）如图，某厂有许多形状为直角梯形的铁皮边角料，为节约资源，现要按图中所示的方法从这些边角料上截取矩形（阴影部分）片备用，当截取的矩形面积最大时，矩形两边长x、y应分别为（）A．x=10，y=14 B．x=14，y=10 C．x=12，y=15 D．x=15，y=12【分析】由直角三角形相似得，得x=•（24﹣y），化简矩形面积S=xy 的解析式为S=﹣（y﹣12）2+180，再利用二次函数的性质求出S 的最大值，以及取得最大值时x、y的值．【解答】解：以直角梯形的下底直角边端点为原点，两直角边方向为x，y轴建立直角坐标系，过点D作DE⊥x轴于点E，∵NH∥DE，∴△CNH∽△CDE，∴=，∵CH=24﹣y，CE=24﹣8，DE=OA=20，NH=x，∴，得x=•（24﹣y），∴矩形面积S=xy=﹣（y﹣12）2+180，∴当y=12时，S有最大值，此时x=15．故选D．【点评】本题考查的是直角梯形以及矩形的性质的相关知识点．12．（2015•玉林）如图，反比例函数y=的图象经过二次函数y=ax2+bx图象的顶点（﹣，m）（m＞0），则有（）A．a=b+2k B．a=b﹣2k C．k＜b＜0 D．a＜k＜0【分析】把（﹣，m）代入y=ax2+bx图象的顶点坐标公式得到顶点（﹣，﹣），再把（﹣，﹣）代入得到k=，由图象的特征即可得到结论．【解答】解：∵y=ax2+bx图象的顶点（﹣，m），∴﹣=﹣，即b=a，∴m==﹣，∴顶点（﹣，﹣），把x=﹣，y=﹣代入反比例解析式得：k=，由图象知：抛物线的开口向下，∴a＜0，∴a＜k＜0，故选D．【点评】本题考查了二次函数的性质，反比例函数图象上点的坐标特征，熟练掌握反比例函数图象上点的坐标特征是解题的关键．二．填空题（共9小题）13．（2016•厦门）已知点P（m，n）在抛物线y=ax2﹣x﹣a上，当m≥﹣1时，总有n≤1成立，则a的取值范围是﹣≤a＜0．【分析】依照题意画出图形，结合函数图形以及已知条件可得出关于a的一元一次不等式组，解不等式组即可得出a的取值范围．【解答】解：根据已知条件，画出函数图象，如图所示．由已知得：，解得：﹣≤a＜0．故答案为：﹣≤a＜0【点评】本题考查了二次函数图象上点的坐标特征以及二次函数的性质，解题的关键是画出函数图象，依照数形结合得出关于a的不等式组．本题属于基础题，难度不大，解决该题型题目时，根据二次函数的性质画出函数图象，利用数形结合解决问题是关键．14．（2016•镇江）a、b、c是实数，点A（a+1、b）、B（a+2，c）在二次函数y=x2﹣2ax+3的图象上，则b、c的大小关系是b＜c（用“＞”或“＜”号填空）【分析】求出二次函数的对称轴，再根据二次函数的增减性判断即可．【解答】解：∵二次函数y=x2﹣2ax+3的图象的对称轴为x=a，二次项系数1＞0，∴抛物线的开口向上，在对称轴的右边，y随x的增大而增大，∵a+1＜a+2，点A（a+1、b）、B（a+2，c）在二次函数y=x2﹣2ax+3的图象上，∴b＜c，故答案为：＜．【点评】本题考查了二次函数图象上点的坐标特征，求出对称轴解析式，然后利用二次函数的增减性求解更简便．15．（2016•内江）二次函数y=ax2+bx+c的图象如图所示，且P=|2a+b|+|3b﹣2c|，Q=|2a﹣b|﹣|3b+2c|，则P，Q的大小关系是P＞Q．【分析】由函数图象可以得出a＜0，b＞0，c＞0，当x=1时，y=a+b+c＞0，x=﹣1时，y=a﹣b+c＜0，由对称轴得出2a+b=0，通过确定绝对值中的数的符号后去掉绝对值再化简就可以求出P、Q的值．【解答】解：∵抛物线的开口向下，∴a＜0，∵﹣＞0，∴b＞0，∴2a﹣b＜0，∵﹣=1，∴b+2a=0，x=﹣1时，y=a﹣b+c＜0．∴﹣b﹣b+c＜0，∴3b﹣2c＞0，∵抛物线与y轴的正半轴相交，∴c＞0，∴3b+2c＞0，∴p=3b﹣2c，Q=b﹣2a﹣3b﹣2c=﹣2a﹣2b﹣2c，∴Q﹣P=﹣2a﹣2b﹣2c﹣3b+2c=﹣2a﹣5b=﹣4b＜0∴P＞Q，故答案为：P＞Q．【点评】本题考查了二次函数的图象与系数的关系，去绝对值，二次函数的性质．熟记二次函数的性质是解题的关键．16．（2016•梅州）如图，抛物线y=﹣x2+2x+3与y轴交于点C，点D（0，1），点P是抛物线上的动点．若△PCD是以CD为底的等腰三角形，则点P的坐标为（1+，2）或（1﹣，2）．【分析】当△PCD是以CD为底的等腰三角形时，则P点在线段CD的垂直平分线上，由C、D坐标可求得线段CD中点的坐标，从而可知P点的纵坐标，代入抛物线解析式可求得P点坐标．【解答】解：∵△PCD是以CD为底的等腰三角形，∴点P在线段CD的垂直平分线上，如图，过P作PE⊥y轴于点E，则E为线段CD的中点，∵抛物线y=﹣x2+2x+3与y轴交于点C，∴C（0，3），且D（0，1），∴E点坐标为（0，2），∴P点纵坐标为2，在y=﹣x2+2x+3中，令y=2，可得﹣x2+2x+3=2，解得x=1±，∴P点坐标为（1+，2）或（1﹣，2），故答案为：（1+，2）或（1﹣，2）．【点评】本题主要考查等腰三角形的性质，利用等腰三角形的性质求得P点纵坐标是解题的关键．17．（2014•宁德）如图，P是抛物线y=﹣x2+x+2在第一象限上的点，过点P分别向x轴和y轴引垂线，垂足分别为A，B，则四边形OAPB周长的最大值为6．【分析】设P（x，y）（2＞x＞0，y＞0），根据矩形的周长公式得到C=﹣2（x﹣1）2+6．根据二次函数的性质来求最值即可．【解答】解：∵y=﹣x2+x+2，∴当y=0时，﹣x2+x+2=0即﹣（x﹣2）（x+1）=0，解得x=2或x=﹣1故设P（x，y）（2＞x＞0，y＞0），∴C=2（x+y）=2（x﹣x2+x+2）=﹣2（x﹣1）2+6．=6，．∴当x=1时，C最大值即：四边形OAPB周长的最大值为6．故答案是：6．【点评】本题考查了二次函数的最值，二次函数图象上点的坐标特征．求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．本题采用了配方法．18．（2016•泰州）二次函数y=x2﹣2x﹣3的图象如图所示，若线段AB在x轴上，且AB为2个单位长度，以AB为边作等边△ABC，使点C落在该函数y轴右侧的图象上，则点C的坐标为（1+，3）或（2，﹣3）．【分析】△ABC是等边三角形，且边长为2，所以该等边三角形的高为3，又点C在二次函数上，所以令y=±3代入解析式中，分别求出x的值．由因为使点C落在该函数y轴右侧的图象上，所以x＞0．【解答】解：∵△ABC是等边三角形，且AB=2，∴AB边上的高为3，又∵点C在二次函数图象上，∴C的纵坐标为±3，令y=±3代入y=x2﹣2x﹣3，∴x=1或0或2∵使点C落在该函数y轴右侧的图象上，∴x＞0，∴x=1+或x=2∴C（1+，3）或（2，﹣3）故答案为：（1+，3）或（2，﹣3）【点评】本题考查二次函数的图象性质，涉及等边三角形的性质，分类讨论的思想等知识，题目比较综合，解决问题的关键是根据题意得出C的纵坐标为±3．19．（2016•大庆）直线y=kx+b与抛物线y=x2交于A（x1，y1）、B（x2，y2）两点，当OA⊥OB时，直线AB恒过一个定点，该定点坐标为（0，4）．【分析】根据直线y=kx+b与抛物线y=x2交于A（x1，y1）、B（x2，y2）两点，可以联立在一起，得到关于x的一元二次方程，从而可以得到两根之和与两根之积，再根据OA⊥OB，可以求得b的值，从而可以得到直线AB恒过的定点的坐标．【解答】解：∵直线y=kx+b与抛物线y=x2交于A（x1，y1）、B（x2，y2）两点，∴kx+b=，化简，得x2﹣4kx﹣4b=0，∴x1+x2=4k，x1x2=﹣4b，又∵OA⊥OB，∴=，解得，b=4，即直线y=kx+4，故直线恒过顶点（0，4），故答案为：（0，4）．【点评】本题考查二次函数的性质、一次函数的性质，解题的关键是明确题意，找出所求问题需要的条件，知道两条直线垂直时，它们解析式中的k的乘积为﹣1．20．（2016•长春）如图，在平面直角坐标系中，菱形OABC的顶点A在x轴正半轴上，顶点C的坐标为（4，3），D是抛物线y=﹣x2+6x上一点，且在x轴上方，则△BCD面积的最大值为15．【分析】设D（x，﹣x2+6x），根据勾股定理求得OC，根据菱形的性质得出BC，=×5×（﹣x2+6x﹣3）=﹣（x﹣3）2+15，然后根据三角形面积公式得出∴S△BCD根据二次函数的性质即可求得最大值．【解答】解：∵D是抛物线y=﹣x2+6x上一点，∴设D（x，﹣x2+6x），∵顶点C的坐标为（4，3），∴OC==5，∵四边形OABC是菱形，∴BC=OC=5，BC∥x轴，∴S=×5×（﹣x2+6x﹣3）=﹣（x﹣3）2+15，△BCD∵﹣＜0，∴S有最大值，最大值为15，△BCD故答案为15．【点评】本题考查了菱形的性质，二次函数的性质，注意数与形的结合是解决本题的关键．21．（2016•自贡）抛物线y=﹣x2+4ax+b（a＞0）与x轴相交于O、A两点（其中O为坐标原点），过点P（2，2a）作直线PM⊥x轴于点M，交抛物线于点B，点B关于抛物线对称轴的对称点为C（其中B、C不重合），连接AP交y轴于点N，连接BC和PC．（1）a=时，求抛物线的解析式和BC的长；（2）如图a＞1时，若AP⊥PC，求a的值．【分析】（1）根据抛物线经过原点b=0，把a=、b=0代入抛物线解析式，即可求出抛物线解析式，再求出B、C坐标，即可求出BC长．（2）利用△PCB∽△APM，得=，列出方程即可解决问题．【解答】解：（1）∵抛物线y=﹣x2+4ax+b（a＞0）经过原点O，∴b=0，∵a=，∴抛物线解析式为y=﹣x2+6x，∵x=2时，y=8，∴点B坐标（2，8），∵对称轴x=3，B、C关于对称轴对称，∴点C坐标（4，8），∴BC=2．（2）∵AP⊥PC，∴∠APC=90°，∵∠CPB+∠APM=90°，∠APM+∠PAM=90°，∴∠CPB=∠PAM，∵∠PBC=∠PMA=90°，∴△PCB∽△APM，∴=，∴=，整理得a2﹣4a+2=0，解得a=2±，∵a＞1，∴a=2+．【点评】本题考查二次函数性质、相似三角形的判定和性质、待定系数法等知识，解题的关键是利用相似三角形性质列出方程解决问题，学会转化的思想，属于中考常考题型．三．解答题（共12小题）22．（2016•黔南州）已知二次函数y=x2+bx+c的图象与y轴交于点C（0，﹣6），与x轴的一个交点坐标是A（﹣2，0）．（1）求二次函数的解析式，并写出顶点D的坐标；（2）将二次函数的图象沿x轴向左平移个单位长度，当y＜0时，求x的取值范围．【分析】（1）将点A和点C的坐标代入抛物线的解析式可求得b、c的值，从而得到抛物线的解析式，然后依据配方法可求得抛物线的顶点坐标；（2）依据抛物线的解析式与平移的规划规律，写出平移后抛物线的解析式，然后求得抛物线与x轴的交点坐标，最后依据y＜0可求得x的取值范围．【解答】解：（1）∵把C（0，﹣6）代入抛物线的解析式得：C=﹣6，把A（﹣2，0）代入y=x2+bx﹣6得：b=﹣1，∴抛物线的解析式为y=x2﹣x﹣6．∴y=（x﹣）2﹣．∴抛物线的顶点坐标D（，﹣）．（2）二次函数的图形沿x轴向左平移个单位长度得：y=（x+2）2﹣．令y=0得：（x+2）2﹣=0，解得：x1=，x2=﹣．∵a＞0，∴当y＜0时，x的取值范围是﹣＜x＜．【点评】本题主要考查的是抛物线与x轴的交点、待定系数法求二次函数的解析式，掌握相关知识是解题的关键．23．（2016•无锡）已知二次函数y=ax2﹣2ax+c（a＞0）的图象与x轴的负半轴和正半轴分别交于A、B两点，与y轴交于点C，它的顶点为P，直线CP与过点B 且垂直于x轴的直线交于点D，且CP：PD=2：3（1）求A、B两点的坐标；（2）若tan∠PDB=，求这个二次函数的关系式．【分析】（1）由二次函数的解析式可求出对称轴为x=1，过点P作PE⊥x轴于点E，所以OE：EB=CP：PD；（2）过点C作CF⊥BD于点F，交PE于点G，构造直角三角形CDF，利用tan∠PDB=即可求出FD，由于△CPG∽△CDF，所以可求出PG的长度，进而求出a 的值，最后将A（或B）的坐标代入解析式即可求出c的值．【解答】解：（1）过点P作PE⊥x轴于点E，∵y=ax2﹣2ax+c，∴该二次函数的对称轴为：x=1，∴OE=1∵OC∥BD，∴CP：PD=OE：EB，∴OE：EB=2：3，∴EB=，∴OB=OE+EB=，∴B（，0）∵A与B关于直线x=1对称，∴A（﹣，0）；（2）过点C作CF⊥BD于点F，交PE于点G，令x=1代入y=ax2﹣2ax+c，∴y=c﹣a，令x=0代入y=ax2﹣2ax+c，∴y=c∴PG=a，∵CF=OB=，∴tan∠PDB=，∴FD=2，∵PG∥BD∴△CPG∽△CDF，∴==∴PG=，∴a=，∴y=x2﹣x+c，把A（﹣，0）代入y=x2﹣x+c，∴解得：c=﹣1，∴该二次函数解析式为：y=x2﹣x﹣1．【点评】本题考查二次函数，涉及待定系数法求出二次函数解析式，相似三角形的性质与判定，锐角三角函数等知识内容，解题的关键是利用作垂线构造直角三角形，再利用相似三角形的对应边的比相等即可得出答案．24．（2016•淄博）已知，点M是二次函数y=ax2（a＞0）图象上的一点，点F的坐标为（0，），直角坐标系中的坐标原点O与点M，F在同一个圆上，圆心Q 的纵坐标为．（1）求a的值；（2）当O，Q，M三点在同一条直线上时，求点M和点Q的坐标；（3）当点M在第一象限时，过点M作MN⊥x轴，垂足为点N，求证：MF=MN+OF．【分析】（1）设Q（m，），F（0，），根据QO=QF列出方程即可解决问题．（2）设M（t，t2），Q（m，），根据K OM=K OQ，求出t、m的关系，根据QO=QM 列出方程即可解决问题．（3）设M（n，n2）（n＞0），则N（n，0），F（0，），利用勾股定理求出MF 即可解决问题．【解答】解：（1）∵圆心Q的纵坐标为，∴设Q（m，），F（0，），∵QO=QF，∴m2+（）2=m2+（﹣）2，∴a=1，∴抛物线为y=x2．（2）∵M在抛物线上，设M（t，t2），Q（m，），。

、填空题:2 .1、函数y (m 1)x m 12mx 1是抛物线，则m = _—2、抛物线y x2 2x 3与x轴交点为______________ ，与y轴交点为.3、二次函数y ax2的图象过点(一1, 2),则它的解析式是_________________当x4 .抛物线y 时，6(xy随x的增大而增大.1)222可由抛物线y 6x 2向平移个单位得到.5. 抛物线y 2 x4x3在x轴上截得的线段长度是6. 抛物线y 2 x2x2m 4的图象经过原点，贝U m7. 抛物线y 2 x x m，若其顶点在x轴上，则m8.如果抛物线3 2y ax2bx c 的对称轴是x = - 2，且开口方向与形状与抛物线y 2X相同，又过原点，那么a= ___________________ , b = ________________ , c9、二次函数y x2 bx c的图象如下左图所示，则对称轴是 __________________ ，当函数值y对应x的取值范围是0时,\‘ yVO x10、已知二次函数y1 2ax bx c(a 0)与一次函数y2kx m(k 0)的图象相交于点A (- 2, 4)和B(8, 2),如上右图所示，则能使y1y成立的x的取值范围二、选择题：11.下列各式中，y是x的二次函数的是A. xy x2 1 B . x2 y 22 2ax 2 D . x y 1 012.在同一坐标系中，作y 2x2、y2x2、A. 都是关于x轴对称，抛物线开口向上BB. 都是关于原点对称，顶点都是原点Dmx m21的图象过原点，则2y1 2-x2的图象，它们共同特点是2都是关于都是关于13.抛物线yA. 0 x2m为(C . - 1y轴对称，抛物线开口向下y轴对称，顶点都是原点)D . ± 121、根据所给条件求抛物线的解析式： (1) 、抛物线过点(0, 2)、(1 , 1 )、(3, 5)(2) 、抛物线关于y 轴对称，且过点(1,— 2)和(一2, 0)bx C 的图像经过 A ( 0, 1), B (2,— 1)两点.(2 )试判断点P (— 1, 2)是否在此函数图像上?14•把二次函数y x 2 2x 1配方成为()2 2A . y (x 1)B . y (x 1) 2C . y 已知原点是抛物线 y (m 1)x 2的最高点，则A. m 1 B . m 115. (x 1)2 m 的范围是m 1D. y (x1)2 216、 函数y 2x 2 x 1的图象经过点(A 、(一 1, 1)B 、( 1 , 1) (0, 1 )、(1 ， 0 )17、 2抛物线y 3x 向右平移1个单位，再向下平移 2个单位, 所得到的抛物线是2y 3(x 1)2 B 、y3(x 21)2C 、y 23(x 1)2 D 、y 3(x1)2 218、已知h 关于t 的函数关系式higt 2 ( g 为正常数，t 为时间)如图，贝U 函数图象为22 2A 、y x 3x 2B 、y 5 xC 、y 2 2x 2x D 、y x 4x 422.已知二次函数 yx 2(1)求b 和c 的值;20三、解答题:c 0，那么它的图象大致是()23、某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米1000元，设矩形一边长为X米，面积为S平方米.(1) 求出S与x之间的函数关系式，并确定自变量x的取值范围;(2) 请你设计一个方案，使获得的设计费最多，并求出这个费用24、某工厂现有80台机器，每台机器平均每天生产384?件产品，现准备增加一批同类机器以提高生产总量，在试生产中发现，？由于其他生产条件没变，因此每增加一台机器，每台机器平均每天将少生产4件产品.(1)如果增加x台机器，每天的生产总量为y件，请你写出y与x之间的关系式；(2)增加多少台机器，可以使每天的生产总量最大？最大生产总量是多少？25、如图，有一个抛物线的拱形立交桥，？这个桥拱的最大高度为16m跨度为40m,现把它放在如图所示的直角坐标系里，？若要在离跨度中心点M5m处垂直竖一根铁柱支撑这个拱顶，铁柱应取多长？1624、如图，抛物线y x2 5x ⑴求抛物线的解析式；⑵P是y轴正半轴上一点，且△n经过点A(1 , 0)，与y轴交于点B.PAB是以AB为腰的等腰三角形，试求P点坐标.。

初三数学常考题型：抛物线经典好题
对于抛物线压轴题，要善于归类总结，掌握常规方法，积累特殊方法。

比如说平行四边形的存在性问题，等腰直角三角形的存在性问题，都是有多种方法求解的。

手写版的参考答案和简单分析：
第一题：考点有待定系数法求抛物线表达式，将军饮马问题，直角三角形的存在性问题，这道题目比较基础，适合初步接触抛物线时练习。

第二题，这道题目也比较常规基础，第一问求直线解析式，知道截距求表达式，可不用列方程组，省下一点时间。

第2问同样是将军饮马问题，送分问。

第3问是求线段长度的最值，最常见的方法就是设坐标列式子求最值。

第三题，这是一道面积问题和平行四边形的存在性问题，用到了水平宽乘以铅垂高求三角形面积。

平行四边形的存在性问题通常有三种方法求点的坐标，我在前面的文章中已经有详细讲解。

这道题我采用的是平行四边形对角坐标公式（中点坐标公式），也可以用点的平移的方法来解决。

第四题，又见将军饮马，可见将军饮马问题有多重要。

第3问求面积的最大值，采用的是直线平移，当直线与抛物线只有一个交点时，高最大，面积最大。

第5题：线段旋转问题，等腰三角形的存在性问题。

第6题：平行四边形的存在性问题和线段最值问题，第三问线段最值问题，用到了转换的思想，通过等腰直角三角形把求直角边的最值转化为求斜边的最值。

五、抛物线与平行四边形15．如图，在平面直角坐标系中，抛物线y=﹣x2+bx+c与轴相交于A、B两点，与轴相交于点C，OA=1，OC=3，连接BC．（1）求b的值；（2）点D是直线BC上方抛物线一动点（点B、C除外），当△BCD的面积取得最大值时，在轴上是否存在一点P，使得|PB﹣PD|最大，若存在，请求出点P的坐标；若不存在，请说明理由．（3）在（2）的条件下，若在平面上存在点Q，使得以点B、C、D、Q为顶点的四边形为平行四边形，请直接写出点Q坐标．【答案】（1）b=2，c=3；（2）P（0，）；（3）（-，），（，-），（，），∴直线BC的解析式为：y=-x+3，如图1，作直线l∥BC，设直线l的解析式为：y=-x+b，由题意可知：△BCD中边BC长一定，当△BCD的面积取得最大值时，即以BC为底边，其高最大，也就是直线l与抛物线有一个交点时，三角形高最大，△BCD的面积最大，则，（3）如图4，分三种情况：①当CD为平行四边形的对角线时，【点睛】本题属于二次函数综合题，考查了二次函数的性质，待定系数法确定抛物线解析式、一次函数解析式，平行四边形的判定，以及坐标与图形性质，确定点D、P、B共线是解决第（2）小题的关键，画出以点B、C、D、Q为顶点的四边形为平行四边形是解决第（3）小题的关键．16．如图，抛物线经过两点，与x轴交于另一点B．点P是抛物线上的动点。

（1）求抛物线的解析式；（2）是否存在点P，使得△BCP是以B C为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；（3）当P运动到第一象限时，过P作直线PM平行y轴，交直线B C于点M。

①求线段PM长度的最大值②D为平面内任意一点，当线段PM最大时，是否存在以C、P、M、D为顶点的平行四边形。

若存在，直接写出所有符合条件的点D坐标.【答案】(1) ;(2)见解析;(3) ①4; ②D1,D2,D3.（3）①求出直线BC解析式,根据PM平行y轴用二次函数表示P M的长度从而表示出PM的最大值;②分3种情况:CM为对角线;MP为对角线;CP为对角线.解:（1）将两点代入到中得，∴抛物线的解析式为.（2）存在．第二种情况，当以B为直角顶点时，过点P作PH⊥x轴，垂足为H.∵∠CBA=45°，∠CBP=90°，∴∠OBP=45°．∴∠HPB=45°，∴PH=HB．即：，解得：（舍去），．∴则P2的坐标是．综上所述，P的坐标是或17．已知，如图，抛物线y=ax2+3ax+c（a＞0）与y轴交于点C，与x轴交于A、B两点，点A在点B 左侧，点B的坐标为（1，0）、C（0，﹣3）．（1）求抛物线的解析式．（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值．（3）若点E在x轴上，点P在抛物线上，是否存在以A、C、E、P为顶点且以AC为一边的平行四边形？如存在，求点P的坐标；若不存在，请说明理由．【答案】（1）y=x2+x﹣3（2）（3）P1（﹣3，﹣3）或P2（，3）或P3（，3）解：（1）解：将点B、C的坐标代入抛物线的解析式得：，解得：a= ，c=﹣3．∴抛物线的解析式为y= x2+ x﹣3.（2）解：令y=0，则x2+ x﹣3=0，解得x1=1，x2=﹣4，∴A（﹣4，0）、B（1，0）.令x=0，则y=﹣3，∴C（0，﹣3），∴S△ABC= ×5×3= .设D（m，m2+ m﹣3），过点D作DE∥y轴交AC于E．直线AC的解析式为y=﹣x﹣3，则E（m，﹣m﹣3），DE=﹣m﹣3﹣（m2+ m﹣3）=﹣（m+2）2+3，当m=﹣2时，DE有最大值为3，此时，S△ACD有最大值为×DE×4=2DE=6.∴四边形ABCD的面积的最大值为6+ = ，18．在平面直角坐标系中，已知抛物线经过A（﹣4，0），B（0，﹣4），C（2，0）三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值．（3）若点P是抛物线上的动点，点Q是直线y=﹣x上的动点，是否存在以点P、Q、B、O为顶点的四边形为平行四边形？若存在，求出点Q的坐标；若不存在，请说明理由．【答案】（1）y=x2+x﹣4；（2）m=﹣2时，S有最大值，S=4；（3）Q（﹣4，4）或（﹣2+2，2﹣2）或（﹣2﹣2，2+2）或（4，﹣4）．【解析】（1）先假设出函数解析式，利用三点法求解函数解析式．（2）∵M点的横坐标为m，且点M在这条抛物线上，∴M点的坐标为：（m，m2+m﹣4），∴S=S△AOM+S△OBM﹣S△AOB=×4×（﹣m2﹣m+4）+×4×（﹣m）﹣×4×4=﹣m2﹣2m+8﹣2m﹣8=﹣m2﹣4m，=﹣（m+2）2+4，∵﹣4＜m＜0，当m=﹣2时，S有最大值为：S=﹣4+8=4．答：m=﹣2时，S有最大值，S=4．（3）设P（x，x2+x﹣4）．当OB为边时，根据平行四边形的性质知PQ∥OB，且PQ=OB，∴Q的横坐标等于P的横坐标，又∵直线的解析式为y=﹣x，则Q（x，﹣x）．由PQ=OB，得|﹣x﹣（x2+x﹣4）|=4，解得x=0，﹣4，﹣2±2．x=0不合题意，舍去．如图，当BO为对角线时，知A与P应该重合，OP=4．四边形PBQO为平行四边形则BQ=OP=4，Q 横坐标为4，代入y=﹣x得出Q为（4，﹣4）．由此可得Q（﹣4，4）或（﹣2+2，2﹣2）或（﹣2﹣2，2+2）或（4，﹣4）．点睛：考查了三点式求抛物线的方法，以及抛物线的性质和最值的求解方法．19．如图，抛物线y=ax2+bx﹣经过A（﹣1，0），B（5，0）两点．（1）求此抛物线的解析式；（2）在抛物线的对称轴上有一点P，使得PA+PC的值最小时，求△ABP的面积；（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，直接写出点N的坐标；若不存在，请说明理由．【答案】（1）y=x2﹣2x﹣；（2）；（3）符合条件的点N的坐标为（4，﹣）、（2+，）或（2﹣，）．种情况分别画出图形，从而得出答案．详解：（1）把A（﹣1，0），B（5，0）代入y=ax2+bx﹣，得到，解得：，即抛物线的解析式为y=x2﹣2x﹣；六、抛物线与动点问题20．如图，在平面直角坐标系中，抛物线y =ax2+bx﹣3（a≠0）与x轴交于点A（﹣2，0）、B（4，0）两点，与y轴交于点C．点P、Q分别是AB、BC上的动点，当点P从A点出发，在线段AB上以每秒3个单位长度的速度向B 点运动，同时点Q 从B 点出发，在线段BC 上以每秒1个单位长度的速度向C 点运动，其中一个点到达终点时，另一个点也停止运动.设P 、Q 同时运动的时间为t 秒（0<t <2).（1）求抛物线的表达式；（2）设△PBQ 的面积为S ，当t 为何值时，△PBQ 的面积最大，最大面积是多少？ （3）当t 为何值时，△PBQ 是等腰三角形？【答案】（1）y =38x 2−34x −3；（2）当t =1时，S △PBQ 最大=910.；（3）当t 的值是32秒或3023秒或4829秒时,△CPQ 为等腰三角形.(2)由题意可知：AP =3t ，BQ =t . ∴PB =6−3t .由题意得,点C 的坐标为(0,−3). 在Rt △BOC 中,BC 22345+=. 如图1，过点Q 作QH ⊥AB 于点H .∴QH∥CO，∴△BHQ∽△BOC∴HQ BQOC BC=,即35HQ t=∴HQ=3 5 t.∴S△PBQ=12PB⋅HQ=12(6−3t)⋅35t=−910t2+95t=−910(t−1)2+910.∴当t=1时，S△PBQ最大=910. （）答：运动1秒使△PBQ的面积最大,最大面积是9 10；∵cos∠HBQ =BD OB BP BC=∴142635tt=-,解得t=4829∴当t=4829秒时，△CPQ 是等腰三角形，即当△CPQ为等腰三角形时,t的值是32秒或3023秒或4829秒.21．如图，在平面直角坐标系中，抛物线（a ≠0）与x轴交于A、B两点，与y轴交于点C，且OA =2，OB=8，OC =6．（1）求抛物线的解析式；（2）点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时，点N从B 出发，在线段BC 上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动，当△MBN存在时，求运动多少秒使△MBN的面积最大，最大面积是多少？（3）在（2）的条件下，△MBN面积最大时，在BC上方的抛物线上是否存在点P，使△BPC的面积是△MBN面积的9倍？若存在，求点P的坐标；若不存在，请说明理由．【答案】（1）；（2）运动秒使△MBN的面积最大，最大面积是；（3）P（3，）或（5，）．（2）设运动时间为t秒，则AM=3t，BN=t，∴MB=10﹣3t．由题意得，点C的坐标为（0，6）．在Rt△BOC 中，BC==10．如图，过点N作NH⊥AB于点H，∴NH∥CO，∴△BHN∽△BOC，∴，即，∴HN=t，∴S△MBN=MB•HN=（10﹣3t）•t==﹣（t﹣）2+，当△MBN存在时，0＜t＜2，∴当t=时，S△MBN最大=．答：运动秒使△MBN的面积最大，最大面积是；（3）设直线BC的解析式为y=kx+c（k≠0）．把B（8，0），C（0，6）代入，得：，解得：，∴直线BC的解析式为．∵点P在抛物线上，∴设点P的坐标为（m，），如图，过点P作PE∥y轴，交BC于点E，则E点的坐标为（m，）．22．如图，已知抛物线与y轴交于点，与x轴交于点，点P是线段AB上方抛物线上的一个动点．求这条抛物线的表达式及其顶点坐标；当点P移动到抛物线的什么位置时，使得，求出此时点P的坐标；当点P从A点出发沿线段AB上方的抛物线向终点B移动，在移动中，点P的横坐标以每秒1个单位长度的速度变动；与此同时点M以每秒1个单位长度的速度沿AO向终点O移动，点P，M移动到各自终点时停止当两个动点移动t秒时，求四边形P AMB的面积S关于t的函数表达式，并求t为何值时，S有最大值，最大值是多少？【答案】（1）抛物线的表达式为，抛物线的顶点坐标为；（2）P点坐标为；（3）当时，S有最大值，最大值为24．解：根据题意，把，代入抛物线解析式可得，解得，抛物线的表达式为，，抛物线的顶点坐标为；如图1，过P作轴于点C，，，当时，，，即，设，则，，把P点坐标代入抛物线表达式可得，解得或，经检验，与点A重合，不合题意，舍去，所求的P点坐标为；七、抛物线与直线、线段的交点问题23．在平面直角坐标系xOy中，抛物线y=mx2﹣4mx+4m+4（m≠0）的顶点为P．P，M两点关于原点O成中心对称．（1）求点P，M的坐标；（2）若该抛物线经过原点，求抛物线的表达式；（3）在（2）的条件下，将抛物线沿x轴翻折，翻折后的图象在0≤x≤5的部分记为图象H，点N为抛物线对称轴上的一个动点，经过M，N的直线与图象H有两个公共点，结合图象求出点N的纵坐标n的取值范围．【答案】（1）点P（2，4），点M（﹣2，﹣4）；（2）y=﹣x2+4x（3）﹣4＜n≤24．已知二次函数y=x2﹣2（k+1）x+k2﹣2k﹣3与x轴有两个交点．（Ⅰ）求k取值范围；（Ⅱ）当k取最小整数时，此二次函数的对称轴和顶点坐标；（Ⅲ）将（Ⅱ）中求得的抛物线在x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分不变，得到一个新图象．请你求出新图象与直线y=x+m有三个不同公共点时m的值．【答案】（Ⅰ）k＞﹣1（Ⅱ）对称轴为：x=1．顶点坐标为（1，﹣4）；（Ⅲ）m的值为1或13 425．在平面直角坐标系中，二次函数y=x2+mx+2m﹣7的图象经过点（1，0）．（1）求抛物线的表达式；（2）把﹣4＜x＜1时的函数图象记为H，求此时函数y的取值范围；（3）在（2）的条件下，将图象H在x轴下方的部分沿x轴翻折，图象H的其余部分保持不变，得到一个新图象M．若直线y=x+b与图象M有三个公共点，求b的取值范围．【答案】（1）抛物线的表达式为y=x2+2x﹣3；（2）y的取值范围是﹣4≤y＜5；（3）b的取值范围是3＜b＜21 4．解：（1）∵二次函数y=x2+mx+2m﹣7的图象经过点（1，0），∴1+m+2m﹣7=0，解得m=2，∴抛物线的表达式为y=x2+2x﹣3；（2）y=x2+2x﹣3=（x+1）2﹣4，∵当﹣4＜x＜﹣1时，y随x增大而减小；当﹣1≤x＜1时，y随x增大而增大，∴当x=﹣1，y 最小=﹣4，当x=﹣4时，y=5，∴﹣4＜x ＜1时，y 的取值范围是﹣4≤y ＜5；26．在平面直角坐标系xOy 中，抛物线2443y mx mx m =-++的顶点为A ．（1）求点A 的坐标；（2）将线段OA 沿x 轴向右平移2个单位得到线段O A ''．①直接写出点O '和A '的坐标；②若抛物线2443y mx mx m =-++与四边形AOO A ''有且只有两个公共点，结合函数的图象，求m 的取值范围．【答案】（1）（2，3）（2）O '（2，0）， A '（4，3）（3）304m -<<（3）如图，∵抛物线y ＝mx 2－4mx ＋4m ＋3与四边形AOO ′A ′有且只有两个公共点，∴m ＜0．由图象可知，抛物线是始终和四边形AOO 'A '的边O 'A '相交，∴抛物线已经和四边形AOO ′A ′有两个公共点，∴将（0，0）代入y ＝mx 2－4mx ＋4m ＋3中，得m ＝34-． ∴34-＜m ＜0． 七、抛物线与整点问题27. 在平面直角坐标系xOy 中，抛物线221(0)y mx mx m m =-+->与x 轴的交点为A,B.(1)求抛物线的顶点坐标；（2）横、纵坐标都是整数的点叫做整点。

初三数学二次函数的性质试题答案及解析1.抛物线y=5（x﹣2）2+1的顶点是．【答案】（2，1）【解析】根据抛物线的顶点式y=a（x﹣h）2+k，顶点坐标是（h，k），可直接写出顶点坐标．解：抛物线y=5（x﹣2）2+1的顶点是（2，1）．故答案为：（2，1）．点评：此题主要考查了二次函数的性质，二次函数顶点式y=a（x﹣h）2+k，顶点坐标是（h，k），对称轴是x=h．2.已知抛物线y=x2﹣2x﹣3与y轴交于点C，则点C的坐标是；若点C′是点的C关于该抛物线的对称轴对称点，则C′点的坐标是．【答案】（0，﹣3），（2，﹣3）【解析】要知抛物线y=x2﹣2x﹣3与y轴交点C的坐标，应知点C的横坐标是0，把0代入即可，抛物线关于对称轴具有对称性，从而可求出点C‘的纵坐标，代入即可求出横坐标．即求出答案．解：抛物线y=x2﹣2x﹣3与y轴交于点C，当x=0时 y=02﹣2×0﹣3=﹣3，∴点C的坐标是（0，﹣3），y=x2﹣2x﹣3，这里a=1，b=﹣2，∴﹣=﹣=1，即：对称轴是x=1，∵点C′是点C关于该抛物线的对称轴对称的点，点C的坐标是（0，﹣3），∴点C′也在抛物线y=x2﹣2x﹣3上，且C′点的纵坐标也是﹣3，当y=﹣3时 x2﹣2x﹣3=﹣3，解得：x1=0，x2=2，∴C′点的坐标是：（2，﹣3），故答案为：（0，﹣3），（2，﹣3）．点评：此题主要考查对抛物线的性质的理解和掌握，能正确求出抛物线上点的坐标；并能利用抛物线的对称轴的对称性，求出对称点的坐标．3.已知抛物线的表达式是y=2（x+2）2﹣1，那么它的顶点坐标是．【答案】（﹣2，﹣1）【解析】已知解析式为抛物线的顶点式，可直接写出顶点坐标．解：∵y=2（x+2）2﹣1是抛物线解析式的顶点式，∴根据顶点式的坐标特点可知，顶点坐标为（﹣2，﹣1）．故答案为（﹣2，﹣1）．点评：本题主要考查了求抛物线的顶点坐标的方法，确定抛物线的顶点坐标的方法可以用配方法或公式法．4.已知抛物线的顶点坐标为（﹣1，﹣2），且通过点（1，10），则该抛物线的解析式为．【答案】y=3（x+1）2﹣2【解析】设抛物线的解析式为y=a（x+1）2﹣2．然后将点（1，10）代入其中，利用待定系数法求该抛物线的解析式即可．解：由题意，可设抛物线的解析式为y=a（x+1）2﹣2．∵该抛物线的解析式通过点（1，10），∴10=a（1+1）2﹣2，解得，a=3；故该抛物线的解析式是：y=3（x+1）2﹣2．点评：本题考查了待定系数法求二次函数的解析式．解答该题时，要充分利用已知条件“抛物线的顶点坐标为（﹣1，﹣2）”来设该抛物线的解析式．5.二次函数y=﹣2（x﹣1）（x﹣3）的图象的对称轴是．【答案】直线x=2【解析】此题先化抛物线的解析式为一般式，再用对称轴公式求解即可．解：∵y=﹣2（x﹣1）（x﹣3）=﹣2x2+8x﹣6，∴x=﹣=2．故答案是：直线x=2．点评：此题主要考查二次函数y=ax2+bx+c（a，b，c为常数，a≠0）对称轴公式，要求掌握并灵活运用．公式为x=﹣．6.根据图中的抛物线可以判断：当x 时，y随x的增大而减小．【答案】＜1【解析】要确定抛物线的单调性首先要知道其对称轴，然后根据对称轴来确定x的取值范围．解：根据图象可知对称轴为x=（﹣1+3）÷2=1，所以当x＜1时，y随x的增大而减小；当x=1时，y有最小值．故答案为：＜1；点评：此题主要考查了函数的单调性与对称性．7.已知抛物线y=x2+（2m+1）x+m+1，根据下列条件分别求m的值．（1）若抛物线过原点；（2）若抛物线的顶点在x轴上；（3）若抛物线的对称轴为x=1．【答案】（1）m=﹣1（2）m=±（3）m=﹣【解析】（1）将原点（0，0）代入抛物线方程，求得m值；（2）根据根的判别式解答；（3）由对称轴方程解答m值．解：（1）∵抛物线y=x2+（2m+1）x+m+1过原点，∴点O（0，0）满足该抛物线方程，∴0=m+1，解得m=﹣1；（2）∵抛物线的顶点在x轴上，∴△=（2m+1）2﹣4（m+1）=0，即4m2﹣3=0，解得，m=±；（3）∵抛物线的对称轴为x=1，∴2m+1=﹣2，解得m=﹣．点评：本题主要考查了待定系数法求二次函数解析式．解答此题时，用到了二次函数的根的判别式△=b2﹣4ac、对称轴方程x=﹣及方程解的意义．8.已知二次函数y=ax2+bx﹣3的图象经过点A（2，﹣3），B（﹣1，0）．求二次函数的解析式．【答案】y=x2﹣2x﹣3【解析】根据题意知，将A（2，﹣3），B（﹣1，0）代入二次函数的解析式，利用待定系数法法求该二次函数的解析式即可．解：根据题意，得，解得，；∴该二次函数的解析式为：y=x2﹣2x﹣3．点评：本题主要考查了待定系数法求二次函数的解析式．解题时，借用了二次函数图象上点的坐标特征：经过图象上的点一定在函数图象上，且图象上的每一个点均满足该函数的解析式．9.一个二次函数的图象经过点（0，0），（﹣1，﹣1），（1，9）三点，求这个函数的关系式．【答案】y=4x2+5x【解析】先设二次函数的一般关系式，然后将已知条件代入其中并解答即可．解：设二次函数的关系式为y=ax2+bx+c（a≠0），∵二次函数的图象经过点（0，0），（﹣1，﹣1），（1，9）三点，∴点（0，0），（﹣1，﹣1），（1，9）满足二次函数的关系式，∴，解得，所以这个函数关系式是：y=4x2+5x．点评：本题主要考查的是利用待定系数法求二次函数解析式．10.根据条件求下列抛物线的解析式：（1）二次函数的图象经过（0，1），（2，1）和（3，4）；（2）抛物线的顶点坐标是（﹣2，1），且经过点（1，﹣2）．【答案】（1）y=x2﹣2x+1（2）y=﹣x2﹣x﹣【解析】（1）设抛物线的解析式是y=ax2+bx+c，把（0，1），（2，1），（3，4）代入得到一个三元一次方程组，求出方程组的解即可；（2）根据抛物线的顶点坐标设抛物线的解析式是：y=a（x+2）2+1，把（1，﹣2）代入得到一个关于a的方程，求出a的值即可．解：（1）设抛物线的解析式是y=ax2+bx+c，把（0，1），（2，1），（3，4）代入得：，解得：，∴y=x2﹣2x+1．（2）设抛物线的解析式是：y=a（x+2）2+1，把（1，﹣2）代入得：﹣2=a（1+2）2+1，∴a=﹣，∴y=﹣（x+2）2+1，即y=﹣x2﹣x﹣．点评：本题考查了用待定系数法求出二次函数的解析式，解三元一次方程组，解一元一次方程等知识点的理解和掌握，关键是看学生如何正确地设抛物线的解析式，注意抛物线的解析式有：①三点式y=ax2+bx+c；②顶点式y=a（x﹣h）2+k，顶点坐标是（h，k）；③交点式y=a（x﹣m）（x﹣n），抛物线与x轴的交点坐标是（m，0），（n，0）．11.已知反比例函数y=与一次函数y=kx﹣2的图象都经过点A（a，﹣4），且一次函数y=kx﹣2的图象与x轴交于点B．（1）求a、k的值；（2）若抛物线y=x2+bx+c过点A、B，求此抛物线的解析式．【答案】（1）k=1（2）y=x2+x﹣6【解析】（1）把A（a，﹣4）代入y=求出a，把A的坐标代入直线求出k即可；（2）根据直线的解析式求出B的坐标，把A、B的坐标代入抛物线得出关于b、c的方程组，求出即可．解：（1）把A（a，﹣4）代入y=得：﹣4=，∴a=﹣2，即A（﹣2，﹣4），代入y=kx﹣2得：﹣4=﹣2k﹣2，∴k=1，答：a=﹣2，k=1．解：（2）直线是y=x﹣2，把y=0代入得：0=x﹣2，∴x=2，∴B（2，0），把A（﹣2，﹣4），B（2，0）代入y=x2+bx+c得：，解得：b=1，c=﹣6，y=x2+x﹣6，答：此抛物线的解析式是y=x2+x﹣6．点评：本题主要考查对解二元一次方程组，解一元一次方程，用待定系数法求抛物线的解析式，反比例函数与一次函数的交点问题，一次函数图象上点的坐标特征等知识点的理解和掌握，能熟练地运用这些性质进行计算是解此题的关键．12.直线y=2x+3与抛物线y=ax2交于A、B两点，已知A点的横坐标是3，求A、B两点的坐标及抛物线的解析式．【答案】（﹣1，1）【解析】首先根据点A的横坐标求得其纵坐标，然后代入抛物线求得其解析式，然后联立组成方程组后求交点坐标即可．解：∵直线y=2x+3与抛物线y=ax2交于A、B两点且A点的横坐标是3，∴点A的纵坐标y=2×3+3=9，∴点A的坐标为（3，9），将点A的坐标代入y=ax2得：a=1，∴抛物线的解析式为y=x2，∴解得：或∴点B的坐标为：（﹣1，1）．点评：本题考查了二次函数的性质，重点是知道如何求两图象的交点坐标．13.抛物线y=（x+1）2﹣3的顶点坐标是（）A．（1，﹣3）B．（﹣1，﹣3）C．（1，3）D．（﹣1，3）【答案】B【解析】已知抛物线的顶点式，可直接写出顶点坐标．解：由y=（x+1）2﹣3，根据顶点式的坐标特点可知，顶点坐标为（﹣1，﹣3），故选B．点评：考查将解析式化为顶点式y=a（x﹣h）2+k，顶点坐标是（h，k），对称轴是x=h．14.抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示．线一定经过点（2，0）；④在对称轴左侧，y随x增大而减小．从表可知，说法正确的个数有（）A.1个 B.2个 C.3个 D.4个【答案】B【解析】根据表中数据和抛物线的对称性，可得到抛物线的开口向下，当x=3时，y=0，即抛物线与x轴的交点为（﹣2，0）和（3，0）；因此可得抛物线的对称轴是直线x=，再根据抛物线的性质即可进行判断．解：根据图表，抛物线与y轴交与（0，6），①正确；∵抛物线经过点（0，6）和（1，6），∴对称轴为x==，∴②正确；设抛物线经过点（x，0），∴x==解得：x=3∴抛物线一定经过（3，0），故③错误；在对称轴左侧，y随x增大而增大，④错误故选B．点评：本题考查了抛物线y=ax2+bx+c的性质：抛物线是轴对称图形，它与x轴的两个交点是对称点，对称轴与抛物线的交点为抛物线的顶点；a＜0时，函数有最大值，在对称轴左侧，y随x增大而增大．15.抛物线y=﹣3（x﹣3）2+5的顶点坐标为（）A．（3，5）B．（﹣3，5）C．（5，﹣3）D．（5，3）【答案】A【解析】因为y=﹣3（x﹣3）2+5是二次函数的顶点式，根据顶点式可直接写出顶点坐标．解：∵抛物线解析式为y=﹣3（x﹣3）2+5，∴二次函数图象的顶点坐标是（3，5）．故选A．点评：本题考查了二次函数的性质，根据抛物线的顶点式，可确定抛物线的开口方向，顶点坐标（对称轴），最大（最小）值，增减性等．16.已知二次函数y=x2+bx+c的图象上有三个点（﹣1，y1）、（1，y2）、（3，y3），若y1=y3，则（）A．y2＞c＞y1B．y2＜c＜y1C．c＞y1＞y2D．c＜y1＜y2【答案】B【解析】根据已知得出（﹣1，y1）和（3，y3）关于二次函数数y=x2+bx+c的对称轴对称，抛物线的开口向上，求出对称轴是直线x=1，根据0＜1＜3即可求出答案．解：∵y1=y3，∴（﹣1，y1）和（3，y3）关于二次函数数y=x2+bx+c的对称轴对称，∴二次函数y=x2+bx+c的对称轴是直线x==1，且二次函数图象的开口向上，∵x=0时，y=c，0＜1＜3，∴y2＜c＜y1，故选B．点评：本题主要考查对二次函数图象上点的坐标特征，二次函数的性质等知识点的理解和掌握，能求出对称轴和根据二次函数的性质求出正确答案是解此题的关键．17.（2011•淮北模拟）给出下列四个命题：正确命题的个数是（）（1）若点A在直线y=2x﹣3上，且点A到两坐标轴的距离相等，则点A在第一或第四象限；（2）若A（a，m）、B（a﹣1，n）（a＞0）在反比例函数y=的图象上，则m＜n；（3）一次函数y=﹣2x﹣3的图象不经过第三象限；（4）二次函数y=﹣2x2﹣8x+1的最大值是9．A．1个B．2个C．3个D．4个【答案】B【解析】根据题意和函数的有关性质，逐一判断每个命题的正确性．解：（1）联立或，解得或所以点A的坐标为（3，3）或（（1，﹣1），在第一或第四象限正确（2）反比例函数y=，在每个象限内y随x的增大而减小，点A在第一象限，而点B不能确定在第几象限，无法比较m、n的大小，错误（3）一次函数y=﹣2x﹣3的图象不经过第一象限，错误（4）二次函数y=﹣2x2﹣8x+1，可化为y=﹣2（x+2）2+9所以二次函数y=﹣2x2﹣8x+1的最大值是9，正确．（1）、（4）正确，故选B．点评：此题考查了二次函数的增减性和最值，一次函数、反比例函数的增减性，以及一次函数的图象性质．18.（2010•无锡一模）二次函数y=x2﹣x+m（m为常数）的图象如图所示，当x=a时，y＜0；那么当x=a﹣1时，函数值（）A．y＜0B．0＜y＜m C．y＞m D．y=m【答案】C【解析】根据对称轴及函数值判断a的取值范围，从而得出a﹣1＜0，因为当x是y随x的增大而减小，所以当x=a﹣1＜0时，函数值y一定大于m．解：当x=a时，y＜0，则a的范围是x1＜a＜x2，又对称轴是x=，所以a﹣1＜0，当x是y随x的增大而减小，当x=0是函数值是m．因而当x=a﹣1＜0时，函数值y一定大于m．故选C．点评：本题主要考查了二次函数的对称轴，以及增减性．19.抛物线y=﹣2（x+1）2+3的顶点坐标是（）A．（1，3）B．（﹣1，﹣3）C．（﹣2，3）D．（﹣1，3）【答案】D【解析】已知抛物线的顶点式，可直接写出顶点坐标．解：由y=﹣2（x+1）2+3，根据顶点式的坐标特点可知，顶点坐标为（﹣1，3），故选D．点评：考查将解析式化为顶点式y=a（x﹣h）2+k，顶点坐标是（h，k），对称轴是x=h．20.已知抛物线y=5（x﹣1）2，下列说法中，你认为不正确的是（）A．顶点坐标为（1，0）B．对称轴为直线x=0C．当x＞1时，y随x的增大而增大D．当x＜1时，y随x的增大而减小【答案】B【解析】根据二次函数y=5（x﹣1）2的性质，利用排除法求解．解：A、顶点坐标为（1，0），正确，不符合题意；B、对称轴为直线x=1，错误，符合题意；C、当x＞1时，y随x的增大而增大，正确，不符合题意；D、当x＜1时，y随x的增大而减小，正确，不符合题意．故选B．点评：本题考查了二次函数的性质，牢记形如y=a（x﹣h）2的二次函数的性质是解答本题的关键．。