抛物线双曲线椭圆知识点

<一>圆的方程(x-a)^2+(y-b)^2=r^2，圆心O（a，b），半径r。

（1）圆的一般式方程：x^2+y^2+Dx+Ey+F=0此方程可用于解决两圆的位置关系：配方化为标准方程：（x+D/2）^2.+(y+E/2)^2=(D^2+E^2-4F)/4其圆心坐标：（-D/2,-E/2）半径为r=√[（D^2+E^2-4F）]/2此方程满足为圆的方程的条件是:D^2+E^2-4F>0若不满足,则不可表示为圆的方程（2）点与圆的位置关系点P（X1,Y1) 与圆(x－a)^2+(y－b) ^2=r^2的位置关系：⑴当(x1－a)^2+(y1－b) ^2>r^2时，则点P在圆外。

⑵当(x1－a)^2+(y1－b) ^2=r^2时，则点P在圆上。

⑶当(x1－a)^2+(y1－b) ^2<r^2时，则点P在圆内。

圆与直线的位置关系判断平面内，直线Ax+By+C=0与圆x^2+y^2+Dx+Ey+F=0的位置关系判断一般方法是：1.由Ax+By+C=0，可得y=(-C-Ax)/B，（其中B不等于0），代入x^2+y^2+Dx+Ey+F=0，即成为一个关于x的一元二次方程f（x）=0。

利用判别式b^2-4ac的符号可确定圆与直线的位置关系如下：如果b^2-4ac>0，则圆与直线有2交点，即圆与直线相交。

如果b^2-4ac=0，则圆与直线有1交点，即圆与直线相切。

如果b^2-4ac<0，则圆与直线有0交点，即圆与直线相离。

2.如果B=0即直线为Ax+C=0，即x=-C/A，它平行于y轴（或垂直于x 轴），将x^2+y^2+Dx+Ey+F=0化为 (x－a)^2+(y－b) ^2=r^2。

令y=b，求出此时的两个x值x1、x2，并且规定x1<x2，那么：当x=-C/A<x1或x=-C/A>x2时，直线与圆相离；当x1<x=-C/A<x2时，直线与圆相交；半径r，直径d在直角坐标系中，圆的解析式为：(x-a)^2+(y-b)^2=r^2;x^2+y^2+Dx+Ey+F=0=> (x+D/2)^2+(y+E/2)^2=(D^2+E^2-4F)/4=> 圆心坐标为(-D/2,-E/2)其实只要保证X方Y方前系数都是1就可以直接判断出圆心坐标为(-D/2,-E/2)这可以作为一个结论运用的且r=根号（圆心坐标的平方和-F）<二>椭圆的标准方程椭圆的标准方程分两种情况：当焦点在x轴时,椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(a>b>0)；当焦点在y轴时,椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(a>b>0)；其中a>0，b>0。

圆椭圆双曲线抛物线知识点汇总一、圆椭圆双曲线抛物线的定义1. 圆：圆是平面上到定点距离相等的所有点的集合。

圆由圆心和半径唯一确定。

2. 椭圆：椭圆是平面上到两个定点的距离之和为常数的所有点的集合。

椭圆由两个焦点和两个半轴唯一确定。

3. 双曲线：双曲线是平面上到两个定点的距离之差为常数的所有点的集合。

双曲线由两个焦点和两个实轴唯一确定。

4. 抛物线：抛物线是平面上到定点距离等于到定直线的距离的所有点的集合。

抛物线由焦点和直线唯一确定。

二、圆椭圆双曲线抛物线的方程1. 圆：圆的标准方程为(x-a)² + (y-b)² = r²，其中圆心为(a, b)，半径为r。

2. 椭圆：椭圆的标准方程为x²/a² + y²/b² = 1，其中a和b分别为x轴和y轴上的半轴长。

3. 双曲线：双曲线的标准方程为x²/a² - y²/b² = 1或者y²/a² - x²/b² = 1，取决于焦点的位置。

4. 抛物线：抛物线的标准方程为y² = 4ax或者x² = 4ay，取决于抛物线开口的方向。

三、圆椭圆双曲线抛物线的性质1. 圆：圆的直径是圆上任意两点之间的最大距离，且所有直径相等。

2. 椭圆：椭圆的离心率介于0和1之间，离心率越接近0，椭圆越接近于圆。

3. 双曲线：双曲线分为两支，每一支的焦点到定点的距离之差相等。

4. 抛物线：抛物线的焦点在抛物线上方，开口方向取决于系数a的正负号。

四、圆椭圆双曲线抛物线的应用1. 圆：在几何中常常与角度和三角函数结合，用于描述正弦和余弦函数的周期性。

2. 椭圆：在天体力学中用于描述行星轨道的形状，以及通信中的极化椭圆。

3. 双曲线：在光学和电磁学中用于描述折射和反射现象。

4. 抛物线：在物理学中用于描述自由落体运动和抛物线运动。

椭圆双曲线抛物线知识点汇总一、椭圆椭圆是平面内到定点 F1、F2 的距离之和等于常数（大于|F1F2|）的动点 P 的轨迹，F1、F2 称为椭圆的焦点，两焦点的距离|F1F2|称为椭圆的焦距。

1、椭圆的标准方程焦点在 x 轴上：＼（＼frac{x^2}｛a^2} ＋＼frac{y^2}｛b^2} ＝ 1\）（＼（a ＞ b ＞ 0\）），其中\（a\）为长半轴长，＼（b\）为短半轴长，＼（c\）为半焦距，满足\（c^2 ＝ a^2 b^2\）。

焦点在 y 轴上：＼（＼frac{y^2}｛a^2} ＋＼frac{x^2}｛b^2} ＝ 1\）（＼（a ＞ b ＞ 0\））。

2、椭圆的性质范围：对于焦点在 x 轴上的椭圆，＼（a ＼leq x ＼leq a\），＼（b＼leq y ＼leq b\）；对于焦点在 y 轴上的椭圆，＼（b ＼leq x ＼leq b\），＼（a ＼leq y ＼leq a\）。

对称性：椭圆关于 x 轴、y 轴和原点对称。

顶点：焦点在 x 轴上时，顶点坐标为\（（＼pm a, 0)＼），＼（（0, ＼pm b)＼）；焦点在 y 轴上时，顶点坐标为\（（0, ＼pm a)＼），＼（（＼pm b, 0)＼）。

离心率：椭圆的离心率\（e ＝＼frac{c}｛a}＼）（＼（0 ＜ e ＜1\）），它反映了椭圆的扁平程度，＼（e\）越接近0，椭圆越接近圆；＼（e\）越接近 1，椭圆越扁。

3、椭圆的参数方程焦点在 x 轴上：＼（＼begin{cases}x ＝ a\cos\theta ＼＼ y ＝b\sin\theta\end{cases}＼）（＼（＼theta\）为参数）焦点在 y 轴上：＼（＼begin{cases}x ＝ b\cos\theta ＼＼ y ＝a\sin\theta\end{cases}＼）（＼（＼theta\）为参数）4、椭圆中的焦点三角形设 P 为椭圆上一点，F1、F2 为焦点，＼（＼angle F1PF2 ＝＼theta\），则三角形 PF1F2 的面积为\（S ＝ b^2\tan\frac{＼theta}｛2}＼）。

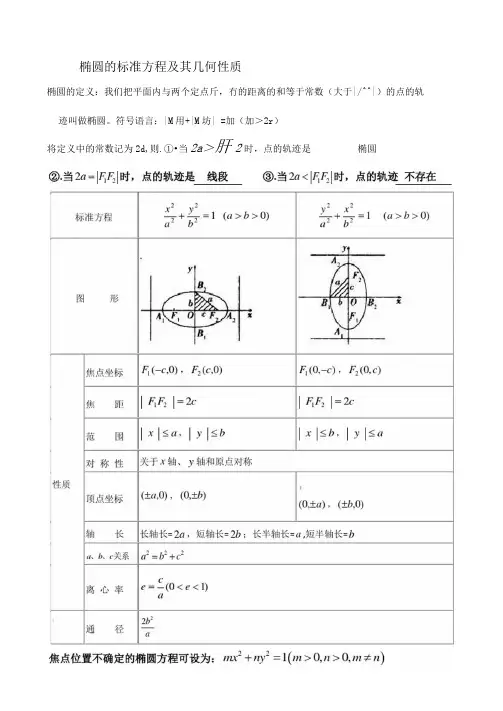
椭圆的标准方程及其几何性质
椭圆的定义：我们把平面内与两个定点斤，冇的距离的和等于常数（大于|/^^|）的点的轨迹叫做椭圆。

符号语言；|M用+|M坊| =加（加＞2r）
肝2时，点的轨迹是椭圆
将定义中的常数记为2d,则.①•当2a＞
与椭圆务卜快焦点的椭圆系方程可设为：£+£*＞»)
双曲线的标准方程及其几何性质
双曲线的定义：我们把平面内与两个定点F F朽的距离的差的绝对值等于常数(小于闪马) 的点的轨迹叫做双曲线。

符号语言；I M歼1 = 2"加＜2c)
将定义中的常数记为2d,则：①•当加＜川^时，点的轨迹是双曲线
焦点位置不确定的双曲线方程可设为：=1（血“>0） 与双曲线P 討共焦点的双曲线系方程可设为七一冷十宀皿 与双曲线yp 咲渐近线的双曲线系方程可设为：P 討（心
抛物线的标准方程及其几何性质
抛物线的定义：我们把平B 内与一个定点F 和一条定直线/ （/不经过点F ）距离相等 的点的轨迹叫做抛物线。

点F 叫做抛物线的焦点，直线/叫做抛物线的准线。

KA
直线与抛物线相交于且直线过抛物线的焦点，则过焦点的弦长公式:
AB =X|
+ p (a 为5纽酗倾斜角) sin a
直线与椭圆（或与双曲线、抛物线）相交于A （Xpy,XB （%.,y,）,则椭圆（或双曲线.抛 物线)的弦长公式：
Jl + k? = +尤2)2 —4西天2 Jl + 疋 标准方程
y~ = 2px(p>Q) y~ =-2px(p>Q) X" = 2py(p>0) X" =-2py(p >0}
AB = x^ -Xj。

椭圆方程、双曲线方程、抛物线方程是平面解析几何中常见的曲线方程类型，它们在数学、物理、工程等领域都有着重要的应用。

通过联立这些方程，不仅可以深入理解曲线的特性，还可以解决一些实际问题。

本文将分别介绍椭圆方程、双曲线方程、抛物线方程的基本定义和性质，以及它们的联立解法，帮助读者更好地理解和应用这些数学知识。

一、椭圆方程的定义和性质椭圆是平面上到两个定点F1和F2的距离之和等于常数2a的点P的轨迹。

椭圆方程的一般形式为：(x-h)²/a² + (y-k)²/b² = 1其中(h, k)为椭圆的中心坐标，a和b分别为椭圆的长半轴和短半轴。

椭圆有许多重要性质，如对称性、焦点、直径等，这些性质都可以通过椭圆方程的分析得到。

二、双曲线方程的定义和性质双曲线是平面上到两个定点F1和F2的距离之差等于常数2a的点P 的轨迹。

双曲线方程的一般形式为：(x-h)²/a² - (y-k)²/b² = 1类似椭圆，双曲线也有许多重要性质，如渐近线、焦点、枝等。

通过双曲线方程的分析，可以深入理解这些性质。

三、抛物线方程的定义和性质抛物线是平面上到一个定点F的距离等于到某条直线L的距离的点P 的轨迹。

抛物线方程的一般形式为：y² = 2px其中p为焦点到抛物线顶点的距离，也是抛物线的焦距。

抛物线也有许多重要性质，如焦点、直径、对称轴等，通过抛物线方程的分析可以得到这些性质。

四、联立椭圆、双曲线和抛物线方程的解法在一些实际问题中，我们需要联立椭圆、双曲线和抛物线方程进行求解。

以二元二次方程组为例，我们可以通过联立椭圆、双曲线和抛物线方程进行求解，得到曲线的交点、切点、共焦点等。

这对于一些物理、工程等领域的问题具有重要意义。

结论：椭圆方程、双曲线方程、抛物线方程是平面解析几何中常见的曲线方程类型，通过对它们的定义、性质和联立解法的深入理解，可以帮助我们更好地应用这些数学知识解决实际问题。

椭圆、双曲线、抛物线相关知识点总结一、椭圆的标准方程及其几何性质椭圆的定义：我们把平面内与两个定点F, F2的距离的和等于常数大于F1F21的点的轨迹叫做椭圆。

符号语言：|MF,| |MF2| 2a 2a 2c将定义中的常数记为2a,贝①.当2a卩人时，点的轨迹是椭圆_____________双曲线的标准方程及其几何性质双曲线的定义：我们把平面内与两个定点F, F2的距离的差的绝对值等于常数小于F”的点的轨迹叫做双曲线。

符号语言：MF t - MF22a 2a 2c将定义中的常数记为2a，贝①.当2a FE时，点的轨迹是双曲线_____________________ ②•当2a |吋2时，点的轨迹是两条射线③.当2a卩占时，点的轨迹不存在焦点位置不确定的双曲线方程可设为：mn 02 2与双曲线仔笃1共焦点的双曲线系方程可设为:a b2y1 ba kb kx22 2 2 2与双曲线笃 耸1共渐近线的双曲线系方程可设为： $ 爲a ba b三、抛物线的标准方程及其几何性质抛物线的定义：我们把平面内与一个定点 F 和一条定直线I （I 不经过点F ）距离相等 的点的轨迹叫做AB x , x 2 p -2^（为弦AB 的倾斜角）sin直线与椭圆（或与双曲线、抛物线）相交于 A （x i ,y i ）,B x 2,y 2，则椭圆（或双曲线、抛 物线）的弦长公式：AB x , x 2| —k 2J x , x 2 2 4%卷—k22 2 2 2与椭圆負b 2 1共焦点的椭圆系方程可设为：和冷1 k b 2标准方程2y 2px (p o )图形焦点坐标(p ,0) 2 (匕0) 2 （0月2(0,上) 2准线方程x& 2x E 2 y 舟 yi范围x 0, y R x 0, y Ry 0,x Ry 0,x R对称性 关于x 轴关于y 轴顶点坐标 (0,0)焦半径M X o ,y o|MF | X 。

1、范围:焦点在x轴上-a≤x≤a -b≤y≤b;焦点在y轴上-b≤x≤b -a≤y≤a[1]2、对称性：关于X轴对称，Y轴对称，关于原点中心对称。

3、顶点：（a，0）（-a，0）（0，b）（0，-b）4、离心率：e=c/a 或e=√1-b^2/a^25、离心率范围 0<e<16、离心率越大椭圆就越扁，越小则越接近于圆7.焦点(当中心为原点时)（-c，0），（c，0）或(0,c),(0,-c)切线法线定理1：设F1、F2为椭圆C的两个焦点，P为C上任意一点。

若直线AB切椭圆C于点P，且A和B在直线上位于P 的两侧，则∠APF1=∠BPF2。

定理2：设F1、F2为椭圆C的两个焦点，P为C上任意一点。

若直线AB为C在P点的法线，则AB平分∠F1PF2。

上述两定理的证明可以查看参考资料。

方程标准方程高中课本在平面直角坐标系中，用方程描述了椭圆，椭圆的标准方程中的“标准”指的是中心在原点，对称轴为坐标轴。

椭圆的标准方程有两种，取决于焦点所在的坐标轴：1）焦点在X轴时，标准方程为：x^2/a^2+y^2/b^2=1 (a>b>0)2）焦点在Y轴时，标准方程为：y^2/a^2+x^2/b^2=1 (a>b>0)其中a>0，b>0。

a、b中较大者为椭圆长半轴长，较短者为短半轴长（椭圆有两条对称轴，对称轴被椭圆所截，有两条线段，它们的一半分别叫椭圆的长半轴和短半轴或半长轴和半短轴）当a>b时，焦点在x轴上，焦距为2*(a^2-b^2）^0.5，焦距与长、短半轴的关系：b^2=a^2-c^2，准线方程是x=a^2/c和x=-a^2/c ，c为椭圆的半焦距。

又及：如果中心在原点，但焦点的位置不明确在X轴或Y轴时，方程可设为mx^2+ny^2=1(m>0，n>0，m≠n）。

即标准方程的统一形式。

椭圆的面积是πab。

椭圆可以看作圆在某方向上的拉伸，它的参数方程是：x=acosθ，y=bsinθ标准形式的椭圆在（x0，y0）点的切线就是：xx0/a^2+yy0/b^2=1。

圆锥曲线知识点一、 椭圆：1、定义：平面内与两个定点1F ，2F 的距离的和等于定长（定长大于两定点间的距离）的点的轨迹叫做椭圆，这两个定点叫焦点，两定点间距离焦距。

{}a MF MF M 221=+()212F F a >2、标准方程：（焦点在x 轴）)0(12222>>=+b a bya x；（焦点在y 轴）：)0(12222>>=+b a b x a y顶点坐标：)0,(a ± (0,)b ± 顶点坐标：),0(a ± (,0)b ±长轴长为a 2，短轴长为b 2焦点坐标：1(,0)F c 2(,0)F c - 焦点坐标：1(0,)F c 2(0,)F c -焦点在长轴上，c = 焦距：122F F c =离 心 率：ac e =(01e <<) ,ab a ac e 22222-==，e 越大椭圆越扁，e 越小椭圆越圆。

二、 双曲线：1、定义：平面内与两个定点1F ，2F 的距离的差的绝对值是常数（小于12F F ）的点的轨迹叫双曲线。

这两个定点叫做双曲线的焦点，两焦点的距离叫焦距。

{}a MF MF M 221=-()212F F a <2、标准方程：（焦点在x 轴）：)0,0(12222>>=-b a by ax ；（焦点在y 轴）：)0,0(12222>>=-b a bx ay焦点坐标：1(,0)F c - 2(,0)F c 1(0,)F c - 2(0,)F c 顶点坐标：（a -,0） (a ,0) (0, a -,) (0，a )离心率： e ac e (=>1)准线方程： c a x 2±= ca y 2±=准线垂直于实轴且在两顶点的内侧；两准线间的距离：ca 22渐近线方程：（焦点在x 轴）xab y±= (实虚) （焦点在y 轴）yab x±= (实虚){MFM =点M 到直线l 的距离}1、()022>=p px y， 焦点坐标：(2p ,0)， 准线方程：2p x -=2、)0(22>-=p px y ， 焦点坐标：(2p -,0)，准线方程：2p x =3、)0(22>=p py x ，焦点坐标：(0,2p )，准线方程：2p y -=4、)0(22>-=p py x ，焦点坐标：(0,2p -)，准线方程：2p y =三、抛物线定义：平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹叫做抛物线，点F 叫做抛物线的焦点，直线l 叫做抛物线的准线。

考点26 椭圆、双曲线与抛物线的方程及几何性质1．基础知识1．椭圆的概念(1)文字形式：在平面内到两定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹(或集合)叫椭圆．这两定点叫做椭圆的焦点 ，两焦点间的距离叫做焦距． (2)代数式形式：集合1212P={M||MF |+|MF |=2a |FF |=2c.} ①若a c >，则集合P 为椭圆；②若a c =，则集合P 为线段；③若a c <，则集合P 为空集． 2．双曲线的定义满足以下三个条件的点的轨迹是双曲线(1)在平面内；(2)动点到两定点的距离的差的绝对值为一定值；(3)这一定值一定要小于两定点的距离． 3．抛物线的定义(1)平面内与一个定点F 和一条定直线l (F ∉l )的距离相等的点的轨迹叫做抛物线．点F 叫做抛物线的焦点，直线l 叫做抛物线的准线．(2)其数学表达式：|MF |＝d (其中d 为点M 到准线的距离)4．重要结论 椭圆：22221x y a b+=（a ＞b ＞0）1、24ABF C a ∆=；2、椭圆22221x y a b+=（a ＞b ＞0）的焦半径公式：10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(F c 3、焦点12PF F ∆中，12F PF θ∠=， （1）1222sin tan 21cos PF F S b bθθθ∆==+； （2）12max ()PF F S bc ∆=；（3）当点P 位于短轴顶点处时，4、焦点弦中， (1) 通径最短，22b AB a=；（2）2112aAF BF b +=． 5、AB 是椭圆22221x y a b +=的不平行于对称轴的弦，M ,(00x 2OM AB a 6、（1）与椭圆22221x y a b +=（a>b>0）共焦点的椭圆方程可设为：22221x y a k b k+=++； （2）中心在原点，坐标轴为对称轴的椭圆方程可设为221(0,0,)mx ny m n m n +=>>≠．双曲线22221x y a b-=（a ＞0,b ＞o ）1、等轴双曲线 （1）22a b =；（2）渐近线为 y x =±；（3）离心率e =2、双曲线22221x y a b-=（a ＞0,b ＞o ）的焦半径公式：(1(,0)F c - , 2(,0)F c当00(,)M x y 在右支上时，10||MF ex a =+,20||MF ex a =-； 当00(,)M x y 在左支上时，10||MF ex a =-+,20||MF ex a =--． 3、焦点到渐近线的距离为b ．4、焦点12PF F ∆中，12F PF θ∠=，12221cos cot2sin PF F S b b θθθ∆+==；5、AB 是双曲线22221x y a b-=（a ＞0,b ＞0）的不平行于对称轴的弦，M ),(00y x 为AB 的中点，则22OM AB b K K a ⋅=，即0202y a x b K AB=． 6、（1）与22221x y a b -=共渐近线的双曲线方程22ax －22y b λ=（0λ≠）．（2）与22221x y a b-=有相同焦点的双曲线方程22x a k -－221y b=（2k a <且2k b ≠-）．抛物线22(0)y p x p =>,11(,)A x y ,22(,)B x y1、212y y p =-，2124p x x =；2、焦半径公式：12pAF x =+；3、焦点弦长公式： （1）121222p pAB x x x x p =+++=++（2）min 2AB p =（即焦点弦中，通径最短）．（3）AF BF p +=； （4）以AB 为直径的圆与准线相切；（5）以AF 或BF 为直径的圆与y 轴相切；【考点分类】考点一 椭圆的标准方程及其几何性质例1．【2015浙江文15】椭圆22221x y a b +=（0a b >>）的右焦点()F ,0c 关于直线by x c=的对称点Q 在椭圆上，则椭圆的离心率是 ．例2．【2015江苏18】如图，在平面直角坐标系xOy 中，已知椭圆()222210x y a b a b +=>>，右焦点F 到左准线2:a l x c=-的距离为3． （1）求椭圆的标准方程；（2）过F 的直线与椭圆交于A ，B 两点，线段AB 的垂直平分线分别交直线l 和A B 于点P ，C ，若PC =2AB ，求直线AB 的方程．【方法总结】1．椭圆的几何性质常涉及一些不等关系，例如对椭圆2222=1x y a b+，有－a ≤x ≤a ，－b ≤y ≤b,0<e <1等，在求与椭圆有关的一些量的范围，或者求这些量的最大值或最小值时，经常用到这些不等关系．2．求解与椭圆几何性质有关的问题时要结合图形进行分析，即使不画出图形，思考时也要联想到图形．当涉及到顶点、焦点、长轴、短轴等椭圆的基本量时，要理清它们之间的关系，挖掘出它们之间的内在联系．3．求椭圆离心率问题，应先将e 用有关的一些量表示出来，再利用其中的一些关系构造出关于e 的等式或不等式，从而求出e 的值或范围．离心率e 与a 、b 的关系：22222222e =1-c a b b ba a a a-==⇔= 巩固练习1． 【2015广东文8】已知椭圆222125x y m+=（0m >）的左焦点为()1F 4,0-，则m =（ ） A ．9 B ．4 C ．3 D ．22．已知椭圆2222:1(0)x y C a b a b+=>>的左焦点为,F C 与过原点的直线相交于,A B 两点，4,.10,6,cos ABF ,5AF BF AB AF C e ==∠=连接若则的离心率= ．3．三个顶点均在椭圆上的三角形称为椭圆的内接三角形．．．．．．已知点A 是椭圆的一个短轴端点，如果以A ．为直．． 角顶点．．．的椭圆内接等腰直角三角形有且仅有三个，则椭圆的离心率的取值范围是（ ）（A ） （B ） （C ） （D ）4．【2015天津文19】已知椭圆22221(a b 0)x y a b+=>>的上顶点为B ,左焦点为F ,（I ）求直线BF 的斜率;（II ）设直线BF 与椭圆交于点P （P 异于点B ）,过点B 且垂直于BP 的直线与椭圆交于点Q （Q 异于点B ）直线PQ 与y 轴交于点M ,||=||PM MQ l ．（i ）求l 的值；（ii ）若||sin PM BQP Ð,求椭圆的方程．5．【2015四川文20】如图，椭圆E ：22221x y a b+=(a >b >0)的离心率是2，点P (0，1)在短轴CD 上，且PC PD⋅＝－1．(Ⅰ)求椭圆E 的方程；(Ⅱ)设O 为坐标原点，过点P 的动直线与椭圆交于A 、B 两点．是否存在常数λ，使得OA OB PA PB λ⋅+⋅为定值？若存在，求λ的值；若不存在，请说明理由．考点二 双曲线的标准方程及其几何性质 例3．【2015湖北文9】将离心率为1e 的双曲线1C 的实半轴长a 和虚半轴长()b a b ≠同时增加(0)m m >个单位长度，得到离心率为2e 的双曲线2C ，则（ ） A ．对任意的,a b ，12e e > B ．当a b >时，12e e >；当a b <时，12e e < C ．对任意的,a b ，12e e <D ．当a b >时，12e e <；当a b <时，12e e >【方法总结】1．双曲线方程的求法(1)若不能明确焦点在哪条坐标轴上，设双曲线方程为mx 2＋ny 2＝1(mn <0)；(2)与双曲线2222=1x y a b -有共同渐近线的双曲线方程可设为2222=x y a bλλ-≠（0）．(3)若已知渐近线方程为mx ＋ny ＝0，则双曲线方程可设为m 2x 2－n 2y 2＝λ(λ≠0)．2．已知渐近线方程y ＝mx ，求离心率时若焦点不确定时，m ＝b a (m >0)或m ＝ba，故离心率有两种可能． 巩固练习1． 【2015天津文5】已知双曲线22221(0,0)x y a b a b-=>>的一个焦点为(2,0)F ,且双曲线的渐近线与圆()222y 3x -+=相切,则双曲线的方程为（ ）(A)221913x y -= (B) 221139x y -= (C) 2213x y -= (D) 2213y x -= 2． 如图，21,F F 是椭圆14:221=+y x C 与双曲线2C 的公共焦点，B A ,分别是1C ，2C 在第二、四象限的公共点．若四边形21BF AF 为矩形，则2C 的离心率是（ ）A ．2 B ．3 C ．23 D ．26 3． 已知直线x=2与双曲线22:14x C y -=的渐近线交于E 1、E 2两点，记2211,e OE e OE ==，任取双曲线C 上的点P ，若),(21R b a be ae OP ∈+=，则（ ）A ．1022<+<b aB ．21022<+<b a C ．122≥+b a D ．2122≥+b a 4．【2015山东文15】过双曲线C ：22221x y a a-=0,0a b >>（）的右焦点作一条与其渐近线平行的直线，交C 于点P ．若点P 的横坐标为2a ,则C 的离心率为 ．5．【2015江苏12】在平面直角坐标系xOy 中，P 为双曲线122=-y x 右支上的一个动点．若点P 到直线01=+-y x 的距离大于c 恒成立，则是实数c 的最大值为 ． 考点三 抛物线的标准方程及其几何性质例4．【2015新课标1文5】已知椭圆E 的中心为坐标原点，离心率为12，E 的右焦点与抛物线2:8C y x =的焦点重合，,A B 是C 的准线与E 的两个交点，则AB = ( ) （A ） 3 （B ）6 （C ）9 （D ）12例5．【2015福建文19】已知点F 为抛物线2:2(0)E y px p =>的焦点，点(2,)A m 在抛物线E 上，且3AF =． （Ⅰ）求抛物线E 的方程；（Ⅱ）已知点(1,0)G -，延长AF 交抛物线E 于点B ，证明：以点F 为圆心且与直线GA 相切的圆，必与直线GB 相切．【方法总结】1．抛物线上点到准线距离转化到点到焦点距离起到化繁为简的作用．注意定义在解题中的应用．研究抛物线的几何性质时，一是注意定义转化应用；二是要结合图形分析，同时注意平面几何性质的应用． 巩固练习1．已知F 是抛物线2yx =的焦点，,A B 是该抛物线上的两点．若线段AB 的中点到y 轴的距离为54，则||||AF BF += （ ） A ．2 B ．52C ．3D ．4 2．已知F 是抛物线2y x =的焦点，点A ，B 在该抛物线上且位于x 轴的两侧，2OA OB ⋅=（其中O 为坐标原点），则ABO ∆面积最小值是（ ） A ．2 B ．8 C ．8D 3．抛物线22y px =（0>p ）的焦点为F ，已知点A ，B 为抛物线上的两个动点，且满足120AFB ∠=︒．过弦AB 的中点M 作抛物线准线的垂线MN ，垂足为N ，则ABMN 的最大值为（ ）A B ．1 C D ．2 4．已知点A(3,4)，F 是抛物线y 2＝8x 的焦点，M 是抛物线上的动点，当|AM|＋|MF|最小时，M 点坐标是( )A ．(0,0)B ．)C ．(2,4)D ．(3，－)5．已知圆P ：x 2+y 2=4y 及抛物线S ：x 2=8y ，过圆心P 作直线l ，此直线与上述两曲线的四个交点，自左向右顺次记为A ，B ，C ，D ，如果线段AB ，BC ，CD 的长按此顺序构成一个等差数列，则直线l 的斜率为( ) A ．22±B ．22 C ．2± D ．2 6． 【2015新课标1，理20】在直角坐标系xoy 中，曲线C ：y =24x 与直线y kx a =+(a ＞0)交与M ,N 两点，（Ⅰ）当k =0时，分别求C 在点M 和N 处的切线方程；（Ⅱ）y 轴上是否存在点P ，使得当k 变动时，总有∠OPM =∠OPN ？说明理由．。

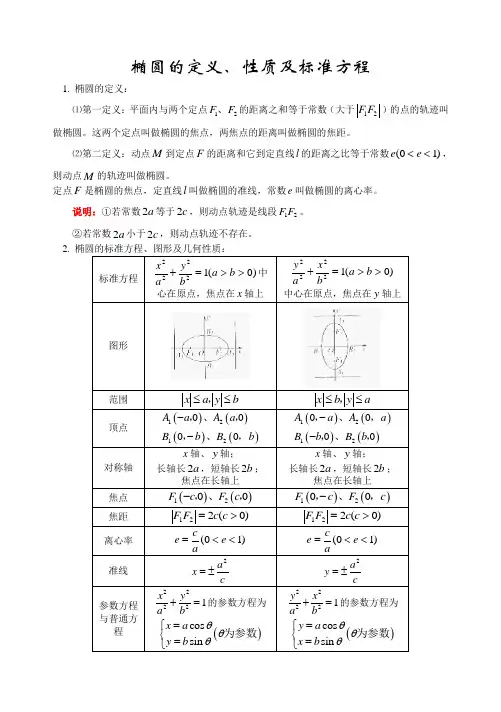
椭圆的定义、性质及标准方程1. 椭圆的定义：⑴第一定义：平面内与两个定点12F F 、的距离之和等于常数（大于12F F ）的点的轨迹叫做椭圆。

这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。

⑵第二定义：动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ，则动点M 的轨迹叫做椭圆。

定点F 是椭圆的焦点，定直线l 叫做椭圆的准线，常数e 叫做椭圆的离心率。

说明：①若常数2a 等于2c ，则动点轨迹是线段12F F 。

②若常数2a 小于2c ，则动点轨迹不存在。

2. 椭圆的标准方程、图形及几何性质：标准方程)0(12222>>=+b a by a x 中心在原点，焦点在x 轴上)0(12222>>=+b a b x a y 中心在原点，焦点在y 轴上图形范围 x a y b ≤≤，x b y a ≤≤，顶点()()()()12120000A a A a B b B b --，、，，、，()()()()12120000A a A a B b B b --，、，，、，对称轴 x 轴、y 轴；长轴长2a ，短轴长2b ；焦点在长轴上x 轴、y 轴；长轴长2a ，短轴长2b ；焦点在长轴上焦点 ()()1200F c F c -，、， ()()1200F c F c -，、， 焦距 )0(221>=c c F F)0(221>=c c F F离心率 )10(<<=e ace )10(<<=e ace 准线2a x c=±2a y c=±参数方程与普通方程22221x y a b +=的参数方程为 ()cos sin x a y b θθθ=⎧⎨=⎩为参数 22221y x a b +=的参数方程为 ()cos sin y a x b θθθ=⎧⎨=⎩为参数3. 焦半径公式：椭圆上的任一点和焦点连结的线段长称为焦半径。

椭圆的定义、性质及标准方程1. 椭圆的定义：⑴第一定义：平面内与两个定点12F F 、的距离之和等于常数〔大于12F F 〕的点的轨迹叫做椭圆。

这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。

⑵第二定义：动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ，那么动点M 的轨迹叫做椭圆。

定点F 是椭圆的焦点，定直线l 叫做椭圆的准线，常数e 叫做椭圆的离心率。

说明：①假设常数2a 等于2c ，那么动点轨迹是线段12F F 。

②假设常数2a 小于2c ，那么动点轨迹不存在。

2. 椭圆的标准方程、图形及几何性质：标准方程)0(12222>>=+b a by a x 中心在原点，焦点在x 轴上)0(12222>>=+b a b x a y 中心在原点，焦点在y 轴上图形范围 x a y b ≤≤，x b y a ≤≤，顶点()()()()12120000A a A a B b B b --，、，，、，()()()()12120000A a A a B b B b --，、，，、，对称轴 x 轴、y 轴；长轴长2a ，短轴长2b ； 焦点在长轴上x 轴、y 轴；长轴长2a ，短轴长2b ；焦点在长轴上焦点 ()()1200F c F c -，、， ()()1200F c F c -，、， 焦距 )0(221>=c c F F)0(221>=c c F F离心率 )10(<<=e ace )10(<<=e ace 准线2a x c=±2a y c=±参数方程与普通方程22221x y a b +=的参数方程为 ()cos sin x a y b θθθ=⎧⎨=⎩为参数 22221y x a b +=的参数方程为 ()cos sin y a x b θθθ=⎧⎨=⎩为参数3. 焦半径公式：椭圆上的任一点和焦点连结的线段长称为焦半径。

课程星级：★★★★★【椭圆】 一、椭圆的定义1、椭圆的第一定义：平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ，这个动点P 的轨迹叫椭圆。

这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距。

注意：若)(2121F F PF PF =+，则动点P 的轨迹为线段21F F ；若)(2121F F PF PF <+，则动点P 的轨迹无图形。

二、椭圆的方程1、椭圆的标准方程（端点为a 、b ，焦点为c ）（1）当焦点在x 轴上时，椭圆的标准方程：12222=+b y a x )0(>>b a ，其中222b a c -=；（2）当焦点在y 轴上时，椭圆的标准方程：12222=+b x a y )0(>>b a ，其中222b a c -=；2、两种标准方程可用一般形式表示：221x y m n += 或者 mx 2+ny 2=1 三、椭圆的性质（以12222=+by a x )0(>>b a 为例）知能梳理1、对称性：对于椭圆标准方程12222=+by a x )0(>>b a ：是以x 轴、y 轴为对称轴的轴对称图形；并且是以原点为对称中心的中心对称图形，这个对称中心称为椭圆的中心。

2、范围：椭圆上所有的点都位于直线a x ±=和b y ±=所围成的矩形内，所以椭圆上点的坐标满足a x ≤，b y ≤。

3、顶点：①椭圆的对称轴与椭圆的交点称为椭圆的顶点。

②椭圆12222=+by a x )0(>>b a 与坐标轴的四个交点即为椭圆的四个顶点，坐标分别为)0,(1a A -，)0,(2a A ，),0(1b B -，),0(2b B 。

③线段21A A ，21B B 分别叫做椭圆的长轴和短轴，a A A 221=，b B B 221=。

a 和b 分别叫做椭圆的长半轴长和短半轴长。

圆锥曲线(椭圆,双曲线,抛物线)的定义、方程和性质知识总结-标准化文件发布号：（9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII2椭圆的定义、性质及标准方程1. 椭圆的定义：⑴第一定义：平面内与两个定点12F F 、的距离之和等于常数（大于12F F ）的点的轨迹叫做椭圆。

这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。

⑵第二定义：动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ，则动点M 的轨迹叫做椭圆。

定点F 是椭圆的焦点，定直线l 叫做椭圆的准线，常数e 叫做椭圆的离心率。

说明：①若常数2a 等于2c ，则动点轨迹是线段12F F 。

②若常数2a 小于2c ，则动点轨迹不存在。

2. 椭圆的标准方程、图形及几何性质：标准方程)0(12222>>=+b a b y a x 中心在原点，焦点在x 轴上)0(12222>>=+b a b xa y 中心在原点，焦点在y 轴上图形范围 x a y b ≤≤，x b y a ≤≤，顶点()()()()12120000A a A a B b B b --，、，，、，()()()()12120000A a A a B b B b --，、，，、，对称轴 x 轴、y 轴； 长轴长2a ，短轴长2b ； 焦点在长轴上 x 轴、y 轴；长轴长2a ，短轴长2b ；焦点在长轴上焦点 ()()1200F c F c -，、， ()()1200F c F c -，、， 焦距 )0(221>=c c F F)0(221>=c c F F离心率)10(<<=e ace )10(<<=e ace33. 焦半径公式：椭圆上的任一点和焦点连结的线段长称为焦半径。

焦半径公式：椭圆焦点在x 轴上时，设12F F 、分别是椭圆的左、右焦点，()00P x y ，是椭圆上任一点，则10PF a ex =+，20PF a ex =-。

椭圆抛物线双曲线公式大全一、椭圆。

（一）椭圆的标准方程。

1. 焦点在x轴上。

设椭圆的标准方程为frac{x^2}{a^2}+frac{y^2}{b^2} = 1(a>b>0)，其中a为长半轴长，b为短半轴长，c为半焦距，且c^2=a^2-b^2，焦点坐标为(± c,0)。

2. 焦点在y轴上。

方程为frac{y^2}{a^2}+frac{x^2}{b^2}=1(a > b>0)，焦点坐标为(0,± c)，同样c^2=a^2-b^2。

（二）椭圆的离心率。

e=(c)/(a)(0 < e<1)，离心率反映了椭圆的扁平程度。

（三）椭圆的参数方程。

<=ft{begin{array}{l}x = acosθ y=bsinθend{array}right.（θ为参数）二、抛物线。

（一）抛物线的标准方程。

1. 焦点在x轴正半轴上。

方程为y^2=2px(p>0)，焦点坐标为((p)/(2),0)，准线方程为x =-(p)/(2)。

2. 焦点在x轴负半轴上。

y^2=-2px(p > 0)，焦点(-(p)/(2),0)，准线x=(p)/(2)。

3. 焦点在y轴正半轴上。

x^2=2py(p>0)，焦点(0,(p)/(2))，准线y =-(p)/(2)。

4. 焦点在y轴负半轴上。

x^2=-2py(p>0)，焦点(0,-(p)/(2))，准线y=(p)/(2)。

（二）抛物线的离心率。

e = 1三、双曲线。

（一）双曲线的标准方程。

1. 焦点在x轴上。

方程为frac{x^2}{a^2}-frac{y^2}{b^2}=1(a>0,b>0)，其中a为实半轴长，b为虚半轴长，c为半焦距，且c^2=a^2+b^2，焦点坐标为(± c,0)。

2. 焦点在y轴上。

frac{y^2}{a^2}-frac{x^2}{b^2} = 1(a>0,b>0)，焦点坐标为(0,± c)，c^2=a^2+b^2。

椭圆双曲线抛物线知识点汇总一、椭圆1、定义平面内与两个定点$F_1$，＄F_2$的距离之和等于常数（大于$｜F_1F_2|＄）的点的轨迹叫做椭圆。

这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。

2、标准方程（1）焦点在$x$轴上：＄＼frac{x^2}｛a^2} ＋＼frac{y^2}｛b^2} ＝ 1$（＄a ＞ b ＞ 0$），其中$a$为长半轴长，＄b$为短半轴长，＄c$为半焦距，满足$c^2 ＝ a^2 b^2$。

（2）焦点在$y$轴上：＄＼frac{y^2}｛a^2} ＋＼frac{x^2}｛b^2} ＝ 1$（＄a ＞ b ＞ 0$）。

3、椭圆的性质（1）对称性：椭圆关于$x$轴、＄y$轴和原点对称。

（2）范围：对于焦点在$x$轴上的椭圆，＄a ＼leq x ＼leq a$，＄b ＼leq y ＼leq b$；对于焦点在$y$轴上的椭圆，＄b ＼leq x ＼leq b$，＄a ＼leq y ＼leq a$。

（3）顶点：焦点在$x$轴上时，顶点坐标为$（＼pm a, 0)＄，＄（0, ＼pm b)＄；焦点在$y$轴上时，顶点坐标为$（0, ＼pm a)＄，＄（＼pm b, 0)＄。

（4）离心率：＄e ＝＼frac{c}｛a}＄（＄0 ＜ e ＜ 1$），反映了椭圆的扁平程度。

4、椭圆中的重要结论（1）过椭圆焦点的弦长：若弦过焦点$F_1$，则弦长$｜AB| ＝ 2a e(x_1 ＋ x_2)＄。

（2）椭圆上一点到焦点的距离：设椭圆上一点$P(x_0, y_0)＄，两焦点为$F_1$，＄F_2$，则$｜PF_1| ＝ a ＋ ex_0$，＄｜PF_2| ＝ aex_0$。

二、双曲线1、定义平面内与两个定点$F_1$，＄F_2$的距离之差的绝对值等于常数（小于$｜F_1F_2|＄）的点的轨迹叫做双曲线。

这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距。

2、标准方程（1）焦点在$x$轴上：＄＼frac{x^2}｛a^2} ＼frac{y^2}｛b^2} ＝1$（＄a ＞ 0$，＄b ＞ 0$），其中$c^2 ＝ a^2 ＋ b^2$。