空间直线方程

空间直线方程的五种形式在空间几何中，直线是最基本的图形之一。

直线的方程是在数学中非常重要的一部分。

空间直线方程的五种形式是基于不同的坐标系和参数化方式，它们各自有其独特的优势和适用范围。

在本文中，我们将探讨这五种形式的具体含义和应用。

1. 点向式方程点向式方程是空间直线方程的最基本形式。

它基于点和向量的概念，可以表示为：$$vec{r}=vec{a}+tvec{b}$$其中，$vec{r}$ 是直线上任意一点的位置向量；$vec{a}$ 是直线上已知的一点的位置向量；$vec{b}$ 是直线的方向向量，它的大小和方向决定了直线的方向；$t$ 是参数，可以取任意实数值。

点向式方程的优势在于它直观地表达了直线的位置和方向。

同时，它也很容易与向量运算相结合，便于进行计算。

但是，它的缺点是不够简洁，需要使用向量的加法和数乘运算，不太方便。

2. 对称式方程对称式方程是空间直线方程的另一种基本形式。

它基于平面和点的概念，可以表示为：$$frac{x-x_0}{a}=frac{y-y_0}{b}=frac{z-z_0}{c}$$ 其中，$(x_0,y_0,z_0)$ 是直线上已知的一点的坐标；$a,b,c$ 是直线的方向比例系数，它们的比值决定了直线的方向；$x,y,z$ 是直线上任意一点的坐标。

对称式方程的优势在于它简洁明了，易于计算。

同时，它也可以很容易地转化为其他形式的方程。

但是，它的缺点是不够直观，不容易理解直线的位置和方向。

3. 参数式方程参数式方程是空间直线方程的常用形式之一。

它基于参数化的概念，可以表示为：$$begin{cases} x=x_0+at y=y_0+bt z=z_0+ct end{cases}$$ 其中，$(x_0,y_0,z_0)$ 是直线上已知的一点的坐标；$a,b,c$ 是直线的方向比例系数，它们的比值决定了直线的方向；$t$ 是参数，可以取任意实数值。

参数式方程的优势在于它直观地表达了直线的位置和方向，同时也很容易进行计算和推导。

空间直线方程的五种形式空间直线是三维几何中的基本概念之一，它在建模、计算机图形学、机器人学、计算机视觉等领域中有着广泛的应用。

本文将介绍空间直线的五种方程形式，分别是点向式、参数式、对称式、标准式和一般式。

一、点向式点向式是一种常用的表示空间直线的方式，它使用一条直线上的一点和该直线的方向向量来描述直线。

设直线上一点为 $P_0$，方向向量为 $vec{v}$，则该直线的点向式方程为：$$vec{OP} = vec{OP_0} + tvec{v}$$其中 $vec{OP}$ 表示直线上任意一点 $P$ 到原点 $O$ 的向量，$t$ 为参数。

点向式方程中的 $vec{v}$ 是直线的方向向量，它的模长为 $|vec{v}|$，方向与直线相同。

点向式方程的优点是简单明了，易于理解和计算。

二、参数式参数式是另一种表示空间直线的方式，它使用一个参数来描述直线上的所有点。

设直线上一点为 $P_0$，方向向量为 $vec{v}$，则该直线的参数式方程为：$$begin{cases}x = x_0 + tv_x y = y_0 + tv_y z = z_0 + tv_z end{cases}$$其中 $(x_0, y_0, z_0)$ 是直线上的一点，$(v_x, v_y,v_z)$ 是直线的方向向量，$t$ 是参数。

参数式方程中的 $t$ 可以取任意实数，它表示直线上的所有点。

参数式方程的优点是方便计算直线上的任意一点的坐标。

三、对称式对称式是一种表示空间直线的方式，它使用一个点和一个平面来描述直线。

设直线上一点为 $P$，平面的法向量为 $vec{n}$，则该直线的对称式方程为：$$vec{OP} cdot vec{n} = vec{OP_0} cdot vec{n}$$ 其中 $vec{OP}$ 表示直线上任意一点 $P$ 到原点 $O$ 的向量，$vec{n}$ 是平面的法向量，$vec{OP_0}$ 是直线上的一点。

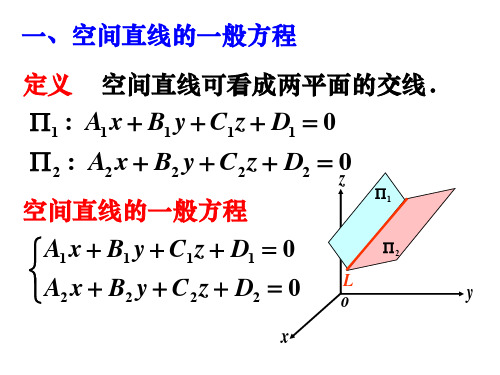
空间直线及其方程§8.4 空间直线及其方程ü直线的一般方程ü直线的参数方程和对称方程ü两直线的夹角ü直线与平面的夹角一、空间直线的一般方程定义空间直线可看成两平面的交线．Π1:A1x+B1y+C1z+D1Π2:A2x+B2y+C2z+D2A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0空间直线的一般方程y注：表示同一直线的一般方程不唯一。

确定空间直线的条件•由两个平面确定一条直线；•由空间的两点确定一条直线；•由空间的一点和一个方向来确定一条直线。

二、空间直线的参数方程与对称式方程r如果一非零向量sr一条已知直线L，向量s线L的方向向量．设定点M0(x0,y0,z0)∈L,方向向量的定义：yr∀M(x,y,z)∈L,0//srs={m,n,p},M0={x−x0,y−y0,z−z0}则{x−x0,y−y0,z−z0}=t{m,n,p} x=x0+mt y=y0+ntz=z+pt0消去参数t，有直线的参数方程x−xy−yz−z==直线的对称式方程mnp直线的一组方向数方向向量的余弦称为直线的方向余弦.注：1. 表示同一直线的对称方程不唯一；2. 对称式方程可转化为一般方程;x=x0,x−x0y−y0z−z0 3.==理解为:y−y=z−z.0np p n4. 任一条直线均可表示为对称式方程.设直线过两点M(x1,y1,z1),N(x2,y2,z2)r则s={x2−x1,y2−y1,z2−z1}x−x1y−y1z−z1直线的对称方程为：==x2−x1y2−y1z2−z1例1用对称式方程及参数方程表示直线x+y+z+1=0.2x−y+3z+4=0解在直线上任取一点(x0,y0,z0)y0+z0+2=0取x0=1⇒,y0−3z0−6=0解得y0=0,z0=−2点坐标(1,0,−2),因所求直线与两平面的法向量都垂直取rrrs=n1×n2={4,−1,−3}, x−1y−0z+2对称式方程==,4−1−3x=1+4t.参数方程y=−tz=−2−3t例2 一直线过点A(2,−3,4)，且和y轴垂直相交，求其方程.解因为直线和y轴垂直相交,所以交点为B(0,−3,0),r取s=={2,0,4},x−2y+3z−4==.所求直线方程204三、两直线的夹角定义两直线的方向向量的夹角称之.（锐角）x−x1y−y1z−z1直线L1:==,p1m1n1x−x2y−y2z−z2直线L2:==,m2n2p2 ^cos(L,L)=12|mm+nn+pp|m1+n1+p1⋅m2+n2+p2两直线的夹角公式222222两直线的位置关系：(1)L1⊥L2⇐⇒m1m2+n1n2+p1p2=0,m1n1p1==,(2)L1//L2⇐⇒m2n2p2r例如，直线L1:s1={1,−4,0},r直线L2:s2={0,0,1},rrrrQs1⋅s2=0,∴s1⊥s2,即L1⊥L2.x−4z=3例3 一直线L过点(-3,2,5)，且和直线2x−y−5z=1平行，求其方程.vi解rrrQs=n1×n2=1vj0vk−4=−{4,3,1}2−1−5∴所求直线方程v方法2:设s={m,n,p}x+3y−2z−5==.431m−4p=0mnpvvvvQs⊥n1,s⊥n2∴⇒==4312m−n−5p=0v取s={4,3,1}………x+1y−1z==例4 一直线过点M0(2,1,3)，且与直线L: 32−1垂直相交，求其方程.解设所求直线为l , 先求两直线的交点。

空间直线的方程与性质一、空间直线的方程在三维空间中，要确定一条直线，我们需要知道直线上的一点和直线的方向。

因此，一般来说，表示空间直线的方程形式为：R: (x-x₁) / l₁ = (y-y₁) / l₂ = (z-z₁) / l₃其中，(x₁, y₁, z₁) 是直线上的一点，l₁, l₂, l₃是直线的方向比例。

二、空间直线的性质1. 直线的方向向量直线上的两个任意点 A(x₁, y₁, z₁) 和 B(x₂, y₂, z₂) ，则直线的方向向量可以表示为：V = [x₂ - x₁, y₂ - y₁, z₂ - z₁]2. 直线的平行与垂直若两个直线的方向向量分别是 V₁=[l₁₁, l₁₂, l₁₃] 和 V₂=[l₂₁,l₂₂, l₂₃]，则有以下条件：- 若 V₁∥ V₂，则直线平行。

- 若 V₁⊥ V₂，则直线垂直。

3. 直线与平面的关系直线与平面相交时，有以下几种情况：- 若直线和平面有且只有一个交点，则交点为直线上的一点。

- 若直线和平面无交点，且直线与平面平行，则直线在平面上。

- 若直线和平面无交点，且直线与平面垂直，则直线与平面互相平行。

4. 直线的距离直线与一点 P (x₀, y₀, z₀) 之间的距离可以通过点到直线的距离公式来计算：d = |(x₀-x₁, y₀-y₁, z₀-z₁) · V| / |V|其中 |·| 表示向量的模，"·" 表示向量的点积。

5. 直线的参数方程若直线的方向向量为 V=[l₁, l₂, l₃]，直线上的一点为 P(x₁, y₁, z₁)，则直线的参数方程形式为：x = x₁ + l₁ * ty = y₁ + l₂ * tz = z₁ + l₃ * t其中 t 为参数。

6. 直线的对称式方程直线的对称式方程形式是通过点和方向向量来表示的，如下：(x - x₁) / l₁ = (y - y₁) / l₂ = (z - z₁) / l₃ = t其中 (x, y, z) 为直线上的任意一点。