判别分析过程

统计学中的判别分析判别分析是统计学中一种常见的分析方法，旨在通过将样本数据归类到一个或多个已知的类别中，来识别和描述不同类别之间的差异。

它在很多领域中都有广泛的应用，例如医学、市场调研、金融等。

本文将介绍判别分析的基本原理、常见的判别分析方法以及其在实际应用中的一些例子。

一、判别分析的原理判别分析的目标是构建一个判别函数，通过输入变量的值来判别或预测样本所属的类别。

它的核心思想是通过最大化类别间的差异和最小化类别内部的差异，来建立一个有效的分类模型。

判别分析的基本原理可以用以下步骤来描述：1. 收集样本数据，包括已知类别的样本和它们的属性值。

2. 对每个样本计算各个属性的平均值和方差。

3. 计算类别内部散布矩阵和类别间散布矩阵。

4. 根据散布矩阵计算特征值和特征向量。

5. 选择最具判别能力的特征值和特征向量作为判别函数的基础。

二、判别分析的方法判别分析有多种方法可以选择，常见的包括线性判别分析（Linear Discriminant Analysis，简称LDA）和二次判别分析（Quadratic Discriminant Analysis，简称QDA）。

1. 线性判别分析（LDA）线性判别分析假设每个类别的样本数据满足多元正态分布，并且各个类别的协方差矩阵相等。

它通过计算最佳投影方向，将多维属性值降低到一维或两维来实现分类。

LDA在分类问题中被广泛应用，并且在特征选择和降维方面也有一定的效果。

2. 二次判别分析（QDA）二次判别分析不同于LDA，它允许每个类别具有不同的协方差矩阵。

QDA通常适用于样本数据的协方差矩阵不相等或不满足多元正态分布的情况。

与LDA相比，QDA在处理非线性问题时可能更有优势。

三、判别分析的应用实例判别分析在多个领域中都有广泛的应用，下面列举了一些实际的例子。

1. 医学领域在医学中，判别分析可以帮助诊断疾病或判断病情。

例如，可以利用病人的临床数据（如血压、血糖等指标）进行判别分析，来预测是否患有某种疾病，或者判断疾病的严重程度。

逐步判别分析的步骤和流程英文回答：Step 1: Define the decision problem.The first step in the Analytic Hierarchy Process (AHP) is to clearly define the decision problem. This involves identifying the goal or objective of the decision, as well as the criteria and alternatives that will be considered. It is important to have a clear understanding of the problem before proceeding to the next steps.Step 2: Develop a hierarchical structure.In this step, a hierarchical structure is developed to represent the decision problem. The goal is placed at the top of the hierarchy, followed by the criteria and alternatives. The criteria are the factors that will be used to evaluate the alternatives, while the alternatives are the options that will be considered. The hierarchicalstructure helps to organize the decision problem and provides a framework for the subsequent analysis.Step 3: Pairwise comparisons.The next step is to perform pairwise comparisons of the criteria and alternatives. This involves comparing each criterion or alternative with every other criterion or alternative and assigning a preference or importance rating. The pairwise comparisons are typically done using a scale, such as a numerical scale or a verbal scale. The goal is to determine the relative importance or preference of each criterion and alternative.Step 4: Calculate priority weights.Once the pairwise comparisons are completed, thepriority weights for each criterion and alternative are calculated. This is done by applying a mathematical method, such as the eigenvector method or the geometric mean method, to the pairwise comparison data. The priority weightsreflect the relative importance of each criterion andalternative in achieving the goal.Step 5: Check for consistency.After calculating the priority weights, it is important to check for consistency in the pairwise comparisons. Inconsistent comparisons can lead to inaccurate results. There are various methods for checking consistency, such as the consistency ratio and the consistency index. If the comparisons are found to be inconsistent, adjustments can be made to improve the consistency.Step 6: Evaluate alternatives.In this step, the alternatives are evaluated based on the priority weights of the criteria. This involves multiplying the priority weights of the criteria by the performance scores of the alternatives for each criterion. The performance scores can be subjective ratings or objective measurements. The goal is to determine theoverall performance of each alternative based on the criteria.Step 7: Make the decision.The final step is to make the decision based on the evaluation of the alternatives. The decision can be made by comparing the overall performance scores of thealternatives or by considering other factors, such as cost or risk. The decision should be based on the priorities and preferences identified in the previous steps.中文回答：步骤1，定义决策问题。

判别分析与聚类分析的基本原理数据分析是在如今信息时代中，越来越重要的一项技能。

在数据分析的过程中，判别分析和聚类分析是两个非常重要的方法。

本文将介绍判别分析和聚类分析的基本原理，以及它们在数据分析中的应用。

一、判别分析的基本原理判别分析是一种用于分类问题的统计方法，其目的是通过学习已知类别的样本数据，来构建一个分类器，从而对未知样本进行分类。

判别分析的基本原理可以简单概括为以下几个步骤：1. 数据预处理：首先需要对数据进行预处理，包括数据清洗、缺失值处理、特征选择等，以获得更好的数据质量。

2. 特征提取：在进行判别分析之前，需要将原始数据转化为有效的特征。

特征提取的方法有很多种，常用的包括主成分分析、线性判别分析等。

3. 训练分类器：利用判别分析算法对已知类别的样本数据进行训练，建立分类模型。

常用的判别分析方法有线性判别分析、二次判别分析等。

4. 分类预测：通过训练好的分类器，对未知样本进行分类预测。

分类预测的结果可以是离散的类标签，也可以是概率值。

判别分析广泛应用于医学、金融、市场营销等领域。

例如，在医学领域，可以利用判别分析来预测疾病的状态，辅助医生做出诊断决策。

二、聚类分析的基本原理聚类分析是一种无监督学习方法，其目的是将相似的数据对象分组，使得同一组内的对象相似度较高，不同组间的相似度较低。

聚类分析的基本原理可以概括为以下几个步骤：1. 选择相似性度量：首先需要选择一个合适的相似性度量，用于评估数据对象之间的相似程度。

常用的相似性度量包括欧氏距离、曼哈顿距离等。

2. 选择聚类算法：根据具体的问题需求，选择合适的聚类算法。

常用的聚类算法有K-means、层次聚类等。

3. 确定聚类数目：根据实际问题，确定聚类的数目。

有些情况下，聚类数目事先是已知的，有些情况下需要通过评价指标进行确定。

4. 根据聚类结果进行分析：将数据对象划分到各个聚类中，并对聚类结果进行可视化和解释。

聚类分析被广泛应用于市场分析、图像处理、社交网络等领域。

解读SPSS 判别分析的计算过程ITELLIN在多元统计分析方法中，多元回归分析使用最普遍，几乎到了快要用滥的程度。

但回归分析要求因变量和自变量的属性为定距以上的变量，如果这个条件不满足，使用起来比较费劲。

在实际工作中，因变量为分类变量，自变量为连续变量的情况比比皆是，如对银行来讲如何辨别良好信用和不良信用的客户，对电信运营商来讲如何辨别大客户，中小客户，对生产企业来讲如何判断新产品的速购者和迟购者等等，这些都是我们经常遇见的问题，判别分析就是解决这类问题的一个优选的统计方法。

现行介绍判别分析方法中，常常见到的有距离判别法，费歇尔判别法，贝叶斯判别法。

这三种方法各有各的产生背景，有不同的使用条件，它们有一个共同的特点就是计算量巨大，以至于靠手算无法进行。

为此现在主流统计软件都把判别分析作为一个专用模块来开发，但由于软件产生的只是结果，对于判别分析的整个推理过程涉及很少，不利于初次接触判别分析的人士学习，所以本文准备从具体的计算过程入手，详细解读SPSS 产生的过程，使得学习者能够做到知其然而知其所以然。

一、 数据整理为了便于验证，考虑g=3个总体，每个总体容量为=3个样品，p=2个变量的观测值。

假定总体有相同的协方差矩阵，先验概率分别为。

利用SPSS 的判别分析过程来求得费歇尔判别函数得分和贝叶斯的分类函数得分。

i n Σ1230.25,0.25,0.50p p p ===来自总体123,πππ和的随机样本为1:π125X 0311−⎛⎞⎜=⎜⎜⎟−⎝⎠⎟⎟ 2:π206X 2412⎛⎞⎜=⎜⎜⎟⎝⎠⎟⎟ 3:π31-2X 00-1-4⎛⎞⎜⎟=⎜⎟⎜⎟⎝⎠1n =33 2n =3n 3=将以上数据按照SPSS 对数据格式的要求录入到SPSS 的数据编辑窗口。

如下图所示：1．在SPSS数据编辑窗口中点选（Analyze）中的分类（Classify）进行判别分析（Discriminant…）。

2．分析时要选择的分析变量如下：3．点选统计量按钮，选择描述统计量，矩阵及判别函数系数中的所有选项。

判别分析的一般步骤和SPSS实现判别分析是一种统计学方法，用于确定一组预测变量对于区分不同组别的目标变量的重要性。

它可以帮助我们理解和解释数据，以及预测未来的观察结果。

下面将介绍判别分析的一般步骤和如何使用SPSS软件来实现。

步骤一：数据收集和准备首先，收集需要的数据，并进行数据清洗和整理。

确保数据的完整性和准确性。

此外，还需要对数据进行标准化，以消除不同变量之间的度量单位差异。

步骤二：设定模型确定分析的目标变量和预测变量。

目标变量是我们想要预测或解释的变量，而预测变量则是用来预测目标变量的变量。

根据实际情况，选择适当的判别分析方法，如线性判别分析或二次判别分析。

步骤三：进行判别函数的计算计算出判别函数，用于将样本分成不同的组别。

判别函数是由预测变量的加权和组成的。

对于线性判别分析，判别函数的形式为：D = a1X1 + a2X2 + ... + anXn + c其中，D是判别分数，X是预测变量，a是权重，n是预测变量的数量，c是常数。

通过计算判别函数，可以根据判别分数将样本分到不同的组别。

步骤四：进行判别分析的检验判别分析的检验包括Wilks' Lambda检验和方差分析。

Wilks' Lambda检验用于检验判别函数是否统计显著，以判断预测变量的组合是否能够显著解释目标变量的变异性。

方差分析用于检验各个预测变量在不同组别之间的差异是否显著。

步骤五：解释和评估结果在判别分析的最后一步，需要对结果进行解释和评估。

根据判别分析的结果，可以判断哪些预测变量对于区分不同组别的目标变量最为重要。

此外，还可以对模型的准确性进行评估，比如使用十折交叉验证等方法。

使用SPSS软件进行判别分析的步骤如下：步骤一：导入数据首先，在SPSS软件中打开数据文件或导入数据。

确保数据的格式正确，包括变量类型、缺失值处理等。

步骤二：设定模型在SPSS中，选择"分析"菜单中的"分类"选项，然后选择"判别分析"。

判别分析实验报告判别分析实验报告一、引言判别分析是一种常用的统计分析方法，广泛应用于数据挖掘、模式识别、生物信息学等领域。

本实验旨在通过对一个真实数据集的分析，探讨判别分析在实际问题中的应用效果。

二、数据集介绍本实验使用的数据集是一份关于肿瘤患者的临床数据，包括患者的年龄、性别、肿瘤大小、转移情况等多个变量。

我们的目标是根据这些变量，建立一个判别模型，能够准确地预测患者是否患有恶性肿瘤。

三、数据预处理在进行判别分析之前，我们首先对数据进行预处理。

这包括数据清洗、缺失值处理、异常值检测等步骤。

通过对数据的观察和分析，我们发现有部分数据存在缺失值，需要进行处理。

我们选择使用均值替代缺失值的方法进行处理，并对替代后的数据进行了异常值检测。

四、判别模型建立在本实验中，我们选择了线性判别分析（LDA）作为判别模型的建立方法。

LDA 是一种经典的判别分析方法，通过将数据投影到低维空间中，使得不同类别的样本在投影后的空间中能够更好地区分开来。

我们使用Python中的scikit-learn 库来实现LDA算法。

五、模型评估为了评估建立的判别模型的性能，我们将数据集划分为训练集和测试集。

使用训练集对模型进行训练，并使用测试集进行模型的评估。

我们选择了准确率、精确率、召回率和F1值等指标来评估模型的性能。

经过多次实验和交叉验证，我们得到了一个较为稳定的模型，并对其性能进行了详细的分析和解释。

六、结果与讨论经过模型评估，我们得到了一个在测试集上准确率为85%的判别模型。

该模型在预测恶性肿瘤时具有较高的精确率和召回率，说明了其在实际应用中的可行性和有效性。

但同时我们也发现，该模型在预测良性肿瘤时存在一定的误判率，可能需要进一步优化和改进。

七、结论本实验通过对一个真实数据集的判别分析，验证了判别分析方法在预测恶性肿瘤的应用效果。

通过建立判别模型，并对其性能进行评估，我们得到了一个在测试集上具有较高准确率的模型。

然而，我们也发现了该模型在预测良性肿瘤时存在一定的误判率，需要进一步的改进和优化。

第19章判别分析判别分析是一种多变量统计分析方法，用于确定两个或多个已知类别的样本在一组变量上的差异程度，从而将未知样本分到合适的类别。

在实际应用中，判别分析具有广泛的应用场景，如医学诊断、金融风险评估、图像识别等领域。

判别分析的目标是确定一个判别函数，该函数可以将样本正确地分类到已知的类别中。

判别分析主要通过以下几个步骤来实现：1.数据准备：首先需要收集并准备训练样本，这些样本包括已知类别的观测值和相关变量的测量值。

2.变量选择：在判别分析中，需要选择与类别之间具有显著差异的变量。

常用的方法包括t检验和方差分析等。

3.建立判别函数模型：判别函数模型是用来将样本正确分类的函数。

常见的判别函数模型包括线性判别函数、二次判别函数、多项式判别函数等。

4.模型评估和选择：需要对模型进行评估和选择，以确保模型的稳定性和准确性。

常见的评估指标包括准确率、召回率、精确率等。

5.判别函数应用：通过判别函数，可以将未知样本分类到合适的类别中，从而实现对未知观测值的预测。

判别分析有几个重要的假设前提：首先，假设样本来自正态分布；其次，假设各个类别的协方差矩阵相等；最后，假设各个类别的先验概率相等。

判别分析的优点在于可以通过变量选择来减少数据的维度，提高判别函数的准确性；同时，判别分析对异常值的鲁棒性较好，不会对判别结果产生较大影响。

然而，判别分析也存在一些限制，如对数据分布的假设较为严格，对样本大小要求较高。

在实际应用中，判别分析可以用于多个领域。

例如，在医学诊断中，可以利用判别分析将病人分为患病和健康两类，从而提供更准确的诊断结果；在金融风险评估中，可以通过判别分析将客户分为高风险和低风险，以便制定相应的风险管理策略；在图像识别中，可以利用判别分析将图像分为不同类别，实现图像的自动分类和识别。

总而言之，判别分析是一种多变量统计分析方法，通过确定样本在一组变量上的差异程度来实现对未知样本的分类。

在实际应用中，判别分析具有广泛的应用场景，可以用于医学诊断、金融风险评估、图像识别等领域。

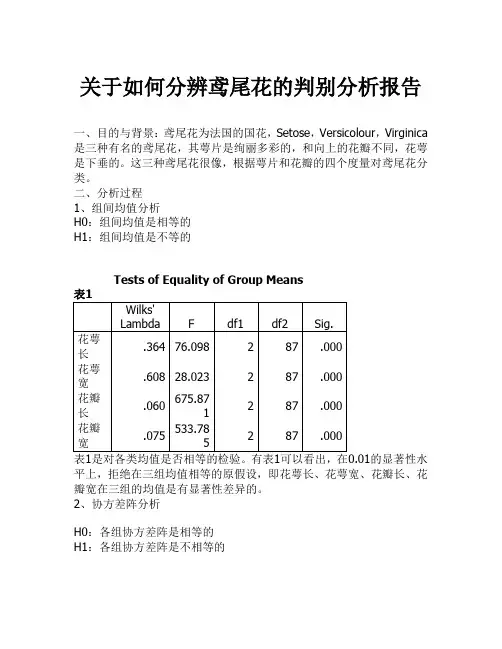
关于如何分辨鸢尾花的判别分析报告一、目的与背景：鸢尾花为法国的国花，Setose，Versicolour，Virginica 是三种有名的鸢尾花，其萼片是绚丽多彩的，和向上的花瓣不同，花萼是下垂的。

这三种鸢尾花很像，根据萼片和花瓣的四个度量对鸢尾花分类。

二、分析过程1、组间均值分析H0：组间均值是相等的H1：组间均值是不等的Tests of Equality of Group Means表1的显著性水平上，拒绝在三组均值相等的原假设，即花萼长、花萼宽、花瓣长、花瓣宽在三组的均值是有显著性差异的。

2、协方差阵分析H0：各组协方差阵是相等的H1：各组协方差阵是不相等的Test Results表2Box's M 92.993F Approx. 4.332df1 20df2 23344.026Sig. .000Tests null hypothesis of equal population covariance matrices.表2是对各总体协方差阵是否相等的统计检验。

在0.05的显著性水平下拒绝原假设，即各总体协方差阵不相等。

3、确定非标准化典型判别函数Canonical Discriminant Function Coefficients表3是非标准化的典型判别函数，表示为y1=-2.063-0.083*Sepal.Lenght-0.132*Sepal.Width+0.212*Petal.Leng th+0.239* Petal.Widthy2=-8.045+0.037*Sepal.Lenght+0.211*Sepal.Width-0.104*Petal.Len gth+0.273* Petal.Width4、函数的显著性检验Eigenvalues表4-1Wilks' Lambda差的比例和典型相关系数。

第一判别函数解释了99%的方差，第二判别函数解释了1%的方差，两个判别函数解释了全部的方差。

判别分析四种方法第六章判别分析§6.1 什么是判别分析判别分析是判别样品所属类型的一种统计方法，其应用之广可与回归分析媲美。

在生产、科研和日常生活中经常需要根据观测到的数据资料,对所研究的对象进行分类。

例如在经济学中，根据人均国民收入、人均工农业产值、人均消费水平等多种指标来判定一个国家的经济发展程度所属类型;在市场预测中,根据以往调查所得的种种指标，判别下季度产品是畅销、平常或滞销;在地质勘探中,根据岩石标本的多种特性来判别地层的地质年代，由采样分析出的多种成份来判别此地是有矿或无矿,是铜矿或铁矿等；在油田开发中,根据钻井的电测或化验数据，判别是否遇到油层、水层、干层或油水混合层；在农林害虫预报中，根据以往的虫情、多种气象因子来判别一个月后的虫情是大发生、中发生或正常; 在体育运动中，判别某游泳运动员的“苗子”是适合练蛙泳、仰泳、还是自由泳等；在医疗诊断中,根据某人多种体验指标（如体温、血压、白血球等）来判别此人是有病还是无病。

总之,在实际问题中需要判别的问题几乎到处可见。

判别分析与聚类分析不同。

判别分析是在已知研究对象分成若干类型(或组别)并已取得各种类型的一批已知样品的观测数据,在此基础上根据某些准则建立判别式，然后对未知类型的样品进行判别分类。

对于聚类分析来说，一批给定样品要划分的类型事先并不知道，正需要通过聚类分析来给以确定类型的。

正因为如此,判别分析和聚类分析往往联合起来使用,例如判别分析是要求先知道各类总体情况才能判断新样品的归类，当总体分类不清楚时,可先用聚类分析对原来的一批样品进行分类,然后再用判别分析建立判别式以对新样品进行判别。

判别分析内容很丰富,方法很多。

判别分析按判别的组数来区分,有两组判别分析和多组判别分析；按区分不同总体的所用的数学模型来分,有线性判别和非线性判别；按判别时所处理的变量方法不同,有逐步判别和序贯判别等。

判别分析可以从不同角度提出的问题，因此有不同的判别准则,如马氏距离最小准则、Fi ｓher 准则、平均损失最小准则、最小平方准则、最大似然准则、最大概率准则等等，按判别准则的不同又提出多种判别方法。

判别分析的一般步骤及SPSS实现判别分析是一种用于分类变量的统计方法，它可以用于确定一个或多个预测变量对于区分不同组之间差异的程度。

判别分析由一系列步骤组成，包括问题的定义、数据的准备、模型的建立、模型的评估和结果的解释。

以下是判别分析的一般步骤以及如何在SPSS中实现这些步骤的详细说明。

第一步：问题的定义在进行判别分析之前，需要明确研究的目的和问题。

例如，我们可能希望根据顾客的一些特征（如性别、年龄、收入等）来预测顾客是否购买一些产品。

这样的问题可以通过判别分析解决。

第二步：数据的准备在进行判别分析之前，需要确保数据满足分析的要求。

数据应包括一个或多个预测变量和一个分类变量。

如果数据中存在缺失值，需要进行缺失值的处理。

如果数据中存在异常值，可以选择忽略或进行适当的修正。

第三步：模型的建立在SPSS中，可以使用“分类函数”来建立判别分析模型。

选择“分析”菜单中的“分类”选项，然后选择“判别”子菜单。

在“判别”对话框中，选择一个或多个预测变量，并将分类变量指定为“因变量”。

此外，还可以选择是否进行卡方检验以及是否使用交叉验证等选项。

卡方检验可以用于评估预测变量与分类变量之间的关联性，而交叉验证可以用于评估模型对于不同样本的预测效果。

第四步：模型的评估在SPSS中，判别分析的模型评估结果可以在“判别”输出中找到。

主要关注以下几个指标：1.方差贡献表：可以查看每个预测变量对于判别函数的贡献程度，以及它们之间的相关性。

2.群组描述：可以查看不同组之间的平均值，以确定最能区分不同组的预测变量。

3.准确性表：可以查看模型的整体分类准确率以及每个组的分类准确率。

4.标准化系数表：可以查看每个预测变量对于判别函数的贡献程度，使用标准化系数来比较不同预测变量的影响。

第五步：结果的解释对于判别分析的结果进行解释是非常重要的，以帮助我们理解预测变量如何影响分类变量，并从中得出有用的结论。

可以通过参考判别函数的系数、标准化系数和方差贡献来解释结果。

判别分析的原理及其操作1 判别分析的原理1．1 判别分析的涵义判别分析（Discriminant Analysis，简称DA）技术是由费舍（R．A．Fisher）于1936年提出的。

它是根据观察或测量到的若干变量值判断研究对象如何分类的方法。

具体地讲，就是已知一定数量案例的一个分组变量（grouping variable）和这些案例的一些特征变量，确定分组变量和特征变量之间的数量关系，建立判别函数（discriminant function），然后便可以利用这一数量关系对其他已知特征变量信息、但未知分组类型所属的案例进行判别分组。

沿用多元回归模型的称谓，在判别分析中称分组变量为因变量，而用以分组的其他特征变量称为判别变量（discriminant variable）或自变量。

判别分析技术曾经在许多领域得到成功的应用，例如医学实践中根据各种化验结果、疾病症状、体征判断患者患的是什么疾病；体育选材中根据运动员的体形、运动成绩、生理指标、心理素质指标、遗传因素判断是否选入运动队继续培养；还有动物、植物分类，儿童心理测验，地理区划的经济差异，决策行为预测等。

1．2 判别分析的假设条件判别分析的基本条件是：分组变量的水平必须大于或等于2，每组案例的规模必须至少在一个以上；各判别变量的测度水平必须在间距测度等级以上，即各判别变量的数据必须为等距或等比数据；各分组的案例在各判别变量的数值上能够体现差别。

判别分析对判别变量有三个基本假设。

其一是每一个判别变量不能是其他判别变量的线性组合。

否则将无法估计判别函数，或者虽然能够求解但参数估计的标准误很大，以致于参数估计统计性不显著。

其二是各组案例的协方差矩阵相等。

在此条件下，可以使用很简单的公式来计算判别函数和进行显著性检验。

其三是各判别变量之间具有多元正态分布，即每个变量对于所有其他变量的固定值有正态分布。

1．3 判别分析的过程1．3．1 对已知分组属性案例的处理此过程为判别分析的第一阶段，也是建立判别分析基本模型的阶段，即分析和解释各组指标特征之间的差异，并建立判别函数。

逐步判别分析1.基本理解逐步判别分析分析过程分两步：1.根据自变量和因变量（分类变量）相关性的大小筛选一部分自变量，这里的相关性是指自变量能否显著地把因变量区分出来；2.用取定的变量做进一步的判别分析。

注：在模型中保留的自变量不是单独的参考每个自变量和因变量的相关性，而是综合考虑由一部分自变量形成的整体对因变量的区分能力。

2.逐步判别分析操作步骤逐步判别函数第一步：首先将已确定分类情况的数据到spss软件中，点击分析、分类、判别式。

图1逐步判别操作第一步第二步：进入判别分析勾选框后首先将变量列表中的变量放入右侧的变量框中，将因变量（已知分组情况变量）放入分组变量框并定义好范围，点击继续，将自变量放入自变量框中。

图2第二步第三步：点击统计，勾选描述里的平均值、博克斯，函数系数勾选费希尔、未标准化。

点击继续。

图3第三步第四步：点击分类、勾选先验概率根据大小计算、显示下的摘要表，图勾选、合并组、领域图。

点击继续，后点击确定。

图4第四步3.逐步判别分析结果分析个案处理摘要、组统计结果。

图5组统计结果对数决定因子、检验结果、输入/除去的变量结果。

图6博克斯等同性检验输入/除去的变量、包括在分析中的变量。

图7步进统计典型判别函数系数、组质心处的函数、分类处理摘要。

图8典型判别函数系数结果分类处理摘要、组先验概率、分类函数系数（费希尔判别函数结果）。

图9费希尔判别函数系数典型判别函数、分类结果（判别函数的准确性）。

图10典则判别函数图4.结果整理结果整理将费希尔判别函数表结果粘贴到表格中，并在右侧加入分类结果中的准确率。

并根据费希尔判别函数系数表整理好每个类别的函数。

图11结果整理。