下载文档原格式
人教版小学数学四年级上册18单元思维导图一、第一单元：认识更大的数1. 数位顺序表2. 整数的读法和写法3. 整数的比较和大小关系4. 整数的加减法5. 乘法口诀表二、第二单元：角的初步认识1. 角的概念2. 角的分类3. 角的度量4. 角的加减法5. 角的周长三、第三单元：观察物体与几何图形1. 长方形和正方形的特征2. 三角形的特征3. 四边形的特征4. 圆的特征5. 立体图形的特征四、第四单元：分数的初步认识1. 分数的概念2. 分数的读法和写法3. 分数的比较和大小关系4. 分数的加减法5. 分数的应用五、第五单元：两位数乘两位数1. 乘法口诀表的应用2. 两位数乘两位数的计算方法3. 两位数乘两位数的进位和借位4. 两位数乘两位数的估算5. 两位数乘两位数的应用六、第六单元：小数的初步认识1. 小数的概念2. 小数的读法和写法3. 小数的比较和大小关系4. 小数的加减法5. 小数的应用七、第七单元：简易方程1. 方程的概念2. 方程的解法3. 方程的应用4. 一元一次方程5. 方程的变形八、第八单元：观察物体与几何图形（二）1. 立体图形的表面积2. 立体图形的体积3. 立体图形的切割与拼接4. 立体图形的应用5. 立体图形的拓展人教版小学数学四年级上册18单元思维导图一、第一单元：认识更大的数1. 数位顺序表：掌握数位的名称和顺序，了解数位之间的关系。
2. 整数的读法和写法：学习如何正确地读出和写出整数，掌握整数的基本表达方式。
3. 整数的比较和大小关系：通过比较整数的大小，建立数的大小概念，培养逻辑思维能力。
4. 整数的加减法：掌握整数加减法的计算方法，能够熟练地进行整数加减运算。
5. 乘法口诀表：学习乘法口诀表，掌握乘法的基本规律，提高计算速度和准确性。
二、第二单元：角的初步认识1. 角的概念：理解角的概念，掌握角的定义和特征。
2. 角的分类：学习不同类型的角，如锐角、直角、钝角等，了解它们之间的区别和联系。
小学数学六年级上册各单元思维导图第一部分：数的认识一、整数1. 自然数：0、1、2、3、4、5、6、7、8、9、10……2. 整数：自然数和它们的相反数3. 整数的分类：正整数、0、负整数二、分数1. 分数的意义：表示一个整体被平均分成若干份，其中的一份或几份2. 分数的表示：分子/分母3. 分数的分类：真分数、假分数、带分数三、小数1. 小数的意义：表示一个整体被平均分成若干份，其中的一份或几份，用小数点表示2. 小数的表示：整数部分和小数部分3. 小数的分类：有限小数、无限小数第二部分：数的运算一、加法1. 整数加法：相同符号的整数相加，异号整数相加2. 分数加法：同分母分数相加，异分母分数相加3. 小数加法：小数点对齐，逐位相加二、减法1. 整数减法：相同符号的整数相减，异号整数相减2. 分数减法：同分母分数相减，异分母分数相减3. 小数减法：小数点对齐，逐位相减三、乘法1. 整数乘法：相同符号的整数相乘，异号整数相乘2. 分数乘法：分子相乘，分母相乘3. 小数乘法：小数点对齐，逐位相乘四、除法1. 整数除法：相同符号的整数相除，异号整数相除2. 分数除法：分子相除，分母相除3. 小数除法：小数点对齐，逐位相除第三部分：数的性质一、数的性质1. 整数的性质：奇数、偶数、质数、合数2. 分数的性质：分子分母同乘（除）一个数，分数的值不变3. 小数的性质：小数点向左（右）移动一位，小数的值缩小（扩大）10倍二、数的运算定律1. 加法交换律：a + b = b + a2. 加法结合律：(a + b) + c = a + (b + c)3. 乘法交换律：a × b = b × a4. 乘法结合律：(a × b) × c = a × (b × c)5. 乘法分配律：a × (b + c) = a × b + a × c三、数的运算顺序1. 先算乘除，后算加减2. 同级运算，从左到右依次计算3. 括号内的运算优先级最高第四部分：数的应用一、整数应用1. 计算长度、面积、体积等2. 解决实际问题，如购物、分配、比较等二、分数应用1. 计算比例、比率等2. 解决实际问题，如分物品、分配资源等三、小数应用1. 计算长度、面积、体积等2. 解决实际问题，如购物、分配、比较等第五部分：几何图形一、平面图形1. 线段、射线、直线：线段是有限长的直线，射线有一个端点，直线无限长2. 角：由两条射线共同确定的图形，有一个顶点和两条边3. 三角形：由三条线段围成的图形，有三个角和三个边4. 四边形：由四条线段围成的图形，有四个角和四个边5. 圆：平面内到一个固定点距离相等的所有点组成的图形二、立体图形1. 长方体：由六个长方形围成的立体图形，有六个面、十二条边和八个顶点2. 正方体：由六个正方形围成的立体图形，有六个面、十二条边和八个顶点3. 圆柱：由两个底面和一个侧面围成的立体图形，底面是圆形4. 圆锥：由一个底面和一个侧面围成的立体图形，底面是圆形5. 球：由一个点向外无限延伸，到该点的距离相等的所有点组成的立体图形第六部分：几何图形的性质一、平面图形的性质1. 线段的性质：线段有长度，线段之间可以比较大小2. 角的性质：角有度数，角之间可以比较大小3. 三角形的性质：三角形的内角和为180度，等腰三角形的底角相等，直角三角形的勾股定理4. 四边形的性质：四边形的内角和为360度，矩形、正方形的对角线互相平分5. 圆的性质：圆的周长与直径的比例是圆周率，圆的面积与半径的平方成正比二、立体图形的性质1. 长方体的性质：长方体的体积等于长、宽、高的乘积2. 正方体的性质：正方体的体积等于边长的立方3. 圆柱的性质：圆柱的体积等于底面积乘以高4. 圆锥的性质：圆锥的体积等于底面积乘以高除以35. 球的性质：球的体积等于半径的立方乘以4/3π第七部分：几何图形的测量一、长度测量1. 线段长度：使用直尺或卷尺进行测量2. 角度测量：使用量角器进行测量二、面积测量1. 平面图形面积：根据公式计算，如长方形面积=长×宽，圆面积=πr²2. 立体图形表面积：根据公式计算，如长方体表面积=2(长×宽+长×高+宽×高)三、体积测量1. 立体图形体积：根据公式计算，如长方体体积=长×宽×高，圆柱体积=底面积×高2. 容器体积：使用量筒或量杯进行测量第八部分：数学应用与拓展一、数学在生活中的应用1. 购物：计算价格、找零等2. 测量：计算长度、面积、体积等3. 分配：分配物品、资源等二、数学在科学中的应用1. 物理学：计算速度、加速度、力等2. 化学：计算物质的量、浓度等3. 生物：计算种群数量、增长率等三、数学在艺术中的应用1. 音乐：计算音高、节奏等2. 绘画：计算比例、透视等3. 建筑设计：计算结构、空间等第九部分：数学问题解决策略一、问题解决步骤1. 理解问题：仔细阅读题目，明确已知条件和求解目标2. 制定计划：根据问题类型和条件，选择合适的解决方法3. 执行计划：按照计划进行计算和推导4. 检查结果：验证计算过程和结果的正确性二、常见问题解决方法1. 图形法：通过绘制图形，直观地表示问题条件，便于理解和解决2. 列表法：将问题条件列成表格，便于分析和比较3. 代数法：使用代数表达式和方程，进行符号运算和推导4. 逻辑推理法：根据已知条件和数学规律，进行逻辑推理和证明第十部分：数学思维培养一、培养逻辑思维能力1. 通过解决数学问题，锻炼逻辑推理和证明能力2. 学习数学定义、定理和公式，理解其背后的逻辑关系二、培养空间想象能力1. 学习几何知识，通过绘制图形和想象空间关系，培养空间想象力2. 参与数学建模活动，将实际问题转化为数学模型，提高空间想象能力三、培养数学建模能力1. 学习数学建模方法，将实际问题转化为数学问题2. 参与数学建模竞赛和活动，提高数学建模能力第十一部分：数学学习资源一、教材和辅导书1. 选择适合自己水平的教材和辅导书，进行系统学习2. 利用辅导书中的例题和习题，巩固所学知识二、在线资源和应用程序1. 利用在线教育平台和数学学习网站，获取丰富的学习资源2. 数学学习应用程序，进行互动式学习和练习三、数学竞赛和活动1. 参与数学竞赛，提高数学水平和竞争意识2. 参加数学讲座、研讨会等活动，拓宽数学视野。
思维导图，英文叫Mind Map，也称 Thinking Map ，就是借助图表来分析问题、理清思路。
今天介绍的都是思维图的基本款，体现了基础的思维框架。
但是每种图都能有无限的延伸，甚至不同种图可以结合起来一起用，可以变得非常复杂。
常见的思维图有这八种：Circle Map 圆圈图、Tree Map 树状图、Bubble Map 气泡图、Double Bubble Map 双重气泡图、Flow Map 流程图、Multi-flow Map 多重流程图、Brace Map 括号图，和Bridge Map 桥型图。
1、圆圈图，定义一件事（Circle Maps - Defining in Context ）Circle map 主要用于把一个主题展开来，联想或描述细节。
它有两个圆圈，里面的小圈圈是主题，而外面的大圈圈里放的是和这个主题有关的细节或特征。
基本形状是这样的：下面是国外一个幼儿园孩子做的圆圈图练习。
左边是一个典型的联想型圆圈图；主题是海滩，可以联想到螃蟹、鱼、遮阳伞、海草、游泳衣、海豚，等等。
而右边的图，反过来，从现象、特征（details）让孩子去推断相关的主题是什么？思维练习的开始就是这么简单！还可以用圆圈图帮孩子理解数学概念，虽然是一个简简单单的10以下数字，也可以让孩子展开很多思考和联想呢！2、气泡图，描述事物性质和特征（Bubble Maps -Describing Qualities ）国外很多幼儿园和小学都在用Bubble Map 来帮助孩子学习知识、描述事物，因为这个真的比较简单和管用，最基本的气泡图是这样的：圆圈图强调的是一个概念的具体展开，而气泡图，则更加侧重于对一个概念的特征描述。
比如这个孩子在用气泡图分析一只鹰有哪些特征。
看起来有点混，是不是？其实，檩子觉得，大家在实际带孩子分析问题的时候，不必太纠结到底该用哪种图，怎么直观怎么来，就行。
气泡图特别能帮助孩子学会使用丰富的形容词，有个孩子读完了《夏洛的网》，为书中的蜘蛛做了这样一张气泡图，在她眼里，这只叫夏洛特的蜘蛛具有一堆美好的品质：聪明、友好、有爱、有才、神奇 ...3、双重气泡图，比较和对照（Double Bubble Maps - Comparing and Contrasting）气泡图还有一个“升级版”，叫双重气泡图（Double Bubble Maps）－这也是一件分析“神器”，它的妙处在于，可以帮孩子对两个事物做比较和对照，找到它们的差别和共同点。
教学设计中常用的八种思维导图思维导图的常见形式有以下几种：圆圈图Circle Map起泡图Bubble Map双起泡图Double Bubble Map树型图Tree Map括号图Brace Map流程图Flow Map复流程图Multi-Flow Map桥型图Bridge Map【拓展阅读】思维导图学习一、在创作思维导图中出现思维阻滞怎么办?1.增加空白线条如果暂时出现了思维障碍，可以先继续在思维导图上加上一些空白线条。
这会对大脑提出挑战，刺激大脑去完成尚未完成的东西，使其在你无限的联想能力帮助下“茅塞顿开”。
2. 提问题提问题是大脑借以积累系列知识的主要方式。
给自己提一些合适的问题，会引起一些打破思维障碍的反应。
3. 增加图像在思维导图上增加图像，可以使进一步触发联想和易于回忆的可能性更大。
4. 保持无限联想的能力意识保持这个意识，会让大脑处于自由状态，而不是受制于既有的习惯。
二、线条分支一定要由粗到细吗?在思维导图的线条中，中央的线条更粗一些，加以突出以后，较粗的线条立即向你的大脑发出一个信号，让你注意中心思想的重要性。
如果你的思维导图是处在探索阶段，也许你会发现，在思维成图的过程中，一些周边思想实际上比中心思想更为重要。
在这些情况下，只要合适，你就可以简单地把外围的线条加粗一些。
有的曲线条会更大程度地增强视觉兴趣。
三、为什么字的长度一定要等于线的长度?线条的长度与词本身的长度一样，让关键词与关键词之间靠的更近，因而也就有助于产生联想。
另外，所节约的空间也让人能够包括更多的信息在一张思维导图上。
四、是否可以把整个支干脉络圈起来?绘制导图时，我们可以为导图的分支添加边界线，定下分支的独特外形。
这个独特的外形可以激发包含在这个分支里的信息记忆。
对于更为高级一些的记忆专家而言，这些外形可以成为“活的图片”，极为成功地强化回忆起来的可能。
思维根据随意的外形构造图像，因而也就让外形更易于记住。
在思维导图中创造外形，会帮你在一个更为容易回忆的形式里组织许多的数据。
八种基本的思维导图思维导图，英文叫Mind MaP ,也称Thi nking MaP ,就是借助图表来分析问题、理清思路.今天介绍的都是思维图的基本款,体现了基础的思维框架。
但是每种图都能有无限的延伸，甚至不同种图可以结合起来一起用,可以变得非常复杂。
常见的思维图有这八种：CirCIeMaP 圆圈图、Tree MaP 树状图、BubbIe MaPBubbIe MaP 双重气泡图、FloW MaP 流程图、多重流程图、BraCe MaP 括号图,和Bridge气泡图、DoubleMUIti-flow MaPMaP桥型图。
BIlACE WAPCff(CLE MAPF(X CEFHW 斗CofflIXFTfIEE MAPD0t∕βtf BUBBLE MAPFLOW MAP MULThFLOWMAPFM CAlSf ΛW ffflΓCT5BRtDGE MAP心AmL YZMi WHOLf MjECTS W PMTS RM AMLQGfES1、圆圈图，定义一件事 (CirCIe MaPS — Defi ning in Con text )CirCIe map 主要用于把一个主题展开来，联想或描述细节.它有两个圆圈，里面的小圈圈是主题，而外面的大圈圈里放的是和这个主题有关的细节或特征。
基本形状是这样的:下面是国外一个幼儿园孩子做的圆圈图练习。
左边是一个典型的联想型圆圈图；主题是海滩，可以联想到螃蟹、鱼、遮阳伞、海草、游泳衣、海豚，等等。
而右边的图，反过来，从现象、特征(details )让孩子去推断相关的主题是什么？思维练习的开始就是这么简单！CrQe35 Vhe mαm ideal还可以用圆圈图帮孩子理解数学概念，虽然是一个简简单单的10以下数字,也可以让孩子展开很多思考和联想呢！2、气泡图，描述事物性质和特征(BubbIe MaPS -DeSCrib ingQualitieS ）国外很多幼儿园和小学都在用BUbbIe MaP 来帮助孩子学习知识、描述事物,因为这个真的比较简单和管用，最基本的气泡图是这样的:圆圈图强调的是一个概念的具体展开, 而气泡图，则更加侧重于对一个概念的特征描述。
思维导图，英文叫 Mind Map，也称Thinking Map ，就是借助图表来分析问题、理清思路。
今天介绍的都是思维图的基本款，体现了基础的思维框架。
但是每种图都能有无限的延伸，甚至不同种图可以结合起来一起用，可以变得非常复杂。
常见的思维图有这八种：Circle Map 圆圈图、Tree Map 树状图、Bubble Map 气泡图、Double Bubble Map 双重气泡图、Flow Map 流程图、Multi-flow Map 多重流程图、Brace Map 括号图，和 Bridge Map 桥型图。
1、圆圈图，定义一件事（Circle Maps - Defining in Context ）Circle map 主要用于把一个主题展开来，联想或描述细节。
它有两个圆圈，里面的小圈圈是主题，而外面的大圈圈里放的是和这个主题有关的细节或特征。
基本形状是这样的：下面是国外一个幼儿园孩子做的圆圈图练习。
左边是一个典型的联想型圆圈图；主题是海滩，可以联想到螃蟹、鱼、遮阳伞、海草、游泳衣、海豚，等等。
而右边的图，反过来，从现象、特征（details）让孩子去推断相关的主题是什么？思维练习的开始就是这么简单！还可以用圆圈图帮孩子理解数学概念，虽然是一个简简单单的10以下数字，也可以让孩子展开很多思考和联想呢！2、气泡图，描述事物性质和特征（Bubble Maps -Describing Qualities ）国外很多幼儿园和小学都在用 Bubble Map 来帮助孩子学习知识、描述事物，因为这个真的比较简单和管用，最基本的气泡图是这样的：圆圈图强调的是一个概念的具体展开，而气泡图，则更加侧重于对一个概念的特征描述。
比如这个孩子在用气泡图分析一只鹰有哪些特征。
看起来有点混，是不是？其实，檩子觉得，大家在实际带孩子分析问题的时候，不必太纠结到底该用哪种图，怎么直观怎么来，就行。
气泡图特别能帮助孩子学会使用丰富的形容词，有个孩子读完了《夏洛的网》，为书中的蜘蛛做了这样一张气泡图，在她眼里，这只叫夏洛特的蜘蛛具有一堆美好的品质：聪明、友好、有爱、有才、神奇 ...3、双重气泡图，比较和对照（Double Bubble Maps - Comparing and Contrasting）气泡图还有一个“升级版”，叫双重气泡图（Double Bubble Maps）－这也是一件分析“神器”，它的妙处在于，可以帮孩子对两个事物做比较和对照，找到它们的差别和共同点。
小学数学思维导图(全)一、数的概念1. 自然数自然数是无限的，可以一直往上数。
自然数是离散的，相邻的自然数之间没有其他数。
自然数是可数的，可以一个一个地数出来。
2. 整数整数是可加的，可以相加得到新的整数。
整数是可减的，可以相减得到新的整数。
整数是可乘的，可以相乘得到新的整数。
整数是可除的，可以相除得到新的整数。
3. 分数分数有分子和分母两部分，分子表示被等分的部分，分母表示等分的总份数。
分数可以相加、相减、相乘、相除。
分数可以化简，即分子和分母同时除以它们的最大公约数。
4. 小数小数有整数部分和小数部分两部分，整数部分表示整体中的整数部分，小数部分表示整体中的小数部分。
小数可以相加、相减、相乘、相除。
小数可以化简，即去掉末尾的0。
二、数的运算1. 加法加法是可交换的，即加数的位置可以交换。
加法是可结合的，即加数可以按照任意顺序相加。
加法的结果是唯一的。
2. 减法减法的结果是唯一的。
减法的结果可以是正数、负数或0。
3. 乘法乘法是可交换的，即乘数的位置可以交换。
乘法是可结合的，即乘数可以按照任意顺序相乘。
乘法的结果是唯一的。
4. 除法除法的结果可以是正数、负数或分数。
除法的结果是唯一的。
三、几何图形1. 线段线段有长度。
线段可以测量。
线段可以比较长度。
2. 角角有大小。
角可以测量。
角可以比较大小。
3. 三角形三角形有面积。
三角形的面积可以用公式计算。
三角形的面积可以比较大小。
4. 四边形四边形有面积。
四边形的面积可以用公式计算。
四边形的面积可以比较大小。
四、数学应用1. 解决实际问题数学可以应用于解决实际问题，例如：计算购物时的找零。
计算路程和时间的关系。
计算物体的面积和体积。
2. 数学游戏数学游戏可以帮助学生提高数学思维能力和兴趣，例如：猜数字游戏。
24点游戏。
数独游戏。
3. 数学竞赛数学竞赛可以激发学生的学习兴趣和竞争意识，例如：数学奥林匹克竞赛。
华罗庚金杯赛。
小学生数学竞赛。
五、数学思维方法1. 归纳法归纳法是一种从具体事例出发，得出一般结论的思维方式。
八种基本的思维导图思维导图，英文叫Mind Map，也称 Thinking Map ，就是借助图表来分析问题、理清思路。
今天介绍的都是思维图的基本款，体现了基础的思维框架。
但是每种图都能有无限的延伸，甚至不同种图可以结合起来一起用，可以变得非常复杂。
常见的思维图有这八种：Circle Map 圆圈图、Tree Map 树状图、Bubble Map 气泡图、Double Bubble Map 双重气泡图、Flow Map 流程图、Multi-flow Map 多重流程图、Brace Map 括号图，和Bridge Map 桥型图。
1、圆圈图，定义一件事（Circle Maps - Defining in Context ）Circle map 主要用于把一个主题展开来，联想或描述细节。
它有两个圆圈，里面的小圈圈是主题，而外面的大圈圈里放的是和这个主题有关的细节或特征。
基本形状是这样的：下面是国外一个幼儿园孩子做的圆圈图练习。
左边是一个典型的联想型圆圈图；主题是海滩，可以联想到螃蟹、鱼、遮阳伞、海草、游泳衣、海豚，等等。
而右边的图，反过来，从现象、特征（details）让孩子去推断相关的主题是什么？思维练习的开始就是这么简单！还可以用圆圈图帮孩子理解数学概念，虽然是一个简简单单的10以下数字，也可以让孩子展开很多思考和联想呢！2、气泡图，描述事物性质和特征（Bubble Maps -Describing Qualities ）国外很多幼儿园和小学都在用Bubble Map 来帮助孩子学习知识、描述事物，因为这个真的比较简单和管用，最基本的气泡图是这样的：圆圈图强调的是一个概念的具体展开，而气泡图，则更加侧重于对一个概念的特征描述。
比如这个孩子在用气泡图分析一只鹰有哪些特征。
看起来有点混，是不是？其实，檩子觉得，大家在实际带孩子分析问题的时候，不必太纠结到底该用哪种图，怎么直观怎么来，就行。
气泡图特别能帮助孩子学会使用丰富的形容词，有个孩子读完了《夏洛的网》，为书中的蜘蛛做了这样一张气泡图，在她眼里，这只叫夏洛特的蜘蛛具有一堆美好的品质：聪明、友好、有爱、有才、神奇 ...3、双重气泡图，比较和对照（Double Bubble Maps - Comparing and Contrasting）气泡图还有一个“升级版”，叫双重气泡图（Double Bubble Maps）－这也是一件分析“神器”，它的妙处在于，可以帮孩子对两个事物做比较和对照，找到它们的差别和共同点。
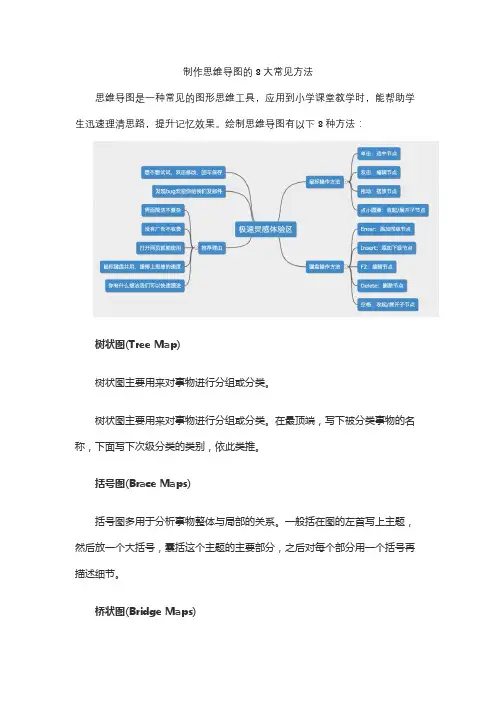
制作思维导图的8大常见方法思维导图是一种常见的图形思维工具，应用到小学课堂教学时，能帮助学生迅速理清思路，提升记忆效果。
绘制思维导图有以下8种方法：树状图(Tree Map)树状图主要用来对事物进行分组或分类。
树状图主要用来对事物进行分组或分类。
在最顶端，写下被分类事物的名称，下面写下次级分类的类别，依此类推。
括号图(Brace Maps)括号图多用于分析事物整体与局部的关系。
一般括在图的左首写上主题，然后放一个大括号，囊括这个主题的主要部分，之后对每个部分用一个括号再描述细节。
桥状图(Bridge Maps)一种主要用来进行类比和类推的图。
这是一种主要用来进行类比和类推的图。
在桥型横线的上面和下面写下具有相关性的一组事物，然后按照这种相关性，列出更多具有类似相关性的事物。
气泡图(Bubble Maps)气泡图通常用于定义事物的属性或相应的联系。
气泡图通常用于定义事物的属性或相应的联系，主要是使用形容词或形容词短语来描述物体。
在画气泡图的时候，一般在中心圆圈内写下被描述的物体，外面圆圈内写下描述性的形容词或短语。
双重气泡图(Double Bubble Maps)双重气泡图也叫气泡图的升级版，这也是一件分析“神器”，主要用于两个主题间的比较和对照。
双重气泡图也叫气泡图的升级版，这也是一件分析“神器”，主要用于两个主题间的比较和对照，从而找到它们的差别和共同点。
具体在绘制的时候是将两个主题分别画在两个圆中，周围的泡泡就是关于主题的属性或者联想，如果一个泡泡和两个主题都关联，那么它就可以用线跟两个主题圆都连起来。
这样的好处是，两个主题有什么共性就可以一目了然了。
流程图(Flow Maps)流程图主要用于描述一件事情的各个过程(包括发生顺序、时间过程、步骤等)。
流程图主要用于描述一件事情的各个过程(包括发生顺序、时间过程、步骤等)。
绘制时通常是在最大的方框内，先写好这个事情的主题，然后用小方框描述完成这个事情所需要的每个步骤，并且用箭头将这些步骤联系起来。
创作编号：BG7531400019813488897SX创作者：别如克*思维导图，英文叫Mind Map，也称 Thinking Map ，就是借助图表来分析问题、理清思路。
今天介绍的都是思维图的基本款，体现了基础的思维框架。
但是每种图都能有无限的延伸，甚至不同种图可以结合起来一起用，可以变得非常复杂。
常见的思维图有这八种：Circle Map 圆圈图、Tree Map 树状图、Bubble Map 气泡图、Double Bubble Map 双重气泡图、Flow Map 流程图、Multi-flow Map 多重流程图、Brace Map 括号图，和Bridge Map 桥型图。
1、圆圈图，定义一件事（Circle Maps - Defining in Context ）Circle map 主要用于把一个主题展开来，联想或描述细节。
它有两个圆圈，里面的小圈圈是主题，而外面的大圈圈里放的是和这个主题有关的细节或特征。
基本形状是这样的：下面是国外一个幼儿园孩子做的圆圈图练习。
左边是一个典型的联想型圆圈图；主题是海滩，可以联想到螃蟹、鱼、遮阳伞、海草、游泳衣、海豚，等等。
而右边的图，反过来，从现象、特征（details）让孩子去推断相关的主题是什么？思维练习的开始就是这么简单！还可以用圆圈图帮孩子理解数学概念，虽然是一个简简单单的10以下数字，也可以让孩子展开很多思考和联想呢！2、气泡图，描述事物性质和特征（Bubble Maps -Describing Qualities ）国外很多幼儿园和小学都在用Bubble Map 来帮助孩子学习知识、描述事物，因为这个真的比较简单和管用，最基本的气泡图是这样的：圆圈图强调的是一个概念的具体展开，而气泡图，则更加侧重于对一个概念的特征描述。
比如这个孩子在用气泡图分析一只鹰有哪些特征。
看起来有点混，是不是？其实，檩子觉得，大家在实际带孩子分析问题的时候，不必太纠结到底该用哪种图，怎么直观怎么来，就行。
