第3讲 集合的基本运算解析版
- 格式:docx
- 大小:615.47 KB
- 文档页数:10


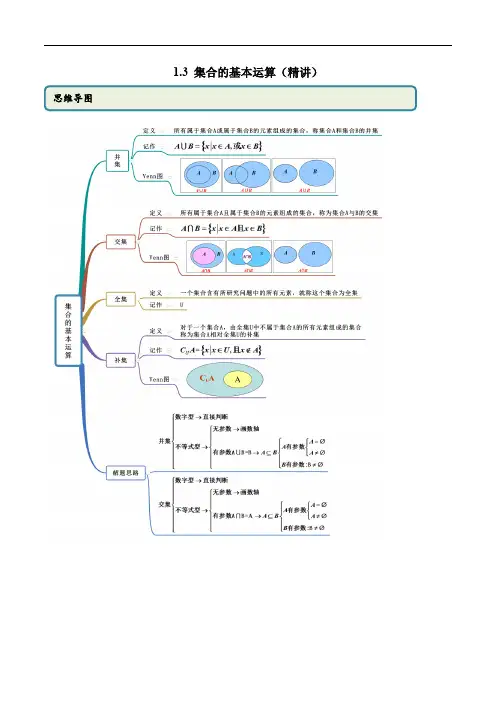
1.3 集合的基本运算(精讲)考点一交集【例1】(1)(2020·上海高一开学考试)设集合A {}3,5,6,8=,集合B {}4,5,7,8=,则A B 等于( )A .{}5,8B .{}3,,6C .{}4,7D .{}3,5,6,8(2)(2020·安徽省庐江金牛中学)已知集合{}|12M x x =-<<,{}|13N x x =≤≤,则M N =( )A .(]1,3-B .(]1,2-C .[)1,2D .(]2,3 【答案】(1)A (2)C【解析】(1)集合A {}3,5,6,8=,集合B {}4,5,7,8=,又集合A 与集合B 中的公共元素为5,8,{}5,8A B ∴⋂=,故选A.(2)集合{}|12M x x =-<<,{}|13N x x =≤≤∴{}[)|121,2M N x x ⋂=≤<=.故选:C.【一隅三反】1.(2020·全国高一课时练习)设集合2{|430}A x x x =-+<,{|230}B x x =->,则AB =( )A .3(3,)2-- B .3(3,)2-C .3(1,)2D .3(,3)2【答案】D【解析】集合()(){}{}|130|13A x x x x x =--<=<<,集合,所以3|32A B x x ⎧⎫⋂=<<⎨⎬⎩⎭,故选D.2(2020·浙江省兰溪市第三中学高三开学考试)已知集合2{|560}A x x x =-+≤,{|15}B x Z x =∈<<,则A B =( )A .[2,3]B .(1,5)C .{}2,3D .{2,3,4}【答案】C 【解析】2560(2)(3)023x x x x x -+≤⇒--≤⇒≤≤,{}23A x x ∴=≤≤,又{}{|15}2,3,4B x Z x =∈<<=,所以{}2,3A B ⋂=,故本题选C.3.(2020·湖南怀化高二期末)设集合{}2|340A x Z x x =∈--≤,{}|21B x x =-<,则AB =( )A .{1,0,1,2}-B .[1,2)-C .{1,0,1}-D .[1,2]-【答案】A【解析】由题意得,{}{}{}2|340|141,0,1,2,3,4A x Z x x x Z x =∈--≤=∈-≤≤=-,{}{}|21|3B x x x x =-<=<,则{}{}{}1,0,1,2,3,4|31,0,1,2A B x x =-<=-,故选:A .考法二 并集【例2】(2020·甘肃城关.兰大附中高三月考(理))若集合{}22A x x =-<≤,{}13B x x =-≤<,则A B =( )A .[)2,3-B .(]1,2-C .(]2,2-D .()2,3-【答案】D【解析】因为{}22A x x =-<≤,{}13B x x =-≤<,所以AB =()2,3-.故选:D .【一隅三反】1.(2020·贵州南明贵阳一中高三其他(理))已知集合{22}A x x =-<<∣,若A B A ⋃=,则B 可能是( )A .{}1,1-B .{}2,3C .[)1,3-D .[]2,1--【答案】A【解析】因为A B A ⋃=,所以B A ⊆,四个选项中只有{}1,1-是集合A 的子集. 故选:A2(2020·上海高一课时练习)满足条件{}{}1,31,3,5A ⋃=的所有集合A 的个数是 ( ) A .1 B .2 C .3 D .4【答案】D【解析】因为{}{}1,31,3,5A ⋃=,所以,集合A 可能为{}{}{}{}5,1,5,5,3,1,3,5, 即所有集合A 的个数是4,故选D.3.(2019·浙江高一期中)已知集合2{|1}P x x ==, 2{|0}Q x x x =-=,那么PQ =( )A .{1,1}-B .{1}C .{1,0,1}-D .{0,1}【答案】C【解析】因为2{|1}{1,1}===-P x x ,2{|0}{0,1}=-==Q x x x , 所以{}1,0,1P Q ⋃=-,故选:C考法三 补集与全集【例3】(2020·上海高一课时练习)已知全集U={1,3,5,7,9},集合A={1,|a -5|,9}, ∁U A={5,7},则a 的值是( ) A .2 B .8C .-2或8D .2或8【答案】D【解析】由由已知得5382a a -=⇒=或;故选D【一隅三反】1.(2020·全国高一)设集合{}0,1,2,3U =,集合{}2|0A x U x mx =∈+=,若{}1,2U C A =,则实数m =_____. 【答案】-3【解析】因为集合{}0,1,2,3U =, {}1,2U C A =,A={0,3},故m= -3.2.(2020·全国高一专题练习)已知全集{}{}2{2,3,23},1,2,3U U a a A a C A a =+-=+=+,则a 的值为__________ 【答案】2【解析】由补集概念及集合中元素互异性知a 应满足()()()()22222233(1)323|1|23(2)|1|3232(3)232233(4)2123433a a a a a a a a A a a B a a a a a a ⎧+=+=+-⎪+=+-⎧⎪⎪⎨+=⎪⎨+-≠⎪⎪+-≠⎪⎪+-≠+-≠⎩⎩或 分两种情况进行讨论:在A 中,由(1)得a=0依次代入(2)、(3)、(4)检验,不合②,故舍去.在B 中,由(1)得a=-3,a=2,分别代入(2、(3)、(4)检验,a=-3不合②,故舍去,a=2能满足②③④,故a=2符合题意.答案为:23.(2019·上海虹口.上外附中高一期中)设全集{}22,3,3U a a =+-,集合{},3A a =,{}2U C A =,则a =___________. 【解析】由{}2U C A =,{}22,3,3U a a =+-可知{}23,3A a a =+-,即{}{}23,3,3a a a +-=.故232,3a a aa ⎧+-=⎪⎨≠⎪⎩ .当0a ≥时,23a a a a +-=⇒=当0a <时,23a a a +-=-即 ()()2230130a a a a +-=⇒-+=,故3a =-.不满足2,3a ≠.故a =考法四 集合运算综合运用【例4】(2020·全国高一课时练习)已知集合{}3|0|31x M x N x x x +⎧⎫=<=≤-⎨⎬-⎩⎭,,则集合 {}|1x x ≥=( ) A .M N ⋂ B .M N ⋃C .()RM N ⋂D .()RM N ⋃【答案】D 【解析】3x +<,解之得,31x -<<,则(,1)M N ⋃=-∞.故选:D. 【一隅三反】1.(2019·浙江高三月考)已知集合{|(3)(1)0}A x x x =-+>,{1|1}B xx =->‖,则()R C A B ⋂=( ) A .[1,0)(2,3]-B .(2,3]C .(,0)(2,)-∞+∞D .(1,0)(2,3)-【答案】A【解析】因为集合{|(3)(1)0}A x x x =-+>,{1|1}B xx =->‖, 所以{|3A x x =>或1}x <-,{|2B x x =>或0}x <,所以{|13}R C A x x =-≤≤,所以()R C A B ⋂={|23x x <≤或10}x -≤<,故选A .2.(2020·浙江高三月考)已知全集{}1,0,1,2,3,4U =-,集合{}|1,=≤∈A x x x N ,{}1,3B =,则()UB A =( )A .{}4B .{}2,4C .{}1,2,4-D .{}1,0,2,4-【答案】C【解析】因为{}|1,=≤∈A x x x N ,{}1,3B =,所以{}0,1,3A B =,则(){}1,2,4UA B =-. 故选:C.3.(2019·浙江高三月考)已知全集{}0,1,2,3,4,5,6U =,集合{}0,1,3,5A =,{}2,3,6B =,则()UA B ⋃=( ) A .{}3 B .{}0,1,3,4 C .{}0,1,3,4,5 D .{}0,1,2,3,5,6【答案】C 【解析】全集{}0,1,2,3,4,5,6U =,集合{}2,3,6B =,则{}0,1,4,5UB =,又集合{}0,1,3,5A =,因此,(){}0,1,3,4,5UA B =.故选:C.考法五 求参数【例5】2.(2020·黑龙江萨尔图.大庆实验中学高二月考(理))已知集合{}2|3210A x x x =--≤,{}|23B x a x a =<<+,若A B =∅,则实数a 的取值范围是( )A .101,,32⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭ B .101,,32⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭ C .()1,2,6⎛⎫-∞-⋃+∞ ⎪⎝⎭D .[)1,2,6⎛⎤-∞-⋃+∞ ⎥⎝⎦【答案】B【解析】{}21|321013A x x x x x ⎧⎫=--≤=-≤≤⎨⎬⎩⎭,当B =∅时,32a a +≤,解得3a ≥,符合题意;当B ≠∅时,2123a a a ≥⎧⎨<+⎩ 或13323a a a ⎧+≤-⎪⎨⎪<+⎩,解得132a ≤<或103a ≤-,综上所述,实数a 的取值范围是101,,32⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭.故选:B【一隅三反】1.(2020·安徽金安六安一中高一期末(理))若不等式组2142x a x a ⎧->⎨-<⎩的解集非空,则实数a 的取值范围是( )A .()1,3-B .(,1)(3,)-∞-+∞C .()3,1-D .(,3)(1,)-∞-⋃+∞【答案】A【解析】由题意2124x a x a ⎧>+⎨<+⎩,∴2124a a +<+,即2230a a --<,解得13a -<<.故选:A .2(2020·湖北高一期末)设全集U =R ,已知集合{3A x x =<或}9x ≥,集合{}B x x a =≥.若()U C A B ≠∅,则a 的取值范围为( )A .3a >B .3a ≤C .9a <D .9a ≤【答案】C【解析】∵{3A x x =<或}9x ≥,∴{}9|3U C A x x =≤<,若()U C A B ≠∅,则9a <,故选:C .3.(2020·浙江高一课时练习)设集合{}2320A x x x =-+=,(){}222150B x x a x a =+++-=.(1)若{}2A B ⋂=,求实数a 的值; (2)若A B A ⋃=,求实数a 的取值范围; (3)若全集U =R ,()UAB A =,求实数a 的取值范围.【答案】(1)1-或3-(2){}3a a ≤-(3){1,3,11a a a a a ≠-≠-≠-≠-- 【解析】(1)由2320x x -+=得{}1,2A =,因为{}2A B ⋂=,所以2B ∈, 所以()244150a a +++-=,整理得2430a a ++=,解得1a =-或3-.当1a =-时,{}{}2402,2B x x =-==-,满足{}2A B ⋂=;当3a =-时,{}{}24402B x xx =-+==,满足{}2A B ⋂=;故a 的值为1-或3-.(2)由题意,知{}1,2A =. 由A B A ⋃=,得B A ⊆.当集合B =∅时,关于x 的方程()222150x a x a +++-=没有实数根,所以()()2241450a a ∆=+--<,即30a +<,解得3a <-.当集合B ≠∅时,若集合B 中只有一个元素,则()()2241450a a ∆=+--=,整理得30a +=,解得3a =-,此时{}{}24402B x x x =-+==,符合题意;若集合B 中有两个元素,则{}1,2B =,所以22220430a a a a ⎧+-=⎨++=⎩,无解.综上,可知实数a 的取值范围为{}3a a ≤-. (3)由()UAB A =,可知A B =∅,所以()()221215044150a a a a ⎧+++-≠⎪⎨+++-≠⎪⎩,所以1113a a a a ⎧≠-≠-⎪⎨≠-≠-⎪⎩且 综上,实数a的取值范围为{1,3,11a a a a a ≠-≠-≠-≠-.故得解.。




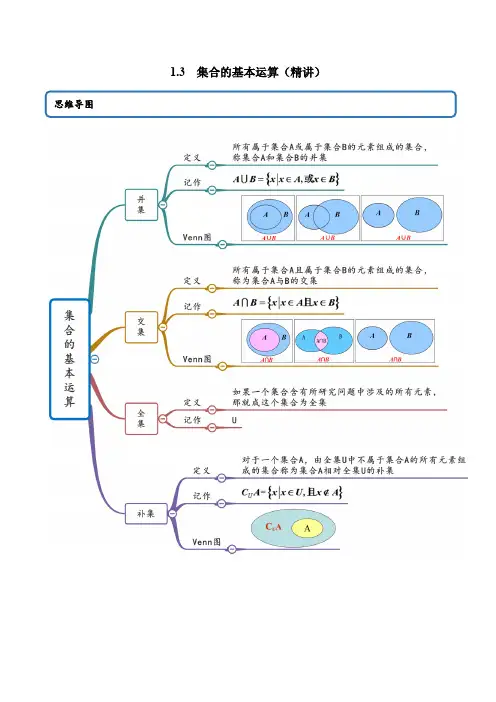
第一章第三节集合的基本运算一、电子版教材二、教材解读知识点 集合的运算1.由所有属于集合A 或属于集合B 的元素组成的集合叫A 与B 的并集,记作A ∪B ;符号表示为A ∪B ={x |x ∈A 或x ∈B } 2.并集的性质A ∪B =B ∪A ,A ∪A =A ,A ∪∅=A ,A ⊆A ∪B .3.对于两个给定的集合A 、B ,由所有属于集合A 且属于集合B 的元素组成的集合叫A 与B 的交集,记作A ∩B 。
符号为A ∩B ={x |x ∈A 且x ∈B }。
4. 交集的性质A ∩B =B ∩A ,A ∩A =A ,A ∩∅=∅,A ∩B ⊆A .5、对于一个集合A ,由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集,记作∁U A 。
符号语言:∁U A ={x |x ∈U ,且x ∉A }。
【例题1】(2020·全国高一)已知集合{}1,2,3,4A =,{}1,4,5B =,C A B =,则C 的子集共有( )A .2个B .3个C .8个D .4个【答案】D 【解析】{1,4}C AB ==,C 的子集有{}1,{}4,{}1,4,∅,共4个.【例题2】(2020·山东省邹城市第一中学高三其他)已知集合{|2}A x x k k ==∈Z ,,{|22}B x x =-≤≤,则AB =( )A .[11]-,B .[22]-,C .{02},D .{202}-,, 【答案】D 【解析】{|2}A x x k k ==∈Z ,,{|22}B x x =-≤≤,∴{202}A B =-,,,故选:D.【例题3】(2020·安徽省舒城中学高二月考(文))已知集合{}}242{60M x x N x x x =-<<=--<,,则M N ⋂= A .}{43x x -<<B .}{42x x -<<-C .}{22x x -<<D .}{23x x <<【答案】C【解析】由题意得,{}{}42,23M x x N x x =-<<=-<<,则{}22M N x x ⋂=-<<.故选C .【例题4】(2020·肥城市教学研究中心高三其他)已知全集U =R ,集合{}1,0,1,2A =-,{}1B x x =≥,则()U A C B ⋂=( )A .{}1,0,1-B .{}1,0-C .{}1x x <D .{}11x x -≤<【答案】B 【解析】由题可知{}1U C B x x =<,则{}()1,0U C A B ⋂=-.【例题5】(2020·重庆高三月考(文))已知全集为R ,集合{}02M x x =<≤,{}1,0,1,2,3N =-,则()R C M N =( )A .{}0,1B .{}1,0,1-C .{}1,0,3-D .{}1,1,2,3-【答案】C 【解析】(](),02,R C M =-∞+∞,则(){}1,0,3R C M N =-.故选:C.【例题6】(2020·全国高一)设全集为R ,{}|37A x x =≤<,{}|210B x x =<<. (1)求A B ;(2)求()R C A B ⋃.【解析】(1)由题意{|37}A B x x =≤<;(2)由题意{|210}A B x x ⋃=<<, ∴(){|2RC A B x x ⋃=≤或10}x ≥.【例题7】(2020·全国高一)已知集合{|121}A x a x a =-<<+,{}B 03x x =<≤,U =R . (1)若12a =,求A B ⋃;()U A C B ⋂. (2)若A B φ⋂=,求实数a 的取值范围.【解析】(1)若12a =时1|22A x x ⎧⎫=-<<⎨⎬⎩⎭,{}|03B x x =<≤,∴1|32AB x x ⎧⎫=-<≤⎨⎬⎩⎭,由{|0U C B x x =≤或3}x >,所以()1|02UA CB x x ⎧⎫⋂=-<≤⎨⎬⎩⎭(2)由AB =∅知当A =∅时121a a -≥+∴2a ≤-当A ≠∅时21113a a a +>-⎧⎨-≥⎩或211210a a a +>-⎧⎨+≤⎩∴4a ≥或122a -<≤-综上:a 的取值范围是1|24a a a ⎧⎫≤-⎨⎬⎩⎭≥或. 三、素养聚焦1.已知集合{}{}2|1,|0A x x B x x ==<≤,则()R AB C =( )A .{|0}x x <B .{|01}x x ≤≤C .{|10}x x -≤<D .【答案】D【解析】{|11},{|0}A x x B x x =-≤≤=<,所以 (){|1}R AB xC x =≤-.故选:D2.已知集合{1,2,3}A =,{|(1)(2)0,}B x x x x Z =+-<∈,则A B ⋃= A .{1} B .{12}, C .{0123},,, D .{10123}-,,,, 【答案】C【解析】集合{}{|12,}0,1B x x x Z =-<<∈=,而{}1,2,3A =,所以{}0,1,2,3A B ⋃=,故选C. 3.已知集合{}0,1,2,3,4,5A =,{}1,3,5,7,9B =则A B =( )A .{}1,2,3,5B .{}0,1,3,5C .{}1,3,5D .{}0,1,2,3,4,5,7,9【答案】C【解析】因为集合{}0,1,2,3,4,5A =,{}1,3,5,7,9B =,故{}1,3,5A B =.故选:C4.若集合{}|03A x x =<<,{}|11B x x =-<<,则A B =( )A .{}13x x -<< B .{}10x x -<< C .{}01x x << D .{}13x x <<【答案】A【解析】由于集合{}|03A x x =<<,{}|11B x x =-<<,所以A B ={}13x x -<<5.已知集合A ={x |﹣1<x <5},B ={1,3,5},则A ∩B =( ) A .{1,3} B .{1,3,5}C .{1,2,3,4}D .{0,1,2,3,4,5} 【答案】A【解析】∵A ={x |﹣1<x <5},B ={1,3,5},∴A ∩B ={1,3}. 故选:A.6.若集合{|2}M x x =<,{|01}N x x =≤≤,则M N =( )A .[0,1]B .[0,2]C .[1,2)D .(,2]-∞【答案】A【解析】因为{|2}M x x =<,{|01}N x x =≤≤, 所以MN ={|01}x x ≤≤.7.已知集合{1,1,2,3,4,5}A =-,{|(1)(5)0}B x x x =∈--<N ,则AB =( ).A .{3}B .{2,3}C .{2,3,5}D .{1,1,5}-【答案】D【解析】{|(1)(5)0}{2,3,4}B x x x =∈--<=N ,所以{1,1,5}AB =-.8.满足条件{}{}1,31,3,5A ⋃=的所有集合A 的个数是 ( ) A .1 B .2C .3D .4【答案】D【解析】因为{}{}1,31,3,5A ⋃=,所以,集合A 可能为{}{}{}{}5,1,5,5,3,1,3,5, 即所有集合A 的个数是4,故选D.9.已知集合P ,S 满足P S P ⋂=,则下列关系式恒成立的是( )A .P ⫋SB .P S ⊆C .P S =D .S ⫋P【答案】B 【解析】集合P ,S 满足P S P ⋂=,∴P 中的元素都在集合S 中, ∴P S ⊆.10.已知集合I ,M ,N 的关系如图,则I ,M ,N 的关系为( ).A .I I C M C N ⊇B .I MC N ⊆C .I I C M C N ⊆D .I M C N ⊇【答案】C【解析】由韦恩图可知,N M I I I C M C N ∴⊆,11.设{}2(,)||1|(2)0A x y x y =++-=,{1,2}B =-,则必有( ). A .A B ⊇ B .A ⊆BC .A B =D .AB =∅【答案】D【解析】{}2(,)||1|(2)0{(1,2)}A x y x y =++-==-,{1,2}B =-,A B ∴⋂=∅12.设全集{,,,,}U a b c d e =,集合{,,}M a c d =,{,,}N b d e =,那么()()U U C M C N 是( ). A .∅ B .{}dC .{,}a cD .{,}b e【答案】A【解析】因为全集{,,,,}U a b c d e =,集合{,,}M a c d =,{,,}N b d e =, 所以{,}U C M b e =,{,}U C N a c =,所以()()UU C M C N ∅=,13.已知集合{}2|1,M y y x x R ==-∈,集合{|N x y ==,MN =( ).A .{}( B .[- C .D .∅【答案】B【解析】[1,)M =-+∞,[N =,故[M N ⋂=-14.已知全集{}1,0,1,2,3U =-,集合{}0,1,2A =,{}1,0,1B =-,则()UA B ⋂=( )A .{}1-B .{}0,1C .{}1,2,3-D .{}1,0,1,3-【答案】A【解析】={1,3}U C A -,则(){1}U C A B =-15.已知集合{1A x x =<-或}2x >,集合{}03B x x =≤<,则()RA B =( )A .{}02x x ≤≤ B .{}02x x <≤C .{}02x x ≤<D .{}02x x <<【答案】A【解析】依题意R C A {}12x x =-≤≤,所以()RA B ={}02x x ≤≤.16.已知函数()f x =A ,则R C A = ( )A .{|0x x ≤或}1x ≥B .{|<0x x 或}>1xC .{}|01x x ≤≤D .{}|0<<1x x【答案】D【解析】已知函数2y x x =-的定义域为A ,所以20x x -≥,得01x x ≤≥,或,即{}01A x x x ,或=≤≥,故C A =R {}1|0x x <<.17.设集合(){}(){}2,2,,A x y x y B x y y x =+===,则AB =( )A .(){}1,1 B .(){}2,4-C .()(){}1,1,2,4-D .∅【答案】C【解析】首先注意到集合A 与集合B 均为点集,联立22x y y x +=⎧⎨=⎩, 解得11x y =⎧⎨=⎩,或24x y =-⎧⎨=⎩,从而集合{(1,1),(2,4)}AB =-,18.下列表示图形中的阴影部分的是( )A .()()A CBC B .()()A B A C C .()()AB B CD .()AB C【答案】A【解析】由已知中阴影部分所表示的集合元素满足 “是A 的元素且是B 的元素,或是C 的元素”, 故阴影部分所表示的集合是()()()CA B A C B C =19.集合A ,B ,C 满足A B A C ⋃=⋃,则成立的等式是( ). A .B C =B .()()R R A BC C C A ⋂=⋂C .A B A C ⋂=⋂D .R R A C B A C C ⋂=⋂【答案】B【解析】因为A B A C ⋃=⋃,所以B A ⊆且C A ⊆,而集合,B C 不一定相等, 所以选项A,C,D 错误; 又由A B A C ⋃=⋃可知()()RR A B A C =∅=,故B 做正确.20.如图所示的韦恩图中,A 、B 是非空集合,定义*A B 表示阴影部分的集合,若x ,y ∈R ,2{|4}{|3,0}x A x y x x B y y x ==-==>,则A *B 为( )A .{|04}x x <≤B .{|01x x ≤≤或4}x >C .{|01x x ≤≤或2}x ≥D .{|01x x ≤≤或2}x >【答案】B【解析】依据定义,*A B 就是指将A B ⋃除去A B ⋂后剩余的元素所构成的集合; 对于集合A ,求的是函数24y x x =-的定义域, 解得:{|04}A x x =≤≤;对于集合B ,求的是函数3(0)xy x =>的值域,解得{}1B y y =;依据定义,借助数轴得:*{|01A B x x =≤≤或4}x >.21.设全集为U 定义集合A 与B 的运算:{*|A B x x A B =∈⋃且}x A B ∉⋂,则(*)*A B A =( ) A .A B .BC .U A C BD .U B C A【答案】B 【解析】{*|A B x x A B =∈⋃且}x A B ∉⋂ ()()U UB C A A C B =(*)*[(*)][(*)]()()U U U A B A A C A B A B C A A B B C A B ∴===22.设集合{}2A x x a=>,{}32B x x a =<-,若AB =∅,则a 的取值范围为( )A .()1,2B .()(),12,-∞⋃+∞C .[]1,2D .(][),12,-∞+∞【答案】D【解析】因为A B φ⋂=,所以232a a ≥-,解得1a ≤或2a ≥.23.设集合{}{}{|08},1,2,4,5,3,5,7U x N x S T =∈<≤==,则()U S C T ⋂=( ) A .{}1,2,4 B .{}1,2,3,4,5,7C .{}1,2D .{}1,2,4,5,6,8【答案】A【解析】∵{}1,2,3,4,5,6,7,8U =,∴{}1,2,4,6,8U C T =,∴{}()1,2,4U S C T ⋂= 24.已知集合A 4{|log (1)1}x x =+≤,{|21,}B x x k k Z ==-∈,则AB =( )A .{}113-,, B .{1,3} C .{1,3}- D .{1,1}-【答案】B【解析】由()411log x +≤可得:014x <+≤解得13x -<≤,即](13A =-, {}|21,B x x k k Z ==-∈, 则{}13A B ,⋂=25.设集合{|10}A x x =+>,{|210}B x x =+>,则()R AB C =( )A .1,2⎛⎤-∞- ⎥⎝⎦B .[)1,-+∞C .11,2⎛⎫- ⎪⎝⎭ D .11,2⎛⎤-- ⎥⎝⎦【答案】D【解析】由题意,集合(){|10}{|1}1,A x x x x =-=+>=>-+∞, 集合1{|210}{|}21(,)2B x x x x =+=->>-+=∞, 所以1,2B ∞-⎛⎤=- ⎥⎝⎦R ,所以()11,2A B ⎛⎤=--⎥⎝⎦R . 故选:D.26.已知非空集合A ,B 满足以下两个条件(){1,i A B ⋃=2,3,4,5,6},A B φ⋂=; ()ii 若x A ∈,则1x B +∈.则有序集合对(),A B 的个数为( ) A .12 B .13C .14D .15【答案】A【解析】由题意分类讨论可得: 若{}1A =,则{2,B =3,4,5,6}; 若{}2A =,则{1,B =3,4,5,6}; 若{}3A =,则{1,B =2,4,5,6}; 若{}4A =,则{1,B =2,3,5,6}; 若{}5A =,则{2,B =3,4,1,6}; 若{}1,3A =,则{2,B =4,5,6}; 若{}1,4A =,则{2,B =3,5,6}; 若{}1,5A =,则{2,B =3,4,6}; 若{}2,4A =,则{1,B =3,5,6}; 若{}2,5A =,则{1,B =3,4,6}; 若{}3,5A =,则{1,B =2,4,6}; 若{1,A =3,5},则{2,B =4,6}. 综上可得:有序集合对(),A B 的个数为12.27.已知集合21,01,2A =--{,,},{}|(1)(2)0B x x x =-+<,则AB =( )A .{}1,0-B .{}0,1C .{}1,0,1-D .{}0,1,2【答案】A【解析】由已知得{}|21B x x =-<<,因为21,01,2A =--{,,},所以{}1,0A B ⋂=-,故选A .28.某单位周一、周二、周三开车上班的职工人数分别是14,10,8.若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是( ) A .5 B .6C .7D .8【答案】B【解析】如图所示,(a +b +c +x )表示周一开车上班的人数,(b +d +e +x )表示周二开车上班人数,(c +e +f +x )表示周三开车上班人数,x 表示三天都开车上班的人数,则有:1410820a b c x b d e x c e f x a b c d e f x +++=⎧⎪+++=⎪⎨+++=⎪⎪++++++=⎩, 即22233220a b c d e f x a b c d e f x ++++++=⎧⎨++++++=⎩,即212b c e x +++=,当b =c =e =0时,x 的最大值为6, 即三天都开车上班的职工人数至多是6.29.设集合{}1,2,3,4,5,6M =,12,,,k S S S 都是M 的含两个元素的子集,且满足:对任意的{},i i i S a b =,{},j j j S a b =((),1,2,3,,i j i j k ≠∈、),都有max ,max ,j j i i i i j j a b a b b a b a ⎧⎫⎧⎫⎪⎪≠⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭({}max ,x y 表示两个数x ,y 中的较大者),则k 的最大值是( )A .10B .11C .12D .13【答案】B【解析】根据题意,对于M ,含2个元素的子集有15个, 但{1,2}、{2,4}、{3,6}只能取一个; {1,3}、{2,6}只能取一个; {2,3}、{4,6}只能取一个,故满足条件的两个元素的集合有11个;30.当一个非空数集G 满足“如果,a b G ∈,则,,a b a b ab G +-∈,且0b ≠时,aG b∈”时,我们称G 就是一个数域,以下四个关于数域的命题:①0是任何数域的元素;②若数域G 有非零元素,则2017G ∈;③集合{}|2,P x x k k Z ==∈是一个数域;④有理数集是一个数域,其中真命题有() A .1个 B .2个C .3个D .4个【答案】C【解析】①:当0a =时,有0aG b=∈,所以0是任何数域的元素,正确; ②:取G 为实数域,令2016a G =∈,1b G =∈,则2017a b G +=∈,正确; ③:若{}|2,P x x k k Z ==∈为数域,取2a =,4b =,则12a Pb =∈不成立,错误; ④:取有理数1x ,2x ,令1a x =,2b x =,则()12a b x x +=+∈有理数集, ()12a b x x -=-∈有理数集,()12a b x x ⋅=⋅∈有理数集,且12x a b x =∈有理数集(20x ≠),所以有理数集是数域.正确的有:①②④.31.全集(){},Z,Z U x y x y =∈∈,非空集合S U ⊆,且S 中的点在平面直角坐标系xOy 内形成的图形关于x 轴、y 轴和直线y x =均对称.下列命题: ①若()1,3S ∈,则()1,3S --∈; ②若()0,4S ∈,则S 中至少有8个元素; ③若()0,0S ∉,则S 中元素的个数一定为偶数;④若(){},4,Z,Z x y x y x y S +=∈∈⊆,则(){},4,Z,Z x y x y x y S +=∈∈⊆.其中正确命题的个数是( ) A .1 B .2C .3D .4【答案】C 【解析】S 中的点在平面直角坐标系xOy 内形成的图形关于x 轴、y 轴和直线y x =均对称.所以当(),x y S ∈,则有(),x y S -∈,(),x y S -∈,(),y x S ∈, 进而有:(),x y S --∈,(),y x S -∈,(),y x S -∈,(),y x S --∈ ①若()1,3S ∈,则()1,3S --∈,正确;②若()0,4S ∈,则()0,4S -∈,()4,0S ∈,()4,0S -∈,能确定4个元素,不正确;③根据题意可知,(),x y S ∈,若00x y =≠,能确定4个元素,当00x y ≠=,也能确定四个,当00x y ≠≠,也能确定8个所以()0,0S ∉,则S 中元素的个数一定为偶数正确;④若(){},4,Z,Z x y x y x y S +=∈∈⊆,由S 中的点在平面直角坐标系xOy 内形成的图形关于x 轴、y 轴和直线y x =均对称可知,(){},4,Z,Z x y x y x y S -=∈∈⊆,(){},4,Z,Z x y x y x y S -+=∈∈⊆,(){},4,Z,Z x y x y x y S --=∈∈⊆,即(){},4,Z,Z x y x y x y S +=∈∈⊆,故正确,综上:①③④正确. 故选C.32.已知集合{}{}2|4,|1A x y x B x a x a ==-=≤≤+,若A B A ⋃=,则实数的取值范围为( )A .(][),32,-∞-⋃+∞ B . C .D .【答案】C 【解析】试题分析:集合{}{}2|4|22A x y x x x ==-=-≤≤,若A B A ⋃=,则B A ⊆,所以有2{12a a ≥-+≤,所以21a -≤≤,故选C.33.(多选题)给定数集M ,若对于任意a ,b M ∈,有M b a ∈+,且a b M -∈,则称集合M 为闭集合,则下列说法中不正确的是( ) A .集合{}4,2,0,2,4M =--为闭集合 B .正整数集是闭集合C .集合{}3,M n n k k Z ==∈为闭集合 D .若集合1A ,2A 为闭集合,则12A A ⋃为闭集合【答案】ABD【解析】A. 当集合{}4,2,0,2,4M =--时,2,4M ∈,而24M +∉,所以集合M 不为闭集合. B.设,a b 是任意的两个正整数,当a b <时,0a b -<不是正整数, 所以正整数集不为闭集合. C .当{}3,M n n k k Z ==∈时,设12123,3,,a k b k k k Z ==∈ 则123abk k M (?为∈),()123a b k k M -=-∈,所以集合M 是闭集合.D .设{}13,A n n k k Z ==∈,{}22,A n n k k Z ==∈由C 可知,集合1A ,2A 为闭集合,122,3A A ∈⋃,而1223A A +∉⋃,此时12A A ⋃不为闭集合. 所以说法中不正确的是ABD34.(多选题)集合A ,B 是实数集R 的子集,定义{|}A B x x A x B -=∈∉且,*()()A B A B B A =-⋃-叫做集合的对称差,若集合{}2|(1)1,03A y y x x ==-+≤≤,{}2|1,13B y y x x ==+≤≤,则以下说法正确的是( ) A .[1,5]A =-B .[2,10]B =C .[1,2)A B -=D .(5,10]B A -=E.*(1,2](5,10]A B =⋃ 【答案】BCD【解析】{}{}2|(1)1,0315A y y x x y y ==-+≤≤=≤≤,{}{}2|1,13210B y y x x y y ==+≤≤=≤≤,故{}{|}12A B x x A x B x x -=∈∉=≤<且,{}{|}510B A x x B x A x x -=∈∉=<≤且.[)*()()1,2(5,10]A B A B B A =--=.35.(多选题)已知集合{}|4A x Z x =∈<,B N ⊆,则( ) A .集合B N N ⋃= B .集合AB 可能是{}1,2,3C .集合AB 可能是{}1,1-D .0可能属于B【答案】ABD【解析】∵B N ⊆,∴B N N ⋃=,故A 正确.∵集合{}4A x Z x =∈<,∴集合A 中一定包含元素1,2,3, ∵B N ⊆,∴集合AB 可能是{}1,2,3,故B 正确;∵1-不是自然数,∴集合AB 不可能是{}1,1-,故C 错误;∵0是最小的自然数,∴0可能属于集合B ,故D 正确.。
1.3 集合的基本运算(精讲)考点一数集之间的基本运算【例1】(1)(2021·辽宁高三其他模拟)已知集合{}{}|3,,1,0,1,2,3A x x x N B =≤∈=-,则A B =( )A .{0,1,2,3}B .{1,2,3}C .{2,3}D .{}0,1,3(2)(2021·北京高考真题)已知集合{}|11A x x =-<<,{}|02B x x =≤≤,则A B =( )A .()1,2-B .(1,2]-C .[0,1)D .[0,1](3)(2021·浙江宁波市)设全集U =R ,集合{}1A x x =≥-,{}23B x x =-≤<,则集合()UA B⋂是( ) A .{}21x x -<<-B .{}21x x -≤<-C .21}x x -<≤- D .{}21x x -≤≤-【答案】(1)A (2)B (3)B【解析】(1)由题得{}{}|3,0,1,2,3A x x x N =≤∈=,{}1,0,1,2,3B =-,所以A B ={0,1,2,3}故选:A(2)由题意可得:{}|12AB x x =-<≤,即(]1,2A B =-.故选:B.(3)由{}1A x x =≥-,则{}U|1A x x =<-又{}23B x x =-≤<,所以(){}U |21A B x x ⋂=-≤<-故选:B 【一隅三反】1.(2021·黑龙江哈尔滨市)已知集合A ={﹣1,0,1,2},B ={x |0<x <3},则A ∩B =( ) A .{﹣1,0,1} B .{0,1} C .{﹣1,1,2} D .{1,2}【答案】D【解析】集合A ={﹣1,0,1,2},B ={x |0<x <3},则A ∩B ={1,2},故选:D 2.(2021·河南焦作市)已知集合{}1,3,5,7,9=U ,{}1,5,7A =,{}1,3B =,则()UA B =( )A .{}3,5,7,9B .{}3,5,7C .{}1,9D .{}9【答案】D 【解析】题意,{}{}{}1,1,5,731,3,5,7AB ==,又∵{}1,3,5,7,9=U ,∴(){}9U AB =.选:D.3.(2021·全国高考真题)设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===,则()UA B =( )A .{3}B .{1,6}C .{5,6}D .{1,3}【答案】B【解析】由题设可得{}U1,5,6B =,故(){}U 1,6A B ⋂=,故选:B.4.(2021·全国)已知全集(){}(){}{N08},{1,2},()5,6,4,7UU U U x x A B A B B A =∈<<⋂=⋃=⋂=∣,则A 集合为( ) A .{1,2,4} B .{1,2,7}C .{1,2,3}D .{1,2,4,7}【答案】C【解析】由题意{1,2,3,4,5,6,7}U =,用Venn 图表示集合,A B ,依次填写()U AB ,()UA B ,()U B A ⋂,最后剩下的数字3只有填写在A B 中,所以{1,2,3}A =.故选:C .5.(2021·辽宁)若集合{{2}A x y B x x ===<∣∣,则A ∩B =( )A .{}12x x << B .{}1x x ≥C .{}2x x <D .{}12x x ≤<【答案】D【解析】由题意,得{}1A x x =≥,所以{}12A B x x ⋂=≤<.故选:D 6.(2021·四川自贡市)设集合A ={x |1≤x ≤3},B ={x |24x x --<0},则A ∩B =( ) A .{x |2<x ≤3} B .{x |2≤x ≤3}C .{x |1≤x <4}D .{x |1<x <4}【答案】A【解析】∵A ={x |1≤x ≤3},B ={x |2<x <4},∴A ∩B ={x |2<x ≤3}.故选:A .考点二 点集之间的基本运算【例2】(2021·河北高三其他模拟)已知集合{}{}3(,)0,(,)M x y x y N x y y x =-===,则M N ⋂中元素的个数为( )A .0B .1C .2D .3【答案】D【解析】因为集合{}{}3(,)0,(,)M x y x y N x y y x=-===,所以{}3(,)(0,0),(1,1),(1,1)y x M N x y y x ⎧⎫=⎧⎪⎪⋂==--⎨⎨⎬=⎩⎪⎪⎩⎭,所以A B 中元素的个数为3,故选:D 【一隅三反】1.(2021·山东济南市)已知集合M ={(x ,y )|y =21x -,xy ≤0},N ={(x ,y )|y =x 24-},则M N ⋂中的元素个数为( ) A .0 B .1C .2D .1或2【答案】A【解析】∵集合M ={(x ,y )|y =2x ﹣1,xy ≤0},N ={(x ,y )|y =x 2﹣4},∴M ∩N ={(x ,y )|22104y x xy y x =-⎧⎨=-⎩,}=∅.∴M ∩N 中的元素个数为0.故选:A . 2.(2021·全国高三其他模拟)已知集合(){}()22,|1,,,{,|2M x y x y x y N x y x y +≤∈∈+≤==Z Z },则集合M ⋂N 中元素的个数是( ) A .6 B .7 C .8 D .9【答案】C【解析】由222x y +≤可得,222,2x y ≤≤,即x y ≤≤N 中的满足,x Z y Z ∈∈的整点有:()()()()()()()()()0,0,0,1,0,1,1,0,1,0,1,1,1,1,1,1,1,1------,共9个点,其中只有(1,1)这一个点不满足1x y +≤,故M N ⋂中的元素个数为8个,故选:C.3.(2021·江苏南通市)若集合{(,)30}M x y x y =-=∣,()22,}0{|N x y x y =+=,则( ) A .M N M ⋂= B .M N M ⋃= C .M N N ⋃= D .M N ⋂=∅【答案】B【解析】∵集合(),30{|}M x y x y =-=,(){}(){}22,00|,0N x y xy =+==,因为2230000x y x x y y -==⎧⎧⇒⎨⎨+==⎩⎩∴(){}0,0M N N ⋂==,所以M N M ⋃=,故选:B.考点三 韦恩图求交并补【例3】(1)(2021·北京101中学高三其他模拟)已知集合{}0,1A =,集合{}1,0,1,2,3B =-,则图中阴影部分表示的集合是( )A .[]1,3B .(]1,3C .{}1,2,3-D .{}1,0,2,3-(2)(2021·山东烟台市)已知集合M ,N 都是R 的子集,且RM N ⋂=∅,则M N =( )A .MB .NC .∅D .R(3)(2021·珠海市)下图中矩形表示集合U ,A ,B 是U 的两个子集,则不能表示阴影部分的是( )A .()UA B ⋂B .()BABC .()()UUA B ⋂D .A BA ⋃【答案】(1)C (2)A (3)C【解析】(1)依题意,由补集的韦恩图表示知,图中阴影部分表示的集合是BA ,因集合{}0,1A =,集合{}1,0,1,2,3B =-,则有{1,2,3}BA =-,所以图中阴影部分表示的集合是{}1,2,3-.故选:C (2)由题知:RM N ⋂=∅,所以M N ⊆,即M N M ⋂=.故选:A(3)由图知:当U 为全集时,阴影部分表示集合A 的补集与集合B 的交集, 当B 为全集时,阴影部分表示A B 的补集,当AB 为全集时,阴影部分表示A 的补集,故选:C.【一隅三反】1.(2021·浙江温州市)设全集U 为实数集R ,集合{A x R x =∈>,集合{0,1,2,3}B =,则图中阴影部分表示的集合为( )A .{}0B .{0,1}C .{3,4}D .{1,2,3,4}【答案】B【解析】图中的阴影部分表示集合B 中不满足集合A 的元素,所以阴影部分所表示的集合为{}0,1. 故选:B.2.(2021·沈阳市)已知非空集合A 、B 、C 满足:A B C ⊆,A C B ⋂⊆.则( ).A .BC = B .()A B C ⊆⋃ C .()B C A ⋂⊆D .A B A C ⋂=⋂【答案】C【解析】因为非空集合A 、B 、C 满足:AB C ⊆,A C B ⋂⊆,作出符合题意的三个集合之间关系的venn 图,如图所示,所以A B A C ⋂=⋂. 故选:D .3.(2021·江苏苏州市)已知U 为全集,非空集合A 、B 满足()UA B =∅,则( )A .AB ⊆ B .B A ⊆C .()()UU A B ⋂=∅ D .()()UU A B U ⋃=【答案】A【解析】如下图所示:()UAB =∅,由图可知,A B ⊆,()()U U U A B B ⋂=,故选:A.4.(2021·全国高三专题练习(文))若集合A ,B ,U 满足:A BU ,则U =( )A .UAB B .UBA C .UAB D .UBA【答案】B【解析】由集合A ,B ,U 满足:ABU ,U UBA ∴,如图所示:UAA U ∴=,UBA U =,UBB U = 故选:B考点四 利用集合运算求参数【例4】(1)(2021·山东泰安市)集合{}{}240,1,,2,.A a B a =-=-若{}2,1,0,4,16A B ⋃=--,则a =( ) A .±1B .2±C .3±D .4±(2)(2021·全国高三专题练习)设集合5,,b A a b a ⎧⎫=-⎨⎬⎩⎭,{},,1B b a b =+-,若{}2,1A B =-,则a =____,b =____.(3)(2021·重庆八中)已知集合{}12A x x =<<,集合{}B x x m =>,若()A B =∅R,则m 的取值范围为( )A .(],1-∞B .(],2-∞C .[)1,+∞D .[)2,+∞(4)(2021·河南安阳市)已知集合{}2230A x N x x *=∈--<,{}20B x ax =+=,若A B B =,则实数a 的取值集合为( ) A .{}1,2--B .{}1,0-C .2,0,1D .{}2,1,0--(5)(2021·全国高三月考(理))设集合{}2|20A x x mx =+-<,{}|13B x x =-≤≤,且{}23A B x x =|-<≤,则A B =( )A .{}|11x x -≤<B .{}|21x x -<<C .{}|21x x -<≤-D .{}|13x x <≤【答案】(1)B (2)1 2 (3)A (4)D (5)A【解析】(1)由{}2,1,0,4,16A B ⋃=--知,24416a a ⎧=⎨=⎩,解得2a =±故选:B(2)由{}2,1A B =-,得21b a a b ⎧=⎪⎨⎪-=-⎩或12ba ab ⎧=-⎪⎨⎪-=⎩.①当21ba ab ⎧=⎪⎨⎪-=-⎩时,解得12a b =⎧⎨=⎩,此时{}5,2,1A =-,{}2,3,1B =-,符合题意;②当12ba ab ⎧=-⎪⎨⎪-=⎩时,解得11a b =⎧⎨=-⎩,此时{}5,2,1A =-,集合B 中的元素不满足互异性,不符合题意.综上所述,1a =,2b =.故答案为:1;2. (3)由题知()AB =∅R,得A B ⊆,则1m ,故选:A .(4){}{}22301,2A x N x x *=∈--<=,因为AB B =,所以B A ⊆,当0a =时,集合{}20B x ax φ=+==,满足B A ⊆; 当0a ≠时,集合{}220B x ax x a ⎧⎫=+===-⎨⎬⎩⎭,由B A ⊆,{}1,2A =得21a -=或22a-=,解得2a =-或1a =-, 综上,实数a 的取值集合为{}2,1,0--.故选:D . (5)由题意,集合{|13}B x x =-≤≤,且{|23}AB x x =-<≤,可得2-是方程220x mx +-=的根,即2(2)(2)20m -+⨯--=,解得1m =, 所以{}{}2|20|21A x x x x x =+-<=-<<,则{|11}A B x x ⋂=-≤<.故选:A. 【一隅三反】1.(2021·全国高三)已知集合{}20,1,,{1,0,23}==+A a B a ,若AB A B =,则实数a 等于( )A .1-或3B .0或1-C .3D .1-【答案】C 【解析】由AB A B =可知A B =,故223a a =+,解得1a =-或3a =.当1a =-时,21a =,与集合元素互异性矛盾,故1a =-不正确. 经检验可知3a =符合题意.故选:C .2.(2021·辽宁沈阳市)已知集合{}{}21,0,1,,A B x x =-=,若AB B =,则实数x =( )A .1-B .1C .±1D .0或±1【答案】A 【解析】由AB B =得B A ⊆,0x =时,20x x ==不合题意,1x =时,21x x ==也不合题意, 1x =-时,21x =,满足题意.故选:A .3.(2021·安徽宣城市){}{}36,72A x x B x a x a =-≤<=-<≤ (1)A B B ⋃=,求a 的取值范围; (2)UA B ,求a 的取值范围.【答案】(1)[)3,4;(2)(],7-∞-.【解析】(1)A B B =,A B ∴⊆,7326a a -<-⎧∴⎨≥⎩,解得34a ≤<,即a 的取值范围为[)3,4;(2)可得{3U A x x =<-或}6x ≥, U A B,若B =∅,则72a a -≥,解得7a ≤-,满足题意; 若B ≠∅,则727326a a a a -<⎧⎪-≥-⎨⎪<⎩,不等式无解,综上,a 的取值范围为(],7-∞-.4.(2021·浙江高一期末)在“①A B =∅,②A B ⋂≠∅”这两个条件中任选一个,补充在下列横线中,求解下列问题:已知集合{|231}A x a x a =-<<+,{|01}B x x =<≤.(Ⅰ)若0a =,求A B ;(Ⅱ)若________(在①,②这两个条件中任选一个),求实数a 的取值范围.注:如果选择多个条件分别解答,按第一个解答记分.【答案】(1){|31}x x -<≤;(2)若选①,(,1][2,)-∞-+∞;若选②,()1,2-【解析】(1)当0a =时,{|31}A x x =-<<,{|01}B x x =<≤;所以{|31}A B x x =-<≤(2)若选①,A B =∅,当A =∅时,231a a -≥+,解得4a ≥,当A ≠∅时,4231a a <⎧⎨-≥⎩或410a a <⎧⎨+≤⎩,解得:24a ≤<或1a ≤-, 综上:实数a 的取值范围(,1][2,)-∞-+∞.若选②,A B ⋂≠∅,则23123110a a a a -<+⎧⎪-<⎨⎪+>⎩,即421a a a <⎧⎪<⎨⎪>-⎩,解得:1a 2-<<,所以实数a 的取值范围()1,2-.考点五 实际生活中集合间的运算【例5】(2021·山东高三专题练习)《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著,某中学为了了解在校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《三国演义》的学生共有80位,阅读过《西游记》的学生共有60位,阅读过《西游记》且阅读过《三国演义》的学生共有40位,则在调查的100位同学中阅读过《三国演义》的学生人数为( )A.60 B.50 C.40 D.20【答案】A【解析】因为阅读过《西游记》或《三国演义》的学生共有80位,阅读过《西游记》的学生共有60位,-=位,所以只阅读了《三国演义》的学生有806020又因为阅读过《西游记》且阅读过《三国演义》的学生共有40位,=位,故选:A.所以只阅读过《三国演义》的学生共有20+4060【一隅三反】1.(2021·云南省云天化中学高一期末)《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著,六盘水市第七中学为了解我校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则在调查的100位同学中阅读过《西游记》的学生人数为()A.80 B.70 C.60 D.50【答案】B【解析】因为阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,-=位,所以《西游记》与《红楼梦》两本书中只阅读了一本的学生共有906030因为阅读过《红楼梦》的学生共有80位,-=位,所以只阅读过《红楼梦》的学生共有806020所以只阅读过《西游记》的学生共有302010位,+=位,故选:B.故阅读过《西游记》的学生人数为1060702.(2021·全国高三专题练习)《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为A.0.5B.0.6C.0.7D.0.8【答案】C【解析】由题意得,阅读过《西游记》的学生人数为90-80+60=70,则其与该校学生人数之比为70÷100=0.7.故选C.3.(2021·吴县中学高一月考)某中学的学生积极参加体育锻炼,其中有95%的学生喜欢篮球或羽毛球,60%的学生喜欢篮球,82%的学生喜欢羽毛球,则该中学既喜欢篮球又喜欢羽毛球的学生数占该校学生总数的比例是( )A .63%B .47%C .55%D .42%【答案】B【解析】设只喜欢篮球的百分比为x ,只喜欢羽毛球的百分比为y ,两个项目都喜欢的百分比为z ,由题意,可得60x z +=,95x y z ++=,82y z +=,解得47z =.∴该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是47%.故选:B .4.(2021·广东清远市·高一期末)某幼儿园满天星班开设“小小科学家”、“小小演说家”兴趣小组,假设每位学员最少参加一个小组,其中有13位学员参加了“小小科学家”兴趣小组,有16位学员参加了“小小演说家”兴趣小组,有8位学员既参加了“小小科学家”兴趣小组,又参加了“小小演说家”兴趣小组,则该幼儿园满天星班学员人数为( )A .19B .20C .21D .37 【答案】C【解析】由条件可知该幼儿园满天星班学员人数为1316821+-=.故选:C。



专题3 集合的基本运算根据参数的取值讨论集合间的包含关系★★★○○○○1.集合的三种基本运算x ∈(1)A ∩A =A ,A ∩∅=∅,A ∪A =A ,A ∪∅=A . (2)A ∩∁U A =∅,A ∪∁U A =U ,∁U (∁U A )=A .(3)A ⊆B ⇔A ∩B =A ⇔A ∪B =B ⇔∁U A ⊇∁U B ⇔A ∩(∁U B )=∅.求集合的交集或并集时,应先化简集合,再利用交集、并集的定义求解.进行集合的混合运算时,一般先运算括号内的部分.当集合是用列举法表示的数集时,可以通过列举集合的元素进行运算;当集合用不等式形式表示时,可借助数轴求解,对于端点值的取舍,应单独检验.已知集合(){}|ln 12 A x y x ==-, {}2| B x x x =≤,全集U A B =⋃,则()U C A B ⋂=( )A. (),0-∞B. 1,12⎛⎤-⎥⎝⎦ C. ()1,0,12⎡⎤-∞⋃⎢⎥⎣⎦ D. 1,02⎛⎤- ⎥⎝⎦KS5U 】福建省2016届高三基地校总复习综合卷数学试题(厦门双十、南安一中、厦门海沧实验中学理科)1.【安徽省安庆市凉亭中学2018届高三上学期9月月考数学理试题】已知集合(){}{}|lg 1,2,1,0,1A x y x B ==+=--,则()R C A B ⋂=( )A. {}2,1--B. []2-C. []1,0,1-D. []0,1 【答案】A【解析】1x +〉0, x >-1,则{}1A x x =-, {}|1R C A x x =≤-则()R C A B ⋂= {}2,1-- 2.【甘肃省武威市第六中学2018届高三第一次阶段性过关考试数学(文)试题】设集合2{|42},{|4}M x x N x x =∈-=<<<Z ,则M N ⋂等于( )A. ()1,1-B. ()1,2-C. {}1,1,2-D. {}1,0,1- 【答案】D 【解析】{}{}{}{}{}2|42M x x =∈-=<<<Z .故选D.3.【河北武邑中学2017—2018高三年级上学期第二次调研考试数学试题理】若全集为实数集R ,集合()12A |210x log x ⎧⎫=->⎨⎬⎩⎭,则R C A =( )A. 12x x ⎧⎫>⎨⎬⎩⎭B. {}1x x >C. 10,12x x x ⎧⎫≤≤≥⎨⎬⎩⎭或 D. 1,12x x x ⎧⎫≤≥⎨⎬⎩⎭或 【答案】D点睛:解对数不等式,注意真数大于零的限制.1.(2016·全国丙卷)设集合S ={x |(x -2)(x -3)≥0},T ={x |x >0},则S ∩T =( ) A .[2,3] B .(-∞,2]∪[3,+∞) C .[3,+∞)D .(0,2]∪[3,+∞)解析:选D 由题意知S ={x |x ≤2或x ≥3},则S ∩T ={x |0<x ≤2或x ≥3}.故选D. 2.(2015·新课标全国卷Ⅱ)已知集合A ={-2,-1,0,1,2},B ={x |(x -1)(x +2)<0},则A ∩B =( ) A .{-1,0} B .{0,1} C .{-1,0,1}D .{0,1,2}解析:选A 由题意知B ={x |-2<x <1},所以A ∩B ={-1,0}.故选A.3.(2012·新课标全国卷)已知集合A ={1,2,3,4,5},B ={(x ,y )|x ∈A ,y ∈A ,x -y ∈A },则B 中所含元素的个数为( ) A .3 B .6 C .8D .10解析:选D 列举得集合B ={(2,1),(3,1),(4,1),(5,1),(3,2),(4,2),(5,2),(4,3),(5,3),(5,4)},共含有10个元素.4.(2016·全国甲卷)已知集合A={1,2,3},B={x|x2<9},则A∩B=()A.{-2,-1,0,1,2,3} B.{-2,-1,0,1,2}C.{1,2,3} D.{1,2}解析:选D∵x2<9,∴-3<x<3,∴B={x|-3<x<3}.又A={1,2,3},∴A∩B={1,2,3}∩{x|-3<x<3}={1,2},故选D.5.(2013·新课标全国卷Ⅰ)已知集合A={1,2,3,4},B={x|x=n2,n∈A},则A∩B=() A.{1,4} B.{2,3} C.{9,16} D.{1,2}解析:选A因为x=n2,所以当n=1,2,3,4时,x=1,4,9,16,所以集合B={1,4,9,16},所以A∩B={1,4}.6.设是全集,集合都是其子集,则下图中的阴影部分表示的集合为()A. B. C. D.KS5U】浙江省杭州四中2017年9月高一单元检测数学试题【答案】B【解析】观察图形得:图中的阴影部分表示的集合为,故选:B.KS5U______________________________________________________________________________ ______________________________________________________________________________ _____________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ ______________________________________________________________________________ _______。
集合的基本关系及运算【学习目标】1.理解集合之间包含与相等的含义,能识别一些给定集合的子集.在具体情境中,了解空集和全集的含义.2.理解两个集合的交集和并集的含义,会求两个简单集合的交集与并集.理解在给定集合中一个子集的补集的含义,会求给定子集的补集.【要点梳理】要点一:集合之间的关系1.集合与集合之间的“包含”关系集合A 是集合B 的部分元素构成的集合,我们说集合B 包含集合A;子集:如果集合A 的任何一个元素都是集合B 的元素,我们说这两个集合有包含关系,称集合A 是集合B 的子集(subset).记作:A B(B A)⊆⊇或,当集合A 不包含于集合B 时,记作A B,用Venn 图表示两个集合间的“包含”关系:A B(B A)⊆⊇或要点诠释:(1)“A 是B 的子集”的含义是:A 的任何一个元素都是B 的元素,即由任意的x A ∈,能推出x B ∈.(2)当A 不是B 的子集时,我们记作“A ⊆B (或B ⊇A )”,读作:“A 不包含于B ”(或“B 不包含A ”).真子集:若集合A B ⊆,存在元素x ∈B 且x A ∉,则称集合A 是集合B 的真子集(proper subset).记作:A B(或B A)规定:空集是任何集合的子集,是任何非空集合的真子集.2.集合与集合之间的“相等”关系A B B A ⊆⊆且,则A 与B 中的元素是一样的,因此A=B要点诠释:任何一个集合是它本身的子集,记作A A ⊆.要点二:集合的运算1.并集一般地,由所有属于集合A 或属于集合B 的元素所组成的集合,称为集合A 与B 的并集,记作:A∪B 读作:“A 并B”,即:A∪B={x|x ∈A,或x ∈B}Venn 图表示:要点诠释:(1)“x ∈A,或x ∈B”包含三种情况:“,x A x B ∈∉但”;“,x B x A ∈∉但”;“,x A x B ∈∈且”.(2)两个集合求并集,结果还是一个集合,是由集合A 与B 的所有元素组成的集合(重复元素只出现一次).2.交集一般地,由属于集合A 且属于集合B 的元素所组成的集合,叫做集合A 与B 的交集;记作:A∩B,读作:“A 交B”,即A∩B={x|x ∈A,且x ∈B};交集的Venn 图表示:要点诠释:(1)并不是任何两个集合都有公共元素,当集合A 与B 没有公共元素时,不能说A 与B 没有交集,而是A B =∅ .(2)概念中的“所有”两字的含义是,不仅“A∩B 中的任意元素都是A 与B 的公共元素”,同时“A 与B 的公共元素都属于A∩B”.(3)两个集合求交集,结果还是一个集合,是由集合A 与B 的所有公共元素组成的集合.3.补集全集:一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集,通常记作U.补集:对于全集U 的一个子集A,由全集U 中所有不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集(complementary set),简称为集合A 的补集,记作:U U A A={x|x U x A}∈∉;即且;痧补集的Venn 图表示:要点诠释:(1)理解补集概念时,应注意补集U A ð是对给定的集合A 和()U A U ⊆相对而言的一个概念,一个确定的集合A ,对于不同的集合U,补集不同.(2)全集是相对于研究的问题而言的,如我们只在整数范围内研究问题,则Z 为全集;而当问题扩展到实数集时,则R 为全集,这时Z 就不是全集.(3)U A ð表示U 为全集时A 的补集,如果全集换成其他集合(如R )时,则记号中“U”也必须换成相应的集合(即R A ð).4.集合基本运算的一些结论:A B A A B B A A=A A =A B=B A ⋂⊆⋂⊆⋂⋂∅∅⋂⋂,,,,A A B B A B A A=A A =A A B=B A ⊆⋃⊆⋃⋃⋃∅⋃⋃,,,,U U (A)A=U (A)A=⋃⋂∅,痧若A∩B=A,则A B ⊆,反之也成立若A∪B=B,则A B ⊆,反之也成立若x ∈(A∩B),则x ∈A 且x ∈B 若x ∈(A∪B),则x ∈A,或x ∈B求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn 图或数轴进而用集合语言表达,增强数形结合的思想方法.【典型例题】类型一:集合间的关系例1.请判断①0{0};②{}R R ∈;③{}∅∈∅;④∅{}∅;⑤{}0∅=;⑥{}0∈∅;⑦{}0∅∈;⑧∅{}0,正确的有哪些?【答案】②③④⑧【解析】①错误,因为0是集合{}0中的元素,应是{}00∈;②③中都是元素与集合的关系,正确;④⑧正确,因为∅是任何集合的子集,是任何非空集合的真子集,而④中的{}∅为非空集合;⑤⑥⑦错误,∅是没有任何元素的集合.【总结升华】集合的符号语言十分简洁,因而被广泛用于现代数学之中,但往往容易混淆,其障碍在于这些符号与具体意义之间没有直接的联系,突破方法是熟练地掌握这些符号的具体含义.举一反三:【变式1】用适当的符号填空:(1){x||x|≤1}{x|x 2≤1};(2){y|y=2x 2}{y|y=3x 2-1};(3){x||x|>1}{x|x>1};(4){(x,y)|-2≤x≤2}{(x,y)|-1<x≤2}.【答案】(1)=(2)(3)(4)【总结升华】区分元素与集合间的关系,集合与集合间的关系.例2.(2015秋确山县期中)已知A ={x |x 2―4=0},B ={x |ax ―6=0},且B 是A 的子集.(1)求a 的取值集合M ;(2)写出集合M 的所有非空真子集.【思路点拨】对(1)根据A 集合中的元素,B A ⊆,分类讨论B 的可能情况,再注解a ,写出集合M .根据含有n 个元素的集合的真子集个数是2n -1,求解(2).【答案】(1)M ={0,3,-3};(2){0},{3},{-3},{0,3},{0,-3},{3,-3}【解析】(1)A ={2,-2}.∵B 是A 的子集,∴B =∅,{2},{-2},①B =∅时,方程ax -6=0无解,得a =0;②B ={2}时,方程ax -6=0的解为x =2,得2a -6=0,所以a =3;③B ={-2}时,方程ax -6=0的解为x =-2,得-2a -6=0,所以a =-3.所以a 的取值集合M ={0,3,-3}.(2)M ={0,3,-3}的非空真子集为{0},{3},{-3},{0,3},{0,-3},{3,-3}【总结升华】本题考查集合的子集问题,含有n 个元素的集合的子集个数是2n ,真子集个数是2n -1;非空真子集个数是2n -2.举一反三:【变式1】已知{},a b A ⊆{},,,,a b c d e ,则这样的集合A 有个.【答案】7个【变式2】同时满足:①{}1,2,3,4,5M ⊆;②a M ∈,则6a M -∈的非空集合M 有()A.16个B.15个C.7个D.6个【答案】C【解析】3a =时,63a -=;1a =时,65a -=;2a =时,64a -=;4a =时,62a -=;5a =时,61a -=;∴非空集合M 可能是:{}{}{}{}{}{}3,1,5,2,4,1,3,5,2,3,4,1,2,4,5,{}1,2,3,4,5共7个.故选C.【变式3】已知集合A={1,3,a},B={a 2},并且B 是A 的真子集,求实数a 的取值.【答案】a=-1,a=3±或a=0【解析】∵,∴a 2∈A,则有:(1)a 2=1⇒a=±1,当a=1时与元素的互异性不符,∴a=-1;(2)a 2=3⇒a=3±(3)a 2=a ⇒a=0,a=1,舍去a=1,则a=0综上:a=-1,a=3±或a=0.注意:根据集合元素的互异性,需分类讨论.例3.设M={x|x=a 2+1,a ∈N +},N={x|x=b 2-4b+5,b ∈N +},则M 与N 满足()A.M=NB.M NC.N MD.M∩N=∅【答案】B【解析】当a ∈N +时,元素x=a 2+1,表示正整数的平方加1对应的整数,而当b ∈N +时,元素x=b 2-4b+5=(b-2)2+1,其中b-2可以是0,所以集合N 中元素是自然数的平方加1对应的整数,即M 中元素都在N 中,但N 中至少有一个元素x=1不在M 中,即M N,故选B.例4.已知},,,0{},,,{y x N y x xy x M =-=若M =N ,则+++2()(x y x )()1001002y x y +++ =.A .-200B .200C .-100D .0【思路点拨】解答本题应从集合元素的三大特征入手,本题应侧重考虑集合中元素的互异性.【答案】D【解析】由M=N,知M,N 所含元素相同.由0∈{0,|x|,y}可知0∈若x=0,则xy=0,即x 与xy 是相同元素,破坏了M 中元素互异性,所以x≠0.若x·y=0,则x=0或y=0,其中x=0以上讨论不成立,所以y=0,即N 中元素0,y 是相同元素,破坏了N 中元素的互异性,故xy≠00,则x=y,M,N 可写为M={x,x 2,0},N={0,|x|,x}由M=N 可知必有x 2=|x|,即|x|2=|x|∴|x|=0或|x|=1若|x|=0即x=0,以上讨论知不成立若|x|=1即x=±1当x=1时,M 中元素|x|与x 相同,破坏了M 中元素互异性,故x≠1当x=-1时,M={-1,1,0},N={0,1,-1}符合题意,综上可知,x=y=-1∴+++2()(x y x )()1001002y x y +++ =-2+2-2+2+…+2=0【总结升华】解答本题易忽视集合的元素具有的“互异性”这一特征,而找不到题目的突破口.因此,集合元素的特征是分析解决某些集合问题的切入点.举一反三:【变式1】设a,b ∈R ,集合b{1,a+b,a}={0,,b}a,则b-a=()【答案】2【解析】由元素的三要素及两集合相等的特征:b1{0,,b},0{1,a+b,a}a 0a b=0a∈∈≠∴+ ,又,∴当b=1时,a=-1,b{0,b}={0,-1,1}a∴,当b=1a时,∴b=a 且a+b=0,∴a=b=0(舍)∴综上:a=-1,b=1,∴b-a=2.类型二:集合的运算例5.(1)(2014湖北武汉期中)已知{}22A y y x ==-;{}22B y y x ==-+,则A ∩B =()A .()){}00,,,B .⎡⎣C .[-2,2]D .{(2)设集合M ={3,a },N ={x |x 2-2x <0,x ∈Z},M ∩N ={1},则M ∪N 为().A .{1,2,a }B .{1,2,3,a }C .{1,2,3}D .{1,3}【思路点拨】(1)先把集合A 、B 进行化简,再利用数轴进行相应的集合运算.(2)先把集合N 化简,然后再利用集合中元素的互异性解题.【答案】(1)C (2)D 【解析】(1)集合A 、B 均表示构成相关函数的因变量取值范围,故可知:A ={y |y ≥-2},B ={y |y ≤2},所以A ∩B ={y |-2≤y ≤2},选C .(2)由N ={x |x 2-2x <0,x ∈Z}可得:N ={x |0<x <2,x ∈Z}={1},又由M ∩N ={1},可知1∈M ,即a =1,故选D .举一反三:【变式1】设A、B 分别是一元二次方程2x 2+px+q=0与6x 2+(2-p)x+5+q=0的解集,且A∩B={21},求A ∪B.【答案】{21,31,-4}【解析】∵A∩B={21},∴21是方程2x 2+px+q=0的解,则有:0q p 2121(22=++(1),同理有:6(21)2+(2-p)·21+5+q=0(2)联立方程(1)(2)得到:⎩⎨⎧-==.4q ,7p ∴方程(1)为2x 2+7x-4=0,∴方程的解为:x 1=21,x 2=-4,∴}4,21{A -=,由方程(2)6x 2-5x+1=0,解得:x 3=21,x 4=31,∴B={21,31},则A∪B={21,31,-4}.【变式2】设集合A={2,a 2-2a,6},B={2,2a 2,3a-6},若A∩B={2,3},求A∪B.【答案】{2,3,6,18}【解析】由A∩B={2,3},知元素2,3是A,B 两个集合中所有的公共元素,所以3∈{2,a 2-2a,6},则必有a 2-2a=3,解方程a 2-2a-3=0得a=3或a=-1当a=3时,A={2,3,6},B={2,18,3}∴A∪B={2,3,6}∪{2,18,3}={2,3,6,18}当a=-1时,A={2,3,6},B={2,2,-9}这既不满足条件A∩B={2,3},也不满足B 中元素具有互异性,故a=-1不合题意,应舍去.综上A∪B={2,3,6,18}.例6.设全集U={x ∈N +|x≤8},若A∩(C u B)={1,8},(C u A)∩B={2,6},(C u A)∩(C u B)={4,7},求集合A,B.【答案】A={1,3,5,8},B={2,3,5,6}【解析】全集U={1,2,3,4,5,6,7,8}由A∩(C u B)={1,8}知,在A 中且不在B 中的元素有1,8;由(C u A)∩B={2,6},知不在A 中且在B 中的元素有2,6;由(C u A)∩(C u B)={4,7},知不在A 中且不在B 中的元素有4,7,则元素3,5必在A∩B 中.由集合的图示可得A={1,3,5,8},B={2,3,5,6}.类型三:集合运算综合应用例7.(2014北京西城学探诊)已知集合A ={x |-4≤x <2},B ={x |-1≤x <3},C ={x |x ≥a ,a ∈R}.(1)若(A ∪B )∩C =∅,求实数a 的取值范围;(2)若(A ∪B )ÜC ,求实数a 的取值范围.【思路点拨】(1)画数轴;(2)注意是否包含端点.【答案】(1)a ≥3(2)a ≤-4【解析】(1)∵A ={x |-4≤x <2},B ={x |-1≤x <3},又(A ∪B )∩C =∅,如图,a ≥3;(2)画数轴同理可得:a ≤-4.【总结升华】此问题从表面上看是集合的运算,但其本质是一个定区间,和一个动区间的问题.思路是,使动区间沿定区间滑动,数形结合解决问题.举一反三:【变式1】已知集合P={x ︱x 2≤1},M={a }.若P ∪M=P,则a 的取值范围是()A .(-∞,-1]B .[1,+∞)C .[-1,1]D .(-∞,-1]∪[1,+∞)【答案】C【解析】P ={x ︱11x -≤≤}又 P M P = ,∴M P ⊆,∴11a -≤≤故选C .例8.设集合{}{}222|40,|2(1)10,A x x x B x x a x a a R =+==+++-=∈.(1)若A B B = ,求a 的值;(2)若A B B = ,求a 的值.【思路点拨】明确A B 、A B 的含义,根据的需要,将其转化为等价的关系式B A ⊆和A B ⊆,是解决本题的关键.同时,在包含关系式B A ⊆中,不要漏掉B =∅的情况.【答案】(1)1a =或1a ≤-;(2)1a =.【解析】首先化简集合A ,得{}4,0A =-.(1)由A B B = ,则有B A ⊆,可知集合B 为∅,或为{}0、{}4-,或为{}0,4-.①若B =∅时,224(1)4(1)0a a ∆=+--<,解得1a <-.②若0B ∈,代入得21011a a a -=⇒==-或.当1a =时,{}{}2|400,4,B x x x A =+==-=符合题意;当1a =-时,{}{}2|00,B x x A ===⊆也符合题意.③若4B -∈,代入得2870a a -+=,解得7a =或1a =.当1a =时,已讨论,符合题意;当7a =时,{}{}2|1648012,4B x x x =++==--,不符合题意.由①②③,得1a =或1a ≤-.(2),A B B A B =∴⊆ .又{}4,0A =-,而B 至多只有两个根,因此应有A B =,由(1)知1a =.【总结升华】两个等价转化:,A B B A B A B B B A =⇔⊆=⇔⊆ 非常重要,注意应用.另外,在解决有条件A B ⊆的集合问题时,不要忽视A ≠∅的情况.举一反三:【变式1】(2015源汇区一模)设A ={x |x 2+4x =0},B ={x |x 2+2(a +1)x +a 2-1=0},其中x ∈R ,如果A ∩B =B ,求实数a 的取值范围.【答案】a =1或a ≤-1【解析】A ={x |x 2+4x =0}={0,-4},∵A ∩B =B 知,B A ⊆,∴B ={0}或B ={-4}或B ={0,-4}或B =∅,若B ={0}时,x 2+2(a +1)x +a 2-1=0有两个相等的根0,则2002(1)001a a +=-+⎧⎨⨯=-⎩,∴a =-1,若B ={-4}时,x 2+2(a +1)x +a 2-1=0有两个相等的根-4,则24(4)2(1)4(4)1a a -+-=-+⎧⎨-⨯-=-⎩,∴a 无解,若B ={0,-4}时,x 2+2(a +1)x +a 2-1=0有两个不相等的根0和-4,则2402(1)401a a -+=-+⎧⎨-⨯=-⎩,∴a =1,当B =∅时,x 2+2(a +1)x +a 2-1=0无实数根,Δ=[2(a +1)]2-4(a 2-1)=8a +8<0,得a <-1,综上,a =1或a ≤-1.。
第3讲 集合的基本运算{AB x x ={AB x x =A A A =A ∅= ∅=∅B BA =B BA =例1. 设{}1,3,4,6A =,{}2,3,5,6B =,{}1,2,3,4,5,6,7,8U =,求:(1)A B = .(2)AB = .(3)U C A = . (4)U C B = . (5)()()U U C A C B = .(6)()()U U C A C B = .(7)()U C A B = . (8)()U C AB = .【答案】(1){}1,2,3,4,5,6;(2){}3,6;(3){}2,5,7,8;(4){}1,4,7,8;(5){}7,8;(6){}1,2,4,5,7,8;(7){}7,8;(8){}1,2,4,5,7,8.例2. 设{}25A x x =-<≤,{}07B x x =≤<,U R =,求:(1) A B = . (2) AB = .(3) U C A = . (4) U C B = . (5) ()()U U C A C B = . (6) ()()U U C A C B = .(7) ()U C A B = . (8) ()U C A B = .【答案】(1){}27x x -<<;(2){}05x x ≤≤;(3){}25x x x ≤->或;(4){}07x x x <≥或;(5){}27x x x ≤-≥或;(6){}05x x x <>或;(7){}27x x x ≤-≥或;(8){}05x x x <>或. 归纳:()()()U U U C A C B C A B =,()()()U U U C A C B C AB =.例3. 如图,U 是全集,,,M P S 是U 的三个子集,则阴影部分所表示的集合是( ) A.()MP SB.()M P SC.()U M P C SD.()U M P C S【答案】C 例4.设集合{}1,3,5A a =+,{}2221,2,21B a a a a a =+++-,当{}2,3AB =时,求A B .【答案】{}5,2,3,5AB =-.【解析】由{}2,3AB =可知2A ∈,所以12a +=,解得1a =或3-.当1a =时,集合B 中元素213a +=,223a a +=,不符合元素的互异性,故1a =舍去; 当3a =-时,{}2,3,5A =,{}5,3,2B =-,{}2,3AB =符合题意,{}5,2,3,5AB =-.例5.已知集合{}23A x x =-≤<,{}29B x m x m =≤≤+.(1)若A B B =,求实数m 的取值范围;(2)若A B ≠∅,求实数m 的取值范围.【答案】(1){}32m m -≤≤-;(2)1132x x ⎧⎫-<<⎨⎬⎩⎭.【解析】(1)A B B =,A B ∴⊆,2293m m ≤-⎧∴⎨+≥⎩,解得32m -≤≤-,所以m 的取值范围是{}32m m -≤≤-;(2)若A B =∅,当B =∅时,则29m m >+,解得9m <-;当B ≠∅时,则29292m m m ≤+⎧⎨+<-⎩或293m m m ≤+⎧⎨≥⎩,解得1192m -≤≤-或3m ≥.综上所述,112m ≤-或3m ≥时,A B =∅, 所以A B ≠∅时,m 的取值范围是1132x x ⎧⎫-<<⎨⎬⎩⎭.例6. 已知集合{}2230A x x x =-->,{}20B x x ax b =++≤,若A B R =,{}34AB x x =<≤,求a b +的值.【答案】7a b +=-【解析】{}{}223013A x x x x x x =-->=<->或,A B R =,{}34AB x x =<≤,{}14B x x ∴=-≤≤,1∴-和4是方程20x ax b ++=的两个根,根据韦达定理得1414a b -+=-⎧⎨-⨯=⎩,解得34a b =-⎧⎨=-⎩,7a b ∴+=-.例7.{}22190A x x ax a =-+-=,{}2560B x x x =-+=,{}2280C x x x =+-=.(1)A B A B =,求a 的值; (2)∅⫋()AB 且AC =∅,求a 的值;(3)A B A C =≠∅,求a 的值.【答案】(1)5a =;(2)2a =-;(3)3a =-.【解析】{}{}25602,3B x x x =-+==,{}{}22802,4C x x x =+-==-(1)A B A B =,A B ∴=,∴2和3是方程22190x ax a -+-=的两个根,根据韦达定理得2232319aa +=⎧⎨⨯=-⎩,解得5a =; (2)∅⫋()A B 且A C =∅,2A ∴∉,3A ∈,4A -∉,将3x =代入22190x ax a -+-=解得2a =-或5,当2a =-时,{}{}221503,5A x x x =+-==-,符合题意;当5a =时,{}{}25602,3A x x x =-+==,不符合题意,综上所述,2a =-; (3)A B A C =≠∅,2A ∴∈,将2x =代入22190x ax a -+-=解得3a =-或5,当3a =-时,{}{}231005,2A x x x =+-==-,符合题意;当5a =时,{}{}25602,3A x x x =-+==,不符合题意,综上所述,3a =-.跟踪训练1. 设集合{}1P x x =<,{}24Q x x =<,则PQ = .【答案】{}21x x -<<.2. 若{}0,1,2,3A =,{}3,B x x a a A ==∈,则A B =( )A. {}1,2B.{}0,1C.{}0,3D.{}3【答案】C 【解析】{}0,1,2,3A =,{}{}3,0,3,6,9B x x a a A ==∈=,{}0,3AB ∴=,故选C.3. 设全集{}8U x N x *=∈<,{}1,3,5,7A =,{}2,4,5B =,则()U C AB = .【答案】{}6 【解析】,{}1,3,5,7A =,{}2,4,5B =,{}1,2,3,4,5,7AB ∴=又{}{}81,2,3,4,5,6,7U x N x *=∈<=,(){}6U C AB ∴=.4. 设集合{}12M x x =-≤<,{}N x x k =≤,若M N ≠∅,则k 的取值范围是( )A.2k ≤B.1k ≥-C.1k >-D.12k -<≤【答案】B5. 设全集U R =,{}220A x x x =--<,{}10B x x =-<,则图中阴影部分所表示的集合为( )A.{}1x x ≥B.{}12x x ≤<C.{}01x x <≤D.{}1x x ≤【答案】B【解析】由Venn 图可知,阴影部分表示集合为()U AC B ,U R =,{}{}22012A x x x x x =--<=-<<,{}{}101B x x x x =-<=<,{}1U C B x x ∴=≥,(){}12U AC B x x ∴=≤<,故选B.6. 设{}260A x x ax =-+=,{}20B x x x c =-+=,{}2AB =,则AB = .【答案】{}1,2,3- 【解析】{}2AB =,2A ∴∈,2B ∈,4260a ∴-+=,420c -+=,5a ∴=,2c =-,{}{}25602,3A x x x ∴=-+==,{}{}2201,2C x x x =--==-,{}1,2,3AB ∴=-.7. 已知(){},1A x y y x ==+,(){}2,B x y y x ==,则AB 的子集个数为( ) A.2B.3C.4D.8【答案】C 【解析】(){},1A x y y x ==+,A 表示函数1y x =+图象上的点集,(){}2,B x y y x ==,B 表示函数2y x =图象上的点集,AB 中的元素为1y x =+和2y x =图象的交点,联立21y x y x=+⎧⎨=⎩得到210x x --=,1450∆=+=>,所以有2个交点, 所以A B 的元素个数为2,其子集个数为224=个,故选C.8. 已知50名学生参加跳远和铅球两项测验,分别及格的人数为40,31人,两项均不及格的人数为4人,那么两项都及格的人数为 人. 【答案】25【解析】依题意画出Venn 图,设两项均及格的人数为x 人,则仅跳远及格人数为40x -人,仅铅球及格人数为31x -人,()()4403150x x x ∴+-++-=,解得25x =.9. 当两个集合中一个集合为另一集合的子集时,称这两个集合构成“全食对集”;当两个集合有公共元素,但互不为对方的子集时,称这两个集合构成“偏食对集”.对于集合11,,12A ⎧⎫=-⎨⎬⎩⎭,{}21,0B x ax a ==≥,若A 与B 构成“全食对集”,则a 的取值集合为 ;若A 与B 构成“偏食对集”,则a 的取值集合为 . 【答案】{}0,1;{}4【解析】{}21,0B x ax a ==≥0a ∴=时,B =∅;0a >时,B⎧=⎨⎩, 又11,,12A ⎧⎫=-⎨⎬⎩⎭,若A 与B 构成“全食对集”,则B A ⊆,当0a =时,满足题意;当0a >时,要使B A ⊆,则{}1,1B =-1=,1a ∴=,综上,A 与B 构成“全食对集”时,a 的取值集合为{}0,1;若A 与B 构成“偏食对集”,则11,22B ⎧⎫=-⎨⎬⎩⎭12=,解得4a =, a ∴的取值集合为{}4.10. 已知集合(){}22,1,,A x y xy x y Z =+≤∈,(){},2,2,,B x y x y x y Z =≤≤∈,定义集合()()(){}12121122,,,,A B x x y y x y A x y B ⊕=++∈∈,则A B ⊕中元素的个数为( )A.77B.49C.45D.30【答案】C 【解析】(){}()()()()(){}22,1,,1,0,0,1,0,0,0,1,1,0A x y xy x y Z =+≤∈=--中有5个元素,(){},2,2,,B x y x y x y Z =≤≤∈中有5525⨯=个元素,即图中正方形ABCD 中的整点,当()()11,1,0x y =-时,()1212,x x y y ++即把()22,x y 向左平移一个单位;()()11,0,1x y =时,()1212,x x y y ++即把()22,x y 向上平移一个单位;()()11,0,0x y =时,()1212,x x y y ++即()22,x y 保持不动;()()11,0,1x y =-时,()1212,x x y y ++即把()22,x y 向下平移一个单位; ()()11,1,0x y =时,()1212,x x y y ++即把()22,x y 向右平移一个单位,()()(){}12121122,,,,A B x x y y x y A x y B ∴⊕=++∈∈的元素可看成图中正方形1111A B C D 中的整点(除去四个顶点),即77445⨯-=个,故选C.。