不等式恒成立问题的解法ppt课件
- 格式:ppt
- 大小:467.93 KB
- 文档页数:17
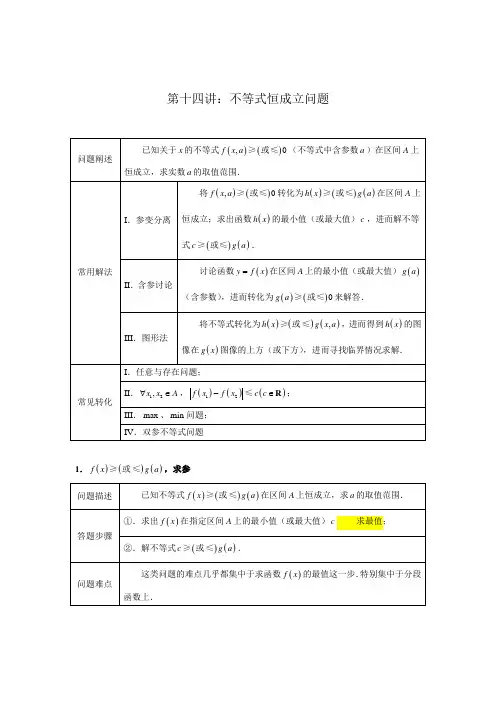
第十四讲:不等式恒成立问题1.()()()f x g a ≥或≤,求参(1)若x ∀∈R ,不等式2121222x x a a -++++≥恒成立,则a ∈_________.(2)已知函数()2,011sin ,13236x x x f x x x ππ⎧-+<⎪=⎨⎛⎫-< ⎪⎪⎝⎭⎩≤≤,若x ∀∈R ,不等式()212f x m m -≤恒成立, 则实数m 的取值范围是_________.(3)已知定义在R 上的函数()f x 满足()()222f x f x +=-,当(]0,2x ∈时,()()[]2,0,11,1,2x x x f x x x⎧-∈⎪=⎨∈⎪⎩.若(]0,4x ∀∈,不等式()2732t t f x t --≤≤恒成立,则t ∈________.1.若x ∀∈R ,不等式2412log x x a -+-≥恒成立,则a ∈_________.2.已知函数()233,11,12xx x x f x x ⎧++-⎪=⎨⎛⎫<-⎪ ⎪⎝⎭⎩≥,若x ∀∈R ,不等式()2f x m m >-恒成立,则实数m的取值范围是_________.3.已知函数()()2,01,0x a x f x x a x x ⎧-⎪=⎨++>⎪⎩≤,若x ∀∈R ,不等式()()0f x f ≥恒成立,则实数a 的取值范围是_________.4.已知定义在R 上的函数()f x 满足()()22f x f x +=,当[)0,2x ∈时,()[)[)2 1.5,0,11,1,22x x x x f x x -⎧-∈⎪=⎨⎛⎫-∈⎪ ⎪⎝⎭⎩,若[)4,2x ∀∈--,不等式()142t f x t -≥成立,则t ∈________.2.参变分离【示例1】已知()21f x x =-,不等式()()()2414x f m f x f x f m m ⎛⎫--+ ⎪⎝⎭≤在区间上3,2⎡⎫+∞⎪⎢⎣⎭恒成立,则实数m 的取值范围是_________.【例2】(1)已知()1,x ∀∈+∞,不等式2201x m x ++>-恒成立,则m 的取值范围是__________.(2)若()0,x ∀∈+∞,不等式2211110a x x a x x ⎛⎫⎛⎫+-++> ⎪ ⎪⎝⎭⎝⎭恒成立,则a ∈_________.(3)已知()2f x x =,若()()()22431a f x a f x f x ⋅++≤在区间[)1,+∞上恒成立,则实数a 的取值范围是__________.(4)已知函数()()2x f x x =∈R ,可以表示为一个奇函数()g x 和一个偶函数()h x 之和,若[]2,3x ∀∈,不等式()()20a g x h x ⋅+≥恒成立,则实数a 的取值范围是_________.(选讲)练习2:1.若(]0,2x ∀∈,不等式2210x ax -+≥恒成立,则实数a 的取值范围是_________.2.若[]2,6x ∀∈,不等式()23110ax a x +-+≥恒成立,则实数a 的取值范围是_________.3.关于x 的不等式144x x a+>在区间[]1,2上恒成立,则a ∈_________.4.已知()()232,2log 1,2x x f x x x -⎧<⎪=⎨-⎪⎩≥,若x ∀∈R ,不等式()()241a f x f x ⋅-≥恒成立,则实数a的最小值是_________.5.已知函数()1f x x x=-,若(]0,1x ∀∈,不等式()221x x t f ⋅-≥恒成立,则实数t 的取值范围是_________.(选做)【示例2】已知a ∈R ,函数()2222,022,0x x a x f x x x a x ⎧++-⎪=⎨-+->⎪⎩≤,若[)3,x ∀∈-+∞,若不等式()f x x ≤在R 上恒成立,则实数a 的取值范围是__________.【例3】已知函数()204,0x f x x x x >=-⎪⎩≤,若不等式()1f x ax -≥恒成立,则a ∈_________.练习3:1.已知函数()011,1x f x x x⎧⎪=⎨>⎪⎩≤≤,若关于x 的不等式()14f x x a -+≥在区间[)0,+∞上恒成立,则实数a 的取值范围是__________.2.若x ∀∈R ,不等式23324x ax x --≥恒成立,则实数a 的取值范围是_________.3.已知a ∈R ,设函数()222,1ln ,1x ax a x f x x a x x ⎧-+=⎨->⎩≤.若关于x 的不等式()0f x ≥在R 上恒成立,则实数a 的取值范围是__________.2.含参讨论2.1 单调函数【例4】(1)若[]1,2x ∀∈-,不等式20ax +>恒成立,则实数a 的取值范围是__________.(2)已知[]1,1a ∀∈-,不等式()24240x a x a +--+>恒成立,则x ∈__________.(3)若函数()()()2log 20,1a f x x x a a =+>≠在区间()0,a 上恒有()0f x >成立,则实数a 的取值范围是__________. 练习4:1.已知1,42a ⎛⎫∀∈ ⎪⎝⎭,不等式2log 10a x a +->恒成立,则x 的取值范围是_________.2.若1,32m ⎡⎤∀∈⎢⎥⎣⎦,不等式2424x mx m x ++>+恒成立,则x 的取值范围是__________.3.若[]1,1a∀∈-,不等式221x ax a->-恒成立,则实数x的取值范围是_________.4.若10,3x⎛⎫∀∈ ⎪⎝⎭,不等式32log1xax+≤恒成立,则实数a的取值范围是_________.(选做)2.2 非单调函数【例5】(2)已知函数()21f x x x =+-,若x ∀∈R ,不等式()()21f x m x +-≥恒成立,则实数m 的取值范围是_________.(2)已知()f x 是R 上的奇函数,当0x <时,()()297a f x x a x=++∈R ,当[)0,x ∈+∞时,不等式()1f x a +≥恒成立,则实数a 的取值范围是_________.(选讲) 练习5:1.若()0,x ∀∈+∞,不等式22944a x a x+-≥恒成立,则a ∈_________.2.已知函数()()f x x x a a a =--∈R ,若[]3,5x ∀∈,()0f x ≥恒成立,则实数a 的取值范围是_________.3.已知()f x 是定义在R 上的奇函数,若当0x >时,()21m f x x x=+-,若(],0x ∀∈-∞,不等式()2f x m -≤恒成立,则实数m 的取值范围是_________.(选做)3.任意与存在问题 3.1 1x A ∀∈,2x D ∃∈ 展现条件 示例图形 不等式转化()()12f x g x ≥()()()1min min f x g x f x c →≥≥()()12f x g x ≤()()()2max max f x g x f x c →≤≤()()12f x g x =()()()()()()1min min 2max max f x g x f x c f x g x f x c ⎧⎧⎪⎪→⎨⎨⎪⎪⎩⎩≥≥≤≤ 答题步骤①.分析()f x 和()g x 之间最值的关系;当()()12f x g x =时,需分析值域之间的关系; ②.转化为不等式恒成立问题处理.问题难点 ①.求确定函数的最值; ②.处理不等式恒成立问题【例6】(1)已知函数()43f x x x=+-,()2g x kx =+,若()11,4x ∀∈,[]21,2x ∃∈-. ①.若()()12g x f x >,则k ∈__________. ②.若()()12g x f x <,则k ∈__________.(2)已知函数()2124,0,411log 3,,124x x f x x x ⎧⎡⎤-∈⎪⎢⎥⎪⎣⎦=⎨⎛⎤⎪-∈ ⎥⎪⎝⎦⎩,()2232g x x a x a =--,若[]10,1x ∀∈,[]20,1x ∃∈,使得()()21f x g x =成立,则a 的最大值为_________.(3)已知函数()221xf x x =+,()()520g x ax a a =+->,若1x ∀∈R ,[]20,1x ∃∈,使得方程()()12f x g x =成立,则实数a 的取值范围是_________.练习6:1.已知函数()12f x x k =-,()13g x x x =-+-.若[]10,2x ∀∈,[]22,4x ∃∈,使得()()12g x f x =成立,则实数k 的取值范围是_________.2.已知函数()21f x x =-,()232g x ax a =-+.若[]10,1x ∀∈,21,22x ⎡⎤∃∈⎢⎥⎣⎦,使得不等式()()12f x g x ≥成立,则实数a 的取值范围是__________.3.已知函数()[)1,2,112,1,211,,22x x x f x x x x x ⎧+∈--⎪⎪⎪⎡⎫=-∈-⎨⎪⎢⎣⎭⎪⎪⎡⎤-∈⎪⎢⎥⎣⎦⎩,设函数()2g x ax =-,若[]12,2x ∀∈-,[]02,2x ∃∈-,使得()()01g x f x =成立,则a ∈__________.4.已知函数()11f x x x =-+,()224g x x ax =-+,若[]10,1x ∀∈,[]21,2x ∃∈,使得不等式()()12f x g x ≥成立,则实数a 的取值范围是_________.3.2 双任意及双存在问题 I .1x A ∀∈,2x D ∀∈展现条件 示例图形 不等式转化()()12f x g x ≥()()()1min max f x g x f x c →≥≥()()12f x g x ≤()()()2max min f x g x f x c →≤≤()()12f x g x =()()()()()()1min min 2max max f x g x f x c f x g x f x c =⎧⎧=⎪⎪→⎨⎨==⎪⎪⎩⎩II .1x A ∃∈,2x D ∃∈展现条件 示例图形 不等式转化 ()()12f x g x ≥()()max min f x g x ≥()()12f x g x ≤()()min max f x g x ≤()()12f x g x =()()()()max minminmax f x g x f x g x ⎧⎪⎨⎪⎩≥≤(交集非空) 【例7】(1)已知函数()213,1log ,1x x x f x x x ⎧-+⎪=⎨>⎪⎩≤,()1g x x k x =-+-,若12x x ∀∈R 、,不等式()()12f x g x ≤恒成立,则实数k 的取值范围是_________.(2)已知函数()()sin2336f x a x a a π=-+>,()222xg x x x =++,若存在[]120,1x x ∈、,使得()()12f x g x =成立,则实数a 的取值范围是_________.(3)已知函数()2,137,1x ax x f x ax x ⎧-+=⎨->⎩≤,若存在12x x ∈R 、且12x x ≠,使()()12f x f x =成立,则实数a 的取值范围是_________.(4)已知函数()f x 的定义域为D ,若c D ∃∈,使得12x x D ∀∈、,c =称()f x 为D 上的“c 平均函数”,已知()[]3,1,2f x x x =∈,若()f x 是区间[]1,2上的“c 平均函数”,则实数c 的值为_________.(5)已知函数()[]2ln ,0,1x f x a x x a x =+-∈,若[]120,1x x ∀∈、,不等式()()121f x f x a --≤恒成立,则实数a 的取值范围是_________.4.运用图像解含参不等式问题描述 已知()0f x ≥(解析式中含参数a ),将不等式分离为()()g x h x ≥(其中一个含参,另一个不含参),则()g x 的图像在()h x 图像的上方.为了便于讨论,下面所有的讲解中,()h x 含参数,()g x 不含参数.分离函数 I .()()()h x kx bh x kx b h x k x b⎧=+⎪=+⎨⎪=+⎩(一次函数模型)II .()()h x g x a =±(左右平移模型)备注 在处理这种问题时,需保证两点:①.将不等式分离成一个含参及一个不含参的函数;②.需保证不含参函数的图像比较“好画”.4.1 一次函数模型问题问题描述 所分离的含参函数()h x 为一次函数或含绝对值的一次式,求参数取值范围图形变换I .()h x 过定点,旋转变换(k 未知) II .()h x 平移变换(b 未知)答题步骤①.不等式分离成()()()g x h x ≥或≤,注意()h x 需分离成含参一次函数; ②.画出()g x (确定函数)的图像;③.旋转(或平移)()h x ,确定临界情况(一般为相切时); ④.求出临界值(求导或用0∆=),写出参数取值范围.【示例3】已知函数()ln f x x =,若(]0,x e ∀∈,不等式()()()11f x f c x --≥恒成立,则实数c 的取值范围是_________.解:()10f =,则()()1f x c x -≥可得()f x 的图像在()()1g x c x =-图像的上方I .确定函数及其图像高低关系.()g x 过点()1,0旋转.画出()()[]ln ,0,1ln ,1,x x f x x x e ⎧-∈⎪=⎨∈⎪⎩的图像,且()g x 恒过()1,0点 II .画出()f x 图像,旋转()g x 找临界.①.若()y g x =在()0,1上满足()()g x f x ≤恒成立,则临界情况为()g x 与()f x 相切于点()1,0; 此时()1f x x'=-,则()11c f '==-;∴当()0,1x ∈时,()()g x f x ≤可得1c -≥;②.若()y g x =在[]1,e 上满足()()g x f x ≤恒成立,则临界情况为11c e =- ∴当[]1,x e ∈时,()()g x f x ≤可得11c e -≤ III .分段分析临界情况,并分别求出对应的c 的取值范围.综上,11,1c e ⎡⎤∈-⎢⎥-⎣⎦IV .求出c 的范围【例8】(1)已知()1f x x =-,若x ∀∈R ,不等式()1f x ax -≥恒成立,则a ∈_________.(2)若x ∀∈R ,不等式()24a x x x ++≥恒成立,则实数a 的取值范围是_________.(3)已知函数()1,12,1x x f x x x x ⎧+<⎪=⎨+⎪⎩≥.设a ∈R ,若关于x 的不等式()2x f x a +≥在R 上恒成立,则实数a 的取值范围是__________.(4)已知函数()()121x f x x e mx +=++,若有且仅有两个整数使得()0f x ≤,则实数m 的取值范围是__________.(选讲) 练习8:1.已知函数()()22log 1,02,0x x f x x x x ⎧+>⎪=⎨-+⎪⎩≤,若x ∀∈R ,不等式()f x mx ≥恒成立,则实数m 的取值范围是_________.2.已知函数()2,04,0x f x x x x ⎧>⎪=⎨-⎪⎩≤,若x ∀∈R ,不等式()1f x ax -≥恒成立,则a ∈______.3.已知()23,032,0x x f x x x ⎧-=⎨->⎩≤,若[]1,1x ∀∈-,不等式()f x ax >恒成立,则实数a 的取值范围是_________.4.若[)0,x ∃∈+∞,使得不等式242x x m --≤成立,则实数m 的取值范围是_________.5.已知(]0,1x ∀∈,函数()2f x x x a =--的值恒为负值,则实数a 的取值范围是_______.6.已知函数()23,12,1x x x f x x x x ⎧-+⎪=⎨+>⎪⎩≤.设a ∈R ,若关于x 的不等式()2x f x a +≥在R 上恒成立,则实数a 的取值范围是__________.7.若关于x 的不等式20x xe ax a -+<的非空解集中无整数解,则a ∈_________.4.2 原函数平移问题(选讲) 问题描述 不等式()()()f x t f x +≤或≥在指定区间A 上恒成立,求参数取值范围.需要注意的是,参数即有可能在解析式中,也有可能为平移幅度(即t )示例图像核心思想 这类问题解决的关键在于找“特定点”.图像平移,图形形态不变.只需找出平移的临界点及其坐标(一般为横坐标)即可求解.核心步骤 ①.画出原函数()f x 的图像,并确定平移方向;②.将()f x 平移至满足()()()f x t f x +≤或≥;③.确认临界点,并求出该点横坐标;④.求出参数取值范围.【例9】(1)已知()f x 是定义在R 上的奇函数,当0x ≥时,()()2221232f x x a x a a =-+--,若x ∀∈R ,不等式()()1f x f x -≤,则实数a 的取值范围是_________.(2)已知函数()()1f x x a x =+. 设关于x 的不等式()()f x a f x +< 的解集为A ,若 11,22A ⎡⎤-⊆⎢⎥⎣⎦, 则实数a 的取值范围是_________.(选讲)练习9:1.定义在R 上的偶函数()f x ,当0x ≥时,()()32ln 1x f x e x x =+++,若()1,x ∀∈-+∞, 不等式()()f x t f x +>恒成立,则实数t 的取值范围是_________.2.设函数()f x 的定义域为D ,若存在非零实数t ,使得()x M M D ∀∈⊆,都有x t D +∈且()()f x t f x +≥,则称()f x 为M 上的“t 高调函数”,若()()()210f x x x =-≥是[)0,+∞上的“m 高调函数”,则实数m 的取值范围是_________.3.已知函数()2,0,0x x f x ax x x -⎧=⎨+>⎩≤,若x ∀∈R ,不等式()()1f x f x -≥恒成立,则实数a 的取值范围是_________.。

第七讲 不等式恒成立问题基本类型及常用解法类型1:设f(x)=ax+bf(x) >0在x ∈[]n m ,上恒成立⇔ ⎩⎨⎧0)(0)( n f m ff(x) <0在x ∈[]n m ,上恒成立⇔⎩⎨⎧0)(0)( n f m f .例1. 设y=(log 2x)2+(t-2)log 2x-t+1,若t 在[-2,2]上变化,y 恒取正值,求实数x 的取值范围。
例2. 对于 -1≤a ≤1,求使不等式(21)ax x +2<(21)12-+a x 恒成立的x 的取值范围。
类型2:设f(x)=ax 2+bx+c (a ≠0)f(x) >0在x ∈R 上恒成立⇔a >0 且△<0;f(x) <0在x ∈R 上恒成立⇔a <0 且△<0. 说明:①.只适用于一元二次不等式②.若未指明二次项系数不等于0,注意分类讨论.例3.不等式3642222++++x x mmx x <1对一切实数x 恒成立,求实数m 的取值范围。
类型3:设f(x)=ax 2+bx+c (a ≠0) (1) 当a >0时① f(x) >0在x ∈[]n m ,上恒成立⇔⎪⎩⎪⎨⎧≤-0)(2 m f m a b 或⎪⎩⎪⎨⎧∆-o n a b m 2或⎪⎩⎪⎨⎧≥-0)(2 n f n ab⇔⎪⎩⎪⎨⎧≤-0)(2 m f m ab 或△<0或⎪⎩⎪⎨⎧≥-)(2 n f n a b. ② f(x) <0在x ∈[]n m ,上恒成立⇔⎩⎨⎧0)(0)( n f m f .(2) 当a <0时① f(x) >0在x ∈[]n m ,上恒成立⇔ ⎩⎨⎧0)(0)( n f m f② f(x) <0在x ∈[]n m ,上恒成立⇔⎪⎩⎪⎨⎧≤-0)(2 m f m a b 或⎪⎩⎪⎨⎧∆-o n a b m 2或⎪⎩⎪⎨⎧≥-0)(2 n f n ab⇔⎪⎩⎪⎨⎧≤-0)(2 m f m ab 或△<0或⎪⎩⎪⎨⎧≥-)(2 n f n a b. 说明:只适用于一元二次不等式.类型4:a >f(x) 恒成立对x ∈D 恒成立⇔a >f(x)max ,a <f(x)对x ∈D 恒成立⇔ a <f(x)min .说明:①. f(x) 可以是任意函数②.这种思路是:首先是---分离变量,其次用---极端值原理。









不等式“恒成立”问题的解法
解决不等式“恒成立”的问题需要采用不等式的性质和规则进行推导和证明。
首先,可以使用分析法来解决不等式“恒成立”的问题。
分析法要求对不等式进行分析和推导,找出其中的规律和特点,从而得出结论。
其次,可以运用数学归纳法来解决不等式“恒成立”的问题。
数学归纳法是通过给出一些特例,然后从其中推导出结论的方法。
另外,可以使用反证法来证明不等式“恒成立”。
反证法是指假设不等式不成立,然后通过推导出矛盾的结论,证明假设的不等式是错误的,从而得出不等式“恒成立”的结论。
最后,可以使用代数法来解决不等式“恒成立”的问题。
代数法是通过对不等式进行变形,转化为“等式”的形式来解决问题。
例如,可以将一个不等式两边分别加上或减去相同的数,或者将不等式两边同时乘以或除以一个正数,从而得出不等式“恒成立”的结论。