2二次函数综合问题例谈
- 格式:doc
- 大小:411.00 KB
- 文档页数:7

(完整版)二次函数综合题分类讨论带答案.doc二次函数综合题分类讨论一、直角三角形分类讨论:11、已知点 A(1 ,0),B( -5,0),在直线y 2 x 2 上存在点C,使得 ABC 为直角三角形,这样的 C 点你能找到个2、如图 1,已知抛物线C1:y a x 2 2 5 的顶点为 P,与 x 轴相较于 A 、 B 两点(点A 在点B 的左边),点B 的横坐标是1.(1)求P 点坐标及a的值;( 2)如图 1,抛物线C2与抛物线C1关于x 轴对称,将抛物线C2向右平移,平移后得到抛物线C3, C,3的顶点为 M ,当点 P、 M 关于点 B 成中心对称时,求C,3的解析式;( 3)如图 2,点 Q 是 x轴正半轴上一点,将抛物线C1绕点Q 旋转180 后得到抛物线C,4,抛物线 C,4的顶点为N,与 x 轴相交于 E、 F 两点(点 E 在点 F 的左边),当以点 P、N、 F 为顶点的三角形是直角三角形时,求点Q 的坐标。
(2013 汇编 P56+P147)3、如图,矩形A’BC’O’是矩形 OABC( 边 OA 在 x 轴正半轴上,边 OC 在 y 轴正半轴上 )绕 B 点逆时针旋转得到的.O’点在 x 轴的正半轴上, B 点的坐标为 (1,3).(1)如果二次函数 y= ax2+ bx+c(a≠0)的图象经过 O、O’两点且图象顶点 M 的纵坐标为—1.求这个二次函数的解析式;(2) 在 (1)中求出的二次函数图象对称轴的右支上是否存在点P,使得POM 为直角三角形若存在,请求出P 点的坐标和POM 的面积;若不存在,请说明理由;(3)求边C’O’所在直线的解析式.练习( 09 成都 28)已知抛物线与x 轴交于 A 、 B 两点 (点 A 在点 B 的左侧 ),与 y 轴交于点C,其顶点为 M ,若直线 MC 的函数表达式为 y=kx-3 ,与 x 轴的交点为N,且cos∠BCO =(3 √ (10) /10).( 1)求此抛物线的解析式;( 2)在此抛物线上是否存在异于点 C 的点 P,使以 N 、 P、C 为顶点的三角形是以NC 为一条直角边的直角三角形?若存在,求出点P 的坐标;( 3)过点 A 作 x 轴的垂线,交直线 MC 于点 Q. 若将抛物线沿其对称轴上下平移,使抛物线与线段NQ 总有公共点,则抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度5 ?4A 二、4321N2 B 2 4 6 8 10 12 14 16 18123P4M56等腰三角形分类讨论1、如图,已知 Rt Rt ABC , ACB 90 , BAC 30 , 在直线BC或直线AC上取一点P,使得 PAB 是等腰三角形,则符合条件的P 点有个2 A的坐标为(12),,点B的坐标为(31),,二次函数 y x2、①,在平面直角坐标系中,点的图象记为抛物线l1.(1)平移抛物线l1,使平移后的抛物线过点A ,但不过点B ,写出平移后的一个抛物线的函数表达式:(任写一个即可).(2)平移抛物线l1,使平移后的抛物线过A,B两点,记为抛物线l2,如图②,求抛物线l2 的函数表达式.(3)设抛物线l2 △△,求点 K 的坐标.的顶点为 C , K 为 y 轴上一点.若S ABK SABC( 4)请在图③上用尺规作图的方式探究抛物线l 2上是否存在点P ,使△ ABP 为等腰三角形.若存在,请判断点P 共有几个可能的位置(保留作图痕迹);若不存在,请说明师.yyyl 2l 1l 2AAA1B1CBx1BO xOO 111图①图②图③解:( 1 )有多种答案,符合条件即可.例如yx 2 1, y x 2 x , y( x 1)22 或y x 2 2x 3 , y (x2 1)2 , y (x 12) 2 .(2)设抛物线 l 2 的函数表达式为 y x 2bxc ,yl 2Q 点 A(12),, B(31),在抛物线 l 2 上,KGA1 b c ,b9 ,2 29 3b c 解得111c.抛物线 l 2 的函数表达式为y x 2 9 x 11 .2 29 x 119 27 ,9,7(3) yx 2 xC 点的坐标为.2 2 4 164 16 过 A , B , C 三点分别作 x 轴的垂线,垂足分别为 D ,E ,F ,则 AD 2 , CF7 , BE1, DE5 , FE316 2 , DF.44 S △ ABCS 梯形ADEBS梯形 ADFCS梯形 CFEB1(2 1) 2 1 2 75 1 1 73 15 .2 2 164 2 164 16延长 BA 交 y 轴于点 G ,设直线 AB 的函数表达式为 y mx n ,2 m ,m1 ,Q 点 A(12),, B(31),在直线 AB 上, n21 3m 解得5n.n.2直线 AB 的函数表达式为 y1x 5 G 点的坐标为52 .0,.22BCO D F E图②设 K 点坐标为(0,h),分两种情况:若 K 点位于 G 点的上方,则KG h 5 .连结AK ,BK .2S△ABK S△BKG S△AKG 1 3 h 5 1 1 h 5 h 5 .2 2 2 2 2Q S△ABK15 5 15,解得 h55K 点的坐标为55 S△ABC ,h16 16.0,.16 2 16若 K 点位于 G 点的下方,则KG 5h .同理可得, h25.2 16 yK 点的坐标为25.l 2 0,16 A(4)作图痕迹如图③所示. B由图③可知,点P 共有3个可能的位置.O图③2、如图:在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形,y点 A 、 C 的坐标分别为A(10 , 0)、 C( 0,4),点 D 是 OA 的中点,点 P 在PCBC 边上运动,当是腰长为 5 的等腰三角形时,点P 的坐标为O D 3、在菱形 ABCD 中,对角线AC , BD 相交于点 O,以 O 为坐标原点,以 BD 所在直线为 x 轴, CA 所在直线为 y 轴建立如图所示的坐标系,且AC=12 ,BD=16 ,E 为 AD 的中点,点 P 在线段 BD 上移动,若为等腰三角形,则所有符合条件的点P 的坐标为三、最值问题 B类型一:两点之间线段最短 C 1、请写出2m 3 2 1 8 2m 2 4 的最小值为 A2、如图,四边形ABCD 是正方形,ABE 是等边三角形,对角线BD 上60 ,得到BN,连EN任一点,将 BM 绕点 B 逆时针旋转EN、 AM 、CM ,求证:( 1)AMB ENB ,(2)M点在何处时,AM+CM值最小,(3)AM+BM+CN 最小值为3 1 时,求正方形的边长(2012 汇编P52+P137) B xBxAyAExDDMC3、( 2010 年天津 25)在平面直角坐标系中,矩形OACB 的顶点 O 在坐标原点,顶点 A 、B 分别在 x 轴、 y 轴的正半轴上,OA=3 ,OB=4 ,D 为边 OB 的中点。

二次函数的综合运用二次函数是一种形式为 y = ax² + bx + c 的函数,其中 a、b、c 是常数且a ≠ 0。
二次函数在数学中有广泛的应用,涉及到诸如物理学、经济学和工程学等多个领域。
本文将探讨二次函数在各个领域中的综合运用,包括最值问题、图像分析、实际问题的建模等。
一、最值问题对于二次函数 y = ax² + bx + c,其中a ≠ 0,我们可以通过一些方法求得其最值。
为了简化讨论,我们以函数 y = x² + 2x - 3 为例。
1. 定义域和值域首先,我们需要确定该二次函数的定义域和值域。
对于二次函数 y= x² + 2x - 3,由于 x²的值始终大于等于 0,所以该函数的定义域为全体实数。
而二次函数在开口向上的情况下,其最小值即为函数的值域的下界。
根据二次函数的顶点公式,可以求得该函数的顶点为(-1, -4),因此该函数的最小值为 -4。
2. 求解极值点我们可以通过求导数的方法求得二次函数的极值点。
对于函数 y =x² + 2x - 3,将其对 x 求导后可得 y' = 2x + 2。
令 y' = 0,解得 x = -1。
将 x = -1 代入函数 y = x² + 2x - 3 中可得 y = -4,即函数在 x = -1 处取得极小值 -4。
同样,对于开口向下的二次函数,可以通过类似的方法求得其极大值。
二、图像分析二次函数的图像一般为抛物线,通过分析图像可以获得更多关于函数的信息。
下面以函数 y = x² + 2x - 3 为例进行具体分析。
1. 对称轴和顶点二次函数的对称轴是由函数的一阶导数确定的直线,其方程形式为x = -b/(2a)。
对于函数 y = x² + 2x - 3,对称轴的方程为 x = -1。
根据二次函数的顶点公式,可以求得该函数的顶点坐标为 (-1, -4)。

二次函数代数推理综合问题解析二次函数是一种常见的二次曲线,其一般形式为:y = ax^2 + bx + c,其中a、b、c为常数,且a ≠ 0。
在代数推理的综合问题中,有一些与二次函数相关的问题需要解析。
下面将介绍几个常见的二次函数代数推理综合问题,并给出解析。
问题一:已知二次函数y = ax^2 + bx + c的顶点坐标为(2,3),且过点(-1,0),求该函数的表达式。
解析:由题可知,二次函数的顶点坐标为(2,3),则顶点坐标中的x坐标为2,代入函数表达式可以得到:3=a*2^2+b*2+c另外,已知过点(-1,0),把该点的坐标代入函数表达式可以得到:0=a*(-1)^2+b*(-1)+c将上述两个方程组成一个方程组:4a+2b+c=3----(1)a-b+c=0----(2)解决方程组(1)和(2),可以采用消元法或代入法:将公式(2)的c解出来得到c=-a+b,代入公式(1)可以得到:4a+2b+(-a+b)=3,整理得到3a+3b=3,整理为a+b=1由公式a+b=1可以得到a=1-b,代入公式(2)可以得到(1-b)-b+c=0,整理得到c=2b-1综上所述,函数表达式为:y = (1 - b)x^2 + bx + (2b - 1)。
问题二:已知二次函数y = ax^2 + bx + c的两个零点为-2和5,求该函数的表达式。
解析:已知二次函数的两个零点为-2和5,可得到两个方程:a*(-2)^2+b*(-2)+c=0a*5^2+b*5+c=0整理得到:4a-2b+c=0----(3)25a+5b+c=0----(4)解决方程组(3)和(4),可以采用消元法或代入法:将公式(3)的c解出来得到c=2b-4a,代入公式(4)可以得到:25a+5b+(2b-4a)=0,整理得到-21a+7b=0,整理为-3a+b=0。
由公式-3a+b=0可以得到b=3a,代入公式(3)可以得到4a-2(3a)+c=0,整理得到c=2a。

二次函数中常见的几种综合题型二次函数常见的几类综合题型一、求线段最大值及根据面积求点坐标问题1.已知抛物线 $y=x^2+bx+c$ 的图象与 $x$ 轴的一个交点为 $B(5,0)$,另一个交点为 $A$,且与 $y$ 轴交于点 $C(0,5)$。
1) 求直线 $BC$ 与抛物线的解析式;2) 若点 $M$ 是抛物线在 $x$ 轴下方图象上的一个动点,过点 $M$ 作 $MN\parallel y$ 轴交直线 $BC$ 于点 $N$,求$MN$ 的最大值;3) 在 (2) 的条件下,$MN$ 取得最大值时,若点 $P$ 是抛物线在 $x$ 轴下方图象上任意一点,以 $BC$ 为边作平行四边形 $CBPQ$,设平行四边形 $CBPQ$ 的面积为 $S_1$,$\triangle ABN$ 的面积为 $S_2$,且 $S_1=6S_2$,求点$P$ 的坐标。
2.对称轴为直线 $x=-1$ 的抛物线$y=ax^2+bx+c(a\neq0)$ 与 $x$ 轴相交于 $A$、$B$ 两点,其中点 $A$ 的坐标为 $(-3,0)$。
1) 求点 $B$ 的坐标;2) 已知 $a=1$,$C$ 为抛物线与 $y$ 轴的交点。
①若点 $P$ 在抛物线上,且 $S_{\trianglePOC}=4S_{\triangle BOC}$,求点 $P$ 的坐标;②设点 $Q$ 是线段 $AC$ 上的动点,作 $QD\perp x$ 轴交抛物线于点 $D$,求线段 $QD$ 长度的最大值。
二、求三角形周长及面积的最值问题3.已知抛物线 $y=ax^2+bx+c$ 经过 $A(-3,a-b+c)$,$B(1,a+b+c)$,$C(c,a+3c-b)$ 三点,其顶点为 $D$,对称轴是直线 $l$,$l$ 与 $x$ 轴交于点 $H$。
1) 求该抛物线的解析式;2) 若点 $P$ 是该抛物线对称轴 $l$ 上的一个动点,求$\triangle PBC$ 周长的最小值;3) 如图 (2),若 $E$ 是线段 $AD$ 上的一个动点($E$ 与$A$、$D$ 不重合),过点 $E$ 作平行于 $y$ 轴的直线交抛物线于点 $F$,交 $x$ 轴于点 $G$,设点 $E$ 的横坐标为 $m$,$\triangle ADF$ 的面积为 $S$。

二次函数的综合应用㈠一、典例精析考点一:二次函数与方程1.已知抛物线与x轴没有交点.(1)求c的取值范围;(2)试确定直线y=cx+l经过的象限,并说明理由.2.已知函数y=mx2-6x+1(m是常数).⑴求证:不论m为何值,该函数的图象都经过y轴上的一个定点;⑵若该函数的图象与x轴只有一个交点,求m的值.考点二:二次函数与最大问题3、如图,二次函数的图像经过点,且与轴交于点. (1)试求此二次函数的解析式;(2)试证明:(其中是原点);(3)若是线段上的一个动点(不与、重合),过作轴的平行线,分别交此二次函数图像及轴于、两点,试问:是否存在这样的点,使?若存在,请求出点的坐标;若不存在,请说明理由。
5、如图,抛物线与x轴交与A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.考点三:二次函数与等腰三角形、直角三角形6.如图,直线交轴于A点,交轴于B点,过A、B两点的抛物线交轴于另一点C (3,0).⑴求抛物线的解析式;⑵在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q 点坐标;若不存在,请说明理由.7、如图,在平面直角坐标系中,△ABC 是直角三角形,∠ACB=90,AC=BC ,OA=1,OC=4,抛物线y=x 2+bx+c 经过A ,B 两点,抛物线的顶点为D .(1)求b ,c 的值;(2)点E 是直角三角形ABC 斜边AB 上一动点(点A 、B 除外),过点E 作x 轴的垂线交抛物线于点F ,当线段EF 的长度最大时,求点E 的坐标;(3)在(2)的条件下:①求以点E 、B 、F 、D 为顶点的四边形的面积;②在抛物线上是否存在一点P ,使△EFP 是以EF 为直角边的直角三角形?若存在,求出所有点P 的坐标;若不存在,说明理由.8如图,抛物线y=21x 2+bx ﹣2与x 轴交于A ,B 两点,与y 轴交于C 点,且A (﹣1,0).(1)求抛物线的解析式及顶点D 的坐标;(2)判断△ABC 的形状,证明你的结论;(3)点M (m ,0)是x 轴上的一个动点,当MC+MD 的值最小时,求m 的值.9.如图所示,在平面直角坐标系Oxy 中,已知点A (-,0),点C (0,3),点B 是x 轴上一点(位于点A 的右侧),以AB 为直径的圆恰好经过点C .(1)求∠ACB 的度数;(2)已知抛物线y =ax 2+bx +3经过A 、B 两点,求抛物线的解析式;(3)线段BC 上是否存在点D ,使△BOD 为等腰三角形.若存在,则求出所有符合条件的点D 的坐标;若不存在,请说明理由.10如图,抛物线254y ax ax =-+经过ABC △的三个顶点,已知BC x ∥轴,点A 在x 轴上,点C 在y 轴上,且AC BC =.(1)求抛物线的对称轴;(2)写出A B C ,,三点的坐标并求抛物线的解析式;(3)探究:若点P 是抛物线对称轴上且在x 轴下方的动点,是否存在PAB △是等腰三角形.若存在,求出所有符合条件的点P 坐标;不存在,请说明理由.11在平面直角坐标系中,已知抛物线经过()40A -,,()04B -,,()20C ,三点. (1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,AMB △的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.(3)若点P 是抛物线上的动点,点Q 是直线y x =-上的动点,判断有几个位置能够使得点P Q B O ,,,为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.12如图,在平面直角坐标系中,直线y=x+2交x 轴于点P ,交y 轴于点A .抛物线y=x 2+bx+c 的图象过点E (﹣1,0),并与直线相交于A 、B 两点.(1)求抛物线的解析式(关系式);(2)过点A 作AC ⊥AB 交x 轴于点C ,求点C 的坐标;(3)除点C 外,在坐标轴上是否存在点M ,使得△MAB 是直角三角形?若存在,请求出点M 的坐标;若不存在,请说明理由.。

完整版)二次函数含参综合专题轴平移3个单位,得到抛物线y=x-2ax+(b+3),求新抛物线的表达式;2)若a=2,b=3,求点P、Q的坐标和抛物线的对称轴;3)将抛物线在x轴上方的部分沿y轴平移2个单位,得到抛物线G,求G与x轴交点的横坐标。
综合专题:二次函数二次函数的特征很多时候是隐藏在式子中的,需要找到关键点才能解决问题。
下面分别对不等关系类、翻折类、平移类的例题进行分析。
例1.在平面直角坐标系xOy中,抛物线y=ax²与x轴交于A、B两点(点A在点B左侧)。
1) 当抛物线过原点时,a的值为0;2) ①对称轴为x=0,顶点纵坐标为0;②顶点为原点,纵坐标为0;3) 当AB≤4时,a∈[-2,2]。
巩固练:在平面直角坐标系xOy中,抛物线y=ax²-4ax+3a(a>0)与x轴交于A、B两点(A在B的左侧)。
1) 对称轴为x=2,A(-a,0),B(3a,0);2) 点C(t,3)在抛物线上,过C作x轴的垂线交x轴于D,①CD=AD时,a=t²-4t+3;②CD>AD时,t∈(-∞,0)∪(1,∞)。
例2.在平面直角坐标系xOy中,抛物线y=nx²-4nx+4n-1(n≠0),与x轴交于点C、D(C在D的左侧),与y轴交于点A。
1) 顶点坐标为(M,n-1),其中M=n;2) A(0,n-1),B(3-n,n-1);3) 翻折后的图象记为G,直线y=n-1与G有一个交点时,m∈(-∞,n-1)。
巩固练:在平面直角坐标系xOy中,抛物线y=ax²-4ax+3a的最高点纵坐标为2.1) 对称轴为x=1,表达式为y=(a-1)²-1;2) 图象G1在x∈[1,4]上,将G1沿直线x=1翻折得到G2,图象G由G1和G2组成,直线y=b与G只有两个公共点时,b∈(-∞,-1)∪(3,∞),x1+x2=2.例3.在平面直角坐标系xOy中,已知抛物线y=x-2ax+b 的顶点在x轴上,P(x1,m)、Q(x2,m)(x1<x2)是此抛物线上的两点。

二次函数综合问题一、转化为最值问题(值域)1、设m 是实数,记M={m |m >1},f(x)=log 3(x 2-4mx+4m 2+m+11-m ). (1)证明:当m ∈M 时,f(x)对所有实数都有意义;反之,若f(x)对所有实数x 都有意义,则m ∈M ; (2)当m ∈M 时,求函数f(x)的最小值;(3)求证:对每个m ∈M,函数f(x)的最小值都不小于1. 解:(1)证明:先将f(x)变形:f(x)=log 3[(x -2m)2+m+11-m ], 当m ∈M 时,m>1,∴(x -m)2+m+11-m >0恒成立,故f(x)的定义域为R 。
反之,若f(x)对所有实数x 都有意义,则只须x 2-4mx+4m 2+m+11-m >0。
令Δ<0,即16m 2-4(4m 2+m+11-m )<0,解得m>1,故m ∈M 。
(2)解析:设u=x 2-4mx+4m 2+m+11-m ,∵y=log 3u 是增函数,∴当u 最小时,f(x)最小。
而u=(x -2m)2+m+11-m ,显然,当x=m 时,u 取最小值为m+11-m ,此时f(2m)=log 3(m+11-m )为最小值。
(3)证明:当m ∈M 时,m+11-m =(m -1)+ 11-m +1≥3,当且仅当m=2时等号成立。
∴log 3(m+11-m )≥log 33=1。
2、x x f f bx ax x f a b a ==+=≠)(0)2()(02,并使方程,且,为常数,,已知有等根 (1)求()x f 的解析式;(2)是否存在实数()n m n m <,,使f(x)的定义域和值域分别为[]n m ,和[]n m 2,2。
解:0)2()(12=+=f bx ax x f ,且)( ∴+=420a b又方程,即f x x ax bx x ()=+=2即有等根ax b x 210+-=()211004)1(2-===⨯⨯--=∆∴a b a b ,从而,即 x x x f +-=∴221)( 2121)1(2121)(222≤+--=+-=x x x x f )( 41212≤≤n n ,则有又f(x)在[m ,n ]上是增函数(或对称轴x =1≥n ) ⎪⎪⎩⎪⎪⎨⎧==≤<∴n n f m m f n m 2)(2)(41 解得,m n =-=20∴存在m =-2,n =0使f(x)的定义域和值域分别为[m ,n ]和[2m ,2n ]。

二次函数综合题解题方法解数学压轴题一般可以分为三个步骤:认真审题,理解题意、探究解题思路、正确解答。
解题方法:1、待定系数法求二次函数的解析式;2、会用配方法、公式法求抛物线的顶点坐标、对称轴方程重要数学思想:转化思想、数形结合思想、分类讨论思想及方程的思想等。
一、距离问题例1:(2014•枣庄)如图,在平面直角坐标系中,二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.例2:(2014年山东泰安)二次函数y=ax2+bx+c的图象经过点(﹣1,4),且与直线y=﹣x+1相交于A、B两点(如图),A点在y轴上,过点B作BC⊥x 轴,垂足为点C(﹣3,0).(1)求二次函数的表达式;(2)点N是二次函数图象上一点(点N在AB上方),过N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;例3:(2014年山东日照)(2014•日照)如图1,在菱形OABC中,已知OA=2,∠AOC=60°,抛物线y=ax2+bx+c(a≠0)经过O,C,B三点.(Ⅰ)求出点B、C的坐标并求抛物线的解析式.(Ⅱ)如图2,点E是AC的中点,点F是AB的中点,直线AG垂直BC于点G,点P在直线AG上.(1)当OP+PC的最小值时,求出点P的坐标;二、面积问题:1、面积最大问题例1:(2009临沂)如图,抛物线经过(40)(10)(02)A B C -,,,,,三点. (1)求出抛物线的解析式;(3)在直线AC 上方的抛物线上有一点D ,使得DCA △的面积最大,求出点D 的坐标.例2:(2014•莱芜)如图,过A (1,0)、B (3,0)作x 轴的垂线,分别交直线y=4﹣x 于C 、D 两点.抛物线y=ax 2+bx+c 经过O 、C 、D 三点. (1)求抛物线的表达式;(3)若△AOC 沿CD 方向平移(点C 在线段CD 上,且不与点D 重合),在平移的过程中△AOC 与△OBD 重叠部分的面积记为S ,试求S 的最大值.2、面积为定值的问题例1:(2014潍坊)如图,抛物线y=ax 2+bx+c (a≠O )与y 轴交于点C(O ,4),与x 轴交于点A 和点B ,其中点A 的坐标为(-2,0),抛物线的对称轴x=1与抛O xyAB C4 12-(第26题图)物线交于点D,与直线BC交于点E(1)求抛物线的解析式;(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC 的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;例2:(2014•枣庄)如图,在平面直角坐标系中,二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).(2)连接CD、BD、DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;三角形相似问题:1、直角三角形相似问题例1:(2014•威海)如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点.(1)求这条抛物线的解析式;xyADBOC(第25题图)(2)E 为抛物线上一动点,是否存在点E 使以A 、B 、E 为顶点的三角形与△COB 相似?若存在,试求出点E 的坐标;若不存在,请说明理由;例2:25.(2014东营) 如图,直线y=2x+2与x 轴交与点A ,与y 轴交与点B ,△AOB 沿y 轴翻折,点A 落到点C ,过点B 的抛物线2y x bx c =-++与直线BC 交于点D (3,4-).(1)求直线BD 和抛物线的解析式;(2)在第一象限内的抛物线上,是否存在一点M ,作MN 垂直于x 轴,垂足为点N ,使得以M 、O 、N 为顶点的三角形与△BOC 相似?若存在,求出点M 的坐标;若不存在,请说明理由;例3:(2011•临沂)如图,已知抛物线经过A (﹣2,0),B (﹣3,3)及原点O ,顶点为C .(1)求抛物线的解析式;:(3)P 是抛物线上的第一象限内的动点,过点P 作PMx 轴,垂足为M ,是否存在点P ,使得以P 、M 、A 为顶点的三角形△BOC 相似?若存在,求出点P 的坐标;若不存在,请说明理由.2、等腰三角形相似问题例1:(2007临沂)如图①,已知抛物线的顶点为A (2,1),且经过原点O ,与x 轴的另一交点为B 。


运用数学思想解决二次函数一次函数及方程等综合问题数学思想是解决各种数学问题的基础,数学的各个分支都离不开数学思想。
二次函数、一次函数和方程是高中数学中的重要内容,其中许多问题需要运用数学思想才能得以解决。
一、二次函数问题1、最值问题对于二次函数$f(x)=ax^2+bx+c(a≠0)$,最值问题是常见的问题之一。
通过求导或者配方法可以得到二次函数的顶点坐标。
但是,在实际问题中,经常需要通过变量代换或者条件限制等方式来解决最值问题。
例如,某面积为$S$的矩形中,正好能容纳一个底边长为$x$的半圆形,问该矩形的长和宽分别为多少?解:设矩形的长和宽分别为$l$和$w$,则根据题意得到方程$\frac{πx^2}{4}=lw$。
要求矩形的长和宽的和最小,可以将$l+w$作为新的变量,即求$f(l,w)=l+w$的最小值。
将$l$用$\frac{πx^2}{4w}$表示代入函数中,得到$f(\frac{πx^2}{4w},w)=\frac{πx^2}{4w}+w$,对变量$w$求导,得到$\frac{df}{dw}=-\fr ac{πx^2}{4w^2}+1$。
令$\frac{df}{dw}=0$,得到$w=\frac{πx^2}{4}$。
将$w$代入原方程,解得$l=x$,因此矩形的长和宽分别为$\frac{πx}{2}$和$\frac{x}{2}$。
2、交点问题对于两个二次函数$f(x)=ax^2+bx+c$和$g(x)=dx^2+ex+f$,交点问题是常见的问题之一。
可以通过解方程或者配方法求解交点。
例如,已知$f(x)=x^2+2x+3$和$g(x)=3x^2-2x+5$,问两个函数有几个交点?解:将两个函数相减得到$h(x)=2x^2-4x+2=2(x-1)^2$,因此两个函数如果有交点,则交点的横坐标为$x=1$。
将$x=1$代入任一函数即可求得交点,$f(1)=6$,$g(1)=6$,因此两个函数有一个交点$(1,6)$。
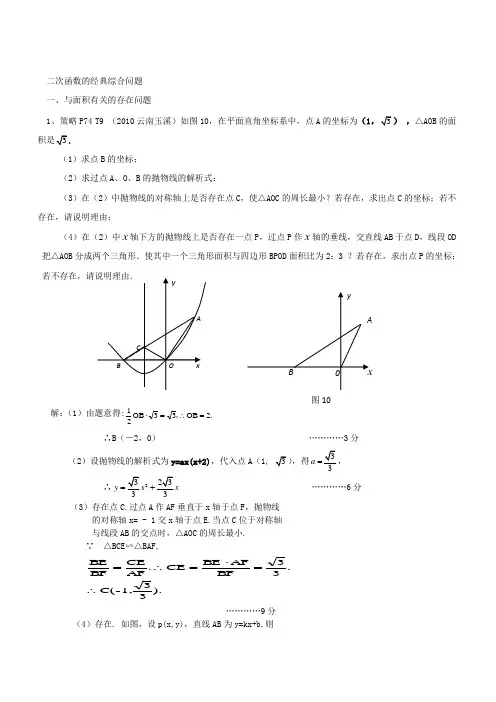
二次函数的经典综合问题 一、与面积有关的存在问题1、策略P74 T9 (2010云南玉溪)如图10,在平面直角坐标系中,点A 的坐标为(1,△AOB 的面(1)求点B 的坐标;(2)求过点A 、O 、B 的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△AOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由;(4)在(2)中x 轴下方的抛物线上是否存在一点P ,过点P 作x 轴的垂线,交直线AB 于点D ,线段OD 把△AOB 分成两个三角形.使其中一个三角形面积与四边形BPOD 面积比为2:3 ?若存在,求出点P 的坐标;解:(1)由题意得: 2.OB 33OB 21=∴=⋅,∴B (-2,0) …………3分(2)设抛物线的解析式为y=ax(x+2),代入点A (,得a , ∴2y =…………6分 (3)存在点C.过点A 作AF 垂直于x 轴于点F ,抛物线的对称轴x= - 1交x 轴于点E.当点C 位于对称轴 与线段AB 的交点时,△AOC 的周长最小. ∵ △BCE ∽△BAF,).33C(-1,.33B FA FB E CE .A F CE B F B E ∴=⋅=∴=…………9分(4)存在. 如图,设p(x,y),直线AB 为y=kx+b,则20.k k b k b b ⎧=⎪⎧+⎪⎪⎨⎨-+=⎪⎩⎪=⎪⎩解得, ∴直线AB为y , BOD BPO BPOD S S S ∆∆+=四 =12|OB||Y P |+12|OB||Y D |=|Y P |+|Y D |=2333x x --+. ∵S △AOD = S △AOB -S △BOD =3-21×2×∣33x+332∣=-33x+33.∴ODB OD S SP A 四∆=33233-33-33332++-x x x =32. ∴x 1=-21, x 2=1(舍去). ∴p(-21,-43) . 又∵S △BOD =33x+332, ∴ODB BOD S SP 四∆ =3323333332332+--+x x x = 32. ∴x 1=-21, x 2=-2. P(-2,0),不符合题意. ∴ 存在,点P 坐标是(-21,-43). …………12分 二 线段长的问题2\策略P77 T18(10四川眉山)26.如图,Rt △ABO 的两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上,O 为坐标原点,A 、B 两点的坐标分别为(3-,0)、(0,4),抛物线223y x bx c =++经过B 点,且顶点在直线52x =上. (1)求抛物线对应的函数关系式;(2)若△DCE 是由△ABO 沿x 轴向右平移得到的,当四边形ABCD 是菱形时,试判断点C 和点D 是否在该抛物线上,并说明理由;(3)若M 点是CD 所在直线下方该抛物线上的一个动点,过点M 作MN 平行于y 轴交CD 于点N .设点M 的横坐标为t ,MN 的长度为l .求M 的坐标.解:(1分) ∴2254()32m =⨯-+ ∴16m =- ……………………………………………………………(3分)∴所求函数关系式为:22251210()432633y x x x =--=-+ …………(4分)(2)在Rt △ABO 中,OA =3,OB =4,∴5AB ==∵四边形ABCD 是菱形∴BC =CD =DA =AB =5 ……………………………………(5分) ∴C 、D 两点的坐标分别是(5,4)、(2,0). …………(6分)当5x =时,2210554433y =⨯-⨯+= 当2x =时,2210224033y =⨯-⨯+=∴点C 和点D 在所求抛物线上. …………………………(7分) (3)设直线CD 对应的函数关系式为y kx b =+,则5420k b k b +=⎧⎨+=⎩解得:48,33k b ==-.∴4833y x =- ………(9分) ∵MN ∥y 轴,M 点的横坐标为t , ∴N 点的横坐标也为t .则2210433M y t t =-+, 4833N y t =-,……………………(10分)∴22248210214202734()3333333322N M l y y t t t t t t ⎛⎫=-=---+=-+-=--+ ⎪⎝⎭∵203-<, ∴当72t =时,32l =最大,此时点M 的坐标为(72,12). ………………………………(12分) 三二次函数中的线段长与面积3(2010山东济宁)指导最后一页最后一题 如图,在平面直角坐标系中,顶点为(4,1-)的抛物线交y 轴于A 点,交x 轴于B ,C 两点(点B 在点C 的左侧). 已知A 点坐标为(0,3).(1)求此抛物线的解析式;(2)过点B 作线段AB 的垂线交抛物线于点D , 如果以点C 为圆心的圆与直线BD 相切,请判断抛物线的对称轴l 与⊙C 有怎样的位置关系,并给出证明;(3)已知点P 是抛物线上的一个动点,且位于A ,C 两点之间,问:当点P 运动到什么位置时,PAC ∆的面积最大?并求出此时P 点的坐标和PAC ∆的最大面积.23.(1)解:设抛物线为2(4)1y a x =--.∵抛物线经过点A (0,3),∴23(04)1a =--.∴14a =. ∴抛物线为2211(4)12344y x x x =--=-+. ……………………………3分 (2) 答:l 与⊙C 相交. …………………………………………………………………4分证明:当21(4)104x --=时,12x =,26x =. ∴B 为(2,0),C 为(6,0).∴AB =设⊙C 与BD 相切于点E ,连接CE ,则90BEC AOB ∠=︒=∠. ∵90ABD ∠=︒,∴90CBE ABO ∠=︒-∠.又∵90BAO ABO ∠=︒-∠,∴BAO CBE ∠=∠.∴AOB ∆∽BEC ∆.x(第23题)x(第23题)∴CE BCOB AB =.∴2CE =.∴2CE =>.…………………………6分 ∵抛物线的对称轴l 为4x =,∴C 点到l 的距离为2.∴抛物线的对称轴l 与⊙C 相交. ……………………………………………7分(3) 解:如图,过点P 作平行于y 轴的直线交AC 于点Q .可求出AC 的解析式为132y x =-+.………………………………………8分 设P 点的坐标为(m ,21234m m -+),则Q 点的坐标为(m ,132m -+).∴2211133(23)2442PQ m m m m m =-+--+=-+.∵22113327()6(3)24244PAC PAQ PCQ S S S m m m ∆∆∆=+=⨯-+⨯=--+,∴当3m =时,PAC ∆的面积最大为274.此时,P 点的坐标为(3,34-). …………………………………………10分作业4、策略P75 T12(10江苏宿迁)28.(本题满分12分)已知抛物线c bx x y ++=2交x 轴于)0,1(A 、)0,3(B ,交y 轴于点C ,其顶点为D .(1)求b 、c 的值并写出抛物线的对称轴;(2)连接BC ,过点O 作直线BC OE ⊥交抛物线的对称轴于点E .求证:四边形ODBE 是等腰梯形; (3)问Q 抛物线上是否存在点Q ,使得△OBQ 的面积等于四边形ODBE 的面积的31?若存在,求出点Q 的坐标;若不存在,请说明理由.(第28题)(第28题2)解:(1)求出:4-=b ,3=c ,抛物线的对称轴为:x=2 ……3分(2) 抛物线的解析式为342+-=x x y ,易得C 点坐标为(0,3),D 点坐标为(2,-1) 设抛物线的对称轴DE 交x 轴于点F ,易得F 点坐标为(2,0),连接OD ,DB ,BE ∵∆OBC 是等腰直角三角形,∆DFB 也是等腰直角三角形,E 点坐标为(2,2), ∴∠BOE= ∠OBD=ο45 ∴OE ∥BD∴四边形ODBE 是梯形 ………………5分 在ODF Rt ∆和EBF Rt ∆中, OD=5122222=+=+DF OF ,BE=5122222=+=+FB EF∴OD= BE∴四边形ODBE 是等腰梯形 ……………7分(3) 存在, ……8分 由题意得:29332121=⨯⨯=⋅=DE OB S ODBE 四边形 ………………9分 设点Q 坐标为(x ,y ), 由题意得:y y OB S OBQ 2321=⋅=三角形=23293131=⨯=ODBE S 四边形 ∴1±=y当y=1时,即1342=+-x x ,∴ 221+=x , 222-=x ,∴Q 点坐标为(2+2,1)或(2-2,1) …………11分 当y=-1时,即1342-=+-x x , ∴x=2, ∴Q 点坐标为(2,-1)综上所述,抛物线上存在三点Q 1(2+2,1),Q 2 (2-2,1) ,Q 3(2,-1) 使得OBQ S 三角形=ODBE S 四边形31. ………………12分EFQ 1 Q 3Q 25、(2010湖南常德)策略P78 T20如图9,已知抛物线212y x bx c x =++与轴交于点A (-4,0)和B (1,0)两点,与y 轴交于C 点. (1)求此抛物线的解析式;(2)设E 是线段AB 上的动点,作EF ∥AC 交BC 于F ,连接CE ,当CEF V 的面积是BEF V 面积的2倍时,求E 点的坐标;(3)若P 为抛物线上A 、C 两点间的一个动点,过P 作y 轴的平行线,交AC 于Q ,当P 点运动到什么位置时,线段PQ 的值最大,并求此时P 点的坐标.25.解:(1)由二次函数212y x bx c =++与x 轴交于(4,0)A -、(1,0)B 两点可得: 221(4)4021102b c b c ⎧--+=⎪⎪⎨⎪⋅++=⎪⎩,. 解得: 322b c ⎧=⎪⎨⎪=-⎩,.故所求二次函数的解析式为213222y x x =+-. ………………3分(2)∵S △CEF =2 S △BEF , ∴1,2BF CF =1.3BF BC = ………………4分 ∵EF //AC , ∴B ,EF BAC BFE BCA ∠=∠∠=∠ , ∴△BEF ~△BAC , ………………5分∴1,3BE BF BA BC ==得5,3BE = ………………6分 故E 点的坐标为(23-,0). ………………7分(3)解法一:由抛物线与y 轴的交点为C ,则C 点的坐标为(0,-2).若设直线AC 的解析式为y kx b =+,则有20,04b k b -=+⎧⎨=-+⎩. 解得:1,22k b ⎧=-⎪⎨⎪=-⎩.故直线AC 的解析式为122y x =--.………………8分图9 x若设P 点的坐标为213,222a a a ⎛⎫+- ⎪⎝⎭,又Q 点是过点P 所作y 轴的平行线与直线AC 的交点,则Q 点的坐标为(1,2)2a a --.则有:2131[(2)](2)222PQ a a a =-+----=2122a a --=()21222a -++即当2a =-时,线段PQ 取大值,此时P 点的坐标为(-2,-3)………10分解法二:延长PQ 交x 轴于D 点,则PD AB ⊥.要使线段PQ 最长,则只须△APC 的面积取大值时即可. ………………8分 设P 点坐标为(),00y x ,则有:ACO DPCO S APC ADP S S S =+-V V V 梯形=111()222AD PD PD OC OD OA OC ⋅++⋅-⋅=()()000001112242222x y y y x --+-+⋅--⨯⨯=0024y x ---=20001322422x x x ⎛⎫-+--- ⎪⎝⎭=2004xx -- =-()22024x ++即02x =-时,△APC 的面积取大值,此时线段PQ 最长,则P 点坐标 为(-2,-3) ……………10分。
二次函数综合(动点与三角形)问题一、知识准备:抛物线与直线形的结合表现形式之一是,以抛物线为载体,探讨是否存在一些点,使其能构成某些特殊三角形,有以下常见的基本形式。
(1)抛物线上的点能否构成等腰三角形;(2)抛物线上的点能否构成直角三角形;(3)抛物线上的点能否构成相似三角形;解决这类问题的基本思路:假设存在,数形结合,分类归纳,逐一考察。
二、例题精析㈠【抛物线上的点能否构成等腰三角形】例一.(2013•铜仁地区)如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c 经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).(1)求抛物线的解析式;(2)求△ABC的面积;(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.的坐标为(﹣得:解得:,OB=×时,解得:))时,,,,),﹣)㈡【抛物线上的点能否构成直角三角形】(2013鞍山)如图,已知一次函数y=0.5x+2的图象与x轴交于点A,与二次函数y=ax2+bx+c 例二.的图象交于y轴上的一点B,二次函数y=ax2+bx+c的图象与x轴只有唯一的交点C,且OC=2.(1)求二次函数y=ax2+bx+c的解析式;(2)设一次函数y=0.5x+2的图象与二次函数y=ax2+bx+c的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标.考点:二次函数综合题.分析:(1)根据y=0.5x+2交x轴于点A,与y轴交于点B,即可得出A,B两点坐标,二次函数y=ax2+bx+c的图象与x轴只有唯一的交点C,且OC=2.得出可设二次函数y=ax2+bx+c=a (x﹣2)2,进而求出即可;(2)根据当B为直角顶点,当D为直角顶点,以及当P为直角顶点时,分别利用三角形相似对应边成比例求出即可.解答:解:(1)∵y=0.5x+2交x轴于点A,∴0=0.5x+2,∴x=﹣4,与y轴交于点B,∵x=0,∴y=2∴B点坐标为:(0,2),∴A(﹣4,0),B(0,2),∵二次函数y=ax2+bx+c的图象与x轴只有唯一的交点C,且OC=2∴可设二次函数y=a(x﹣2)2,把B(0,2)代入得:a=0.5∴二次函数的解析式:y=0.5x2﹣2x+2;(2)(Ⅰ)当B为直角顶点时,过B作BP1⊥AD交x轴于P1点由Rt△AOB∽Rt△BOP1∴=,∴=,得:OP1=1,∴P1(1,0),(Ⅱ)作P2D⊥BD,连接BP2,将y=0.5x+2与y=0.5x2﹣2x+2联立求出两函数交点坐标:D点坐标为:(5,4.5),则AD=,当D为直角顶点时∵∠DAP2=∠BAO,∠BOA=∠ADP2,∴△ABO∽△AP2D,∴=,=,解得:AP2=11.25,则OP2=11.25﹣4=7.25,故P2点坐标为(7.25,0);(Ⅲ)当P为直角顶点时,过点D作DE⊥x轴于点E,设P3(a,0)则由Rt△OBP3∽Rt△EP3D得:,∴,∵方程无解,∴点P3不存在,∴点P的坐标为:P1(1,0)和P2(7.25,0).点评:此题主要考查了二次函数综合应用以及求函数与坐标轴交点和相似三角形的与性质等知识,根据已知进行分类讨论得出所有结果,注意不要漏解.㈢【抛物线上的点能否构成相似三角形】例三.(2013•恩施州)如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB 沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).(1)求直线BD和抛物线的解析式.(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.(﹣((×﹣三、形成训练1.(2013•湘西州)如图,已知抛物线y=﹣x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).(1)求抛物线的解析式及它的对称轴方程;(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;(3)试判断△AOC与△COB是否相似?并说明理由;(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若不存在,求出符合条件的Q点坐标;若不存在,请说明理由.x=)根据﹣∴﹣,x+x x+4=(,﹣+,即﹣+,,y=,=AQ====,==±﹣4+2 :已知:直线12y x =+与y 轴交于A ,与x 轴交于D ,抛物线22y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0).(1)求抛物线的解析式;(2)动点P 在x 轴上移动,当△P AE 是直角三角形时,求点P 的坐标.3、如图,抛物线21222y x x =-++与x 轴交于A B 、两点,与y 轴交于C 点.(1)求A B C 、、三点的坐标;(2)证明ABC △为直角三角形;(3)在抛物线上除C 点外,是否还存在另外一个点P ,使ABP △是直角三角形,若存在,请求出点P 的坐标,若不存在,请说明理由.4、如图,已知抛物线224233y x x =-++的图象与x 轴交于A ,B 两点,与y 轴交于点C ,抛物线的对称轴与x 轴交于点D . 点M 从O 点出发,以每秒1个单位长度的速度向B 运动,过M 作x 轴的垂线,交抛物线于点P ,交BC 于Q .(1)求点B 和点C 的坐标;(2)设当点M 运动了x (秒)时,四边形OBPC 的面积为S ,求S 与x 的函数关系式,并指出自变量x 的取值范围.(3)在线段BC 上是否存在点Q ,使得△DBQ成为以.BQ ..为一腰...的等腰三角形?若存在, 求出点Q 的坐标,若不存在,说明理由.5、(09年成都)在平面直角坐标系xOy 中,已知抛物线y=2(1)(0)a x c a ++>与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,其顶点为M,若直线MC 的函数表达式为3y kx =-,与x 轴的交点为N ,且COS ∠BCO =10。
成都市中考压轴题(二次函数)精选【例一】.如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,﹣2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.(1)求此抛物线的解析式;(2)求证:AO=AM;(3)探究:①当k=0时,直线y=kx与x轴重合,求出此时的值;②试说明无论k取何值,的值都等于同一个常数.考点:二次函数综合题.专题:代数几何综合题.分析:(1)把点C、D的坐标代入抛物线解析式求出a、c,即可得解;(2)根据抛物线解析式设出点A的坐标,然后求出AO、AM的长,即可得证;(3)①k=0时,求出AM、BN的长,然后代入+计算即可得解;②设点A(x1,x12﹣1),B(x2,x22﹣1),然后表示出+,再联立抛物线与直线解析式,消掉未知数y得到关于x的一元二次方程,利用根与系数的关系表示出x1+x2,x1•2,并求出x12+x22,x12•x22,然后代入进行计算即可得解.解答:(1)解:∵抛物线y=ax2+c(a≠0)经过C(2,0),D(0,﹣1),∴,解得,所以,抛物线的解析式为y=x2﹣1;(2)证明:设点A的坐标为(m,m2﹣1),则AO==m 2+1,∵直线l 过点E (0,﹣2)且平行于x 轴, ∴点M 的纵坐标为﹣2,∴AM=m 2﹣1﹣(﹣2)=m 2+1,∴AO=AM ;(3)解:①k=0时,直线y=kx 与x 轴重合,点A 、B 在x 轴上, ∴AM=BN=0﹣(﹣2)=2, ∴+=+=1;②k 取任何值时,设点A (x 1,x 12﹣1),B (x 2,x 22﹣1),则+=+==,联立,消掉y 得,x 2﹣4kx ﹣4=0,由根与系数的关系得,x 1+x 2=4k ,x 1•x 2=﹣4, 所以,x 12+x 22=(x 1+x 2)2﹣2x 1•x 2=16k 2+8, x 12•x 22=16, ∴+===1,∴无论k 取何值,+的值都等于同一个常数1.点评: 本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,勾股定理以及点到直线的距离,根与系数的关系,根据抛物线上点的坐标特征设出点A 、B 的坐标,然后用含有k 的式子表示出+是解题的关键,也是本题的难点,计算量较大,要认真仔细.【例二】. 如图,在平面直角坐标系xOy 中,△OAB 的顶点A的坐标为(10,0),顶点B 在第一象限内,且AB 5,sin ∠OAB=55. (1)若点C 是点B 关于x 轴的对称点,求经过O 、C 、A 三点的抛物线的函数表达式;(2)在(1)中,抛物线上是否存在一点P ,使以P 、O 、C 、A 为顶点的四边形为梯形?若存在,求出点P 的坐标;若不存在,请说明理由;(3)若将点O 、点A 分别变换为点Q ( -2k ,0)、点R (5k ,0)(k>1的常数),设过Q 、R 两点,且以QR 的垂直平分线为对称轴的抛物线与y 轴的交点为N ,其顶点为M ,记△QNM 的面积为QMN S ,△QNR的面积QNR S ∆,求QMN S ∆∶QNR S ∆的值.解:(1)如图,过点B 作BD OA ⊥于点D . 在Rt ABD △中,35AB =5sin OAB ∠=5sin 3535BD AB OAB ∴=∠==. 又由勾股定理, 得2222(35)36AD AB BD =-=-=.1064OD OA AD ∴=-=-=.点B 在第一象限内,∴点B 的坐标为(43),.∴点B 关于x 轴对称的点C 的坐标为(43)-,. ··················································· 2分 设经过(00)(43)(100)O C A -,,,,,三点的抛物线的函数表达式为2(0)y ax bx a =+≠.由11643810010054a ab a b b ⎧=⎪+=-⎧⎪⇒⎨⎨+=⎩⎪=-⎪⎩,.∴经过O C A ,,三点的抛物线的函数表达式为21584y x x =-. ····························· 2分 (2)假设在(1)中的抛物线上存在点P ,使以P O C A ,,,为顶点的四边形为梯形.①点(43)C -,不是抛物线21584y x =-的顶点, ∴过点C 作直线OA 的平行线与抛物线交于点1P .y F P 3BEC D A P 2P 1O则直线1CP 的函数表达式为3y =-. 对于21584y x x =-,令34y x =-⇒=或6x =. 1143x y =⎧∴⎨=-⎩,;2263x y =⎧⎨=-⎩,.而点(43)C -,,1(63)P ∴-,. 在四边形1P AOC 中,1CP OA ∥,显然1CP OA ≠.∴点1(63)P -,是符合要求的点. ······································································· 1分 ②若2AP CO ∥.设直线CO 的函数表达式为1y k x =. 将点(43)C -,代入,得143k =-.134k ∴=-. ∴直线CO 的函数表达式为34y x =-.于是可设直线2AP 的函数表达式为134y x b =-+. 将点(100)A ,代入,得131004b -⨯+=.1152b ∴=.∴直线2AP 的函数表达式为31542y x =-+.由223154246001584y x x x y x x ⎧=-+⎪⎪⇒--=⎨⎪=-⎪⎩,即(10)(6)0x x -+=. 11100x y =⎧∴⎨=⎩,;22612x y =-⎧⎨=⎩,;而点(100)A ,,2(612)P ∴-,. 过点2P 作2P E x ⊥轴于点E ,则212P E =. 在2Rt AP E △中,由勾股定理,得220AP ===.而5CO OB ==.∴在四边形2P OCA 中,2AP CO ∥,但2AP CO ≠.∴点2(612)P -,是符合要求的点. ······································································ 1分③若3OP CA ∥.设直线CA 的函数表达式为22y k x b =+.将点(100)(43)A C -,,,代入,得22222211002435k b k k b b ⎧+==⎧⎪⇒⎨⎨+=-⎩⎪=-⎩,.∴直线CA 的函数表达式为152y x =-. ∴直线3OP 的函数表达式为12y x =.由22121401584y x x x y x x ⎧=⎪⎪⇒-=⎨⎪=-⎪⎩,即(14)0x x -=. 1100x y =⎧∴⎨=⎩,;22147x y =⎧⎨=⎩,. 而点(00)O ,,3(147)P ∴,. 过点3P 作3P F x ⊥轴于点F ,则37P F =. 在3Rt OP F △中,由勾股定理,得3OP ===而CA AB ==∴在四边形3P OCA 中,3OP CA ∥,但3OP CA ≠.∴点3(147)P ,是符合要求的点. ········································································ 1分 综上可知,在(1)中的抛物线上存在点123(63)(612)(147)P P P --,,,,,, 使以P O C A ,,,为顶点的四边形为梯形. ······················································· 1分 (3)由题知,抛物线的开口可能向上,也可能向下.①当抛物线开口向上时,则此抛物线与y 轴的负半轴交于点N . 可设抛物线的函数表达式为(2)(5)(0)y a x k x k a =+->.即22310y ax akx ak =--2234924a x k ak ⎛⎫=-- ⎪⎝⎭.如图,过点M 作MG x ⊥轴于点G .3(20)(50)02Q k R k G k ⎛⎫- ⎪⎝⎭,,,,,,22349(010)24N ak M k ak ⎛⎫-- ⎪⎝⎭,,,,3||2||7||2QO k QR k OG k ∴===,,,22749||||10||24QG k ON ak MG ak ===,,.23117103522QNR S QR ON k ak ak ∴==⨯⨯=△.QNM QNO QMG ONMG S S S S =+-△△△梯形111()222QO ON ON GM OG QG GM =++- 2222114931749210102242224k ak ak ak k k ak ⎛⎫=⨯⨯+⨯+⨯-⨯⨯ ⎪⎝⎭ 3314949212015372884ak ak ⎛⎫=++⨯-⨯= ⎪⎝⎭. 3321::(35)3:204QNM QNR S S ak ak ⎛⎫∴== ⎪⎝⎭△△. ················································· 2分②当抛物线开口向下时,则此抛物线与y 轴的正半轴交于点N .同理,可得:3:20QNM QNR S S =△△. ································································· 1分 综上可知,:QNM QNR S S △△的值为3:20.【例三】、 如图,在平面直角坐标系xOy 中,一次函数54y x m =+ (m 为常数)的图象与x 轴交于点A(3-,0),与y 轴交于点C .以直线x=1为对称轴的抛物线2y ax bx c =++ (a b c ,, 为常数,且a ≠0)经过A ,C 两点,并与x 轴的正半轴交于点B . (1)求m 的值及抛物线的函数表达式;(2)设E 是y 轴右侧抛物线上一点,过点E 作直线AC 的平行线交x 轴于点F .是否存在这样的点E ,使得以A ,C ,E ,F 为顶点的四边形是平行四边形?若存在,求出点E 的坐标及相应的平行四边形的面积;若不存在,请说明理由;(3)若P 是抛物线对称轴上使△ACP 的周长取得最小值的点,过点P 任意作一条与y 轴不平行的直线交抛物线于111M ()x y , ,222M ()x y ,两点,试探究2112P PM M M M ⋅ 是否为定值,并写出探究过程.考点:二次函数综合题。
二次函数综合题分类解析二次函数是高中数学中常见的函数,它是一些常见的一元二次多项式的求导函数,在考试中也是比较重要的知识点。
关于二次函数的综合题也是比较多见的,这些题型中涉及到的知识点也是比较多,因此,了解二次函数综合题的分类以及解题方法是非常有必要的。
首先,让我们来看一下关于二次函数综合题的分类:一、求函数值这类题目主要涉及求二次函数的值,比如已知二次函数y=ax2+bx+c的参数a、b、c值,当x的值给定时,求二次函数的函数值y。
此类题的解题思路是:根据y=ax2+bx+c的表达式,把参数a、b、c和x的值带入到表达式中,即可求得y的值。
二、求函数图象这类题主要涉及求二次函数的图象,比如已知ax2+bx+c=0的参数a、b、c值,求这个二次函数的图象。
此类题的解题思路是:根据a、b、c的值可以先求得直线y=ax2+bx+c的方程,然后根据方程的极值或者零点可以求得二次函数的图象。
三、求函数的最大值、最小值这类题目主要涉及求二次函数的最大值或者最小值,比如已知ax2+bx+c=0的参数a、b、c值,求这个二次函数的最大值或者最小值。
此类题的解题思路是:根据二次函数y=ax2+bx+c的形式,求解出它的最大和最小值,即可求得最大值和最小值。
四、求函数的极值点这类题目主要涉及求二次函数的极值点,比如已知ax2+bx+c=0的参数a、b、c值,求这个二次函数的极大值点或者极小值点。
此类题的解题思路是:根据二次函数y=ax2+bx+c的形式,求出它的极值点,即可求得极值点。
五、求函数的零点此类题目主要涉及求二次函数的零点,比如已知ax2+bx+c=0的参数a、b、c值,求这个二次函数的零点。
此类题的解题思路是:根据二次函数y=ax2+bx+c的形式,采用二元一次方程组的求解方法,求出它的零点,即可求得零点。
六、求函数的对称轴这类题目主要涉及求二次函数的对称轴,即求出它的离散点集中所包含的点关于对称轴对称的概念。
例谈二次函数综合与学科核心素养培养二次函数是描述现实世界中变量之间关系的一种重要的数学模型,是学生学习其他高等函数的重要基础.同时二次函数在解决一些数学实际问题时,也是非常有力的工具。
对学生而言既能培养他们严谨的数学思维能力;也能提高他们的运算、分析问题、解决问题的核心素养. 下面就某地区中考最后一道二次函数综合题与大家谈谈二次函数与核心素养的问题.一、试题呈现抛物线y=-x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足E,连接BD.(1)求抛物线的解析式及D的坐标;(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P 在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q 的坐标.二、解题分析1.解题思路分析(1)由B,C的坐标,利用待定系数法可求得抛物线解析式,再求其顶点D 的坐标即可;(2)过F作FG⊥x轴于点G,可设出F点坐标,利用△FBG∽△BDE,由相似三角形的性质可得到关于F点坐标的方程,可求得F点的坐标;(3)由于M,N两点关于对称轴对称,可知点P为对称轴与x轴的交点,点Q在对称轴上,可设出Q点的坐标,则可表示出M的坐标,代入抛物线解析式可求得点Q的坐标.2.解题过程展示(1)把B,C两点坐标代入抛物线解析式,可得-18+6b+6=0,解得b=2.∴抛物线解析式为y=-x2+2x+6.∵y=-x2+2x+6=-(x-2)2+8,∴点D的坐标为(2,8) .(2)过点F作FG⊥x轴于点G.∵点F在抛物线上,∴设点F的坐标为(x,-x2+2x+6).则FG=∣-x2+2x+6∣.∵∠FBA=∠BDE,∠FGB=∠BED=90°,∴△FGB∽△BED=90°. ∴= .∵点B(6,0),点D(2,8),∴点E(2,0).∴BE=4,DE=8,OB=6,∴BG=6-x.∴= .当点F在x轴上方时,有= .解得,x=-1或x=6(舍去),此时点F的坐标为(-1,).当点F在x轴下方时,有=- .解得,x=-3或x=6(舍去),此时点F的坐标为(-3,-).(3)如图,设MN与PQ交于点O′.∵点M,N关于抛物线的对称轴对称,且四边形MPNQ为正方形,∴点P为抛物线的对称轴与x轴的交点,且点Q在抛物线的对称轴上.设点Q的坐标为(2,n)则点M的坐标可表示为(2-n,n).∵点M在抛物线y=-x2+2x+6上,∴n=-(2-n)2+2(2-n)+6.解得n=-1+或n=-1-.∴点Q的坐标为(2,-1+)或(2,-1-).三、试题特点本题为二次函数与几何图形的综合应用。
二次函数综合题例析一、二次函数综合题的解题方法二次函数综合题是一类解题项目,按照问题和求解条件的不同可以分为求函数值、求函数的图像、解二次方程和分析图像等几类。
1、求函数值。
求二次函数值时,要先确定函数的系数,再求函数的值。
常用的方法有识别法和计算法,前者把函数参数代入识别函数解出,后者将函数参数代入函数求解出。
2、求函数图像。
要求解函数图像,首先要确定二次函数方程式,然后将该函数方程式求解得出二次函数的几何图像,有的时候还要将图像改写成可计算的方形式,方便计算此函数的最大值、最小值等内容。
3、解二次方程。
解决二次方程要先进行因式分解,然后再项聚合,最后对称求根。
另外,对于一般二次方程还可以应用完全平方式求解,完全平方式是把传统的常规运算稍加改变,由于其因式分解之后系数都被除去,因此求解起来较为简单,容易计算。
4、分析图像。
分析二次函数的图像可以先求出抛物线的轴对称性,再找出图像的上下凸点,最后得出图像的外观特点及其大致的函数表达式。
二、二次函数综合题的应用一般而言,二次函数综合题都有一定的实际应用,可以用于求解图形性质、经济学问题、地理学和政治学问题等等,以下是一些典型的应用例子:1、经济学问题。
经济学中的二次函数综合题可以用来求解企业经营过程中的成本函数,帮助经营者进行最优化控制,并可以将函数用于分析企业的竞争力,根据函数的几何图形,企业可以清楚自己的优势企业和优势市场。
2、地理学问题。
二次函数综合题可以用来计算地理信息系统中各种物体之间的距离,以便更好地了解地球上各地之间的关系并使其在适当的地理环境中进行有效的安排和管理。
3、政治学问题。
政治学领域中的二次函数。
二次函数中常见的几类综合题型一求线段最大值及根据面积求点坐标问题1.如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).(1)求直线BC与抛物线的解析式;(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标.分析:(1)设直线BC的解析式为y=mx+n,将B(5,0),C(0,5)两点的坐标代入,运用待定系数法即可求出直线BC的解析式;同理,将B(5,0),C(0,5)两点∑的坐标代入y=x2+bx+c,运用待定系数法即可求出抛物线的解析式;(2)MN的长是直线BC的函数值与抛物线的函数值的差,据此可得出一个关于MN的长和M点横坐标的函数关系式,根据函数的性质即可求出MN的最大值;(3)先求出△ABN的面积S2=5,则S1=6S2=30.再设平行四边形CBPQ的边BC上的高为BD,根据平行四边形的面积公式得出BD=3,过点D作直线BC的平行线,交抛物线与点P,交x轴于点E,在直线DE上截取PQ=BC,则四边形CBPQ为平行四边形.证明△EBD为等腰直角三角形,则BE=BD=6,求出E的坐标为(﹣1,0),运用待定系数法求出直线PQ的解析式为y=﹣x﹣1,然后解方程组,即可求出点P的坐标.解答:解:(1)设直线BC的解析式为y=mx+n,将B(5,0),C(0,5)两点的坐标代入,得,解得,所以直线BC的解析式为y=﹣x+5;将B(5,0),C(0,5)两点的坐标代入y=x2+bx+c,得,解得,所以抛物线的解析式为y=x2﹣6x+5;(2)设M(x,x2﹣6x+5)(1<x<5),则N(x,﹣x+5),∵MN=(﹣x+5)﹣(x2﹣6x+5)=﹣x2+5x=﹣(x﹣)2+,∴当x=时,MN有最大值;(3)∵MN取得最大值时,x=2.5,∴﹣x+5=﹣2.5+5=2.5,即N(2.5,2.5).解方程x2﹣6x+5=0,得x=1或5,∴A(1,0),B(5,0),∴AB=5﹣1=4,∴△ABN的面积S2=×4×2.5=5,∴平行四边形CBPQ的面积S1=6S2=30.设平行四边形CBPQ的边BC上的高为BD,则BC⊥BD.∵BC=5,∴BC•BD=30,∴BD=3.过点D作直线BC的平行线,交抛物线与点P,交x轴于点E,在直线DE上截取PQ=BC,则四边形CBPQ为平行四边形.∵BC⊥BD,∠OBC=45°,∴∠EBD=45°,∴△EBD为等腰直角三角形,BE=BD=6,∵B(5,0),∴E(﹣1,0),设直线PQ的解析式为y=﹣x+t,将E(﹣1,0)代入,得1+t=0,解得t=﹣1∴直线PQ的解析式为y=﹣x﹣1.解方程组,得,,∴点P的坐标为P1(2,﹣3)(与点D重合)或P2(3,﹣4).2.如图,对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).(1)求点B的坐标;(2)已知a=1,C为抛物线与y轴的交点.①若点P在抛物线上,且S△POC=4S△BOC.求点P的坐标;②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值分析:(1)由抛物线y=ax2+bx+c的对称轴为直线x=﹣1,交x轴于A、B两点,其中A点的坐标为(﹣3,0),根据二次函数的对称性,即可求得B点的坐标;(2)①a=1时,先由对称轴为直线x=﹣1,求出b的值,再将B(1,0)代入,求出二次函数的解析式为y=x2+2x﹣3,得到C点坐标,然后设P点坐标为(x,x2+2x﹣3),根据S△POC=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;②先运用待定系数法求出直线AC的解析式为y=﹣x﹣3,再设Q点坐标为(x,﹣x﹣3),则D点坐标为(x,x2+2x﹣3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.解答:解:(1)∵对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,∴A、B两点关于直线x=﹣1对称,∵点A的坐标为(﹣3,0),∴点B的坐标为(1,0);(2)①a=1时,∵抛物线y=x2+bx+c的对称轴为直线x=﹣1,∴=﹣1,解得b=2.将B(1,0)代入y=x2+2x+c,得1+2+c=0,解得c=﹣3.则二次函数的解析式为y=x2+2x﹣3,∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.设P点坐标为(x,x2+2x﹣3),∵S△POC=4S△BOC,∴×3×|x|=4××3×1,∴|x|=4,x=±4.当x=4时,x2+2x﹣3=16+8﹣3=21;当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.所以点P的坐标为(4,21)或(﹣4,5);②设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,﹣3)代入,得,解得,即直线AC的解析式为y=﹣x﹣3.设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D点坐标为(x,x2+2x﹣3),QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣(x+)2+,∴当x=﹣时,QD有最大值.二求三角形周长及面积的最值问题3.如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.(1)求该抛物线的解析式;(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y 轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.①求S与m的函数关系式;②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.分析:(1)根据函数图象经过的三点,用待定系数法确定二次函数的解析式即可;(2)根据BC是定值,得到当PB+PC最小时,△PBC的周长最小,根据点的坐标求得相应线段的长即可;(3)设点E的横坐标为m,表示出E(m,2m+6),F(m,﹣m2﹣2m+3),最后表示出EF的长,从而表示出S于m的函数关系,然后求二次函数的最值即可.解答:解:(1)由题意可知:解得:∴抛物线的解析式为:y=﹣x2﹣2x+3;(2)∵△PBC的周长为:PB+PC+BC∵BC是定值,∴当PB+PC最小时,△PBC的周长最小,∵点A、点B关于对称轴I对称,∴连接AC交l于点P,即点P为所求的点∵AP=BP∴△PBC的周长最小是:PB+PC+BC=AC+BC∵A(﹣3,0),B(1,0),C(0,3),∴AC=3,BC=;故△PBC周长的最小值为3+.(3)①∵抛物线y=﹣x2﹣2x+3顶点D的坐标为(﹣1,4)∵A(﹣3,0)∴直线AD的解析式为y=2x+6∵点E的横坐标为m,∴E(m,2m+6),F(m,﹣m2﹣2m+3)∴EF=﹣m2﹣2m+3﹣(2m+6)=﹣m2﹣4m﹣3∴S=S△DEF+S△AEF=EF•GH+EF•AG=EF•AH=(﹣m2﹣4m﹣3)×2=﹣m2﹣4m﹣3;②S=﹣m2﹣4m﹣3=﹣(m+2)2+1;∴当m=﹣2时,S最大,最大值为1此时点E的坐标为(﹣2,2).4. 如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).(1)求抛物线的解析式;(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.分析:(1)利用待定系数法求二次函数解析式解答即可;(2)利用待定系数法求出直线AC的解析式,然后根据轴对称确定最短路线问题,直线AC与对称轴的交点即为所求点D;(3)根据直线AC的解析式,设出过点E与AC平行的直线,然后与抛物线解析式联立消掉y得到关于x 的一元二次方程,利用根的判别式△=0时,△ACE的面积最大,然后求出此时与AC平行的直线,然后求出点E的坐标,并求出该直线与x轴的交点F的坐标,再求出AF,再根据直线l与x轴的夹角为45°求出两直线间的距离,再求出AC间的距离,然后利用三角形的面积公式列式计算即可得解.解答:解:(1)∵抛物线y=ax2+bx+3经过点A(1,0),点C(4,3),∴,解得,所以,抛物线的解析式为y=x2﹣4x+3;(2)∵点A、B关于对称轴对称,∴点D为AC与对称轴的交点时△BCD的周长最小,设直线AC的解析式为y=kx+b(k≠0),则,解得,所以,直线AC的解析式为y=x﹣1,∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的对称轴为直线x=2,当x=2时,y=2﹣1=1,∴抛物线对称轴上存在点D(2,1),使△BCD的周长最小;(3)如图,设过点E与直线AC平行线的直线为y=x+m,联立,消掉y得,x2﹣5x+3﹣m=0,△=(﹣5)2﹣4×1×(3﹣m)=0,即m=﹣时,点E到AC的距离最大,△ACE的面积最大,此时x=,y=﹣=﹣,∴点E的坐标为(,﹣),设过点E的直线与x轴交点为F,则F(,0),∴AF=﹣1=,∵直线AC的解析式为y=x﹣1,∴∠CAB=45°,∴点F到AC的距离为×=,又∵AC==3,∴△ACE的最大面积=×3×=,此时E点坐标为(,﹣).三为等腰或直角三角形是求点坐标问题5.如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).(1)求抛物线的解析式;(2)求△ABC的面积;(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.分析:(1)根据直线解析式求出点A及点B的坐标,然后将点A及点B的坐标代入抛物线解析式,可得出b、c的值,求出抛物线解析式;(2)由(1)求得的抛物线解析式,可求出点C的坐标,继而求出AC的长度,代入三角形的面积公式即可计算;(3)根据点M在抛物线对称轴上,可设点M的坐标为(﹣1,m),分三种情况讨论,①MA=BA,②MB=BA,③MB=MA,求出m的值后即可得出答案.解答:解:(1)∵直线y=3x﹣3分别交x轴、y轴于A、B两点,∴可得A(1,0),B(0,﹣3),把A、B两点的坐标分别代入y=x2+bx+c得:,解得:.∴抛物线解析式为:y=x2+2x﹣3.(2)令y=0得:0=x2+2x﹣3,解得:x1=1,x2=﹣3,则C点坐标为:(﹣3,0),AC=4,故可得S△ABC=AC×OB=×4×3=6.(3)抛物线的对称轴为:x=﹣1,假设存在M(﹣1,m)满足题意:讨论:①当MA=AB时,,解得:,∴M1(﹣1,),M2(﹣1,﹣);②当MB=BA时,,解得:M3=0,M4=﹣6,∴M3(﹣1,0),M4(﹣1,﹣6)(不合题意舍去),③当MB=MA时,,解得:m=﹣1,∴M5(﹣1,﹣1),答:共存在4个点M1(﹣1,),M2(﹣1,﹣),M3(﹣1,0),M4(﹣1,﹣1)使△ABM为等腰三角形.6.如图,抛物线y=x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0)(1)求该抛物线的解析式.(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.分析:(1)利用待定系数法求出抛物线的解析式;(2)首先求出△PCE面积的表达式,然后利用二次函数的性质求出其最大值;(3)△OMD为等腰三角形,可能有三种情形,需要分类讨论.解答:解:(1)把点C(0,﹣4),B(2,0)分别代入y=x2+bx+c中,得,解得∴该抛物线的解析式为y=x2+x﹣4.(2)令y=0,即x2+x﹣4=0,解得x1=﹣4,x2=2,∴A(﹣4,0),S△ABC=AB•OC=12.设P点坐标为(x,0),则PB=2﹣x.∵PE∥AC,∴∠BPE=∠BAC,∠BEP=∠BCA,∴△PBE∽△ABC,∴,即,化简得:S△PBE=(2﹣x)2.S△PCE=S△PCB﹣S△PBE=PB•OC﹣S△PBE=×(2﹣x)×4﹣(2﹣x)2=x2﹣x+=(x+1)2+3∴当x=﹣1时,S△PCE的最大值为3.(3)△OMD为等腰三角形,可能有三种情形:(I)当DM=DO时,如答图①所示.DO=DM=DA=2,∴∠OAC=∠AMD=45°,∴∠ADM=90°,∴M点的坐标为(﹣2,﹣2);(II)当MD=MO时,如答图②所示.过点M作MN⊥OD于点N,则点N为OD的中点,∴DN=ON=1,AN=AD+DN=3,又△AMN为等腰直角三角形,∴MN=AN=3,∴M点的坐标为(﹣1,﹣3);(III)当OD=OM时,∵△OAC为等腰直角三角形,∴点O到AC的距离为×4=,即AC上的点与点O之间的最小距离为.∵>2,∴OD=OM的情况不存在.综上所述,点M的坐标为(﹣2,﹣2)或(﹣1,﹣3).7.如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).(1)求抛物线的解析式;(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.分析:(1)已知抛物线上的三点坐标,利用待定系数法可求出该二次函数的解析式;(2)过点P作x轴的垂线,交AC于点N,先运用待定系数法求出直线AC的解析式,设P点坐标为(x,x2+2x﹣3),根据AC的解析式表示出点N的坐标,再根据S△PAC=S△PAN+S△PCN就可以表示出△PAC的面积,运用顶点式就可以求出结论;(3)分三种情况进行讨论:①以A为直角顶点;②以D为直角顶点;③以M为直角顶点;设点M的坐标为(0,t),根据勾股定理列出方程,求出t的值即可.解答:解:(1)由于抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),可设抛物线的解析式为:y=a(x+3)(x﹣1),将C点坐标(0,﹣3)代入,得:a(0+3)(0﹣1)=﹣3,解得 a=1,则y=(x+3)(x﹣1)=x2+2x﹣3,所以抛物线的解析式为:y=x2+2x﹣3;(2)过点P作x轴的垂线,交AC于点N.设直线AC的解析式为y=kx+m,由题意,得,解得,∴直线AC的解析式为:y=﹣x﹣3.设P点坐标为(x,x2+2x﹣3),则点N的坐标为(x,﹣x﹣3),∴PN=PE﹣NE=﹣(x2+2x﹣3)+(﹣x﹣3)=﹣x2﹣3x.∵S△PAC=S△PAN+S△PCN,∴S=PN•OA=×3(﹣x2﹣3x)=﹣(x+)2+,∴当x=﹣时,S有最大值,此时点P的坐标为(﹣,﹣);(3)在y轴上是存在点M,能够使得△ADM是直角三角形.理由如下:∵y=x2+2x﹣3=y=(x+1)2﹣4,∴顶点D的坐标为(﹣1,﹣4),∵A(﹣3,0),∴AD2=(﹣1+3)2+(﹣4﹣0)2=20.设点M的坐标为(0,t),分三种情况进行讨论:①当A为直角顶点时,如图3①,由勾股定理,得AM2+AD2=DM2,即(0+3)2+(t﹣0)2+20=(0+1)2+(t+4)2,解得t=,所以点M的坐标为(0,);②当D为直角顶点时,如图3②,由勾股定理,得DM2+AD2=AM2,即(0+1)2+(t+4)2+20=(0+3)2+(t﹣0)2,解得t=﹣,所以点M的坐标为(0,﹣);③当M为直角顶点时,如图3③,由勾股定理,得AM2+DM2=AD2,即(0+3)2+(t﹣0)2+(0+1)2+(t+4)2=20,解得t=﹣1或﹣3,所以点M的坐标为(0,﹣1)或(0,﹣3);综上可知,在y轴上存在点M,能够使得△ADM是直角三角形,此时点M的坐标为(0,)或(0,﹣)或(0,﹣ 1)或(0,﹣3).四四边形与二次函数问题8、如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点.(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.分析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(﹣1,0),B(5,0),C(0,)三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点A的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.解答:解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),∵A(﹣1,0),B(5,0),C(0,)三点在抛物线上,∴,解得.∴抛物线的解析式为:y=x2﹣2x﹣;(2)∵抛物线的解析式为:y=x2﹣2x﹣,∴其对称轴为直线x=﹣=﹣=2,连接BC,如图1所示,∵B(5,0),C(0,﹣),∴设直线BC的解析式为y=kx+b(k≠0),∴,解得,∴直线BC的解析式为y=x﹣,当x=2时,y=1﹣=﹣,∴P(2,﹣);(3)存在.如图2所示,①当点N在x轴下方时,∵抛物线的对称轴为直线x=2,C(0,﹣),∴N1(4,﹣);②当点N在x轴上方时,如图,过点N2作ND⊥x轴于点D,在△AN2D与△M2CO中,∴△AN2D≌△M2CO(ASA),∴N2D=OC=,即N2点的纵坐标为.∴x2﹣2x﹣=,解得x=2+或x=2﹣,∴N2(2+,),N3(2﹣,).综上所述,符合条件的点N的坐标为(4,﹣),(2+,)或(2﹣,).9.如图,抛物线y=x2+bx+c与x轴交于点A(2,0),交y轴于点B(0,).直线y=kx过点A与y轴交于点C,与抛物线的另一个交点是D.(1)求抛物线y=x2+bx+c与直线y=kx的解析式;(2)设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作 y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为l,点P的横坐标为x,求l与x的函数关系式,并求出l的最大值.分析:(1)将A,B两点分别代入y=x2+bx+c进而求出解析式即可;(2)首先假设出P,M点的坐标,进而得出PM的长,将两函数联立得出D点坐标,进而得出CE的长,利用平行四边形的性质得出PM=CE,得出等式方程求出即可;(3)利用勾股定理得出DC的长,进而根据△PMN∽△CDE,得出两三角形周长之比,求出l与x的函数关系,再利用配方法求出二次函数最值即可.解答:解:(1)∵y=x2+bx+c经过点A(2,0)和B(0,)∴由此得,解得.∴抛物线的解析式是y=x2﹣x+,∵直线y=kx﹣经过点A(2,0)∴2k﹣=0,解得:k=,∴直线的解析式是 y=x﹣,(2)设P的坐标是(x,x2﹣x+),则M的坐标是(x,x﹣)∴PM=(x2﹣x+)﹣(x﹣)=﹣x2﹣x+4,解方程得:,,∵点D在第三象限,则点D的坐标是(﹣8,﹣7),由y=x﹣得点C的坐标是(0,﹣),∴CE=﹣﹣(﹣7)=6,由于PM∥y轴,要使四边形PMEC是平行四边形,必有PM=CE,即﹣x2﹣x+4=6解这个方程得:x1=﹣2,x2=﹣4,符合﹣8<x<2,当x=﹣2时,y=﹣×(﹣2)2﹣×(﹣2)+=3,当x=﹣4时,y=﹣×(﹣4)2﹣×(﹣4)+=,因此,直线AD上方的抛物线上存在这样的点P,使四边形PMEC是平行四边形,点P的坐标是(﹣2,3)和(﹣4,);(3)在Rt△CDE中,DE=8,CE=6 由勾股定理得:DC=∴△CDE的周长是24,∵PM∥y轴,∵∠PMN=∠DCE,∵∠PNM=∠DEC,∴△PMN∽△CDE,∴=,即=,化简整理得:l与x的函数关系式是:l=﹣x2﹣x+,l=﹣x2﹣x+=﹣(x+3)2+15,∵﹣<0,∴l有最大值,当x=﹣3时,l的最大值是15.10.如图,抛物线经过A(﹣1,0),B(5,0),C(0,)三点.(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.分析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(﹣1,0),B(5,0),C(0,)三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点A的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.解答:解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),∵A(﹣1,0),B(5,0),C(0,)三点在抛物线上,∴,解得.∴抛物线的解析式为:y=x2﹣2x﹣;(2)∵抛物线的解析式为:y=x2﹣2x﹣,∴其对称轴为直线x=﹣=﹣=2,连接BC,如图1所示,∵B(5,0),C(0,﹣),∴设直线BC的解析式为y=kx+b(k≠0),∴,解得,∴直线BC的解析式为y=x﹣,当x=2时,y=1﹣=﹣,∴P(2,﹣);(3)存在.如图2所示,①当点N在x轴下方时,∵抛物线的对称轴为直线x=2,C(0,﹣),∴N1(4,﹣);②当点N在x轴上方时,如图,过点N2作ND⊥x轴于点D,在△AN2D与△M2CO中,∴△AN2D≌△M2CO(ASA),∴N2D=OC=,即N2点的纵坐标为.∴x2﹣2x﹣=,解得x=2+或x=2﹣,∴N2(2+,),N3(2﹣,).综上所述,符合条件的点N的坐标为(4,﹣),(2+,)或(2﹣,).。
二次函数综合问题例谈二次函数是中学代数的基本内容之一,它既简单又具有丰富的内涵和外延. 作为最基本的初等函数,可以以它为素材来研究函数的单调性、奇偶性、最值等性质,还可建立起函数、方程、不等式之间的有机联系;作为抛物线,可以联系其它平面曲线讨论相互之间关系. 这些纵横联系,使得围绕二次函数可以编制出层出不穷、灵活多变的数学问题. 同时,有关二次函数的内容又与近、现代数学发展紧密联系,是学生进入高校继续深造的重要知识基础. 因此,从这个意义上说,有关二次函数的问题在高考中频繁出现,也就不足为奇了. 学习二次函数,可以从两个方面入手:一是解析式,二是图像特征. 从解析式出发,可以进行纯粹的代数推理,这种代数推理、论证的能力反映出一个人的基本数学素养;从图像特征出发,可以实现数与形的自然结合,这正是中学数学中一种非常重要的思想方法. 本文将从这两个方面研究涉及二次函数的一些综合问题.1.代数推理由于二次函数的解析式简捷明了,易于变形(一般式、顶点式、零点式等),所以,在解决二次函数的问题时,常常借助其解析式,通过纯代数推理,进而导出二次函数的有关性质.1.1 二次函数的一般式c bx ax y ++=2)0(≠c 中有三个参数c b a ,,. 解题的关键在于:通过三个独立条件“确定”这三个参数.例1 已知f x ax bx ()=+2,满足1≤-≤f ()12且214≤≤f (),求f ()-2的取值范围. 分析:本题中,所给条件并不足以确定参数b a ,的值,但应该注意到:所要求的结论不是()2-f 的确定值,而是与条件相对应的“取值范围”,因此,我们可以把1≤-≤f ()12和4)1(2≤≤f 当成两个独立条件,先用()1-f 和()1f 来表示b a ,.解:由()b a f +=1,()b a f -=-1可解得:))1()1((21)),1()1((21--=-+=f f b f f a (*) 将以上二式代入f x ax bx ()=+2,并整理得()()⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛+=2)1(2122x x f x x f x f ,∴ ()()()1312-+=f f f .又∵214≤≤f (),2)1(1≤-≤f ,∴ ()1025≤≤f .例2 设()()f x ax bx c a =++≠20,若()f 01≤,()f 11≤,()f -11≤, 试证明:对于任意-≤≤11x ,有()f x ≤54. 分析:同上题,可以用()()()1,1,0-f f f 来表示c b a ,,.解:∵ ()()()c f c b a f c b a f =++=+-=-0,1,1,∴ ()()()()0)),1()1((21),0211(21f c f f b f f f a =--=--+=, ∴ ()()()()()222102121x f x x f x x f x f -+⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛+=. ∴ 当01≤≤-x 时,()()()().4545)21(1)1(2212210212122222222222≤++-=+--=-+⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛+-=-+-++≤-⋅+-⋅-++⋅≤x x x x x x x x x x x x x x f x x f x x f x f当10-≤≤x 时, ()()()()222102121x f x x f x x f x f -⋅+-⋅-++⋅≤ 222122x x x x x -+-++≤ )1(22222x x x x x -+⎪⎪⎭⎫ ⎝⎛+-+⎪⎪⎭⎫ ⎝⎛+= .4545)21(122≤+--=++-=x x x 综上,问题获证.1.2 利用函数与方程根的关系,写出二次函数的零点式()().21x x x x a y --=例3 设二次函数()()f x ax bx c a =++>20,方程()f x x -=0的两个根x x 12,满足0112<<<x x a . 当()x x ∈01,时,证明()x f x x <<1.分析:在已知方程()f x x -=0两根的情况下,根据函数与方程根的关系,可以写出函数()x x f -的表达式,从而得到函数)(x f 的表达式.证明:由题意可知))(()(21x x x x a x x f --=-.a x x x 1021<<<< , ∴ 0))((21>--x x x x a ,∴ 当()x x ∈01,时,x x f >)(.又)1)(())(()(211211+--=-+--=-ax ax x x x x x x x x a x x f ,,011,0221>->+-<-ax ax ax x x 且∴ 1)(x x f <,综上可知,所给问题获证. 1.3紧扣二次函数的顶点式,44222a b ac a b x a y -+⎪⎭⎫ ⎝⎛+=对称轴、最值、判别式显合力 例4 已知函数x z a x f 22)(-=。
(1)将)(x f y =的图象向右平移两个单位,得到函数)(x g y =,求函数)(x g y =的解析式;(2)函数)(x h y =与函数)(x g y =的图象关于直线1=y 对称,求函数)(x h y =的解析式;(3)设)()(1)(x h x f a x F +=,已知)(x F 的最小值是m 且72+>m ,求实数a 的取值范围。
解:(1)()();22222---=-=x x ax f x g(2)设()x h y =的图像上一点()y x P ,,点()y x P ,关于1=y 的对称点为()y x Q -2,,由点Q 在()x g y =的图像上,所以 y ax x -=---22222, 于是 ,22222--+-=x x a y 即 ();22222--+-=x x a x h(3)22)14(2411)()(1)(+-+⎪⎭⎫ ⎝⎛-=+=x x a a x h x f a x F . 设x t 2=,则21444)(+-+-=ta t a a x F . 问题转化为:7221444+>+-+-ta t a a 对0>t 恒成立. 即 ()0147442>-+--a t t aa 对0>t 恒成立. (*) 故必有044>-a a .(否则,若044<-aa ,则关于t 的二次函数()14744)(2-+--=a t t a a t u 开口向下,当t 充分大时,必有()0<t u ;而当044=-aa 时,显然不能保证(*)成立.),此时,由于二次函数()14744)(2-+--=a t t a a t u 的对称轴0847>-=a a t ,所以,问题等价于0<∆t ,即()⎪⎪⎩⎪⎪⎨⎧<-⋅-⋅->-0144447044a a a a a , 解之得:221<<a . 此时,014,044>->-a a a ,故21444)(+-+-=t a t a a x F 在aa a t --=4)14(4取得最小值()214442+-⋅-=a aa m 满足条件. 2. 数形结合二次函数()0)(2≠++=a c bx ax x f 的图像为抛物线,具有许多优美的性质,如对称性、单调性、凹凸性等. 结合这些图像特征解决有关二次函数的问题,可以化难为易.,形象直观.2.1 二次函数的图像关于直线a b x 2-=对称, 特别关系ab x x -=+21也反映了二次函数的一种对称性.例 5 设二次函数()()f x ax bx c a =++>20,方程()f x x -=0的两个根x x 12,满足0112<<<x x a . 且函数()f x 的图像关于直线x x =0对称,证明:x x 012<. 解:由题意 ()c x b ax x x f +-+=-)1(2.由方程()f x x -=0的两个根x x 12,满足0112<<<x x a, 可得 ,121021a x a b x <<--<<且ab x x a b 212121---=---, ∴ a b a a b x x a b 211212121---<---=---, 即 1x ab <-,故 x x 012<. 2.2 二次函数)(x f 的图像具有连续性,且由于二次方程至多有两个实数根. 所以存在实数n m ,使得n m <且0)()(<n f m f ⇔在区间()n m ,上,必存在0)(=x f 的唯一的实数根. 例6 已知二次函数)0,,(1)(2>∈++=a R b a bx ax x f ,设方程x x f =)(的两个实数根为1x 和2x .(1)如果4221<<<x x ,设函数)(x f 的对称轴为0x x =,求证:10->x ;(2)如果21<x ,212=-x x ,求b 的取值范围.分析:条件4221<<<x x 实际上给出了x x f =)(的两个实数根所在的区间,因此可以考虑利用上述图像特征去等价转化.解:设1)1()()(2+-+=-=x b ax x x f x g ,则0)(=x g 的二根为1x 和2x . (1)由0>a 及4221<<<x x ,可得 ⎩⎨⎧><0)4(0)2(g g ,即⎩⎨⎧>-+<-+034160124b a b a ,即 ⎪⎪⎩⎪⎪⎨⎧<+⋅--<-⋅+,043224,043233a a b a a b 两式相加得12<ab ,所以,10->x ; (2)由aa b x x 4)1()(2221--=-, 可得 1)1(122+-=+b a . 又0121>=a x x ,所以21,x x 同号. ∴ 21<x ,212=-x x 等价于⎪⎩⎪⎨⎧+-=+<<<1)1(1220221b a x x 或⎪⎩⎪⎨⎧+-=+<<-<1)1(1202212b a x x ,即 ⎪⎪⎩⎪⎪⎨⎧+-=+>>1)1(120)0(0)2(2b a g g 或⎪⎪⎩⎪⎪⎨⎧+-=+>>-1)1(120)0(0)2(2b a g g解之得 41<b 或47>b . 2.3 因为二次函数()0)(2≠++=a c bx ax x f 在区间]2,(a b --∞和区间),2[+∞-ab 上分别单调,所以函数()x f 在闭区间上的最大值、最小值必在区间端点或顶点处取得;函数)(x f 在闭区间上的最大值必在区间端点或顶点处取得.例7 已知二次函数f x ax bx c ()=++2,当-≤≤11x 时,有-≤≤11f x (),求证:当-≤≤22x 时,有-≤≤77f x ().分析:研究)(x f 的性质,最好能够得出其解析式,从这个意义上说,应该尽量用已知条件来表达参数c b a ,,. 确定三个参数,只需三个独立条件,本题可以考虑)1(f ,)1(-f ,)0(f ,这样做的好处有两个:一是c b a ,,的表达较为简洁,二是由于01和±正好是所给条件的区间端点和中点,这样做能够较好地利用条件来达到控制二次函数范围的目的.要考虑()x f 在区间[]7,7-上函数值的取值范围,只需考虑其最大值,也即考虑()x f 在区间端点和顶点处的函数值.解:由题意知:c b a f c f c b a f ++==+-=-)1(,)0(,)1(,∴ )0()),1()1((21)),0(2)1()1((21f c f f b f f f a =--=--+=, ∴ f x ax bx c ()=++2()2221)0(2)1(2)1(x f x x f x x f -+⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛+=. 由-≤≤11x 时,有-≤≤11f x (),可得 ,1)1(≤f (),11≤-f ()10≤f . ∴ ()()()()7)0(3)1(1303113)2(≤+-+≤--+=f f f f f f f ,()()()()7)0(3)1(3103131)2(≤+-+≤--+=-f f f f f f f .(1)若[]2,22-∉-ab ,则()x f 在[]2,2-上单调,故当[]2,2-∈x 时, ))2(,)2(max()(max f f x f -=∴ 此时问题获证.(2)若[]2,22-∈-a b ,则当[]2,2-∈x 时,)2,)2(,)2(max()(max ⎪⎭⎫ ⎝⎛--=a b f f f x f 又()72411214)1()1(2022422<=+⋅+≤--⋅+=⋅+≤-=⎪⎭⎫ ⎝⎛-f f ab f b a bc a b c a b f , ∴ 此时问题获证.综上可知:当-≤≤22x 时,有-≤≤77f x ().。