抛物线中的直角三角形存在性问题一对一教案

直角三角形的存在性问题（教案）学习目标：1、经历探索直角三角形存在性问题的过程，熟练掌握解题技巧。

2、体会分类讨论的数学思想，体验解决问题方法的多样性。

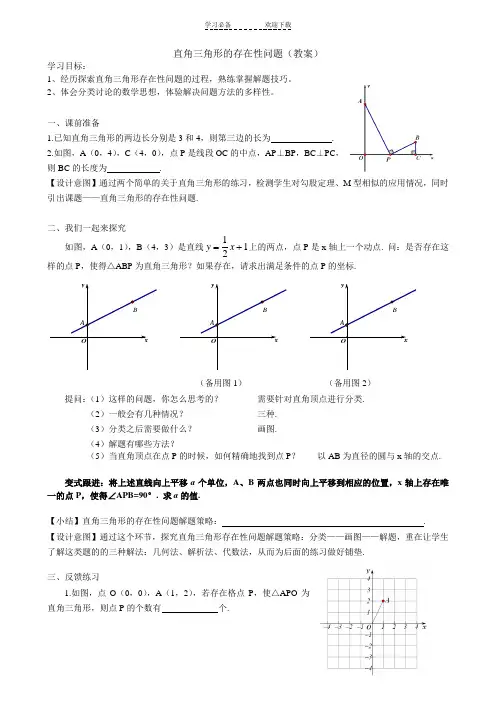
一、课前准备1.已知直角三角形的两边长分别是3和4，则第三边的长为 .2.如图，A （0，4），C （4，0），点P 是线段OC 的中点，AP ⊥BP ，BC ⊥PC ，则BC 的长度为 .【设计意图】通过两个简单的关于直角三角形的练习，检测学生对勾股定理、M 型相似的应用情况，同时引出课题——直角三角形的存在性问题.二、我们一起来探究如图，A （0，1），B （4，3）是直线121+=x y 上的两点，点P 是x 轴上一个动点. 问：是否存在这样的点P ，使得△ABP 为直角三角形？如果存在，请求出满足条件的点P 的坐标.yxBA OyxBA OyxBAO（备用图1） （备用图2）提问：（1）这样的问题，你怎么思考的？ 需要针对直角顶点进行分类. （2）一般会有几种情况？ 三种. （3）分类之后需要做什么？ 画图.（4）解题有哪些方法？（5）当直角顶点在点P 的时候，如何精确地找到点P ？ 以AB 为直径的圆与x 轴的交点.变式跟进：将上述直线向上平移a 个单位，A 、B 两点也同时向上平移到相应的位置，x 轴上存在唯一的点P ，使得∠APB=90°. 求a 的值.【小结】直角三角形的存在性问题解题策略： . 【设计意图】通过这个环节，探究直角三角形存在性问题解题策略：分类——画图——解题，重在让学生了解这类题的的三种解法：几何法、解析法、代数法，从而为后面的练习做好铺垫.三、反馈练习1.如图，点O （0，0），A （1，2），若存在格点P ，使△APO 为直角三角形，则点P 的个数有 个.2.在△ABC 中，∠C=90°，AC=8cm ，BC=6cm ，动点P 、Q 分别同时从A 、B 出发，其中点P 在线段AB 上向点B 移动，速度是2cm/s. 点Q 在线段BC 上向点C 运动，速度为1cm/s.设运动时间为t s ，当t= 时，△BPQ 是直角三角形.3.如图，已知A 、B 是线段MN 上的两点，4=MN ，1=MA ，1>MB ．以A 为中心顺时针旋转点M ，以B 为中心逆时针旋转点N ，使M 、N 两点重合成一点C ，构成△ABC ，设x AB =角形，求x 的值；追问：x 的取值范围如何？【设计意图】通过这三个题的练习，让学生了解尽管题目的背景不同，但是方法是一样的，旨在检测学生对分类讨论思想的应用，学会针对直角顶点进行分类画图，并采用合适的方法予以解答.四、链接中考（2011 济南）如图，矩形OABC 中，点O 为原点，点A 的坐标为（0，8），点C 的坐标为（6，0）. 抛物线834942++-=x x y 经过A 、C 两点，与AB 边交于点D ，Q 是AC 上一点，且AQ ＝5. 请问在抛物线对称轴l 上是否存在点F ，使得△FDQ 为直角三角形？若存在，请直接写出所有符合条件的点F 的坐标，若不存在，请说明理由。

抛物线与直角三角形说课稿讲解抛物线三条围成的三角形（一般称为抛物线的外切三角形）与圆综合的几个的有趣而深刻的性质，以及四条切线围成的图形性质。

39 求证：FA*FB*FC=FA’*FB’*FC’，40 △A’B’C’的外接圆是否经过某个定点？41 求△A’B’C’垂心H的轨迹。

42 证明斯坦纳定理：△ABC外接圆上任一点关于三边对称点与△ABC 垂心共线。

43 抛物线的四条切线，每两条切线交点与另两条切线交点连线中点共线（牛顿线定理）44 对于一般的四条直线，交成四个三角形，证明这四个三角的外接圆交于一点。

这四个三角形的垂心在同一条直线上。

39 求证：FA*FB*FC=FA’*FB’*FC’，思路：这显然和性质27有关。

以上三式相乘并开方即得FA*FB*FC=FA’*FB’*FC’。

注：本题是性质27的推论，当然也可以直接计算证明。

40 △A’B’C’的外接圆是否经过某个定点？思路分析一：切线的关键是切点，所以可以设出三条切线的切点为A,B,C,求出切线的交点坐标，然后设出外接圆的一般方程，将坐标代入，求出系数的表达式。

最后让变量系数为0，即可求出定点坐标。

△A’B’C’的外接圆是否经过某个定点？解答一：思路分析二：如果此圆过定点，此定点一定关于抛物线对称，因此最可疑的就是焦点F了。

下面只需证明A’B’FC’共圆即可，只需利用到角公式算出一个角的正切值，对称得到另一个，说明其相等即可。

解答二：思路分析三：纯几何证明想到了前面性质9，从而得到∠FPB=∠FQC=∠FQA=90°,可以得到共圆，倒角即得结果。

解法三：由前面性质9得∠FPB=∠FQC=∠FQA=90°,故A'PQF共圆，则∠FA'P=∠FQR,同理∠FB'A=∠FQR,故∠FB'A=∠FA'P,故A'C'B'F共圆。

即△A’B’C’外接圆恒过抛物线焦点F。

202!年第2期抛物我中角的存在性问题■罗峻\段利芳2摘要:在数学学习中，不少同学实行“题海”战，通 过做大量的习题，来掌握所学的数学定理，巩固解题技 能.虽然学生学得辛苦，但是数学知识掌握得并不好， 缺乏系统性和逻辑性，解题能力并没有发生实质性的 提升.为打破这一僵局，本文通过一道典型习题的“一 题五问”来设置问题，破解抛物线中角的存在性问题， 让学生了解抛物线存在性问题的题目设置特点及解答 策略，培养学生逻辑思维能力和综合运用几何知识构 造基本图形，运用函数、方程思想解决问题的能力，从 而领悟解题方法，提高解题效益.关键词：二次函数；角的存在性；一题多问函数与几何是初中数学的重点知识和核心内容， 将这两方面的内容结合在同一题目中，难度及综合性 有所增大，这类题目可以考查学生灵活运用知识的能 力，创新意识和数学素养.下面通过一个问题的五问来 破解函数与几何相结合的角的存在性问题，供大家参 考⑴.图1题目：如图1，二次函数;K = -2* -6与坐标轴交于4、B 、C ，Z)为顶点•1. 75°角存在问题问题1:如图2，P 是下方抛物线上一动点，若 乙P C B = 75。

，求点P 的坐标•图2图3分析：由=易发现乙OCfi =45°,构造平行线，将75°分成45°和30°角之和，出现30°的特殊角， 利用30°的条件，构造直角三角形并运用含30°角的直 角三角形的三边之比，用某一字母表示点P 坐标，代入 函数解析式则问题获解.解:易求/l(-2,0)，B(6,0)，C (0，-6)，如图3，过点C 作C £ // /1B交抛物线于点£，过点 户作^^的垂线，垂足为F.易求乙=乙 0B C = 45。

，则乙 E C /5 = 30。

.设 P F =爪，则 C F =，一 6 - m )，- 6 - m) i X A y - -^-x 2 - 2x - 6,作者简介：罗峻（1973 -)，男，湖北省黄石人，本科，中学一级教师，主要从事初中数学教学研究 段利芳（1976 -)，女，湖北省武汉人，本科，中学高级教师，主要从事初中数学教学研究•41•-数理化学习 —--------------—_-_—_-_—_______________________:____________________；____；____________解得m =4j 3 - 2所以尸(2. 45。

抛物线与直角三角形结合的解题方法在数学中，抛物线和直角三角形是两个常见且重要的概念。

它们在解决实际问题和理论推导中都扮演着重要的角色。

本文将探讨如何将抛物线与直角三角形结合起来，以更全面地解决一些数学问题。

一、基本概念1. 抛物线抛物线是一种特殊的曲线，其定义可以是平面内到定点和一条定直线的距离相等的点的轨迹。

抛物线在物理学、工程学和数学等领域都有着广泛的应用。

2. 直角三角形直角三角形是一种特殊的三角形，其中包含一个90度的直角。

直角三角形的性质和定理在几何学中具有重要意义，也是解决三角函数和特殊角度问题的基础。

二、抛物线与直角三角形的关系在实际问题中，抛物线与直角三角形常常会相互联系，特别是在物体的抛体运动和轨迹分析中。

当我们需要分析一个抛体运动的轨迹时，通常会涉及到抛物线的方程和直角三角形的性质。

当我们需要求解一个物体从抛出到落地的时间、速度和位置等问题时，我们可以通过解析几何的方法，将抛物线的轨迹和直角三角形的性质结合起来，从而得到更加全面和深入的解答。

三、抛物线与直角三角形结合的解题方法1. 利用抛物线方程构建直角三角形在解决与抛物线和直角三角形相关的问题时，可以先利用抛物线的方程构建出相关的直角三角形。

当我们需要分析抛体运动的轨迹时，可以通过抛物线的方程构建出相关的直角三角形，从而推导出物体的运动规律和轨迹特性。

2. 利用直角三角形的性质求解抛物线方程另一种常见的方法是利用直角三角形的性质来求解抛物线的方程。

在一些特殊的问题中，可以通过构建直角三角形、利用三角函数和三角恒等式等方法，从而简化抛物线方程的求解过程，使问题得到更加清晰和简化的解答。

四、个人观点和总结在数学问题的解决过程中，抛物线与直角三角形的结合是一种常见且有效的方法。

通过将抛物线的特性和方程与直角三角形的性质相结合，不仅可以更全面地理解和分析问题，也可以从不同角度和方法解决问题，使解题过程更灵活和丰富。

抛物线与直角三角形的结合在解决实际问题和理论推导中具有重要的意义。

课题：二次函数图像中直角三角形的存在性问题一、教学目标1、掌握求二次函数表达式的方法。

2、掌握判断直角三角形可以从边和角两个角度入手。

3、掌握二次函数与直角三角形结合的动点问题的解决方法。

二、重、难点重点：线段的表示与分类讨论难点：分类讨论三、教学过程情境创设：存在性问题是中考中的热点问题，所涉知识点多，难度较大，也是学生比较荆手的问题，但它也是有解题方法可循的。

比如我们本节课将复习的直角三角形存在性问题，就可利用坐标系中两点的距离公式，正确得到所求三角形三边长的平方的代数式；根据勾股定理的逆定理得到方程，并解方程即可。

知识梳理：1、二次函数的表达式有哪些？一般式：对轴称为顶点坐标（，）项点式：对轴称为顶点坐标（，）交点（两根）式：对轴称为顶点坐标（，）（设计意图：让学生能根据所给条件选用恰当的表达式求二次函数解析式）2、直角三角形的判定方法有哪些？（设计意图：让学生知道判断一个三角形是直角三角形可从边和角两个角度入手，重点是对勾股定理逆定理的运用）3、已知点P(x,y)，则点P到x轴的距离为，到y轴的距离为。

（设计意图：让学生知道点的坐标的实际意义）4、两点间的距离公式：用A，B两点的坐标来表示线段AB的长。

（设计意图：让学生知道用两点坐标来表示该两点的线段长）习题展示：oy B( x2,y2)A( x1,y1)x如图，已知抛物线y=-x 2+bx+c 与x 轴交于点A 、B （3，0），与y 轴交于点C （0，3），直线l 经过点B 、C 两点，抛物线的顶点为D 。

（1）求此抛物线和直线l 的解析式；（2）判断ΔBCD 的形状并说明理由；（3）如图，在抛物线的对称轴上求点P ，使ΔPBC 为直角三角形；思考题：如图，在对称轴右侧的抛物线上，是否存在点P ，使ΔPDC 为等腰三角形。

若存在，请求出符合条件点P 的坐标，若不存在，请说明理由；C B A O y xD CBDA yLO C B A O y xD 思路分析：将B （3，0），C （0，3）代入y=-x 2+bx+c 中，得关于b ，c 的二元一次方程组，解出b ，c 的值，从而得到抛物线的解析式；设y=kx+z,将B （3，0），C （0，3）代入y=kx+z ，得关于k ，z 的二元一次方程组，解出k ，z 的值，从而得到直线l 的解析式。

抛物线中直角三角形存在性问题(勾股定理与K值法)[例]已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于A（x1，0）、B（x2，0）（x1＜x2）两点，与y轴交于点C，x1，x2是方程x2+4x﹣5=0的两根．（1）若抛物线的顶点为D，求S△ABC：S△ACD的值；（2）若∠ADC=90°，求二次函数的解析式．【解答】解：（1）解方程x2+4x﹣5=0，得x=﹣5或x=1，由于x1＜x2，则有x1=﹣5，x2=1，∴A（﹣5，0），B（1，0）．抛物线的解析式为：y=a（x+5）（x﹣1）（a＞0），∴对称轴为直线x=﹣2，顶点D的坐标为（﹣2，﹣9a），令x=0，得y=﹣5a，∴C点的坐标为（0，﹣5a）．依题意画出图形，如右图所示，则OA=5，OB=1，AB=6，OC=5a，过点D作DE⊥y轴于点E，则DE=2，OE=9a，CE=OE﹣OC=4a．S△ACD=S梯形ADEO﹣S△CDE﹣S△AOC=（DE+OA）•OE﹣DE•CE﹣OA•OC=（2+5）•9a﹣×2×4a﹣×5×5a=15a，而S△ABC=AB•OC=×6×5a=15a，∴S△ABC：S△ACD=15a：15a=1：1.注：作铅垂线求S△ACD也是可以的（2）方法一：如解答图，过点D作DE⊥y轴于E在Rt△DCE中，由勾股定理得：CD2=DE2+CE2=4+16a2，在Rt△AOC中，由勾股定理得：AC2=OA2+OC2=25+25a2，设对称轴x=﹣2与x轴交于点F，则AF=3，在Rt△ADF中，由勾股定理得：AD2=AF2+DF2=9+81a2．∵∠ADC=90°，∴△ACD为直角三角形，由勾股定理得：AD2+CD2=AC2，即（9+81a2）+（4+16a2）=25+25a2，化简得：a2=，∵a＞0，∴a=，∴抛物线的解析式为：y=（x+5）（x﹣1）=x2+x﹣．方法二：（K 值法）结论1：直线1111:l y k x b =+与直线2222:l y k x b =+垂直⇔121k k =-； 结论2：点11(,)A x y 、22(,)B x y （12x x ≠）分别是直线:l y kx b =+上两个不同的点，则2121y y k x x -=-.（证明：11y kx b =+……①22y kx b =+……②， ②－①得，2121()y y k x x -=-，2121y y k x x -=-） 解：90932(5)3AD a a k a ---===----，9(5)42202CD a a a k a ----===---， ∵∠ADC =90°，∴1AD CD k k =-，即23261a a a -⨯=-=-，12a a ==. ∴抛物线的解析式为：y =（x +5）（x ﹣1）=x 2+x ﹣． 练习.已知抛物线c bx x y ++-=221与y 轴交于点C ，与x 轴的两个交点分别为A （﹣4，0），B （1，0）．（1）求抛物线的解析式； （2）已知点P 在抛物线上，连接PC ，PB ，若△PBC 是以BC 为直角边的直角三角形，求点P 的坐标；（3）已知点E 在x 轴上，点F 在抛物线上，是否存在以A ，C ，E ，F 为顶点的四边形是平行四边形？若存在，请直接写出点E 的坐标；若不存在，请说明理由．。

中考专题讲解：直角三角形的存在性问题解题策略有关直角三角形的存在性问题，一般都是放在平面直角坐标系中和抛物线结合起来考察，这种题的解法套路一般都是固定的，在学习的过程中只需要牢固掌握直角三角形存在的基本模型：两线一圆，多加练习，这类问题就可以轻松掌握。

一、模型讲解“两线一圆”模型：在平面直角坐标系中遇到直角三角形的相关问题时，通常是以直角顶点作为分类标准，如下图，分别以点A、点B、点M为直角定点来构造直角三角形，然后根据相关条件来进行求解即可。

已知:定点A(2，1)、B(6，4)和动点M(m，0)，存在直角三角形。

具体有以下三种情况：（1）过点A作直线AM垂直AB，交x轴于点M；（2）过点B作直线BM垂直AB，交x轴于点M；（3）根据直径所对的圆周角为90度，以AB为直径作圆，交x轴的点即为满足条件的点M（一般情况下有两个交点，特殊情况下只有一个交点），然后根据相关条件来进行求解即可。

作出图形后，具体求解方法有三种：方法一：“K型”图（有的叫“一线三等角”），三角形相似易得△ACM∽△BEA，求得CM，从而求出点M的坐标。

易得△AEB ∽△BFM求得BF，从而得M的坐标方法二：勾股定理∵BH²=BG²-GH² ∵AC²+CM²=AM²BH²=BM²-HM² MD²+BD²=BM²∴BG²-GH² =BM²-HM² AM²+BM²=AB²∴AC²+CM²+MD²+BD²=AB²方法三：解析法（来源于高中的解析几何，虽然有点超纲，但是很多老师都教学生这种方法）K AB ·K AM =-1，直线BM 与x 轴的交点即为M 。

K AB ·K BM =-1，直线A 与x 轴的交点即为M 。

年级九科目数学班型一对一学生第次课课题名称抛物线中的直角三角形存在性问题授课老师授课时间2018年3月20日8:00——10:00教学目标经历探索直角三角形存在性问题的过程，熟练掌握解题技巧；体会分类讨论的数学思想，体验解决问题方法的多样性。

教学重点.能够正确的分析问题、转化问题，合理利用条件解决问题2.确定动点位置的方法及数形结合、分类讨论思想和方程思想的培养教学难点能够正确的分析问题、转化问题，合理利用条件解决问题教学过程：一、课前小测：1.直角三角形的两边长分别是3和4，则第三边的长是2.已知Rt△ABC中，∠C=90°,AC=8,BC=6,动点P、Q分别同时从A、B出发，其中点P在线段AB上向点B移动，速度是2单位每秒；点Q在线段BC上向点C运动，速度是1单位每秒。

设运动时间为t〔秒〕，当t= 秒时，△BPQ是直角三角形。

二、新课学习：〔一〕经典模型模型再现：已知：定点A(2, 1) 、B(6, 4)和动点M〔m, 0〕, 存在直角三角形ABM,求点M的坐标。

两线一圆找直角模型：在平面直角坐标系中遇到直角三角形的相关问题时，通常是以直角顶点作为分类标准，如下列图，分别以点A、点B、点M为直角定点来构造直角三角形，然后根据相关条件来进行求解即可。

具体有以下三种情况：比方：〔1〕当以点A为直角顶点时，过点A作AB的垂线交x轴的点即为所求；〔2〕当以点B为直角顶点时，过点B 作AB的垂线交x轴的点即为所求；〔3〕当以点M为直角顶点时，只需要以AB为直径作辅助圆与x轴的交点〔一般情况下有两个交点，特殊情况下只有一个交点〕即为所求。

〔二〕解法：1.“K型相似”〔一线三直角〕提示：竖直型，上减下；水平型，右减左。

遇直角，构矩形，得相似，求结果。

2.勾股定理〔暴力法---两点间距离公式〕利用两点间距离公式.勾股定理及其逆定理的应用进行求解。

其基本解题思路是列点.列线.列式。

第一步，列出构建所求直角三角形的三个点，定点找到后，动点用参数表示其坐标；第二步，采用分类讨论思想，列出构建所求直角三角形的三个边，并分类讨论两两垂直的三种可能性；第三步，把定点坐标及参数点坐标代入两点间距离公式，利用勾股定理的逆定理列出等式求解。

复习课《二次函数与几何图形存在性问题——直角三角形的存在性问题》教学设计普定县第二中学孙家坤：精例如图，已知抛物线y＝1／2x2＋bx＋c经过点B(4，0)和点C(0，－2)，与x轴的另一个交点为点A，其对称轴l与x轴交于点E，过点C且平行x轴的直线交抛物线于点D，连接AD。

(1)求该抛物线的解析式；【思路点拨】解：略(2)判断△ABD的形状；【思路点拨】判断三角形形状，一般为特殊三角形，若两边相等，则为等腰三角形；若三边相等，则为等边三角形；若两条边的平方和等于第三边的平方，则为直角三角形。

解：略(3)P为线段AD上一点，连接PE，若△APE是直角三角形，求点P的坐标；【思路点拨】观察思考，带着问题进入学习。

解：略(4)抛物线的对称轴上是否存在一点P，使△APD是直角三角形，若存在，求出P点坐标；若不存在，请说明理由．【思路点拨】学生书写求解过程。

分别利用勾股定理，列出方程求解．若有解，则存在；若无解，则不存在．解：略：总（满分对于抛物线与直角三角形的综合问题，解题时，一般需做好以下几点：1．利用坐标系中两点距离公式，得到所求三角形三边平方的代数式；2．确定三角形中的锐角，若存在锐角，则只需使得另外两个角中任意一个角为直角，并利用勾股定理列方程求解；若无法确定哪个角是锐角，则需要讨论三个角；3．根据勾股定理得到方程，并解方程即可，若方总结归纳，得出解决这类问题的方法。

：针对1.如图，已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝－1，且抛物线经过A(1，0)，C(0，3)两点，与x轴交于点B.(1)若直线y＝mx＋n经过B、C两点，求直线BC和抛物线的解析式；(2)设点P为抛物线的对称轴x＝－1上的一个动点，求使△BPC为直角三角形的点P的坐标．第1题图解：(1)依题意得⎩⎪⎨⎪⎧－b2a＝－1a＋b＋c＝0c＝3，解得⎩⎨⎧a＝－1b＝－2c＝3，∴抛物线解析式为y＝－x2－2x＋3，∵对称轴为x＝－1，抛物线经过A(1，0)，∴B(－3，0)，把B(－3，0)，C(0，3)分别代入y＝mx＋n得，⎩⎨⎧－3m＋n＝0n＝3，解得⎩⎨⎧m＝1n＝3，∴直线BC的解析式为y＝x＋3；学分题意，探思路，并成答程。

抛物线与直角三角形结合的解题方法【最新版3篇】篇1 目录1.引言：抛物线与直角三角形的结合问题在数学题目中十分常见，本文将探讨如何利用抛物线的性质和直角三角形的特征来解题。

2.抛物线的基本性质：介绍抛物线的定义、标准方程和顶点坐标等基本概念。

3.直角三角形的特征：介绍直角三角形的定义、直角边和斜边的关系等特征。

4.抛物线与直角三角形结合的解题方法：通过实例分析，讲解如何利用抛物线和直角三角形的性质求解相关问题。

5.结论：总结抛物线与直角三角形结合的解题方法，并鼓励读者在实际解题中灵活运用。

篇1正文一、引言在数学题目中，抛物线与直角三角形的结合问题常常出现，这类问题不仅考验了学生的计算能力，还考验了他们的几何直观和逻辑思维能力。

为了更好地解决这类问题，本文将从抛物线的基本性质和直角三角形的特征出发，探讨如何利用它们来解题。

二、抛物线的基本性质抛物线是平面上到定点距离与到定直线距离相等的点的轨迹。

它有以下基本性质：1.抛物线的定义：设焦点 F 和直线 l，满足到定点 F 的距离与到定直线 l 的距离相等的点的轨迹称为抛物线。

2.标准方程：抛物线的标准方程为 y^2=2px，其中 p 为焦点到准线的距离。

3.顶点坐标：抛物线的顶点坐标为 (0, p)。

三、直角三角形的特征直角三角形是指有一个内角为 90 度的三角形，它有以下特征：1.定义：有一个内角为 90 度的三角形称为直角三角形。

2.直角边和斜边的关系：直角三角形的两条直角边的长度满足勾股定理，即 a^2 + b^2 = c^2，其中 a、b 为直角边，c 为斜边。

四、抛物线与直角三角形结合的解题方法在解决抛物线与直角三角形结合的问题时，我们可以利用抛物线的性质和直角三角形的特征，通过以下几个步骤来求解：1.画图：首先画出抛物线和直角三角形，标出已知条件。

2.寻找关键点：观察图形，找到可能对解题有帮助的关键点，如抛物线的顶点、直角三角形的直角顶点等。

探究抛物线中特定三角形的存在性以抛物线为载体、满足某种条件的几何图形是否存在的问题，是中考的热点和难点．解决这类问题的关键是，弄清函数与几何图形之间的联系，在解题过程中将函数问题几何化，几何问题数量化，数形统一，同时要学会将大题分解为小题，各个击破，本文选取“抛物线中特定三角形的存在性”为例，说明这类问题的解题策略．一、抛物线中等腰三角形的存在性例1（湖南湘西州中考题）如图1，已知抛物线y ＝－14x 2＋bx ＋4与x 轴相交于A 、B 两点，与y 轴相交于点C ，若已知A 点坐标为A （－2，0）．(1)求抛物线的解析式及它的对称轴方程；(2)求C 点坐标，连结AC 、BC 并求线段BC 所在直线的解析式；(3)试判断△AOC 与△COB 是否相似？并说明理由；(4)在抛物线的对称轴上是否存在点Q ，使△ACQ 为等腰三角形，若存在，求出符合条件的Q 点坐标；若不存在，请说明理由．解 (1)易得抛物线解析式为配方得，y ＝()2125344x --+， 所以对称轴方程为x ＝3；(2)在213442y x x =-++中，令x ＝0， 则y ＝4，所以点C(0，4).令y ＝0，则2134042x x -++= 解得x 1＝8，x 2＝－2，∴A （－2，0），B(8，0).设直线BC 的解析式为y ＝kx ＋b ，把B(8，0)，C(0，4)的坐标分别代入解析式，解得直线BC 的解析式为142y x =-+； (3) △AOC ∽△COB ．理由：在△AOC 与△COB 中∵OA ＝2，OC ＝4，OB ＝8， ∴2141,4282OA OC OC OB ==== ∴OA OC OC OB =．又∠AOC ＝∠BOC ＝90°，∴△AOC ∽△COB ；(4)因为抛物线的对称轴方程为x ＝3，Q 点在对称轴x ＝3上，如图2．点评 本题点的移动贯穿始终，其中对于等腰三角形的确定需要分类讨论，在具体求点Q 坐标时，还要充分注意图形的几何特点，利用数形结合思想．二、抛物线中的直角三角形的存在性例2 （广州市中考题）如图3，抛物线y ＝－38x 2－34x ＋3与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ．(1)求点A 、B 的坐标；(2)设D 为已知抛物线的对称轴上的任意一点，当△ACD 的面积等于△ACB 的面积时，求点D 的坐标；(3)若直线l 过点E(4，0)，M 为直线l 上一动点，当以A 、B 、M 为顶点所作的直角三角形有且只有三个时，求直线l 解析式．解 (1)A （－4，0），B(2，0)（过程略）；(2)因为抛物线y ＝－38x 2－34x ＋3的对称轴为x ＝－1， 与y 轴交点C 的坐标为(0，3)，所以直线AC 的解析式为y ＝34x ＋3．且当x ＝－1时，有y ＝94，所以直线AC 与对称轴x ＝－1的交点H 的坐标为（－1，94）． 因为AB ＝6，CO ＝3，所以△ACB 的面积为，S △ACE ＝9．不妨设点D 的坐标为（－1，m ），如图4，则△ACD 的面积为S △ACD ＝12×DH ×AO ＝9．当点D 位于AC 上方时，DH ＝m －94， 代入解得m ＝274； 当点D 位于AC 下方时，DH ＝94－m ， 代入解得m ＝－94．所以点D 的坐标为 （－1，274），或（－1，－94） (3)如图5，以AB 为直径作⊙P ，当且仅当直线l 与⊙P 相切时符合题意．因为Rt △PME 中，∠PME ＝90°，PM ＝3，PE ＝5，所以由勾股定理，可得ME ＝4．利用三角形相似可以求得点M 的坐标M （45，125） 设直线l 的解析式为y=kx+b ，代入M （45，125），E(4，0)，解得 4125540k b k b ⎧+=⎪⎨⎪+=⎩，即343k b ⎧=-⎪⎨⎪=⎩ 所以直线l 的解析式为y ＝－34x ＋3 同理可得直线l 的另一个解析式为y ＝34x －3． 点评 此题借助于几何图形的知识考查函数的综合应用，这是初中阶段的重点，解答这类题型时要注意数形结合、综合分析思考，第3问具有较高的区分度，对学生的能力要求特别高，学生必须具有较强的观察能力、分析能力和综合运用知识的能力．三、抛物线中相似三角形的存在例3 （山东日照中考题）已知，如图6，抛物线y＝ax2＋bx＋c经过点A（x1，0），B(x2，0)，C(0，－2)，其顶点为D．以AB为直径的⊙M交y轴于点E、F，过点E作⊙M的切线交x轴于点N．∠ONE＝30°，128x x-=．(1)求抛物线的解析式及顶点D的坐标；(2)连结AD、BD，在(1)中的抛物线上是否存在一点P，使得△ABP与△ADB相似？若存在，求出P点的坐标；若不存在，说明理由；(3)如图7，点Q为弧EBF上的动点（Q不与E、F重合），连结AQ交y轴于点H，问：AH·AQ是否为定值？若是，请求出这个定值；若不是，请说明理由．(2)如图8，由抛物线的对称性可知：AD＝BD，△ADB为等腰三角形．若在抛物线对称轴的右侧图象上存在点P，使△ABP与△ADB相似，必须有∠BAP＝∠BPA＝∠BAD．设AP交抛物线的对称轴于D’点，显然同理可说明在对称轴左边的抛物线上也不存在符合条件的P点．所以在该抛物线上不存在点P，使得与△PAB与△ADB相似；点评解决存在性问题的基本思路是：先假设存在，然后根据问题的已知条件去探索，但对于按部分条件得出的结论，还需要验证是否满足题目的全部要求．。

抛物线中特殊三角形的存在性问题专题复习一、学情分析：近几年来中考的25题均与图形的动态变化有关，尤其是以二次函数为载体, 然后在二次函数中出现，是否存在等腰三角形、是否存在直角三角形等作为考察对象。

二次函数与特殊三角形的存在性问题主要分为两类，一类是静态的特殊三角形的存在性问题，一类是动态的特殊三角形的存在性问题。

在实际授课中发现静态的特殊三角形的存在性问题难度相对较小，可根据抛物线的对称性以及三角形的特点为切入点来解决，而动态的特殊三角形的存在性问题对学生来说难度较大，因此在教学中我们要找到合适的解题方法，降低难度，突破难点难度。

二、学习目标1.通过二次函数的图象回顾抛物线的基础知识并能表示出图象中线段的长度，进而探究得到特殊三角形的条件。

2.让学生能够从对称轴和抛物线上分别引入一个动点两个维度体会分类讨论和数形结合的思想方法。

三、教学重点培养学生的问题意识并根据题意分析出动点在动的过程一些不变的量以及不变的关系四、教学难点熟练掌握知识之间的关联与转化，提升思维的灵活性与深刻性。

五、教学设计：1、知识回顾设计意图：通过开放性的问题，让学生有广阔的思维空间和充足的思考方式，并让学生的思维得到充分展示提高学生的参与度。

通过图象学生可以求出点的坐标, 水平线段的长度，斜线段的长度及用待定系数法求函数表达式，体现了数学的数形结合思想，初步体现思维深刻的课堂，预热学生的思维，为后面的探究性学习做好有效的思维铺垫。

2：探究新知一：已知抛物线y= - x2 +2x+3的图像如图所示,点P是抛物线对称轴上一动点，连结AC、AP、CP,你能提出一个与AACP形状有关的探究性的问题吗？设计意图：当点P是抛物线对称轴上任意一动点时，学生是否能类比第一个环节当点P 为抛物线的顶点时用勾股定理分别求出AACP三边的长的方法把AACP的三边表示出来，注重知识之间的关联与转化，从而培养学生类比的学习方法。

然后根据三边的长分析出动点在动的过程一些不变的量以及不变的关系，只要能清楚找到不变的关系，利用它可列出相应的式子，便能将问题解决。

抛物线上存在性问题的探究教案一、教学目标1、通过本节课的复习，进一步提高学生运用二次函数、平行四边形、矩形、菱形、正方形等知识解决问题的能力。

2能从数和形的角度探究抛物线上图形的若干综合问题二、重点和难点重点：利用抛物线上的图形的特性，如何将问题转化为基本的数学问题难点：根据题意找出能使四边形转变成平行四边形、矩形、菱形、正方形的条件。

三、教学过程一、平行四边形与抛物线1、（2012•钦州）如图甲，在平面直角坐标系中，A、B的坐标分别为（4，0）、（0，3），抛物线y=x2+bx+c经过点B，且对称轴是直线x=﹣．（1）求抛物线对应的函数解析式；（2）将图甲中△ABO沿x轴向左平移到△DCE（如图乙），当四边形ABCD是菱形时，请说明点C和点D都在该抛物线上；（3）在（2）中，若点M是抛物线上的一个动点（点M不与点C、D重合），经过点M作MN∥y轴交直线CD于N，设点M的横坐标为t，MN的长度为l，求l与t之间的函数解析式，并求当t为何值时，以M、N、C、E为顶点的四边形是平行四边形．（参考公式：抛物线y=ax2+bx+c（a≠0）的顶点坐标为（﹣，），对称轴是直线x=﹣．）1、解：（1）由于抛物线y=x2+bx+c与y轴交于点B（0，4），则c=4；∵抛物线的对称轴x=﹣=﹣，∴b=5a=；即抛物线的解析式：y=x2+x+4．（2）∵A（4，0）、B（3，0）∴OA=4，OB=3，AB==5；若四边形ABCD是菱形，则BC=AD=AB=5，∴C（﹣5，3）、D（﹣1，0）．将C（﹣5，3）代入y=x2+x+4中，得：×（﹣5）2+×（﹣5）+4=3，所以点C在抛物线上；同理可证：点D也在抛物线上．（3）设直线CD的解析式为：y=kx+b，依题意，有：，解得∴直线CD：y=﹣x﹣．由于MN∥y轴，设M（t，t2+t+4），则N（t，﹣t﹣）；①t＜﹣5或t＞﹣1时，l=MN=（t2+t+4）﹣（﹣t﹣）=t2+t+；②﹣5＜t＜﹣1时，l=MN=（﹣t﹣）﹣（t2+t+4）=﹣t2﹣t﹣；若以M、N、C、E为顶点的四边形是平行四边形，由于MN∥CE，则MN=CE=3，则有：t2+t+=3，解得：t=﹣3±2；二、梯形与抛物线1、已知，在Rt△OAB中，∠OAB=90°，∠BOA=30°，AB=2．若以O为坐标原点，OA所在直线为x轴，建立如图所示的平面直角坐标系，点B在第一象限内．将Rt△OAB沿OB折叠后，点A落在第一象限内的点C处．（1）求点C的坐标；（2）若抛物线y=ax2+bx（a≠0）经过C、A两点，求此抛物线的解析式；（3）若上述抛物线的对称轴与OB交于点D，点P为线段DB上一动点，过P作y轴的平行线，交抛物线于点M，问：是否存在这样的点P，使得四边形CDPM为等腰梯形？若存在，请求出此时点P的坐标；若不存在，请说明理由．1、解：（1）过点C作CH⊥x轴，垂足为H；∵在Rt△OAB中，∠OAB=90°，∠BOA=30°，AB=2，∴OB=4，OA=2；由折叠的性质知：∠COB=30°，OC=AO=2，∴∠COH=60°，OH=，CH=3；∴C点坐标为（，3）．（2）∵抛物线y=ax2+bx（a≠0）经过C（，3）、A（2，0）两点，∴，解得；∴此抛物线的函数关系式为：y=﹣x2+2x．（3）存在．因为y=﹣x2+2x的顶点坐标为（，3），即为点C，MP⊥x轴，垂足为N，设PN=t；因为∠BOA=30°，所以ON=t，∴P（t，t）；作PQ⊥CD，垂足为Q，ME⊥CD，垂足为E；把x=t代入y=﹣x2+2x，得y=﹣3t2+6t，∴M（t，﹣3t2+6t），E（，﹣3t2+6t），同理：Q（，t），D（，1）；2.（2012•玉林）如图，在平面直角坐标系xOy中，矩形AOCD的顶点A的坐标是（0，4），现有两动点P，Q，点P从点O出发沿线段OC（不包括端点O，C）以每秒2个单位长度的速度匀速向点C运动，点Q从点C出发沿线段CD（不包括端点C，D）以每秒1个单位长度的速度匀速向点D运动．点P，Q同时出发，同时停止，设运动时间为t（秒），当t=2（秒）时，PQ=2．（1）求点D的坐标，并直接写出t的取值范围．（2）连接AQ并延长交x轴于点E，把AE沿AD翻折交CD延长线于点F，连接EF，则△AEF 的面积S是否随t的变化而变化？若变化，求出S与t的函数关系式；若不变化，求出S的值．（3）在（2）的条件下，t为何值时，四边形APQF是梯形？.解：（1）由题意可知，当t=2（秒）时，OP=4，CQ=2，在Rt△PCQ中，由勾股定理得：PC===4，∴OC=OP+PC=4+4=8，又∵矩形AOCD，A（0，4），∴D（8，4）．点P到达终点所需时间为=4秒，点Q到达终点所需时间为=4秒，由题意可知，t的取值范围为：0＜t＜4．（2）结论：△AEF的面积S不变化．∵AOCD是矩形，∴AD∥OE，∴△AQD∽△EQC，∴，即，解得CE=．由翻折变换的性质可知：DF=DQ=4﹣t，则CF=CD+DF=8﹣t．S=S梯形AOCF+S△FCE﹣S△AOE=（OA+CF）•OC+CF•CE﹣OA•OE=[4+（8﹣t）]×8+（8﹣t）•﹣×4×（8+）化简得：S=32为定值．所以△AEF的面积S不变化，S=32．（3）若四边形APQF是梯形，因为AP与CF不平行，所以只有PQ∥AF．由PQ∥AF可得：△CPQ∽△DAF，∴，即，化简得t2﹣12t+16=0，解得：t1=6+2，t2=6﹣2，由（1）可知，0＜t＜4，∴t1=6+2不符合题意，舍去．∴当t=（6﹣2）秒时，四边形APQF是梯形．三、等腰三角形、菱形与抛物线1、（2012•龙岩）在平面直角坐标系xOy中，一块含60°角的三角板作如图摆放，斜边AB在x轴上，直角顶点C在y轴正半轴上，已知点A（﹣1，0）．（1）请直接写出点B、C的坐标：B、C；并求经过A、B、C三点的抛物线解析式；（2）现有与上述三角板完全一样的三角板DEF（其中∠EDF=90°，∠DEF=60°），把顶点E 放在线段AB上（点E是不与A、B两点重合的动点），并使ED所在直线经过点C．此时，EF所在直线与（1）中的抛物线交于点M．①设AE=x，当x为何值时，△OCE∽△OBC；②在①的条件下探究：抛物线的对称轴上是否存在点P使△PEM是等腰三角形？若存在，请写出点P的坐标；若不存在，请说明理由．1、解：（1）∵点A（﹣1，0），∴OA=1，由图可知，∠BAC是三角板的60°角，∠ABC是30°角，所以，OC=OA•tan60°=1×=，OB=OC•cot30°=×=3，所以，点B（3，0），C（0，），设抛物线解析式为y=ax2+bx+c，则，解得，所以，抛物线的解析式为y=﹣x2+x+；（2）①∵△OCE∽△OBC，∴=，即=，解得OE=1，所以，AE=OA+OE=1+1=2，即x=2时，△OCE∽△OBC；②存在．理由如下：抛物线的对称轴为x=﹣=﹣=1，所以，点E为抛物线的对称轴与x轴的交点，∵OA=OE，OC⊥x轴，∠BAC=60°，∴△ACE是等边三角形，∴∠AEC=60°，又∠DEF=60°，∴∠FEB=60°，∴∠BAC=∠FEB，∴EF∥AC，由A（﹣1，0），C（0，）可得直线AC的解析式为y=x+，∵点E（1，0），∴直线EF的解析式为y=x﹣，联立，解得，（舍去），∴点M的坐标为（2，），EM==2，分三种情况讨论△PEM是等腰三角形，当PE=EM时，PE=2，所以，点P的坐标为（1，2）或（1，﹣2），当PE=PM时，∵∠FEB=60°，∴∠PEF=90°﹣60°=30°，PE=EM÷cos30°=×2÷=，所以，点P的坐标为（1，），当PM=EM时，PE=2EM•cos30°=2×2×=2，所以，点P的坐标为（1，2），综上所述，抛物线对称轴上存在点P（1，2）或（1，﹣2）或（1，）或（1，2），使△PEM是等腰三角形．四、直角三角形与抛物线1、（2012•广州）如图，抛物线y=与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．（1）求点A、B的坐标；（2）设D为已知抛物线的对称轴上的任意一点，当△ACD的面积等于△ACB的面积时，求点D的坐标；（3）若直线l过点E（4，0），M为直线l上的动点，当以A、B、M为顶点所作的直角三角形有且只有三个时，求直线l的解析式．1、解：（1）令y=0，即=0，解得x1=﹣4，x2=2，∴A、B点的坐标为A（﹣4，0）、B（2，0）．（2）S△ACB=AB•OC=9，在Rt△AOC中，AC===5，设△ACD中AC边上的高为h，则有AC•h=9，解得h=．如答图1，在坐标平面内作直线平行于AC，且到AC的距离=h=，这样的直线有2条，分别是l1和l2，则直线与对称轴x=﹣1的两个交点即为所求的点D．设l1交y轴于E，过C作CF⊥l1于F，则CF=h=，∴CE==．设直线AC的解析式为y=kx+b，将A（﹣4，0），B（0，3）坐标代入，得到，解得，∴直线AC解析式为y=x+3．直线l1可以看做直线AC向下平移CE长度单位（个长度单位）而形成的，∴直线l1的解析式为y=x+3﹣=x﹣．则D1的纵坐标为×（﹣1）﹣=，∴D1（﹣4，）．同理，直线AC向上平移个长度单位得到l2，可求得D2（﹣1，）综上所述，D点坐标为：D1（﹣4，），D2（﹣1，）．（3）如答图2，以AB为直径作⊙F，圆心为F．过E点作⊙F的切线，这样的切线有2条．连接FM，过M作MN⊥x轴于点N．∵A（﹣4，0），B（2，0），∴F（﹣1，0），⊙F半径FM=FB=3．又FE=5，则在Rt△MEF中，ME==4，sin∠MFE=，cos∠MFE=．在Rt△FMN中，MN=MN•sin∠MFE=3×=，FN=MN•cos∠MFE=3×=，则ON=，∴M点坐标为（，）直线l过M（，），E（4，0），设直线l的解析式为y=kx+b，则有，解得，所以直线l的解析式为y=x+3．同理，可以求得另一条切线的解析式为y=x﹣3．综上所述，直线l的解析式为y=x+3或y=x﹣3．五、相似三角形与抛物线1、（2012•福州）如图1，已知抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4）两点．（1）求抛物线的解析式；（2）将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个公共点D，求m 的值及点D的坐标；（3）如图2，若点N在抛物线上，且∠NBO=∠ABO，则在（2）的条件下，求出所有满足△POD∽△NOB的点P坐标（点P、O、D分别与点N、O、B对应）．1、解：（1）∵抛物线y=y=ax2+bx（a≠0）经过A（3，0）、B（4，4）∴，解得：∴抛物线的解析式是y=x2﹣3x．（2）设直线OB的解析式为y=k1x，由点B（4，4），得：4=4k1，解得：k1=1∴直线OB的解析式为y=x，∴直线OB向下平移m个单位长度后的解析式为：y=x﹣m，∵点D在抛物线y=x2﹣3x上，∴可设D（x，x2﹣3x），又点D在直线y=x﹣m上，∴x2﹣3x=x﹣m，即x2﹣4x+m=0，∵抛物线与直线只有一个公共点，∴△=16﹣4m=0，解得：m=4，此时x1=x2=2，y=x2﹣3x=﹣2，∴D点的坐标为（2，﹣2）．（3）∵直线OB的解析式为y=x，且A（3，0），∴点A关于直线OB的对称点A′的坐标是（0，3），设直线A′B的解析式为y=k2x+3，过点（4，4），∴4k2+3=4，解得：k2=，∴直线A′B的解析式是y=，∵∠NBO=∠ABO，∴点N在直线A′B上，∴设点N（n，），又点N在抛物线y=x2﹣3x上，∴=n2﹣3n，解得：n1=﹣，n2=4（不合题意，舍去）∴N点的坐标为（﹣，）．方法一：如图1，将△NOB沿x轴翻折，得到△N1OB1，则N1（，），B1（4，﹣4），∴O、D、B1都在直线y=﹣x上．∵△P1OD∽△NOB，∴△P1OD∽△N1OB1，∴，∴点P1的坐标为（，）．将△OP1D沿直线y=﹣x翻折，可得另一个满足条件的点P2（，），综上所述，点P的坐标是（，）或（，）．六、抛物线中的翻折问题1、（2012•天门）如图，抛物线y=ax2+bx+2交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点．（1）求抛物线解析式及点D坐标；（2）点E在x轴上，若以A，E，D，P为顶点的四边形是平行四边形，求此时点P的坐标；（3）过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′．是否存在点P，使Q′恰好落在x轴上？若存在，求出此时点P的坐标；若不存在，说明理由．1、解：（1）∵抛物线y=ax2+bx+2经过A（﹣1，0），B（4，0）两点，∴，解得：∴y=﹣x2+x+2；当y=2时，﹣x2+x+2=2，解得：x1=3，x2=0（舍），即：点D坐标为（3，2）．（2）A，E两点都在x轴上，AE有两种可能：①当AE为一边时，AE∥PD，∴P1（0，2），②当AE为对角线时，根据平行四边形对顶点到另一条对角线距离相等，可知P点、D点到直线AE（即x轴）的距离相等，∴P点的纵坐标为﹣2，代入抛物线的解析式：﹣x2+x+2=﹣2解得：x1=，x2=，∴P点的坐标为（，﹣2），（，﹣2）综上所述：p1（0，2）；p2（，﹣2）；p3（，﹣2）．（3）存在满足条件的点P，显然点P在直线CD下方，设直线PQ交x轴于F，点P的坐标为（a，﹣a2+a+2），①当P点在y轴右侧时（如图1），CQ=a，PQ=2﹣（﹣a2+a+2）=a2﹣a，又∵∠CQ′O+∠FQ′P=90°，∠COQ′=∠Q′FP=90°，∴∠FQ′P=∠OCQ′，∴△COQ′～△Q′FP，，，∴Q′F=a﹣3，∴OQ′=OF﹣Q′F=a﹣（a﹣3）=3，CQ=CQ′==，此时a=，点P的坐标为（，），②当P点在y轴左侧时（如图2）此时a＜0，，﹣a2+a+2＜0，CQ=﹣a，PQ=2﹣（﹣a2+a+2）=a2﹣a，又∵∠CQ′O+∠FQ′P=90°，∠CQ′O+∠OCQ′=90°，∴∠FQ′P=∠OCQ′，∠COQ′=∠Q′FP=90°，∴△COQ′～△Q′FP，，，Q′F=3﹣a，∴OQ′=3，CQ=CQ′=，此时a=﹣，点P的坐标为（﹣，）．综上所述，满足条件的点P坐标为（，），（﹣，）．2、（2010•恩施州）如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．（1）求这个二次函数的表达式．（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．（3）当点P运动到什么位置时，四边形ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积．。

抛物线背景下特殊三角形存在性问题的解题策略【专题综述】动态问题是近几年来中考数学的热点题型，常与存在性问题结合，这类问题综合性较强，对学生分析问题和解决问题的能力要求较高，解题时要特别关注运动和变化过程中的不变量、不变关系和特殊关系．本文以中考题为例，对二次函数背景下，一些特殊三角形存在性问题的解题策略进行探究．【方法解读】一、探究等腰三角形的存在性例1 如图1，已知抛物线y＝ax2＋b x＋c经过A（－1，0）、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．(1)求抛物线的函数关系式；(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．解(1)易得y＝－x2＋2x－3；(2)分析由图知，A，B两点关于抛物线的对称轴对称，那么根据对称性以及两点之间线段最短可知，若连结BC，那么BC与直线l的交点即为符合条件的P点．易求得BC的函数关系式为y＝－x＋3，当x＝1时，y＝2，所以P(1，2)；评注例1(3)中，由于△MAC的腰和底不明确，因此要分上述三种情况来讨论．可先设出M的坐标，然后用M点纵坐标表示△MAC的三边长，再分别按三种情况列式求解．同学们可根据上述解题思路分析解决下题：如图2，在平面直角坐标系中，直角三角形AOB的顶点A、B分别落在坐标轴上．O为原点，点A的坐标为(6，0)，点B的坐标为(0，8)．动点M从点O出发．沿OA向终点A以每秒1个单位的速度运动，同时动点N从点A出发，沿AB向终点B以每秒53个单位的速度运动．当一个动点到达终点时，另一个动点也随之停止运动，设动点M、N运动的时间为t秒(t>0)．(1)当t＝3秒时，直接写出点Ⅳ的坐标，并求出经过O、A、N三点的抛物线的解析式；(2)在此运动的过程中，△MNA的面积是否存在最大值？若存在，请求出最大值；若不存在，请说明理由；(3)当t为何值时，△MNA是一个等腰三角形？二、探究直角三角形的存在性例2 如图3，已知抛物线y＝x2＋bx＋c与x轴交于A、B两点（A点在B点左侧），与y轴交于点C(0，－3)，对称轴是直线x＝1，直线BC与抛物线的对称轴交于点D．(1)求抛物线的函数表达式；(2)求直线BC的函数表达式；(3)点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限．①当线段PQ＝34AB时，求tan∠CED的值；②当以点C、D、E为顶点的三角形是直角三角形时，请直接写出点P的坐标．评注例2(3)②中直角三角形的存在性问题有三部曲：先罗列三边，再分类列方程，后解方程检验．罗列三边时，应将三边由同一变量的表达式进行表示，分类列方程的分类标准为直角顶点的不同，求解后注意取舍．三、探究相似三角形的存在性例3 如图4，已知二次函数y＝148(x＋2)（a x＋b）的图象过点A（－4，3），B(4，4)．(1)求二次函数的解析式：(2)求证：△ACB是直角三角形；(3)若点P在第二象限，且是抛物线上的一动点，过点P作PH垂直戈轴于点H，是否存在以P、H、D为顶点的三角形与△ABC相似？若存在，求出点P的坐标；若不存在，请说明理由．评注由动点产生的相似三角形问题的一般解题途径为：①若两个三角形各边均未给出，则应先设所求点的坐标，进而用变量表达式来表示各边的长度，再利用相似关系列方程求解．②求相似三角形的第三个顶点时，先要分析已知三角形的边和角的特点，进而得出其是否为特殊三角形，再根据未知三角形中，已知边与已知三角形中边的对应情形分类讨论．【强化训练】1.（2017辽宁省辽阳市）如图，抛物线223y x x =--与y 轴交于点C ，点D 的坐标为（0，﹣1），在第四象限抛物线上有一点P ，若△PCD 是以CD 为底边的等腰三角形，则点P 的横坐标为（ ）A ．12+B ．12-C ． 21-D ．12-或12+2.（2017山东省莱芜市）二次函数2y ax bx c =++（a ＜0）图象与x 轴的交点A 、B 的横坐标分别为﹣3，1，与y 轴交于点C ，下面四个结论： ①16a ﹣4b +c ＜0；②若P （﹣5，y 1），Q （52，y 2）是函数图象上的两点，则y 1＞y 2；③a =﹣13c ；④若△ABC 是等腰三角形，则b =﹣273．其中正确的有 （请将结论正确的序号全部填上） 3.如图，二次函数2y ax bx c =++（a ＞0）图象的顶点为D ，其图象与x 轴的交点A 、B 的横坐标分别为﹣1和3，则下列结论正确的是（ ）A ．2a ﹣b =0B ．a +b +c ＞0C ．3a ﹣c =0D ．当a =12时，△ABD 是等腰直角三角形 4.已知直线33y x =-+与坐标轴分别交于点A ，B ，点P 在抛物线21(3)43y x =--+上，能使△ABP为等腰三角形的点P 的个数有（ ）A ．3个B ．4个C ．5个D ．6个5. 如图，抛物线223y x x =-++与y 轴交于点C ，点D （0，1），点P 是抛物线上的动点．若△PCD 是以CD 为底的等腰三角形，则点P 的坐标为 ．6. 如图1，抛物线23[(2)]5y x n =--+与x 轴交于点A （m ﹣2，0）和B （2m +3，0）（点A 在点B 的左侧），与y 轴交于点C ，连结BC ． （1）求m 、n 的值；（2）如图2，点N 为抛物线上的一动点，且位于直线BC 上方，连接CN 、BN ．求△NBC 面积的最大值； （3）如图3，点M 、P 分别为线段BC 和线段OB 上的动点，连接PM 、PC ，是否存在这样的点P ，使△PCM 为等腰三角形，△PMB 为直角三角形同时成立？若存在，求出点P 的坐标；若不存在，请说明理由． 7.（2017辽宁省盘锦市）如图，直线y =﹣2x +4交y 轴于点A ，交抛物线212y x bx c =++ 于点B （3，﹣2），抛物线经过点C （﹣1，0），交y 轴于点D ，点P 是抛物线上的动点，作PE ⊥DB 交DB 所在直线于点E ． （1）求抛物线的解析式；（2）当△PDE 为等腰直角三角形时，求出PE 的长及P 点坐标；（3）在（2）的条件下，连接PB ，将△PBE 沿直线AB 翻折，直接写出翻折点后E 的对称点坐标．8.（2017四川省雅安市）如图，已知抛物线2y x bx c =++的图象经过点A （l ，0），B （-3，0），与y 轴交于点C ，抛物线的顶点为D ，对称轴与x 轴相交于点E ，连接BD ． （1）求抛物线的解析式．（2）若点P 在直线BD 上，当PE =PC 时，求点P 的坐标．（3）在（2）的条件下，作PF ⊥x 轴于F ，点M 为x 轴上一动点，N 为直线PF 上一动点，G 为抛物线上一动点，当以点F ，N ，G ，M 四点为顶点的四边形为正方形时，求点M 的坐标．9.（2017四川省眉山市）如图，抛物线22y ax bx =+-与x 轴交于A 、B 两点，与y 轴交于C 点，已知A （3，0），且M （1，83-）是抛物线上另一点． （1）求a 、b 的值；（2）连结AC ，设点P 是y 轴上任一点，若以P 、A 、C 三点为顶点的三角形是等腰三角形，求P 点的坐标； （3）若点N 是x 轴正半轴上且在抛物线内的一动点（不与O 、A 重合），过点N 作NH ∥AC 交抛物线的对称轴于H 点．设ON =t ，△ONH 的面积为S ，求S 与t 之间的函数关系式．10.（2017内蒙古包头市）如图，在平面直角坐标系中，已知抛物线232y x bx c =++与x 轴交于A （﹣1，0），B （2，0）两点，与y 轴交于点C ． （1）求该抛物线的解析式；（2）直线y =﹣x +n 与该抛物线在第四象限内交于点D ，与线段BC 交于点E ，与x 轴交于点F ，且BE =4EC ． ①求n 的值；②连接AC ，CD ，线段AC 与线段DF 交于点G ，△AGF 与△CGD 是否全等？请说明理由；（3）直线y =m （m ＞0）与该抛物线的交点为M ，N （点M 在点N 的左侧），点 M 关于y 轴的对称点为点M '，点H 的坐标为（1，0）．若四边形OM 'NH 的面积为53．求点H 到OM '的距离d 的值．。

教师姓名学生姓名年级初三上课时间2018/ /学科数学课题名称直角三角形的存在性问题解题策略待提升的知识点/题型考点提炼一、解直角三角形的存在性问题，一般分三步走，第一步寻找分类标准，第二步列方程，第三步解方程并验根．二、一般情况下，按照直角顶点或者斜边分类，然后按照三角比或勾股定理列方程．有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便．解直角三角形的问题，常常和相似三角形、三角比的问题联系在一起．如果直角边与坐标轴不平行，那么过三个顶点作与坐标轴平行的直线，可以构造两个新的相似直角三角形，这样列比例方程比较简便．三、在平面直角坐标系中，两点间的距离公式常常用到．怎样画直角三角形的示意图呢？如果已知直角边，那么过直角边的两个端点画垂线，第三个顶点在垂线上；如果已知斜边，那么以斜边为直径画圆，直角顶点在圆上（不含直径的两个端点）．考点精析例❶如图1-1，在△ABC中，AB＝AC＝10，cos∠B＝45．D、E为线段BC上的两个动点，且DE＝3（E在D右边），运动初始时D和B重合，当E和C重合时运动停止．过E作EF//AC交AB 于F，连结DF．设BD＝x，如果△BDF为直角三角形，求x的值．图1-1【解析】△BDF中，∠B是确定的锐角，那么按照直角顶点分类，直角三角形BDF存在两种情况．如果把夹∠B的两条边用含有x的式子表示出来，分两种情况列方程就可以了．如图1-2，作AH⊥BC，垂足为H，那么H是BC的中点．在Rt△ABH中，AB＝10，cos∠B＝45，所以BH＝8．所以BC＝16．由EF//AC，得BF BEBA BC=，即31016BF x+=．所以BF＝5(3)8x+．图1-2 图1-3 图1-4①如图1-3，当∠BDF＝90°时，由4cos5BDBBF∠==，得45BD BF=．解方程45(3)58x x=⨯+，得x＝3．②如图1-4，当∠BFD＝90°时，由4cos5BFBBD∠==，得45BF BD=．解方程5154885x x+=，得757x=．我们看到，在画示意图时，无须受到△ABC的“限制”，只需要取其确定的∠B．例❷如图2-1，已知A、B是线段MN上的两点，4=MN ，1=MA，1>MB．以A为中心顺时针旋转点M ，以B 为中心逆时针旋转点N ，使M 、N 两点重合成一点C ，构成 △ABC ，设AB ＝x ，若△ABC 为直角三角形，求x 的值．图2-1【解析】△ABC 的三边长都可以表示出来，AC ＝1，AB ＝x ，BC ＝3－x ． 如果用斜边进行分类，每条边都可能成为斜边，分三种情况：①若AC 为斜边，则22)3(1x x -+=，即0432=+-x x ，此方程无实根．②若AB 为斜边，则1)3(22+-=x x ，解得35=x （如图2-2）． ③若BC 为斜边，则221)3(x x +=-，解得34=x （如图2-3）．因此当35=x 或34=x 时，△ABC 是直角三角形．图2-2 图2-3例❸ 如图3-1，已知在平面直角坐标系中，点A 的坐标为（-2, 0），点B 是点A 关于原点的对称点，P 是函数)0(2>=x xy 图象上的一点，且△ABP 是直角三角形，求点P 的坐标．图3-1【解析】A 、B 两点是确定的，以线段AB 为分类标准，分三种情况．如果线段AB 为直角边，那么过点A 画AB 的垂线，与第一象限内的一支双曲线没有交点；过点B 画AB 的垂线，有1个交点．以AB 为直径画圆，圆与双曲线有没有交点呢？先假如有交点，再列方程，方程有解那么就有交点．如果是一元二次方程，那么可能是一个交点，也可能是两个交点．由题意，得点B 的坐标为（2，0），且∠BAP 不可能成为直角． ①如图3-2，当∠ABP ＝90°时，点P 的坐标为（2，1）．②方法一：如图3-3，当∠APB ＝90°时，OP 是Rt △APB 的斜边上的中线，OP ＝2． 设P 2(,)x x ，由OP 2＝4，得2244x x+=．解得2x =±．此时P (2,2)．图3-2 图3-3方法二：由勾股定理，得P A 2＋PB 2＝AB 2．解方程2222222(2)()(2)()4x x x x+++++=，得2x =±． 方法三：如图3-4，由△AHP ∽△PHB ，得PH 2＝AH ·BH ． 解方程22()(2)(2)x x x=+-，得2x =±．图3-4 图3-5这三种解法貌似差异很大，转化为整式方程之后都是(x 2－2)2＝0．这个四次方程的解是x 1＝x 2＝2，x 3＝x 4＝2-，它的几何意义就是以AB 为直径的圆与双曲线相切于P 、P ′两点（如图3-5）．例❹ 如图4-1，已知直线y ＝kx －6经过点A (1,－4)，与x 轴相交于点B ．若点Q 是y 轴上一点，且△ABQ 为直角三角形，求点Q 的坐标．图4-1【解析】和例题3一样，过A 、B 两点分别画AB 的垂线，各有1个点Q ．和例题3不同，以AB 为直径画圆，圆与y 轴有没有交点，一目了然．而圆与双曲线有没有交点，是徒手画双曲线无法肯定的．将A (1,－4)代入y ＝kx －6，可得k ＝2．所以y ＝2x －6，B (3,0)． 设OQ 的长为m ．分三种情况讨论直角三角形ABQ ：①如图4-2，当∠AQB ＝90°时，△BOQ ∽△QHA ，BO QH OQ HA =．所以341mm -=． 解得m ＝1或m ＝3．所以Q (0,－1)或(0,－3)． ②如图4-3，当∠BAQ ＝90°时，△QHA ∽△AGB ，QH AG HA GB =．所以4214m -=．解得72m =．此时7(0,)2Q -．③如图4-4，当∠ABQ ＝90°时，△AGB ∽△BMQ ，AG BM GB MQ =．所以243m=． 解得32m =．此时3(0,)2Q ．图4-2 图4-3 图4-4三种情况的直角三角形ABQ ，直角边都不与坐标轴平行，我们以直角顶点为公共顶点，构造两个相似的直角三角形，这样列比例方程比较简便．已知A (1,－4)、B (3,0)，设Q (0, n )，那么根据两点间的距离公式可以表示出AB 2，AQ 2和BQ 2，再按照斜边为分类标准列方程，就不用画图进行“盲解”了．例❺ 如图5-1，抛物线233384y x x =--+与x 轴交于A 、B 两点（点A 在点B 的左侧）．若直线l 过点E (4, 0)，M 为直线l 上的动点，当以A 、B 、M 为顶点所作的直角三角形有且只有．．．．三个时，求直线l 的解析式．图5-1【解析】有且只有三个直角三角形ABM 是什么意思呢？过A 、B 两点分别画AB 的垂线，与直线l 各有一个交点，那么第三个直角顶点M 在哪里？以AB 为直径的⊙G 与直线l 相切于点M 啊！由23333(4)(2)848y x x x x =--+=-+-，得A (－4, 0)、B (2, 0)，直径AB ＝6．如图5-2，连结GM，那么GM⊥l．在Rt△EGM中，GM＝3，GE＝5，所以EM＝4．因此3 tan4GEM∠=．设直线l与y轴交于点C，那么OC＝3．所以直线l（直线EC）为334y x=-+．根据对称性，直线l还可以是334y x=-．图5-2例❻如图6-1，在△ABC中，CA＝CB，AB＝8，4cos5A∠=．点D是AB边上的一个动点，点E与点A关于直线CD对称，连结CE、DE．（1）求底边AB上的高；（2）设CE与AB交于点F，当△ACF为直角三角形时，求AD的长；（3）连结AE，当△ADE是直角三角形时，求AD的长．图6-1【解析】这道题目画示意图有技巧的，如果将点D看作主动点，那么CE就是从动线段．反过来画图，点E在以CA为半径的⊙C上，如果把点E看作主动点，再画∠ACE的平分线就产生点D 了．（1）如图6-2，设AB边上的高为CH，那么A H＝BH＝4．在Rt△ACH中，AH＝4，4cos5A∠=，所以AC＝5，CH＝3．（2）①如图6-3，当∠AFC＝90°时，F是AB的中点，AF＝4，CF＝3．在Rt△DEF中，EF＝CE－CF＝2，4cos5E∠=，所以52DE=．此时52AD DE==．②如图6-4，当∠ACF＝90°时，∠ACD＝45°，那么△ACD的条件符合“角边角”．作DG⊥AC，垂足为G．设DG＝CG＝3m，那么AD＝5m，AG＝4m．由CA＝5，得7m＝5．解得57m=．此时2557AD m==．图6-2 图6-3 图6-4（3）因为DA＝DE，所以只存在∠ADE＝90°的情况．①如图6-5，当E在AB下方时，根据对称性，知∠CDA＝∠CDE＝135°，此时△CDH是等腰直角三角形，DH＝CH＝3．所以AD＝AH－DH＝1．②如图6-6，当E在AB上方时，根据对称性，知∠CDA＝∠CDE＝45°，此时△CDH是等腰直角三角形，DH＝CH＝3．所以AD＝AH＋DH＝7．图6-5 图6-6课堂测评（2018届黄浦二模）25．（本题满分14分）如图，四边形ABCD 中，∠BCD =∠D =90°，E 是边AB 的中点.已知AD =1，AB =2. （1）设BC =x ，CD =y ，求y 关于x 的函数关系式，并写出定义域； （2）当∠B =70°时，求∠AEC 的度数； （3）当△ACE 为直角三角形时，求边BC 的长.25. 解：（1）过A 作AH ⊥BC 于H ，————————————————————（1分） 由∠D =∠BCD =90°，得四边形ADCH 为矩形.在△BAH 中，AB =2，∠BHA =90°，AH =y ，HB =1x -，所以22221y x =+-，——————————————————————（1分） 则()22303y x x x =-++<<.———————————————（2分）BEDAC（2）取CD 中点T ，联结TE ，————————————————————（1分） 则TE 是梯形中位线，得ET ∥AD ，ET ⊥CD .∴∠AET =∠B =70°. ———————————————————————（1分） 又AD =AE =1，∴∠AED =∠ADE =∠DET =35°. ——————————————————（1分） 由ET 垂直平分CD ，得∠CET =∠DET =35°，————————————（1分） 所以∠AEC =70°＋35°=105°. ——————————————————（1分）（3）当∠AEC =90°时，易知△CBE ≌△CAE ≌△CAD ，得∠BCE =30°， 则在△ABH 中，∠B =60°，∠AHB =90°，AB =2，得BH =1，于是BC =2. ——————————————————————（2分）当∠CAE =90°时，易知△CDA ∽△BCA ，又2224AC BC AB x =-=-，则221411724AD CAx x AC CBx x -±=⇒=⇒=-（舍负）—————（2分） 易知∠ACE <90°. 所以边BC 的长为2或1172+.——————————————————（1分）回顾总结一、直角三角形存在问题的解题策略分哪三步？二、直角三角形存在问题的分类的一般方法是什么？三、直角三角形在直角坐标系中有哪些特定的解题思路和方法？中考演练（上海市2015年14分）25.已知：如图，AB 是半圆O 的直径，弦//CD AB ，动点P 、Q 分别在线段OC 、CD 上，且DQ OP =，AP 的延长线与射线OQ 相交于点E 、与弦CD 相交于点F （点F 与点C 、D 不重合），20AB =，4cos 5AOC ∠=．设OP x =，CPF ∆的面积为y ． （1）求证：AP OQ =；（2）求y 关于x 的函数关系式，并写出它的定义域； （3）当OPE ∆是直角三角形时，求线段OP 的长．【答案】（1）通过证明AOP ∆≌ODQ ∆，过程略；（2）236030050(10)13x x y x x -+=<<；（3）8OP =（3）分成三种情况讨论，充分利用已知条件4cos 5AOC ∠=、以及（1）（2）中已证的结论，注意要对不符合（2）中定义域的答案舍去.∠，∴OP90时，9090时，CQ==cos-CD CQ90时，∵APO，∴，此时弦种情况不符合题意，舍；圆的综合应用（2017年上海市第25题）如图，已知⊙O的半径长为1，AB、AC是⊙O的两条弦，且AB=AC，BO 的延长线交AC于点D，联结OA、OC．（1）求证：△OAD∽△ABD；（2）当△OCD是直角三角形时，求B、C两点的距离；（3）记△AOB、△AOD、△COD 的面积分别为S1、S2、S3，如果S2是S1和S3的比例中项，求OD的长．【答案】（1）证明见解析；（2）BC=3．（3）OD=5-1 2．【解析】试题分析：（1）由△AOB≌△AOC，推出∠C=∠B，由OA=OC，推出∠OAC=∠C=∠B，由∠ADO=∠ADB，即可证明△OAD∽△ABD；试题解析：（1）如图1中，在△AOB和△AOC中，OA OAAB ACOB OC=⎧⎪=⎨⎪=⎩，∴△AOB≌△AO C，∴∠C=∠B，∵OA=OC，∴∠OAC=∠C=∠B，∵∠ADO=∠ADB，∴△OAD∽△ABD．（2）如图2中，∵BD⊥AC，OA=OC，∴AD=DC，∴BA=BC=AC，∴△ABC是等边三角形，在Rt△OAD中，∵OA=1，∠OAD=30°，∴OD=12OA=12，∴AD=22OA OD- =32，∴BC=AC=2AD=3．（3）如图3中，作OH⊥AC于H，设OD=x．∵△DAO∽△DBA，∴AD OD OADB AD AB== ,∴11AD xx AD AB==+，∴AD=()1x x+，AB=()1x xx+，∵S2是S1和S3的比例中项，∴S22=S1S3，∵S2=12ADOH，S1=S△OAC=12AC﹒OH，S3=12CD﹒OH，∴（12AD﹒OH）2=12AC﹒OH﹒12CD﹒OH，∴AD2=ACCD，∵AC=AB．CD=AC﹣AD=()1x xx+﹣()1x x+，∴（()1x x +）2=()1x x x+（()1x x x+﹣()1x x +），∴OD=5-12． 考点：1.圆综合题；2.全等三角形的判定和性质；3.相似三角形的判定和性质；4.比例中项.。