中考第23题专题之-----抛物线与特殊的四边形的存在性问题

中考数学总复习《二次函数中的特殊四边形存在性问题 》专题训练-附答案学校:___________班级：___________姓名：___________考号：___________1．如图，已知抛物线223y x x =+-的图像与坐标轴分别交于、、A B C 三点，连接AC ，点M 是AC 的中点，抛物线的对称轴交x 轴于点F ，作直线FM ．(1)直接写出下列各点的坐标：F ______，M ______；(2)若点P 为直线FM 下方抛物线上动点，过点P 作PQ y ∥轴，交直线FM 于点Q ，当PQM 为直角三角形时，求点P 的坐标；(3)若点N 是x 轴上一动点，则在坐标平面内是否存在点E ，使以点F M N E 、、、为顶点的四边形是正方形？若存在，请直接写出点E 的坐标：若不存在，请说明理由．2．如图所示，在平面直角坐标系中，直线3y x =-+交坐标轴于B 、C 两点，抛物线23y ax bx =++经过B 、C 两点，且交x 轴于另一点()1,0A -．点D 为抛物线在第一象限内的一点，过点D 作DQ CO ∥，DQ 交BC 于点P ，交x 轴于点Q ．(1)求抛物线的解析式；(2)设点P 的横坐标为m ，在点D 的移动过程中，存在DCP DPC ∠=∠，求出m 值；(3)在抛物线上取点E ，在平面直角坐标系内取点F ，问是否存在以C 、B 、E 、F 为顶点且以CB 为边的矩形？如果存在，请求出点F 的坐标；如果不存在，请说明理由．3．如图，已知抛物线223y x x =--+的顶点为D 点，且与x 轴交于B ，A 两点（B 在A 的左侧），与y 轴交于点C ．点E 为抛物线对称轴上的一个动点：(1)当点E 在x 轴上方且CE BD ∥时，求sin DEC ∠的值；(2)若点Р在抛物线上，是否存在以点B ，E ，C ，P 为顶点的四边形是平行四边形﹖请求出点Р的坐标；(3)若抛物线对称轴上有点E ，使得55AE DE +取得最小值，连接AE 并延长交第二象限抛物线为点M ，请直接写出AM 的长度．4．如图，抛物线22y ax bx =++与x 轴交于()1,0A -和()4,0B ，与y 轴交于点C ．(1)求抛物线的解析式；(2)如图1，若点D 是第一象限内抛物线上的一个动点，连接AC ，CD ，DB ，试求四边形ABDC 面积的最大值；(3)如图2，点(),1D m m -是第一象限内抛物线上的一点，连接AD ，BD ，点E 是线段AB 上的任意一点（不与点A ，B 重合），过点E 分别作EM AD ∥交BD 于点M ，EN BD ∥交AD 于点N ．①判断四边形EMDN 的形状，并证明你的结论；①四边形EMDN 是否能成为正方形？若能，请直接写出点E 的坐标；若不能，请说明理由．5．如图，在平面直角坐标系中，AOC 绕原点O 逆时针旋转90︒得到DOB ，其中1OA =，OC=3．(1)若二次函数经过A 、B 、C 三点，求该二次函数的解析式；(2)在（1）条件下，在二次函数的对称轴l 上是否存在一点P ，使得PA PC +最小？若P 点存在，求出P 点坐标；若P 点不存在，请说明理由．(3)在（1）条件下，若E 为x 轴上一个动点，F 为抛物线上的一个动点，使得B 、C 、E 、F 构成平行四边形时，求E 点坐标．6．如图，在平面直角坐标系中，抛物线234y x bx c =++与直线AB 交于点()0,3A -和()4,0B ．(1)求抛物线的函数解析式；(2)点P 是直线AB 下方抛物线上一点，过点P 作y 轴的平行线，交AB 于点E ，过点P 作AB 的垂线，垂足为点F ，求PEF 周长的最大值及此时点P 的坐标；(3)在（2）中PEF 取得最大值的条件下，将该抛物线沿水平方向向左平移3个单位，点Q 为点P 的对应点，点N 为原抛物线对称轴上一点．在平移后抛物线上确定一点M ，使得以点B ，Q ，M ，N 为顶点的四边形是平行四边形，写出所有符合条件的点M 的坐标，并写出求解点M 的坐标的其中一种情况的过程．7．如图，在平面直角坐标系中，抛物线()230y ax bx a =+-≠与x 轴交于()1,0A -，()3,0B 两点，与y 轴交于C 点．(1)求抛物线的函数表达式；(2)点P 是直线BC 下方抛物上一动点，连接PB ，PC ，求PBC 面积的最大值以及此时点P 的坐标；(3)在（2）中PBC 的面积取得最大值的条件下，将该抛物线沿水平方向向左移动2个单位，平移后的抛物线顶点坐标为Q ，M 为y 轴上一点，在平移后的抛物线上确定一点N ，使得以点P ，Q ，M ，N 为顶点的四边形是平行四边形，写出所有符合条件的N 的坐标，并写出求解点N 的坐标的其中一种情况的过程．8．如图，在平面直角坐标系中，抛物线()240y ax bx a =+-≠与x 轴交于()4,0A ，()2,0B -两点，与y 轴交于点C ，连接BC ，y 轴上有一点()0,3D -．(1)求抛物线的函数表达式；(2)点P 是直线AD 下方抛物线上的一个动点，过点P 作PH x ⊥轴于点H ，PH 交直线AD 于点E ，作PF BC 交直线AD 于点F ，求11510PF PH +的最大值，及此时点P 的坐标； (3)在（2）的条件下，将点P 向右平移152个单位长度，再向上平移398个单位长度得到点P '；将抛物线沿着射线BC 方向平移5个单位长度得到一条新抛物线，点M 为新抛物线与y 轴的交点，N 为新抛物线上一点，Q 为新抛物线对称轴上一点，请写出所有使得以点P '，M ，Q ，N 为顶点的四边形是平行四边形的点Q 的坐标，并写出求解点Q 的坐标的其中一种情况的过程．9．如图，抛物线212y x bx c =-++的图象经过点C ，交x 轴于点()1,0A -、()4,0B （A 点在B 点左侧），顶点为D ．(1)求抛物线的解析式；(2)点P 在直线BC 上方的抛物线上，过点P 作y 轴的平行线交BC 于点Q ，过点P 作x 轴的平行线交y 轴于点F ，过点Q 作x 轴的平行线交y 轴于点E ，求矩形PQEF 的周长最大值；(3)抛物线的对称轴上是否存在点M ，使45BMC ∠=︒？若存在，请直接写出点M 的纵坐标；若不存在，请说明理由．10．如图1，抛物线232y ax x c =++与x 轴交于点A 、(4,0)B （A 点在B 点左侧），与y 轴交于点(0,6)C ，点P 是抛物线上一个动点，连接,,PB PC BC(1)求抛物线的函数表达式；(2)如图2所示，当点P 在直线BC 上方运动时，连接AC ，求四边形ABPC 面积的最大值，并写出此时P 点坐标．(3)若点M 是x 轴上的一个动点，点N 是抛物线上一动点，P 的横坐标为3．试判断是否存在这样的点M ，使得以点,,,B M N P 为顶点的四边形是平行四边形，若存在，请直接写出点M 的坐标；若不存在，请说明理由．11．如图，已知抛物线2y x bx c =-++与y 轴交于点C ，与x 轴交于(1,0)A -，(3,0)B 两点．(1)求抛物线的解析式． (2)连接AC ，在抛物线的对称轴上是否存在点P ，使得ACP △的周长最小？若存在，求出点P 的坐标和ACP △的周长的最小值，若不存在，请说明理由．(3)点M 为抛物线上一动点，点N 为x 轴上一动点，当以A ，C ，M ，N 为顶点的四边形为平行四边形时，直接写出点M 的横坐标．12．在平面直角坐标系中，抛物线24y x x c =--+与x 轴交于点A ，B （点A 在点B 的左侧），与y 轴交于点C ，且点A 的坐标为()5,0-．(1)求点C 的坐标；(2)如图1，若点P 是第二象限内抛物线上一动点，求三角形ACP 面积的最大值；(3)如图2，若点M 是抛物线上一点，点N 是抛物线对称轴上一点，是否存在点M 使以A ，C ，M ，N 为顶点的四边形是平行四边形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．13．如图，在平面直角坐标系中，抛物线()10A -，，()30B ，和()01C -，三点．(1)求该抛物线的表达式与顶点坐标；(2)点Q 在y 轴上，点P 在抛物线上，要使Q 、P 、A 、B 为顶点的四边形是平行四边形，求所有满足条件点P 的坐标．14．如图，抛物线2()y a x h k =-+的顶点坐标是19,24⎛⎫ ⎪⎝⎭，与x 轴交于点A 、点()2,0B ，与y 轴交于点C ．(1)求抛物线的解析式；(2)点P 在抛物线的对称轴上，点Q 在抛物线上，是否存在点Q ，使得以B 、C 、P 、Q 为顶点的四边形是平行四边形？若存在，请求出点Q 的坐标；若不存在，请说明理由．15．综合与探究如图，抛物线2142y x x =+-与x 轴交于点A 和B ，点A 在点B 的左侧，与y 轴交于点C ，点P 在直线AC 下方的抛物线上运动．(1)求点B 的坐标和直线AC 的解析式；(2)如图1，过点P 作PD y ∥轴交直线AC 于点D ，过点P 作PE AC ⊥，垂足为E ，当PDE △的面积最大时，求点P 的坐标；(3)点M 在抛物线上运动，点N 在x 轴上运动，以点B ，C ，M 和N 为顶点的四边形是平行四边形，借助图2探究，请直接写出符合条件的点M 的坐标．参考答案： 1．(1)(1,0)F - 13(,)22M - (2)点P 的坐标为：1P （210322---，） 21555(,)22P ---- (3)存在，13(,)22E 或3(1,)2E --2．(1)223y x x =-++(2)2m =(3)存在，此时点F 的坐标为()4,1或()5,2--3．(1)55(2)存在 ()2,3P - ()4,5P -- ()2,5P -(3)754AM =4．(1)213222y x x =-++ (2)四边形ABDC 面积的最大值为9(3)①矩形①能，7,03E ⎛⎫ ⎪⎝⎭5．(1)2=23y x x --(2)存在(3)(72,0)-或(72,0)--或(1,0)6．(1)239344y x x =-- (2)365 92,2P ⎛⎫- ⎪⎝⎭ (3)13693,216M ⎛⎫ ⎪⎝⎭ 727,216M ⎛⎫-- ⎪⎝⎭ 333,216M ⎛⎫ ⎪⎝⎭7．(1)2=23y x x --(2)315(,)24P - (3)17(,)24N -或533(,)24N 或57(,)24N --8．(1)2142y x x =-- (2)11510PF PH +最大值为758，此时点P 的坐标为335,28⎛⎫- ⎪⎝⎭ (3)点Q 的坐标为()2,39或()2,29或()2,10-9．(1)213222y x x =-++ (2)9(3)3132+或3912--10．(1)233642y x x =-++ (2)2t =时，ABPC S 四边形有最大值，最大值为24，点P 的坐标为(2,6)(3)存在，点M 的坐标为(0,0)或()14,0-或(14,0)或(8,0)11．(1)223y x x =-++(2)(1,2)P 1032+(3)2或17+或17-12．(1)(0,5)(2)1258(3)存在，点M 的坐标为：()3,8-或()3,16-或(7,16)--13．(1)212133y x x =--，顶点坐标为413⎛⎫- ⎪⎝⎭， (2)()21-，或543⎛⎫ ⎪⎝⎭，或()47-，14．(1)22y x x =-++(2)存在，点Q 的坐标为：35,24Q ⎛⎫ ⎪⎝⎭或37,24⎛⎫-- ⎪⎝⎭或57,24⎛⎫- ⎪⎝⎭15．(1)点B 的坐标为()20，，直线AC 的解析式为4y x =-- (2)()24--，(3)()24--，或()1174--，或()1174-+，；。

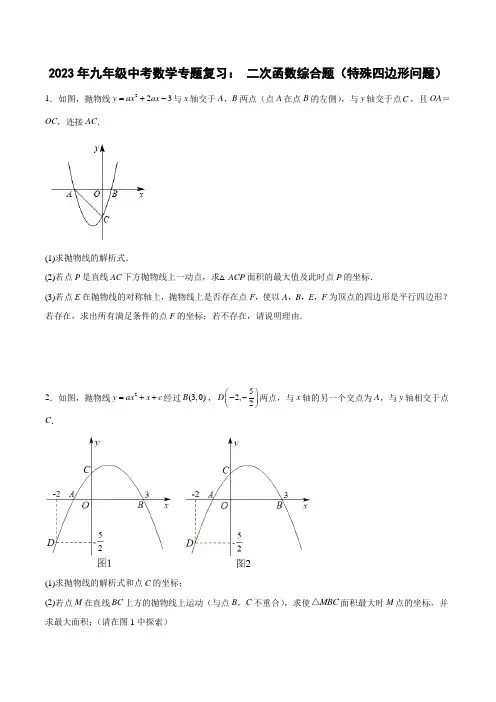
2023年九年级中考数学专题复习： 二次函数综合题（特殊四边形问题） 1．如图，抛物线223y ax ax =+-与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，且OA ＝OC ，连接AC ．(1)求抛物线的解析式．(2)若点P 是直线AC 下方抛物线上一动点，求△ACP 面积的最大值及此时点P 的坐标．(3)若点E 在抛物线的对称轴上，抛物线上是否存在点F ，使以A ，B ，E ，F 为顶点的四边形是平行四边形？若存在，求出所有满足条件的点F 的坐标；若不存在，请说明理由．2．如图，抛物线2y ax x c =++经过(3,0)B ，52,2D ⎛⎫-- ⎪⎝⎭两点，与x 轴的另一个交点为A ，与y 轴相交于点C ．(1)求抛物线的解析式和点C 的坐标；(2)若点M 在直线BC 上方的抛物线上运动（与点B ，C 不重合），求使MBC △面积最大时M 点的坐标，并求最大面积；（请在图1中探索）(3)设点Q 在y 轴上，点P 在抛物线上，要使以点A ，B ，P ，Q 为顶点的四边形是平行四边形，求所有满足条件的点P 的坐标．（请在图2中探索）3．如图，抛物线经过A (﹣1，0)，B (3，0)，C (0，32)三点．(1)求抛物线的解析式；(2)在抛物线的对称轴上有一点P ，使P A +PC 的值最小，求点P 的坐标；(3)点M 为x 轴上一动点，在抛物线上是否存在一点N ，使以A ，C ，M ，N 四点构成的四边形为平行四边形？若存在，求点的坐标；若不存在，请说明理由．4．如图，在平面直角坐标系中，矩形OABC 的两边OA ，OC 分别在x 轴和y 轴上，3OA =，4OC =，抛物线24y ax bx =++经过点B ，且与x 轴交于点()1,0D -和点E ．(1)求抛物线的表达式：(2)若P 是第一象限抛物线上的一个动点，连接CP ，PE ，当四边形OCPE 的面积最大时，求点P 的坐标，此时四边形OCPE 的最大面积是多少；(3)若N 是抛物线对称轴上一点，在平面内是否存在一点M ，使以点C ，D ，M ，N 为顶点的四边形是矩形？若存在，请直接写出点M 的坐标；若不存在，说明理由．5．已知二次函数2(0)y x bx c a =++≠的图像与x 轴的交于A 、(1,0)B 两点，与y 轴交于点(0,3)C -．(1)求二次函数的表达式及A 点坐标；(2)D 是二次函数图像上位于第三象限内的点，求点D 到直线AC 的距离取得最大值时点D 的坐标；(3)M 是二次函数图像对称轴上的点，在二次函数图像上是否存在点N ．使以M 、N 、B 、O 为顶点的四边形是平行四边形？若有，请写出点N 的坐标（不写求解过程）．6．如图，已知抛物线y＝x2﹣5x+4与x轴交于点A和点B（点A在点B的左侧），与y轴交于点C.(1)求A、B、C三点的坐标；(2)如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ，当线段PQ长度最大时，判断四边形OCPQ的形状，并说明理由；(3)如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且∠DQE＝2∠ODQ.在y轴上是否存在点F，使得△BEF为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由.7．如图，在平面直角坐标系中，抛物线y＝x2+bx+c与x轴交于点A（-1，0），B（3，0），与y轴交于点C，作直线BC，点P是抛物线在第四象限上一个动点（点P不与点B，C重合），连结PB，PC，以PB，PC为边作平行四边形CPBD，点P的横坐标为m．(1)求抛物线对应的函数表达式；(2)当平行四边形CPBD有两个顶点在x轴上时，点P的坐标为；(3)当平行四边形CPBD是菱形时，求m的值．8．如图，在平面直角坐标系中，抛物线2y x bx c =-++经过点()1,6A -，()2,0B ．(1)求该抛物线的解析式；(2)点P 为直线AB 上方抛物线上一动点，过点P 作PQ x ⊥轴，交AB 于点Q ，过点P 作PM AB ⊥于M ，当线段PM 的长度取得最大值时，求点P 的坐标和线段PM 的长度；(3)把抛物线2y x bx c =-++沿射线AB C 是新抛物线对称轴上一点，D 为平面上任意一点，直接写出所有使得以A 、B 、C 、D 为顶点的四边形为菱形的点D 的坐标．9．如图1，在平面直角坐标系中，抛物线与x 轴分别交于A 、B 两点，与y 轴交于点C （O ，6），抛物线的顶点坐标为E （2，8），连接BC 、BE 、CE ．(1)求抛物线的表达式；(2)判断△BCE 的形状，并说明理由；(3)如图2，点F 为线段BE 的中点，点P ，Q 分别为x 轴，y 轴上的动点，当四边形EFPQ 的周长取最小值时，求P ，Q 两点的坐标．10．如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于A、B两点（点A在点B的左侧），点B坐标（3，0），抛物线与y轴交于点C（0，﹣3），点D为抛物线顶点，对称轴x＝1与x轴交于点E，连接BC、EC．(1)求抛物线的解析式；(2)点P是BC下方异于点D的抛物线上一动点，若S△PBC＝S△EBC，求此时点P的坐标；(3)点Q是抛物线上一动点，点M是平面上一点，若以点B、C、Q、M为顶点的四边形为矩形，直接写出满足条件的点Q的横坐标．11．如图，一次函数y＝kx＋2的图象分别交y轴，x轴于A，B两点，B的坐标为（4，0），抛物线y＝－x2＋bx＋c经过A，B两点．(1)求k的值及抛物线的解析式．(2)直线x＝t在第一象限交直线AB于点M，交抛物线于点N，当t取何值时，线段MN的长有最大值？最大值是多少？(3)在（2）的情况下，以A，M，N，D为顶点作平行四边形，直接写出第四个顶点D的坐标，并直接写出所有平行四边形的面积是多少．12．如图，一次函数3y x =-+的图象与x 轴和y 轴分别交于点B 和点C ，二次函数2y x bx c =-++的图象经过B ，C 两点，并与x 轴交于点A ．点(),0M m 是线段OB 上一个动点（不与点O 、B 重合），过点M 作x 轴的垂线，分别与二次函数图象和直线BC 相交于点D 和点E ，连接CD ．(1)求这个二次函数的解析式．(2)①求DE 、CE 的值（用含m 的代数式表示）．②当以C ，D ，E 为顶点的三角形与△ABC 相似时，求m 的值．(3)点F 是平面内一点，是否存在以C ，D ，E ，F 为顶点的四边形为菱形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．13．如图，已知抛物线2y ax bx c =++与x 轴交于A （1，0）、B （－3，0）两点，与y 轴交于C （0，3）．(1)求抛物线的函数表达式：(2)设P 为抛物线上一动点，点P 在直线BC 上方时，求△BPC 面积的最大值：(3)若M 为抛物线上动点，点N 在抛物线对称轴上，是否存在点M 、N 使点A 、C 、M 、N 为平行四边形？如果存在，直接写出点N 的坐标：如果不存在，请说明理由．14．如图已知二次函数2y x bx c =++（b ，c 为常数）的图像经过点(3,1)A -，点(0,4)C -，顶点为点M ，过点A 作AB x ∥轴，交y 轴于点D ，交二次函数2y x bx c =++的图象于点B ，连接BC ．(1)求该二次函数的表达式及点M 的坐标；(2)若将该二次函数图象向上平移(0)m m >个单位，使平移后每到的二次函数图象的顶点落在ABC 的内部（不包括ABC 的边界），求m 的取值范围；(3)若E 为y 轴上且位于点C 下方的一点，P 为直线AC 上一点，在第四象限的抛物线上是否存在一点Q ，使以C 、E 、P 、Q 为顶点的四边形是菱形？若存在，请求出点Q 的横坐标；若不存在，请说明理由．15．如图，在平面直角坐标系中，二次函数y ＝x 2+bx +c 的图象与x 轴交于点A (﹣1，0)，B (3，0)，与y 轴交于点C ．(1)b ＝______，c ＝______；(2)若点D 为第四象限内抛物线上的一个动点，过点D 作DE ∥y 轴交BC 于点E ，过点D 作DF ⊥BC 于点F ，过点F 作FG ⊥y 轴于点G ，求出DE +FG 的最大值及此时点D 的坐标；(3)若点P 是该抛物线对称轴上的一点，点Q 为坐标平面内一点，那么在抛物线上且位于x 轴上方是否存在点M ，使四边形OMPQ 为正方形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．16．如图，在平面直角坐标系中，已知抛物线()220y ax bx a =+-≠与x 轴交于点A （1，0），B （5，0）两点，与y 轴交于点C ，点D 为抛物线的顶点．(1)求抛物线的解析式和点D 的坐标；(2)求△BCD 的面积；(3)点M 为抛物线上一动点，点N 为平面内一点，以A ，M ，I ，N 为顶点作正方形，是否存在点M ，使点I恰好落在对称轴上？若存在，直接写出点M 的坐标；若不存在，请说明理由．17．如图，二次函数2y ax 2x c =++（0a ≠）的图象经过点()0,3C ，与x 轴分别交于点A ，点()3,0B ．(1)求该二次函数的解析式及其图象的顶点坐标；(2)点P 是直线BC 上方的抛物线上任意一点，点P 关于y 轴的对称点记作点P '，当四边形POP C '为菱形时，求点P 的坐标；(3)点P 是抛物线上任意一点，过点P 做PD BC ⊥，垂足为点D ．过点P 作PQ x ∥轴，与抛物线交于点Q ．若PQ =，求点P 的坐标．18．如图，在平面直角坐标系中，二次函数223y mx mx =-+的图像与x 轴交于A 和点B （点A 在点B 的左侧），与y 轴交于点C ，且AB ＝4．(1)求这个函数的解析式，并直接写出顶点D 的坐标；(2)点E 是二次函数图像上一个动点，作直线EF x ∥轴交抛物线于点F （点E 在点F 的左侧），点D 关于直线EF 的对称点为G ，如果四边形DEGF 是正方形，求点E 的坐标；(3)若射线AC 与射线BD 相交于点H ，求∠AHB 的大小．19．如图，已知直线3y =-与x 轴，y 轴分别交于点A ，B ，抛物线213y x bx c =++的顶点是)1-，且与x 轴交于C ，D 两点，与y 轴交于点E ，P 是抛物线上一个动点，过点P 作PG AB ⊥于点G ．(1)求b 、c 的值；(2)若点M 是抛物线对称轴上任意点，点N 是抛物线上一动点，是否存在点N ，使得以点C ，D ，M ，N 为顶点的四边形是菱形？若存在，请你求出点N 的坐标；若不存在，请你说明理由．(3)当点P 运动到何处时，线段PG 的长最小？最小值为多少？20．综合与探究 如图，抛物线249y x bx c =-++与y 轴交于点()0,8A ，与x 轴交于点()6,0B ，C ，过点A 作AD x ∥轴与抛物线交于另一点D ．(1)求抛物线的表达式；(2)连接AB ，点P 为AB 上一个动点，由点A 以每秒1个单位长度的速度沿AB 运动（不与点B 重合），运动时间为t ，过点P 作PQ y ∥轴交抛物线于点Q ，求PQ 与t 的函数关系式；(3)点M 是y 轴上的一个点，点N 是平面直角坐标系内一点，是否存在这样的点,M N ，使得以,,,B D M N 为顶点的四边形是矩形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．参考答案：2．(1)223y x x =+-(2)当32x =-时，△ACP 面积的最大值为278，此时点3(2,)4P --； (3)点F 的坐标为（﹣5，12）或（3，12）或（﹣1，﹣4）3．(1)21322y x x =-++，30,2C ⎛⎫ ⎪⎝⎭(2)315,28M ⎛⎫ ⎪⎝⎭，当32m =时，S 有最大值为2716 (3)满足条件的点P 坐标为154,2P ⎛⎫- ⎪⎝⎭，2214,2P ⎛⎫-- ⎪⎝⎭，332,2P ⎛⎫ ⎪⎝⎭4．(1)21322y x x =-++ (2)（1，1）(3)存在，3(2,)2，(13)2，(13)25．(1)y ＝－x 2＋3x ＋4(2)P （2，6）；四边形OCPE 的面积最大为16(3)存在； M 113,28⎛⎫- ⎪⎝⎭或M 252728,⎛⎫ ⎪⎝⎭或M 355,22⎛⎫- ⎪⎝⎭或M 453,22⎛⎫- ⎪⎝⎭6．(1)223y x x =+-，(3,0)A -(2)315,24D ⎛⎫-- ⎪⎝⎭(3)存在，(2,3)--或(0,3)-或(2,5)7．(1)点A （1，0），点B （4，0），点C （0，4）(2)平行四边形(3)存在；F （0，1）或（0，﹣1）或（0，258）8．(1)223y x x =--(2)（2，-3）(3)12m m ==9．(1)26y x x =--+(2)1(2P ，21)4；PM =(3)5(2-，6或5(2-，6或7(2或7(2， 10．(1)y 212x =-+2x +6 (2)直角三角形(3)P ，Q 两点的坐标分别为（2，0），（0，4）11．(1)y =x 2-2x -3(2)(2，-3)(3)1或-212．(1)k =-12，y =-x 2+72x +2； (2)当t =2时，MN 有最大值4；(3)点D 的坐标为（0，-2）或（0，6）或（4，4）时，以A 、M 、N 、D 为顶点的四边形是平行四边形，平行四边形的面积均为8．13．(1)2y x 2x 3=-++(2)①23DE m m =-，CE =；②m 的值为32或53(3)存在以C ，D ，E ，F 为顶点的四边形为菱形，点M 的坐标为(1，0)或(2，0)或(3，0)．14．(1)223y x x =--+(2)278(3)存在，(1-，0)或(1-，8)15．(1)二次函数解析式为224y x x =--，点M 的坐标为（1，-5）(2)24m <<(3)当点Q 的横坐标为3时，四边形CEQP 为顶点的四边形为菱形16．(1)﹣2，3(2)GF +DE 有最大值258，D 57,24⎛⎫- ⎪⎝⎭(3)存在，M 点的坐标为或 17．(1)2212y x x 255=-+-，顶点D 的坐标是（3，85） (2)6(3)存在，点M ）或18．(1)2y x 2x 3=-++(2)32P ⎫⎪⎪⎝⎭(3)()2,3P 或1,0或⎝⎭或⎝⎭19．(1)2y x 2x 3=-++；D （1，4）；(2)E （0，3）；(3)45AHB ︒∠=．20．(1)b =3c =．(2)存在，符合条件的点N 的坐标为或(0,3)或)1-．(3)当点P PG 21．(1)244893y x x =-++ (2)PQ 与t 的函数关系式为248255PQ t t =-+（010t ≤<）； (3)存在点,M N ，使得以,,,B D M N 为顶点的四边形是矩形，点N 的坐标为(3,)98-或()233,4-.。

中考专题复习《抛物线与四边形》解抛物线与四边形相关的问题，特殊四边形的性质与判定是解题的基础，而待定系数法、数形结合、分类讨论是解题的关键。

以抛物线为背景，探讨是否存在一些点，使其能构成某些特殊的四边形，有以下基本形式：（1）抛物线上的点能否构成平行四边形;（2）抛物线上的点能否构成矩形、菱形或正方形；（3）抛物线上的点能否构成梯形;下面，我就通过几个具体的实例来探讨解析抛物线与四边形结合的综合题。

一、抛物线与平行四边形将二次函数与方程（组）、平行四边形的知识有机的结合在一起。

这类试题难度较大，解这类试题关键是善于将函数问题转化为方程问题，善于利用平行四边形的有关性质定理与判定定理，二次函数的知识，并充分挖掘题目中的隐含条件，用分类讨论的方法分析答案有几种可能。

例1、如图，在平面直角坐标系中，抛物线A（-1，0），B（3，0），C（0，-1）三点．（1）求该抛物线的表达式；（2）点Q在y轴上，点P在抛物线上，要使Q、P、A、B为顶点的四边形是平行四边形，求所有满足条件点P的坐标．分析：（1）设出抛物线的表达式为y=ax2+bx+c，由于抛物线经过A（-1，0），B（3，0），C（0，-1）三点，把三点代入表达式，联立解方程组，求出a、b、c．（2）要分类讨论AB 是边还是对角线两种情况，AB 为边时，只要PQ ∥AB 且PQ =AB=4，进而求出P 点坐标，当AB 为对角线时，只要线段PQ 与线段AB 互相平分，进而求出P 点坐标．解答：（1）设该抛物线的表达式为y=ax 2+bx+c 根据题意，得：⎪⎩⎪⎨⎧-==++=+-10390c c b a c b a 解得：⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-=-=13231c b a ∴所求抛物线的表达式为y=132312---x x （2）①AB 为边时，只要PQ ∥AB 且PQ=AB=4即可。

又知点Q 在y 轴上，∴点P 的横坐标为4或-4，这时符合条件的点P 有两个，分别记为P1，P2 而当x=4时，y=32；当x=-4时，y=7， 此时P1（4，32）,P2（-4,7） ②当AB 为对角线时，只要线段PQ 与线段AB 互相平分即可又知点Q 在Y 轴上，且线段AB 中点的横坐标为1∴点P 的横坐标为2，这时符合条件的P 只有一个记为P3而且当x=2时y=-1 ，此时P3（2，-1）综上，满足条件的P 为P1（4，32）,P2（-4,7）,P3（2，-1） 二、抛物线与矩形、菱形或正方形我们解决这类问题要能够熟练运用配方法求抛物线的对称轴、顶点坐标以及与x 轴、y 轴的交点坐标，并且要充分理解矩形、菱形和正方形的性质和判定，注意它们之间的联系与区别。

专题二二次函数背景下的平行四边形的存在性问题知识梳理平行四边形的存在性问题是分类讨论中的一大难点。

此类题目多在直角坐标平面内，辅以二次函数为背景.一般会根据两个或者三个定点,在某个特定的位置上找另两个顶点或者第四个顶点，这样的顶点往往不止一个,需要仔细考虑解题策略,如:若已知两点构成的线段是平行四边形的一边或者对角线.如何利用平行四边形的性质确定出其他的顶点的位置，否则在分类时就容易漏解.【典型例题】【例1】如图.抛物线y= ax2 +bx+c与y轴正半轴交于点C，与x轴交于点A(1，0)、B (4，0)，∠OCA=∠OBC.(1)求抛物线的解析式;(2)在直角坐标平面内确定点M，使得以点M、A、B、C为顶点的四边形是平行四边形,请直接写出点M的坐标.[思路分析]本题在平行四边形分类讨论中已经有三个点是定点,则第四个顶点可利用平行四边形两组对边分别平行的方法去找，AC，AB，BC中任意两边可作为平行四边形的邻边，分别作这两邻边的平行线，它们的交点就是所求的平行四边形的第四个顶点.解：当CA和CB为平行四边形的邻边时，M在第四象限，BH=AO=1,M,=−2所以M3(5, −2)综上所述:M点的坐标为M1(3，2)或M2(−3，2)或M3(5， −2).[点评]M1，M2的坐标相对易求得，而M3的坐标利用平行四边形的性质:对角顶点到对角线距离相等或者三角形全等求得M3的坐标.【例2】如图，抛物线y=ax2+ 2ax+3与y轴交于点C，与x轴交于A、B两点(点A和点B分别在x轴的正、负半轴上)，cot∠OCA = 3.(1)求抛物线的解析式;(2)平行于x轴的直线l与抛物线交于点E, F(点F在点E的左边)，如果四边形OBFE是平行四边形,求点E的坐标.[思路分析]由题意得BO不可能是平行四边形的对角线,所以只可能OB = EF =3,又因为EF被对称轴平分,根据对称轴的方程便能求得点E的坐标[点评]本题借助于抛物线的一条重要性质：抛物线关于对称轴对称.因为EF // AB，所以E，F关于对称轴对称,同时线段EF被对称轴垂直平分.【例3】如图,抛物线y= ax2+ bx +3与y轴交于点C,与x轴交于A, B两点，tan∠OCA =1 3S△ABC = 6.(1)求点B的坐标;解：(2)求抛物线的解析式及顶点坐标;(3)若E 点在x 轴上，F 点在抛物线上,如果A, C, E, F 构成平行四边形,写出点E 的坐标。

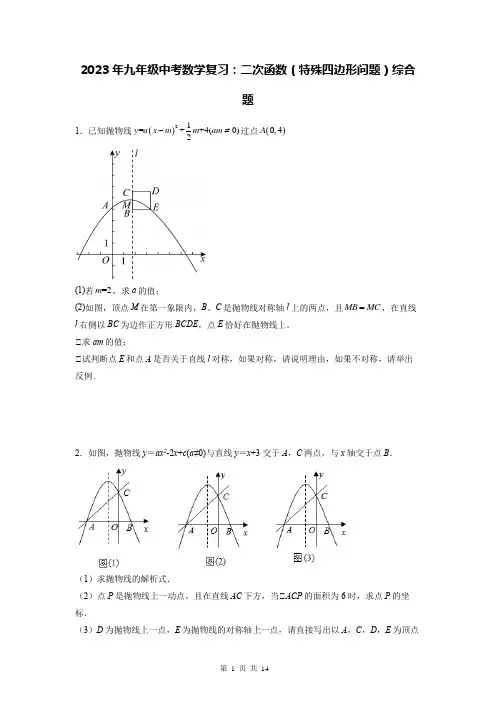
2023年九年级中考数学复习：二次函数（特殊四边形问题）综合题1．已知抛物线()21=++4(0)2y a x m m am -≠过点()0,4A(1)若=2m ，求a 的值；(2)如图，顶点M 在第一象限内，B 、C 是抛物线对称轴l 上的两点，且MB MC =，在直线l 右侧以BC 为边作正方形BCDE ，点E 恰好在抛物线上．①求am 的值；①试判断点E 和点A 是否关于直线l 对称，如果对称，请说明理由，如果不对称，请举出反例．2．如图，抛物线y ＝ax 2-2x +c (a ≠0)与直线y ＝x +3交于A ，C 两点，与x 轴交于点B ．（1）求抛物线的解析式．（2）点P 是抛物线上一动点，且在直线AC 下方，当①ACP 的面积为6时，求点P 的坐标．（3）D 为抛物线上一点，E 为抛物线的对称轴上一点，请直接写出以A ，C ，D ，E 为顶点的四边形为平行四边形时点D 的坐标．3．如图1，二次函数y ＝ax 2+bx +c （a ≠0）的图象与x 轴交于A （﹣1，0）、B （3，0），与y 轴交于点C ，连接AC 和BC ，①OAC ＝60°．（1）求二次函数的表达式．（2）如图2，线段BC 上有M 、N 两动点（N 在M 上方），且MN 3P 是直线BC 下方抛物线上一动点，连接PC 、PB ，当①PBC 面积最大时，连接PM 、AN ，当MN 运动到某一位置时，PM +MN +NA 的值最小，求出该最小值．（3）如图3，在（2）的条件下，连接AP ，将AP 绕着点A 逆时针旋转60°至AQ ．点E 为二次函数对称轴上一动点，点F 为平面内任意一点，是否存在这样的点E 、F ，使得四边形AEFQ 为菱形，若存在，请直接写出点E 的坐标，若不存在，请说明理由．4．直线3y x =-+与x 轴相交于点A ，与y 轴相交于点B ，抛物线2y ax 2x c =++经过点A ，B ，与x 轴的另一个交点为C ．（1）求抛物线的解析式；（2）如图1，若点P为直线AB上方的抛物线上的一动点，求四边形APBO的面积的最大值；D为抛物线上的一点，直线CD与AB相交于点M，点H在抛物线上，（3）如图2，(2,3)∥轴，交直线CD于点K．P是平面内一点，当以点M，H，K，P为顶点的四过H作HK y边形是正方形时，请直接写出点P的坐标．5．综合与探究如图1所示，直线y=x+c与x轴交于点A（-4，0），与y轴交于点C，抛物线y=-x2+bx+c经过点A，C．（1）求抛物线的解析式；（2）点E在抛物线的对称轴上，求CE+OE的最小值为______．（3）如图2所示，M是线段OA的上一个动点，过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N①当ANC面积最大时的P点坐标为______；最大面积为______．①点F是直线AC上一个动点，在坐标平面内是否存在点D，使以点D、F、B、C为顶点的四边形是菱形？若存在，请直接写出点D的坐标；若不存在，请说明理由．。

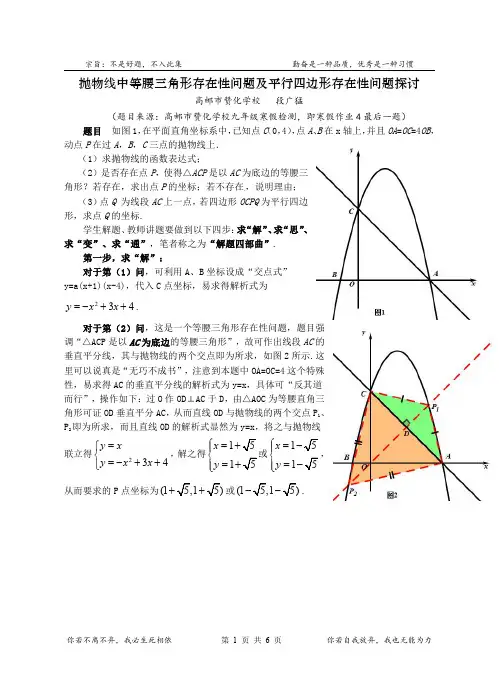
抛物线中等腰三角形存在性问题及平行四边形存在性问题探讨高邮市赞化学校段广猛（题目来源：高邮市赞化学校九年级寒假检测，即寒假作业4最后一题）题目如图1，在平面直角坐标系中，已知点C （0，4），点A 、B 在x 轴上，并且OA =OC =4OB ，动点P 在过A ，B ，C 三点的抛物线上．（1）求抛物线的函数表达式；（2）是否存在点P ，使得△ACP 是以AC 为底边的等腰三角形？若存在，求出点P 的坐标；若不存在，说明理由；（3）点Q 为线段AC 上一点，若四边形OCPQ 为平行四边形，求点Q 的坐标.学生解题、教师讲题要做到以下四步：求“解”、求“思”、求“变”、求“通”，笔者称之为“解题四部曲”.第一步，求“解”：对于第（1）问，可利用A、B 坐标设成“交点式”y=a(x+1)(x-4)，代入C 点坐标，易求得解析式为234y x x =-++.对于第（2）问，这是一个等腰三角形存在性问题，题目强调“△ACP 是以AC 为底边的等腰三角形”，故可作出线段AC 的垂直平分线，其与抛物线的两个交点即为所求，如图2所示.这里可以说真是“无巧不成书”，注意到本题中OA=OC=4这个特殊性，易求得AC 的垂直平分线的解析式为y=x，具体可“反其道而行”，操作如下：过O 作OD ⊥AC 于D，由△AOC 为等腰直角三角形可证OD 垂直平分AC，从而直线OD 与抛物线的两个交点P 1、P 2即为所求，而且直线OD 的解析式显然为y=x，将之与抛物线联立得234y x y x x =⎧⎨=-++⎩，解之得1515x y ⎧=+⎪⎨=+⎪⎩或1515x y ⎧=-⎪⎨=-⎪⎩，从而要求的P 点坐标为(15,15)++或(15,15)--.对于第（3）问，这是一个平行四边形存在性问题，题目已强调其“名字”，即“四边形OCPQ 为平行四边形”，顺序已定，并且“点Q 为线段AC 上一点”，导致本题只有一种可能，无需分类，但需画图分析，如图3所示.由抛物线解析式及直线AC：y=-x+4，可设P（t,234t t -++），Q（t,-t+4），于是PQ=P y -Q y =2(34)(4)t t t -++--+=24t t -+，因为OC=4，所以PQ=4，即244t t -+=，解得122t t ==，故要求的Q 点坐标为（2,2）.第二步，求“思”：学生解题后、教师改题后都需要有反思的习惯.对于第（2）问中等腰三角形的存在性问题，本题的解题策略是求出AC 的垂直平分线，进而与抛物线联立解方程求出P 点坐标，对于这点也可以用“确定性思想”去分析，A、C 两点是确定的，线段AC 的垂直平分线也随之确定，这样其与抛物线的交点也就确定了，即为所求，而且借助“因果关系”分析，最终的P 是由最初的A、C 两点形成的，也应该可以由AC 两点一步一步逐渐求出，先想办法求线段AC 的垂直平分线的解析式，进而联立抛物线求交点即可，这就是我所要表达的“基于确定性思想的因果关系分析法”（详见本人作品《圆与等腰三角形存在性问题综合一例———浅谈确定性思想及因果关系分析法》）.另外，此题中动点P 的确定依赖于定边AC，也体现了出了“以不变应万变——抓不变量”的重要性.在批改学生作业的过程中，发现部分学生直接利用PA=PC，用勾股定理（或两点间距离公式）建立方程，表面上得出了一个四次方程导致无功而返.当动点P 在抛物线运动时，一般情况下不用此方法，不是因为这个方法不对，是限于学生不会解高次方程导致行不通，不是方法超纲而是解方程超纲，这一点学生也需要进行反思、琢磨，而且此法对于很多等腰三角形的存在性问题都不失为一种通法，在第三步“变”的过程中，同学们会进一步体会到什么时候均可以采用此法实现“通杀”.难道此法真的在此题中行不通吗？请往下看：由题易知A （4,0），C （0,4），设P （t,234t t -++），则2222(t 4)(34)PA t t =-+-++，2222t (3)PC t t =+-+，当△ACP 是以AC 为底边的等腰三角形时，有PA=PC，即22PA PC =，即222222(t 4)(34)t (3)t t t t -+-++=+-+，即22(t 4)t --=2222(3)(34)t t t t -+--++，24(2t 4)4(264)t t --=--++，整理得2240t t --=，解之得11t =+，21t =-故要求的P 点坐标为(1+或(1-.上面解法中的解方程过程中巧妙利用了“移项”技巧结合“平方差公式”将四次方完美消掉，如果看不出这种技巧，将22(34)t t -++中“23t t -+”看成一个整体，采取整体思想进行展开，依然可以消去四次方，所以表面上是一个四次方程，其实质根本就是一元二次方程，因而行得通，只不过可能你缺乏了“计算到底”的耐心与信心罢了！另外此法里学生需关注到“两点间距离公式”的熟练使用，即设P 1（x 1,y 1）,P 2(x 2,y 2)，则P 1与P 2两点间的距离为P 1P 2，其本质即为勾股定理，如图4所示.对于第（3）问中平行四边形的存在性问题，本题已给出该平行四边形的“名字”，即四个字母已有顺序性，若是没有“名字”，本问应该要分类解决.首先抓住这个四边形中不变的两个顶点O 和C，采取“抓不变量——以不变应万变”的解题策略，分OC 作为边及OC 作为对角线两种情况，画图分析解决，请记住养成“没事画画图”的好习惯，只有借助于草图来分析，才能更好地找到解决问题的出路，而且“画图越准确越好”！另外，此问中还有一个简化条件“点Q 为线段AC 上一点”，若将该条件弱化成“点Q 为直线AC 上一点”，此题难度顿时提升，真正能拿到满分的同学估计会少之又少，而且此时能真正采取最佳解题策略的同学更会是“凤毛麟角”.具体如何操作我会在第三步求“变”中一一展开.第三步，求“变”：梁启超先生在《变法通议》中说道“变者，天下之公理也！”数学解题又何尝不是呢！上一步求“思”过程中已有一些对本题条件的变化，只有“灵活多变”，才能把握住数学规律，进而能运用自如.对于第（2）问中等腰三角形的存在性问题，此题可以说是太“巧”了！若是△AOC 不是等腰直角三角形，又该如何确定AC 的垂直平分线的解析式，进而通过“求交点坐标”的方法确定点P 的坐标呢？变式1：如图5，在平面直角坐标系中，已知点A（4,0），B （-1,0），C （0,3），动点P 在过A ，B ，C 三点的抛物线上．是否存在点P ，使得△ACP 是以AC 为底边的等腰三角形？若存在，求出点P 的坐标；若不存在，说明理由.首先求出抛物线的解析式为239344y x x =-++.然后依然可以作出线段AC 的垂直平分线，其与抛物线的两个交点即为所求，如图6所示.此题中不再具有OA=OC 这个特殊性，线段AC 的垂直平分线不再过原点了，该如何求呢？这成了解题的关键点也是难点所在了！关注到这条垂直平分线的画法：先取线段AC 的中点D，再过点D 作AC 的垂线即可.既然如此，我们只要仅仅抓住这个中点D 及“垂直”这个条件即可解决，这正是“因果关系分析法”的核心所在，需要同学们学会并熟练应用的一种最基本的分析问题的方式与方法.如图7所示，狠抓“垂直”这个条件，可以过垂足D 作一条平行于x 轴的直线交y 轴于点F，再过点P 1作该直线的垂线于点E，构造出“一线三直角”型相似.则易知134DE CF CO PE DF AO ===.下面抓住“134DE PE =”这个结论，给同学们介绍两种求P 1点坐标的方式.方式一“设坐标法”：可设P 1（t,239344t t -++），由“中点坐标公式”易知D 点坐标为（2，32），则P 1E=1P D y y -=2393442t t -++，DE=1P D x x -=2t -，所以有2233934442t t t -=-++，解之得t=1118，其中负值也无需舍去，它其实就是图7中点P 2的横坐标.而对于P 点纵坐标的求法，其实也无需代入抛物线中计算，利用上面的方程，只要我们静下心来就可以观察到，点P 的纵坐标为239344t t -++，这个整体其实等于4(t 2)3+32-，将t 代入这个一次式口算即可得P点坐标为（1118，1954-+）或者（1130118-，19230154--）.这个变式中数据可能凑得不好，但正因此，更加考验学生灵活计算的能力，而不是不动脑筋，强行带入，导致计算量更大而算错，近年来扬州中考对于学生计算能力的要求日益加强.另外，更有趣的是上面求点P 的纵坐标的一次式“4(t 2)3+32-”，其实对应着线段AC 的垂直平分线的解析式，即为y=4(x 2)3+32-=4736x -，这一点也会在方式二中提及.关于“设坐标法”，上面利用了抛物线设出点P 的坐标，利用“134DE PE =”来列方程，进而求出P 点坐标.其实也可以反过来操作，利用“134DE PE =”来巧设出点P 的坐标，然后代入抛物线解析式求解即可，具体如下：如图7所示，由D 点坐标（2，32）及134DE PE =，可设P 1（2+3k,32+4k），再将其代入抛物线239344y x x =-++即可解出k 的值，进而写出P 点坐标即可.对于上面的坐标巧设，同学们可以用心琢磨下，而且这个原理也自然能引出接下来的的方式二中求线段AC 垂直平分线的方法.方式二“联立解析式求交点坐标”：如图8所示，要求线段AC 的垂直平分线的解析式需要两个点的坐标，点D 的坐标为（2，32），只需再找一点个即可.为此，在前面图7的基础上，在FD 的延长线上取DM=3，则同理由基本模型“一线三直角”型相似可知MN=4，则N 点坐标为（5，112），设DN 解析式为：y=kx+b，代入D、N 坐标得y=4736x -，再与抛物线联立得2473639344y x y x x ⎧=-⎪⎪⎨⎪=-++⎪⎩，解之即可得到两个P 点坐标，即为所求.上面两种方式可以说是求某个点坐标的最常用的两种方法，一个是“设坐标法”，另一个是“求交点坐标法”，两种方法相得益彰，建议学生都要掌握.另外，无论是哪一种方式，最基本的构图都是“见直角，造一线三直角”，这个模型应用广泛，具体操作方式可通过垂足以及其他已知的点作平行于坐标轴的直线得到，这是一种重要的“斜化直”思想.在变式1中如果执意利用PA=PC，用勾股定理（或两点间距离公式）建立方程，又会怎么样呢？试试便知：由A （4,0），C （0,3），设P （t,239344t t -++），则222239(t 4)(3)44PA t t =-+-++，222239t ()44PC t =+-+，当△ACP 是以AC 为底边的等腰三角形时，有PA=PC，即22PA PC =，即22239(t 4)(3)44t t -+-++=22239t ()44t t +-+，至此依然可以同前面那样要么移项利用平方差公式消去四次方，要么将“23944t t -+”看成整体展开消去四次方，在此不再赘述.本文后续预告，暂未完成，敬请期待：本题中动点P 是抛物线上的一个动点，这使得“代数方法”的求解显得“惊心动魄”，差点导致了四次方程的出现，若是动点P 在直线上运动，有什么样的方法可以“通杀”此类题型呢？若动点P 在双曲线上运动呢？对于第（3）问中平行四边形的存在性问题，此题可以说是太“简”了！一简在条件“点Q 为线段AC 上一点”上，二简在该平行四边形的“名字”，即顺序已定上.若这些条件都再弱化一些又会如何呢？如何轻松搞定所有的“平行四边形存在性”问题呢？第四步，求“通”：这个环节又会如何总结呢？敬请期待。

特殊四边形存在性问题平行四边形：如果已知三个定点，则形成三条定线段，把每条定线段看成对角线，利用对角形互相平分解决。

如果已知两个定点，一般是把确定的一条线段按照边或对角线分为两种情况．菱形：通常转化为等腰三角形存在问题。

矩形：通常转化为直角三角形存在问题。

正方形：通常转化为等腰直角三角形存在问题。

针对训练1．如图，已知抛物线y ＝－x 2－2x ＋3与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，顶点为P ．若以A 、C 、P 、M 为顶点的四边形是平行四边形，求点M 的坐标．2．如图，在平面直角坐标系xOy 中，已知抛物线y ＝－x 2+2x ＋3与x 轴交于A 、B 两点，点M 在这条抛物线上，点P 在y 轴上，如果以点P 、M 、A 、B 为顶点的四边形是平行四边形，求点M 的坐标．3.如图（1），抛物线与x 轴交于A 、B 两点，与y 轴交于点C ，其中点A 的坐标为（﹣2，0）．（1）求此抛物线的解析式；（2）①若点D 是第一象限内抛物线上的一个动点，过点D 作DE ⊥x 轴于E ，连接CD ，以OE 为直径作⊙M ，如图（2），试求当CD 与⊙M 相切时D 点的坐标；②点F 是x 轴上的动点，在抛物线上是否存在一点G ，使A 、C 、G 、F 四点为顶点的四边形是平行四边形？若存在，求出点G 的坐标；若不存在，请说明理由．21y x x c 4=-++4．如图1，在平面直角坐标系中，抛物线y ＝ax 2＋bx －3a 经过A (－1,0)、B (0,3)两点，与x 轴交于另一点C ，顶点为D ．（1）求该抛物线的解析式及点C 、D 的坐标；（2）经过点B 、D 两点的直线与x 轴交于点E ，若点F 是抛物线上一点，以A 、B 、E 、F 为顶点的四边形是平行四边形，求点F 的坐标；（3）如图2，P （2，3）是抛物线上的点，Q 是直线AP 上方的抛物线上一动点，求△APQ 的最大面积和此时Q 点的坐标．5.如图，在平面直角坐标系中，直线AB 与x 轴、y 轴分别交于点A ，B ，直线CD 与x 轴、y 轴分别交于点C ，D ，AB 与CD 相交于点E ，线段OA ，OC 的长是一元二次方程x 2﹣18x+72=0的两根（OA ＞OC ），BE=5，tan ∠ABO=．（1）求点A ，C 的坐标；（2）若反比例函数y=的图象经过点E ，求k 的值； （3）若点P 在坐标轴上，在平面内是否存在一点Q ，使以点C ，E ，P ，Q 为顶点的四边形是矩形？若存在，请写出满足条件的点Q 的个数，并直接写出位于x 轴下方的点Q 的坐标；若不存在，请说明理由．43kx6.将抛物线c 1：2y =x 轴翻折，得到抛物线c 2，如图所示．现将抛物线c 1向左平移m 个单位长度，平移后得到新抛物线的顶点为M ，与x 轴的交点从左到右依次为A 、B ；将抛物线c 2向右也平移m 个单位长度，平移后得到新抛物线的顶点为N ，与x 轴的交点从左到右依次为D 、E ．在平移过程中，是否存在以点A 、N 、E 、M 为顶点的四边形是矩形的情形？若存在，请求出此时m 的值；若不存在，请说明理由．7．已知平面直角坐标系xOy （如图），一次函数334y x =+的图像与y 轴交于点A ，点M 在正比例函数32y x =的图像上，且MO ＝MA ．二次函数y ＝x 2＋bx ＋c 的图像经过点A 、M ．（1）求线段AM 的长； （2）求这个二次函数的解析式；（3）如果点B 在y 轴上，且位于点A 下方，点C 在上述二次函数的图像上，点D 在一次函数334y x =+的图像上，且四边形ABCD 是菱形，求点C 的坐标．8.如图，直线y=x ﹣4与x 轴、y 轴分别交于A 、B 两点，抛物线经过A 、B 两点，与x 轴的另一个交点为C ，连接BC ．（1）求抛物线的解析式及点C 的坐标； （2）点M 在抛物线上，连接MB ，当∠MBA+∠CBO=45°时，求点M 的坐标；（3）点P 从点C 出发，沿线段CA 由C 向A 运动，同时点Q 从点B 出发，沿线段BC 由B 向C 运动，P 、Q 的运动速度都是每秒1个单位长度，当Q 点到达C 点时，P 、Q 同时停止运动，试问在坐标平面内是否存在点D ，使P 、Q 运动过程中的某一时刻，以C 、D 、P 、Q 为顶点的四边形为菱形？若存在，直接写出点D 的坐标；若不存在，说明理由．9．已知抛物线2(2)y a x b =-+ (0)ab <的顶点为A ，与x 轴的交点为B ，C （点B 在点C 的左侧）．（1)直接写出抛物线对称轴方程；（2）若抛物线经过原点，且△ABC 为直角三角形，求a ，b 的值；（3）若D 为抛物线对称轴上一点，则以A 、B 、C 、D 为顶点的四边形能否为正方形？若能，请求出a ，b 满足的关系式；若不能，说明理由．21y x bx c 3=++10．如图，已知双曲线6yx与直线AB交于A、B两点，与直线CD交于C、D两点．（1）求证四边形ACBD是平行四边形；（2）四边形ACBD可能是矩形吗？可能是正方形吗？（3）如果点A的横坐标为3，点C的横坐标为m(m＞0)，四边形ACBD的面积为S，求S与m的之间的关系式．。

中考数学“特殊四边形的存在性问题”题型解析由抛物线上的点构成特殊四边形的问题，需要根据特殊四边形的性质与判定去确定点的坐标，然后求解 . 具体而言，解该类题时，我们要根据题目中的条件，科学地进行分类，然后画出图形，再根据这个四边形的性质或判定求出这点的坐标，若这一点是根据特殊四边形的特性得到的坐标，我们还应将这一点代入到抛物线的解析式中去验证是否是抛物线上的点 .本节主要来讨论下特殊四边形：平行四边形、菱形、矩形的存在性问题 .类型一：平行四边形问题【例题1】如图，抛物线y = 1/2 x^2 + bx + c 经过点A（-1,0）和点B（3,0），同时交y 轴于点C .（1）求抛物线的解析式；（2）若点Q 在y 轴上，点P 在抛物线上，且以A , B , Q , P 为顶点的四边形是平行四边形，求满足条件的点P 的坐标 .【分析】（1）根据抛物线经过A , B 两点即可求得b , c 的值，可解题；（2）以A , B , Q , P 为顶点的四边形是平行四边形，则点P 横坐标为4 或- 4，将x = 4 或- 4 代入抛物线解析式即可求得y 的值，即可解题 .【解析】（1）把A（-1,0），B（3,0）代入y = 1/2 x^2 + bx + c 中，∴抛物线的解析式是y = 1/2 x^2 - x - 3/2 .（2）①当AB 为边时，只要PQ∥AB 且PQ = AB = 4 即可 .又知点Q 在y 轴上，∴点P 的横坐标为4 或- 4 ，这时符合条件的点P 有两个，分别记为P1 , P2，把x = 4 代入y = 1/2 x^2 - x - 3/2 ,得y = 5/2 ,把x = - 4 代入y = 1/2 x^2 - x - 3/2 ,得y = 21/2 ,此时P1（4 , 5/2），P2（- 4 , 21/2）；②当AB 为对角线时，只要线段PQ 与线段AB 互相平分即可 .又知点Q 在y 轴上，且线段AB 中点的横坐标为1，∴点P 的横坐标为2，这时符合条件的P 只有一个记为P3 ,而且当x = 2 时，y = - 3/2 ,此时P3（2，- 3/2），综上，满足条件的P 为P1（4 , 5/2），P2（- 4 , 21/2），P3（2，-3/2）.类型二：菱形问题【例题2】如图，在平面直角坐标系中，点O 为坐标原点，直线y = -x + b 与坐标轴交于C，D 两点，直线AB 与坐标轴交于A , B 两点，线段OA , OC 的长是方程x^2 - 3x + 2 = 0 的两个根（OA > OC）.（1）求点A , C 的坐标；（2）直线AB 与直线CD 交于点E，若点E 是线段AB 的中点，反比例函数y = k/x （k ≠0 ）的图象的一个分支经过点E，求k 的值；（3）在（2）的条件下，点M 在直线CD 上，坐标平面内是否存在点N，使以点B , E , M , N 为顶点的四边形是菱形？若存在，请直接写出满足条件的点N 的坐标；若不存在，请说明理由 .【分析】（1）利用分解因式法解一元二次方程x^2 - 3x + 2 = 0 即可得出OA , OC 的值，再根据点所在的位置即可得出A , C 的坐标；（2）根据点C 的坐标利用待定系数法即可求出直线CD 的解析式，根据点A , B 的横坐标结合点E 为线段AB 的中点即可得出点E 的横坐标，将其代入直线CD 的解析式中即可求出点E 的坐标，再利用待定系数法即可求出k 的值；（3）假设存在，设点M 的坐标为（m , - m + 1）, 分别以BE 为边、BE 为对角线来考虑 .根据菱形的性质找出关于m 的方程，解方程即可得出点M 的坐标，再结合点B , E 的坐标即可得出点N 的坐标 .【解析】（1）x^2 - 3x + 2 = （x - 1）（x - 2）= 0 ,∴x1 = 1 , x2 = 2 ,∵OA > OC ,∴OA = 2 , OC = 1 ,∴A（-2,0），C（1,0）；（2）将C（1,0）代入y = - x + b 中，得0 = - 1 + b , 解得b = 1 ,∴直线CD 的解析式为y = - x + 1 .∵点E 为线段AB 的中点，A（-2,0），B 的横坐标为0 ，∴点E 的横坐标为- 1 .∵点E 为直线CD 上一点，∴E（-1,2）.将点E（-1,2）代入y = k/x （k ≠0 ）中，得2 = k / -1 , 解得k = -2 ;（3）假设存在，设点M 的坐标为（m , - m + 1）,以点B , E , M , N 为顶点的四边形是菱形分两种情况（如上图所示）类型三：矩形问题【例题3】【解题策略】这三道例题分别呈现了运动变化过程中的平行四边形、菱形、矩形的存在性问题，三道例题的思路都是要依据特殊四边形的性质构图并建立方程求点的坐标 .特别地，由于菱形任意三个顶点组成的三角形都是等腰三角形，因此可将菱形问题转化为等腰三角形的存在性问题；而矩形问题则可转化为直角三角形的问题，要注意体会相关知识之间的联系 .。

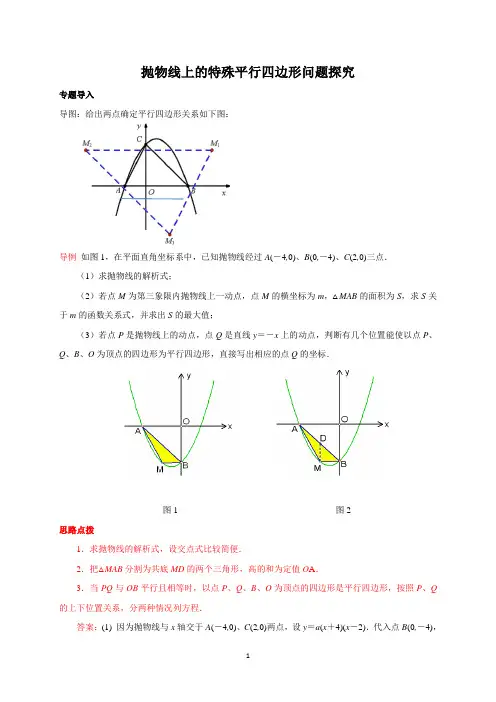
抛物线上的特殊平行四边形问题探究专题导入导图：给出两点确定平行四边形关系如下图：导例如图1，在平面直角坐标系中，已知抛物线经过A(－4,0)、B(0,－4)、C(2,0)三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△MAB的面积为S，求S关于m的函数关系式，并求出S的最大值；（3）若点P是抛物线上的动点，点Q是直线y＝－x上的动点，判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．图1 图2思路点拨1．求抛物线的解析式，设交点式比较简便．2．把△MAB分割为共底MD的两个三角形，高的和为定值O A．3．当PQ与OB平行且相等时，以点P、Q、B、O为顶点的四边形是平行四边形，按照P、Q 的上下位置关系，分两种情况列方程．答案：(1) 因为抛物线与x轴交于A(－4,0)、C(2,0)两点，设y＝a(x＋4)(x－2)．代入点B(0,－4)，求得12a =．所以抛物线的解析式为211(4)(2)422y x x x x =+-=+-． (2)如图2，直线AB 的解析式为y ＝－x －4．过点M 作x 轴的垂线交AB 于D ，那么2211(4)(4)222MD m m m m m =---+-=--．所以2142MDA MDB S S S MD OA m m ∆∆=+=⋅=--2(2)4m =-++．因此当2m =-时，S 取得最大值，最大值为4．(3) 如果以点P 、Q 、B 、O 为顶点的四边形是平行四边形，那么PQ //OB ，PQ ＝OB ＝4． 设点Q 的坐标为(,)x x -，点P 的坐标为21(,4)2x x x +-． ①当点P 在点Q 上方时，21(4)()42x x x +---=．解得225x =-±．此时点Q 的坐标为(225,225)-+-（如图3），或(225,225)--+（如图4）． ②当点Q 在点P 上方时，21()(4)42x x x --+-=．解得4x =-或0x =（与点O 重合，舍去）．此时点Q 的坐标为(－4,4) （如图5）．图3 图4 图5典例类型一：已知“两点”判断平行四边形存在性问题例1、如图，在平面直角坐标系中，抛物线y =x 2+mx +n 经过点A （3，0）、B （0，﹣3），点P 是直线AB 上的动点，过点P 作x 轴的垂线交抛物线于点M ，设点P 的横坐标为t ． （1）分别求出直线AB 和这条抛物线的解析式．（2）若点P 在第四象限，连接AM 、BM ，当线段PM 最长时，求△ABM 的面积．（3）是否存在这样的点P ，使得以点P 、M 、B 、O 为顶点的四边形为平行四边形？若存在，请直接写出点P 的横坐标；若不存在，请说明理由．【分析】：（1）分别利用待定系数法求两函数的解析式：把A（3，0）B（0，﹣3）分别代入y=x2+mx+n 与y=kx+b，得到关于m、n的两个方程组，解方程组即可；（2）设点P的坐标是（t，t﹣3），则M（t，t2﹣2t﹣3），用P点的纵坐标减去M的纵坐标得到PM 的长，即PM=（t﹣3）﹣（t2﹣2t﹣3）=﹣t2+3t，然后根据二次函数的最值得到当t=﹣=32时，PM最长为=94，再利用三角形的面积公式利用S△ABM=S△BPM+S△APM计算即可；（3）由PM∥OB，根据平行四边形的判定得到当PM=OB时，点P、M、B、O为顶点的四边形为平行四边形，然后讨论：当P在第四象限：PM=OB=3，PM最长时只有，所以不可能；当P在第一象限：PM=OB=3，（t2﹣2t﹣3）﹣（t﹣3）=3；当P在第三象限：PM=OB=3，t2﹣3t=3，分别解一元二次方程即可得到满足条件的t的值．类型二：菱形的存在性问题例2 如图2所示，直线y＝x＋c与x轴交于点A(－4，0)，与y轴交于点C，抛物线y＝－x2＋bx＋c 经过点A，C.(1)求抛物线的解析式；(2)点E在抛物线的对称轴上，求CE＋OE的最小值；(3)如图2所示，点M是线段OA上的一个动点，过点M作垂直于x轴的直线与直线AC和抛物线分别交于点P，N.若点P恰好是线段MN的中点，点F是直线AC上一个动点，在坐标平面内是否存在点D，使以点D，F，P，M为顶点的四边形是菱形？若存在，请直接写出点D的坐标；若不存在，请说明理由．注：二次函数y＝ax2+bx+c（a≠0）的顶点坐标为（﹣，）【分析】（1）把已知点坐标代入解析式；（2）取点C关于抛物线的对称轴直线l的对称点C′，由两点之间线段最短，最小值可得；（3）①由已知，注意相似三角形的分类讨论．②设出M坐标，求点P坐标．注意菱形是由等腰三角形以底边所在直线为对称轴对称得到的．本题即为研究△CPN为等腰三角形的情况．类型三：正方形的存在性问题例3如图1，在平面直角坐标系中，直线y＝x+4与抛物线y＝﹣x2+bx+c（b，c是常数）交于A、B两点，点A在x轴上，点B在y轴上．设抛物线与x轴的另一个交点为点C．（1）求该抛物线的解析式；（2）P 是抛物线上一动点（不与点A 、B 重合），①如图2，若点P 在直线AB 上方，连接OP 交AB 于点D ，求的最大值；②如图3，若点P 在x 轴的上方，连接PC ，以PC 为边作正方形CPEF ，随着点P 的运动，正方形的大小、位置也随之改变．当顶点E 或F 恰好落在y 轴上，直接写出对应的点P 的坐标．【分析】（1）利用直线解析式求出点A 、B 的坐标，再利用待定系数法求二次函数解析式解答； （2）作PF ∥BO 交AB 于点F ，证△PFD ∽△OBD ，得比例线段，则PF 取最大值时，求得的最大值；（3）（i ）点F 在y 轴上时，P 在第一象限或第二象限，如图2，3，过点P 作PH ⊥x 轴于H ，根据正方形的性质可证明△CPH ≌△FCO ，根据全等三角形对应边相等可得PH ＝CO ＝2，然后利用二次函数解析式求解即可；（ii ）点E 在y 轴上时，过点PK ⊥x 轴于K ，作PS ⊥y 轴于S ，同理可证得△EPS ≌△CPK ，可得PS ＝PK ，则P 点的横纵坐标互为相反数，可求出P 点坐标；点E 在y 轴上时，过点PM ⊥x 轴于M ，作PN ⊥y 轴于N ，同理可证得△PEN ≌△PCM ，可得PN ＝PM ，则P 点的横纵坐标相等，可求出P 点坐标．由此即可解决问题． 专题突破1、如图，抛物线2y x bx c =-++与直线122y x =+交于,C D 两点，其中点C 在y 轴上，点D 的坐标为7(3,)2。

专题08二次函数中特殊四边形存在性问题的四种考法类型一、平行四边形存在性问题(1)求抛物线的表达式；(2)如图1，连接BC ，PB ，PC ，设PBC 的面积为①求S 关于t 的函数表达式；②求P 点到直线BC 的距离的最大值，并求出此时点(3)如图2，设抛物线的对称轴为l ，l 与x 轴的交点为边形CDPM 是平行四边形？若存在，直接写出点【答案】(1)22y x=-(2)①23922S t t =-+；②点P 到直线BC 的距离的最大值为(3)存在，()1,6M 【分析】（1）待定系数法求解析式即可求解；（2）①在图1中，过点P 作PF y ∥轴，交BC 于点P 的坐标为()2,23t t t -++，则点F 的坐标为(t 2139222S PF OB t t =⋅=-+；②根据二次函数的性质得出当32t =时，S 取最大值，最大值为面积法求得点P 到直线BC 的距离，进而得出P （3）如图2，连接PC ，交抛物线对称轴l 于点设直线BC 的解析式为将()3,0B 、()0,3C 代入30,3m n n +=⎧⎨=⎩，解得：∴直线BC 的解析式为∵点P 的坐标为(,t t -∴点F 的坐标为(,t -∴(223PF t t =-++-∴1322S PF OB =⋅=-②12S PF OB =⋅=-∵302-<，∴当32t =时，S 取最大值，最大值为抛物线2y x bx =-++∴抛物线的对称轴为直线 1D C x x -=，∴1P M x x -=，∴2P x =，()2,3P ∴，在223y x x =-++中，当()0,3C ∴，∴3C D y y -=，∴3M P y y -=，∴6M y =，∴点M 的坐标为()1,6；当2P x ¹时，不存在，理由如下，若四边形CDPM 是平行四边形，则 点C 的横坐标为0，点∴点P 的横坐标12t =⨯又 2P x ¹，(1)求点C 的坐标；(2)点P 为直线AC 下方抛物线上一点，过点此时点P 的坐标；(3)抛物线顶点为M ，在平面内是否存在点若存在请求出N 点坐标并在备用图中画出图形；若不存在，请说明理由．【答案】(1)()4,5C (2)315,24P ⎛⎫- ⎪⎝⎭(3)存在，点N 的坐标为：()154N -，，【详解】（1）解：在2=23y x x --中，令解得：11x =-，23x =，()()1,0,3,0A B ∴-，直线y x m =+经过点()1,0A -，∴01m =-+，解得：1m =，∴直线AC 的解析式为1y x =+，联立方程组，得2123y x y x x =+⎧⎨=--⎩，解得：1110x y =-⎧⎨=⎩，2245x y =⎧⎨=⎩()4,5C ∴；（2）如图1，设点2(,23)P n n n --，则点∴2212334()PE n n n n n =+---=-++ 10-<，∴当32n =时，PE 取得最大值254，此时，（3） 2223(1)4y x x x =--=--，∴抛物线顶点为()14M -，，如图2，点,,,A B M N 为顶点的四边形是平行四边形时，设①BM 为对角线时，AN 的中点与BM ∴(1)3122m +-+=，04022n +-+=，解得：∴()154N -，，②AM 为对角线时，BN 的中点与AM ∴31122m +-+=，04022n +-+=，解得：(1)求此拋物线的解析式；(2)在抛物线的对称轴上有一点P ，使得PA PC +值最小，求最小值；(3)点M 为x 轴上一动点，在拋物线上是否存在一点N ，使以边形为平行四边形？若存在，直接写出点N 的坐标；若不存在，请说明理由．【答案】(1)215222y x x =--(2)552(3)54,2⎛⎫- ⎪⎝⎭，5214,2⎛⎫+ ⎪⎝⎭，5214,2⎛⎫- ⎪⎝⎭【分析】（1）把()1,0A -，()5,0B 两点代入求出a 、b 的值即可；（2）因为点A 关于对称轴对称的点B 的坐标为()5,0，连接BC 点坐标即可；（3）分点N 在x 轴下方或上方两种情况进行讨论．拋物线的解析式为212y x =-∴其对称轴为直线2b x a =-=-当0x =时，52y =-，50,2C ⎛⎫∴- ⎪⎝⎭，又()5,0B ，∴设BC 的解析式为(y kx b =+5052k b b +=⎧⎪∴⎨=-⎪⎩，解得：12k =，52b =-，∴BC 的解析式为1522y x =-，当2x =时，1532222y =⨯-=-，①当点N 在x 轴下方时，抛物线的对称轴为2x =，0,C ⎛- ⎝154,2N ⎛⎫∴- ⎪⎝⎭，②当点N 在x 轴上方时，如图，过点在2AN D △和2M CO △中，22N AD AN N DA ∠⎧⎪⎨⎪∠⎩252N D OC ∴==，即2N 点的纵坐标为21552222x x ∴--=，解得：2x =+25214,2N ⎛⎫∴+ ⎪⎝⎭，35214,2N ⎛⎫- ⎪⎝⎭综上所述符合条件的N 的坐标有⎛ ⎝【点睛】本题考查的是二次函数综合题，式、平行四边的判定与性质、全等三角形等知识，两点间距离的求解，在解答（意进行分类讨论．(1)求抛物线的解析式：(2)在抛物线的对称轴上是否存在点P ，使PCD 是以CD 为腰的等腰三角形？如果存在，求出点P 的坐标；如果不存在，请说明理由；(3)点E 在x 轴上运动，点F 在抛物线上运动，当以点B ，C ，E ，F 为顶点的四边形是平行四边形，直接写出点E 的坐标．【答案】(1)213222y x x =-++(2)存在，3,42⎛⎫ ⎪⎝⎭或35,22⎛⎫ ⎪⎝⎭或35,22⎛⎫- ⎪⎝⎭(3)541,02⎛⎫-+ ⎪ ⎪⎝⎭或541,02⎛⎫-- ⎪ ⎪⎝⎭或(7,0)或(1,0)【分析】（1）用待定系数法即可求解；（2）分两种情况：以C 为顶点，即CP CD =；以D 为顶点，即CD =等腰三角形的定义建立方程即可完成；（3）分三种情况：当BC 是对角线时；当BE 是对角线时；当BF 是对角线时；分别设点与F 的坐标，利用中点坐标公式即可求解．【详解】（1）解：∵点B 的坐标是(40)，，点C 的坐标是(02)，，∴16602a c c ++=⎧⎨=⎩，解得：122a c ⎧=-⎪⎨⎪=⎩，∴所求抛物线解析式为213222y x x =-++；（2）解：存在(1)求抛物线的表达式；(2)若点E 在第一象限内对称右侧的抛物线上，四边形ODEB 的面积为(3)在（2）的条件下，若点F 是对称轴上一点，点H 是坐标平面内一点，在对称轴右侧的抛物线上是否存在点G ，使以E ，F ，G ，H 为顶点的四边形是菱形，且存在，请直接写出点G 的坐标；如果不存在，请说明理由．【答案】(1)232333y x x =-++(2)()2,33E 2039⎫⎪⎭或532,339⎛⎫⎪⎝⎭）根据待定系数法求解即可；∵232333y x x =-++()23143x =--+，∴()1,43D ．令232333y x x =-++中0y =，则解得=1x -或3x =，抛物线的对称轴与x轴交于点M，过点∵四边形EFGH 是菱形，EFG ∠∴EF FG GH EG ===，∵60EFG ∠=︒，∴EFG 是等边三角形．∴60FEG EF FG ∠=︒=，，∵()2,33E ，()0,33C ，(1,4D ∴2CE CD ==，()24333-+同理可证： EFG 是等边三角形，∵CF FE =，=GE FE ，∴DG ∴CDG CEG ∆∆≌．∴DCG ∠=∴直线CG 的表达式为：33y =与抛物线表达式联立得33y y ⎧=⎪⎨⎪=-(1)求抛物线的表达式；(2)若点D 是直线AC 上方拋物线上一动点，连接BC ，AD ADM △的面积为1S ，BCM 的面积为2S ，当121S S -=时，求点(3)如图2，若点P 是抛物线上一动点，过点P 作PQ x ⊥轴交直线上是否存在点E ，使以P ，Q ，E ，C 为顶点的四边形是菱形，若存在，请直接写出点坐标；若不存在，请说明理由【答案】(1)223y x x =-++(2)271,22⎛⎫+ ⎪ ⎪⎝⎭或271,22⎛⎫- ⎪ ⎪⎝⎭．(3)符合条件的点E 有三个，坐标为：()0,1E ，(10,132E -【分析】（1）把点()30A ，和()10B -，代入解析式求解即可；（2）由121S S -=得121S S =+从而121ABM ABM S S S S +=++ 程求解即可；（3）分类当CQ 为对角线和菱形边时，利用直线AC 与x 轴成标的方程，进而求出点的坐标．【详解】（1）把点()3,0A 和()1,0B -代入得：93330a b a b ++=⎧⎨-+=⎩解得：12a b =-⎧⎨=⎩，∴抛物线的解析式为223y x x =-++；（2）设(),D x y ，对于抛物线223y x x =-++，令0x =，则()0,3C ∴．121S S -= ，121S S ∴=+．∵()30A ，，()0,3C ，∴3OA OB ==，45OCA ∴∠=︒，此时四边形CEQP 是正方形．PQ EQ ∴=．设()2,23P m m m -++，则23PQ m m =-+，23m m m ∴-+=，解得m =此时32OE OC m =-=-=②当CQ 为菱形的边时，如图设()2,23P m m m -++，则∴HQ m =，2PQ m =-+作QH OC ⊥于点H ，45OCA ∠︒= ，∴22CQ HQ m ==．∴23CE PQ m m ==-+=解得：132m =-，23m =()323213OE =+-=+()10,132E ∴-，(20,1E +综上所述，符合条件的点【点睛】本题考查待定系数法求函数的解析式，二次函数的性质，二次函数与几何综合，数形结合是解题的关键．【变式训练2】如图1，在平面直角坐标系中，点（点A 在点B 左侧），与(1)求ABC 的面积；（3）解：∵抛物线212y x x =--∴()211942212y x x x =--+=-2＋＋∵将抛物线2142y x x =--+沿着水平方向向右平移∴新抛物线为：()112y x =--2＋∴原抛物线与新抛物线的交点，∴()()1111992222x x -=--22＋＋＋，∴解得：0x =，【点睛】本题考查了二次函数的图象及性质，二次函数与特殊图形，二次函数的平移规律，掌握二次函数与特殊图形的位置关系是解题的关键．类型三、矩形存在性问题(1)求抛物线的解析式；(2)如图，点P 是抛物线上位于直线直线AC 于点D ，交x 轴于点E ，(3)在抛物线上是否存在点M ，对于平面内任意点一条边的四边形为矩形，若存在，请直接写出【答案】(1)2142y x x =--(2)335,28P ⎛⎫- ⎪⎝⎭；254(3)()4,8M -、()8,4N -【分析】（1）把点()4,0A 和点B a 、b 的值；（2）先用待定系数法求出直线2211,422D t t t t ⎛⎫--- ⎪⎝⎭，然后求出最大值时t 的值，即可求出点P （3）假设抛物线上是存在点M ，一条边的四边形为矩形，过点O 点A 且与OH 平行的直线解析式，经计算验证可得过点立方程可求得M 的坐标，通过平移即可求得点【详解】（1）解：把点()4,0A 和点∵()4,0A ，()0,4C -，∴OAC 为等腰直角三角形，∴点H 为AC 的中点，即(H 则OH 所在的直线方程为y =∵四边形AMNC 为矩形，∴过A 与直线AC 相垂直的直线函数解析式中的∴设AM 所在的直线解析式为∵点A 在直线AM 上，(1)求点A 、B 、C 的坐标；(2)将抛物线L 向右平移1个单位，得到新抛物线对称轴l 上是否存在点D ，使得以点D 的坐标；若不存在，请说明理由．【答案】(1)()1,0A -，()3,0B (2)存在，点D 的坐标为()2,1或【分析】（1）分别令0y =和x （2）先求得平移后的抛物线L 角线时，根据矩形的性质求解即可．【详解】（1）解：令0y =，则解得11x =-，23x =，当AD 为对角线时，连接AC ，过点 ()1,0A -，()0,1C -，∴1OA OC ==，∴45OCA ∠=︒∴45OCG ∠=︒∴1OG OC ==，∴()1,0G ．设CG 所在直线解析式为y kx =+将()0,1C -，()1,0G 代入得，⎧⎨⎩解得11k b =⎧⎨=-⎩，∴CG 所在直线解析式为1y x =-当2x =时，1211y x =-=-=．∴()2,1D ．当AD 为边时，同理过点A 作AC 易得AH 所在直线解析式为y =当AC 为对角线时，DE 也为对角线，∴此种情况不存在．(1)求抛物线的表达式；(2)若点P 为第一象限内抛物线上的一点，设PBC 的面积为S ，求S 坐标；(3)已知M 是抛物线对称轴上一点，在平面内是否存在点N ，使以B 的四边形是矩形？若存在，直接写出N 点坐标；若不存在，请说明理由．【答案】(1)22+3y x x =-+(2)S 最大值为278，315(,)24P (3)存在，点1(2,(317))2N +或1(2,(317))2-或(2,1)-或(4,1)．【分析】（1）运用抛物线交点式解析式求解，设抛物线(1)(y a x x =+解；（2）如图，过点P 作PD AC ⊥，垂足为点D ，交BC 于点E ，设(,P m 的解析式3y x =-+，于是23PE m m =-+，从而13(22S PE OC m ==- 时，S 最大值为278，进而求得315(,)24P ；设2(,23)P m m m -++设直线BC 的解析式为y kx =033k hh =+⎧⎨=⎩，解得13k h =-⎧⎨=⎩∴3y x =-+则点(,3)E m m -+，2PE m =-∴2113(22S PE OC m ==´-+ ∴当32m =时，S 最大值为2782915233344m m -++=-++=∴315(,)24P ；（3）存在．设(1,)M p ，如图，223BC =222(13)(0)CM p p =-+-=如图，当BM 为对角线时，∠222BM CM BC =+，即26p p -+01330n p q +=+⎧⎨+=+⎩解得21n q =-⎧⎨=⎩∴点(2,1)N -如图，当CM 为对角线时，MBC ∠222BM BC CM +=，即26p p -+(1)求抛物线的对称轴方程；(2)若点P 满足PAB PBA ∠=∠，求点P 的坐标；(3)设M 是抛物线的对称轴上一点，N 是坐标平面内一点，正方形的面积．【答案】(1)32x =-(2)()51,51P --+(3)正方形AMPN 的面积为172或372【分析】（1）由4y x =+可知()4,0A -，()0,4B ，进而求得抛物线解析式为即可得抛物线的对称轴方程；（2）由题意可知PAB PBA ∠=∠，可知PA PB =，进而值OP 其与AB 交于点Q ，可得()2,2Q -，可求得OP 的解析式为则90PDM ACM ∠=∠=︒∴DPM PMD PMD ∠+∠=∠∴(AAS PDM MCA △≌△∴PD MC =，MD AC =，∵()4,0A -，3,02C ⎛⎫- ⎪⎝⎭，∴35422MD AC ==-=，则90PEM ACM ∠=∠=︒∴EPM PME PME ∠+∠=∠∴(AAS PEM MCA △≌△∴PE MC =，ME AC =，∵()4,0A -，3,02C ⎛⎫- ⎪⎝⎭，∴35422ME AC ==-=，则P y CE MC ME ==+=即：32P x m =-，P y m =-(1)求A ，B ，C 三点的坐标，并直接写出直线(2)在点P 的运动过程中，求使四边形(3)点N 为平面内任意一点，在（2N 为顶点的四边形是正方形？若存在，请直接写出点【答案】(1)()1,0A -，()3,0B ，C (2)32m =-(3)()1221,2Q +，2252,2Q ⎛+ ⎝【分析】（1）分别令0y =，0x =，可求出点∵()3,0B ，()0,3C ，∴3OB OC ==，∴BOC 是等腰直角三角形，∴点()221,2Q +，∴()22132322EQ =+--=-∴PE EQ =，此时点()221,2Q +使得以P ，E 如图，过点E 作EQ PM ⊥于点Q ，过点由（2）得：45BED ∠=︒，∵PM BC ∥，∴45BED DPQ ∠=∠=︒，∴PEQ ，PSQ 是等腰直角三角形，∴此时点Q 使得以P ，E ，Q ，N 为顶点的四边形是正方形；∴132222PS SE PE -===，∴点5232,12S ⎛⎫-- ⎪ ⎪⎝⎭，对于321y x =-++，当5212y =-时，222x =+，(1)求抛物线的解析式；(2)点E 在第一象限内，过点E 作EF y ∥轴，交BC 于点F ，作EH 点H 在点E 的左侧，以线段,EF EH 为邻边作矩形EFGH ，当矩形求线段EH 的长；(3)点M 在直线AC 上，点N 在平面内，当四边形OENM 是正方形时，请直接写出点标．【答案】(1)抛物线的解析式为2142y x x =-++；(2)4EH =；(3)点N 的坐标为()44，或7322⎛⎫- ⎪⎝⎭，．【分析】（1）利用待定系数法即可求解；（2）先求得直线BC 的解析式为4y x =-+，设2142x E x x ⎛ ⎝-++，对称性质求得21422H x x x ⎛⎫- ⎪+⎝-+⎭，，推出2122GH EF x -=-+矩形周长公式列一元二次方程计算即可求解；（3）先求得直线AC 的解析式为24y x =+，分别过点M 、E 作90OPE MQO ∠=∠=︒，90OEP ∠=︒∴OEP MOQ ≌△△，∴PE OQ =，PO MQ =，设2142m E m m ⎛⎫ ⎪⎝-++⎭，，∴PE OQ m ==-，12P m O M Q ==-∵点M 在直线AC 上，∴244212m m m -⎛⎫=+ ⎪⎝⎭-，解得m =当4m =时，()04M ，，()40E ，，即点M 与点C 重合，点E 与点B 重合时，四边形当1m =-时，512M ⎛⎫-- ⎪⎝⎭，，512E ⎛- ⎝，点O 向左平移52个单位，再向下平移则点E 向左平移52个单位，再向下平移∴551122N ⎛⎫--- ⎪⎝⎭，，即7322N ⎛⎫- ⎪⎝⎭，．课后训练(1)求抛物线的解析式；(2)如图2，点P 、Q 为直线BC 下方抛物线上的两点，点Q 的横坐标比点过点P 作PM y ∥轴交BC 于点M ，过点Q 作QN y ∥轴交BC 于点N ，求值及此时点Q 的坐标；(3)如图3，将抛物线()230y ax bx a =+-≠先向右平移1个单位长度，再向下平移长度得到新的抛物线y '，在y '的对称轴上有一点D ，坐标平面内有一点E D 、E 为顶点的四边形是矩形，请直接写出所有满足条件的点E 的坐标．【答案】(1)抛物线的解析式为2=23y x x --(2)当1a =时，max ()4PM QN +=，()2,3Q -(3)()1,2E --或()5,2-或3171,2⎛⎫-- ⎪ ⎪⎝⎭或3171,2⎛⎫-+ ⎪ ⎪⎝⎭【分析】（1）直接运用待定系数法即可解答；（2）设()2,23P a a a --，则()21,4Q a a +-，进而得到(),3M a a -，(N 出222422(1)4PM QN a a a +=-++=--+，最后根据二次函数的性质即可解答；（3）分以BC 为矩形一边和对角线两种情况，分别根据等腰直角三角形的性质、平移和矩形的判定定理解答即可．【详解】（1）解：把()1,0A -和()3,0B 代入()230y ax bx a =+-≠，得309330a b a b --=⎧⎨+-=⎩，解得1a =，2b =-∴222422(1)4PM QN a a a +=-++=--+∴当1a =时，max ()4PM QN +=∴()2,3Q -．（3）解：由题意可得：()()()222=1213152x y x x x x --'---=---=-，∴y '的对称轴为2x =∵抛物线()230y ax bx a =+-≠与y 轴交于点C ．∴()0,3C -,∵()3,0B ,∴3OC OB ==,45BCO CBO ∠=∠=︒；如图：当BC 为矩形一边时，且点D 在x 轴的下方，过D 作DF y ⊥轴，∵D 在y '的对称轴为2x =，∴2FD =，∴2CF FD ==,325OF =+=,即点()2,5D -，∴点C 向右平移2个单位、向下平移3个单位可得到点D ，则点B 向右平移2个单位、向下平移3个单位可得到()5,3E -；如图：当BC 为矩形一边时，且点D 在x 轴的上方，y '的对称轴为2x =与x 轴交于F ，∵D 在y '的对称轴为2x =，∴2FO =，∴321BF =-=，∵45CBO ∠=︒，即45DBO ∠=︒，∴321BF FD ==-=,即点()2,1D ，∴点B 向左平移1个单位、向上平移1个单位可得到点D ，则点C 向左平移1个单位、向上平移1个单位可得到点()1,2E --；如图：当BC 为矩形对角线时，设∴BC 的中点F 的坐标为32⎛ ⎝∴2322322m d n +⎧=⎪⎪⎨+⎪=⎪⎩，解得：m d =⎧⎨+⎩又∵DE BC =,∴()()22222133d n -+-=+联立173d n d n ⎧-=±⎪⎨+=⎪⎩，解得：∴点E 的坐标为3171,2⎛-- ⎝综上，存在()1,2E --或(5,的四边形是矩形．【点睛】本题主要考查了运用待定系数法求解析式、与几何的综合等知识点，掌握二次函数的性质和矩形的判定定理是解答本题的关键．2．如图，在平面直角坐标系中，抛物线与y 轴交于点C ，点P 为抛物线上的动点．(1)求该抛物线的函数表达式；(2)点D 为直线y x =上的动点，当点P 在第四象限时，求四边形PBDC 面积的最大值及此时点P 的坐标；(3)已知点E 为x 轴上一动点，点Q 为平面内任意一点，是否存在以点P ，C ，E ，Q 为顶点的四边形是以PC 为对角线的正方形，若存在，请直接写出点Q 的坐标，若不存在，请说明理由．【答案】(1)2=23y x x --(2)278，315,24P ⎛⎫- ⎪⎝⎭(3)3333,2⎛⎫+- ⎪ ⎪⎝⎭；3333,2⎛⎫-- ⎪ ⎪⎝⎭；(3,3)-；(3,2)【分析】（1）用待定系数法求函数的解析式即可；（2）作直线BC ，过P 作PH x ⊥轴于点G ，交BC 于点H ．设()2,23P m m m --，则(,3)H m m -，23PH m m =-+，则2139()228BPC S t ∆=--+，当32t =时，BPC △的面积最大值为从而求出此时四边形PBDC 面积的最大值，P 点坐标；（3）设()2,23P m m m --，(,0)E n ，分四种情况画出图形，利用正方形性质求解即可．【详解】（1）解：将(1,0)A -，(3,0)B 代入23y ax bx =+-中，得309330a b a b --=⎧⎨+--⎩，解得12a b =⎧⎨=-⎩．∴该抛物线的函数表达式为2=23y x x --．（2）解：作直线BC ，过P 作PH x ⊥轴于点G ，交BC 于点H ．设直线BC 的表达式为：y kx =+得303k n n +=⎧⎨=-⎩，解得13k n =⎧⎨=-⎩，3y x ∴=-．设()2,23P m m m --，则(,H m m ∵BPC CPH BPHS S S =+△△△∴1122BPC S PH OG PH BG =⋅+⋅△∴(21322BPC S PH OB m =⨯=-+△∴28323272BPC S m ⎛⎫=-+ ⎪⎝-⎭△，∴当32m =时，BPC △面积的最大值为BC 与直线y x =平行，1122DBC OBC S S OB OC ∴==⋅=△△∴四边形PBDC 面积的最大值为当32m =时，2332322y ⎛⎫-⨯- ⎪⎝⎭=315,24P ⎛⎫∴- ⎪⎝⎭（3）解：设()2,23P m m m --，I.如图，当点E 在原点时，即点∵四边形PECQ 为正方形，∴点3(3,)Q -，II.如解图3-2，当四边形PECQ 作PI x ⊥轴，垂足为I ，作QH ⊥又∵90CEO OCE ∠+∠=︒，∴OCE PEO ∠=∠，∴(ASA)OCE PEI ≅ △∴3CO IE ==，22EO IP m ==-同理可得：3QH CO IE ===，∴3OE OI IE m =+=+，HO IO=∴2323m m m +=--，解得：m ∴3332HO IO +==，∴点)33(3,32Q +-，同理可得：PI OE CH ==，IE QH =∴3OE IE IO m =-=+，∴2233m m m =---，解得：m =∴3332HO IO -+==，∴点3,(Q -IV.如解图3-4，当四边形PECQ 为正方形时，同理可得：PI OE CH ==，EI HQ =∴2323m m m -=--，解得：m =∴2HO IO ==，∴点(3,2)Q ，综上所述：点Q 坐标为3333,2⎛+- ⎝【点睛】此题重点考查二次函数的图象与性质、数解析式、正方形性质、全等三角形的判定与性质、一元二次方程的解法、数形结合与分类讨论数学思想的运用等知识与方法，此题综合性强，难度较大，属于考试压轴题．3．如图，抛物线212y x bx c =++与物线交于A 、D 两点，与y 轴交于点综上所述，341,22N ⎛⎫+ ⎪ ⎪⎝⎭或341,22N ⎛- ⎝【点睛】本题考查了待定系数法求解析式，面积问题，平行四边形的性质，熟练掌握是二次函数的性质解题的关键．4．在平面直角坐标系中，抛物线2y ax =(1)求抛物线的表达式；(2)若直线x m =与x 轴交于点求出抛物线上点M 的坐标；(3)若点P 为抛物线y ax =位长度后，Q 为平移后抛物线上一动点，在（构成平行四边形？若能构成，求出【答案】(1)223y x x =-++(2)315,24⎛⎫ ⎪⎝⎭(3)1(2-，15)4或3(2-，7)4或【分析】（1）利用待定系数法，即可求出抛物线的表达式；（2）由“直线x m =与x 轴交于点的坐标，进而可得出AN 再利用二次函数的性质，即可求出（3）利用平移的性质，可得出平移后抛物线的表达式为点的坐标特征，可求出点点P 的坐标为(1,)m ，点Q 线三种情况考虑，由平行四边形的对角线互相平分，可得出关于得出n 值，再将其代入点【详解】（1）解：将(1,0)-09303a b c a b c c -+=⎧⎪++=⎨⎪=⎩，解得：∴抛物线的表达式为y =-（2） 直线x m =与x 轴交于点∴点M 的坐标为2(,m m -。

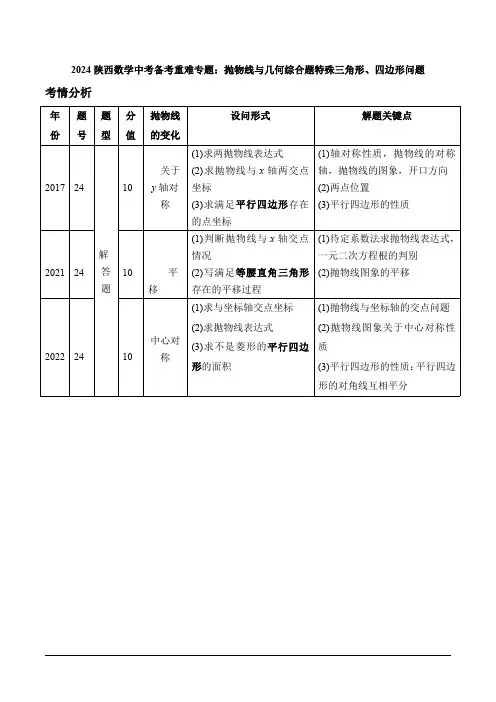
2024陕西数学中考备考重难专题：抛物线与几何综合题特殊三角形、四边形问题考情分析年份题号题型分值抛物线的变化设问形式解题关键点201724解答题10关于y轴对称(1)求两抛物线表达式(2)求抛物线与x轴两交点坐标(3)求满足平行四边形存在的点坐标(1)轴对称性质，抛物线的对称轴，抛物线的图象，开口方向(2)两点位置(3)平行四边形的性质20212410平移(1)判断抛物线与x轴交点情况(2)写满足等腰直角三角形存在的平移过程(1)待定系数法求抛物线表达式，一元二次方程根的判别(2)抛物线图象的平移20222410中心对称(1)求与坐标轴交点坐标(2)求抛物线表达式(3)求不是菱形的平行四边形的面积(1)抛物线与坐标轴的交点问题(2)抛物线图象关于中心对称性质(3)平行四边形的性质：平行四边形的对角线互相平分例(2022陕西逆袭卷改编)如图，抛物线L：y＝x2＋2x－c的图象与x轴交于A，B两点(点B 在点A的左侧)，与y轴交于点C(0，-3)，过点A的直线与y轴交于点D，与抛物线交于点M，且tan∠BAM＝1.(1)求点A，B的坐标及抛物线解析式;(2)抛物线M与抛物线L关于y轴对称，求抛物线M与y轴交点坐标；(3)若点P为抛物线L上一动点，E为直线AD上一动点，则是否存在点P，使得以点A，P，E 为顶点的三角形为等腰直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．例题图①(4)抛物线M上存在一点F，抛物线L上存在一点G，使得四边形ABFG为平行四边形，求出F，G两点坐标.例题图②探究平行四边形存在性问题的步骤：1.三定点(A、B、C)，一动点(D)：分别过点A、B、C作BC、AC、AB的平行线，三条平行线的交点即为所求作的点D 2.两定点(A、C)，两动点(E、F)：分AC为边和AC为对角线两种情况来讨论：①AC为边，平移AC，利用平行四边形的对边平行且相等确定点E、F位置②AC为对角线，取AC中点，利用平行四边形对角线互相平分来确定点E、F位置练习(2022山西逆袭复诊卷)综合与探究如图，抛物线y＝38x2－94x－6与x轴交于点A，C，与y轴交于点B，点P是抛物线上任意一点，连接PB，PC，BC.练习题图(1)求点A，B，C的坐标；(2)当△PBC的面积为24时，求点P的坐标；(3)若点Q是直线x＝4上一点，是否存在以点P，Q，B，C为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由．练习1(2022陕西原创卷)在平面直角坐标系中，抛物线L：y＝x2＋bx＋c与x轴交于A、B(3，0)两点，与y轴交于点C(0，－3)，抛物线L′与抛物线L关于y轴对称．练习1题图(1)求抛物线L的表达式；(2)抛物线L′的顶点为D，在x轴上是否存在一点P，使得以B、D、P为顶点的三角形是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．练习2(2022陕西黑白卷白卷)如图，抛物线y＝ax2＋bx＋c(a≠0)与直线y＝23x－2分别交x轴、y轴于点A，B，且抛物线与x轴的另一个交点为C(－1，0).(1)求抛物线的表达式；(2)点P是平面内任意一点，在抛物线对称轴上是否存在点Q，使得以A，B，P，Q为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由．练习2题图答案典例精讲例解：(1)∵C(0，－3)∴抛物线L解析式为y＝x2＋2x－3，令y＝0，即x2＋2x－3＝0，解得x＝1或x＝－3，∴A(1，0)，B(－3，0)；(2)将抛物线L化为顶点式为y＝(x+1)2－4∵抛物线M与抛物线L关于y轴对称，∴抛物线M的解析式为y＝(x－1)2－4令x=0，则y=－3，∴抛物线M与y轴交点坐标为(0，－3)(3)存在．在Rt△AOD中，∵tan∠BAM＝tan∠OAD＝ODOA＝1，∴OD＝OA，∠BAD＝45°.如解图，分三种情况讨论：例题解题①①当AE＝PE时，∠AEP＝90°，∴∠EPA＝∠EAP＝45°，∵∠DAB＝45°，∴此时点P与点B重合，∴点P 的坐标为(－3，0)；②当AP ＝PE 时，∠EPA ＝90°，∴∠PEA ＝∠EAP ＝45°，∴此时点P 与点B 重合，∴点P 的坐标为(－3，0)；③当AP ＝AE 时，∠EAP ＝90°，设AP 与y 轴交于点F ，则∠OFA ＝∠OAF ＝45°，∴OF ＝OA ＝1，∴点F 的坐标为(0，－1)，设直线AF 的表达式为y ＝kx ＋b (k ≠0)，将A (1，0)，F (0，－1)代入y ＝kx ＋b 中，＝k ＋b1＝b ＝1＝－1，∴直线AF 的表达式为y ＝x －1，设点P 的坐标为(x ，x 2＋2x －3)，∴x 2＋2x －3＝x －1，解得x 1＝1(舍去)，x 2＝－2，当x ＝－2时，y ＝－2－1＝－3，∴点P 的坐标为(－2，－3)．综上所述，满足条件的点P 的坐标为(－3，0)或(－2，－3)．(4)∵A (1，0)，B (－3，0)∴AB ＝4∵点F 在抛物线M 上，点G 在抛物线L 上，且四边形ABFG 是平行四边形∴FG ∥AB ，FG =AB =4∵抛物线M 与抛物线L 关于y 轴对称∴两抛物线上纵坐标相同的点，横坐标关于y 轴对称∴4F G x x +=，x F ＝－x G分两种情况讨论，当F 、G 在x 轴上方时，即x F ＝－2时，x G ＝2当F、G在x轴下方时，即x F＝2时，x G＝－2将x F＝－2代入抛物线M解析式y＝x2－2x－3可得y F＝5，x G＝2，y G＝5，此时F(－2，5)，G(2，5)将x F＝2代入抛物线M解析式y＝x2－2x－3可得y F＝－3，x G＝－2，y G＝－3，此时F(2，－3)，G(－2，－3)∴综上所述，F(－2，5)，G(2，5)或F(2，－3)，G(－2，－3).例题解图②课堂练兵练习解：(1)在y＝38x2－94x－6中，令y＝0，得38x2－94x－6＝0，解得x＝－2或x＝8，令x＝0，得y＝－6，∴点A(－2，0)，点B(0，－6)，点C(8，0)；(2)当点P在直线BC下方时，如解图①，过点P作PD⊥x轴于点D，交BC于点E，设直线BC的表达式为y＝kx＋d(k≠0)，将点B(0，－6)，C(8，0)代入，得＝－68＋＝0，解得＝34＝－6，∴直线BC的表达式为y＝34x－6.设点P (m ，38m 2－94m －6)(0<m <8)，则点E (m ，34m －6)，∴PE ＝(34m －6)－(38m 2－94m －6)＝－38m 2＋3m ，∴S △PBC ＝12PE ·OC ＝12(－38m 2＋3m )×8＝－32m 2＋12m ，当S △PBC ＝24时，即－32m 2＋12m ＝24，解得m ＝4，此时P (4，－9)；当点P 在直线BC 上方时，如解图②，由平移易求得lP 1P 2：y ＝34x ，联立＝34＝382－94－6，解得1＝4＋421＝3＋32，2＝4－422＝3－32，此时P 1(4＋42，3＋32)，P 2(4－42，3－32)．综上所述，点P 的坐标为(4，－9)或(4＋42，3＋32)或(4－42，3－32)；解图①解图②练习题(3)存在．当以点P ，Q ，B ，C 为顶点的四边形是平行四边形时，分两种情况：①如解图③，当BC 作为平行四边形的一条边时，PQ ∥BC ，且PQ ＝BC ，∵点Q 的横坐标为4，∴|x p －4|＝8，解得x p ＝－4或x p ＝12，∴P 1(－4，9)，P 2(12，21)；②如解图④，当BC 为平行四边形的对角线时，设对角线交于点R ，则BR ＝CR ，∴点R (4，－3)，＋2＝4，点Q 在直线x ＝4上，∴点P 的横坐标为4，此时P 3(4，－9)．综上所述，存在满足题意的点P ，点P 的坐标为(－4，9)或(12，21)或(4，－9)．解图③解图④练习题课后小练练习1解：(1)分别将点B (3，0)，C (0，－3)的坐标代入y ＝x 2＋bx ＋c 中得9＋3＋＝0＝－3，解得＝－2＝－3，∴抛物线L 的表达式为y ＝x 2－2x －3；(2)存在．∵抛物线L ′与抛物线L 关于y 轴对称，∴抛物线L ′的表达式为y ＝x 2＋2x －3＝(x ＋1)2－4，∴D (－1，－4)，设点P 的坐标为(m ，0)，∴BD 2＝(3＋1)2＋[0－(－4)]2＝32，DP 2＝(m ＋1)2＋(0＋4)2，则PB 2＝(m －3)2，∵△PBD 为等腰三角形，分三种情况讨论：①当PB ＝BD 时，即(m －3)2＝32，解得m ＝3＋42或m ＝3－42，∴P 1(3＋42，0)，P 2(3－42，0)；②当BD ＝PD 时，即32＝(m ＋1)2＋(0＋4)2，解得m ＝3(舍去)或m ＝－5，∴P 3(－5，0)；③当PB ＝PD 时，即(m －3)2＝(m ＋1)2＋(0＋4)2，解得m ＝－1，∴P 4(－1，0)综上所述，点P 点坐标为(3＋42，0)，(3－42，0)，(－5，0)，(－1，0).练习2解：(1)在y ＝23x －2中，当x ＝0时，y ＝－2.∴B (0，－2).令y ＝23x －2＝0，得x ＝3.∴A (3，0).设抛物线的表达式为y ＝a (x ＋1)(x －3)，将点B(0，－2)代入，得－2＝－3a，解得a＝2 3 .∴抛物线的表达式为y＝23(x＋1)(x－3)＝23x2－43x－2；(2)存在．∵A(3，0)，B(0，－2)，∴AB2＝13.由(1)可知抛物线的对称轴为直线x＝1，∴设Q(1，m)，则AQ2＝22＋m2，BQ2＝1＋(m＋2)2，要使以A，B，P，Q为顶点的四边形是菱形，则分三种情况讨论：①当AQ＝AB，即AQ2＝AB2时，四边形ABPQ为菱形，∴22＋m2＝13，解得m＝3或m＝－3，∴点Q的坐标为(1，3)或(1，－3)；②当AB＝BQ，即AB2＝BQ2时，四边形ABQP为菱形，∴13＝1＋(m＋2)2，解得m＝23－2或m＝－23－2，∴点Q的坐标为(1，23－2)或(1，－23－2)，③当AQ＝BQ，即AQ2＝BQ2时，四边形AQBP为菱形，∴22＋m2＝1＋(m＋2)2，解得m＝－1 4∴点Q的坐标为(1，－1 4 ).综上所述，点Q的坐标为(1，3)或(1，－3)或(1，23－2)或(1，－23－2)或(1，－1 4 ).。

专题 24《特别平行四边形的存在性》破解策略在平行四边形的基础上增添一些条件，即可获得特别的平行四边形因此能够联合”等腰三角形的存在性”，”直角三角形的存在性”和”平行四边形的存在性”来解决这种问题．例题解说例 1：如图，在平面直角坐标系xOy 中，抛物线y＝ ax2－ 2ax－3a（ a＜ 0）与 x 轴交于 A，B两点（点 A 在点 B 的左边）．经过点 A 的直线 l： y＝ax＋ a 与抛物线的另一交点为C，设 P是抛物线的对称轴上的一点，点Q 在抛物线上，那么以点A，C，P，Q 为极点是四边形可否成为矩形若能，求出点P 的坐标 ;若不可以，请说明原因．解：以点A， C，P，Q 为都极点的四边形能成为矩形．令 ax2－ 2a－ 3a＝ ax＋ a．解得 x1＝－ 1，x2＝ 4，因此点 A 的坐标为（－ 1， 0）， C 的坐标为（ 4， 5a）．由于 y＝ ax2－ 2ax－ 3a，因此抛物线的对称轴为 x＝1．则 x P＝ 1．①若 AC 是矩形的一条边，如图，则x A＋x P＝x C＋x Q，可得x Q＝－4，进而点Q 坐标为（－4，21a ）．相同 y A＋ y P＝y C＋y Q，可得 y P＝ 26a，进而点 P 坐标为（ 1，26a）．由于 AC＝ PQ，因此有 22＋（ 26a ）2＝82＋（ 16a）2，解得 a1 7, a27(舍去 ) ，此时点P的坐标为（1，26 7 ）7 7 7②若 AC 是矩形的一条对角线，如图．则x A＋x C＝x P＋x Q，可得x Q＝2，进而点Q 坐标为（2，－3a）．相同y A＋y C＝y P＋y Q，可得y P＝8a，进而点P 坐标为（1，8a）．由于 AC＝ PQ，因此有 52＋（ 5a）2＝12＋（ 11a）2，算得 a3 1, a41(舍) ，因此此时点P 的坐标为（ 1，－ 4）2 2综上可得，以点A， C， P， Q 为极点的四边形能成为矩形，点P 的坐标为（ 1，26 7）7或（ 1，－ 4）．例 2：如图，在平面直角坐标系 xOy 中，菱形 ABCD的中心与原点重合， C，D 两点的坐标分别为（ 4， 0），（ 0， 3）．现有两动点 P， Q 分别从 A，C 同时出发，点 P 沿线段 AD 向终点 D 运动，点Q 沿折线 CBA 向终点 A 运动，设运动时间为t 秒．（1）菱形 ABCD的边长是 _____，面积是 _____，高 BE 的长是 _____;（2）若点 P 的速度为每秒 1 个单位．点 Q 的速度为每秒 k 个单位．在运动过程中，任何时辰都有对应的 k 值，使得△ APQ 沿它的一边翻折，翻折前后两个三角形构成的四边形为菱形．请研究当t ＝ 4 秒时的情况，并求出k 的值．解：（ 1） 5，24， 4． 8．（ 2）要使△ APQ 沿它的一边翻折，翻折前后的两个三角形构成的四边形为菱形，依据轴对称的性质， 翻折前后两个图形是全等的， 因此要知足四边形是菱形只要△ APQ 为等腰三角形即可．当 t ＝4 时， AP ＝ 4．①如图，当点 Q 在线段 BC 上时， PQ ≥BE ＞AP ，同理， AQ ＞ AP ，因此只存在 QA ＝ QP 的等腰三角形．过点 Q 作 QH ⊥ AP 于点 H ，交 AC 于点 F ，则 AH ＝ PH ＝1AP ＝ 22易证：△ AFH ∽△ CFQ ∽△ ADO ， 因此FH=FQ =DO =3AH CQ AO 4可得FH=3 ,FQ = 33 ,CQ= 222105进而 k ＝CQ=114 10②当 Q 在 BA 上时，有两种状况的等腰三角形存在：（i ）如图 1，当 AP ＝ AQ 时，此时点 P ， Q 对于 x 轴对称， BQ ＝ PD ＝ 1 因此， k ＝CB +BQ=342（ⅱ ）如图 3，当 PA ＝ PQ 时，过点 P 作 PH ⊥ AB 于点 H ．易证 △ AHP ∽ △ AEB ，因此AH AP，此中 AE ＝ AB 2 BE27 .AEAB5因此 AH ＝28， AQ ＝ 2AH ＝56，因此 k ＝CBBQ97 ．2525450（ⅲ ）由 ① 可得， AP 的垂直均分线与 BC 订交，因此点 Q 在线段 AB 上时，不存在 AQ ＝ PQ 这种状况．综上所得，知足条件的k 值为 3，11，97．21050y PDExOCA HQB例 3 如图，二次函数12c 的图象与 x 轴分别交于 A ， B 两点，极点 M 对于 x 轴yx x2的对称点是 M ′．问：能否存在抛物线y1 x2 x c 使得四边形 AMBM ′为正方形若存在， 2恳求出抛物线的表达式；若不存在，请说明原因．yM ′xAOBM解：存在易得 AMBM ’是菱彤，因此当 AB ＝ MM ′时，四边彤 AMBM ′是正方形设点 A 的坐标为（ x 1 ，0）， B 的坐标为（ x 2， 0）．令 1xx c 022因此 x ＋x ＝2， x ·x ＝2c1212因此 AB ＝x 1 24x 1 x 2 ＝ 4 8c.x 2点 M 的纵坐标为 4 acb 2 2c 1 .4 a 2 若四边形 AMBM ’为正方形，则有 4 8c 2c 12 ．2 解得 c 11, c 23 .2 2又由于已知抛物线与 x 轴有两个交点，因此b24ac24 1 c 0.12 解得 c ＜ 1，2因此 c 的值为3. ．2因此存在抛物线 y 1 x 2 x3，使得四边彤AMBM '为正方形．22进阶训练1．已知抛物线 C 1： y ＝－ 2x 2＋ 8x －6 与抛物线点 A ， B 两点（点 A 在点 B 的左边），极点为 C在点 D 的左边）极点为 N ．（1）求抛物线 C 2 的表达式；C 对于原点对称，抛物线 C 2 与 x 轴分别交于M ，抛物线 C 2 与 x 轴分别交于 C ，D 两点（点（2）若抛物线 C 1 与抛物线 C 2 同时以每秒 1 个单位的速度沿 x 轴方向分别向左、 向右运动，此时记 A，B， C， D， M， N 在某一时辰的新地点分别为A'，B'， C'， D'， M' ， N'，当点 A'与点 D'重合时运动停止，在运动过程中，四边形B'， M' ，C'， N'可否形成矩形若能，求出此时运动时间 t （秒）的值；若不可以，请说明原因．解：（ 1）抛物线 C2的表达式为 y 2x2 8x 6 （ 2）能． 1＝[提示 ]（2）如图，由轴对称的性质可得四边形C'N' B'M' 为平行四边形．因此当∠ B' M'C'＝ 90 或 B'C'＝ M 'N'时．四边形为矩形，由此可列方程，从面求得t ．2．如图，抛物线y2 (x 7)225与x轴的右交点为A，与y轴的交点为B，设E（x，y）32 6是抛物线上一动点，且位于第四象限，若四边形OEAF是以 OA 为对角线的平行四边形．（1）该四边形的面积为24 时，判断平行四边形OEAF能否为菱形；（2）能否存在点 E，使平行四边形 OEAF为正方形若存在，求出点 E 的坐标；若不存在，请说明原因．yBFxO AE解：（ 1）当点 E 的坐标为（ 3，－ 4）时，平行四边形OAEF是菱形 ;（2）不存在，原因：若平行四边形 OEAF是正方形，则 OA⊥ EF且 OA＝ EF．此时的点 E 不在抛物线上．3．如图，抛物线经过原点 O 与 x 轴上一点 A（ 4，0 ），抛物线的极点为 E，它的对称轴x 轴交于点 D，直线 y＝－ 2x－ 1 经过抛物线上一点 B（－ 2， m），与抛物线的对称轴交于点F．（1）求抛物线的表达式；（2）Q 是平面内随意一点，点M 从点 F 出发，沿对称轴向上以每秒 1 个单位长度的速度均速运动，设点 M 的运动时间为t 秒，能否能使以 Q，A，E， M 四点极点的四边形是菱形若能，请直接写出点M 的运动时间；若不可以，请说明原因．yBD xO AEF解：（ 1）抛物线的表达式为 y 1 x2 x ；4（2 ）能， t 的值为 4 5，6，4 5 或13．2[提示 ]（2）如图，点 M 的运动过程中，以Q， A， E， M 为极点的四边形是菱形有以下四种状况，依据菱形的性质即可求得对应的t 的值．yB BDQ2x D xO A O A EEQ1F Fy yBQ3BQ4D x D x O A O AE EF F24．如图，抛物线 y＝－ x ＋ bx＋c 经过 A（－ 1，0）两点，且与 y 轴交于点 C，D 是抛物线的极点，抛物线的对称轴 DE 交 x 轴于点 E，连接 BD．（1） P 是线段 BD 上一点，当 PE＝ PC时，恳求出点 P 的坐标；（2）在（ 1）的条件下，过点 P 作 PF⊥ x 轴于点 F，G 为抛物线上一动点， M 为 x 轴上一动点， N 为直线 PF 上一动点，当以 F，M，N，G 为极点的四边形是正方形时，恳求出点 M 的坐标．yDCPxA O EB解：（ 1）点 P 的坐标为（2， 2），（2）点 M 的坐标为 1 21，，1 21，，3 13，，3 13 ，2 0 0 0 0 .2 2 2[提示 ]（ 1）易求得抛物线的 l 表达式为 yx 2 2 x 3 ．因此 C （ 0，3）， D （1， 4）， E （ 1， 0），进而直线 BD 的表达式为 y ＝－ 2x ＋ 6．设点 P 的 坐标为（ t ，－ 2t ＋6）．若 PE ＝ PC ．则有 t 2＋（－ 2t ＋ 6－ 3） 2 t 12t 6 2，解得 t ＝2，进而获得点 P 的坐标为（ 2． 2）．（2）可设点 M 的坐标为（ m ，0），则点 G 的坐标为（ m ， m 2 2m 3 ）．而以 F ，M ，N ，G 为极点的四边形是正方形． 因此 MF ＝ MG ，进而 m 2m 2 2m 3 ，解得 m121，2或 m313，即得点 M 的坐标．2。

考向二：两定两动
2．如图，抛物线 y＝13x2－23x－1 与 x 轴交于 A，B 两点．点 Q 在 y 轴上， 点 P 在抛物线上，要使 Q，P，A，B 为顶点的四边形是平行四边形，请求 出所有满足条件的点 P 的坐标．
解：在 y＝13x2－23x－1 中， 令13x2－23x－1＝0， 解得 x1＝－1，x2＝3， ∴A(_－__1_，__0__)，B(__3_，__0___).
－1＝__t__．解得 t＝53.∴P2(__4_，__53___).
②如图，当 AB 为对角线，若四边形 P3BQ3A 为平行四边形， 则xyPP33－－xyBB＝＝xyAA－－xyQQ33，. ∴xyPP33－ －_0＝_3_0_－＝t－.1－__0__，解得xyPP33＝＝_－_2_t._， ∴P3(__2__，－t). 将点 P3 的坐标代入抛物线解析式 y＝13x2－23x－1，得13×__2_2_－23×__2__
若以点 P，A，B，D 为顶点的四边形是平行四边形， 则 PA＝BD，即 PA2＝BD2. 设 P(m，m－5)，则_P_A_2_＝(m－1)2＋(m－5＋4)2＝2(m－1)2.
又_B_D_2_＝32＋32＝18，
∴2(m－1)2＝18.解得 m1＝4，m2＝－2. ∴P1(4，－1)，P2(－2，－7). 综上所述，存在满足条件的点 P，点 P 的坐标分别为 P1(_4_，__－__1__)或 P2(－__2_，__－__7_).
－ 综1上＝所_述 _－_，_t_符__合_．条解件得的_点__－_P_t的__坐_＝标－为1.P∴1(_P－_3(_4__，_2__，_7___－__)_1，_)P.2(__4_，__53___)， P3(__2_，__－_1__).

二次函数中考精品压轴题（四边形与存在性问题）解析精选【例1】综合与实践：如图，在平面直角坐标系中，抛物线y=﹣x 2+2x+3与x 轴交于A ．B 两点，与y 轴交于点C ，点D 是该抛物线的顶点．（1）求直线AC 的解析式及B ．D 两点的坐标；（2）点P 是x 轴上一个动点，过P 作直线l ∥AC 交抛物线于点Q ，试探究：随着P 点的运动，在抛物线上是否存在点Q ，使以点A ．P 、Q 、C 为顶点的四边形是平行四边形？若存在，请直接写出符合条件的点Q 的坐标；若不存在，请说明理由．（3）请在直线AC 上找一点M ，使△BDM 的周长最小，求出M 点的坐标．【答案】解：（1）当y=0时，﹣x 2+2x+3=0，解得x 1=﹣1，x 2=3。

∵点A 在点B 的左侧，∴A ．B 的坐标分别为（﹣1，0），（3，0）。

当x=0时，y=3。

∴C 点的坐标为（0，3）。

设直线AC 的解析式为y=k 1x+b 1（k 1≠0），则111b =3k +b =0⎧⎨-⎩，解得11k =3b =3⎧⎨⎩。

∴直线AC 的解析式为y=3x+3。

∵y=﹣x 2+2x+3=﹣（x ﹣1）2+4，∴顶点D 的坐标为（1，4）。

（2）抛物线上有三个这样的点Q 。

如图，①当点Q 在Q 1位置时，Q 1的纵坐标为3，代入抛物线可得点Q 1的坐标为（2，3）；②当点Q 在点Q 2位置时，点Q 2的纵坐标为﹣3，代入抛物线可得点Q 2坐标为（1+7，﹣3）；③当点Q 在Q 3位置时，点Q 3的纵坐标为﹣3，代入抛物线解析式可得，点Q 3的坐标为（1﹣7，﹣3）。

综上可得满足题意的点Q 有三个，分别为：Q 1（2，3），Q 2（1+7，﹣3），Q 3（1﹣7，﹣3）。

（3）点B 作BB′⊥AC 于点F ，使B′F=BF ，则B′为点B 关于直线AC 的对称点．连接B′D 交直线AC 与点M ，则点M 为所求。

过点B′作B′E ⊥x 轴于点E 。

专题7 二次函数图象抛物线中特殊四边形存在性问题（原卷版）第一部分典例剖析+针对训练类型一二次函数与平行四边形典例1（2023•淄博）如图，一条抛物线y＝ax2+bx经过△OAB的三个顶点，其中O为坐标原点，点A（3，﹣3），点B在第一象限内，对称轴是直线x=94，且△OAB的面积为18．（1）求该抛物线对应的函数表达式；（2）求点B的坐标；（3）设C为线段AB的中点，P为直线OB上的一个动点，连接AP，CP，将△ACP沿CP翻折，点A 的对应点为A1．问是否存在点P，使得以A1，P，C，B为顶点的四边形是平行四边形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．针对训练1．（2023•济宁）如图，直线y＝﹣x+4交x轴于点B，交y轴于点C，对称轴为x=32的抛物线经过B，C两点，交x轴负半轴于点A，P为抛物线上一动点，点P的横坐标为m，过点P作x轴的平行线交抛物线于另一点M，作x轴的垂线PN，垂足为N，直线MN交y轴于点D．（1）求抛物线的解析式；（2）若0＜m＜32，当m为何值时，四边形CDNP是平行四边形？2．（2023•聊城）如图①，抛物线y＝ax2+bx﹣9与x轴交于点A（﹣3，0），B（6，0），与y轴交于点C，连接AC，BC．点P是x轴上任意一点．（1）求抛物线的表达式；（2）点Q在抛物线上，若以点A，C，P，Q为顶点，AC为一边的四边形为平行四边形时，求点Q的坐标；类型二二次函数与矩形典例2（2023•内蒙古）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴的交点分别为A和B（1，0）（点A在点B的左侧），与y轴交于点C（0，3），点P是直线AC上方抛物线上一动点．（1）求抛物线的解析式；（2）如图1，过点P做x轴平行线交AC于点E，过点P做y轴平行线交x轴于点D，求PE+PD的最大值及点P的坐标；（3）如图2，设点M为抛物线对称轴上一动点，当点P，点M运动时，在坐标轴上确定点N，使四边形PMCN为矩形，求出所有符合条件的点N的坐标．1．（2023•东营）如图，抛物线过点O（0，0），E（10，0），矩形ABCD的边AB在线段OE上（点B在点A的左侧），点C，D在抛物线上．设B（t，0），当t＝2时，BC＝4．（1）求抛物线的函数表达式；（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？（3）保持t＝2时的矩形ABCD不动，向右平移抛物线，当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形ABCD的面积时，求抛物线平移的距离．类型三二次函数与菱形典例3（2023•重庆）如图，在平面直角坐标系中，抛物线y＝ax2+bx+2过点（1，3），且交x轴于点A（﹣1，0），B两点，交y轴于点C．（1）求抛物线的表达式；（2）点P是直线BC上方抛物线上的一动点，过点P作PD⊥BC于点D，过点P作y轴的平行线交直线BC于点E，求△PDE周长的最大值及此时点P的坐标；（3）在（2）中△PDE周长取得最大值的条件下，将该抛物线沿射线CB方向平移√5个单位长度，点M 为平移后的抛物线的对称轴上一点．在平面内确定一点N，使得以点A，P，M，N为顶点的四边形是菱形，写出所有符合条件的点N的坐标，并写出求解点N的坐标的其中一种情况的过程．1．（2023•西藏）在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）如图甲，在y轴上找一点D，使△ACD为等腰三角形，请直接写出点D的坐标；（3）如图乙，点P为抛物线对称轴上一点，是否存在P、Q两点使以点A，C，P，Q为顶点的四边形是菱形？若存在，求出P、Q两点的坐标，若不存在，请说明理由．2．（2023•锦州）如图，抛物线y=−√3x2+bx+c交x轴于点A（﹣1，0）和B，交y轴于点C（0，3√3），顶点为D．（1）求抛物线的表达式；（2）若点E在第一象限内对称轴右侧的抛物线上，四边形ODEB的面积为7√3，求点E的坐标；（3）在（2）的条件下，若点F是对称轴上一点，点H是坐标平面内一点，在对称轴右侧的抛物线上是否存在点G，使以点E，F，G，H为顶点的四边形是菱形，且∠EFG＝60°，如果存在，请直接写出点G的坐标；如果不存在，请说明理由．3．（2023•雅安）在平面直角坐标系中，已知抛物线y＝x2+bx+c过点A（0，2），对称轴是直线x＝2．（1）求此抛物线的函数表达式及顶点M的坐标；（2）若点B在抛物线上，过点B作x轴的平行线交抛物线于点C，当△BCM是等边三角形时，求出此三角形的边长；（3）已知点E在抛物线的对称轴上，点D的坐标为（1，﹣1）是否存在点F，使以点A，D，E，F为顶点的四边形为菱形？若存在，请直接写出点F的坐标；若不存在，请说明理由．类型四二次函数与正方形典例4（2023•绥化）如图，抛物线y1＝ax2+bx+c的图象经过A（﹣6，0），B（﹣2，0），C（0，6）三点，且一次函数y＝kx+6的图象经过点B．（1）求抛物线和一次函数的解析式；（2）点E，F为平面内两点，若以E、F、B、C为顶点的四边形是正方形，且点E在点F的左侧．这样的E，F两点是否存在？如果存在，请直接写出所有满足条件的点E的坐标；如果不存在，请说明理由；针对训练1．（2023•日照）在平面直角坐标系xOy 内，抛物线y ＝﹣ax 2+5ax +2（a ＞0）交y 轴于点C ，过点C 作x 轴的平行线交该抛物线于点D ．（1）求点C ，D 的坐标；（2）当a =13时，如图1，该抛物线与x 轴交于A ，B 两点（点A 在点B 的左侧），点P 为直线AD 上方抛物线上一点，将直线PD 沿直线AD 翻折，交x 轴于点M （4，0），求点P 的坐标；（3）坐标平面内有两点E （1a ，a +1），F （5，a +1），以线段EF 为边向上作正方形EFGH ． ①若a ＝1，求正方形EFGH 的边与抛物线的所有交点坐标；②当正方形EFGH 的边与该抛物线有且仅有两个交点，且这两个交点到x 轴的距离之差为52时，求a 的值．2．（2023•长沙）我们约定：若关于x 的二次函数y 1＝a 1x 2+b 1x +c 1与y 2＝a 2x 2+b 2x +c 2同时满足√a 2−c 1+（b 2+b 1）2+|c 2﹣a 1|＝0，（b 1﹣b 2）2023≠0，则称函数y 1与函数y 2互为“美美与共”函数．根据该约定，解答下列问题：（1）若关于x 的二次函数y 1＝2x 2+kx +3与y 2＝mx 2+x +n 互为“美美与共”函数，求k ，m ，n 的值；（2）对于任意非零实数r ，s ，点P （r ，t ）与点Q （s ，t ）（r ≠s ）始终在关于x 的函数y 1＝x 2+2rx +s 的图象上运动，函数y 2与y 1互为“美美与共”函数．①求函数y 2的图象的对称轴；②函数y 2的图象是否经过某两个定点？若经过某两个定点，求出这两个定点的坐标；否则，请说明理由；（3）在同一平面直角坐标系中，若关于x 的二次函数y 1＝ax 2+bx +c 与它的“美美与共”函数y 2的图象顶点分别为点A ，点B ，函数y 1的图象与x 轴交于不同两点C ，D ，函数y 2的图象与x 轴交于不同两点E ，F ．当CD ＝EF 时，以A ，B ，C ，D 为顶点的四边形能否为正方形？若能，求出该正方形面积的取值范围；若不请说明理由．第二部分专题提优训练1．（2023•枣庄）如图，抛物线y＝﹣x2+bx+c经过A（﹣1，0），C（0，3）两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与y轴交于点D．（1）求该抛物线的表达式；（2）若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；（3）若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．2．（2023•巴中）在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）经过点A（﹣1，0）和B（0，3），其顶点的横坐标为1．（1）求抛物线的表达式．（2）若直线x＝m与x轴交于点N，在第一象限内与抛物线交于点M，当m取何值时，使得AN+MN有最大值，并求出最大值．（3）若点P为抛物线y＝ax2+bx+c（a≠0）的对称轴上一动点，将抛物线向左平移1个单位长度后，Q为平移后抛物线上一动点．在（2）的条件下求得的点M，是否能与A、P、Q构成平行四边形？若能构成，求出Q点坐标；若不能构成，请说明理由．3．（2023•自贡）如图，抛物线y=−43x2+bx+4与x轴交于A（﹣3，0），B两点，与y轴交于点C．（1）求抛物线解析式及B，C两点坐标；（2）以A，B，C，D为顶点的四边形是平行四边形，求点D坐标；4．（2023•南充）如图1，抛物线y＝ax2+bx+3（a≠0）与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）点P在抛物线上，点Q在x轴上，以B，C，P，Q为顶点的四边形为平行四边形，求点P的坐标；（3）如图2，抛物线顶点为D，对称轴与x轴交于点E，过点K（1，3）的直线（直线KD除外）与抛物线交于G，H两点，直线DG，DH分别交x轴于点M，N．试探究EM•EN是否为定值，若是，求出该定值；若不是，说明理由．5．（2023•辽宁）如图，抛物线y=−12x2+bx+c与x轴交于点A和点B（4，0），与y轴交于点C（0，4），点E在抛物线上．（1）求抛物线的解析式；（2）点E在第一象限内，过点E作EF∥y轴，交BC于点F，作EH∥x轴，交抛物线于点H，点H在点E的左侧，以线段EF，EH为邻边作矩形EFGH，当矩形EFGH的周长为11时，求线段EH的长；（3）点M在直线AC上，点N在平面内，当四边形OENM是正方形时，请直接写出点N的坐标．6．（2023•邵阳）如图，在平面直角坐标系中，抛物线y＝ax2+x+c经过点A（﹣2，0）和点B（4，0），且与直线l：y＝﹣x﹣1交于D、E两点（点D在点E的右侧），点M为直线l上的一动点，设点M的横坐标为t．（1）求抛物线的解析式．（2）过点M作x轴的垂线，与抛物线交于点N．若0＜t＜4，求△NED面积的最大值．（3）抛物线与y轴交于点C，点R为平面直角坐标系上一点，若以B、C、M、R为顶点的四边形是菱形，请求出所有满足条件的点R的坐标．7．（2023•广安）如图，二次函数y＝x2+bx+c的图象交x轴于点A、B，交y轴于点C，点B的坐标为（1，0），对称轴是直线x＝﹣1，点P是x轴上一动点，PM⊥x轴，交直线AC于点M，交抛物线于点N．（1）求这个二次函数的解析式；（2）若点P在线段AO上运动（点P与点A、点O不重合），求四边形ABCN面积的最大值，并求出此时点P的坐标；（3）若点P在x轴上运动，则在y轴上是否存在点Q，使以M、N、C、Q为顶点的四边形是菱形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．8．（2023•达州）如图，抛物线y＝ax2+bx+c过点A（﹣1，0），B（3，0），C（0，3）．（1）求抛物线的解析式；（2）设点P是直线BC上方抛物线上一点，求出△PBC的最大面积及此时点P的坐标；（3）若点M是抛物线对称轴上一动点，点N为坐标平面内一点，是否存在以BC为边，点B、C、M、N为顶点的四边形是菱形，若存在，请直接写出点N的坐标；若不存在，请说明理由．9．（2023•扬州）在平面直角坐标系xOy中，已知点A在y轴正半轴上．（1）如果四个点（0，0）、（0，2）、（1，1）、（﹣1，1）中恰有三个点在二次函数y＝ax2（a为常数，且a≠0）的图象上．①a＝1；②如图1，已知菱形ABCD的顶点B、C、D在该二次函数的图象上，且AD⊥y轴，求菱形的边长；③如图2，已知正方形ABCD的顶点B、D在该二次函数的图象上，点B、D在y轴的同侧，且点B在点D的左侧，设点B、D的横坐标分别为m、n，试探究n﹣m是否为定值．如果是，求出这个值；如果不是，请说明理由．（2）已知正方形ABCD的顶点B、D在二次函数y＝ax2（a为常数，且a＞0）的图象上，点B在点D 的左侧，设点B、D的横坐标分别为m、n，直接写出m、n满足的等量关系式．。

类型五 特殊四边形存在性问题
(3)存在．
①当点 P 在 x 轴上方时，要使以 A、C、P、N 为顶点的四边形为平行四
边形，如解图，过点 C 作 CP1∥x 轴，交对称轴于点 P1，对称轴与 x 轴交
于点 D，
∵点 P1 在对称轴直线 x＝－3 上，点 C 的坐标为(0，5)，
∴点 P1(－3，5)，
由勾股定理得 OG2＝OD2＋DG2＝9＋g2，AG2＝AD2＋GD2＝4＋g2，
∵GK∥AO，
①当 OG＝AO＝5，且 GK＝AO 时，四边形 OGKA 是菱形，
此时有 9＋g2＝25，
解得 g1＝4，g2＝－4， ∴点 G 的坐标为(－3，4)或(－3，－4)，
则相对应的点 K 的坐标为(－8，4)或(－8，－4)；
解得 g1＝6，g2＝－1， 此时点 G 的坐标为(－3，6)或(－3，－1)；
例题图⑦
综上所述，存在满足题意的点 G，点 G 的坐标为(－3，8)或(－3，－2)或
(－3，6)或(－3，－1)；
类型五 特殊四边形存在性问题 (8)设 P 是抛物线上一点，Q 是 x 轴上一点，R 为坐标平面内一点，若以 A、 P、Q、R 为顶点的四边形是正方形，求出点 Q 的坐标．
∴x1＝0，x2＝－6， ∴CP1＝AN1＝6， ∴ON1＝6＋5＝11， 此时 N1(－11，0)． 若点 P 在 x 轴下方，不存在；
例题解图
类型五 特殊四边形存在性问题
②当 AC 为平行四边形的对角线时，如解图，
满足 AN2＝P2C＝6，
∴ON2＝6－5＝1，
此时 N2(1，0)．
例题解图
综上所述，存在满足题意的点 N，点 N 的坐标为(－11，0)或(1，0)；