青岛版-数学-九年级上册-例析点的坐标与位似变换

1.4 图形的位似第1课时教学目标1．了解位似图形及其有关概念，了解位似与相似的联系和区别，掌握位似图形的性质．2．掌握位似图形的画法，能够利用作位似图形的方法将一个图形放大或缩小．重点、难点1．重点：位似图形的有关概念、性质与作图．2．难点：利用位似将一个图形放大或缩小．一、创设情境位似图形的探究一:如何探究这两个相似图形之间的内在关系呢？对应点的连线相交于一点除对应点连线外，我们还可以怎样去探究？(观察图像)对应边互相平行位似图形的探究二:对类似的这两个相似图形，同学们知道怎样去探究了吗？对应点的连线相交于一点根据经验，我们从对应边的位置关系去探究。

(观察图片)对应边平行位似图形的探究三:对应点的连线相交于一点对应边平行二、定义及性质：如果两个图形不仅是相似图形，而且是每组对应点连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形.这个点叫做位似中心.知道了位似图形的特征，如何按要求去画位似图形呢？三、位似图形的画法以0为位似中心把△ABC在同侧缩小为原来的一半。

步骤：1.画出ABC2.选取中心点3.连结OA.OB.OC。

4.在OA.OB.OC上分别选取A′、B′、C′，使OA′：OA=1：2.OB′：OB=1：2.OC′：OC=1：2。

5.连结A′B′C′，所连成的图形就是所求作图形。

四.典例讲解例1.如下图，已知△ABC与点O.以点O为位似中心，画出△A′B′C′，使它与△ABC是位似图形，并且相似比为3:2.画法1 ：(1)作射线OA ,OB ,OC ;(2)在射线OA ,OB ,OC 上分别取点A ′，B ′，C ′，使 333,,;222OA OA OB OB OC OC '''=== (3)连接A ′B ′，B ′C ′，C ′A ′.如下图，△A ′B ′C ′就是所要画的图形.画法2(1)作射线AO , BO , CO ;(2)在射线AO , BO , CO 上分别取点A ′，B ′，C ′，使333,,;222OA OA OB OB OC OC '''=== (3)连接A ′B ′，B ′C ′，C ′A ′.如下图，△A ′B ′C ′就是所要画的图形.五. 课堂小结学习本节课有什么收获?六.作业课本练习题教后反思。

如何画位似图形位似变换是新课程标准中涉及的一个重要知识点，它是图形变换的一种，实际上它是相似变换的一种特殊情形，存在位似中心———即对应顶点连线的交点．其位似比就是相似比．作为一个新的知识点，越来越受到中考命题者的青睐．图形放大、缩小通常用位似变换的思想作图，位似中心的位置可在图形顶点处、图形边上、图形内部、图形外部．本文以一道中考题为例介绍几种常见画法，供同学们参考．（锦州）如图1，己知四边形ABCD ，用尺规将它放大，使放大前后的图形对应线段的比为1:2．画法一：延长AD 到1D ，使1DD AD =，延长AC 到点1C ，使1CC AC =，延长AB 到点1B ，使1BB AB =，连接11D C ，11C B ，则四边形1111A B C D 即为所求（如图2）． 说明：延长AD 得到1D 后，也可以过点1D 作11D C DC ∥，交AC 的延长线于1C ，再过点1C 作11B C BC ∥，交AC 的延长线于1B ，得到四边形1111A B C D ．画法二：延长DA 到点1D ，使12AD AD =，延长CA 到点1C ，使12AC AC =，延长BA 到点1B ，使12AB AB =连接11B C ，11C D ，则四边形1111A B C D 即为所求（如图3）．画法三：任取一点O ，连接OA 并延长到点1A ，使1AA OA =，连接OB 并延长到点1B ，使1BB OB =、连接OC 并延长到点1C ，使1CC OC =，连接OD 并延长到点1D ，使1DD OD =，顺次连接11A B ，11B C ，11C D ，11D A ，则四边形1111A B C D 即为所求（如图4）． 运用这些作图方法可以解决不少数学问题．现举例说明：例 如图5，在给定的锐角ABC △中，求作一个正方形DEFG ，使D E ，落在BC 上，F G ，分别落在AC AB ，边上，要求写出画法． 画法：第一步：画一个有三个顶点落在ABC △两边上的正方形D E F G ''''（如图5）；第二步：连接BF '并延长交AC 于点F ；第三步：过F 点作FE BC ⊥，垂足为点E ；第四步：过F 作FG BC ∥交AB 于点G ；第五步：过G 作GD BC ⊥，垂足为点D ．四边形DEFG 即为所求的正方形．（如图5）想一想：为什么四边形DEFG 是正方形？请读者思考．。

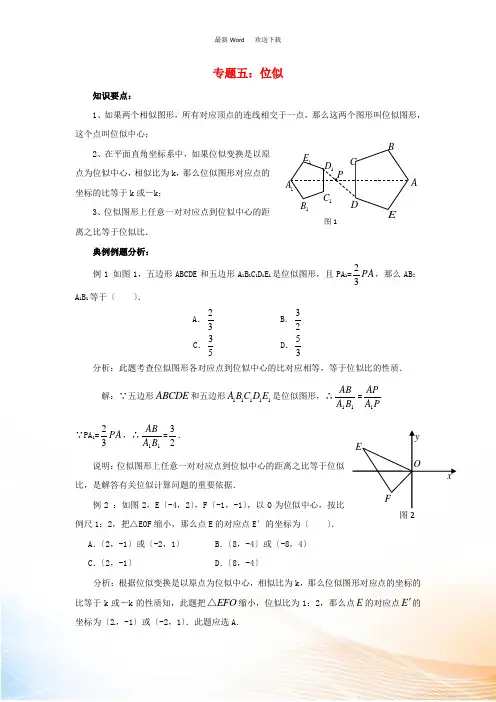
专题五：位似知识要点：1、如果两个相似图形，所有对应顶点的连线相交于一点，那么这两个图形叫位似图形，这个点叫位似中心；2、在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标的比等于k 或－k ；3、位似图形上任意一对对应点到位似中心的距离之比等于位似比．典例例题分析：例1 如图1，五边形ABCDE 和五边形A 1B 1C 1D 1E 1是位似图形，且PA 1=PA 32，那么AB ：A 1B 1等于〔 〕．A ．23 B ．32 C ．35D ．53分析：此题考查位似图形各对应点到位似中心的比对应相等，等于位似比的性质． 解：∵五边形ABCDE 和五边形11111A B C D E 是位似图形，∴11B A AB =PA AP1 ∵PA 1=PA 32，∴11B A AB =23． 说明：位似图形上任意一对对应点到位似中心的距离之比等于位似比，是解答有关位似计算问题的重要依据．例2 ：如图2，E 〔-4，2〕，F 〔-1，-1〕，以O 为位似中心，按比例尺1：2，把△EOF 缩小，那么点E 的对应点E′的坐标为〔 〕． A ．〔2，-1〕或〔-2，1〕 B ．〔8，-4〕或〔-8，4〕C ．〔2，-1〕D ．〔8，-4〕分析：根据位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标的比等于k 或－k 的性质知，此题把EFO △缩小，位似比为1：2，那么点E 的对应点E 的坐标为〔2，-1〕或〔-2，1〕．此题应选A ．1A 1E 1D 1C 1B P CBA D图1图2xy EFO说明：在直角坐标系中放大或缩小图形，可以将一个多边形的各点的横坐标与纵坐标都乘以k 〔或除以k 〕，所得新多边形与原多边形是以坐标原点为位似中心的位似图形．专题训练：1．如图3，电影胶片上每一个图片的规格为3．5 cm×3．5 cm ，放映屏幕的规格为2 m×2 m ，假设放映机的光源S 距胶片20 cm ，那么光源S 距屏幕 ，米时，放映的图象刚好布满整个屏幕．2．如图4，△ABC 与△A′B′C′是位似图形，且位似比是1：2，假设AB =2cm ，那么A′B′是 cm ，并在图中画出位似中心O ．3．如图5，四边形木框ABCD 在灯泡发出的光照射下形成的影子是四边形A ’B ’C ’D ’，假设AB ∶A ’B ’＝1∶2，那么四边形ABCD 的面积∶四边形A ’B ’C ’D ’的面积为〔 〕．A ．4∶1 B．2∶1 C．1∶2 D ．1∶4参考答案1．780； 2．4cm ； 3．D 图5DA BCD ’B ’C ’A ’灯泡图3′A BC AB C′ ′图4。

青岛版数学初三上册教案第一章图形的相似《图形的位似》教案传授目标根据新课标要求，连合课本特点，本节课应抵达以下几个目标：1、理解图形的位似概念.2、会利用作位似图形的要领把一个图形举行放大或缩小.3、掌握直角坐标系中图形的位似变化与对应点坐标变化的纪律.4、利用图形的位似办理一些简略的实际标题，并在此历程中培育学生的数学应用意识.5、成长学生的合情推理能力和初步的逻辑推理能力.传授重难点重点图形的位似概念、位似图形的性质及利用位似把一个图形放大或缩小.难点直角坐标系中图形的位似变化与对应点坐标的干系.传授历程一、创设情形，构建新知1、位似图形的概念下列两幅图有什么互助特点？议决对图的查看能从生活中找到一种感觉吗？（像一种什么镜头）图片的形状相同，而且每组对应极点都在由联合点出发的一条射线上.要是两个图形不仅形状相同，而且每组对应点所在的直线都议决联合点，那么这样的两个图形叫做位似图形，这个点叫做位似中心.比方上图中的任何两个五角星都是位似图形，点O是它们的位似中心；放影戏时，胶片与屏幕的画面也是位似图形，光源便是它们的位似中心.2、引导学生查看位似图形下列图形中，每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别查看这五个图，并鉴别哪些是位似图形，哪些不是位似图形？为什么？每个图形中的两个四边形不仅相似，而且各对应点所在的直线都议决联合点.所以都是位似图形.各对应点所在的直线都议决联合点的相似图形是位似图形.其相似比又叫做它们的位似比.显然，位似图形是相似图形的特殊环境.它们的对应边互相平行（或在联合条直线上）. 例题剖析例1 如图1-30（书本第27页），已知△ABC 与点O .以点O 为位似中心，画出△A'B'C'，使它与△ABC 是位似图形，而且相似比为3:2.二、应用新知1、作位似图形如图，请以坐标原点O 为位似中心，作ABCD 的位似图形，并把ABCD 的边长放大3倍.剖析：根据位似图形上恣意一对对应点到位似中心的隔断之比即是位似比，我们只要连合位似中心O 和ABCD 的各极点，并把线段延长（或反向延长）到原来的3倍，就得到所求作图形的各个极点.作法：如图所示1、连合OA ，OB ，OC ，OD .2、分别延长OA ，OB ，OC ，OD 到G ，C ，E ，F ，使3OG OC OE OF OA OB OC OD====. 3、依次连合GC ，CE ，EF ，FG .四边形GCEF 便是所求作的四边形.要是反向延长OA ，OB ，OC ，OD ，就得到四边形G′C′E′F′，也是所求作的四边形.4、直角坐标系中图形的位似变化与对应点坐标变化的纪律想一想：1、四边形GCEF 与四边形G ′C ′E ′F ′具有怎样的对称性？2、怎样运用像与原像对应点的坐标干系，画出以原点为位似中心的位似图形？ 比较图形中各对应点的坐标，我们还不难发觉要是多边形有一个极点在坐标原点，有一条边在x 轴上，那么将这个多边形的极点坐标分别扩大（或缩小）相同的倍数，所得到的图形与原图形式位似图形，坐标原点是它们的位似中心.例2 如讲义第29页图1-35，四边形OABC 的极点坐标分别为（0,0），（2,0），（4,4），（-2,2）.(1)要是四边形O′A′B′C′与四边形OABC位似，位似中心是原点，它的面积即是四边形OABC面积的94倍，分别写出点A′，B′，C′的坐标.(2)画出四边形OA′B′C′三、讲堂小结本日你学会了什么？1.位似图形的定义要是两个多边形不仅相似，而且对应极点所在直线相交于一点，那么这两个多边形叫做位似图形形．这个点叫做位似中心．2.推论要是多边形有一个极点在坐标原点，有一条边在x轴上，那么将这个多边形的极点坐标分别扩大（或缩小）相同的倍数，所得到的图形与原图形式位似图形，坐标原点是它们的位似中心.。

如何放大与缩小图形对一个图形放大或缩小，实际上就是画一个图形的位似图形．那么如何才能画出一个图形的位似图形呢？现通过一道试题为例说明如下．例如图1，在8×8的网格中，每个小正方形的顶点叫做格点，△OAB的顶点都在格点上，请在网格中画出．．．．．△OAB的一个位似图形，使两个图形以O为位似中心，且所画图形与△OAB 的位似比为2:1．分析：位似是相似的特殊情况，要使所画图形与△OAB的位似比为2:1，即过位似中心O分别作点A、B的对应点A1、B1，使O A1:OA=OB1=OB=2:1，然后连结A1B1，所得的△O A1B1即为所画的图形．解：〔1〕分别延长AO到A1、BO到B1，使OA1=2OA、OB1=2OB；〔2〕连结A1B1．那么△O A1B1即为所画的图形，如图1-1所示．拓展：此题如果不限定O为位似中心，也不限定在8×8的网格中，要画出△OAB的一个位似图形，使其位似比为2:1，其方法有多种，常见的方法是随位似中心的选取而定．方法一：在△OAB外任取一点P，如图1-2，以P为端点作射线PO、PA、PB，分别在射线PO、PA、PB上截取点O1、A1、B1，使PO1=2PO、PA1=2PA、PB1=2PB，连结O1A1、A1B1、B1O1，△O1A1B1即为所画的图形．方法二：在△OAB外任取一点P，如图1-3，作直线PO、PA、PB，在点P的另一侧截取点O1、A1、B1，使PO1=2PO、PA1=2PA、PB1=2PB，也可以画出与△OAB的位似比为2:1的位似图形．方法三：在△OAB内任取一点P，如图1-4，以P为端点作射线PO、PA、PB，分别在射线PO、PA、PB上截取点O1、A1、B1，使PO1=2PO、PA1=2PA、PB1=2PB，同样可出与△OAB的位似比为2:1的位似图形．、方法四：也可以把位似中心P取在△OAB的任意一边上，这种画法，请同学们自己完成．点评：从上面的几种画法可以看出，作一个图形的位似图形的关键是确定位似中心的位置．要注意如果题目中没有给出位似中心，一般来说位似中心可取在原图形的外部、内部、一边或一顶点上．。