当前位置：文档之家 › 离散随机变量的概率分布

离散随机变量的概率分布

  • 格式：ppt
  • 大小：397.00 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

第二节常见离散型随机变量的概率分布

第二节常见离散型随机变量的概率分布

例2.20 某种玻璃器皿在汽车运输中的破损率为2%，现 在一次运送1200件，试求，(1) 破损件数X的概率分布； (2) 最多破损30件的概率α．
解 (1) 为求破损件数X的概率分布，考虑n=1200次伯努 利试验，每次试验成功的概率为p=0.02，可见X的概率 分布是参数为的二项分布．由于n=1200和p=0.02显然满 足泊松定理的条件，可见近似服从参数为np=24的泊松 分布．
第二节、常见离散型随机变 量的概率分布
一、两点分布（0－1分布）
只有两个可能值的随机变量X的概率分布称做两点分布：
X
~
x1 q
x2 p
(q
1
p,
0
p
1)
特别，若x1 =0 , x2 =1,则称X服从参数为p的0-1分布，亦称伯
努利分布．只计“成功”和“失败”两种结局的试验称做伯
努利
试验．设X是试验成1功 , 的若次试数验：成功 ， X ~ 0 , 若试验失败 ,
n})
；
四、泊松分布、泊松定理和泊松流
称随机变量X服从参数为 0 的泊松分布，如果
PX k λ k eλ (k 0,1,2,)
k!
1、泊松定理 假设X服从二项分布，参数年n充分大，而 p充分小，且 n p 适中，则可以利用泊松分布概率近似计 算二项分布概率．
Ckn
pk (1
p)nk
(np)k k!
因此，至少需要安排3个人值班．
例2.15 假设一部设备在一个工作日因故停用的概率为0.2．一
周使用5个工作日可创利润10万元；使用4个工作日可创利润7
万元；使用3个工作日只创利润2万元；停用3个及多于3个工
作日亏损2万元．求所创利润的概率分布．

离散型随机变量的概率分布

离散型随机变量的概率分布

解
设 p 为每组信号灯禁止汽车通过的概率, 则有
X0
1
2
3
4
pk p (1 p) p (1 p)2 p (1 p)3 p (1 p)4
将 p 1 代入得 2
X0
1
pk 0.5 0.25
2
0.125
3
4
0.0625 0.0625
离散型随机变量分布律与分布函数的关系
分布律
pk P{X xk }
3.二项分布
(1) 重复独立试验 将试验 E 重复进行 n 次, 若各次试验的结果互 不影响 , 即每次试验结果出现的概率都不依赖于其 它各次试验的结果, 则称这 n 次试验是相互独立的, 或称为 n 次重复独立试验.
(2) n 重伯努利试验
伯努利资料
设试验 E 只有两个可能结果: A 及 A,则称 E 为伯努利试验. 设 P( A) p (0 p 1),此时P( A) 1 p.
正面, 反面.
随机变量 X 服从 (0—1) 分布.
其分布律为
X
0 1
1
1
pk
2
2
实例2 200件产品中,有190件合格品,10件不合格 品,现从中随机抽取一件,那么,若规定
X
1, 0,
取得不合格品, 取得合格品.
X0
1
pk
190 200
10 200
则随机变量 X 服从(0 —1)分布.
说明
两点分布是最简单的一种分布,任何一个只有 两种可能结果的随机现象, 比如新生婴儿是男还是 女、明天是否下雨、种籽是否发芽等, 都属于两点 分布.
P{X = a} = 1 则称 X 服从 a处的退化分布.
2.两点分布（Bernoulli分布)

2.2离散型随机变量及其概率分布

2.2离散型随机变量及其概率分布

8
5
k
24
小结
离 散 型 随 机 变 量 的 分 布
二项分布 泊松分布
两点分布
两点分布
n1
二项分布
n 10, p 0.1, np
泊松分布
25
二项分布与 (0 1) 分布、泊松分布之间的 关系 .
二项分布是 (0 1) 分 布 的 推 广 , 对 于n 次 独 立重复伯努利试验 ,每 次 试 验 成 功 的 概 率 为 p, 设 , 1, 若 第 i 次 试 验 成 功 Xi ( i 1,2, , n) . 0, 若 第 i 次 试 验 失 败 它们都服从 (0 1) 分 布 并 且 相 互 独 立 , 那末 X X1 X 2 X n 服 从 二 项 分 布 , 参 数 为( n, p).
定义2 如果随机变量 X 只有两个可能取 值，其概率分布为
P{ X x1 } P , P{ X x2 } q 1 p(0 p 1, p q 1)
则称X服从 x1 , x2 处参数为p的两点分布. 特别，若X服从
x1 1, x 0 处参数为p的两点分布，即
p
k 1
5
k
1
1 a . 15
5
关于分布律的说明：
若已知一个离散型随机变量X的概率分布 X P x1 p1 x2 p2 ... ... xn ... pn ...
则可以求X所生成的任何事件的概率，特别地：
P{a X b} P{ { X xi }} pi
a xi b a xi b
26
以 n, p ( np ) 为参数的二项分布 ,当 n 时趋 于以 为参数的泊松分布 ,即

2.2 离散型随机变量的概率分布

2.2 离散型随机变量的概率分布

P(X=2)=C (0.05) (0.95) = 0.007125
2 3 2
注:若将本例中的"有放回"改为"无放 将本例中的"有放回"改为" 那么各次试验条件就不同了, 回",那么各次试验条件就不同了,不是贝 努里概型,此时,只能用古典概型求解. 努里概型,此时,只能用古典概型求解
C C P(X=2)= ≈ 0.001 P { X = 0} P { X = 1}
= 1 C 0.01 × 0.99 C 0.01 × 0.99
0 20 0 20 1 20 1
19
≈ 0.0169 重贝努利概型, (2)这是 )这是n=80重贝努利概型,参数为 重贝努利概型 参数为p=0.01,需维 , 修的机床数X~B(80, 0.01),故不能及时维修的概率为 修的机床数 故不能及时维修的概率为
eλ = ∑
k=0
λk
k!
某射手连续向一目标射击, 例4. 某射手连续向一目标射击,直到命中为 已知他每发命中的概率是p, 止 , 已知他每发命中的概率是 , 求所需射击 发数X 的概率函数. 发数 的概率函数 显然, 可能取的值是1,2,… , 解: 显然,X 可能取的值是 为计算 P(X =k ), k = 1,2, …, , , 设 Ak = {第k发命中 ,k =1, 2, …, 发命中}, 第 发命中 , 于是 P(X=1)=P(A1)=p,
P(X=k)=C (0.8) (0.2) , k = 0,1,2,3 把观察一个灯泡的使用
时数看作一次试验, 时数看作一次试验 P(X ≤ =P(X=0)+P(X=1) 1)
k 3 k
3k
"使用到 使用到1000小时已坏" 小时已坏" 使用到 小时已坏 视为事件A,每次试验, 视为事件 )3+3(0.8)(0.2)2 ,每次试验 =(0.2 A发生的概率为 发生的概率为0.8 发生的概率为

离散型随机变量的概率分布

离散型随机变量的概率分布

用随机变量表示随机事件:
在灯泡寿命试验中， {灯泡的寿命不低于1000小时} 可用随机变量X表示为{X≥1000}
用随机变量X表示玉米穗位，则{玉米穗位在100到 120厘米之间}可以表示为{100≤X≤120}
在投硬币试验中， {正面朝上}可以表示为{X=1} 一般地：{X=k} ，{X ≤a} ，{a＜X≤b}表示一个随机 事件。
C130
X
0
1
2
3
pk
1
6
1
3
1
2
10
30
山东农业大学
概率论与数理统计
主讲人：程述汉 苏本堂
三、几种常见的离散型随机变量的概率分布
1. 0-1分布 若随机变量 X 只可能取 0 和 1 两个值，概率分布为
P{X 1} p, P{X 0} q 1 p
( 0＜p＜1，p+q=1) 则称 X 服从0-1分布（p为参数）, 也称为贝努里分布.
50次射击试验中命中的次数等都可以用一个随机变量X
来表示，它可能取0，1，…，50中的任一非负整数；
(2) 一个传呼台单位时间内接到的传唤次数，城市某 十字路口一分钟内通过的机动车数、单位时间内到达 某公交车站等车的人数等都可以用随机变量X来表示， 它所有可能的取值为一切非：h）是一个可以在 (0, +∞)上取值的随机变量，{X>10000}表示“电视机使用 寿命超过10000 h”这一事件．类似的，测量的误差X也 是一个随机变量，它可能的取值为(﹣∞,﹢∞)上任意实 数，{︱x︱ <0.1 }表示“测量的误差在(-0.1, 0.1)内”．
山东农业大学
概率论与数理统计
主讲人：程述汉 苏本堂

离散型随机变量的概率分布

离散型随机变量的概率分布
概率函数具有下面两条性质 ：
(1) pn 0 n 1, 2,
(2) pn 1
n
凡满足上述两条性质的 任意一组 pn , n 1,2, 都可
以成为一个d .r .v .的概率分布。称之为离 散型 概率分布。
对于集合 xn : n 1,2, 中的任何一个子集 A，事件
“X 在A 中取值”，即事件“ X A”的概率为 P ( X A) Pn
xnA
例1：做一次试验，其结果只有两种，成功和失败，
若令成功的概率为 p，用 X表示试验成功的次，则 X的分
布律为：
X P
0
1 p
1
p
此类试验即为伯努利试验，此分布称为0-1分布。
不难求出X的分布函数
例2：设d.r.v.X的概率分布为：

这样的试验E称为伯努利试验 .
概率论
将伯努利试验E独立地重复地进行n次 ,则称这一串重复 的独立试验为n重伯努利试验 .
“重复”是指这n次试验中P(A)= p 保持不变. “独立”是指各次试验的结果互不影响 . 实际模型 设事件A在一次试验中发生的概率为 p, (0 p 1), 令X = “n次试验中A事件发生的次数”， 现独立地重复试验n次，
X P
-1 0.3
0 0.3
1 0.2
2 0.2
P ( X 1, X 0) P ( X 1 X 0) P ( X 0) P ( X 1) 0.3 3 1 P ( X 0) 0.7 7
二、常见离散型随机变量
1.退化分布
P{ X a } 1
2.Bernoulli分布(两点分布,0-1分布) 记为X ～ B(1,p)

离散型随机变量的概率分布

离散型随机变量的概率分布

n次试验中A发生的总次数，则
X的可能值为 0,1,2,…,n, 且
P(X
k)
C
k n
pk (1
p)nk , k
0,1,2,...,
n
称 X ~ B(n, p) 二项分布
n重
A发生的概率
证明：指定的k次（如前k次）让A发生，其余
的（n-k）为 A发生
而事件A在n次试验中发生k次的方式为：C
k n
P(X
§2 离散型随机变量的概率分布
主要内容
一、离散型随机变量的定义及其分布律 二、常用分布 三、常用分布之间的联系
一、离散型随机变量的定义及其分布
1. 定义 如果随机变量X所有可能值是有限个或无限可 列个，则称X为离散型随机变量。 2. 概率分布
要掌握一个离散型随机变量的分布，必须
且只需知道以下两点
(1) X所有可能的取值: x1, x2, , xk ,
例 2 某一城市每天发生火灾的次数X服从参数为 0.8的泊松分布. 求:该城市一天内发生3次以上火灾 的概率.
解: P( X 3) 0.8k e
k3 k!
查表
0.0474
上页 下页 返回
三. 常用分布的联系 1. 0-1分布和B(n,p)
X ~ B(n, p)中，当n 1时，X ~ 0 1分布，且X分解为
2
b 3 2b 1
1
2 3
b 1 2
练习1: 设随机变量X的分布律为：
P( X k) a , k 1,2, ,10. 10
试求常数a. (a 1)
练习2: 设随机变量X的分布律为：
P( X k) a k , k 0,1,2,...., 0为常数。

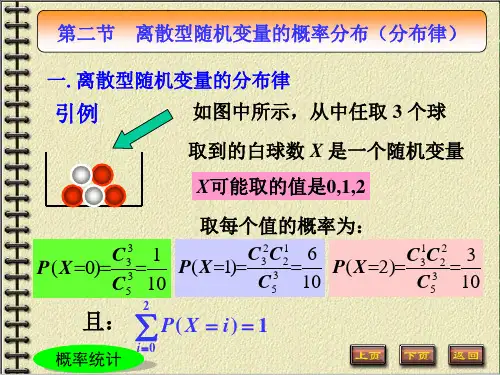
第二节离散型随机变量的概率分布(分布律)

第二节离散型随机变量的概率分布(分布律)

例6. 将一枚均匀骰子抛掷 3 次， 令:X 表示 3 次中出现“4”点的次数
求: X的概率函数
解: 显然， X的概率函数是：
1 k 5 3 k P {X k } C ( ) ( ) , 6 6
k 3
k 0 ,1, 2 , 3
概率统计
3
0 .
定理
设一次试验中事件A发生的概率为 p , (0 p 1)
4 5 4 5 5 5 0
0.98
概率统计
(2). 二项分布 若用X表示 n 重贝努利概型中事件A 发生的次数， 它的分布 律为：
Pn ( k) C p (1 p )
k n k
n k
k 0,1,2
n
则称 X 服从参数为 n, p (0<p<1) 的二项分布，
记为: 列表:
X～B(n, p)
概率 Pn ( k ) 就等于二项式 [(1 p) px ]n 的展开式中 x k 注 ▲ 显然它满足： 的系数，这也是二项分布的名称的 P ( X k ) 0, 由来.
k C n p k (1 p)n k ( p q )n 1 k 0 n
概率统计
例7. 设某炮手射击的命中率为 0.8，为炸毁某个目 标， 经预测只要命中两发就够炸毁.
思考题： 从中抽取3只，求次品数不大于1只 例2. 某篮球运动员投中篮圈概率是0.9， 的概率有多大？ 求：他两次独立投篮投中次数 X 的概率分布. 12 22 答案： P ( X 1) P ( X 0) P ( X 1) 解： X 可能取值为 0、1、2 则： 35 35
问:希望发射5发炮弹就能炸毁目标的可能性有多大?
解: A : 发射 5 发炮弹就炸毁了目标

离散型随机变量的概率分布

离散型随机变量的概率分布

例 保险公司为一单位500名员工办理了一年期 医疗保险，每张保单最多理赔一次。假设员工 是否发生医疗费用是相互独立的，理赔概率为 0.01，问保险期内最可能发生几次理赔，并求 相应的概率。
4. 泊松分布
设随机变量所有可能取的值为0, 1, 2, ,而取各个 值的概率为
P{ X k} ke , k 0,1,2, ,
将 E 独立地重复地进行n 次,则称这一串重 复的独立试验为n 重伯努利试验.
实例1 抛一枚硬币观察得到正面或反面. 若将硬 币抛 n 次,就是n重伯努利试验.
实例2 抛一颗骰子n次,观察是否 “出现 1 点”, 就 是 n重伯努利试验.
(3) 二项概率公式 若 X 表示 n 重伯努利试验中事件 A 发生的次数, 则 X 所有可能取的值为
n pkqnk k
得 X 的分布律为
X0
1
k
n
pk
qn
n pqn1 1
n pkqnk k
pn
称这样的分布为二项分布.记为 X ~ b(n, p).
二项分布 n 1 两点分布
二项分布的图形
例如 在相同条件下相互独立地进行 5 次射击,每 次射击时击中目标的概率为 0.6 ,则击中目标的次 数 X 服从 b (5,0.6) 的二项分布.
设 Ai 表示“抽到的第 i 个产品是正品”, P{ X k} P( A1A2 Ak1 Ak )
P( A1) P( A2 ) P( Ak1) P( Ak )
(1 p)(1 p) (1 p) p qk1 p.
( k 1)
(k 1,2, )
若随机变量 X 的分布律为
X 1 2 k , p q 1, pk p qp qk1 p
k0 k!

常用离散型随机变量的概率分布

常用离散型随机变量的概率分布

常用离散型随机变量的概率分布一、离散型随机变量简介离散型随机变量是指只能取有限个或可数个值的随机变量。

在概率论与数理统计中，离散型随机变量的概率分布描述了该随机变量每个可能取值的概率。

在实际问题中，常用的离散型随机变量包括伯努利分布、二项分布、泊松分布和几何分布等。

二、伯努利分布伯努利分布是一种表示两个可能结果的离散型概率分布。

它的特点是每次试验只有两个可能结果：成功和失败。

该分布由一个参数p确定，表示成功的概率，成功的概率为p，失败的概率为1-p。

伯努利分布的概率质量函数如下：P(X=x) = p^x * (1-p)^(1-x)其中，x为随机变量X的取值（0或1），p为成功的概率。

三、二项分布二项分布是一种多次独立重复实验的离散型概率分布。

它描述了n次重复独立实验中成功次数的概率分布。

每次实验都有两个可能结果：成功和失败。

每次实验成功的概率为p，失败的概率为1-p。

二项分布的概率质量函数如下：P(X=k) = C(n,k) * p^k * (1-p)^(n-k)其中，X为成功次数的随机变量，k为取值，n表示实验的次数，p为每次实验成功的概率。

四、泊松分布泊松分布是描述单位时间（或单位空间）内某种事件发生次数的离散型概率分布。

泊松分布适用于很多事件发生的情况，例如到达人口数量、电话交换机接收到的呼叫数量等。

泊松分布的特点是事件的发生率稳定且独立。

泊松分布的概率质量函数如下：P(X=k) = (λ^k * e^(-λ)) / k!其中，X为事件发生次数的随机变量，k为取值，λ表示单位时间（或单位空间）内事件的平均发生次数。

五、几何分布几何分布是描述进行独立重复实验，直到第一次成功出现时的实验次数的离散型概率分布。

每次实验成功的概率为p，失败的概率为1-p。

几何分布的概率质量函数如下：P(X=k) = (1-p)^(k-1) * p其中，X为成功所需的实验次数的随机变量，k为取值，p为每次实验成功的概率。

2.2离散型随机变量及其概率分布

2.2离散型随机变量及其概率分布

a P X k , k 1,2,, N , N
试确定常数a.
解 由离散型随机变量分布列的性质（2）规范性，
a a P{ X k} N N N 1 k 1 k 1
N
N
a 1
旧书（56页1题）
1. 判断下面各数列是否为随机变量的分布列，并说明理由．
易于验证：
1) P{ X k}

k
k!
e 0, k 0,1,2,, 非负性

2)
P{ X k}
k 0 k 0
k
k!
e
k

规范性
e

k!
k 0



e e

1
例6：某商店根据过去的销售记录,总结出某种商品每 月的销售量可以用参数为 5 的泊松分布来描述,求： (1)下个月该商店销售2件此种商品的概率是多少？
的概率为：
记为
k n k n k
X ~ B(n, p).源自P X k C p (1 p)
(k 0,1 n)
练习：某射手每次射击时命中10环的概率为 p, 现 进行 4 次独立射击，求 恰有 k 次命中10环的概率。
解：用X 表示 4 次射击后, 命中10环的次数, 则
X 的概率分布为
参数为 np 1 的泊松分布近似计算，得
1 解 因为 500 个错字随机分布在 500 页书上，所以错字出现在每一页的概率都是 ． 500 1 )， 设 X 表示在给定的某一页上出现错字的个数，则 X ~ B(500 , 500
1, X ( ) 0,
X
反面, 正面.
1

1.5 概率论——离散型随机变量的概率分布

1.5 概率论——离散型随机变量的概率分布

1
即，kk00
np np
p p
1
因此 np p 1 k0 np p
于是
np p k0 np p 1
[np p]
当np p是整数时 当np p是整数时
其它
二项分布的概率计算;
B(k;n, p) P( X k) Cnk pk (1 p)nk
1.直接计算; n 较小 2.查表 n 较大时,ｐ不太大或小时 3.利用泊松分布; n 较大, p较小 4.利用中心极限定理; n 较大
二项分布的概率最大值(众数); 二项分布中 X 可以取值 0,1,2, , n,使概率 Pk 取最大值
的 k记作 k0 , 称 k0为二项分布的最可能取值。已知 n, p 来求 k0
np p k0 np p 1
[np p]
当np p是整数时 当np p是整数时
其它
设P( X k0 )为最大，则有下面不等式组：
因此 X概率分布为 X -1
0
1
2
P 0.3 0.3 0.2 0.2
P( X 1 X 0) P( X 1, X 0) P( X 0)
P( X 1) 0.3 3 1 P( X 0) 0.7 7
二、常见离散型随机变量
1.退化分布
P{X a} 1
2.Bernoulli分布(两点分布,0-1分布) 记为X ～ B(1,p)
(1)P( X 10) 0.9510 0.599
(2)P( X 8) C180 0.958 0.052 0.075 (3)P( X 9) C190 0.959 0.05 0.9510 0.914
4.超几何分布
模型: 一般地，如果有 N个元素分为两大类，第一类 N1个 元素，第二类 N2个元素(N1 N2 N ), 采用不重复抽样， 从N个元素中取出n个元素，那么所取到的第一类元素的 个数 X的分布称为超几何分布。

常用离散型随机变量的概率分布

常用离散型随机变量的概率分布

常用离散型随机变量的概率分布一、离散型随机变量的概念及特点离散型随机变量是指在一定条件下，其取值只能是有限个或者可数个的随机变量。

与连续型随机变量相对应，离散型随机变量的取值只能是整数或者某些特定的值。

因此，它们具有以下几个特点：1. 取值有限或可数2. 每个取值的概率都不为03. 不连续4. 概率分布可以用概率质量函数来描述二、常用离散型随机变量的概率分布及其性质1. 伯努利分布伯努利分布是一种最简单的二项分布，它只涉及到一个试验和两种结果。

伯努利分布表示为：X~B(1,p)，其中p表示事件发生的概率，1-p表示事件不发生的概率。

性质：（1）期望：E(X)=p（2）方差：Var(X)=p(1-p)2. 二项分布二项分布是多次独立重复进行相同试验中成功次数的概率分布。

二项分布表示为：X~B(n,p)，其中n表示试验次数，p表示每次试验成功的概率。

性质：（1）期望：E(X)=np（2）方差：Var(X)=np(1-p)3. 泊松分布泊松分布是描述单位时间内某事件发生次数的概率分布。

泊松分布表示为：X~P(λ)，其中λ表示单位时间内事件发生的平均次数。

性质：（1）期望：E(X)=λ（2）方差：Var(X)=λ4. 几何分布几何分布是描述在一系列独立重复试验中，第一次成功所需的试验次数的概率分布。

几何分布表示为：X~G(p)，其中p表示每次试验成功的概率。

性质：（1）期望：E(X)=1/p（2）方差：Var(X)=(1-p)/p^25. 超几何分布超几何分布是描述从有限个物品中抽取不放回地抽取n个物品，其中有m个特定类型的物品的概率分布。

超几何分布表示为：X~H(N,M,n)，其中N表示总共有多少个物品，M表示特定类型的物品有多少个，n表示抽取多少个物品。

性质：（1）期望：E(X)=nM/N（2）方差：Var(X)=nM/N*(N-M)/(N-1)三、离散型随机变量的应用离散型随机变量在实际生活中有广泛的应用。

2.1,2.2离散型随机变量的概率分布

2.1,2.2离散型随机变量的概率分布

解 k可取值0，1，2
P{X＝k}＝
C2k C33k C53
.
例2.某射手对目标独立射击5次，每次命中目标的概 率为p，以X表示命中目标的次数，求X的分布律。
解：设Ai第i次射击时命中目标，i=1,2,3,4,5 则A1,A2,…A5,相互独立且 P(Ai)=p,i=1,2,…5. SX={0,1,2,3,4,5},
e e 3e2 2
P{X 3} 1 P{X 0} P{X 1} P{X 2}
1 e2 21 e2 22 e2 1 5e2 0.323
1!
2!
解 设X表示400次独立射击中命中的次数， 则X～B(400, 0.02)，故
P{X2}＝1－ P{X＝0}－P {X＝1} ＝1－0.98400－(400)(0.02)(0.98399)=…
泊松定理 设随机变量Xn～B(n, p), (n＝0, 1, 2,…), 且n很大，p很小，记=np，则
P{X k} k e ,
随机变量通常用X、Y、Z 或 、、等表示。 用小写字母x,y,z,…表示它们可能的取值。
随机变量的特点: 1 X的全部可能取值是互斥且完备的. 2 X的部分可能取值描述随机事件.
例1．引入适当的随机变量描述下列事件：
①将3个球随机地放入三个格子中， 事件A={有1个空格}，B={有2个空格}，C={全有球}。 ②进行5次试验，事件D={试验成功一次}，F={试验至少成 功一次}，G={至多成功3次}.
X
X (e)
0, 1,
eT eH
则这个有两个可能值的变量X代表了抛1枚硬币这一
试验的结果。
作为随机试验的结果，这些数量与以往用来表示时 间，位移等的变量有很大的不同，这就是其取值的 变化情况取决于随机试验的结果，即是不能完全预 言的，这种随机取值的变量就是随机变量。

离散型随机变量的概率分布

离散型随机变量的概率分布

离散型随机变量的概率分布一、定义与性质1.离散型随机变量：随机变量X的取值是 countable 的，即X的所有可能取值可以构成一个可数集合。

2.概率分布：离散型随机变量的概率分布是指随机变量取每一个可能值的概率。

3.概率的基本性质：a.非负性：概率值非负，即P(X=x)≥0。

b.归一性：所有可能取值的概率之和为1，即ΣP(X=x)=1。

c.互斥性：不同取值之间的概率没有交集，即P(X=x1)∩P(X=x2)=0（x1≠x2）。

二、概率分布的数学描述1.概率质量函数（Probability Mass Function, PMF）：离散型随机变量的概率分布通常用概率质量函数f(x)来描述，定义为P(X=x)=f(x)。

2.概率分布表：将所有可能的取值及其对应的概率列成表格，称为概率分布表。

3.伯努利分布（Bernoulli distribution）：定义在随机试验成功（记为1）和失败（记为0）上的两点分布，其概率质量函数为P(X=1)=p，P(X=0)=1-p。

4.二项分布（Binomial distribution）：在n次独立重复试验中，成功次数的离散型随机变量遵循二项分布，其概率质量函数为P(X=k)=C(n,k)p k(1-p)(n-k)，其中，n为试验次数，k为成功次数，p为每次试验成功的概率。

5.几何分布（Geometric distribution）：在伯努利试验中，第一次成功之前试验次数的离散型随机变量遵循几何分布，其概率质量函数为P(X=k)=(1-p)^(k-1)p。

6.负二项分布（Negative binomial distribution）：在伯努利试验中，试验次数达到r次之前成功次数的离散型随机变量遵循负二项分布，其概率质量函数为P(X=k)=C(r-1,k-1)(1-p)(r-k)p k。

7.超几何分布（Hypergeometric distribution）：从N个对象中抽取n 个，其中有K个成功对象，抽取k个成功对象的离散型随机变量遵循超几何分布，其概率质量函数为P(X=k)=C(K,k)C(N-K,n-k)/C(N,n)。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

P(X k)
b( 2)k
b2 3
k 1
k 1 3
1 2
2
b
3 1
2b
1
3
3
b 1. 2
几种常见的离散型分布
0-1分布(二点分布 ) 定义： 若随机变量X的分布列为:
X
0
1
P
1－p
p
则称X服从参数为p 的二点分布或(0-1)分布,
应用范围：样本空间只有两个样本点的情况 都可以用两点分布来 描述。
解：X的可能取值为 0，1，2
P{X=0}
C127
C
2 20
136 =P(抽得的两件全为正品) 190
P{X=1}
C31C117 C220
51 190
ቤተ መጻሕፍቲ ባይዱ
=P(只有一件为次品)
P{X=2}
C32
C
2 20
3 =P(抽得的两件全为次品) 190
故 X的分布列为
X0 1 2
pk
136 190
51
3
190
例已知某电话交换台每分钟接到的呼唤次数X服从
4 的普阿松分布，分别 求（1）每分钟内恰好接到3
次呼唤的概率；（2）每分钟不超过4次的概率
解 P( X k) k e
k!
4, k 3
P( X
3) 43 e4 3!
0.19563
P( X 4) P( X 0) P( X 1) P( X 2)
分布列确定概率
例 设X的分布列为
X -1 1 2
P 1/3 1/2
1/6
求 P(0<X≤2)
解 P(0<X≤2)=P（X=1）+P（X=2） =1/2+1/6=2/3
求分布列举例
例 设有一批产品20件，其中有3件次品，从中任意
抽取2件，如果用X表示取得的次品数，求随机变量X 的分布列及事件“至少抽得一件次品”的概率。
C52
1 4
2
1
1 52 4
L
例 一大批种子发芽率为90%，今从中任取10粒.
求播种后, 求（1）恰有8粒发芽的概率；（2） 不小于8粒发芽的概率。
解
X～B（10, 0.9）
(1) P(X=8)= C180 0.98 0.12 0.1937
(2) P(x 8)= P(X=8)+P(X=9)+P(X=10)
P( X 3) P( X 4) 0.628838
二项分布的泊松近似
泊松定理
Cnk pk (1
p)nk
k
k!
e
np
实际应用中：当n较大,p较小，np适中时，即可 用泊松公式近似替换二项概率公式
例 某人骑摩托车上街,出事故率为0.02，独立重 复上街400次，求出事故至少两次的概率.
解 400次上街400重Bernoulii实验
离散随机变量的概率分布
设离散型随机变量 X 的所有可能取值是
x1, x2 ,L , xn ,L ，而取值 xk的概率为 pk
即
PX xk pk
称此式为X的分布列
离散随机变量分布列的表格表示法
公式法
PX xk pk
表格法
X x1， x2， … xk， …
p1 ， p2 ，… p K …
性质 1) pk 0 k 1, 2,L 2) pk 1 k 1
( X=k )对应着事件 A1 A2 Ak1 Ak
X的所有可能取值为 1，2，3，… ,k,…
P(X=k)=P(A1A2 Ak1 Ak ) (1-p)k-1p ,k=1,2,…
例 设随机变量X的分布列为
PX k b( 2)k , k 1, 2,3,L
3
试确定常数b.
解
由分布列的性质,有
C180 0.98 0.12 C190 0.99 0.1
C10 10
0.910
0.9298
普阿松分布
若随机变量 X 的分布列为:
P( X k ) k e , k 0,1,2...
k! 其中 >0, 则称X服从参数为的普阿松分布
X～P()
实际问题中R.v.X是服从或近似服从普阿松分布的例子。
X～B( n, p)
例 从一批由9件正品、3件次品组成的产品中,有放回地
抽取5次,每次抽一件,求恰好抽到两次次品的概率.
解有放回地抽取5件,可视为5重Bernoulli实验
A=“一次实验中抽到次品”，P(A)=3/12,
n=5 p=1/4
记X为共抽到的次品数，则
X ~ B(5, 1 ) 4
P{X
2}
记X为出事故的次数，则 X ~ B(400,0.02)
P{x
k}
Ck 400
0.02 k
0.98 400k
8k e8
k!
P(X≥2)=1-P(X=0)-P(X=1)
≈1- e-8 - 8e-8
=1-0.98 400-400（0.02)(0.98 399) ≈0.9970 ≈0.9972
表明随着实验次数的增多，小概率事件总会发生的！
EX 若某人做某事的成功率为1%，他重复努力400次， 则至少成功一次的概率为
P{X 1} 1 P{X 0} =1 0.99400 0.9820
成功次数服从二项概率 B(400, 0.01)
有百分之一的希望，就要做百分之百的努力
1、服务台在某时间段内接待的服务次数X； 2、交换台在某时间段内接到呼叫的次数Y; 3、矿井在某段时间发生事故的次数; 4、显微镜下相同大小的方格内微生物数目； 5、单位体积空气中含有某种微粒的数目等等。
体积相对小的物质在较大的空间内的稀疏 分布，都可以看作普阿松分布,其参数 可以 由观测值的平均值求出。
即X服从两点分布。
二项分布
在n重贝努利试验中,若以X表示事件A发生的次数,
则X可能的取值为0,1,2,3,…,n. 随机变量X的分布列
P{X k} Cnk pk (1 p)nk k 0,1, 2..., n;
其中0< p <1, 则称X服从参数为 n, p 的二项分布 (也称Bernoulli 分布）,记为
如：上抛一枚硬币。
例 设一个袋中装有3个红球和7个白球，现在从中
随机抽取一球，如果每个球抽取的机会相等，
并且用数“1”代表取得红球，“0”代表取得
白球，则随机抽取一球所得的值是一个离散型
随机变量
1 X 0
（取得红球） （取得白球）
其概率分布为 P( X 1) 3 10
P(X 0) 7 10
190
而“至少抽得一件次品”={X≥1} = {X=1}{X=2}
注意：{X=1}与{X=2}是互不相容的！
故
P{X≥1}=
P{X=1}+P{X=2}
51 190
3 190
54 190
27 95
例
从一批次品率为p的产品中，有放回抽样直到抽到 次品为止。求抽到次品时，已抽取的次数X的分布列。
解 记Ai=“第i次取到正品”,i=1,2,3,… 则 Ai , i=1,2,3,… 是相互独立的！ 且