逻辑变量与基本运算.
- 格式:ppt
- 大小:1.69 MB
- 文档页数:25




课题:逻辑变量与基本运算授课教师:平利职教中心屈垚垚一、教学目标:1、知识与技能:(1)理解逻辑变量的概念,掌握三种逻辑基本运算;(2)通过逻辑运算的学习,使学生的逻辑思维能力得到锻炼和提高。
2、过程与方法:发现式教学。
通过创设情境,引出课题;观察动画,激发兴趣;再引导学生不断讨论、归纳、总结,在探索中不断提高。
3、情感态度与价值观:(1)学生通过观察电路的拟真动画演示,体会数学知识与专业课程以及现实世界的联系,提高对数学课程的重视;(2)学生动脑发现规律,总结知识,培养其主动参与、积极探究的主体意识。
二、重点与难点:1、重点:理解并掌握逻辑变量的含义,掌握逻辑变量的三种基本运算;2、难点:区分三种基本逻辑运算之间的区别与联系。
三、教学方法与教学手段:1、教学方法:借助多媒体教学,教师以引导为主,学生合作探索、积极思考的探究式教学方法,教学中主要采用观察发现法、与讲练结合法,注重启发式引导、反馈式评价,充分调动学生的学习积极性。
2、教学用具:黑板、教学课件、flash拟真动画、多媒体设备,以及提前按小组分发给学生的学案。
四、教学设计:创设情境、引出课题(3分钟)↓观察动画、总结规律(3分钟)↓师生合作、共探新知(20分钟)↓讨论探究、例题演练(7分钟)↓运用知识、强化练习(5分钟)↓课堂小结、布置作业(2分钟)本节课的总体设计思想是建构主义思想,强调数学知识的建构过程,让学生亲历基本逻辑运算的运算规则的发现之旅。
首先通过列举生活中的“只有两种对立状态的量”,创设情境,激发兴趣;然后观察两个开关并联控制灯泡工作的电路拟真动画,总结因果逻辑关系,为学习逻辑变量的概念做准备;再通过分别观察三个不同的电路拟真动画来总结学习逻辑变量及三种基本逻辑运算,突出本节课的重点;接着对比对比分析三个电路图和对应的逻辑运算,找到区别和联系,突破难点;最后通过分析例题、强化练习巩固所学知识;课堂小结、作业布置分享成长体会,达到教学目的。


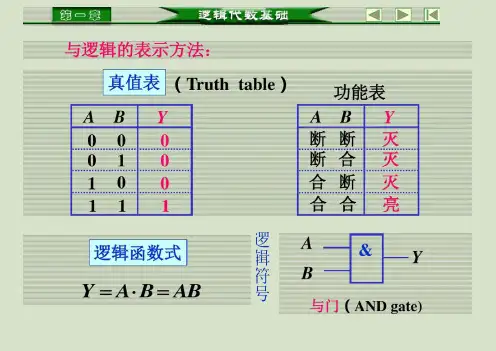
逻辑符号真值表逻辑函数式逻辑变量:量逻辑山山亠亠川畐隸■」「逻垢弯量亚值逻辑匿变量的取值不是1就是爨。
删8[]反血皿■ 3丄山兀砂的称加逻辑函数:如果输入逻辑变量丛B、O 啲取值确定之后,输出逻辑变量丫的值也被唯尋确^■u称疑八、zk门…菊Y2的真值表=(5)同或逻辑(异或非)I 刖mm曲g—闯“叭尋__ ■ B鉉O章鉉O章鉉o章^■□11 Er s三三三方法二:真值表法(将变量的各;=r 二‘y f一 -—^――"W^ + _ ■将y式中"・〃换成"+〃,"+"换成"・〃_ I "0〃换成"1" , "i n换成"0"原变量换成反变量,反变量换成原变量注意:将y 式中"・"换成"+",换成"・〃"0"换成"1" , "1〃 换成"0"原变量换成反变量,反变量换成原变量运算顺序:=A (B +C )+CD J 七暂"V 亠入右i 尊不属于单个变量上例如:已知 括号i 与i 或_______________________ 丿已知的反号应保留不变S ____________ _________ 7偶式也一定相等。
将丫中"・”换成"+”,"+"换成"・""0"换成"1〃,"1〃换成"0"例如X = MT? id I门〃—人・(A + 1KJ)心+“)臺y -4ff+c + n+r —» rj =(?i+fi)c D(M对偶规则的应用:证明等式成立0 * 0 ■ 0 ■运算顺序:括号i与i或__ _____ yI0 + P H G +P )W + P )IIII H H E )IR +P ^l ■■®o ®推——■ AB+AC + 〃C£> = A〃+AC芹M AH・AR =(A + ")fA + yn 尋同理WHE精品课件V1 ••r精品课件V1 ••r■w===■[□Mi=5律律律和量变和。


逻辑运算逻辑代数的基本运算比较简单,只有三种:“与”运算、“或”运算和“非”运算。
任何复杂的逻辑运算都可由这三种基本逻辑运算构成。
如,广泛采用的“与非”、“或非”、“与或非”、“异或” 。
、“同或”等逻辑运算,它们的逻辑关系可以由以上三种基本运算导出。
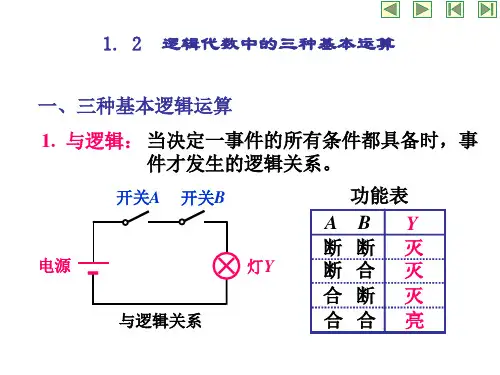
1.“与”运算当决定一事件的所有条件都具备之后,这事件才会发生,称这种因果关系为“与”逻辑关系,或称为“与”逻辑运算或逻辑乘。
条件用逻辑变量“A,B…..”表示,变量取值为1,表示条件具备;取值为0,表示条件不具备。
事件用F表示,只有发生(用1表示)和不发生(用0表示)两种取值。
“与”逻辑运算用表达式表示为:F=A·B 或者F=A ∧B一般简写为:F=AB,把此式称为变量A、B相“与”的逻辑表达式。
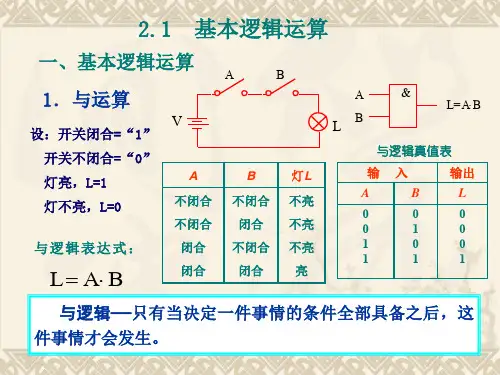
用两个串联的开关A、B控制一盏灯,如图1(a)所示。
灯亮的条件是开关A“与”开关B同时处在合上位置。
假定灯亮为“1”,不亮为“0”,开关在合上位置为“1”,在断开位置为“0”,那么,把灯的状态和两个开关所处位置之间的关系列表,如图1(b)所示。
把这种表称为真值表(或称为功能表)。
常用真值表来表示逻辑命题的真假关系。
把所有的条件(输入变量)的全部组合以表格形式列出来,这里为A、B,再把在每一种组合下对应的事件(函数)的值F求出,这张表格就是真值表。
因为每个条件有两种状态“0”、“1”,因此,n个条件就有2n个组合。
图1(b)为A“与”B 的真值表。
同一逻辑函数只可能有唯一的真值表!2.“或”运算当决定事件发生的各种条件中,只要有一个或一个以上条件具备时,这事件就会发生,这样的因果关系称为“或”逻辑关系,或称逻辑加。
“或”运算的逻辑表达式为:F=A+B 或者F=A∨B 。
用并联的两个开关A、B控制一盏灯,如图2(a)所示,只要开关A“或”开关B在合上位置,灯就亮。
按照前面假定来赋值“0”、“1”,列出真值表,如图2(b)所示。
3.“非”运算“非”运算,就是否定,或者称为求反。