基本逻辑运算解读

逻辑代数的三个基本运算逻辑代数是一种数学分支，研究命题和命题之间的逻辑关系。

它主要包括命题逻辑和谓词逻辑两个部分。

在逻辑代数中，有三个基本运算，即合取、析取和否定。

接下来，我将一步一步回答有关逻辑代数的这三个基本运算的问题。

一、合取运算（AND）合取运算，也称为与运算，用∧（圆圈上有一个小竖杠）表示。

在逻辑代数中，合取运算指的是将两个或多个命题连接起来，当且仅当这些命题都为真时，合取命题才为真。

1. 合取命题的真值表首先，我们可以通过真值表来表示合取命题。

假设有两个命题P和Q，可以通过以下真值表来表示合取命题：P Q P∧QT T TT F FF T FF F F从上表可以看出，当且仅当P和Q的值均为真时，合取命题才为真。

2. 合取的代数表达式除了使用真值表，我们还可以使用代数表达式来表示合取命题。

例如，我们可以用“P ∧Q”来表示“P和Q的合取”。

在逻辑代数中，合取的代数表达式遵循以下规则：- 合取满足交换律：P ∧Q = Q ∧P- 合取满足结合律：(P ∧Q) ∧R = P ∧(Q ∧R)- 合取满足吸收律：P ∧(P ∨Q) = P二、析取运算（OR）析取运算，也称为或运算，用∨（有一个小竖杠在圆圈顶部）表示。

在逻辑代数中，析取运算是将两个或多个命题连接起来，当且仅当这些命题中至少有一个为真时，析取命题才为真。

1. 析取命题的真值表与合取运算类似，我们可以使用真值表来表示析取命题。

假设有两个命题P和Q，可以通过以下真值表来表示析取命题：P Q P∨QT T TT F TF T TF F F从上表可以看出，只有当P和Q的值至少有一个为真时，析取命题才为真。

2. 析取的代数表达式类似于合取运算，我们可以使用代数表达式来表示析取命题。

例如，我们可以用“P ∨Q”来表示“P或Q的析取”。

在逻辑代数中，析取的代数表达式遵循以下规则：- 析取满足交换律：P ∨Q = Q ∨P- 析取满足结合律：(P ∨Q) ∨R = P ∨(Q ∨R)- 析取满足分配律：P ∨(Q ∧R) = (P ∨Q) ∧(P ∨R)三、否定运算（NOT）否定运算，也称为非运算，用¬表示。

78个逻辑类型及总结在计算机科学中，逻辑类型是指变量或表达式的类型，用于表示真值逻辑运算的结果。

逻辑类型通常只有两个取值：真(True)和假(False)。

在本文中，我们将介绍并总结78种常见的逻辑类型。

逻辑类型的基本运算1.逻辑与 (AND): 当两个表达式都为真时，结果为真；否则为假。

2.逻辑或 (OR): 当两个表达式至少一个为真时，结果为真；否则为假。

3.逻辑非 (NOT): 对单个表达式求反，即真变为假，假变为真。

基本逻辑类型4.布尔型 (Bool): 最基本的逻辑类型，只有真和假两个取值。

数字比较类型5.相等 (Equal): 判断两个数值是否相等。

6.不等 (Not equal): 判断两个数值是否不相等。

7.大于 (Greater than): 判断一个数值是否大于另一个数值。

8.小于 (Less than): 判断一个数值是否小于另一个数值。

9.大于等于 (Greater than or equal to): 判断一个数值是否大于等于另一个数值。

10.小于等于 (Less than or equal to): 判断一个数值是否小于等于另一个数值。

字符串比较类型11.相等 (Equal): 判断两个字符串是否相等。

12.不等 (Not equal): 判断两个字符串是否不相等。

13.大于 (Greater than): 判断一个字符串是否大于另一个字符串。

14.小于 (Less than): 判断一个字符串是否小于另一个字符串。

15.大于等于 (Greater than or equal to): 判断一个字符串是否大于等于另一个字符串。

16.小于等于 (Less than or equal to): 判断一个字符串是否小于等于另一个字符串。

集合比较类型17.集合相等 (Set equal): 判断两个集合是否相等。

18.集合不等 (Set not equal): 判断两个集合是否不相等。

逻辑的运算规则逻辑是一门研究思维和推理的学科，它通过运用一定的规则和方法来研究思维的合理性和推理的正确性。

逻辑的运算规则是逻辑学中的基础知识，它们是推理过程中必须遵循的规则，用于保证推理的准确性和有效性。

本文将介绍几个常用的逻辑运算规则，包括命题逻辑中的合取、析取、蕴含和等价运算规则，以及谓词逻辑中的全称量词和存在量词运算规则。

一、命题逻辑中的运算规则1. 合取运算规则：合取是指将两个命题同时成立的情况，用符号“∧”表示。

在合取运算中，有以下两个重要的规则：（1）合取交换律：P∧Q与Q∧P是等价的，即合取运算可以交换位置。

（2）合取结合律：(P∧Q)∧R与P∧(Q∧R)是等价的，即合取运算可以按照任意顺序进行。

2. 析取运算规则：析取是指将两个命题中至少有一个成立的情况，用符号“∨”表示。

在析取运算中，有以下两个重要的规则：（1）析取交换律：P∨Q与Q∨P是等价的，即析取运算可以交换位置。

（2）析取结合律：(P∨Q)∨R与P∨(Q∨R)是等价的，即析取运算可以按照任意顺序进行。

3. 蕴含运算规则：蕴含是指从一个命题推导出另一个命题的过程，用符号“→”表示。

在蕴含运算中，有以下两个重要的规则：（1）蕴含的传递性：如果P蕴含Q，Q蕴含R，则P蕴含R。

（2）蕴含的假设消除：如果假设P成立，然后通过推理得出Q成立，那么可以得出P蕴含Q。

4. 等价运算规则：等价是指两个命题具有相同的真值，用符号“↔”表示。

在等价运算中，有以下两个重要的规则：（1）等价交换律：P↔Q与Q↔P是等价的，即等价运算可以交换位置。

（2）等价结合律：(P↔Q)↔R与P↔(Q↔R)是等价的，即等价运算可以按照任意顺序进行。

二、谓词逻辑中的运算规则1. 全称量词运算规则：全称量词是指对于所有的元素都成立，用符号“∀”表示。

在全称量词运算中，有以下两个重要的规则：（1）全称量词的交换律：∀x∀yP(x,y)与∀y∀xP(x,y)是等价的，即全称量词可以交换位置。

1.6 逻辑运算逻辑运算在我们今后的编程中会经常使用到的。

本节必须掌握的知识点:掌握逻辑运算计算机中所有的数据都是使用二进制保存，但是这些复杂的电路又是如何做运算的呢？1.6.1【逻辑运算】逻辑运算是CPU运算的本质，不管是计算机能处理多么复杂的事情，它最终还是通过电路的开关来实现的。

逻辑是指对某个事物的推理，“真”和“假”是两个对立的逻辑状态，逻辑运算是指用数学符号来表示逻辑状态，以便于用数学方法研究逻辑问题。

我们通常将电路通电状态表示为“真”，用数字“1”表示，不通电表示为“假”，用数字“0”表示。

“或”、“与”、“非”是三种基本逻辑运算，计算机逻辑运算也包含“异或”、“位”。

1、或运算或运算：汇编中用“OR”表示，C语言中用“|”来表示，可以理解为“或者”，即只要有一个条件满足就为“真”，用电路来描述：只要有一条电路通电这条总电路就能通电，原理如图1-6-1：图1-6-1：OR运算等效电路这是一个并联电路图，不管是A为闭合状态、还是B为闭合状态，还是AB都处于闭合状态，电灯泡都能亮。

我们把电路图用符号0和1来表示，或运算表示只要有一个为1，结果就为1。

我们来看一个宽度为8的或运算：1 0 1 1 0 1 0 0or 1 0 0 1 1 1 1 01 0 1 1 1 1 1 0总结:或（or）运算“有1为1”。

2、与运算与运算：汇编中用“and”表示，C语言中用“&”来表示，它表示两个条件都成立才能为真，即两个都为1结果为1，其他为0，电路实现原理如图1-6-2：图1-6-2：AND运算等效电路这是一个串联电路图，A和B都为闭合状态，灯泡才能亮。

如果有一个开关没有闭合，灯泡是不能亮的。

即两个都为1，结果为1，只要有一个为0 ，结果为0。

我们来看一下下面的运算：1 0 1 1 0 1 0 0and 1 0 0 1 1 1 1 01 0 0 1 0 1 0 0总结：与（and）运算的法则：“有0为0”。

逻辑运算1.逻辑常量与变量：逻辑常量只有两个，即0和1，用来表示两个对立的逻辑状态。

逻辑变量与普通代数一样，也可以用字母、符号、数字及其组合来表示，但它们之间有着本质区别，因为逻辑常量的取值只有两个，即0和1，而没有中间值。

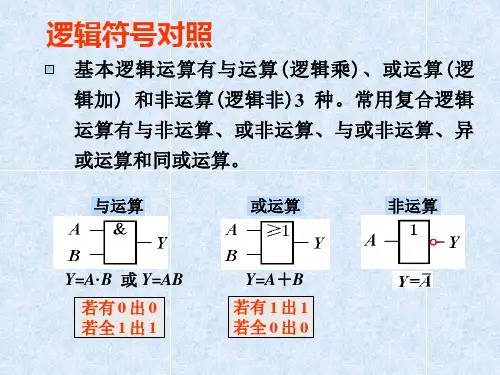
2.逻辑运算：在逻辑代数中，有与、或、非三种基本逻辑运算。

表示逻辑运算的方法有多种，如语句描述、逻辑代数式、真值表、卡诺图等。

3.表示方法"∨" 表示"或""∨" 表示"与"."┐" 表示"非"."=" 表示"等价".1和0表示"真"和"假"逻辑或对于逻辑或，如果一个操作数或多个操作数为true，则逻辑或运算符返回true；只有全部操作数为false，结果才是false。

在决定一事物的若干条件中，只要有一个条件能满足时，结果就会出现；只有当所有条件都起；只有两个开关都不闭合，电灯EL才不会亮。

亮）。

1 V 1结果就是1，0 V 1结果就是1，0 V 0结果就是0。

逻辑与只有两个操作数都是真，结果才是真。

逻辑与操作属于短路操作，既如果第一个操作数能够决定结果，那么就不会对第二个操作数求值。

对于逻辑与操作而言，如果第一个操作数是假，则无论第二个操作数是什么值，结果都不可能是真，相当于短路了右边。

亮。

一个是0（开关不闭合）那么结果就是0（灯不亮）1^1结果就是1，1^0结果就是0，0^0结果就是0例题101001^000111 →000001从左到右1^0 00^1 01^0 00^0 00^1 01^1 (1)→000001。

高中数学掌握数学中的逻辑运算逻辑运算是高中数学中的一个重要概念，它涉及到命题和命题之间的关系，通过逻辑运算可以从已知的命题中推导出新的结论。

在解决数学问题的过程中，掌握逻辑运算的方法和规则，对于正确理解和应用数学知识起到至关重要的作用。

本文将介绍高中数学中常用的几种逻辑运算，包括与运算、或运算、非运算以及条件语句等。

一、与运算与运算是指将两个命题同时满足的结果，用符号“∧”表示。

当且仅当两个命题同时为真时，与运算的结果为真，否则为假。

例如，如果命题P：“今天是周一”和命题Q：“天空是晴朗的”都为真，则它们的与运算结果为真，即P∧Q为真。

二、或运算或运算是指两个命题中至少有一个为真的结果，用符号“∨”表示。

当且仅当两个命题中至少有一个为真时，或运算的结果为真，否则为假。

例如，如果命题P：“今天是周一”为真，命题Q：“天空是晴朗的”为假，则它们的或运算结果为真，即P∨Q为真。

三、非运算非运算是指对一个命题取反的结果，用符号“¬”表示。

当命题为真时，非运算的结果为假，当命题为假时，非运算的结果为真。

例如，如果命题P：“今天是周一”为真，则它的非运算结果为假，即¬P为假。

四、条件语句条件语句是指一个命题关于另一个命题的陈述，其中一个命题称为条件，另一个命题称为结论。

条件语句的真值依赖于条件和结论之间的关系。

条件语句通常用符号“→”表示，读作“如果……，那么……”。

例如，条件语句P→Q表示如果命题P为真，则命题Q也为真。

在数学中，我们常常需要根据已知的命题进行推理。

通过运用逻辑运算的规律和方法，我们可以从已知的命题出发，推导出新的结论，进而解决问题。

在应用逻辑运算时，需要注意以下几点：首先，要准确理解命题的含义。

在解题过程中，要明确每个命题的真值以及与其他命题之间的关系，确保理解正确。

其次，要熟练掌握逻辑运算的规则和定义。

了解与运算、或运算、非运算等的定义和规则，掌握它们的真值表和性质，能够灵活运用。

逻辑运算功能的原理和方法逻辑运算是一种基本的数学运算，它代表我们在进行推理和判断时所使用的方法和原则。

逻辑运算的原理和方法涉及到命题、符号、真值表、逻辑关系和逻辑推理等多方面的知识。

下面将从这些方面逐一阐述逻辑运算功能的原理和方法。

首先，逻辑运算的基础是命题。

命题是陈述一个判断或描述一个事实的句子，它要么为真，要么为假。

例如，"今天是星期一"就是一个命题。

命题可以用符号来表示，常用的符号包括大写字母P、Q、R等。

通过符号化，我们可以将逻辑运算简化为符号的操作，从而更方便地进行分析和推理。

其次，逻辑运算采用了符号逻辑的方法。

在符号逻辑中，我们使用一系列的逻辑符号来表示不同的逻辑关系。

常见的逻辑符号包括非（¬）、合取（∧）、析取（∨）、蕴含（→）和等价（↔）等。

这些符号为我们提供了进行命题间逻辑关系运算的工具。

然后，逻辑运算可以通过真值表来描述。

真值表是一种将命题和逻辑连接词所代表的关系列出来的表格。

通过真值表，我们可以清晰地了解不同命题间逻辑关系的结果。

例如，在合取运算中，当两个命题都为真时，合取运算的结果为真；在蕴含运算中，只有当前提命题为真而结论命题为假时，蕴含运算的结果为假。

此外，逻辑运算还涉及到逻辑关系的分析和判断。

在逻辑关系中，我们需要判断不同命题之间的逻辑关系，如是否满足蕴含、合取和等价等。

逻辑关系的判断可通过真值表、推理等方法进行。

通过分析逻辑关系，我们可以推导出一些新的命题。

例如，如果我们知道了"如果下雨，那么路滑"和"下雨"两个命题，就可以推导出"路滑"这个命题。

最后，逻辑运算还包括逻辑推理的方法。

逻辑推理是通过已知的命题之间的逻辑关系，推导出其他的命题的过程。

逻辑推理可以分为直接推理和间接推理两种方法。

直接推理是通过明确的逻辑关系进行推理，如通过合取关系推导出其中一个元素的真值。

间接推理则是通过构建一个推理过程，通过前提和规则进行推导，最终得出结论。

基本逻辑运算的运算规则
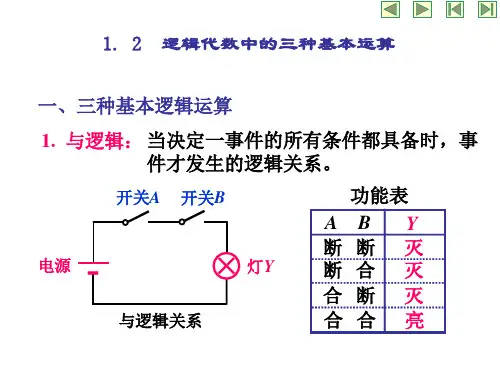
1. 与运算就像两个人都点头同意呀！比如说，你和朋友都想去吃冰淇淋，只有你们俩都想去，那这才算是真正的与运算成功啦，就像电灯的两个开关都得闭合灯才会亮。

2. 或运算就像是有一条路能走就行！比如你想去一个地方，要么坐公交可以去，要么打车可以去，只要满足其中一个条件，那就是或运算达成了呀，这不是很简单嘛！
3. 非运算哎呀，就是完全反过来呢！比如你本来很高兴，非一下就变得不高兴啦！就像一件事本来是真的，非运算后就变成假的了。

4. 与非运算就像是要先同意再反对。

比如大家说去爬山，先都同意了，但最后又决定不去了，这就是与非运算呀。

5. 或非运算则有点像只要有一个不行就都不行。

就好比去看电影，要么你没时间，要么朋友没时间，只要有一个不行，那就去不成了，这不就是或非运算吗？
6. 异或运算可有意思啦，就像两个人只能有一个对。

比如说你和朋友猜硬币正反，只有你们俩一个猜对一个猜错，那才是异或运算的结果呢！
7. 同或运算呢，就是要两个人一样才行哦！就像你们俩都猜对或者都猜错硬币，这就是同或运算呀，挺好玩的吧？
8. 基本逻辑运算规则可太重要啦！就像搭积木，这是基础呀！如果基础没打好，那后面怎么能搭出漂亮的建筑呢？所以一定要好好掌握呀！
我的观点结论：基本逻辑运算规则简单又有趣，理解并熟练运用它们会让很多事情变得清晰明了！。

逻辑运算总结
逻辑运算是计算机科学中的重要概念，其主要目的是在程序中对逻辑值进行计算。

逻辑运算通常包括与、或、非等操作。

与运算是指两个操作数都为真时结果为真，否则为假。

与运算可以用符号“&”来表示。

例如，如果a和b都为真，则a&b的结果为真。

或运算是指两个操作数中至少有一个为真时结果为真，否则为假。

或运算可以用符号“|”来表示。

例如，如果a和b中至少有一个为真，则a|b的结果为真。

非运算是指一个操作数为真时结果为假，反之亦然。

非运算可以用符号“!”来表示。

例如，如果a为真，则!a的结果为假。

除了上述基本的逻辑运算，还有其他一些常见的逻辑运算，如异或运算、条件运算等。

异或运算是指两个操作数相等时结果为假，不相等时结果为真。

条件运算是指根据一个条件来选择两个操作数中的一个。

例如，如果a为真，则选择b作为结果，否则选择c作为结果。

总之，逻辑运算在计算机科学中具有非常重要的意义，掌握各种逻辑运算的使用方法对于编写高效的程序非常重要。

- 1 -。