基本逻辑运算

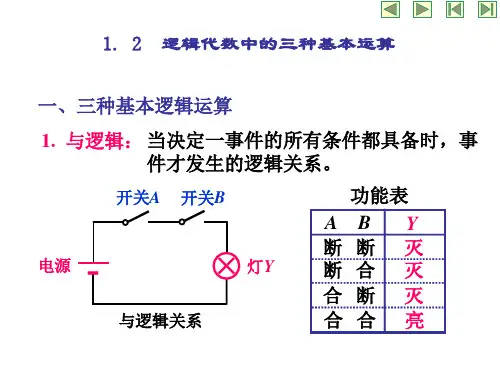
计算机基础逻辑运算计算机基础逻辑运算是计算机科学中的重要概念，它是计算机进行数据处理和决策的基础。

逻辑运算是指根据一定的规则对逻辑命题进行推导和判断的过程。

在计算机中，逻辑运算主要涉及与、或、非三种基本逻辑运算符号，它们分别用符号“∧”、“∨”和“¬”表示。

与运算是指逻辑命题同时为真时，结果为真；或运算是指逻辑命题其中之一为真时，结果为真；非运算是指逻辑命题取反的运算。

这三种逻辑运算符号可以通过组合使用，构建更复杂的逻辑表达式。

在计算机中，逻辑运算是通过逻辑门电路实现的。

逻辑门电路是由逻辑门组成的电路，逻辑门是一种电子设备，能够根据输入信号的逻辑关系输出相应的逻辑结果。

常见的逻辑门有与门、或门、非门等。

通过逻辑门的组合和连接，可以构建出各种复杂的逻辑电路，实现不同的逻辑运算。

逻辑运算在计算机中的应用非常广泛。

例如，在程序设计中，逻辑运算常用于判断条件的真假，根据不同的条件执行不同的代码块。

逻辑运算还可以用于逻辑推理和证明，如在人工智能领域中，逻辑推理是实现智能决策和问题求解的重要方法。

除了基本的逻辑运算，计算机还能进行更复杂的逻辑运算，如位运算和布尔运算。

位运算是指对二进制数进行逐位的逻辑运算，常见的位运算有与运算、或运算、异或运算等，它们可以对数据的各个位进行操作。

布尔运算是指对布尔值进行逻辑运算，布尔值只有两个值，即真和假，布尔运算可以对多个布尔值进行逻辑运算，得出一个最终的逻辑结果。

逻辑运算在计算机科学中有着广泛的应用。

它不仅是计算机硬件实现的基础，也是计算机软件设计和算法分析的基础。

了解和掌握逻辑运算对于理解计算机工作原理和开发高效的程序非常重要。

此外，逻辑运算还与数学、哲学、语言学等学科密切相关，是这些学科中重要的研究对象之一。

总结起来，计算机基础逻辑运算是计算机科学中的重要概念，它涉及与、或、非三种基本逻辑运算符号，可以通过逻辑门电路实现。

逻辑运算在计算机中的应用非常广泛，不仅是计算机硬件实现的基础，也是计算机软件设计和算法分析的基础。

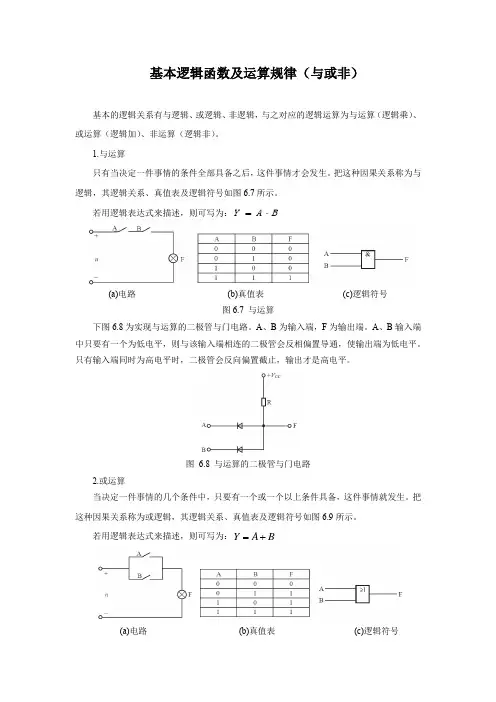
基本逻辑函数及运算规律（与或非）基本的逻辑关系有与逻辑、或逻辑、非逻辑，与之对应的逻辑运算为与运算（逻辑乘）、或运算（逻辑加）、非运算（逻辑非）。

1.与运算只有当决定一件事情的条件全部具备之后，这件事情才会发生。

把这种因果关系称为与逻辑，其逻辑关系、真值表及逻辑符号如图6.7所示。

若用逻辑表达式来描述，则可写为：B A Y ⋅=(a)电路 (b)真值表 (c)逻辑符号图6.7 与运算下图6.8为实现与运算的二极管与门电路。

A 、B 为输入端，F 为输出端。

A 、B 输入端中只要有一个为低电平，则与该输入端相连的二极管会反相偏置导通，使输出端为低电平。

只有输入端同时为高电平时，二极管会反向偏置截止，输出才是高电平。

图 6.8 与运算的二极管与门电路2.或运算当决定一件事情的几个条件中，只要有一个或一个以上条件具备，这件事情就发生。

把这种因果关系称为或逻辑，其逻辑关系、真值表及逻辑符号如图6.9所示。

若用逻辑表达式来描述，则可写为：B A Y +=(a)电路 (b)真值表 (c)逻辑符号图6.9 或运算下图6.10为实现与运算的二极管或门电路。

A、B为输入端，F为输出端。

A、B输入端中只要有一个为高电平，则输出端为高电平。

只有当A、B同时为低电平，输出端才会输出低电平。

图 6.10或运算的二极管与门电路3.非运算某事情发生与否，仅取决于一个条件，而且是对该条件的否定，即条件具备时事情不发生；条件不具备时事情才发生，其逻辑关系、真值表及逻辑符号如图6.11所示。

(a)电路(b)真值表(c)逻辑符号图6.11 或运算Y若用逻辑表达式来描述，则可写为：A下图6.12为晶体管非门电路。

当输入为高电平，晶体管饱和，输出为低电平；当输入为电平，晶体管截止，输出为高电平，实现了非门功能。

图 6.12 非运算的二极管与门电路二、常用逻辑运算1.与非运算下图6.13为2输入与非运算的电路、逻辑符号及真值表。

它由二极管与门和晶体管非门串接而成，当输入中至少有一个为低电平，P点输出为低电平，晶体管截止，F输出为高电平；当输入全为高电平时，P点输出为高电平，晶体管饱和，F输出为低电平，实现了与非的逻辑功能。

四种基本逻辑运算
在数学和计算机科学中，有四种基本逻辑运算。

这些运算是： 1. 与运算（AND）：当两个条件都为真时，与运算才为真。

如果有一个条件为假，则整个表达式为假。

2. 或运算（OR）：在两个条件中，只要有一个为真，或运算就为真。

只有当两个条件都为假时，整个表达式才为假。

3. 非运算（NOT）：非运算是一元运算符，它的结果是条件的相反值。

如果条件为真，则非运算为假；如果条件为假，则非运算为真。

4. 异或运算（XOR）：异或运算只有在两个条件不同的情况下为真。

如果两个条件都为真或都为假，则整个表达式为假。

这些基本逻辑运算在计算机科学中非常重要，因为它们可以用来创建复杂的逻辑表达式和控制流程。

例如，在编程语言中，可以使用这些运算符来创建条件语句和循环语句，以控制程序的执行流程。

- 1 -。

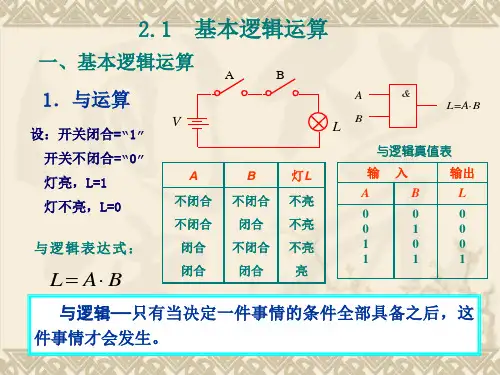
基本的逻辑运算逻辑运算是数学和计算机科学中重要的概念之一。

它是指通过一些特定的规则和操作，将一个或多个输入值映射为一个输出值的过程。

本文将从逻辑运算的基本形式出发，逐步介绍与之相关的概念和应用。

我们需要了解逻辑运算的基本组成部分——逻辑门。

逻辑门是一种由电子元件组成的电路，它能够实现特定的逻辑运算。

最常见的逻辑门有与门、或门、非门和异或门等。

与门的输出只有在所有输入都为真时才为真，或门的输出只要有一个输入为真就为真，非门的输出是输入的反值，异或门的输出只有在输入值不同时才为真。

逻辑运算可以通过组合多个逻辑门来实现更复杂的功能。

例如，通过将多个与门和非门连接起来，可以构建出一个与非门（NAND）电路。

与非门的输出只有在所有输入都为真时才为假，否则为真。

事实上，与非门本身已经足够强大，可以用来实现所有其他的逻辑门，因此被广泛应用于计算机的设计和制造中。

逻辑运算在计算机科学中扮演着重要的角色。

例如，在逻辑电路中，逻辑门的组合可以实现各种计算和控制功能。

在计算机的中央处理器中，逻辑运算用于实现算术运算、逻辑判断和控制流程等操作。

逻辑运算也被广泛应用于数字电路、通信系统和人工智能等领域，为各种应用提供了强大的计算和决策能力。

除了基本的逻辑运算，还有一些常用的逻辑运算符号和表达方式。

例如，逻辑与运算可以用符号“∧”表示，逻辑或运算可以用符号“∨”表示，逻辑非运算可以用符号“¬”表示。

这些符号可以使逻辑表达更加简洁和直观。

逻辑运算在数学推理和证明中也发挥着重要的作用。

通过运用逻辑运算的规则和定律，我们可以从已知条件推导出新的结论。

逻辑运算可以帮助我们识别和排除逻辑错误，提高思维的准确性和严谨性。

在生活中，逻辑运算也有着广泛的应用。

例如，在解决问题和做决策时，我们常常需要进行逻辑思考和逻辑推理。

通过运用逻辑运算的原理和方法，我们可以更好地分析问题、归纳总结和做出正确的判断。

逻辑运算是数学和计算机科学中重要的概念，它通过一些特定的规则和操作将输入映射为输出。

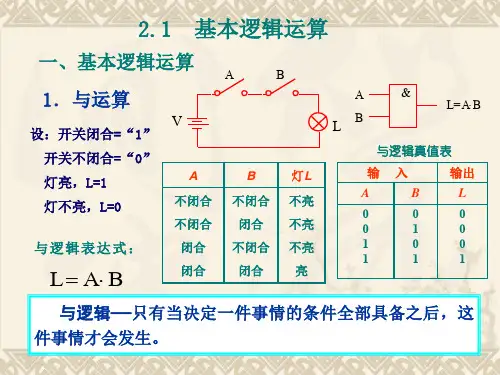
三种基本的逻辑运算关系在数学和计算机科学中，逻辑运算关系是基本的逻辑概念，它们帮助我们理解和操控事物之间的关系。

逻辑运算关系主要有三种：与（AND）、或（OR）和非（NOT）。

下面我们将对每一种逻辑运算关系进行详细解释，以帮助读者更好地理解它们的含义和应用。

首先，我们来介绍与运算（AND）。

与运算是指两个条件同时满足时结果为真，否则结果为假。

与运算可以用来判断多个条件是否同时成立。

比如，在一个餐厅中，为了让顾客享受到美味的菜品，我们可以设置一个与运算条件，只有当顾客同时点了主菜和甜点时，才会上菜，否则不会上菜。

这样可以保证顾客们只有在满足两个条件的情况下才能获得他们所期望的美食。

其次，让我们介绍或运算（OR）。

或运算是指两个条件中只要有一个满足时结果为真，只有当两个条件都不满足时结果为假。

或运算可以用来判断多个条件中是否有至少一个成立。

例如，假设你参加了一场晚会，门口有一个守卫，他会检查你是否持有邀请函或者是否是VIP。

只要你满足其中一种条件，就可以进入晚会，否则你将无法进入。

这就是或运算的用途。

最后，让我们介绍非运算（NOT）。

非运算是指对某个条件取反，如果原来的条件为真，则取反后为假；如果原来的条件为假，则取反后为真。

非运算可以用来转换一个条件的逻辑状态。

例如，如果你希望你的自行车不被小偷盗走，你可以在停车处贴上一个标志，上面写着“此车容易损坏”。

这个标志的作用是利用非运算，通过传递一个虚假的信息，让小偷们误以为你的自行车不值得被盗窃，从而不会选择你的车作为目标。

综上所述，与、或和非是三种基本的逻辑运算关系。

它们在我们日常生活中无处不在，用来判断和操纵不同条件之间的关系。

通过了解和灵活运用这些逻辑运算关系，我们可以更加理性地思考和决策，提高我们的生活品质和工作效率。

“与”、“或”、“非”逻辑的基本运算公式是and、or、not。

用逻辑运算符将关系表达式或逻辑量连接起来的有意义的式子称为逻辑表达式。

逻辑表达式的值是一个逻辑值，即“true”或“false”。

有三种最基本的逻辑运算：
1）逻辑与-- 用AB表示：当A，B都为1时，其值为1，否则为零。

2）逻辑或-- 用A+B 表示：当A，B都为0时，其值为0，否则为1。

3）逻辑非-- 用A上'¯'表示，当A=0时，A的非为1，A=1时，A的非为0。

产生
布尔用数学方法研究逻辑问题，成功地建立了逻辑演算。

他用等式表示判断，把推理看作等式的变换。

这种变换的有效性不依赖人们对符号的解释，只依赖于符号的组合规律。

这一逻辑理论人们常称它为布尔代数。

20世纪30年代，逻辑代数在电路系统上获得应用，随后，由于电子技术与计算机的发展，出现各种复杂的大系统，它们的变换规律也遵守布尔所揭示的规律。