第1章 逻辑代数基础作业

X Y Z
F
图1.28 习题1-2(1)逻辑图
解：
X Y Z
00001111 00110011 01010101
00001111 11001100
11001111 01000101 01010101 00100000 01100101 F
11110000 00110011 10101010
真值表 X 0 0 0 0 1 1 1 1 Y 0 0 1 1 0 0 1 1 Z 0 1 0 1 0 1 0 1 F 0 1 1 0 0 1 0 1
CD AB 00 01 11 10 00 1 0 0 1 01 0 0 0 0 11 0 0 1 1 10 1 0 0 1
1-5 以卡诺图法化简下列函数，写成或-与表达式的形式。 (1) F AB (C D) A B DC 解： F (C D)( A C )( A D)( B D)( B C )
图1.29 习题1-2(6)的卡诺图
真值表 A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F 1 0
(2) F

A, B , C
m(1,2,5,7)
真值表 A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 F 0 1 1 0 0 1 0 1
(3) F

W , X ,Y , Z
M (2,3,6,7,10,12)
真值表 W 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 X 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 Y 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 Z 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F 1 1 0 0 1 1 0 0 1 1 0 1 0 1 1 1

《逻辑代数基础》练习题及答案[1.1]将下列二进制数转为等值的十六进制数的等值的十进制数。

（1）(10010111)2 ；（2）(1101101)2 ；（3）(0.01011111)2 ；（4）(11.001)2 。

[解]（1）(10010111)2 = (97)16 = (151)10，（2）(11011101)2 = (6D)16 = (109)10（3）(0.01011111)2 = (0.5F)16 = (0.37109375)10，（4）(11.001)2 = (3.2)16 = (3.125)10[1.2]将下列十六进制数化为等值的二进制数和等值的十进制数。

（1）(8C)16 ；（2）(3D.BE)16；（3）(8F.FF)16 ；（4）(10.00)16[解]（1）(8C)16 = (10001100)2 = (140)10（2）(3D·BE)16 = (111101.1011111)2 = (61.7421875)10（3）(8F·FF)16 = (10001111.11111111)2 = (143.99609375)10（4）(10.00)16 = (10000.00000000)2 = (16.00000000)10[1.3]将下列十进制数转换成等效的二进制数和等效的十进制数。

要求二进制数保留小数点以后4位有效数字。

（1）(17)10 ；（2）(127 )10 ；（3）(0.39)10 ;（4）(25.7)10[解]（1）(17)10 =(10001)2 =(11)16 ；（2）(127)10 = (1111111)2 = (7F)16（3）(0.39)10 = (0.0110)2 = (0.6)16；（4）(25.7)10 = (11001.1011)2 = (19.B)16[1.4]写出下列二进制数的原码和补码。

（1）(+1011)2 ；（2）(+00110)2 ；（3）(-1101)2 ；（4）(-00101)2 。

5、三个重要运算规则
①代入规则：任何一个含有变量 A 的等式，如果将所有出现 A 的位置都用
同一个逻辑函数代替，则等式仍然成立。这个规则称为代入规则。 例如，已知等式 AB A B ，用函数 Y=AC 代替等式中的 A，
根据代入规则，等式仍然成立，即有：
( AC) B AC B A B C
A
E
B Y
4
第1章 逻辑代数基础---三种基本运算
功能归纳：
真值表：
开关 A 开关 B 断开 断开 闭合 闭合 断开 闭合 断开 闭合
灯Y 灭 灭 灭 亮
A 0 0 1 1
B 0 1 0 1
Y 0 0 0 1
将开关接通记作1，断开记作0；灯亮记作1，灯灭记作0。可以作出如
上表格来描述与逻辑关系，这种把所有可能的条件组合及其对应结果一一列
的逻辑函数， 并记为：
F f ( A, B, C , )
3
第1章 逻辑代数基础---三种基本运算
②三种基本运算
a.与逻辑（与运算）
定义:仅当决定事件（Y）发生的所有条件（A，B，C，…）均满足 时，事件（Y）才能发生。表达式为：
Y=A· C· B· …=ABC…
描述:开关A，B串联控制灯泡Y
法进行描述。每种方法各具特点，可以相互转换。 ①真值表
将输入变量的各种可能取值和相应的函数值排列在一起而组成的表格。
真值表列写方法：每一个变量均有0、1两种取值，n个变量共有2n种不 同的取值，将这2n种不同的取值按顺序（一般按二进制递增规律）排列起
来，同时在相应位置上填入函数的值，便可得到逻辑函数的真值表。
原式左边
AB A C ( A A ) BC

1.3集合的基本运算（同步练习）一、单选题1．若集合{|23}A x x =-，{|1B x x =<-或4}x >，则集合A B 等于（ ） A ．{|3x x 或4}x > B ．{|13}x x -< C ．{|21}x x -<- D ．{|34}x x < 2．已知全集U =A B 中有m 个元素，()()U U A B ⋃中有n 个元素．若A B 非空，则A B 的元素个数为A ．mnB ．m n +C ．n m -D ．m n - 3．设M ，N 是非空集合，且M N U ⊆⊆（U 为全集），则下列集合表示空集的是（ ）A ．()U M NB ．()U M NC ．()()U U M ND ．M N ⋂ 4．已知集合M={1，2，3，4}，N={-2,2}，下列结论成立的是A ．N ⊆MB ．M∪N=MC ．M∩N=ND ．M∩N={2} 5．设集合M={-1,0,1}，N={x |2x =x }，则M∩N=A ．{-1，0，1}B ．{0,1}C ．{1}D ．{0} 6．已知集合A={（x ，y ）|x ，y 为实数，且x 2+y 2=1}，B=|（x ，y ）|x ，y 为实数，且x+y=1}，则A∩B 的元素个数为（ ）A ．4B ．3C ．2D ．17．设全集U={1，2，3，4，5，6} ，设集合P={1，2，3，4}， Q={3，4，5}，则P∩（C U Q ）=A ．{1，2，3，4，6}B ．{ 1，2，3，4，5}C ．{1，2，5}D ．{1,2} 8．已知全集{}0,1,2,3,4U =，集合{}1,2,3A =，{}2,4B =，则()U A B ⋃为 A ．{1,2,4}B ．{2,3,4}C ．{0,2,4}D ．{0,2,3,4}二、填空题9．设U R = ，{}0A x x =，{}1B x x =，则()U A B ⋂=_____．10．设M ，P 是两个非空集合，定义集合M ，P 的差集运算为{,M P x x M -=∈且},x P ∉设集合{}2,4,6,8,B =请你写出一个集合A ，使得{}5,A B -=则集合A =___________.11．设全集U ＝{a ，b ，c ，d }，集合A ＝{a ，b }，B ＝{b ，c ，d }，则()()U U A B ⋃=_____．12．某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为_______13．如图所示，U 是全集，A B 、是U 的子集，则阴影部分所表示的集合是__________三、解答题14．设全集U =R ，集合13{|}A x x =-≤<，{|242}B x x x =-≥-（1）求A B ；（2）若集合{}|20C x x a =+>，满足C C =B ∪，求实数a 的取值范围.15．已知全集{}{}{}14,11,03,U x x A x x B x x =-≤≤=-≤≤=<≤求(),.U U A B A 16．已知下列三个方程：24430x ax a +-+=，22(1)0x a x a +-+=，2220x ax a +-=至少有一个方程有实根，求实数a 的取值范围.参考答案：1．C【解析】【分析】根据交集的定义写出A B ．【详解】集合{|23}A x x =-，{|1B x x =<-或4}x >，∴集合{|21}A B x x =-<-．故选：C ．【点睛】本题考查交集的运算，属于基础题.2．D【解析】【详解】因为()()()U U U B A B A ⋃=⋂ 所以()()U U U A B A B ⋂=⋃⎡⎤⎣⎦，所以A B 共有m n -个元素，故选D ．3．A【解析】【分析】由集合的包含关系结合集合的运算即可得解.【详解】集合M 是非空集合，对集合M 中任一元素x ，∪M N U ⊆⊆，∪x ∈N ，∪U x N ∉，又若U y N ∈，则y N ∉，∪M N ⊆，∪y M ∉，∪()U M N ⋂=∅.故选：A.4．D【解析】【详解】试题分析：由M={1，2，3，4}，N={﹣2，2}，则可知，﹣2∪N ，但是﹣2∪M ，则N∪M ，M∪N={1，2，3，4，﹣2}≠M ，M∩N={2}≠N ，从而可判断．解：A 、由M={1，2，3，4}，N={﹣2，2}，可知﹣2∪N ，但是﹣2∪M ，则N∪M ，故A 错误；B 、M∪N={1，2，3，4，﹣2}≠M ，故B 错误；C 、M∩N={2}≠N ，故C 错误；D 、M∩N={2}，故D 正确．故选D ．考点：集合的包含关系判断及应用．5．B【解析】【详解】{}0,1N = M="{-1,0,1}" ∴M∩N={0,1}【点评】本题考查了集合的基本运算，较简单，易得分.先求出{}0,1N =，再利用交集定义得出M∩N6．C【解析】【详解】由题得221,{1,x y x y +=+= ∪1,{0,x y ==或0,{1,x y ==A∩B={(1,0),(0,1)}. 故选C.7．D【解析】【详解】{}{}1,2,6()1,2.U U C Q P C Q =∴⋂=，选D.【考点定位】此题主要考察集合运算8．C【解析】【分析】先根据全集U 求出集合A 的补集U A ，再求U A 与集合B 的并集()U A B ⋃． 【详解】由题得，{}0,4,U A ={}{}{}()0,42,40,2,4.U A B ∴⋃=⋃=故选C. 【点睛】本题考查集合的运算，属于基础题．9．{|01}x x <≤；【解析】【详解】试题分析：由题：{|1}U C B x x =≤，则：(){|01}U A C B x x ⋂=<≤考点：集合的运算.10．{}5(答案不唯一)【解析】【分析】由集合的新定义转化条件为5A ∈，且A 中不再含U B 中的其他任何元素，即可得解. 【详解】由题意，知5A ∈，且A 中不再含U B 中的其他任何元素，而是否再含B 中的元素则不影响等式{}5A B -=，因此{}5A =符合题意.故答案为：{}5(答案不唯一)11．{},,a c d【解析】先分别求出U A ，U B ，即可求出并集.{},U A c d =，{}U B a =，()(){},,U U A B a c d ∴⋃=.故答案为：{},,a c d .【点睛】本题考查集合的补集并集混合运算，属于基础题.12．12【解析】【详解】设两者都喜欢的人数为x 人，则只喜爱篮球的有(15-x )人，只喜爱乒乓球的有(10-x )人,(15-x )+(10-x )+x +8= 30解得x =3,所以15- x = 12故喜爱篮球运动但不喜爱乒乓球运动的人数为12人.13．()U B A ⋂【解析】【分析】试题分析：根据韦恩图可知，图中阴影部分为集合B 与集合A 在U 中的补集的交集，即()U B A ⋂.考点：1.韦恩图；2.集合的交集，并集，补集.14．（1）{}|23A B x x =≤<；（2）4a >-.【解析】（1）化简集合B ，根据交集运算即可求解；（2）由C C =B ∪可得B C ⊆，据此建立不等式求解即可.【详解】（1）∪{}|13A x x =-≤<，{}{}|242|2B x x x x x =-≥-=≥∪{}|23A B x x =≤<；（2）由集合C 中的不等式20x a +>，解得2a x >-， ∪|2a C x x ⎧⎫=>-⎨⎬⎩⎭， ∪C C =B ∪，∪B C ⊆， ∪22a -<， 解得4a >-15．{}14U A x x =<≤，(){}10U B A x x ⋂=-≤≤.【解析】【分析】由集合的交、并、补的定义即可得解.【详解】∪{}14U x x =-≤≤，11A x x ，{}03B x x =<≤，{}14U A x x ∴=<≤，{34U B x x =<≤或}10x -≤≤，(){}10U B A x x ∴⋂=-≤≤.16．32a ≤-或1a ≥- 【解析】【分析】至少有一个方程有实根的对立面是三个方程都没有根，由于正面解决此问题分类较多，而其对立面情况单一，故求解此类问题一般先假设没有一个方程有实数根，然后由根的判别式解得三方程都没有根的实数a 的取值范围，其补集即为个方程 24430x ax a +-+=，22(1)0x a x a +-+=，2220x ax a +-=至少有一个方程有实根成立的实数a 的取值范围．此种方法称为反证法【详解】假设没有一个方程有实数根，则：2122223(4)4(43)0(1)40(2)41(2)0a a a a a a ⎧∆=--+<⎪∆=--<⎨⎪∆=-⨯⨯-<⎩得2224430321020a a a a a a ⎧+-<⎪+->⎨⎪+<⎩解得：312a -<<- 所以至少有一个方程有实根，则实数a 的取值范围为32a ≤-或1a ≥-.。

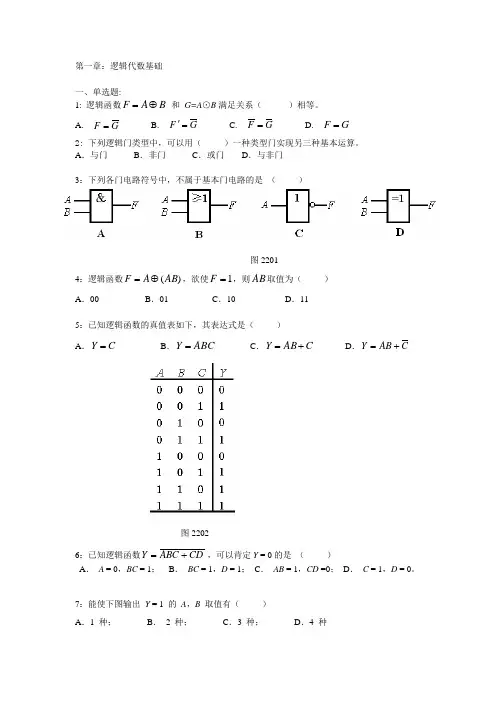
第一章：逻辑代数基础一、单选题:1: 逻辑函数B A F ⊕= 和 G=A ⊙B 满足关系（ ）相等。

A. G F = B. G F =' C. G F = D. G F = 2: 下列逻辑门类型中，可以用（ ）一种类型门实现另三种基本运算。

A ．与门 B ．非门 C ．或门 D ．与非门3：下列各门电路符号中，不属于基本门电路的是 （ ）图22014：逻辑函数)(AB A F ⊕=，欲使1=F ，则AB 取值为（ ） A ．00B ．01C ．10D ．115：已知逻辑函数的真值表如下，其表达式是（ ）A ．C Y =B ．ABC Y = C ．C AB Y +=D ．C AB Y +=图22026：已知逻辑函数 CD ABC Y +=，可以肯定Y = 0的是 （ ）A ． A = 0，BC = 1；B ． BC = 1，D = 1； C ． AB = 1，CD =0； D ． C = 1，D = 0。

7：能使下图输出 Y = 1 的 A ，B 取值有（ ）A ．1 种；B ． 2 种；C ．3 种；D ．4 种图22038：下图电路，正确的输出逻辑表达式是（ ）。

A ． CD AB Y += B ． 1=YC ． 0=YD ． D C B A Y +++=图22049：根据反演规则，E DE C C A Y ++⋅+=)()(的反函数为（ ） A. E E D C C A Y ⋅++=)]([ B. E E D C C A Y ⋅++=)( C. E E D C C A Y ⋅++=)( D. E E D C C A Y ⋅++=)(10：若已知AC AB C A B A =+=+,，则（ ）A ． B=C = 0B ． B=C =1 C ． B=CD ． B ≠C11：在什么情况下，“与非”运算的结果是逻辑0。

（ ）A ．全部输入是0 B. 任一个输入是0 C. 仅一个输入是0 D. 全部输入是112：逻辑函数=⊕⊕=)(B A A F （ ）A ．B B ．AC ．B A ⊕D ． B A ⊕13：逻辑式=⋅+⋅+A A A 10 （ ）A ． 0B ． 1C ． AD ．A14：逻辑函数ACDEF C AB A Y +++=的最简与或式为（ ）A ．C A Y += B.B A Y += C. AD Y = D. AB Y =15：下列逻辑函数中不相等的是（ ）。

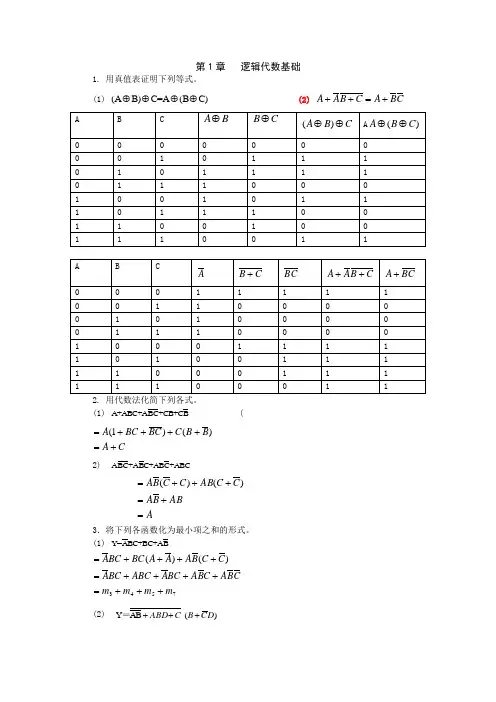
第1章 逻辑代数基础1. 用真值表证明下列等式。

(1) (A B)C=A (B C)⊕⊕⊕⊕ (2) C B A C B A A +=++(1) A+ABC+ABC+CB+CB (CA B B C BC BC A +=++++=)()1(2) ABC+ABC+ABC+ABCAABB AC C AB C C B A =+=+++=)()(3．将下列各函数化为最小项之和的形式。

(1) Y=ABC+BC+AB7543)()(m m m m C B A C B A BC A ABC BC A C C B A A A BC BC A +++=++++=++++= (2) )( AB Y D C B C ABD +++＝DC ABD C B D C AB D C B C D B D A D C B C AD B BD A D C B C ABD B A =+=+++++=+++++=++++=)()()()(4．根据下列各逻辑式， 画出逻辑图。

①Y=（A+B ）C ； ②Y=AB+BC ； ③Y=（A+B ）（A+C ）；5．试对应输入波形画出下图中 Y 1 ~ Y 4 的波形。

6.如果“与”门的两个输入端中， A 为信号输入端， B 为控制端。

设当控制端B=1和B=0两种状态时，输入信号端A 的波形如图所示， 试画出输出端Y 的波形。

如果A 和B 分别是“与非”门、“或”门、“或非”门的两个输入端，则输出端Y 的波形又如何？总结上述四种门电路的控制作用。

第2章 组合逻辑电路1.分析图示电路的逻辑功能。

要求写出逻辑式，列出真值表，然后说明逻辑功能。

ABY B A B A Y =+=21 半加器 真值表略2.已知逻辑式B A AB Y +=：①列出逻辑真值表，说明其逻辑功能；②画出用“与非”门实现其逻辑功能的逻辑图；③画出用双2/4线译码器74LS139实现其逻辑功能的逻辑图； ④画出用4选1数据选择器74LS153实现其逻辑功能的逻辑图；③双2/4线译码器74LS139 有两个2-4线译码器④用4选1数据选择器74LS1533.证明图（a ）和（b ）所示的两个逻辑电路具有相同的逻辑功能。

第 20 页
数字电子技术
第 1 章 逻辑代数基础
单项选择题
20、当变量 A、B、C 取值为101 时，下列三变量函数最小项中等于
1 的是
( )。
A m1
×
B m3
×
C m5
√
D m7
×
分析提示
将 ABC = 101 代入各最小项： m 1AB C1010 m3ABC 1010 m5ABC1011 m 7AB 1C 010
第 30 页
数字电子技术
第 1 章 逻辑代数基础
单项选择题
30、函数 Y = ABC + ABC + ABC + ABC 的最简化简结果为 ( ) 。
须先变换成同一进制，再比较大小、相等关系。
如统一表示成十进制数：
( 101111 ) 2 = ( 47 ) 10 ( 3A ) 16= ( 58 ) 10
( 55 ) 8= ( 45 ) 10 ( 01010110 ) 8421BCD= ( 56 ) 10
第2页
数字电子技术
第 1 章 逻辑代数基础
8
6
9
3
3
3
5
3
6
第4页
数字电子技术
第 1 章 逻辑代数基础
单项选择题
7、常用的BCD码有8421码、2421码、余3码等，其中既是有权码
又是自补码的是
( )。
A 8421码 C 余3码
×
B 2421码
√
×
D 余3循环码
×
分析提示
2421码代码中从左至右每一位的权分别为 2、4、2、1，为有 权码； 2421码代码中 0和9、 1和8、 2和7、 3和6、 4和5 互 补， 为自补码。

第一章（数制、编码与逻辑代数）作业及答案1、数制、编码转换题（1）(74.3 )8=( 60.375 )10=( 111100.011)2=( 0111 0100.0011 )8421BCD（2）(45.24 )10=(101101.001111 )2 精确到小数点后6位（3）(110101.11 )2=(35.C )16=( 65.6 )8（4）(71.45 )8=( 39.94 )16（5）(010********* )8421BCD =(1113)8=( 24B)162、求下列函数的反函数。

（1）)(B D A C C B A F +++=（2）))()((B A D C C D A B F +++=3、写出下列函数的对偶式。

（1）（2）4、用公式法将下列各逻辑函数表达式化成最简“与—或”式，并继而将其转换成相应的“与非—与非”式、“或—与”式和“与或非”式。

（1）)() (C B C B A C B BC A F +++=（2）ABD D C ABC C B A AC F ++++=D（3）BC C B A BC A A F ++++=)D (（4）C B C A AB F ++=（5）))()()()()((F E D F B F E C A D B C A B A A F +++++++++=答案:（1）A （2）D C AC +=D C AC ∙=(A+C )(C+D)=D C C A +（3）BC A +=BC A ∙=(A+B)(A+C)=C A B A +（4）C AB +=C AB ∙=(A+C)(B+C)=C B C A +（5）))((F B D B AC F ++==CD B A ABCF ∙=))((F B D B AC ++=F B C D B A +++5、写出下列逻辑函数的最小项表达式，并用卡诺图法将其化为最简“与—或”式。

（1）D C A D C A C B A D C AB ABC F +++++= D 解：C A AB D A ++（2）B C A BD F )(+= 解：D A D C B ++6、用卡诺图法将下列逻辑函数化为最简“与—或”式。

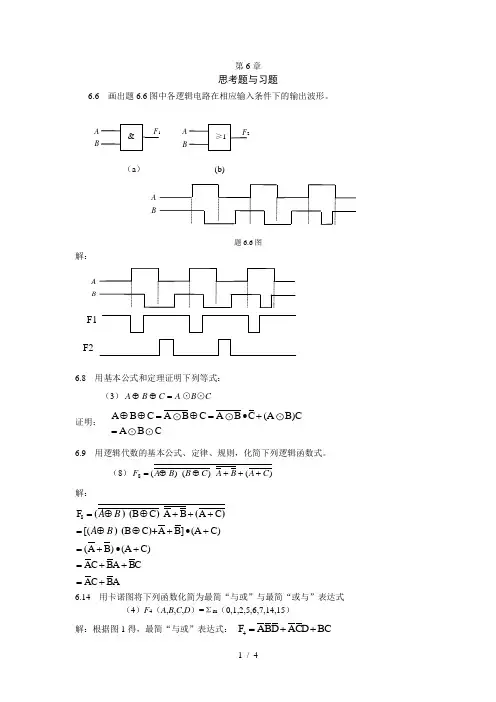
第6章思考题与习题6.6 画出题6.6图中各逻辑电路在相应输入条件下的输出波形。

（a ） (b)题6.6图解：A BF1F26.8 用基本公式和定理证明下列等式： （3）A C B A =⊕⊕⊙B ⊙C 证明：A B C A B C A B C (A B)CABC⊕⊕=⊕=•+=6.9 用逻辑代数的基本公式、定律、规则，化简下列逻辑函数式。

（8）)()()(8C A B A C B B A F +++⊕⊕= 解：8F B C A B A C [(B C A B](A C)(A B)(A C)AC BA BC AC BA()()())()+A B A B =⊕⊕+++=⊕⊕+•+=+•+=++=+6.14 用卡诺图将下列函数化简为最简“与或”与最简“或与”表达式（4）F 4（A ,B ,C ,D ）=Σm （0,1,2,5,6,7,14,15）解：根据图1得，最简“与或”表达式： 4F ABD ACD BC =++F 1 。

F 2。

A B根据图2得，最简“或与”表达式：4F BCD AC AB BCD (B C D)(A C)(A B)(B C D)=+++=++++++6.16 用卡诺图将下列函数化简为最简“与或”式（2）F 2（A ,B ,C ,D ）=Σm （1,3,4,9,11,12,14,15）+Σd （5,6,7,13）（3）D C B A ABC C B A F ++=3，约束条件0=⊕B A 解：（2）根据图1：F 2=B+D约束条件：A C A A C B D BCD BCD AB D=0+++（3）根据图2：3F AC BC CD =++，约束条件0=⊕B A6.21 写出题6.21图所示各电路的逻辑表达式，化成最简“与或”式，并用“与非”门重新实现。

6.21图图1图2F 1。

F 2（a ）（b ）解：1F A B BC A B)BC=ABC BC=BC (=++=++)()C 2F A B+B+C A B B+C AB AB B C AB AB =⊕=⊕•=++=+（）（用“与非”门实现：6.28 已知逻辑函真值表如图表题6.28所示，写出逻辑函数式，化简并用“与非”门实现。

逻辑代数基础试题及答案1. 逻辑代数中，与运算的符号是什么？答案：与运算的符号是“∧”。

2. 逻辑代数中，或运算的符号是什么？答案：或运算的符号是“∨”。

3. 逻辑代数中，非运算的符号是什么？答案：非运算的符号是“¬”。

4. 逻辑代数中，异或运算的符号是什么？答案：异或运算的符号是“⊕”。

5. 逻辑代数中，同或运算的符号是什么？答案：同或运算的符号是“≡”。

6. 逻辑代数中，如何表示变量A和变量B的与运算？答案：变量A和变量B的与运算表示为“A∧B”。

7. 逻辑代数中，如何表示变量A和变量B的或运算？答案：变量A和变量B的或运算表示为“A∨B”。

8. 逻辑代数中，如何表示变量A的非运算？答案：变量A的非运算表示为“¬A”。

9. 逻辑代数中，如何表示变量A和变量B的异或运算？答案：变量A和变量B的异或运算表示为“A⊕B”。

10. 逻辑代数中，如何表示变量A和变量B的同或运算？答案：变量A和变量B的同或运算表示为“A≡B”。

11. 在逻辑代数中，德摩根定律是什么？答案：德摩根定律包括两个部分，即(¬A)∨(¬B) = ¬(A∧B)和 (¬A)∧(¬B) = ¬(A∨B)。

12. 逻辑代数中，如何证明A∧(A∨B) = A？答案：根据分配律，A∧(A∨B) = (A∧A)∨(A∧B)。

由于A∧A = A，所以表达式简化为A∨(A∧B)。

由于A∨A = A，最终表达式简化为A。

13. 逻辑代数中，如何证明A∨(¬A∧B) = A∨B？答案：根据分配律，A∨(¬A∧B) = (A∨¬A)∧(A∨B)。

由于A∨¬ A = 1（真），表达式简化为1∧(A∨B)。

由于任何变量与1的与运算结果都是该变量本身，最终表达式简化为A∨B。

14. 逻辑代数中，如何证明A∧(¬A∨B) = ¬A∨B？答案：根据分配律，A∧(¬A∨B) = (A∧¬A)∨(A∧B)。

1-13（1） 用卡诺图简化下面逻辑函数
Y BC AC AB
1
1
1
1
五邑大学
第一章 逻辑代数基础 习题
数 字 Y ( A, B, C, D) m(0,1,2,3,4,6,7,8,9,10,11,14) 电 表2.4.16 Y的卡诺图 路 CD 与 解: AB 00 01 11 10 逻 00 1 1 1 1 辑 01 1 Y CD AD B AC 1 1 设 11 1 计
10
1-14(4)简化下列逻辑函数，写最简成与或式
01
11
10
× × 1
1
×
1
1
五邑大学
字 电 路 Y ABC ABC ABC 与 ABC ABC 逻 辑 AB C 设 计
数
A B C 0 0 0 0 0 0 1 1 0 1 1 0 0 1 0 1 0 1 Y 0 1 0 1 0 1
1 1
1 1
0 1
1 1
五邑大学
第一章 逻辑代数基础 习题
• 题1-2已知真值表如表所示，试写出输出的逻辑函 数
第一章 逻辑代数 习题
数 字 电 路 与 逻 辑 设 计
题1-1、题1-7(2) 、题1-8(5) 题1-9(2) 题1-2、题1-3、题1-4(a) 题1-10(3)(8) 题1-11(1) 、题1-12(1) 题1-13(1)(5)、题1-14(1)(4)
五邑大学
第一章 逻辑代数基础 习题
• 题1-1 如图，列出真值表，试写出输出的逻辑函 数
3.
将这些变量相加即得 Y。
五邑大学
第一章 逻辑代数基础 习题
• 题1-2已知真值表如表所示，试写出输出的逻辑函 数

第1章逻辑代数基础概述一、填空题1、将十进制数（10）10转换成二进制数是__，转换成八进制数是。

2、二进制数10111111对应的八进制数为,十进制数为。

3、(35.75)10=()24、(10011010)B =()D =()H 。

二、选择题1、十进制整数转换为二进制数一般采用（）A 、除2取余法B 、除2取整法C 、除10取余法D 、除10取整法2、将十进制小数转换为二进制数一般采用（）A 、乘2取余法B 、乘2取整法C 、乘10取余法D 、乘10取整法3、一位十六进制数可以用（）位二进制数来表示。

A 、2B 、3C 、4D 、54、与十进制数（53.5）10等值的数或代码为（）A 、(01010011.0101)8421BCDB 、(35.8)16C 、(110101.1)2D 、(65.4)85、与八进制数(47.3)8等值的数为（）。

A 、(100111.011)2B 、(27.6)16C 、(27.3)16D 、(100111.11)26、和二进制数(1100110111)2等值的十六进制数是()。

A.(337)16B.(637)16C.(1467)16D.(C37)167、下列数中,最大的数是（）A.(3D )16B ．(111010)2C ．(57)10D ．(65)88、在N 进制中，字符N 的取值范围为：（）A ．01N - B ．1NC ．11N -D ．0N9、欲对全班53个学生以二进制代码表示，至少需要二进制码的位数是()A.6B.5C.10D.5310、n 位二进制数最大可以表示的十进制数为（）A 、nB 、2nC 、n2D 、12-n三、判断题（）1、模拟量是连续的，数字量是离散的，所以模拟电路的精度要高于数字电路。

（）模拟电路相比，数字电路具有较强的抗干扰能力。

（）3、数字电路中用“1”和“0”分别表示两种状态,二者无大小之分。

（）4、八进制数（17）8比十进制数（17）10小。

第一章 数字逻辑基础 作业及参考答案P431-7 列出下列问题的真值表，并写出逻辑函数表达式（1）3个输入信号A 、B 、C ，如果3个输入信号都为1或其中两个信号为0，输出信号F 为1，其余情况下输出信号F 为0 。

（2）4个输入信号A 、B 、C 、D ，如果4个输入信号出现偶数个0时，输出信号F 为1，其余情况下，输出信号F 为0.（1）解：根据题意列出真值表如下：（2）解：根据题意列出真值表如下：ABC C B A C B A C B A F +++=ABCD D C AB D C B A D C B A D BC A D C B A D C AB D C B A F +++++++=1-8 写出下列函数的反函数表达式和对偶函数表达式解：（1）C AB F += C B A F ⋅+=)( C B A F ⋅+=)('（2）C B A F +⊕= C B A F +⊕=C B A B A F ⋅+⋅+=)()('（3）E BD AC D B A F )()(+++= ])()[()]([E D B C A D B A F ++⋅+⋅++= ])()[()('E D B C A BD A F ++⋅+⋅+=(4) CD A C B A B A F ++=)( )(CD A C B A B A F ++=)()('D C A C B A B A F ++⋅+++=1-9 证明下列等式（1）))(())()((C A B A C B C A B A ++=+++证明：))(())()((C B BC B A AC C B C A B A +++=+++BC BC A B A AC ABC ++++=BC B A AC ++=))((C A B A ++= 证毕。

（2）E CD A E D C CD A ABC A ++=++++)(证明：E D C CD A A E D C CD A ABC A )()(+++=++++ E D C A E D C D C A E D C CD A +++=++++=+++=)()(E CD A ++=证毕。

第一章数字逻辑基础作业及参考答案P43()1-11已知逻辑函数F AB BC CA ，试用真值表、卡诺图和逻辑图表示该函数。

解：(1)真值表表示如下:1-12用与非门和或非门实现下列函数，并画出逻辑图。

解: (1) F(A,B,C)= AB + BC = AB ?B C(2) F(A,B,C,D) = (A+B)?(C + D)二 A+B + C + D输入输出 A B C F 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 11100 01 11 10 由卡诺图可得(3)逻辑图表示如下：F 二 A + B C + B C =A?B C ?B CACA BC BCABC AC ? ABC ? BC ABC(A 1C)?(A BC)?(BC) AB C(AB AC AC B C C)?(B C) ABCABC ABC AC ABC AC BC BC C ABC ABCABCACABCACBCBC CABCCAD AD AB AC BD ACE BE DE题 1-12(1) 题 1-12(2)1-14利用公式法化简下列函数为最简与或式。

解(3) F解：(2) FA AC BD BE DE(2)卡诺图表示如下:0 10 111111=A + C + BD + BE解(5) F (A B C D)(A B C D)(A BCD)F' ABCD ABCD ABCD BCD ABCD BCD ABD••• F =(B + C + D)(A+B + D)二 AC + B+ DP441-15利用卡诺图化简下列函数为最简与或式。

解：(3) F = (A +B + C + D)(A+B+C + D)(A +B + C + D)(A + B + C +D) 方法 i ： F = (A+B+C + D)(A + B + C + D)(A + B+C + D)(AB AC AD AB B BC BDACCDAD CD D)(ABCD)(AC B AC D)(A B C D)AC ABCACD ABBC BDABC ACACD AD BDCD=AC + AB + BC + B D + AC + AD + BD + CD解(5) F(A, B,C, D) = Rm o ,m 2,m 5,m 6,m 8,m 10m 12,m 14,m 15)-CDAB 、00 01111000 01F(A,B,C,D) CD AD BD ABCABCD001、01 I 1「1「0 111 JF 110I 11 JaV .F = AC + AC + BD+BD +AD1 0 0 1 01 0 1 10 1 1 10 0 1F 的卡诺图00 01 1110F 的卡诺图11 101-16(1)F(A,B,C,D) (m2,m4,m6,m9,m13,m14)解：画出函数F的卡诺图如下:(d0, d1, d3 , d11 , d15)00 XXX1 01 1 0 01 11 0 1 X 1 10 01X经化简可得F (代B,C,D) AD AD ABC1- 16(3) F(A,B,C,D)(m 0，m 13，m 14，m 15)(aa ，d 3，d 9，d 10，dn)解：画出函数F 的卡诺图如下：■ CD AB 、 00 01111000 01 11 101-18 (1) Y AB AC BC Z AB 解：画出函数 Y 、Z 的卡诺图如下：1-18 (2) Y (A B C)(AB CD) 解：Y (AB C)(AB CD) AB1 XXX0 0 0 0 0 111XXX经化简可得F(A,B,C,D) ABAD AC 0 0 1 0 0 0 1 0 1 1 1 1 00 10100 01 11 10的卡诺图11 10 ACBC由卡诺图可知：Y Z1 1 0 1 1 0 0 0AB^CD 00Z AB CDACD BCD ABC CD 0 1Z 的卡诺图00 丫2的卡诺图1-19已知 0 0 1 00 0 1 01 1 1 1 0 0 1 0 0111 10 Z 的卡诺图 A B 、C 、D 是一个十进制数 X 的8421BCD 码，当X 为奇数时，输出 Y 为1,否则Y 为0。

组合逻辑电路中的竞争与冒险
分析电路中可能出现的竞争与冒险现象，采取相应措施进行消除或 抑制。
时序逻辑电路分析与设计
分析时序逻辑电路
了解时序逻辑电路的基本概念和组成，包括触发器、寄存器、计数器等。根据给定的电路图，分 析电路的工作原理和功能。
设计时序逻辑电路
根据实际需求，确定输入与输出之间的逻辑关系以及电路的状态转换关系。选择合适的触发器类 型，设计状态转换表和状态转换图，并进行电路连接。
备考策略指导
明确考试要求
了解考试形式和评分标准，明确备考方向和重 点。
制定复习计划
根据考试要求和自身情况，制定合理的复习计 划，并按照计划有序进行复习。
多做模拟试题
通过做模拟试题来检验自己的学习成果，找出自己的不足之处，有针对性地进 行弥补。
考试技巧点拨
仔细审题
在考试时，认真阅读题目，理解题意和要求 ，避免因为误解题意而导致失分。
题目1：逻辑代数中，基本的逻辑运算包括哪些？
02
A. 与、或、非
03
B. 与、或、异或
选择题解析
C. 与、非、同或 D. 或、非、异或 答案：A. 与、或、非
选择题解析
• 题目2：在逻辑代数中，下列哪个公式是正 确的？
选择题解析
C. A + A'B = A + B
B. A(A + B) = AB
表示方法
逻辑函数可以用多种方法表示，如真值表、逻辑表达式、卡诺图等。其中，真值表是列出所有输入组合及对应输 出的表格；逻辑表达式是用逻辑运算符和逻辑变量表示的式子；卡诺图是一种图形化表示方法，用于简化逻辑函 数。
02 逻辑代数化简方法
公式化简法
利用基本公式进行化简

逻辑代数基础一、选择题1. 以下代码中为相邻两个码字之间只有一位码有差异的是 。

A . 8421BCD 码B . 自然二进制码C . 余三码D . 格雷码2. 一位十六进制数可以用 位二进制数来表示。

A . １B . ２C . ４D . 163. 十进制数25用8421BCD 码表示为 。

A .10 101B .0010 0101C .100101D .101014. 当逻辑函数有n 个变量时，共有 个变量取值组合？A. nB. 2nC. n 2D. 2n5. 逻辑函数的表示方法中具有唯一性的是 。

A .真值表 B.表达式 C.逻辑图 D.卡诺图6. 逻辑函数F=)(B A A ⊕⊕ = 。

A.BB.AC.B A ⊕D. B A ⊕7. A+BC= 。

A .A+B B.A+C C.（A+B）（A+C） D.B+C8. 在何种输入情况下，“与非”运算的结果是逻辑0。

A．全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是19. 在何种输入情况下，“或非”运算的结果是逻辑0。

A．全部输入是0 B.全部输入是1 C.任一输入为0，其他输入为1 D.任一输入为110. 与十进制数（53.5）10等值的数或代码为 。

A .(0101 0011.0101)8421BCDB .(35.8)16C .(110101.1)2D .(65.4)811. 与八进制数(47.3)8等值的数为 。

A. (100111.011)2B.(27.6)16C.(27.3 )16D. (100111.11)212.与模拟电路相比，数字电路主要的优点有 。

A.容易设计B.通用性强C.保密性好D.抗干扰能力强13.以下表达式中符合逻辑运算法则的是 。

A.C·C=C2B.1+1=10C.0<1D.A+1=114.逻辑变量的取值１和０可以表示： 。

A.开关的闭合、断开B.电位的高、低C.真与假D.电流的有、无二、判断题（正确打√，错误的打×）1.8421码1001比0001大。

《数字电子技术基础》第1章 逻辑代数技术基础单元测试一、选择题(每题10分，共10分)1. 以下表达式中符合逻辑运算法则的是 。

A.C ·C =C 2B.1+1=10C.0<1D.A +1=12. 逻辑变量的取值１和０可以表示： 。

A.开关的闭合、断开B.电位的高、低C.真与假D.电流的有、无3. 当逻辑函数有n 个变量时，共有 个变量取值组合？A. nB. 2nC. n 2D. 2n4. 逻辑函数的表示方法中具有唯一性的是 。

A .真值表 B.表达式 C.逻辑图 D.卡诺图5.F=A B +BD+CDE+A D= 。

A.D B A +B.D B A )(+C.))((D B D A ++D.))((D B D A ++6.逻辑函数F=)(B A A ⊕⊕ = 。

A.BB.AC.B A ⊕D. B A ⊕7．求一个逻辑函数F 的反函数式，可将F 中的 。

A .“·”换成“+”，“+”换成“·”B.原变量换成反变量，反变量换成原变量C.变量不变D.常数中“0”换成“1”，“1”换成“0”E.常数不变8．A+BC= 。

A .A +B B.A +C C.（A +B ）（A +C ） D.B +C9．在何种输入情况下，“与非”运算的结果是逻辑0。

A ．全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是110．在何种输入情况下，“或非”运算的结果是逻辑0。

A ．全部输入是0 B.全部输入是1 C.任一输入为0，其他输入为1 D.任一输入为1二、判断题（正确打√，错误的打×）(每题10分，共10分)1．逻辑变量的取值，１比０大。

（ ）。

2．异或函数与同或函数在逻辑上互为反函数。

（ ）。

3．若两个函数具有相同的真值表，则两个逻辑函数必然相等。

（ ）。

4．因为逻辑表达式A+B+AB=A+B 成立，所以AB=0成立。

（ ）5．若两个函数具有不同的真值表，则两个逻辑函数必然不相等。