南京信息工程大学第一学期《高等数学》(上)期中考试样卷

南京信息工程大学_高等数学试卷南京信息工程大学高等数学试卷（A ）年级:___ _____专业:___ _____时间:__ _ 2010.07. __学号:________________姓名:_________________得分:________________一、填空题（本题共5小题，每小题3分，满分15分）1．若0),,(=z y x F ，且F 可微，z y x F F F ,,非零，则=x z z y y x _______。

2．交换积分次序，=?xxdy y x f dx 331),(_______。

3．过点()4,2,1-与平面0432=-+-z y x 垂直的直线方程为_______。

4．设有点()3,2,1A 和()4,1,2-B ，则线段AB 的垂直平分面的方程为_______。

5．微分方程02=+'-''y y y 的通解是:二、选择题（本题共5小题，每小题3分，满分15分）1．二元函数),(y x f 在点()00,y x 处两个偏导数),(00y x f x ，),(00y x f y 存在是),(y x f 在该点连续的______。

（A ）充分而非必要条件； (B) 必要而非充分条件； (C) 充分必要条件； (D) 既非充分又非必要条件 2．两平面34=-z x 和152=--z y x 与直线153243-=-=+z y x ______。

（A ）垂直； (B) 平行； (C) 异面； (D) 相交但不垂直。

3．设∑为球面2222a z y x =++，则()=++??∑ds z y x222_____。

（A ）42a π； (B) 48a π； (C) 44a π； (D)434a π。

4．方程xxe y y 22='-''的一个特解具有_______形式。

（A ） ()x e B Ax 2+； (B) xAxe 2； (C) xe Ax 22； (D) ()xe B Ax x 2+。

南京信息工程大学20XX ─ 20XX 学年 第 2 学期高等数学2课程试卷( Ｂ 卷) 及参考答案注意：1、本课程为 （表明必修或选修）， 学时为 ，学分为2、本试卷共 页；考试时间 分钟； 出卷时间： 年 月3、姓名、学号等必须写在指定地方； 考试时间： 年 月 日4、本考卷适用专业年级： 任课教师： XXX以上内容为教师填写）专业年级 班级学号 姓名一、填充题 (每小题 3 分，共 15 分)1．设L 是周长为a 的椭圆22143x y +=，则曲线积分22(234)L xy x y ds ++⎰=__12a ______． 2．已知:z ∑=zdS ∑=⎰⎰3R π. 3．设{(,,)|,01}D x y z a x b y =≤≤≤≤，且()1Dyf x d σ=⎰⎰，则()baf x dx =⎰_______2_____.4．将xoy 坐标面上的椭圆14922=+y x 绕x 轴旋转一周, 所生成的旋转曲面方程为 222194x y z ++= 5．微分方程230y y y '''--=的通解为 312x x y C e C e -=+，（12,C C 为常数）.二、选择题(每小题 3 分，共 15 分)1．级数11(1)n n n ∞=+∑ （ A ）（A ）发散 （B ） 收敛于1 （C ） 收敛于0 （D ）无法判断收敛性2． 22xydx ax dy +在xOy 面内是某一函数(,)u x y 的全微分，则a = （ C ）. (A) 1- (B) .2- (C) 1 (D) 23．2．设y x z =, 则zx∂=∂ ( A ) A. 1y yx - B. ln ||y x x C. (ln )y y x x x+ D. ln y x x 4．若区域222:1x y z Ω++≤取外侧，则积分222()xy z dv Ω++⎰⎰⎰等于 ( B )(A) 2120sin d d r dr ππθϕϕ⎰⎰⎰ (B)2140sin d d r dr ππθϕϕ⎰⎰⎰(C)211221()d d z dz πθρρρ-+⎰⎰⎰ (D)21d d πθρρ⎰⎰5．若级数1nn a∞=∑收敛 ，1nn b∞=∑发散，则级数1()nn n ab ∞=+∑ ( Ａ )(A) 一定发散 (B) 一定收敛 (C) 条件收敛 (D) 不能确定三、判别下列各级数是否收敛？若收敛，是绝对收敛还是条件收敛？(本题２０分) 1．1(1)sin3n nn π∞=-∑ 绝对收敛解 因为|(1)sin|sin333nnnnπππ-=≤，--------------------------------------------------------4分而级数13nn π∞=∑收敛，所以原级数1(1)sin3n nn π∞=-∑绝对收敛.------------------------------１０分2．132nnn n ∞=⋅∑ 解 因为1133(1)2lim1322n n n n nn n ++→∞+⋅=>⋅，--------------------------------------------------------------4分 由比值审敛法知，该级数发散.---------------------------------------------------------------１０分四．已知曲线方程:sin ,1cos ,4sin2t x t t y t z Γ=-=-=, 求对应于2t π=的点处的切线 及法平面方程 (本题１０分)解 (1,1,2)T = -------------------------------------------------------------------------------４分切线方程11211x y π-+-==-----------------------------------------------------８分 法平面方程402x y π+--= -----------------------------------------------------１０分五．求微分方程2x y y y e -'''++=的通解 (本题10分)解 对应的齐次方程的通解12()x y C x C e -=+， --------------------------------------4分 设非次方程的特解2x y Ax e *-=， ---------------------------------------------------------6分 则2(2)x y Ax Ax e -'=-，2(24)x y A Ax Ax e -''=-+代入解得12A =- ------------------------------------------------------------------------------8分 从而原方程的通解为2121()2xy C x C x e -=++ （12,C C 为常数） ------------10分六．求幂级数11n n n x n ∞=+∑的收敛域及和函数，并求1(1)2nn nn ∞=+∑ 的值(本题10分). 解 (2)lim1(1)(1)n n nR n n →∞+==++， --------------------------------------------------------------2分当1x =±时级数发散，故原级数的收敛域为11x -<<， -----------------------------4分又 111111n n n n n n x x n n ∞∞==+-=++∑∑1111n nn n x x n ∞∞===-+∑∑11ln(1),0||110,0x x x xx ⎧+-<<⎪=-⎨⎪=⎩， -------------------------------------------------------8分 令12x =，得12(1ln 2)(1)2nn n n ∞==-+∑. --------------------------------------------------10分 七．将1()arctan1xf x x+=-展为x 的幂级数 (本题10分). 解 221()(1),(11)1n n n f x x x x ∞='==--<<+∑-----------------------------------------------4分 0()(0)()xf x f f x dx '-=⎰221000(1)(1)21n x n nn n n x dx x n ∞∞+==-=-=+∑∑⎰------------------------------------------------------------8分 所以 2101(1)arctan ,(11)1421n n n x x x x n π∞+=+-=+-<<-+∑--------------------------------------10分八．计算曲面积分2(81)(1)4I y xdydz z y dzdx yzdxdy ∑=++-=⎰⎰，其中∑是由曲线13z y x ⎧=≤≤⎪⎨=⎪⎩ 绕y 轴旋转一周所成的曲面，它的法向量与y 轴正向的夹角恒大于2π.(本题10分) 解 曲面∑：221y x z -=+，设2212:3x z y ⎧+≤∑⎨=⎩，取右侧， ---------------------------2分则11I ∑+∑∑=-⎰⎰⎰⎰，由高斯公式212312dv d d dy πρθρπ+∑+∑Ω===⎰⎰⎰⎰⎰⎰⎰， --------------------------------------------6分而122(13)32zxD dzdx π∑=-=-⎰⎰⎰⎰- --------------------------------------------------------------8分从而 23234I πππ=+=. ----------------------------------------------------------------------10分。

南京信息工程大学-高等数学(上册)-试卷B(含答案)南京信息工程大学试卷学年 第 1学期 高等数学 课程试卷( B 卷)本试卷共 页；考试时间 120分钟；任课教师 课程组 ；一、单项选择题 (本大题有4小题, 每小题4分, 共16分) 1.)(0),sin (cos )(　处有则在设=+=x x x x x f .（A ）(0)2f '= （B ）(0)1f '=（C ）(0)0f '= （D ）()f x 不可导.2.　）时（　，则当，设133)(11)(3→-=+-=x x x x xx βα.（A ）()()x x αβ与是同阶无穷小，但不是等价无穷小； （B ）()()x x αβ与是等价无穷小；（C ）()x α是比()x β高阶的无穷小； （D ）()x β是比()x α高阶的无穷小.3. 若()()()02xF x t x f t dt=-⎰，其中()f x 在区间上(1,1)-二阶可导且'>()0f x ，则（ ）.（A ）函数()F x 必在0x =处取得极大值； （B ）函数()F x 必在0x =处取得极小值；（C ）函数()F x 在0x =处没有极值，但点(0,(0))F 为曲线()y F x =的拐点； （D ）函数()F x 在0x =处没有极值，点(0,(0))F 也不是曲线()y F x =的拐点。

4.)()( , )(2)( )(1=+=⎰x f dt t f x x f x f 则是连续函数，且设（A ）22x（B ）222x +（C ）1x - （D ）2x +.二、填空题（本大题有4小题，每小题4分，共16分） 5. =+→xx x sin 2)31(lim .6. ,)(cos 的一个原函数是已知x f x x =⋅⎰x x xx f d cos )(则 .7.lim(cos cos cos )→∞-+++=22221L n n nnn n ππππ .8.=-+⎰21212211arcsin －dx xx x .三、解答题（本大题有5小题，每小题8分，共40分）9. 设函数=()y y x 由方程sin()1x y e xy ++=确定，求'()y x 以及'(0)y .10. .d )1(177x x x x ⎰+-求11.．　求，， 设⎰--⎪⎩⎪⎨⎧≤<-≤=132)(1020)(dx x f x x x x xe x f x12. 设函数)(x f 连续，=⎰1()()g x f xt dt，且→=0()limx f x A x ，A 为常数.求'()g x 并讨论'()g x 在=0x 处的连续性.13. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、 解答题（本大题10分）14. 已知上半平面内一曲线)0()(≥=x x y y ，过点(,)01，且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和，求此曲线方程.五、解答题（本大题10分）15. 过坐标原点作曲线x y ln =的切线，该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ；(2) 求D 绕直线x = e 旋转一周所得旋转体的体积六、证明题（本大题有2小题，每小题4分，共8分）16. 设函数)(x f 在[]0,1上连续且单调递减，证明对任意的[,]∈01q ，1()()≥⎰⎰qf x d x q f x dx.17. 设函数)(x f 在[]π,0上连续，且0)(0=⎰πx d x f ，cos )(0=⎰πdx x x f .证明：在()π,0内至少存在两个不同的点21,ξξ，使.0)()(21==ξξf f （提示：设⎰=xdxx f x F 0)()(）解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题（本大题有4小题，每小题4分，共16分）5. 6e . 6.c x x +2)cos (21　.7. 2π. 8.3π.三、解答题（本大题有5小题，每小题8分，共40分） 9. 解：方程两边求导(1)cos()()0x y e y xy xy y +''+++= cos()()cos()x y x ye y xy y x e x xy +++'=-+0,0x y ==，(0)1y '=-10. 解：767u x x dx du == 1(1)112()7(1)71u du duu u u u -==-++⎰⎰原式 1(ln ||2ln |1|)7u u c =-++ 7712ln ||ln |1|77x x C =-++11. 解：1033()x f x dx xe dx ---=+⎰⎰⎰3()x xd e --=-+⎰⎰00232cos (1sin )x x xe e d x πθθθ----⎡⎤=--+-=⎣⎦⎰令3214e π=--12. 解：由(0)0f =，知(0)0g =。

20.
lim
n

n2
1 n
1

n2
2 n

2
L

n2
n n

n


1 2 n n2 n n

n2
1 n1
n2
2 n2

n2
n nn
1 2 n n2 n 1
…………2 分
lim
n
1
n
2 n 2 nn
x arctan t

y

t2

ln(1
t2
)
所确定,
求 dy ， d 2 y dx dx2
解： dy dx

2t

1
2t t
2
1
2t3
， d2y dx2
6t 2 1
6t2 6t4 …………6 分
1 t2
1 t2
2
阅卷教师
五、证明题(本大题共 2 小题，每小题 6 分，共计 12 分)
|
x0
A.0 B.
C.
D.不存在
8.函数 f (x) 在区间 (a,b) 内有定义，则 f (x) 在 (a,b) 一定有界.（ × ）
订
9.同一极限过程中，若 f (x) 极限存在，g(x) 极限不存在，则 f (x) g(x) 极限不存在（. √ ）
学号：
班级 ：
|
2.若 lim f (x) , lim g(x) ，则必有（ D ）
e y xy e 确定隐函数 y y(x) ，求 dy dx
x0
解： x 0 时， y(0) 1 ………………………………………………3 分

第一学期高等数学期中考试试卷答案一．填空题（本题满分15分，共有5道小题，每道小题3分），请将合适的答案填在空中．1．已知()()212x x f x f =-+，则()=x f ______________________________．2．设x x x y arcsin 12-+=，则='y ______________________．3．设函数()x y y =由方程42ln 2x y y =+所确定，则=dxdy _______________． 4．设()x f 为可导的奇函数，且()50='x f ，则()=-'0x f ________________．5．函数()22sin x x e x f x +--=在区间()∞+∞-，上的最小值为_____________． 答案：⒈ 3132312-+x x ； ⒉ x x xa r c s i n122--； ⒊ 2212yy x +； ⒋ 5；⒌ 1-．二．选择填空题（本题满分15分，共有5道小题，每道小题3分）。

以下每道题有四个答案，其中只有一个答案是正确的，请选出合适的答案填在空中，多选无效．1．数列极限()[]n n n n ln 1ln lim --∞→是________ ． ()A ．1 ； ()B ．1-； ()C ．∞； ()D ．不存在但非∞．2．函数()()x x x x x f ---=322不可导点的个数是______________．()A . 3 ； ()B . 2 ； ()C . 1 ； ()D . 0 ．3．设()x f 可导且()210='x f ，则0→∆x 时，()x f 在0x 点处的微分dy 是____． ()A .比x ∆低阶的无穷小； ()B .比x ∆高阶的无穷小；()C .与x ∆同阶的无穷小； ()D .与x ∆等价的无穷小．4．已知函数()x f 具有任意阶导数，且()()[]2x f x f ='，则当n 为大于2的正整数时，()x f 的n 阶导数()()x f n 为___________．()A .()[]nx f n 2!； ()B . ()[]1+n x f n ； ()C . ()[]n x f 2； ()D .()[]1!+n x f n ． 5．设()()[]2x x f ψ='，其中()x ψ在()∞+∞-，上恒为正值，其导数()x ψ'为单调减少函数，且()00='x ψ，则___________ ．()A ．曲线()x f y =在点()()00x f x ，处有拐点；()B ．0x x =是函数()x f 的极大值点；()C ．曲线()x f y =在()∞+∞-，上是凹的；()D ．()0x f 是()x f 在()∞+∞-，上的最小值．答案：⒈ ()B ；⒉ ()A ；⒊ ()C ；⒋ ()D ；⒌ ()A ．三．（本题满分6分）设0>>a b ，()2a a f ='，求极限()()ab a f b f a b ln ln lim --→． 解：()()()()ab a b a b a f b f a b a f b f a b a b ln ln lim ln ln lim--⋅--=--→→ ()()()()a b a b a b a f b f a b a f b f a b a b a b ln ln lim lim ln ln lim --⋅--=--=→→→ ()3a a a f =⋅'=，四．（本题满分7分）设()A x f x x =→0lim ，极限()x g x x 0lim →不存在，试问极限 ()()[]x g x f x x +→0lim是否存在？并证明之．解：极限()()[]x g x f x x +→0lim 不存在． 反证法：如果极限()()[]x g x f x x +→0lim 存在，由极限()A x f x x =→0lim 存在，可知极限 ()()()()[]()()[]()x f x g x f x f x g x f x x x x x x 000lim lim lim →→→-+=-+ 存在，即极限()x g x x 0lim →存在，这与题设中()x g x x 0lim →不存在矛盾，因此极限()()[]x g x f x x +→0lim 不存在．五．（本题满分7分）设()⎪⎪⎩⎪⎪⎨⎧->+-=-<-=1arccos 1112x x a x bx x x f ，试确定a 、b 之值，使得函数()x f 在点1-=x 处连续．解：()b f =-1，()()01lim lim 0120101=-==----→--→x x f f x x ，()()()π+=+==+-+-→+-→a x a x f f x x a r c c o s lim lim 010101， 所以，由()()101-=--f f ，得0=b ；由()()101-=+-f f ，得π-=a ．因此，当π-=a ，0=b 时，函数()x f 在点1-=x 处连续．六．（本题满分8分）设函数()x y y =由参数方程⎩⎨⎧=+=ty t x cos 12所确定，求22dx y d ． 解：tt t t dtdx dt dydx dy 2sin 2sin -=-== ， dtdxdx dy dt d dx dt dx dy dt d dx dy dx d dx y d 122⋅⎪⎭⎫ ⎝⎛=⋅⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛= ()3224c o s s i n 21s i n c o s 21112s i n t t t t t t t t t t t t dt d t -=⋅--='+⋅⎪⎭⎫ ⎝⎛-= ．七．（本题满分8分）求对数螺线θρe =（由极坐标方程给出）在点()⎪⎪⎭⎫ ⎝⎛=22πθρπ，e 处的切线的直角坐标方程．解：我们将其转换为参数方程()()⎩⎨⎧==θθρθθρsin cos y x ．在本题中，转换后的参变量方程为⎩⎨⎧==θθθθsin cos e y e x ．这时，我们将θ看作参变量，利用参变量方程的求导方法，我们有()()θθθθθθθθθθθs i n c o s s i n c o s s i n c o s s i n c o s -+=-+==e e d d dydx dy ． 当2πθ=时，1s i n c o s s i nc o s 22-=-+===πθπθθθθθdx dy ，0cos 22==⎪⎭⎫⎝⎛=πθθθπe x ，22sin 2ππθθθπe e y ==⎪⎭⎫ ⎝⎛=． 因此，所求切线方程为()()012--=-x e y π，即2πe y x =+ ．八．（本题满分8分）求曲线5412--=x x y 的铅直渐近线与水平渐近线．解：由于0541limlim 2=--=∞→∞→x x y x x ； 所以，0=y 是曲线5412--=x x y 的水平渐近线；由于 ∞=--=-→-→541lim lim 211x x y x x ，∞=--=→→541lim lim 255x x y x x 所以，1-=x 与5=x 都是曲线5412--=x x y 的两条铅直渐近线． 九．（本题满分8分）求数列⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛n n 322的最大项() ，，，321=n ．（已知41.05.1ln ≈） 解：设()xx x f ⎪⎭⎫ ⎝⎛⋅=322 ()+∞<≤x 1， 则()⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⋅='23ln 232x x x f x，令()0='x f ，得()x f 在()∞+，0内的唯一驻点为 9.423ln 20≈=x 当23ln 21<≤x 时，()0>'x f ；当x <23ln 2时，()0<'x f ． 所以2ln 20=x 是函数()x x x f ⎪⎭⎫ ⎝⎛⋅=322在区间()+∞<≤x 1上的极大值点，也是最大值点． 由于59.423ln 240<≈=<x ，且()44232163244⎪⎭⎫ ⎝⎛⋅=⎪⎭⎫ ⎝⎛⋅=f ，()()4323503255452f f >⎪⎭⎫ ⎝⎛⋅=⎪⎭⎫ ⎝⎛⋅=， 所以数列⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛n n 322的最大项为()2438005=f ． 十．（本题满分9分）论证πe 与e π的大小．解：由于ππln e e e =，因此只需讨论π与πln e 的大小．设()x e x x f ln -=，则()xe xf -='1 令()0='x f ，得函数()x e x x f ln -=的驻点e x =0．由于()02>=''xe xf ，所以函数()x e x x f ln -=在点e x =0处取极小值 ()0=-=e e e f由于点e x =0是函数()x e x x f ln -=的唯一极值点，因而也是函数()x e x x f ln -=的最小值点．因此当e x >时，()()0=>e f x f ．因此由e >π，知()0>πf ，即0ln >-ππe ，或ππln e >所以，ππln e e e >，即ee ππ>． 十一．（本题满分9分）设函数()x f 在闭区间[]10，上可微，对闭区间[]10，上的每一点x ，函数()x f 的值都在开区间()10，内，且()1≠'x f ．证明：在开区间()10，内仅有唯一的一点x ，使得()x x f =．解：（存在性）：令()()x x f x F -=，则函数()x F 在闭区间[]10，上连续，且当[]10，∈x 时，由()10<<x f ，所以，()()0000>-=f F ，()()111-=f F ．因此由连续函数的零点定理，知至少存在一点()10，∈x ，使得()()0=-=x x f x F ．即至少存在一点()10，∈x ，使得()x x f =．（唯一性）：若存在两点()1021，，∈x x ，21x x <，使得()11x x f =， ()22x x f =由Lagrange 中值定理，知至少存在一点1021<<<<x x ξ，使得()()()112121212=--=--='x x x x x x x f x f f ξ 这与题设中任意()10，∈x ，()1≠'x f 相矛盾．因此，在开区间()10，内仅有唯一的一点x ，使得()x x f =．。

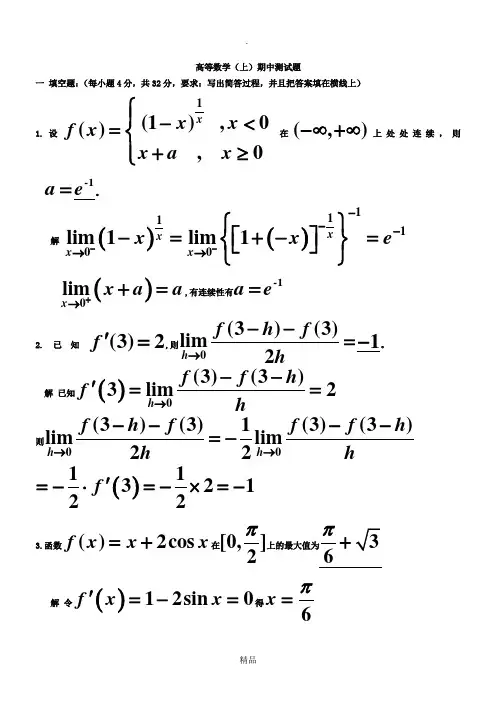
高等数学（上）期中测试题一 填空题：（每小题4分，共32分，要求：写出简答过程，并且把答案填在横线上）1.设1(1),0(),0x x x f x x a x ⎧⎪-<=⎨⎪+≥⎩在(,)-∞+∞上处处连续，则a =-1e。

解()()111100lim 1lim 1xxx x x x e -----→→⎧⎫⎡⎤-=+-=⎨⎬⎣⎦⎩⎭()0lim x x a a +→+=,有连续性有a =-1e2. 已 知 (3)2f '=,则0(3)(3)lim2h f h f h →--=1-。

解 已知()0(3)(3)3lim2h f f h f h→--'== 则00(3)(3)1(3)(3)lim lim 22h h f h f f f h h h →→----=-()1132122f '=-⋅=-⨯=-3.函数()2cos f x x x =+在[0,]2π上的最大值为6π+解 令()12sin 0f x x '=-=得6x π=()026622f f f ππππ⎛⎫⎛⎫==+= ⎪ ⎪⎝⎭⎝⎭则最大值为6π+4. 设5(sin )5(1cos )x t t y t =+⎧⎨=-⎩ ， 则 0t dydx ==0,22t d ydx==120解()05sin 051cos t t t dy dy t dt dx dxt dt======+220t t t dy d dy dx d d y dx dt dx dxdxdt===⎛⎫ ⎪⎛⎫⎝⎭ ⎪⎝⎭==()()()22cos 1cos sin 1cos 151cos 20t t t tt t =+++==+5. 设1(0)xy xx +=>，则y '=()1ln xx x x x ++解 两边取对数有()ln 1ln y x x =+两边关于x 求导得1ln y xx y x'+=+,整理后即得结果 6. 设函数()y y x =由方程cos()0x y xy ++=确定，则dy =sin 11sin y xy dx x xy --。

= 9.
(10分)
2301
3
六. (10分) 设
A
=
2 1 4
−1 1 −6
−1 −2 2
1 1 −2
2 4 4
,
3 6 −9 7 9
求矩阵A的秩, 并求A的一个最高阶非零子式.
解: 对矩阵A作初等行变换将其化为行阶梯形矩阵:
A
=
2 1 4
−1 1 −6
−1 −2 2
1 1 −2
2 4 4
∼
1 0 0
解: 对增广矩阵B = (A, b)作初等行变换将其化为行阶梯形矩阵:
B
=
1+λ 1
1 1+λ
1 1
0 3
∼
1 0
1 λ
1+λ −λ
λ 3−λ
(3分)
1 1 1+λ λ
0 0 −λ(3 + λ) (1 − λ)(3 + λ)
(1) 当λ ̸= 0且λ ̸= 3时, R(A) = R(B) = 3, 方程组有唯一解; (2分)
C. A, B中至少有一个不可逆; D. A + B = O.
4. 设A∗为n阶方阵A的伴随矩阵, 则下列说法不正确的是(C ).
A. 若|A| ̸= 0, 则|A∗| ̸= 0;
B. 若|A| = 10, 则|A∗| = 10n−1;
C. 若R(A) = n − 2, 则A∗ ̸= O;
D. AA∗ = |A|E (其中E 为n阶单位矩阵).
A = EA = (A∗)−1A∗A = (A∗)−10 = 0,
从而与A ̸= 0矛盾. (4分)
(2) 由(1) A ̸= 0, 在A∗A = A E 两侧同时求行列式, A∗ A = A n, 从而 A∗ = A n−1. (3分)

' '' '''
1
1
1
1
1
1
2 1
1
1 48
f ( 1 )
'''
'''
1 48
f ( 2 )
'''
'''
f ( 1 ) f ( 2 ) 48
''' ''' ''' ''' '''
2 | f ( ) | | f ( 1 ) | | f ( 2 ) | | f ( 1 ) f ( 2 ) | 48
dy dx
3
y( x )
由方程
y
2
2 ln y x
4
所确定，则

2x y y 1
2
8．设函数
f ( 2 x ) ln x
，则
f ( x )
1 x
9．曲线
y x e
x
在 x 0 处的切线方程是 y 2 x 1
10．若函数 f ( x ) x 1 在区间[ 1 , 4 ] 上满足拉格朗日中值定理的条件，则定理结论中的ຫໍສະໝຸດ e e 2x

e
x
lim
x
2 2
1 a rc ta n x
1 x
2

2 所以 lim a rc ta n n e n
n

4．设函数
所确定，求
x 1 t y y ( x ) 由参数方程 y cos t 2 d y

《高等数学A（1）》课程期中测试试卷一
命题教师：审核人：适用年级专业：理工类本科
大项
一
二
三
四
Байду номын сангаас总分
统分人
得分
一.计算题
1.求 定义域。（3分）
2.求 （4分）
3.求 （3分）
4．已知当 时， 与 是等价无穷小，求常数 。（4分）
5. 求 （3分）
6．设 则 是 的什么点。（3分）
7.已知 ，求 。（3分）
8.设 ，则 求 （4分）
9.求函数 在点 处的导数。（4分）
10．若 在 处可导,求 , .（5分）
11.已知 ，求 （4分）
12.已知 ，求 。（4分）
13.求曲线 在 处的切线与 轴正方向的夹角。（3分）
14.求曲线 在当 处的切线方程和法线方程。（4分）
15．设 ，求 。（3分）
16.设 可导， ，求 。（3分）
17.求 （3分）
18.求 （3分）
19.求函数 的单调区间和极值。（3分）
20．求曲线 的拐点。（3分）
21.求 （2分）
22.已知 ，求 （4分）
23.求 （3分）
24.求 （3分）
25.计算 （4分）
26. 计算积分 （3分）
27.若 为 的一个原函数，求 。（4分）
二．应用题（8分）
28.某商人如果将进货单价为8元的商品按每件10元售出时，每天可售出100件。 现在他采用提高售出价，减少进货量的办法增加利润，已知这种商品每件提价1元，其销售量就要减少10件，问他将售出价定为多少元时，才能使每天所赚得的利润最大？并求出最大利润。

南京信息工程大学试卷20XX －20XX 学年 第 一 学期 高等代数(上) 课程试卷( A 卷)本试卷共 2 页；考试时间 120 分钟；任课教师 杨兴东 昝立博 ；出卷时间20XX 年12月学院 专业 年级 班 学号 姓名 得分一、填空题（15分）1. 设四阶行列式111222333444a b c d a b c d D a b c d a b c d=，ij A 表示行列式D 的第i 行第j 列元素的代数余子式，则11213141A A A A +++= . 2. 设A 为3阶矩阵，且1||2A =，则1*1()43A A --= . 3. 设123(1,2,3),(3,1,2),(2,3,)t ααα==-=，若123,,ααα线性相关，则t = ． 4. 若A 为n 级实对称阵，并且T AA O =，则A = .5. 设12410113X ⎛⎫⎛⎫= ⎪ ⎪--⎝⎭⎝⎭，则X = .二、选择题（15分）1. 设()2421(1)x Ax Bx -++，则,A B =（ ）(A) 1,2 (B) 1,2- (C) 1,2- (D) 1,2- 2. 设A 为n 阶矩阵，*A 是A 的伴随矩阵，则有（ ）成立(A) *1||||n A A -= (B) *||||n A A = (C) *||||A A = (D) *1||||A A -= 3. 设A 为n 阶方阵，且()r A r n =<，则A 中（ ）. （A ）必有r 个列向量线性无关； （B ）任意r 个列向量线性无关； （C ）任意r 个行向量构成一个极大无关组；（D ）任意一个行向量都能被其他r 个行向量线性表示4. 设,A B 是n 阶方阵，下列结论正确的是（ ） (A) 22()()A B A B A B -=+- (B) ||||AB BA = (C) ||||||A B A B +=+ (D) ||||kA k A =5. ,,A B C 均为n 阶矩阵，E 为n 阶单位矩阵，若ABC E =，则有( ) (A) ACB E = （B ）BAC E = （C ）CAB E = （D ）CBA E = 三、判别下列多项式在有理数域上是否可约. (10分) 1. 65322877221153x x x x x +-+--； 2．771x x -+.四、(10分) 计算行列式1111111111111111111111111xx D x x x++=+++五、(10分) 设021112111A -⎛⎫ ⎪= ⎪ ⎪---⎝⎭，试用两种方法求矩阵A 的逆矩阵.六、(10分) 求向量组123413130110,,,320541510αααα-⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪====⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的秩与一个极大线性无关组，并将其余向量用此极大无关组线性表示.七、(10分) 证明((),())1f x g x =当且仅当(()(),()())1f x g x f x g x += 八、(10分) 讨论λ取何值时，非齐次线性方程组⎪⎩⎪⎨⎧=+++=+++=+++λλλλ321321321)1(3)1(0)1(x x x x x x x x x (1) 无解；(2) 有唯一解；(3) 有无穷多解？有无穷多解时，求其全部解.九、(10分) 已知A 为n 阶矩阵，E 为n 阶单位矩阵，证明：(2)()r A E r A E n -++= 的充要条件是22A A E O --=.20xx-20xx 学年第一学期《高等代数》（上）期末试卷（A 卷）参考答案一、填空题（本题满分15分, 每题3分）1. 0；2. 2；;3. 5；4. O ；5.6713X ⎛⎫= ⎪--⎝⎭.二、选择题（本题满分15分, 每题3分）1. D2. A3. A4. B5. C三、解：1、取p =3，则 ①p 不整除2；②|87p ，72|-p ，21|p ，|15p -，3|-p ； ③2p =9不整除-3，故由艾森斯坦因判别法，()x f 在有理数域上不可约. -------------------5分 2、 令1-=y x ，77()71(1)7(1)1f x x x y y =-+=---+7654327213535217y y y y y y =-+-+-+.取p =7，由艾森斯坦因判别法，()x f 在有理数域上不可约. --------5分四、解: 12511111555551111111111111111111111111111111111111111r r r xx x x x x x x x x x x x x+++++++++++=++++++213141511111111111111110000(5)(5)111110000111110000111110000r r r r r r r r x x x x xx x x x x----+=+=++++ 4(5)x x =+ ------------10分五、解：法一：因为02111220111A -==-≠---，所以A 可逆。

⾼等数学1期中考试试题参考答案《⾼等数学（Ⅰ）》试卷学院：______ 班级：_____学号：________姓名：________任课教师：_____⼀、选择题（每题2分，共16分）1、下列极限存在的是…………………………………………………………( ) （A ）xx 21l i m ∞→（B ） 1310lim -→x x （C ） e x 1l i m ∞→（D ） xx 3lim ∞→2、0)(lim =→x f ax ，∞=→)(lim x g ax ，则下列不正确的是…………………………( )（A ） ∞=+→)]()([lim x g x f ax （B ） ∞=→)]()([lim x g x f ax（C ） 0][lim )()(1=+→x g x f ax （D ） 0)](/)(lim[=→x g x f ax3、,0)(lim >=→A x f ax ,0)(lim <=→B x g ax 则下列正确的是…………………………( )（A ） f (x )>0, （B ） g(x )<0, （C ） f (x )>g (x ) （D ）存在a 的⼀个空⼼邻域，使f (x )g (x )<0。

4、已知， ,2lim )(0=→xx f x 则=→)2x (sin3x 0f x ………………………………………………( )（A ） 2/3, （B ） 3/2 （C ） 3/4 （D ）不能确定。

5、若函数在[1，2]上连续，则下列关于函数在此区间上的叙述，不正确的是……（）（A ）有最⼤值（B ）有界（C ）有零点（D ）有最⼩值6、下列对于函数y =x cos x 的叙述，正确的⼀个是………………………………………( ) （A ）有界，且是当x 趋于⽆穷时的⽆穷⼤，（B ）有界，但不是当x 趋于⽆穷时的⽆穷⼤，（C ）⽆界，且是当x 趋于⽆穷时的⽆穷⼤，（D ）⽆界，但不是当x 趋于⽆穷时的⽆穷⼤。

南京信息工程大学试卷学年 第 1学期 高等数学 课程试卷( B 卷)本试卷共 页；考试时间 120分钟；任课教师 课程组 ；《高等数学A 》考试试卷一．填空题（本题共5小题，每小题4分，共20分）1.设⎩⎨⎧<+≥=0x 1x 0x e f(x) x ，则 f(x)的一个原函数是 .2.曲线12x 11y ++=与x 轴、y 轴和直线4x =所围成的面积是 .3.已知曲线f(x)y =上的任一点f(x))(x,的切线斜率是2x41+，而且曲线经过定点(2,0)，则曲线方程 .4.1x x 12x 4x f(x)234-+++=在Ｒ上的零点有 个.5.已知(1)'' f 存在，且1xdx)f(e lim3x2xx =⎰→，则=(1)'' f .二．选择题（本题共5小题，每小题4分，共20分）1.已知F(x)具有二阶连续导数(x)'F'，则下面正确的是（ ） A.⎰=F(x)dF(x)B. ⎰+=+1]dx (x)'[F'x]dx (x)[F'dC. ⎰+=C F(x)(x)dF'D. ⎰++=+C (x)F'F(x)(x)]dx 'F'(x)[F' 2.=∑=∞→1-n 1i ni 2n e n2lim（ ）A. ⎰2x dx e 2 B. ⎰1x 2dx e 2C. ⎰2 0x2dx e D. ⎰1x 2dx e3.已知F(x)的一阶导数(x)F'在Ｒ上连续，且0F(0)=， 则⎰=0x (t)dt xF'd （ ）A. (x)dx xF'-B. (x)dx xF'C. (x)dx]xF'[F(x)+-D. (x)]dx xF'[F(x)+-4.设f(x)的导数在x=a 处连续，又x a()lim1f x x a→'=--，则 （ ）A.x=a 是f(x)的极小值点B.x=a 是f(x)的极大值点C.(a,f(a))是曲线y=f(x)的拐点D.x=a 不是f(x)的极值点，(a,f(a))也不是曲线y=f(x)的拐 点。

南京信息工程大学试卷学年 第 1学期 高等数学 课程试卷( B 卷)本试卷共 页；考试时间 120分钟；任课教师 课程组 ；一、单项选择题 (本大题有4小题, 每小题4分, 共16分) 1. )(0),sin (cos )(　处有则在设=+=x x x x x f .（A ）(0)2f '= （B ）(0)1f '=（C ）(0)0f '= （D ）()f x 不可导.2. ）时（　，则当，设133)(11)(3→-=+-=x x x x xx βα.（A ）()()x x αβ与是同阶无穷小，但不是等价无穷小； （B ）()()x x αβ与是等价无穷小；（C ）()x α是比()x β高阶的无穷小； （D ）()x β是比()x α高阶的无穷小.3. 若()()()02xF x t x f t dt=-⎰，其中()f x 在区间上(1,1)-二阶可导且'>()0f x ，则（ ）.（A ）函数()F x 必在0x =处取得极大值； （B ）函数()F x 必在0x =处取得极小值；（C ）函数()F x 在0x =处没有极值，但点(0,(0))F 为曲线()y F x =的拐点； （D ）函数()F x 在0x =处没有极值，点(0,(0))F 也不是曲线()y F x =的拐点。

4.)()( , )(2)( )(1=+=⎰x f dt t f x x f x f 则是连续函数，且设（A ）22x （B ）222x+（C ）1x - （D ）2x +.二、填空题（本大题有4小题，每小题4分，共16分） 5. =+→xx x sin 2)31(l i m .6. ,)(cos 的一个原函数是已知x f xx=⋅⎰x xxx f d cos )(则.7.lim(cos cos cos )→∞-+++=22221n n nnn n ππππ .8. =-+⎰21212211arcsin －dx xx x .三、解答题（本大题有5小题，每小题8分，共40分）9. 设函数=()y y x 由方程sin()1x ye xy ++=确定，求'()y x 以及'(0)y .10. .d )1(177x x x x ⎰+-求11. ．　求，， 设⎰--⎪⎩⎪⎨⎧≤<-≤=1 32)(1020)(dx x f x x x x xe x f x12. 设函数)(x f 连续，=⎰10()()g x f xt dt，且→=0()limx f x A x ，A 为常数. 求'()g x 并讨论'()g x 在=0x 处的连续性.13. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、 解答题（本大题10分）14. 已知上半平面内一曲线)0()(≥=x x y y ，过点(,)01，且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和，求此曲线方程. 五、解答题（本大题10分）15. 过坐标原点作曲线x y ln =的切线，该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ；(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V .六、证明题（本大题有2小题，每小题4分，共8分）16. 设函数)(x f 在[]0,1上连续且单调递减，证明对任意的[,]∈01q ，1()()≥⎰⎰qf x d x q f x dx.17. 设函数)(x f 在[]π,0上连续，且0)(0=⎰πx d x f ，0cos )(0=⎰πdx x x f .证明：在()π,0内至少存在两个不同的点21,ξξ，使.0)()(21==ξξf f （提示：设⎰=xdxx f x F 0)()(）解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题（本大题有4小题，每小题4分，共16分）5. 6e . 6.c x x +2)cos (21　.7. 2π. 8.3π.三、解答题（本大题有5小题，每小题8分，共40分） 9. 解：方程两边求导(1)c o s ()()x ye y xy xy y +''+++= cos()()cos()x y x ye y xy y x e x xy +++'=-+0,0x y ==，(0)1y '=- 10. 解：767u x x dx du == 1(1)112()7(1)71u du duu u u u -==-++⎰⎰原式 1(ln ||2ln |1|)7u u c =-++ 7712ln ||ln |1|77x x C =-++11.解：1330()xf x dx xe dx ---=+⎰⎰⎰3()xxd e --=-+⎰⎰00232cos (1sin )x x xe e d x πθθθ----⎡⎤=--+-=⎣⎦⎰　令3214e π=--12. 解：由(0)0f =，知(0)0g =。

চ.
故答案为：B.
【分析】先计算出 茘 চ ，再代入函数从而求出 茘茘. 4．【答案】B
6
【解析】【解答】解：由不等式性质可知，
充分性：若
ྦྷ
t t
，则有 x+y>3，故“
”是“ྦྷ t ”的充分条件，
取
x=-1，y=5，显然
x+y>3，但不满足
ྦྷ
t t
，故“
所以“
ྦྷ
t t
”是 “x+y>3”的充分不必要条件.
所以，ሻ ྦྷ茘 ྦྷ茘ሻ是偶函数，D 正确.
故答案为：D.
ྦྷ চ ྦྷ ，即 ྦྷ 为偶函
【分析】利用函数奇偶性的定义逐项判断，从而得出结论.
11．【答案】B,C,D
【解析】【解答】解：对于 A，
，当 চ 时，方程 ྦྷ
实数 a 的取值可以为 0，故 A 错误；
চ 无解，则 চ ；
对于 B，由题意可知：方程 ྦྷ ྦྷ চ 的解为ྦྷ চ ，ྦྷ চ ，且 a<0，
当 ྦྷ ， 茘时，ྦྷ ， 故答案为：B.
茘， ྦྷ ， 茘，所以 ྦྷ茘 t ，故 A 错误，B 满足题意；
【分析】根据函数的奇偶性以及判断函数的单调性即可求解. 7．【答案】D
7
【解析】【解答】解：对任意的ྦྷ ，ྦྷ ， 茘ྦྷ ྦྷ 茘，不妨设ྦྷ t ྦྷ ，则ྦྷ ྦྷ t ， 又因为ྦྷ ྦྷ 茘 ྦྷ 茘 ྦྷ 茘 t ， 所以 ྦྷ 茘 ྦྷ 茘 t ，则 ྦྷ 茘 t ྦྷ 茘， 所以，函数 ྦྷ茘在 ， 茘上为增函数，
，则 茘茘 চ（ ）
ྦྷ ，ྦྷ t
A．1
B．3
C．
D．
4．“
”是“ྦྷ t ”的（ ）条件.
A．充要 C．必要且不充分

南京信息工程大学试卷学年 第 1学期 高等数学 课程试卷( B 卷)本试卷共 页；考试时间 120分钟；任课教师 课程组 ；一、单项选择题 (本大题有4小题, 每小题4分, 共16分) 1. )(0),sin (cos )(　处有则在设=+=x x x x x f .（A ）(0)2f '= （B ）(0)1f '=（C ）(0)0f '= （D ）()f x 不可导.2. ）时（　，则当，设133)(11)(3→-=+-=x x x x xx βα.（A ）()()x x αβ与是同阶无穷小，但不是等价无穷小； （B ）()()x x αβ与是等价无穷小；（C ）()x α是比()x β高阶的无穷小； （D ）()x β是比()x α高阶的无穷小.3. 若()()()02xF x t x f t dt=-⎰，其中()f x 在区间上(1,1)-二阶可导且'>()0f x ，则（ ）.（A ）函数()F x 必在0x =处取得极大值； （B ）函数()F x 必在0x =处取得极小值；（C ）函数()F x 在0x =处没有极值，但点(0,(0))F 为曲线()y F x =的拐点； （D ）函数()F x 在0x =处没有极值，点(0,(0))F 也不是曲线()y F x =的拐点。

4.)()( , )(2)( )(1=+=⎰x f dt t f x x f x f 则是连续函数，且设（A ）22x （B ）222x+（C ）1x - （D ）2x +.二、填空题（本大题有4小题，每小题4分，共16分） 5. =+→xx x sin 2)31(lim .6.,)(cos 的一个原函数是已知x f xx=⋅⎰x xxx f d cos )(则.7. lim (cos cos cos )→∞-+++=22221L n n n n n n ππππ .8. =-+⎰21212211arcsin －dx xx x .三、解答题（本大题有5小题，每小题8分，共40分）9. 设函数=()y y x 由方程sin()1x ye xy ++=确定，求'()y x 以及'(0)y .10. .d )1(177x x x x ⎰+-求11. ．　求，， 设⎰--⎪⎩⎪⎨⎧≤<-≤=1 32)(1020)(dx x f x x x x xe x f x12. 设函数)(x f 连续，=⎰10()()g x f xt dt，且→=0()limx f x A x ，A 为常数. 求'()g x 并讨论'()g x 在=0x 处的连续性.13. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、 解答题（本大题10分）14. 已知上半平面内一曲线)0()(≥=x x y y ，过点(,)01，且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和，求此曲线方程. 五、解答题（本大题10分）15. 过坐标原点作曲线x y ln =的切线，该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ；(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V .六、证明题（本大题有2小题，每小题4分，共8分）16. 设函数)(x f 在[]0,1上连续且单调递减，证明对任意的[,]∈01q ，1()()≥⎰⎰qf x d x q f x dx.17. 设函数)(x f 在[]π,0上连续，且0)(0=⎰πx d x f ，0cos )(0=⎰πdx x x f .证明：在()π,0内至少存在两个不同的点21,ξξ，使.0)()(21==ξξf f （提示：设⎰=xdxx f x F 0)()(）解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题（本大题有4小题，每小题4分，共16分）5. 6e . 6.c x x +2)cos (21　.7. 2π. 8.3π.三、解答题（本大题有5小题，每小题8分，共40分） 9. 解：方程两边求导(1)cos()()0x ye y xy xy y +''+++=cos()()cos()x y x ye y xy y x e x xy +++'=-+0,0x y ==，(0)1y '=- 10. 解：767u x x dx du == 1(1)112()7(1)71u du duu u u u -==-++⎰⎰原式 1(ln ||2ln |1|)7u u c =-++ 7712ln ||ln |1|77x x C =-++11. 解：1033()x f x dx xe dx ---=+⎰⎰⎰03()x xd e --=-+⎰⎰00232cos (1sin )x xxe e d x πθθθ----⎡⎤=--+-=⎣⎦⎰令3214e π=--12. 解：由(0)0f =，知(0)0g =。

高等数学（上）期中考试试卷1 高等数学（上）期中考试试卷1一、选择题（每题5分，共30分）1. 设函数f(x) = 2x^3 + ax^2 + bx + 3，若f(x)的导函数为f'(x) = 6x^2 + 2ax + b，则a的值为（）A. 2B. -2C. 3D. -32. 函数y = x^3 - 3x^2 + 2x + k的图像必经过的点为（）A. (-1, -1)B. (1, -1)C. (2, 2)D. (-2, 2)3. 设函数y = e^x + a，若a = 1，求y在x = 0处的切线方程为（）A. y = x + 2B. y = 2x + 1C. y = x + 1D. y = 2x + 24. 函数y = a^x在点(0, b)处的切线方程为y = x + 1，求a和b的值。

A. a = 1, b = 1B. a = e, b = eC. a = 2, b = 2D. a = e, b = 15. 函数y = ln(x)在点(1, 0)处的切线方程为y = 2x - 2，求曲线在x = 1处的切线方程。

A. y = xB. y = x - 1C. y = 2x - 1D. y = 2x6. 函数y = cos(x)在区间[0, π/2]上的最小值为（）A. -1B. -√2/2C. -1/2D. 0二、计算题（共70分）1. 求函数y = 2x^3 - 3x^2 + 4x在区间[0, 2]上的定积分。

2. 求曲线y = x^2 - 2x的长度。

3. 求函数y = 2x^3 - 3x^2 + 4x的最大值和最小值，并求出取得最大值和最小值的点。

4. 求函数y = ln(x)与y = x的交点坐标。

5. 已知函数y = e^x满足条件∫(1, a) y dx = 5，求a的值。

6. 求函数y = x^2 - 2在区间[-2, 2]上的平均值。

三、证明题（共20分）1. 设函数f(x) = x^3 - 3x + 4，证明f(x)在区间[-1, 1]上有且仅有一个零点。

南京信息工程大学试卷学年 第 1学期 高等数学 课程试卷( B 卷)本试卷共 页；考试时间 120分钟；任课教师 课程组 ；一、单项选择题 (本大题有4小题, 每小题4分, 共16分) 1.)(0),sin (cos )(　处有则在设=+=x x x x x f .（A ）(0)2f '= （B ）(0)1f '=（C ）(0)0f '= （D ）()f x 不可导.2.　）时（　，则当，设133)(11)(3→-=+-=x x x x xx βα.（A ）()()x x αβ与是同阶无穷小，但不是等价无穷小； （B ）()()x x αβ与是等价无穷小；（C ）()x α是比()x β高阶的无穷小； （D ）()x β是比()x α高阶的无穷小.3. 若()()()02xF x t x f t dt=-⎰，其中()f x 在区间上(1,1)-二阶可导且'>()0f x ，则（ ）.（A ）函数()F x 必在0x =处取得极大值； （B ）函数()F x 必在0x =处取得极小值；（C ）函数()F x 在0x =处没有极值，但点(0,(0))F 为曲线()y F x =的拐点； （D ）函数()F x 在0x =处没有极值，点(0,(0))F 也不是曲线()y F x =的拐点。

4.)()( , )(2)( )(10=+=⎰x f dt t f x x f x f 则是连续函数，且设（A ）22x （B ）222x +（C ）1x - （D ）2x +.二、填空题（本大题有4小题，每小题4分，共16分） 5. =+→xx x sin 2)31(lim .6. ,)(cos 的一个原函数是已知x f x x =⋅⎰x x xx f d cos )(则 .7.lim(cos cos cos )→∞-+++=22221n n nnnn ππππ .8.=-+⎰21212211arcsin －dx xx x .三、解答题（本大题有5小题，每小题8分，共40分）9. 设函数=()y y x 由方程sin()1x y e xy ++=确定，求'()y x 以及'(0)y .10. .d )1(177x x x x ⎰+-求11.．　求，， 设⎰--⎪⎩⎪⎨⎧≤<-≤=132)(1020)(dx x f x x x x xe x f x12.设函数)(x f 连续，=⎰1()()g x f xt dt，且→=0()limx f x A x ，A 为常数. 求'()g x 并讨论'()g x 在=0x 处的连续性.13.求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、 解答题（本大题10分）14. 已知上半平面内一曲线)0()(≥=x x y y ，过点(,)01，且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和，求此曲线方程.五、解答题（本大题10分）15. 过坐标原点作曲线x y ln =的切线，该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ；(2) 求D 绕直线x = e 旋转一周所得旋转体的体积六、证明题（本大题有2小题，每小题4分，共8分）16. 设函数)(x f 在[]0,1上连续且单调递减，证明对任意的[,]∈01q ，1()()≥⎰⎰qf x d x q f x dx.17. 设函数)(x f 在[]π,0上连续，且0)(0=⎰πx d x f ，0cos )(0=⎰πdx x x f .证明：在()π,0内至少存在两个不同的点21,ξξ，使.0)()(21==ξξf f （提示：设⎰=xdxx f x F 0)()(）解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题（本大题有4小题，每小题4分，共16分）5. 6e . 6.c x x +2)cos (21　.7. 2π. 8.3π.三、解答题（本大题有5小题，每小题8分，共40分） 9. 解：方程两边求导(1)cos()()0x y e y xy xy y +''+++= cos()()cos()x y x ye y xy y x e x xy +++'=-+0,0x y ==，(0)1y '=-10. 解：767u x x dx du == 1(1)112()7(1)71u du duu u u u -==-++⎰⎰原式1(ln ||2ln |1|)7u u c =-++ 7712ln ||ln |1|77x x C =-++11. 解：1033()xf x dx xe dx ---=+⎰⎰⎰3()xxd e --=-+⎰⎰00232cos (1sin )x xxe e d x πθθθ----⎡⎤=--+-=⎣⎦⎰令3214e π=--12. 解：由(0)0f =，知(0)0g =。