初中阶段函数及图像
- 格式:docx
- 大小:63.42 KB
- 文档页数:7


初中高中数学七大函数的性质图像1.一次函数(包括正比例函数)最简单最常见的函数,在平面直角坐标系上的图象为直线。
定义域(下面没有说明的话,都是在无特殊要求情况下的定义域):R值域:R奇偶性:无周期性:无平面直角坐标系解析式(下简称解析式):①ax+by+c=0[一般式]②y=kx+b[斜截式](k为直线斜率,b为直线纵截距,正比例函数b=0)③y-y1=k(x-x1)[点斜式](k为直线斜率,(x1,y1)为该直线所过的一个点)④(y-y1)/(y2-y1)=(x-x1)/(x2-x1)[两点式]((x1,y1)与(x2,y2)为直线上的两点)⑤x/a-y/b=0[截距式](a、b分别为直线在x、y轴上的截距)解析式表达局限性:①所需条件较多(3个);②、③不能表达没有斜率的直线(平行于x轴的直线);④参数较多,计算过于烦琐;⑤不能表达平行于坐标轴的直线和过圆点的直线。
倾斜角:x轴到直线的角(直线与x轴正方向所成的角)称为直线的倾斜角。
设一直线的倾斜角为a,则该直线的斜率k=tg(a)。
2.二次函数:题目中常见的函数,在平面直角坐标系上的图象是一条对称轴与y轴平行的抛物线。
定义域:R值域:(对应解析式,且只讨论a大于0的情况,a小于0的情况请读者自行推断)①[(4ac-b^2)/4a,正无穷);②[t,正无穷)奇偶性:偶函数周期性:无解析式:①y=ax^2+bx+c[一般式]⑴a≠0⑵a>0,则抛物线开口朝上;a<0,则抛物线开口朝下;⑶极值点:(-b/2a,(4ac-b^2)/4a);⑷Δ=b^2-4ac,Δ>0,图象与x轴交于两点:([-b+√Δ]/2a,0)和([-b+√Δ]/2a,0);Δ=0,图象与x轴交于一点:(-b/2a,0);Δ<0,图象与x轴无交点;②y=a(x-h)^2+t[配方式]此时,对应极值点为(h,t),其中h=-b/2a,t=(4ac-b^2)/4a);3.反比例函数在平面直角坐标系上的图象为双曲线。





一次函数的图象和性质一、知识要点:1、一次函数:若两个变量x,y存在关系为y=kx+b (k≠0, k,b为常数)的形式,则称y是x的函数。
注意:(1)k≠0,否则自变量x的最高次项的系数不为1;(2)当b=0时,y=kx,y叫x的正比例函数。
2、图象:一次函数的图象是一条直线(1)两个常有的特殊点:与y轴交于(0,b);与x轴交于(- ,0)。
(2)正比例函数y=kx(k≠0)的图象是经过(0,0)和(1,k)的一条直线;一次函数y=kx+b(k≠0)的图象是经过(- ,0)和(0,b)的一条直线。
(3)由图象可以知道,直线y=kx+b与直线y=kx平行,例如直线:y=2x+3与直线y=2x-5都与直线y=2x平行。
3、一次函数图象的性质:(1)图象在平面直角坐标系中的位置:(2)增减性:k>0时,y随x增大而增大;k<0时,y随x增大而减小。
4、求一次函数解析式的方法求函数解析式的方法主要有三种:一是由已知函数推导,如例题1;二是由实际问题列出两个未知数的方程,再转化为函数解析式,如例题4的第一问。
三是用待定系数法求函数解析式,如例2的第二小题、例7。
其步骤是:①根据题给条件写出含有待定系数的解析式;②将x、y的几对值或图象上几个点的坐标代入上述的解析式中,得到以待定系数为未知数的方程或方程组;③解方程,得到待定系数的具体数值;④将求出的待定系数代入要求的函数解析式中。
二、例题举例:例1、已知变量y与y1的关系为y=2y1,变量y1与x的关系为y1=3x+2,求变量y与x的函数关系。
分析:已知两组函数关系,其中共同的变量是y1,所以通过y1可以找到y与x 的关系。
解:∵y=2y1y1=3x+2,∴y=2(3x+2)=6x+4,即变量y与x的关系为:y=6x+4。
例2、解答下列题目(1)(甘肃省中考题)已知直线与y轴交于点A,那么点A的坐标是()。
(A)(0,–3)(B)(C)(D)(0,3)(2)(杭州市中考题)已知正比例函数,当x=–3时,y=6.那么该正比例函数应为()。
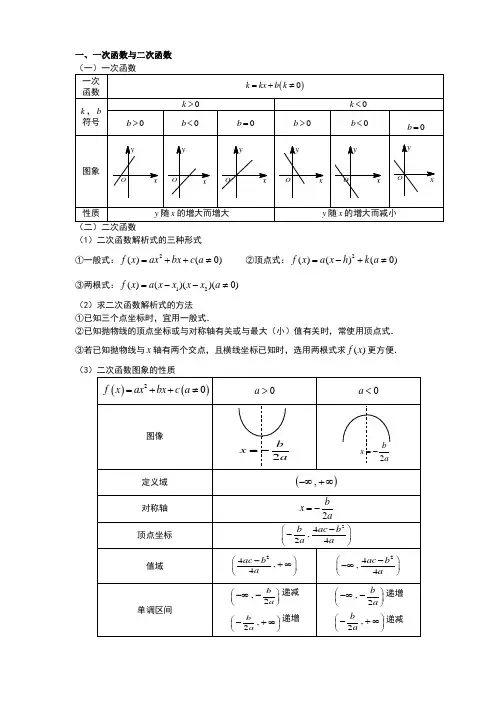
一、一次函数与二次函数(1)二次函数解析式的三种形式①一般式:2()(0)f x ax bx c a =++≠ ②顶点式:2()()(0)f x a x h k a =-+≠ ③两根式:12()()()(0)f x a x x x x a =--≠(2)求二次函数解析式的方法①已知三个点坐标时,宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式. ③若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便. (3①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为,2bx a=-顶点坐标是24(,)24b ac b a a--②当0a >时,抛物线开口向上,函数在(,]2b a -∞-上递减,在[,)2b a-+∞上递增,当2bx a =-时,2min 4()4ac b f x a -=;当0a <时,抛物线开口向下,函数在(,]2b a -∞-上递增,在[,)2b a -+∞上递减,当2b x a=-时,2max 4()4ac b f x a -=.二、幂函数(1)幂函数的定义一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数. (2)幂函数的图象过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1).(1)根式的概念:如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是:1()0,,,m m nn a a m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. (3)运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈(1)对数的定义: ①若(0,1)x a N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数. ②负数和零没有对数.③对数式与指数式的互化: log (0,1,0)xa x N a N a a N =⇔=>≠>. (2)几个重要的对数恒等式: log 10a =,log 1a a =,log ba ab =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a aM M N N-= ③数乘:log log ()na a n M M n R =∈ ④log a N a N =⑤log log (0,)b n a a nM M b n R b =≠∈⑥换底公式:log log (0,1)log b a b N N b b a =>≠且 (5)对数函数五、反函数(1)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x f y -=,习惯上改写成1()y fx -=.(2)反函数的求法①确定反函数的定义域,即原函数的值域; ②从原函数式()y f x =中反解出1()x f y -=;③将1()x fy -=改写成1()y f x -=,并注明反函数的定义域.(3)反函数的性质①原函数()y f x =与反函数1()y f x -=的图象关于直线y x =对称. ②函数()y f x =的定义域、值域分别是其反函数1()y fx -=的值域、定义域.③若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y f x -=的图象上.④一般地,函数()y f x =要有反函数则它必须为单调函数.六、三角函数的图像和性质(一)正弦与余函数的图像与性质 函数 x y sin =x y cos =图像定域义 RR值域 []1,1-[]1,1-最值2,1 22,1 2x k y k Zx k y k Zππππ=+=∈=-+=-∈最大最小时,时,2, 1 2,1x k y k Zx k y k Z πππ==∈=+=-∈最大最小时,时,单调性[2,2]223[2,2]22Zk k k k k ππππππππ-++++∈在每个上递增在每个上递减[2,2][2,2] Zk k k k k ππππππ-++∈在每个上递增在每个上递减奇偶性 奇函数偶函数周期性 是周期函数,2π为最小正周期 是周期函数,2π为最小正周期 对称性对称中心(,0)k π,:,()2x k k Z ππ=+∈对称轴 对称中心(,0)2k ππ+,:,()x k k Z π=∈对称轴2. 正切与余切函数的图像与性质函数 x y tan = x y cot =图像定域义 {|,}2x x R x k k Z ππ∈≠+∈且 {|,}x x R x k k Z ππ∈≠+∈且值域 RR单调性(,)22Zk k k ππππ-++∈在每个上递增(,) Zk k k πππ+∈在每个上递减奇偶性 奇函数奇函数周期性 是周期函数,π为最小正周期 是周期函数,π为最小正周期 对称性对称中心(,0)2k π 对称中心(,0)2k π七、反三角函数的图像与性质1. 反正弦与反余函数的图像与性质函数反正弦函数arcsin y x =是sin ,22y x x ππ⎡⎤=∈-⎢⎥⎣⎦,的反函数反余弦函数arccos y x =是[]cos 0,y x x π=∈,的反函数图像定域义 []1,1-[]1,1-值域 ,22ππ⎡⎤-⎢⎥⎣⎦[]0,π 单调性 [1,1]-+在上递增[1,1]-+在上递减奇偶性 奇函数 非奇非偶 周期性 无 无对称性对称中心(0,0)对称中心(0,)2π2. 反正切与反余切函数的图像与性质 函数反正切函数arctan y x = 是tan (,)22y x x ππ=∈-,的反函数反余切函数arccot y x = 是()cot 0,y x x π=∈,的反函数图像定域义 (,,)-∞+∞(,,)-∞+∞值域,22ππ⎛⎫- ⎪⎝⎭ ()0,π。



初中数学函数大全文档编制序号:[KK8UY-LL9IO69-TTO6M3-MTOL89-FTT688]初中数学函数大全(分类I、与定义式:自x变量y关系:y=kx+b(kb数k≠0)则称yx函数特别b=0yx比例函数II、:y变化值与应x变化值比例k即△y/△x=kIII、函数及性质:1.作与:通3(1)列表(般找4-6点);(2)描点;(3)连线作函数图象(用平滑连接)2.性质:函数图象任意点P(xy)都满足:y=kx+b3.kb与函数图象所k>0直线必通、三象限y随x增增;k<0直线必通二、y随x增减b>0直线必通、二象限;b<0直线必通三、四象限特别b=0直线通O(00)表示比例函数图象k>0直线通、三象限;k<0直线通二、四象限IV、确定函数:已知点A(x1y1);B(x2y2)请确定点A、表达式(1)设函数表达式(叫)y=kx+b(2)函数任意点P(xy)都满足等式y=kx+b所列2程:y1=kx1+b①y2=kx2+b②(3)解二元程kb值(4)函数表达式V、y=kx+b,两必定经(0,b)(-b/k,0)VI、函数应用1.间t定距离s速度v函数s=vt2.水池抽水速度f定水池g抽水间设水池量Sg=S-ft反比例函数形y=k/x(k数且k≠0)函数叫做自变量x等于0切实数反比例图面给k别负(2-2)函数图像二函数般自变量x变量y间存关系:y=ax^2+bx+c(a≠0)(abc数a≠0且a决定函数口向a>0口向向a<0口向向IaI决定口,IaI越口越,IaI越口越)则称yx二函数二函数表达式通二三项式x自变量yx函数二函数三种表达式般式:y=ax^2+bx+c(abc数a≠0)顶点式:y=a(x-h)^2+k[抛物线顶点P(hk)]于二函数y=ax^2+bx+c其顶点坐标(-b/2a,(4ac-b^2)/(4a))交点式:y=a(x-x?)(x-x?)[仅限于与x轴交点A(x?0)B(x?0)抛物线]其x12=(-b±√(b^2-4ac))/(2a)注:3种互相转化关系:______h=-b/(2a)k=(4ac-b^2)/(4a)x?,x?=(-b±√b^2-4ac)/2a二函数图像平面直角坐标系作二函数y=x^2二函数看二函数图像条抛物线二函数标准画步骤()(1)列表(2)描点(3)连线抛物线性质1.抛物线轴称图形称轴直线x=-b/2a称轴与抛物线唯交点抛物线顶点P特别b=0抛物线称轴y轴(即直线x=0)2.抛物线顶点P坐标P(-b/2a(4ac-b^2)/4a)-b/2a=0Py轴;Δ=b^2-4ac=0Px轴3.二项a决定抛物线口向a>0抛物线;a<0抛物线向口|a|越则抛物线口越4.项系数b二项系数a共同决定称轴位置a与b(即ab>0)称轴y轴左;a与b异号(即ab<0)称轴y轴右5.数项c决定抛物线与y轴交点抛物线与y轴交于(0c)6.抛物线与x轴交Δ=b^2-4ac>0抛物线与x轴2交点Δ=b^2-4ac=0抛物线与x轴1交点_______Δ=b^2-4ac<0抛物线与x轴没交点X取值(x=-b±√b^2-4ac值相反数乘虚数i除2a)a>0函数x=-b/2a处取值f(-b/2a)=4ac-b^2/4a;{x|x<-b/2a}{x|x>-b/2a};抛物线口向;函数{x|x≥4ac-b^2/4a}相反变b=0抛物线称轴y轴函数解析式变形y=ax^2+c(a≠0)二函数与元二程特别二函数(称函数)y=ax^2+bx+cy=0二函数关于x元二程(称程)即ax^2+bx+c=0函数图像与x轴交点即程函数与x轴交点即1.二函数y=ax^2y=a(x-h)^2y=a(x-h)^2+ky=ax^2+bx+c(各式a≠0)图象相同位置同顶点坐标及称轴表:解析式y=ax^2y=a(x-h)^2y=a(x-h)^2+ky=ax^2+bx+c顶点坐标(00)(h0)(hk)(-b/2a(4ac-b^2)/4a)称轴x=0x=hx=hx=-b/2ah>0y=a(x-h)^2图象由抛物线y=ax^2平行移h单位h<0则平行移|h|单位.h>0,k>0抛物线y=ax^2向右平行移h单位再向移k单位y=a(x-h)^2+k图象;h>0,k<0抛物线y=ax^2向右平行移h单位再向移|k|单位y=a(x-h)^2+k图象; h<0,k>0抛物线向左平行移|h|单位再向移k单位y=a(x-h)^2+k图象;h<0,k<0抛物线向左平行移|h|单位再向移|k|单位y=a(x-h)^2+k图象;研究抛物线y=ax^2+bx+c(a≠0)图象般式化y=a(x-h)^2+k形式确定其顶点坐标、称轴抛物线体位置清楚.给画图象提供便.2.抛物线y=ax^2+bx+c(a≠0)图象:a>0口向a<0口向称轴直线x=-b/2a顶点坐标(-b/2a[4ac-b^2]/4a).3.抛物线y=ax^2+bx+c(a≠0)若a>0x≤-b/2ay随x增减;x≥-b/2ay随x增增.若a<0x≤-b/2ay随x增增;x≥-b/2ay随x增减.4.抛物线y=ax^2+bx+c图象与交点:(1)图象与y轴定相交交点坐标(0c);(2)△=b^2-4ac>0图象与x轴交于两点A(x?0)B(x?0)其x1,x2元二程ax^2+bx+c=0(a≠0)两根.两点间距离AB=|x?-x?|另外抛物线任何称点距离由|2×(-b/2a)-A|(A其点)△=0.图象与x轴交点;△<0.图象与x轴没交点.a>0图象落x轴x任何都y>0;a<0图象落x轴x任何实数都y<0.5.抛物线y=ax^2+bx+c值:a>0(a<0)则x=-b/2ay()值=(4ac-b^2)/4a.顶点横坐标取值自顶点值取值.6.用待定系数求二(1)题给条件已知图象经三已知点或已知x、y三应值设解析式般形式:y=ax^2+bx+c(a≠0).(2)题给条件已知图象顶点坐标或称轴设解析式顶点式:y=a(x-h)^2+k(a≠0).(3)题给条件已知图象与x轴两交点坐标设解析式两:y=a(x-x?)(x-x?)(a≠0).7.二函数知识容易与其知识综合应用形较复杂综合二函数知识主综合性题目考热点往往题形式现.。
函数知识点总结(掌握函数的定义、性质和图像)平面直角坐标系1、定义:平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系2、各个象限内点的特征:第一象限:(+,+) 第二象限:(-,+) 第三象限:(-,-) 第四象限:(+,-)3、坐标轴上点的坐标特征:x 轴上的点,y 为零;y 轴上的点,x 为零;原点的坐标为(0 , 0)。
4、点的对称特征:已知点P(m,n),关于x 轴的对称点坐标是(m,-n), 横坐标相同,纵坐标反号 关于y 轴的对称点坐标是(-m,n) 纵坐标相同,横坐标反号 关于原点的对称点坐标是(-m,-n) 横,纵坐标都反号 5、平行于坐标轴的直线上的点的坐标特征:平行于x 轴的直线上的任意两点:纵坐标相等; 平行于y 轴的直线上的任意两点:横坐标相等。
6、各象限角平分线上的点的坐标特征:第一、三象限角平分线上的点横、纵坐标相等。
第二、四象限角平分线上的点横、纵坐标互为相反数。
7、点P (x,y )的几何意义:点P (x,y )到x 轴的距离为 |y|,点P (x,y )到y 轴的距离为 |x|。
点P (x,y )到坐标原点的距离为22y x +8、两点之间的距离:X 轴上两点为A )0,(1x 、B )0,(2x |AB|||12x x -= Y 轴上两点为C ),0(1y 、D ),0(2y |CD|||12y y -=已知A ),(11y x 、B ),(22y x AB|=212212)()(y y x x -+-9、中点坐标公式:已知A ),(11y x 、B ),(22y x M 为AB 的中点,则:M=(212x x + , 212y y +) 10、点的平移特征: 在平面直角坐标系中,将点(x,y )向右平移a 个单位长度,可以得到对应点( x-a ,y ); 将点(x,y )向左平移a 个单位长度,可以得到对应点(x+a ,y ); 将点(x,y )向上平移b 个单位长度,可以得到对应点(x ,y +b ); 将点(x,y )向下平移b 个单位长度,可以得到对应点(x ,y -b )。
一、一次函数与二次函数(1)二次函数解析式的三种形式①一般式:2()(0)f x ax bx c a =++≠ ②顶点式:2()()(0)f x a x h k a =-+≠ ③两根式:12()()()(0)f x a x x x x a =--≠(2)求二次函数解析式的方法①已知三个点坐标时,宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式. ③若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便. (3①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为,2bx a=-顶点坐标是24(,)24b ac b a a--②当0a >时,抛物线开口向上,函数在(,]2b a -∞-上递减,在[,)2b a-+∞上递增,当2bx a =-时,2min 4()4ac b f x a -=;当0a <时,抛物线开口向下,函数在(,]2b a -∞-上递增,在[,)2b a -+∞上递减,当2b x a=-时,2max 4()4ac b f x a -=.二、幂函数(1)幂函数的定义一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数. (2)幂函数的图象过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1).(1)根式的概念:如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是:1()0,,,m m nn a a m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. (3)运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈(1)对数的定义: ①若(0,1)x a N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数. ②负数和零没有对数.③对数式与指数式的互化: log (0,1,0)xa x N a N a a N =⇔=>≠>. (2)几个重要的对数恒等式: log 10a =,log 1a a =,log ba ab =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a aM M N N-= ③数乘:log log ()na a n M M n R =∈ ④log a N a N =⑤log log (0,)b n a a nM M b n R b =≠∈ ⑥换底公式:log log (0,1)log b a bN N b b a =>≠且 (5)对数函数五、反函数(1)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x f y -=,习惯上改写成1()y fx -=.(2)反函数的求法①确定反函数的定义域,即原函数的值域; ②从原函数式()y f x =中反解出1()x f y -=;③将1()x fy -=改写成1()y f x -=,并注明反函数的定义域.(3)反函数的性质①原函数()y f x =与反函数1()y f x -=的图象关于直线y x =对称. ②函数()y f x =的定义域、值域分别是其反函数1()y fx -=的值域、定义域.③若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y f x -=的图象上.④一般地,函数()y f x =要有反函数则它必须为单调函数.六、三角函数的图像和性质(一)正弦与余函数的图像与性质 函数 x y sin =x y cos =图像定域义 RR值域 []1,1-[]1,1-最值2,1 22,1 2x k y k Zx k y k Zππππ=+=∈=-+=-∈最大最小时,时,2, 1 2,1x k y k Zx k y k Z πππ==∈=+=-∈最大最小时,时, 单调性[2,2]223[2,2]22k k k k ππππππππ-++++在每个上递增在每个上递减[2,2][2,2] k k k k ππππππ-++在每个上递增在每个上递减奇偶性 奇函数偶函数周期性 是周期函数,2π为最小正周期 是周期函数,2π为最小正周期 对称性对称中心(,0)k π,:,()2x k k Z ππ=+∈对称轴 对称中心(,0)2k ππ+,:,()x k k Z π=∈对称轴2. 正切与余切函数的图像与性质函数 x y tan = x y cot =图像定域义 {|,}2x x R x k k Z ππ∈≠+∈且 {|,}x x R x k k Z ππ∈≠+∈且值域 RR单调性(,)22Zk k k ππππ-++∈在每个上递增(,) Zk k k πππ+∈在每个上递减奇偶性 奇函数奇函数周期性 是周期函数,π为最小正周期 是周期函数,π为最小正周期 对称性对称中心(,0)2k π 对称中心(,0)2k π七、反三角函数的图像与性质1. 反正弦与反余函数的图像与性质函数反正弦函数arcsin y x =是sin ,22y x x ππ⎡⎤=∈-⎢⎥⎣⎦,的反函数反余弦函数arccos y x =是[]cos 0,y x x π=∈,的反函数图像定域义 []1,1-[]1,1-值域 ,22ππ⎡⎤-⎢⎥⎣⎦[]0,π 单调性 [1,1]-+在上递增[1,1]-+在上递减奇偶性 奇函数 非奇非偶 周期性 无 无对称性对称中心(0,0)对称中心(0,)2π2. 反正切与反余切函数的图像与性质 函数反正切函数arctan y x = 是tan (,)22y x x ππ=∈-,的反函数反余切函数arccot y x = 是()cot 0,y x x π=∈,的反函数图像定域义 (,,)-∞+∞(,,)-∞+∞值域 ,22ππ⎛⎫- ⎪⎝⎭ ()0,π单调性 (,,)-∞+∞在上递增(,,)-∞+∞在上递减奇偶性 奇函数 非奇非偶 周期性 无无对称性 对称中心(0,0)对称中心(0,π/2)。
函数及图象、学习的目标:掌握正、反比例、一次函数、二次函数的图象及性质 、知识点归纳:1、 平面直角坐标系: 平面内两条有公共原点且互相垂直的数轴构成了平面直角坐标系,坐标平面内一点对 应的有序实数对叫做这点的坐标•在平面内建立了直角坐标系,就可以把“形” (平面内的点)和(有序实数对)紧密结合起来.2、 函数的概念:设在某个变化过程中有两个变量 x 、y ,如果对于x 在某一范围内的每一个确定的值,有唯一确定的值与它相对应,那么就说 y 是x 的函数,x 叫做自变量.3、 自变量的取值范围: 对于实际问题,自变量取值必须使实际问题有意义.对于纯数学问题,自变量取值 应保证数学式子有意义. 4、 正比例函数:如果y = kx (k 是常数,k 丰0),那么,y 叫做x 的正比例函数.5、 正比例函数 y = kx 的图象:过(0, 0), (1, K )两点的一条直线.6、 正比例函数y = kx 的性质(1 )当k > 0时,y 随x 的增大而增大 (2 )当k v 0时,y 随x 的增大而减小 7、 反比例函数及性质園数y =悬常数,此工0)叫做反比例函数。
X(1) 当k >0时,在每个象限内分别是 y 随x 的增大而减小; (2) 当k v 0时,在每个象限内分别是 y 随x 的增大而增大.8、 一次函数如果y = kx + b ( k , b 是+常数,k 丰0),那么y 叫做x 的一次函数.9、 一次函数y = kx + b 的图象—系钦特征国飲特征不疑过的象限图例k>ob>0 青銭从左 到右取向上方 向 直銭与y 轴 的交点M (0, IQ 在N 轴上 四h<0 右£就轴下片k<0b>0克談从左 到右取冋 直钱与F 轴 的宏点 M(o a b)在用铀上 方M |Xy——Xb<0柱M 轴下 ■10克递記詡艮卫瑟社二匹象眼1过的一条直线。
k(1 )当k > 0时,y 随x 的增大而增大; (2 )当k v 0时,y 随x 的增大而减小.(1) 函数y = ax 2 + bx + c (其中a 、b 、c 是常数,且a 0)叫做的二次函数.2(2) 禾ij 用配方,可以把二次函数表示成 y = a (x + b ) 2 + 4ac b 或y = a (x — h ) 2 + k 的形式2a 4a (3) 二次函数的图象是抛物线,当 a >0时抛物线的开口向上,当a v 0时抛物线开口向下.抛物线的对称轴是直线 x =— 2或x = h2a(4) 抛物线的顶点是(一_b , 4ac b )或(h, k )2a4a•、选择题: 1 .函数y 'x 1中,自变量x 的取值范围是()A . x v 1 B. x > 1C . x > 1D. x 丰 1 2.在函数..中,自变量的取值范围是()x-lA.二 一 :B. -C.-■< D. 飞 v I3 .在函数y 5 中,自变量x 的取值范围是() J x 3A 、 x > 3B 、x 工 3C 、 x > 3D、x v 34.点 P (—1, 2)关于 y 轴对称的点的坐标是().A . (1, 2: )B • (— 1, 2) c . (1,— 2) D . (— 1,— 2)5.点 M (1 , 2) 关于x 轴对称点的坐标为( )A、 (—1, 2) E I 、(— 1, — 2) C 、 (1 ,— 2) D (2,— 1)6 .在直角坐标系中,点’1;'一定在( )A. 抛物线匸—'上B. 双曲线 上C.直线「二厂上D.直线丁二- ■■上4*411. 为解决药价虚高给老百姓带来的求医难的问题,国家决定对某药品分两次降价.若设平均每次降 价的百分率为x ,该药品的原价是 m 元,降价后的价格是 y 元,贝U y 与x 的函数关系式是(2A 、y = 2m (1 — x )B 、y = 2m (1 + x )C 、y = m (1 — x ) 13 . 一辆汽车由淮安匀速驶往南京,下列图象中,能大致反映汽车距南京的路程间t (小时)的关系的是()15、关于函数y 2x1,下列结论正确的是(A . 2s1、sOtAO14、某小工厂现在年产值 是( ) A . y 150x 20 tt150万元,计划今后每年增加y 15 2x C20万元,年产值y (万元)与年数x 的函数关系式.y 150 20x D . y 20xA 、图象必经过点(- 2, 1)、图象经过第一、二、三象限 C 、当x 1时,y216、一次函数y = ax + b 的图像如图所示,则下面结论中正确的是 、y 随x 的增大而增大A . a v 0, b v 0B . a v 0, C. a >0, b >0 D . a > 0,17、若反比例函数A.k 工0xB.k 工3C.k v 3D.k > 318、函数y1的图象与坐标轴围成的三角形的面积是(7.若反比例函数y 兰(kx0)的图象经过点(一1, 2),则k 的值为2 函数y = — x + 3的图象经过( 第一、二、三象限 B 、第一■、 .函数y = 2x — 1的图象不经过( A 、 B.第二象限 ) 三、四象限 )C .第三象限第二、三、四象限 D 、第一、二、四象限D.第四象限10 、如图所示,函数x 2的图象最可能是(、y = m (1 + x )2 s (千米)和行驶时19、 抛物线y -X x 4的对称轴是()4A 、x =— 2B 、x = 2C 、x =— 4 20、 抛物线y = 2(x — 3)2的顶点在()A 、第一象限B 、第二象限C 、x 轴上、填空题: 1. 抛物线yX? 2x 3与x 轴分别交A B 两点,贝y AB 的长为3•若反比例函数y 巴图象经过点A (2 , — 1),贝U k= _________ .x4.若将二次函数 y = x 2 — 2x + 3配方为y = (x — h )2+ k 的形式,则y= ____________ 5•若反比例函数y k 的图象过点(3,— 4),则此函数的解析式为 y —x6. ______________________________________________ 函数y _J —的自变量x 的取值范围是 .2x 37. 写出一个图象经过点 (1,一 1)的函数解析式: _______________________ &已知一次函数 y 2x b ,当x = 3时,y = 1,贝U b = _________________14 .函数y =豎-:中自变量x 的取值范围是 ___________n =、解答题:1、求下列函数中自变量 x 的取值范围:/ 八 5x 7 (1) y =2(2) y = x — x — 2; (3) y = ;(4) y = -:f x 324x 8解:(1) _______________________________________________________________________(2) ______________________________________________________________________ (3) _____________________________________________________________________3的图象在每一象限内,y 随x 的增大而增大,则有( )D D.、x = 4 、y 轴上2. y直线2 1x3 2不经过第_______ 象限. 10. 函数y ax b 的图像如图所示,贝U y 随x 的增大而.11. 反比例函数 y 5的图像在 x象限.12. 函数 y 3x 24x 5中自变量x 的取值范围是 .2x 113. 当k =时,反比例函数yk(x 0)的图象在第一象限15.若正比例函数 y = mx (m z 0)和反比例函数y = n (n 丰0)的图象都经过点(2 , 3),贝U m =x9.已知点P (— 2, 3),则点P 关于x 轴对称的点坐标是( ___ , _____ ).(只需填一个数)(4) _____________________________________________________________________2、分别写出下列各问题中的函数关系式及自变量的取值范围:(1)某市民用电费标准为每度 0.50元,求电费y (元)关于用电度数 x 的函数关系式;数关系式;(3)在一个半径为10 cm 的圆形纸片中剪去一个半径为 r (cm )的同心圆,得到一个圆环 .设圆环的 面积为S (cm 2),求S 关于r 的函数关系式.3、 已知弹簧的长度 y (厘米)在一定的限度内是所挂重物质量x (千克)的一次函数•现已测得不挂重物时弹簧的长度是 6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米•求这个一次函数的关系式.解:设所求函数的关系式是 y = kx + b,根据题意,得k------------- 解这个方程组,得---------------- b所以所求函数的关系式是 ________________________ •4、 一次函数中,当x 1时,y 3 ;当x 1时,y 7,求出相应的函数关系式.5、已知一次函数 y = _kx + b 的图象经过点(一1, 1)和点(1, - 5),求四、综合题:(E 在F 的左边),求出 E 、F 两点的坐标.x 取什么时,y >0, y v 0, y = 0通过配方,求函数的顶点 P 的坐标;已知一个二次函数的图象经过A - 2, 5)、 2 B (0,3)和Q1 , - 2)三点.2(2)已知等腰三角形的面积为 20cm * 2 * *,设它的底边长为 x( cm ),求底边上的高y ( cm )关于x 的函 (1)函数的解析式(2)当x = 5时,函数y 的值.(1) (2) (3)求出这个二次函数的解析式;若函数的图象与x轴相交于点E、F, 作出函数的图象并根据图象回答:当函数及图象答案.选择题: C B C A C D A D B C C B C D A C C B C •填空题:1 . 4 2. 三3. -2 4.y = (x —1) + 2 5. y7. y = —x 等8.7 9.(—2, —3) 10.减小31. 62-三.解答题:1 . (1) 一切实数(2 )一切实数(3) x 22 . (1) y = 0.5x (x> 0)(2) y =40x3.分析:kx + b k0 0k& b 6k0.3解:y 4k b7.2b611.二、四13.321—1 等14.x >且x 12(4) x>—3(3) s= 100 —r2 (0 v r v 10)=0.3x + 6kx b333解:y = kx + b k y = x —3b322b 3kx b3b55.解:y= kx + b y =—2x + 5k b7k24.分析:(2, 0) ( 0,—3)k b 1b25.(1) y = —3x —2k b 5k3(2) y =—172四.① y = 0.5x —x — 1.52② y = 0.5(x —1) — 2 p(1 , —2)③ E( —1, 0 ) F(3 , 0) ④ 图略.当X V—1或X>3时y> 0 .当一1 v X v 3时y v 0 当X=—1, X= 3 时y = 0。