下载文档原格式
轴承的摩擦系数
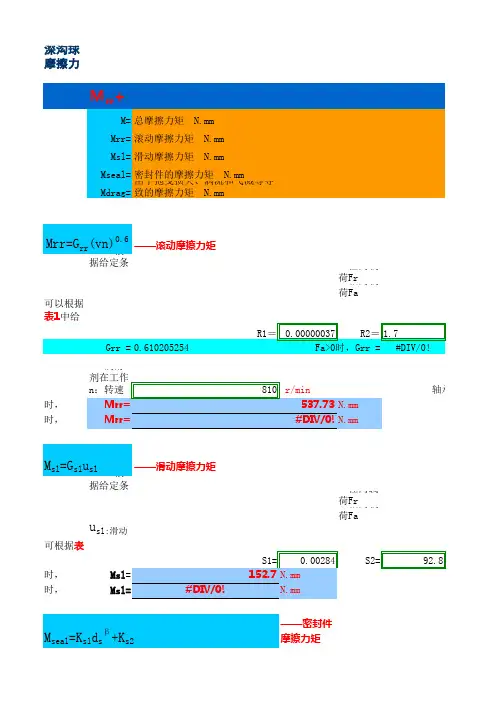
为便于与滑动轴承比较，滚动轴承的摩擦力矩可按轴承内径由下式计算：M=uPd/2
这里,
M：摩擦力矩，
u：摩擦系数，表1
P：轴承负荷，N
d：轴承公称内径，mm
摩擦系数u受轴承型式、轴承负荷、转速、润滑方式等的影响较大，一般条件下稳定旋转时的摩擦系数参考值如表１所示。
对于滑动轴承，一般u=，有时也达。
各类轴承的摩擦系数u
轴承型式摩擦系数u
深沟球轴承
角接触球轴承
调心球轴承
圆柱滚子轴承
满装型滚针轴承
带保持架滚针轴承
圆锥滚子轴承
调心滚子轴承
推力球轴承
推力调心滚子轴承由轴承摩擦引起的轴承功率损失可用以下计算公式得出
NR = 1,05 x 10-4 Mn
其中
NR = 功率损失，W
M = 轴承的总摩擦力矩，Nmm
n = 转速，r/min
电机扭矩公式：T=9550*P/n
T：电机转矩
P：电机功率KW
n：转速r/min。
转盘轴承力矩载荷下的变形计算摘要:通过分析四点接触转盘轴承受倾覆力矩时的套圈位移与接触变形、轴承接触角变化的关系，得出转盘轴承倾覆力矩载荷下套圈倾角变形计算公式，为转盘轴承力矩载荷下变形提供了精确的计算方法。
最后用所得的力矩计算公式进行实例计算，并做出力矩-变形曲线。
关键词:四点接触;转盘轴承;力矩载荷;变形计算转盘轴承主要用在起重、建筑工程等大型机械设备中，国内也对其进行了较多的研究。
转盘轴承主要承受的是轴向力和倾覆力矩，而在很多情况下，倾覆力矩是轴承的主要载荷。
在力矩作用下，轴承的转角变形将很大的影响着整个机械的刚度和工作精度等性能。
所以有必要对转盘轴承力矩载荷承载-变形关系进行分析。
以往的转盘轴承在力矩作用下变形计算公式复杂，且计算过程中有时难以收敛。
这里对四点接触转盘轴承承载时变形的几何关系进行分析，得到轴承转角位移与接触变形的关系计算式。
在此基础上，推导出转盘轴承的倾覆力矩与变形计算式。
一、转盘轴承的受力变形四点接触转盘轴承受倾覆力矩时，轴承内、外套圈产生相对倾角，设外圈保持固定不动。
忽略倾角引起的径向位移，则受力后的处在位置角i处滚珠(0≤<)由于转角而引起的轴向位移为:ai= cosi (1)式中:Dw——滚珠中心圆直径(mm)。
转盘轴承的套圈位移和滚珠接触变形如图1所示。
在外沟道曲率中心Oe建立坐标系，变形前的内沟道中心为Oi，坐标分别为(x，y)。
变形后的内沟道中心Oii，坐标分别为(xi，yi)。
A和Ai分别是变形前后的沟道中心距。
则变形前内外沟道中心距:A=re+ri-Dw(2)式中:ri、re——内、外沟道曲率半径(mm);Dw——滚珠直径(mm)。
变形前内沟道曲率中心Oi的坐标(x，y):y=Acos(3)式中:——初始接触角x=Asin (4)转盘轴承受矩载荷引起内外套圈位移后，位置角i处内、外圈沟道曲率中心距为:Ai=re+ri-(Dw-i)(5)式中:i——内外套圈和滚珠接触变形总量(mm)。
回转转盘轴承承载计算实例详解假设我们需要设计一个能够承受1000吨荷载的回转转盘，直径为10米。
我们将使用滚子转盘轴承来支撑和传递荷载。
下面是计算的详细步骤：第一步：确定所使用的轴承类型和参数根据设计要求，我们选择了滚子转盘轴承。
根据轴承的类型和尺寸，我们可以得到一些必要的参数，如滚子直径、滚子数量、接触角、滚子材料等信息。
第二步：计算滚子的等效负荷根据滚子的材料和几何参数，我们可以得到滚子的基本动态载荷额定值C。
然后，根据荷载特性，在垂直和水平方向上计算滚子的等效负荷。
对于水平方向上的荷载，我们需要考虑滚子对称排列的情况。
第三步：计算滚子转盘的等效负荷滚子转盘的等效负荷可以通过将滚子的等效负荷乘以滚子数量得到。
在纵向和横向方向上都要进行计算，以考虑荷载的不同作用方向。
第四步：根据滚子转盘的等效负荷计算负载接触应力根据滚子转盘的等效负荷和轴承的几何参数，可以计算滚子转盘的接触应力。
第五步：根据滚子转盘的接触应力判断轮廓变形情况根据滚子转盘的接触应力和材料弹性参数，可以计算出轮廓变形。
如果轮廓变形过大，会影响到传递荷载的能力和轴承的寿命。
第六步：根据回转转盘的尺寸和材料回转转盘的自身重量对轴承的承载能力也会造成一定的影响。
根据回转转盘的尺寸和材料密度，可以计算出其自身重量。
第七步：根据合成荷载计算轴承的等效动态负荷根据回转转盘的荷载和自身重量，可以计算出合成荷载。
根据荷载特性和标准系数，可以将合成荷载转化为等效动态负荷。
第八步：检查轴承的额定动态负荷是否满足要求根据轴承的额定动态负荷额定值和计算得到的等效动态负荷，可以判断轴承是否能够满足设计要求。
如果额定动态负荷大于等效动态负荷，则说明轴承能够满足要求。
总结：通过以上的步骤，我们可以根据回转转盘的设计要求和参数，计算出所使用的滚子转盘轴承的承载能力和使用寿命。
同时，我们还可以对轴承的安全性能进行评估和优化，以提高回转转盘的使用寿命和可靠性。
滚动轴承的校核计算及公式1 基本概念1．轴承寿命：轴承中任一元件出现疲劳剥落扩展迹象前运转的总转数或一定转速下的工作小时数。
批量生产的元件，由于材料的不均匀性，导致轴承的寿命有很大的离散性，最长和最短的寿命可达几十倍，必须采用统计的方法进行处理。
2．基本额定寿命：是指90%可靠度、常用材料和加工质量、常规运转条件下的寿命，以符号L10（r）或L10h（h）表示。
3．基本额定动载荷（C）：基本额定寿命为一百万转（106）时轴承所能承受的恒定载荷。
即在基本额定动载荷作用下，轴承可以工作106 转而不发生点蚀失效，其可靠度为90%。
基本额定动载荷大，轴承抗疲劳的承载能力相应较强。
4．基本额定静载荷（径向C0r，轴向C0a）：是指轴承最大载荷滚动体与滚道接触中心处引起以下接触应力时所相当的假象径向载荷或中心轴向静载荷。
在设计中常用到滚动轴承的三个基本参数：满足一定疲劳寿命要求的基本额定动载荷Cr（径向）或Ca（轴向），满足一定静强度要求的基本额定静强度C0r（径向）或C0a（轴向）和控制轴承磨损的极限转速N0。
各种轴承性能指标值C、C0、N0等可查有关手册。
2 寿命校核计算公式图17-6滚动轴承的寿命随载荷的增大而降低，寿命与载荷的关系曲线如图17-6，其曲线方程为PεL10=常数其中 P-当量动载荷，N；L10-基本额定寿命，常以106r为单位（当寿命为一百万转时，L10=1）；ε-寿命指数，球轴承ε=3，滚子轴承ε=10/3。
由手册查得的基本额定动载荷C是以L10=1、可靠度为90%为依据的。
由此可得当轴承的当量动载荷为P时以转速为单位的基本额定寿命L10为Cε×1=Pε×L10L10=(C/P)ε 106r (17.6)若轴承工作转速为n r/min，可求出以小时数为单位的基本额定寿命h （17.7）应取L10≥L h'。
L h '为轴承的预期使用寿命。
通常参照机器大修期限的预期使用寿命。
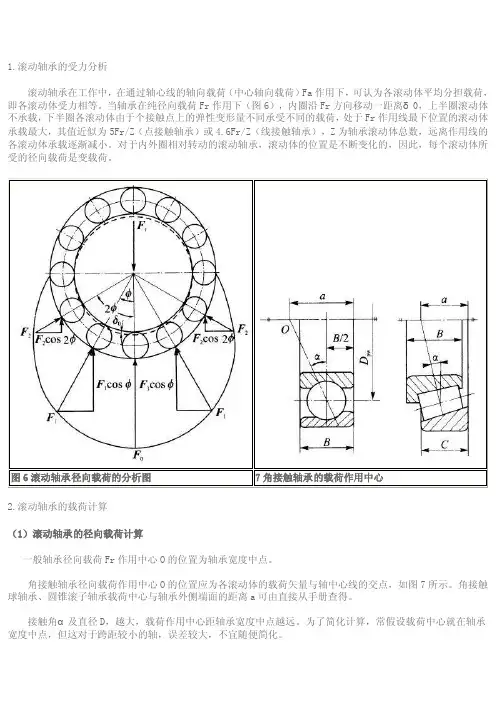
1.滚动轴承的受力分析滚动轴承在工作中，在通过轴心线的轴向载荷（中心轴向载荷）Fa作用下，可认为各滚动体平均分担载荷，即各滚动体受力相等。
当轴承在纯径向载荷Fr作用下（图6），内圈沿Fr方向移动一距离δ0，上半圈滚动体不承载，下半圈各滚动体由于个接触点上的弹性变形量不同承受不同的载荷，处于Fr作用线最下位置的滚动体承载最大，其值近似为5Fr/Z（点接触轴承）或4.6Fr/Z（线接触轴承），Z为轴承滚动体总数，远离作用线的各滚动体承载逐渐减小。
对于内外圈相对转动的滚动轴承，滚动体的位置是不断变化的，因此，每个滚动体所受的径向载荷是变载荷。
2.滚动轴承的载荷计算（1）滚动轴承的径向载荷计算一般轴承径向载荷Fr作用中心O的位置为轴承宽度中点。
角接触轴承径向载荷作用中心O的位置应为各滚动体的载荷矢量与轴中心线的交点，如图7所示。
角接触球轴承、圆锥滚子轴承载荷中心与轴承外侧端面的距离a可由直接从手册查得。
接触角α及直径D，越大，载荷作用中心距轴承宽度中点越远。
为了简化计算，常假设载荷中心就在轴承宽度中点，但这对于跨距较小的轴，误差较大，不宜随便简化。
图8角接触轴承受径向载荷产生附加轴向力1)滚动轴承的轴向载荷计算当作用于轴系上的轴向工作合力为FA，则轴系中受FA作用的轴承的轴向载荷Fa=FA，不受FA作用的轴承的轴向载荷Fa=0。
但角接触轴承的轴向载荷不能这样计算。
角接触轴承受径向载荷Fr时，会产生附加轴向力FS。
图8所示轴承下半圈第i个球受径向力Fri。
由于轴承外圈接触点法线与轴承中心平面有接触角α，通过接触点法线对轴承内圈和轴的法向反力Fi将产生径向分力Fri；和轴向分力FSi。
各球的轴向分力之和即为轴承的附加轴向力FS。
按一半滚动体受力进行分析，有FS ≈ 1.25 Frtan α(1)计算各种角接触轴承附加轴向力的公式可查表5。
表中Fr为轴承的径向载荷；e为判断系数，查表6；Y 为圆锥滚子轴承的轴向动载荷系数，查表7。
转盘轴承力矩载荷下的变形计算
摘要:通过分析四点接触转盘轴承受倾覆力矩时的套圈位移与接触变形、轴承接触角变化的关系，得出转盘轴承倾覆力矩载荷下套圈倾角变形计算公式，为转盘轴承力矩载荷下变形提供了精确的计算方法。
最后用所得的力矩计算公式进行实例计算，并做出力矩-变形曲线。
关键词:四点接触;转盘轴承;力矩载荷;变形计算
转盘轴承主要用在起重、建筑工程等大型机械设备中，国内也对其进行了较多的研究。
转盘轴承主要承受的是轴向力和倾覆力矩，而在很多情况下，倾覆力矩是轴承的主要载荷。
在力矩作用下，轴承的转角变形将很大的影响着整个机械的刚度和工作精度等性能。
所以有必要对转盘轴承力矩载荷承载-变形关系进行分析。
以往的转盘轴承在力矩作用下变形计算公式复杂，且计算过程中有时难以收敛。
这里对四点接触转盘轴承承载时变形的几何关系进行分析，得到轴承转角位移与接触变形的关系计算式。
在此基础上，推导出转盘轴承的倾覆力矩与变形计算式。
一、转盘轴承的受力变形
四点接触转盘轴承受倾覆力矩时，轴承内、外套圈产生相对倾角，设外圈保持固定不动。
忽略倾角引起的径向位移，则受力后的处在位置角i处滚珠(0≤<)由于转角而引起的轴向位移为:
ai= cosi (1)
式中:Dw——滚珠中心圆直径(mm)。
转盘轴承的套圈位移和滚珠接触变形如图1所示。
在外沟道曲率中心Oe建立坐标系，变形前的内沟道中心为Oi，坐标分别为(x，y)。
变形后的内沟道中心Oii，坐标分别为(xi，yi)。
A和Ai分别是变形前后的沟道中心距。
则变形前内外沟道中心距:
A=re+ri-Dw(2)
式中:ri、re——内、外沟道曲率半径(mm);
Dw——滚珠直径(mm)。
变形前内沟道曲率中心Oi的坐标(x，y):
y=Acos(3)
式中:——初始接触角
x=Asin (4)
转盘轴承受矩载荷引起内外套圈位移后，位置角i处内、外圈沟道曲率中心距为:
Ai=re+ri-(Dw-i)(5)
式中:i——内外套圈和滚珠接触变形总量(mm)。
套圈移动后内沟道曲率中心Oii坐标(xi，yi):
yi=Aicosi (6)
xi=Aisini(7)
式中:i ——套圈位移后，位置角i处的接触角。
即有Ai=(8)
轴承位移前后内沟道曲率中心的坐标关系:
xi=x+ai(9)
yi=y(10)
由式(3)、式(6)、式(8)、式(9)和式(10)可以得到转盘轴承受力位移后的接触角:
cosi =(11)
将式(8)、式(9)和式(10)代入式(5)中得出转盘轴承位移ai和滚珠接触弹性变形i关系式:
i=Dw -(re+ri-)(12)
二、转盘轴承倾覆力矩的计算
四点接触转盘轴承某滚珠上的接触受力由点接触的受力变形关系计算公式 : Qi=Ki i3/2 (13)
式中:Qi——滚珠和套圈接触受力(N);
i——滚子与内外套圈接触处的总的弹性变形量(mm);
Ki——系数。
对于滚珠与内外套圈接触的系数:
Ki=1/(2.97×10-4[(∑ii)1/3+(∑ie)1/3])3/2
式中，、是滚珠与内、外圈点接触相关的系数，可根据文献[7]计算内、外沟道主曲率函数F(ii)、F(ie)进行查表得到。
内、外沟道主曲率和∑ii (ie)=×(2+-)，参数i=，fi、fe分别为内、外沟道沟曲率半径系数。
主曲率和以内圈接触“±”取“-”，以外圈接触计算“±”取“+”。
在转盘轴承承受倾覆力矩时，内外圈产生相对倾角，使每个滚子的受力大小各不相同。
由图2可知，每个滚珠上由接触受力产生的力矩
将式(13)带入上式，得到:
Mi=Kii3/2sinicosi(15)
根据四点接触转盘轴承在力矩载荷下，外载荷与内部滚子负荷平衡的条件，轴承受到总力矩
M=Mi=Kii3/2sinicosi(16)
式中，sini由式(11)得sini=(1-()2)1/2。
将式(1)、(12)、(13)带入式(16)中，得
M=Ki(Dw-(re+ri-((x+cosi)2+y2)1/2))3/2 •(1-)1/2cosi(17)
上式可知，倾覆力矩M是倾角的非线性函数，可经过计算机非线性数值计算方法反复进行迭代求解。
三、实例分析
某四点接触转盘轴承，结构参数:Dw=40，Dw=1900，初始接触角a=50°，滚珠数Z=120，内、外沟曲率半径系数fi(e)==0.53。
试分析其倾覆力矩M与倾角的关系曲线。
该轴承初始中心距由式(1)得:
A=re+ri-Dw =2.4mm
初始内沟道曲率中心Oi的坐标(x，y)由式(2)、式(3)得:
y=Acos=2.4cos50°1.54269mm
x=Acos=2.4sin50°1.83851mm
滚珠受力过程中接触角增加使系数Ki略有增加。
经过计算表明，系数Ki在接触角为80°比接触角为50°大0.4%。
因此，简便起见，系数Ki按初始接触角50°计算。
具体计算结果如下:
ri===0.01353237
∑ii=0.0535160889
∑ie=0.053506931
F(ii)=0.894230362
查表并插值计算得=0.689077493
(ie)=0.891485912
查表并插值计算得=0.692919723
则Ki=1/(2.97×10-4[(∑ii)1/3+(∑ie)1/3])3/2
≈570954
将已知相关数据带入式(17)进行计算，得:
M=570954(Dw-(re+ri-((x+cosi)2+y2)1/2))3/2 •(1-)1/2cosi
用MATLAB对上式进行牛顿法非线性数值计算。
经过程序运算后，倾覆力矩M与轴承倾角变形的关系曲线如图3所示:
四、结语
四点接触转盘轴承力矩载荷下倾角变形对机械的工作性能有很大的影响。
通过
对转盘轴承承载时变形的几何关系进行分析，推导出转盘轴承的倾覆力矩与变形关
系计算式。
并进行了实例计算，绘制出力矩-变形曲线。
整个计算过程简便，为四点接触转盘轴承力矩载荷下变形分析提供了理论依据。
这将有助于四点接触转盘轴承
的设计、使用以及刚度、振动的分析。
参考文献
[1]徐立民，陈卓.回转支承[M].合肥:安徽科学技术出版社，1988.
[2]杜睿，吴志军.单排球式回转支承的承载能力分析[J].机械设计与制造，2006，(9).
[3]苏立樾，苏健.转盘轴承静载荷承载曲线的创建[J].轴承，2004，(6).
[4]汪洪，陈原.转盘轴承承载能力及额定寿命的计算方法[J].轴承，2008，(2).
[5]郑兰疆，李彦，赵武，等.大型回转轴承的承载性能分析[J].机械设计与研
究，2008，(4).
[6]Harris T A.Rolling Bearing Analysis(Third Edition)[M].New York: John Wilcy and Sons.Inc.，1991.
[7]万长森.滚动轴承的分析方法[M].北京:机械工业出版社，1987.
[8]常巍，谢光军，黄朝峰.MATLABR2007基础与提高[M].北京:电子工业出版社，2007.。
