西藏昌都第四高级中学2019高三月考数学(理)试卷

西藏昌都第四高级中学2019届高三数学第三次周考试题 理一、选择题 1.设集合 A = {x x — 2x —3 兰0},B = {x y = l n( x —1)},贝 U AcB =()A .[2,3] B. 1,31 C.1,31D.1 -1,1 2i=( )22.(1-i )A 111 1.1i B.i C. -1 - i D.-1—22223.卜列命题说法止确的是 ( )A.命题“若 2 x =1,则 X 二 1 的否命题为: “若 2 x =1,贝y x=1 ”B. “0<xc3”是“ x —1 <1 ”的必要不充分条件C.命题 “ -x ■ R ,使得 x 2 • x -1 ：：： 0 ”的否定是：“- x 门 R ,均有 x 2 • x -1 • 0 ”D.命题“若x = y ，贝U sin x = sin y ”的逆命题为真命题4在一个几何体的三视图中，正视图和俯视图如图所示,则该几何体的体积为()比为()A = 2B =4C 二丄D =22A.360B.180C.90D.456数列On '是公差不为 0的等差数列,且a 1,a 3,a 7为等比数列 £鳥的连续三项，则数列U 的公10.某校进行了一次创新作文大赛，共有 100名同学参赛，经过评判，这 100名参赛者的得分都在［40,90］之间，其得分的频率分布直方图如图，则下列结论错误的是（ ）A. 得分在［40,60）之间的共有40人B. 从这100名参赛者中随机选取 1人，其得分在［60,80）的概率为0.5C. 估计得分的众数为 55D. 这100名参赛者得分的中位数为65+ sin(- + x)：y h (x)为. 的导函数，则的图象大致是8若是2和8的等比中项,则圆锥曲线心=1m 的离心率是（ B = 5C 3 或.529.抛掷一枚质地均匀的硬币,如果连续抛掷1000次,那么第999次出现正面朝上的概率是A.1 999B. C.999 D.100010007已知),那么输出的］(10题A.22B.46C.94D.190 12三个数a =0.76,b =60.7,C = log°.7 6的大小关系为(A.c<a<bB.a<b<cC.c<b<aD.a<c<b二、填空题13.已知向量a =(1,2),b =(2, m)，且a//b，则m= ______________14.直线y=2x+3被圆x2+y2—6x—8y = 0所截得的弦长等于_________________15.若点P(cosa,sin a)在直线y = -2x 上,则tan(ax-2y 4 _016. 已知变量x, y满足彳x-2兰0 ,则y +1的取值范围是______________ .c c x+2x y-2 _0三、解答题17. △ ABC的内角A, B,C的对边分别为a,b,c,已知b,c,2acosB成等差数列1. 求角A ;2. 若a =、.l3,b =3,D为BC中点，求AD的长.28.某医疗科研项目对5只实验小白鼠体内A,B两项指标数据进行收集和分析，得到的数据如表所示指标1号小白鼠2号小白鼠3号小白鼠4号小白鼠5号小白鼠A57698B223441. 若通过数据分析，得知A项指标数据与B项指标数据具有线性相关关系。

44西藏昌都第四高级中学届高三数学四月周考试题理（考试时间：分钟 试卷满分：分）第I 卷一、选择题（本题共小题，每小题分，共分•在每小题给出的四个选项中，只有一项是符合 题目要求的）.已知集合 A=「_1,0,1〉B=1x| _1 d 则 A 'B n ( ).. (-1,0} . g,i . 「-1,0,1.已知复数z 满足iz=1+i ,则z 的共轭复数z =(). 1 i .1 -i . 、、2 . -1 -i.已知随机变量「，"食… '二哄,则J wn （） .将函数y 二cos3x 的图象向左平移 一个单位长度,所得函数的解析式是（4=cos i 3x y = COS i 3x - -La 为三角形的一个内角；.,则二（)125 n.n5△的内角，，的对边分别为， ,.已知°,6 ,,则（）30 .60 .751206(2—x )(2x+1 )的展开式中 4x 的系数为 ()13.有一个圆柱形笔筒如图放置,它的侧视图是（.函数f X 的图象如图所示,则f' X 的图像可能是()31JI3.2设函数.■-- ■--''-,若实数 满足=二］,则( )• — . :.若函数f(x)=xl nx -x 3 • x 2-ax 有两个不同的零点，则实数a 的取值范围是( ).0, ：： ? . 0,1】. 1-1,0 . -：：,0第n 卷二、填空题(本题共小题，每小题分，共分).已知向量 a , b 满足 | a |=1 , a b = -1，则 a (2 a —b )=x -y _0•若x , y 满足约束条件 x ，y-2^0，则z=3x-4y 的最小值为.［八0•设等比数列、a n '满足-,--,则..直线y =x 1与圆x 2 • y 2，2y -3 =0交于A , B 两点，贝U AB =.y = COS i 3x —I 4丿y =COS3x .已知双曲线b 2=1的离心率为2,则其两条渐进线的夹角为2三、解答题(本大题共小题，共分•解答应写出文字说明、证明过程或演算步骤) .(分)已知等差数列：a n /中,2a 2 a 3 a^20,且前10项和S 10 =100 ()求数列的通项公式1()若b n,求数列血:■的前n 项和a n an 卅•(分)年双当天，某购物平台的销售业绩高达亿人民币 •与此同时，相关管理部门推出了针对电商的商品和服务的评价体系，现从评价系统中选出次成功交易 ，并对其评价进行统计，对商品的好评率为，对服务的好评率为，其中对商品和服务都做出好评的交易为次 •()请完成下表，并判断是否可以在犯错误概率不超过的前提下 ，认为商品好评与服务好评有关？()若将频率视为概率，某人在该购物平台上进行的次购物中 ，设对商品和服务全好评的次数为X .① 求随机变量X 的分布列； ② 求X 的数学期望和方差•2附： K 2n(ad一bc)，其中 n = a b c d.(a+b)(c+d)(a+c)(b+d)k.（分）如图，m 是直角梯形，—n二u-一.匸「-二又二一，:=-■■--，直线二*与直线「._所成的角4正磅拟育（）求证：平面PAC1平面匸一；（）求二面角M-AC-B的大小；.（分）已知椭圆C的对称中心为原点O ,焦点在x轴上，左，右焦点分别为F1,F2,上顶点和右顶点分别为B, A,线段AB的中点为D ,且k OD k AB二-1 JAOB的面积为2 2（）求椭圆C的方程（）过F i的直线I与椭圆C相交于M , N两点，若MF2N的面积为16,求以F2为圆心且与直3线I相切的圆的方程1 2（分）已知函数f x ax^ 1 a x In x a _ 02（）求函数f x的单调区间（）当a =0时,关于x方程f x i；= mx在区间i,e2上有唯一实数解，求实数m取值范围请考生在第、两题中任选一题作答•注意：只能做所选定的题目•如果多做，则按所做的第一个题目计分..（本小题满分分）选修：坐标系与参数方程在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，已知点A的极坐标为' J2,工：直线I的极坐标方程为Pcos £||= a ,且点A在直线I上.I 4丿I 4丿()求a的值及直线I的直角坐标方程；X =1 +COSG()圆C的参数方程为｛(:为参数)，试判断直线I与圆C的位置关系y =s ina(本小题满分分)选修：不等式选讲已知定义在R上的函数f (x)= —2的最小值为a.()求a的值；()若p,q, r釣正实数，且p q r二a,求证：p2q2r^3.、选择题、填空题三、解答题.）设公差为，由已知得,（分）解得，（分）所以｛｝的通项公式为（），（分）（）由（）可知？（）X,所以XXX…（）X （）X,① XXX…（）X （）X,②（分）①②得：X （…）（）X,X(•••)()X(分)())0XX()()X(分)()X(分)由题意可得关于商品和服务评价的列联表则宀2°° (14°°-4°°) so?.15^< 5^18^20显然有:0, 由于7.407 -7.879,则不可以在犯错误概率不超过 0.5%的前提下，认为商品好评与服务好评有关..①每次购物时，对商品和服务都好评的概率为 —10且X 的取值可以是0,1,2,3,则271000343 1000故的分布列为 ②由于xLI B(3,—)10则 E(X) =3 — 21,D(X^3 — (1 7) 63 .10 10 10 10 100P(XP(X=1）=c 3（?）2 7 189 10 110 441 1000设椭圆方程为a 22^=1(a b 0)P(X2b由已知得A a，0, B 0，b , D I b ,所以k OD k A^ ——12 2 丿 a -a2又S AOB ab = 2、、2 ,所以ab = 4、、2 ,②22 2 由①②解得a2 =8,b2=4 ,所以椭圆方程为—1 1 .8 4 1,即a2=2b2,①2.①当直线I —x轴时，易得M -2,、、2 ,N -2,-、、2 , MF2N的面积为4*2,不合题意.②当直线I与x轴不垂直时，设直线I的方程为y二k x • 2 ,代入椭圆方程得2 2 2 21 2k x 8k x 8k -8 =0.显然有:0,- 10 - / 10所以所求圆的方程为 x - 2 2 • y 2 =8当0 ::: a ::: 1时，函数f x 的单调递增区间为（0,1）和单调递减区间为'1 1 I;◎丿「a 丿当a =1时，函数f x 的单调递增区间为 0,匸：；当a 1时，函数f x 的单调递增区间为'1 - i 和（1,母）单调递减区间为'-11'aa'm| - 仁 m ：：三 一1 或 m 二 I 1 e 2 J IL （H 兀）、、2 cos -14 4丿所以即为的直角坐标方程• .圆的方程（为参数）,可化为， 圆心到直线的距离为， 所以直线与圆相交..当a=0时,函数f x 的单调递增区间为0,1, 单调递减区间为（1,畑设 M X i , y i ,N X 2,y 2 ,则花 x ?二2 2 -8k 8k -8 川6X1X 22 ,所以 1 2k1 2kMN = 1 k 21 x X2 $ —4^X 2 = 1 kf -8k 2丿-4 8宀8 1 2k 2化简得MN心i 2 .又圆的半径-4kj1+k 21 2k 2所以S MF 2NJ MN r 21 4j2 1 k 2—X21 2k 24k 1 k 2 & 2 k 1k 2 16 31 2k 2化简得k 「k 2-2=0,解得k = 1,所以r= 2 2,..因为点A直线I 上，。

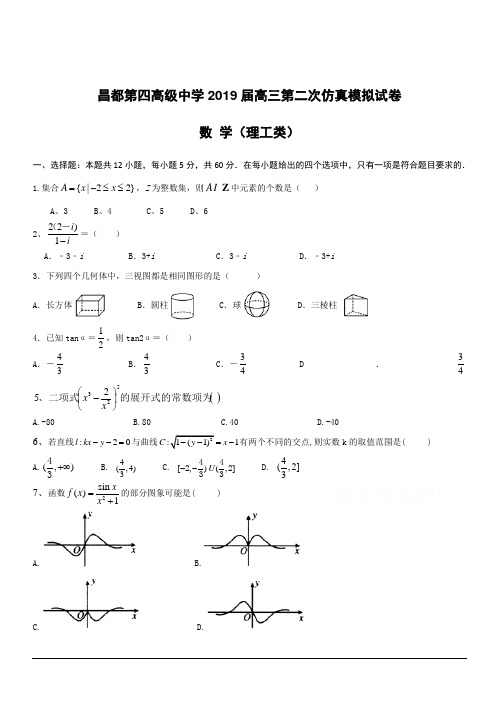
昌都第四高级中学2019届高三第二次仿真模拟试卷数 学（理工类）一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1.集合{|22}A x x =-≤≤，Z 为整数集，则AZ 中元素的个数是（ ）A 、3B 、4C 、5D 、6 2、22)1i i-（－＝（ ） A ．﹣3﹣iB ．3+iC ．3﹣iD ．﹣3+i3．下列四个几何体中，三视图都是相同图形的是（ ） A ．长方体B ．圆柱C ．球D ．三棱柱4．已知tan α＝12，则tan2α＝（ ） A ．－43B ．43C ．－34D ．34()的展开式的常数项为、二项式52325⎪⎭⎫ ⎝⎛-x xA.-80B.80C.40D.-406、若直线:20l kx y --=与曲线1C x -有两个不同的交点,则实数k 的取值范围是( )A.(,)+∞43B. 4(,4)3C. [,)(,]--442233 D. 4(,2]37、函数2sin ()1xf x x =+的部分图象可能是( ) A. B.C. D.8、已知随机变量()~,X N σ22,若()()P X a P X a ≤-+≤+=1121,则实数a = ( )A.0B.1C.2D.4 9、设1423log ,ln 2,5a b c ===, 则( )A. b a c <<B. b c a <<C. a b c <<D. c b a <<10. 已知函数()sin(2)3f x x ωπ=-（0>ω）的最小正周期为2π，则下列说法正确的是（ ） A ．1=ω B ．函数()f x 在(,)42ππ上单调递增C ．函数()f x 的图象关于直线2x π=对称D ．函数()f x 的图象关于点(,0)3π对称11. 已知B A ,是球O 的球面上两点，且球的半径为3，︒=∠90AOB ，C 为该球面上的动点．当三棱锥ABCO -的体积取得最大值时，则过C B A ,,三点的截面的面积为（ ） A ．π6B ．π12C ．π18D ．π3612. 已知函数21-2)(,1ln )(x e x g x x f =+=，若)(=)(n g m f 成立，则n m -的最小值是（ ）A.21-2ln B.2-e C.2ln +21 D. 21-e 二、填空题：本题共4小题，每小题5分，共20分．13、已知向量()()1,2,,4,p q x =-=且//,p q 则p q ⋅的值为__________. 14、已知数列{a n }的前n 项和S n 满足2a n ＝2+S n ．求a n= 。

昌都市高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 如图，空间四边形ABCD 中，M 、G 分别是BC 、CD的中点，则等（ ）A． B． C． D．2． 某几何体的三视图如图所示（其中侧视图中的圆弧是半圆），则该几何体的表面积为（ ）A ．20+2πB ．20+3πC ．24+3πD ．24+3π3． 已知U=R ，函数y=ln （1﹣x ）的定义域为M ，集合N={x|x 2﹣x ＜0}．则下列结论正确的是（ ） A ．M ∩N=N B ．M ∩（∁U N ）=∅ C ．M ∪N=U D ．M ⊆（∁U N ）4．下面是关于复数的四个命题：p 1：|z|=2， p 2：z 2=2i ，p 3：z 的共轭复数为﹣1+i ， p 4：z 的虚部为1． 其中真命题为（ ）A ．p 2，p 3B ．p 1，p 2C ．p 2，p 4D ．p 3，p 45． 函数y=a x +2（a ＞0且a ≠1）图象一定过点（ ）A ．（0，1）B ．（0，3）C ．（1，0）D ．（3，0）6． 在△ABC中，已知，则∠C=（ ） A ．30°B ．150°C ．45°D ．135°7． 两圆C 1：x 2+y 2﹣4x+3=0和C 2：的位置关系是（ ）A ．相离B ．相交C ．内切D ．外切班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________8．将正方形的每条边8等分，再取分点为顶点（不包括正方形的顶点），可以得到不同的三角形个数为（）A．1372 B．2024 C．3136 D．44959．已知函数f（x）=xe x﹣mx+m，若f（x）＜0的解集为（a，b），其中b＜0；不等式在（a，b）中有且只有一个整数解，则实数m的取值范围是（）A．B． C．D．10．“x2﹣4x＜0”的一个充分不必要条件为（）A．0＜x＜4 B．0＜x＜2 C．x＞0 D．x＜411．下面的结构图，总经理的直接下属是（）A．总工程师和专家办公室B．开发部C．总工程师、专家办公室和开发部D．总工程师、专家办公室和所有七个部12．现要完成下列3项抽样调查：①从10盒酸奶中抽取3盒进行食品卫生检查．②科技报告厅有32排，每排有40个座位，有一次报告会恰好坐满了听众，报告会结束后，为了听取意见，需要请32名听众进行座谈．③高新中学共有160名教职工，其中一般教师120名，行政人员16名，后勤人员2名．为了了解教职工对学校在校务公开方面的意见，拟抽取一个容量为20的样本．较为合理的抽样方法是（）A．①简单随机抽样，②系统抽样，③分层抽样B．①简单随机抽样，②分层抽样，③系统抽样C．①系统抽样，②简单随机抽样，③分层抽样D．①分层抽样，②系统抽样，③简单随机抽样二、填空题13．已知△ABC中，内角A，B，C的对边分别为a，b，c，asinA=bsinB+（c﹣b）sinC，且bc=4，则△ABC 的面积为．14．对于集合M，定义函数对于两个集合A，B，定义集合A△B={x|f A（x）f B（x）=﹣1}．已知A={2，4，6，8，10}，B={1，2，4，8，12}，则用列举法写出集合A△B的结果为．15．棱长为2的正方体的顶点都在同一球面上，则该球的表面积为 ．16．设等差数列{a n }的前n 项和为S n ，若﹣1＜a 3＜1，0＜a 6＜3，则S 9的取值范围是 ．17．复数z=（i 虚数单位）在复平面上对应的点到原点的距离为 ．18．已知f （x ）=，则f[f （0）]= ．三、解答题19．（本小题满分12分） 已知函数21()x f x x +=，数列{}n a 满足：12a =，11n n a f a +⎛⎫= ⎪⎝⎭（N n *∈）. （1）求数列{}n a 的通项公式；（2）设数列{}n a 的前n 项和为n S ，求数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和n T .【命题意图】本题主要考查等差数列的概念，通项公式的求法，裂项求和公式，以及运算求解能力.20．已知平面直角坐标系xoy 中的一个椭圆，它的中心在原点，左焦点为，右顶点为D （2，0），设点A （1，）． （1）求该椭圆的标准方程；（2）若P 是椭圆上的动点，求线段PA 的中点M 的轨迹方程；（3）过原点O 的直线交椭圆于B ，C 两点，求△ABC 面积的最大值，并求此时直线BC 的方程．21．（本小题满分12分）某媒体对“男女延迟退休”这一公众关注的问题进行名意调查，下表是在某单位 得到的数据：（Ⅱ）从赞同“男女延迟退休”的80人中，利用分层抽样的方法抽出8人，然后从中选出2人进行陈述 发言，求事件“选出的2人中，至少有一名女士”的概率．参考公式：22()K ()()()()n ad bc a b c d a c b d -=++++，()n a b c d =+++【命题意图】本题考查统计案例、抽样方法、古典概型等基础知识，意在考查统计的思想和基本运算能力22．（本小题满分12分） 设函数mx x x x f -+=ln 21)(2（0>m ）． （1）求)(x f 的单调区间； （2）求)(x f 的零点个数；（3）证明：曲线)(x f y =没有经过原点的切线．23．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ．已知b 2+c 2=a 2+bc ． （Ⅰ）求A 的大小； （Ⅱ）如果cosB=，b=2，求a 的值．24．（本小题满分12分）已知函数f （x ）＝12x 2＋x ＋a ，g （x ）＝e x .（1）记曲线y ＝g （x ）关于直线y ＝x 对称的曲线为y ＝h （x ），且曲线y ＝h （x ）的一条切线方程为mx －y －1＝0，求m 的值；（2）讨论函数φ（x ）＝f （x ）－g （x ）的零点个数，若零点在区间（0，1）上，求a 的取值范围．昌都市高级中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题13．．14．{1，6，10，12}．15．1216．（﹣3，21）．17．．18．1．三、解答题19．20．21．22．23．24．。

昌都第四高级中学2019届高三第二次全真模拟考试理科综合能力测试注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上；2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3.考试结束后，只将答题卡交回。

4.可能用到的相对原子质量：H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 S 32 Cr 52 Zn 65 I 127第I卷（选泽题共计126分）一、选择题:本题共13小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一个．．．．符合题目要求的。

1．有研究人员发现了一种含有集光绿色体的喜氧罕见细菌，每个集光绿色体含有大量叶绿素，使得细菌能够同其他生物争夺阳光，维持生存。

下列有关该细菌的叙述，不正确的是() A．该菌的基本结构包括细胞壁、细胞膜、细胞质和拟核等B．该菌是好氧细菌，其生命活动所需能量主要由线粒体提供C．细菌也可以是生产者D．该菌是光能自养细菌，其光合作用的场所是细胞质2.颜色变化常作为生物实验的一项重要观察指标，下面相关叙述正确的是()A．在花生子叶薄片上滴加苏丹Ⅲ染液，若发现满视野都呈现橘黄色，可以滴1～2滴50%盐酸洗去浮色B．酒精在重铬酸钾的作用下由橙色变成灰绿色C．紫色洋葱鳞片叶外表皮细胞发生质壁分离复原过程中，细胞液颜色变浅是液泡里的色素渗透出细胞所致D．用纸层析法分离绿叶中的色素，蓝绿色色带最宽，可判断叶绿素a含量最多3．以下关于遗传的说法，错误的是（）A.基因是具有遗传效应的DNA片段B.RNA是在细胞核中，以DNA的一条链为模板合成的，这一过程称为转录C.DNA由4种脱氧核苷酸，通过氢键链接而成。

D.自然界中一共有5种含氮碱基、8种核苷酸4．有关血糖平衡调节的叙述中，正确的是()A．饥饿状态下，胰岛B细胞的代谢活动增强，分泌的激素使脂肪等非糖物质转化为糖类的速度加快B．血糖浓度过高时，葡萄糖会合成肝糖原和肌糖原；过低时，肝糖原和肌糖原会分解成葡萄糖，进入血液，从而维持血糖的平衡C．能使血糖升高的激素有胰高血糖素和肾上腺素，二者表现为协同作用D．血糖平衡的调节与多种激素有关，神经系统不参与血糖平衡的调节5．今年，我国较多城市雾霾天气频发，改善生态环境势在必行。

昌都市第四高级中学2018-2019学年高二上学期第二次月考试卷数学班级__________ 姓名__________ 分数__________一、选择题1．若函数f（x）=3﹣|x﹣1|+m的图象与x轴没有交点，则实数m的取值范围是（）A．m≥0或m＜﹣1B．m＞0或m＜﹣1C．m＞1或m≤0D．m＞1或m＜02．设长方体的长、宽、高分别为2a、a、a，其顶点都在一个球面上，则该球的表面积为（）A．3πa2B．6πa2C．12πa2D．24πa23．已知两条直线ax+y﹣2=0和3x+（a+2）y+1=0互相平行，则实数a等于（）A．1或﹣3B．﹣1或3C．1或3D．﹣1或﹣34．已知某市两次数学测试的成绩ξ1和ξ2分别服从正态分布ξ1：N1（90，86）和ξ2：N2（93，79），则以下结论正确的是（）A．第一次测试的平均分比第二次测试的平均分要高，也比第二次成绩稳定B．第一次测试的平均分比第二次测试的平均分要高，但不如第二次成绩稳定C．第二次测试的平均分比第一次测试的平均分要高，也比第一次成绩稳定D．第二次测试的平均分比第一次测试的平均分要高，但不如第一次成绩稳定5．=（）A．﹣i B．iC．1+i D．1﹣i6．为得到函数的图象，只需将函数y=sin2x的图象（）A．向左平移个长度单位B．向右平移个长度单位C．向左平移个长度单位D．向右平移个长度单位7．已知点P（x，y）的坐标满足条件，（k为常数），若z=3x+y的最大值为8，则k的值为（）A．B．C．﹣6D．68．下列函数中，在区间（0，+∞）上为增函数的是（）A．y=x﹣1B．y=（）x C．y=x+D．y=ln（x+1）9．函数f（x）是以2为周期的偶函数，且当x∈（0，1）时，f（x）=x+1，则函数f（x）在（1，2）上的解析式为（）A．f（x）=3﹣x B．f（x）=x﹣3C．f（x）=1﹣x D．f（x）=x+110．设a=sin145°，b=cos52°，c=tan47°，则a，b，c的大小关系是（）A．a＜b＜c B．c＜b＜a C．b＜a＜c D．a＜c＜b11．设x∈R，则“|x﹣2|＜1”是“x2+x﹣2＞0”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件12．从一群学生中抽取一个一定容量的样本对他们的学习成绩进行分析，已知不超过70分的人数为8人，其累计频率为0.4，则这样的样本容量是（）A．20人B．40人C．70人D．80人二、填空题13．已知（2x﹣）n展开式的二项式系数之和为64，则其展开式中常数项是 ．14．一组数据2，x，4，6，10的平均值是5，则此组数据的标准差是 ．15．抛物线y2=﹣8x上到焦点距离等于6的点的坐标是 ．16．已知点E、F分别在正方体的棱上，且, ,则面AEF与面ABC所成的二面角的正切值等于 .17．已知数列的前项和是, 则数列的通项__________18．某慢性疾病患者，因病到医院就医，医生给他开了处方药（片剂),要求此患者每天早、晚间隔小时各服一次药，每次一片，每片毫克．假设该患者的肾脏每小时从体内大约排出这种药在其体内残留量的，并且医生认为这种药在体内的残留量不超过毫克时无明显副作用．若该患者第一天上午点第一次服药，则第二天上午点服完药时，药在其体内的残留量是毫克，若该患者坚持长期服用此药明显副作用（此空填“有”或“无”）三、解答题19．已知数列{a n}与{b n}，若a1=3且对任意正整数n满足a n+1﹣a n=2，数列{b n}的前n项和S n=n2+a n．（Ⅰ）求数列{a n}，{b n}的通项公式；（Ⅱ）求数列{}的前n项和T n．20．已知集合A={x|2≤x ≤6}，集合B={x|x ≥3}．（1）求C R （A ∩B ）；（2）若C={x|x ≤a}，且A C ，求实数a 的取值范围．⊆21．（本小题满分10分）已知函数.()|||2|f x x a x =++-（1）当时，求不等式的解集；3a =-()3f x ≥（2）若的解集包含，求的取值范围.()|4|f x x ≤-[1,2]22．已知命题p ：x 2﹣2x+a ≥0在R 上恒成立，命题q ：若p 或q 为真，p 且q为假，求实数a 的取值范围．　23．设函数f （x ）=ax 2+bx+c （a ≠0）为奇函数，其图象在点（1，f （1））处的切线与直线x ﹣6y ﹣7=0垂直，导函数f ′（x ）的最小值为﹣12．（1）求a ，b ，c 的值；（2）求函数f （x ）的单调递增区间，并求函数f （x ）在[﹣1，3]上的最大值和最小值．24．在中已知，，试判断的形状.ABC ∆2a b c =+2sin sin sin A B C =ABC ∆昌都市第四高级中学2018-2019学年高二上学期第二次月考试卷数学（参考答案）一、选择题1．【答案】A【解析】解：∵函数f（x）=3﹣|x﹣1|+m的图象与x轴没有交点，∴﹣m=3﹣|x﹣1|无解，∵﹣|x﹣1|≤0，∴0＜3﹣|x﹣1|≤1，∴﹣m≤0或﹣m＞1，解得m≥0或m＞﹣1故选：A．2．【答案】B【解析】解：根据题意球的半径R满足（2R）2=6a2，所以S球=4πR2=6πa2．故选B3．【答案】A【解析】解：两条直线ax+y﹣2=0和3x+（a+2）y+1=0互相平行，所以=≠，解得a=﹣3，或a=1．故选：A．4．【答案】C【解析】解：∵某市两次数学测试的成绩ξ1和ξ2分别服从正态分布ξ1：N1（90，86）和ξ2：N2（93，79），∴μ1=90，▱1=86，μ2=93，▱2=79，∴第二次测试的平均分比第一次测试的平均分要高，也比第一次成绩稳定，故选：C．【点评】本题考查正态分布曲线的特点，考查学生分析解决问题的能力，比较基础．5．【答案】B【解析】解：===i．故选：B．【点评】本题考查复数的代数形式混合运算，复数的除法的运算法则的应用，考查计算能力．6．【答案】A【解析】解：∵，只需将函数y=sin2x的图象向左平移个单位得到函数的图象．故选A．【点评】本题主要考查诱导公式和三角函数的平移．属基础题．7．【答案】B【解析】解：画出x，y满足的可行域如下图：z=3x+y的最大值为8，由，解得y=0，x=，（，0）代入2x+y+k=0，∴k=﹣，故选B．【点评】如果约束条件中含有参数，可以先画出不含参数的几个不等式对应的平面区域，分析取得最优解是哪两条直线的交点，然后得到一个含有参数的方程（组），代入另一条直线方程，消去x，y后，即可求出参数的值．8．【答案】D【解析】解：①y=x﹣1在区间（0，+∞）上为减函数，②y=（）x是减函数，③y=x+，在（0，1）是减函数，（1，+∞）上为，增函数，④y=lnx在区间（0，+∞）上为增函数，∴A，B，C不正确，D正确，故选：D【点评】本题考查了基本的函数的单调区间，属于基本题目，关键掌握好常见的函数的单调区间．9．【答案】A【解析】解：∵x∈（0，1）时，f（x）=x+1，f（x）是以2为周期的偶函数，∴x∈（1，2），（x﹣2）∈（﹣1，0），f（x）=f（x﹣2）=f（2﹣x）=2﹣x+1=3﹣x，故选A．10．【答案】A【解析】解：∵a=sin145°=sin35°，b=cos52°=sin38°，c=tan47°＞tan45°=1，∴y=sinx在（0，90°）单调递增，∴sin35°＜sin38°＜sin90°=1，∴a＜b＜c故选：A【点评】本题考查了三角函数的诱导公式的运用，正弦函数的单调性，难度不大，属于基础题．11．【答案】A【解析】解：由“|x﹣2|＜1”得1＜x＜3，由x2+x﹣2＞0得x＞1或x＜﹣2，即“|x﹣2|＜1”是“x2+x﹣2＞0”的充分不必要条件，故选：A．12．【答案】A【解析】解：由已知中的频率分布直方图可得时间不超过70分的累计频率的频率为0.4，则这样的样本容量是n==20．故选A．【点评】本题考查的知识点是频率分布直方图，熟练掌握频率的两个公式频率=矩形高×组距=是解答的关键．二、填空题13．【答案】　60　．【解析】解：由二项式系数的性质，可得2n=64，解可得，n=6；（2x﹣）6的展开式为为T r+1=C66﹣r•（2x）6﹣r•（﹣）r=（﹣1）r•26﹣r•C66﹣r•，令6﹣r=0，可得r=4，则展开式中常数项为60．故答案为：60．【点评】本题考查二项式定理的应用，注意系数与二项式系数的区别．14．【答案】　2　．【解析】解：∵一组数据2，x，4，6，10的平均值是5，∴2+x+4+6+10=5×5，解得x=3，∴此组数据的方差[（2﹣5）2+（3﹣5）2+（4﹣5）2+（6﹣5）2+（10﹣5）2]=8，∴此组数据的标准差S==2．故答案为：2．【点评】本题考查一组数据的标准差的求法，解题时要认真审题，注意数据的平均数和方差公式的求法．15．【答案】　（﹣4，）　．【解析】解：∵抛物线方程为y2=﹣8x，可得2p=8，=2．∴抛物线的焦点为F（﹣2，0），准线为x=2．设抛物线上点P（m，n）到焦点F的距离等于6，根据抛物线的定义，得点P到F的距离等于P到准线的距离，即|PF|=﹣m+2=6，解得m=﹣4，∴n2=8m=32，可得n=±4，因此，点P的坐标为（﹣4，）．故答案为：（﹣4，）．【点评】本题给出抛物线的方程，求抛物线上到焦点的距离等于定长的点的坐标．着重考查了抛物线的定义与标准方程等知识，属于基础题．16．【答案】【解析】延长EF交BC的延长线于P，则AP为面AEF与面ABC的交线，因为，所以为面AEF与面ABC所成的二面角的平面角。

西藏昌都第四高级中学2019届高三数学四月周考试题 文（考试时间：120分钟 试卷满分：150分）第Ⅰ卷一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1. 设全集为R ,集合{}21<≤-=x x M ,{}3,2,1,0,1,2--=N 则M N ⋂= ( ){}3,2.-A {}1,0,1-=B {}2,1,0,1-=C {}1,0=D2. 设1i2i 1iz -=++，则z =（ ）A ．0B ．12C ．1D 3．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（ ） A ．月接待游客量逐月增加 B ．年接待游客量逐年增加C ．各年的月接待游客量高峰期大致在7，8月D ．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4.有一个圆柱形笔筒如图放置,它的侧视图是( )A. B. C. D.5.α为三角形的一个内角,αtan =125-,则αcos =( )A.1312 B.135C.135-D.1312-6.某兴趣小组有2名男生和4名女生，现从中任选2名学生去参加活动，则恰好选中2名女生的概率为( )107.A103.B 53.C 52.D7.已知函数()222cos sin 2f x x x =-+，则（ ）A ．()f x 的最小正周期为π，最大值为3B ．()f x 的最小正周期为π，最大值为4C ．()f x 的最小正周期为2π，最大值为3D ．()f x 的最小正周期为2π，最大值为48.函数y =||2x sin2x 的图象可能是（ ）A ．B ．C ．D ．9.将函数cos3y x =的图象向左平移4π个单位长度,所得函数的解析式是( ) A.cos 34y x 3π⎛⎫=+⎪⎝⎭ B.cos 34y x π⎛⎫=+ ⎪⎝⎭ C.cos 34y x π⎛⎫=- ⎪⎝⎭D.cos 34y x 3π⎛⎫=- ⎪⎝⎭10．△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知C =60°，b ，c =3，则A =( )A. ︒30B.︒60C.︒75D.︒12011.已知双曲线2222:1x y C a b-=的离心率为2,则其两条渐进线的夹角为( )A.6π B.3π C.2π D.23π 12.若函数32()ln f x x x x x ax =-+-有两个不同的零点,则实数a 的取值范围是( )A. ),0(+∞B. (]0,1C. [)1,0- D. (),0-∞第Ⅱ卷二、填空题（本题共4小题，每小题5分，共20分）13.已知向量a ，b 满足||1=a ，1⋅=-a b ，则(2)⋅-=a a b ________.14．若x ，y 满足约束条件y 0200x x y y -≥⎧⎪+-≤⎨⎪≥⎩，则z 34x y =-的最小值为__________．15．设等比数列{}n a 满足a 1 + a 2 = –1, a 1 – a 3 = –3，则a 4 = ___________． 16. 直线1y x =+与圆22230x y y ++-=交于A B ，两点，则AB =________． 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤） 17.已知等差数列{}n a 中, 235220a a a ++=,且前10项和10100S = （1）求数列{}n a 的通项公式 （2）若11n n n b a a +=,求数列{}n b 的前n 项和18．（12分）某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：以最高气温位于各区间的频率代替最高气温位于该区间的概率。

2019年高三年级周考试卷理科数学（考试时间：120分钟 试卷满分：150分）第Ⅰ卷一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知集合{}{}=1,0,1,=|11A B x x --≤<,则A B ⋂= ( ) A. {}0 B.{}1,0- C.{}0,1 D.{}1,0,1-2.已知复数z 满足z=1+i i ,则z 的共轭复数z = ( )A. 1i +B. 1i - D. 1i -- 3.有一个圆柱形笔筒如图放置,它的侧视图是( )A. B. C. D.4.α为三角形的一个内角,tan =-,则cos =( )A. B. C.- D.-5．△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知C =60°，b ，c =3，则A =( )A. ︒30B.︒60C.︒75D.︒1206.()()6221x x -+的展开式中4x 的系数为( )A.-160B.320C.480D.640 7.已知随机变量x~,,则( ) A.0.16B.0.32C.0.68D. 0.848.将函数cos3y x =的图象向左平移4π个单位长度,所得函数的解析式是( ) A.cos 34y x π⎛⎫=+⎪⎝⎭ B.cos 34y x π⎛⎫=- ⎪⎝⎭C.cos 34y x 3π⎛⎫=-⎪⎝⎭ D.cos 34y x 3π⎛⎫=+ ⎪⎝⎭ 9.函数()f x 的图象如图所示,则()'f x 的图像可能是()A. B. C. D.10.已知双曲线2222:1x y C a b-=的离心率为2,则其两条渐进线的夹角为( )A.6π B.3π C.2π D.23π11设函数,若实数满足,则( ) A. B. C.D.12.若函数32()ln f x x x x x ax =-+-有两个不同的零点,则实数a 的取值范围是( ) A. ()0,?+∞ B. (]0,1 C. [)1,0- D. (),0-∞第Ⅱ卷二、填空题（本题共4小题，每小题5分，共20分）13.已知向量a ，b 满足||1=a ，1⋅=-a b ，则(2)⋅-=a a b ________.14．若x ，y 满足约束条件y 0200x x y y -≥⎧⎪+-≤⎨⎪≥⎩，则z 34x y =-的最小值为__________．15．设等比数列{}n a 满足a 1 + a 2 = –1, a 1 – a 3 = –3，则a 4 = ___________． 16. 直线1y x =+与圆22230x y y ++-=交于A B ，两点，则AB =________．三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤） 17.(12分)已知等差数列{}n a 中, 235220a a a ++=,且前10项和10100S = （1）求数列{}n a 的通项公式 （2）若11n n n b a a +=,求数列{}n b 的前n 项和18.（12分）2018年双11当天,某购物平台的销售业绩高达2135亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.9,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为140次.（1）请完成下表,并判断是否可以在犯错误概率不超过0.5%的前提下,认为商品好评与服务好评有关?（2）若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为X .①求随机变量X 的分布列; ②求X 的数学期望和方差.附: 22()()()()()n ad bc K a b c d a c b d -=++++,其中.n a b c d =+++19.（12分）如图，是直角梯形，又，，直线与直线所成的角（1）求证：平面平面；（2）求二面角的大小；20. （12分）已知椭圆 C 的对称中心为原点 O ,焦点在 x 轴上,左,右焦点分别为12,F F ,上顶点和右顶点分别为,B A ,线段AB 的中点为D ,且 12OD AB k k ⋅=-,AOB ∆的面积为（1）求椭圆C 的方程（2）过1F 的直线l 与椭圆C 相交于,M N 两点,若2MF N ∆的面积为163,求以2F 为圆心且与直线l 相切的圆的方程21. （12分）已知函数()()()211ln 02f x ax a x x a =-++≥ （1）求函数()f x 的单调区间（2）当0a =时,关于x 方程()f x mx =在区间21,e ⎡⎤⎣⎦上有唯一实数解,求实数m 取值范围请考生在第22、23两题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做的第一个题目计分．22．（本小题满分10分）选修4-4：坐标系与参数方程在平面直角坐标系中,以坐标原点为极点, x 轴的非负半轴为极轴建立极坐标系,已知点A 的极坐标为4π⎫⎪⎭,直线l 的极坐标方程为cos 4a πρθ⎛⎫-= ⎪⎝⎭,且点A 在直线l 上. （1）求a 的值及直线l 的直角坐标方程; （2）圆C 的参数方程为 1cos {sin x y αα=+= (α为参数),试判断直线l 与圆 C 的位置关系.23．（本小题满分10分)选修4-5：不等式选讲已知定义在R 上的函数()12f x x x =++-的最小值为a . （1）求a 的值;（2）若,,?p q r 为正实数,且p q r a ++=,求证: 2223p q r ++≥.BACDC BADBB AD二、填空题13.314.-115.-816.三、解答题17. I）设公差为d，由已知得2a2+a3+a5=4a1+8d=2010a1+10×92d=10a1+45d=100，（2分）解得a1=1d=2，（4分）所以{a n}的通项公式为a n=5+2（n-3）=2n-1，（5分）（ II）由（ I）可知a n•b n=(2n-1)×22n-1，所以S n=1×21+3×23+5×25+…+(2n-3)×22n-3+(2n-1)×22n-1，①4S n=1×23+3×25+5×27+…+(2n-3)×22n-1+(2n-1)×22n+1，②（7分）①-②得：-3S n=2+2×(23+25+…+22n-1)-(2n-1)×22n+1，∴S n=2+2×(23+25+…×22n+1-3（9分）=2+2×(8(1-4n-1)1-4)-(2n-1)×22n+1-3=-6+2×8(1-4n-1)+(6n-3)×22n+19（11分）=10+(6n-5)×22n+19（12分）列联表: 18. 1.由题意可得关于商品和服务评价的22则2200(1400400)7.4071505018020K ⨯-=≈⨯⨯⨯.由于7.4077.879<,则不可以在犯错误概率不超过0.5%的前提下,认为商品好评与服务好评有关.2.①每次购物时,对商品和服务都好评的概率为710且X 的取值可以是0,1,2,3,则3327(0)()101000P X ===12337189(1)()10101000P X C ===22337441(2)()()10101000P X C ===37343(3)()101000P X ===故X 的分布列为②由于7(3,)10XB则7217763()3,()3(1)10101010100E X D X =⨯==⨯⨯-=. 20. 1.设椭圆方程为22221(0)x y a b ab+=>>由已知得()(),0,0,,,22a b A aB b D ⎛⎫⎪⎝⎭,所以1·22OD AB bb a k k a a =⋅=--,即222a b =,① 又12AOB S ab ∆==所以ab =② 由①②解得228,4a b ==,所以椭圆方程为22184x y +=. 2.①当直线l x ⊥轴时,易得((,2,,M N --2MF N ∆的面积为不合题意.②当直线l 与 x 轴不垂直时,设直线l 的方程为()2,y k x =+代入椭圆方程得()2222128880k xk x k +++-=.显然有0∆>,设()()1122,,,,M x y N x y 则22121222888,,1212k k x x x x k k--+==++所以MN ==, 化简得)22112k MN k+=+.又圆的半径r =,所以212MF NS MN r ∆=⋅)2211162123k k +=⨯==+, 化简得4220k k +-=,解得1k =±,所以r =所以所求圆的方程为()2228x y -+=21. 1.当0a =时,函数()f x 的单调递增区间为()0,1,单调递减区间为()1,+∞; 当01a <<时,函数()f x 的单调递增区间为()0,1和1,a ⎛⎫+∞⎪⎝⎭,单调递减区间为11,a ⎛⎫⎪⎝⎭;当1a =时,函数()f x 的单调递增区间为()0,+∞;当1a >时,函数()f x 的单调递增区间为11,a ⎛⎫ ⎪⎝⎭和()1,+∞,单调递减区间为1,1a ⎛⎫⎪⎝⎭2. 22|11m m e ⎧⎫-≤<-⎨⎬⎩⎭或11m e ⎧⎫=-⎨⎬⎩⎭22. 1.因为点4A π⎫⎪⎭在直线l 上 , 44a ππ⎛⎫-= ⎪⎝⎭,a ∴=cos -4πρθ⎛⎫∴= ⎪⎝⎭,()cos sin 2ρθρθ+=所以2x y +=即为的直角l 坐标方程. 2.圆C 的方程1cos {sin x y αα=+= (α为参数),可化为()2211x y -+=,圆心()1,0到直线l 的距离为12d ==<, 所以直线l 与圆C 相交.。

西藏昌都第四高级中学2019高三理综月考试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

可能用到的相对原子质量：H 1 C12N14O16 Na 23 Mg 24 Al 27 S 32 Cr 52 Zn 65一、选择题：本题共13个小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列关于物质和结构的叙述，不正确的是( )A．磷脂是生物膜的主要成分，其组成元素为C、H、O、N、PB．ADP由磷酸、腺嘌呤和脱氧核糖组成，其中含有高能磷酸键C．核孔能实现核质之间频繁的物质交换和信息交流D．细胞骨架是由蛋白质组成的，能维持细胞的形态2. 下列与某些疾病有关的叙述，正确的是( )A．致癌病毒能够引起细胞癌变，是因为它们具有与致癌有关的核酸序列B．过敏反应和自身免疫病都不会破坏自身器官、组织和细胞C．糖尿病病人的尿液带走了大量的糖，所以其血糖浓度很低D．运动性失语症患者能听懂别人的谈话，不能看懂文字也不能讲话3．下列实验材料的选择理由不合理的是( )A．孟德尔选择豌豆的理由之一是豌豆属于自花传粉、闭花受粉植物B．赫尔希和蔡斯选择T2噬菌体的理由之一是它只有蛋白质和RNAC．在探究细胞呼吸方式时选择酵母菌的理由之一是它属于兼性厌氧菌D．比较H2O2在不同条件的分解实验中选择肝脏研磨液的理由是其中含过氧化氢酶4．下列关于性染色体和人类红绿色盲的叙述，不恰当的是( )A．位于性染色体上的基因在遗传时总和性别相关联B．人类的X和Y染色体无论大小和携带的基因种类都有差异C．人类红绿色盲形成的根本原因是基因突变D．红绿色盲基因和白化病基因在遗传时不遵循自由组合定律5．取生长状态一致的菠菜新鲜叶片，用打孔器打出若干圆片，均分成四组，各置于相同的密闭装置内，在其他条件相同且适宜的情况下，分别置于四种不同温度下(T1＜T2＜T3＜T4)。

昌都市第四高级中学2018-2019学年高二上学期第二次月考试卷数学班级__________ 姓名__________ 分数__________一、选择题1． 在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c，若﹣+1=0，则角B 的度数是（ ）A ．60°B ．120°C ．150°D ．60°或120°2． 若a ＜b ＜0，则下列不等式不成立是（ ）A．＞B．＞C ．|a|＞|b|D ．a 2＞b 23． 已知数列{}n a 的各项均为正数，12a =，114n n n na a a a ++-=+，若数列11n n a a +⎧⎫⎨⎬+⎩⎭的前n 项和为5，则n =（ ）A ．35B ． 36C ．120D ．1214．已知双曲线﹣=1的一个焦点与抛物线y 2=4x 的焦点重合，且双曲线的渐近线方程为y=±x ，则该双曲线的方程为（ ） A．﹣=1B ．﹣y 2=1 C ．x 2﹣=1 D．﹣=15． 函数f （x ）=sin ωx （ω＞0）在恰有11个零点，则ω的取值范围（ ） A ． C ． D ．时，函数f （x ）的最大值与最小值的和为（ ） A ．a+3 B ．6 C ．2D ．3﹣a6． 已知命题:()(0xp f x a a =>且1)a ≠是单调增函数；命题5:(,)44q x ππ∀∈，sin cos x x >.则下列命题为真命题的是（ ）A ．p q ∧B ．p q ∨⌝ C. p q ⌝∧⌝ D ．p q ⌝∧ 7． 若复数a 2﹣1+（a ﹣1）i （i 为虚数单位）是纯虚数，则实数a=（ ） A ．±1B ．﹣1C ．0D ．18． 奇函数f （x ）在区间[3，6]上是增函数，在区间[3，6]上的最大值为8，最小值为﹣1，则f （6）+f （﹣3）的值为（ ） A ．10B ．﹣10C ．9D ．159． 函数f （x ）＝kx ＋bx ＋1，关于点（－1，2）对称，且f （－2）＝3，则b 的值为（ ）A ．－1B ．1C ．2D ．410．已知数列{}n a 为等差数列，n S 为前项和，公差为d ，若201717100201717S S -=，则d 的值为（ ） A ．120 B ．110C ．10D ．20 11．已知集合，则A0或 B0或3C1或D1或312．若函数()()22f x x πϕϕ⎛⎫=+< ⎪⎝⎭的图象关于直线12x π=对称，且当12172123x x ππ⎛⎫∈-- ⎪⎝⎭，，，12x x ≠时，()()12f x f x =，则()12f x x +等于（ ）AB D 二、填空题13．直线l 过原点且平分平行四边形ABCD 的面积，若平行四边形的两个顶点为B （1，4），D （5，0），则直线l 的方程为 ．14．设实数x ，y 满足，向量=（2x ﹣y ，m ），=（﹣1，1）．若∥，则实数m 的最大值为 ．15．如果椭圆+=1弦被点A （1，1）平分，那么这条弦所在的直线方程是 ．16．如图，函数f （x ）的图象为折线 AC B ，则不等式f （x ）≥log 2（x+1）的解集是 ．17．已知数列{a n }中，2a n ，a n+1是方程x 2﹣3x+b n =0的两根，a 1=2，则b 5= ．18．已知变量x，y，满足，则z=log4（2x+y+4）的最大值为．三、解答题19．在平面直角坐标系xOy中，圆C：x2+y2=4，A（，0），A1（﹣，0），点P为平面内一动点，以PA为直径的圆与圆C相切．（Ⅰ）求证：|PA1|+|PA|为定值，并求出点P的轨迹方程C1；（Ⅱ）若直线PA与曲线C1的另一交点为Q，求△POQ面积的最大值．20f x=sin x+002x 0y 1 0 ﹣1（2）求函数g（x）=f（x）+sin2x的单调递增区间．21．设M是焦距为2的椭圆E：+=1（a＞b＞0）上一点，A、B是椭圆E的左、右顶点，直线MA与MB的斜率分别为k1，k2，且k1k2=﹣．（1）求椭圆E 的方程；（2）已知椭圆E ：+=1（a ＞b ＞0）上点N （x 0，y 0）处切线方程为+=1，若P是直线x=2上任意一点，从P 向椭圆E 作切线，切点分别为C 、D ，求证直线CD 恒过定点，并求出该定点坐标．22．设函数f （x ）=mx 2﹣mx ﹣1．（1）若对一切实数x ，f （x ）＜0恒成立，求m 的取值范围； （2）对于x ∈[1，3]，f （x ）＜﹣m+5恒成立，求m 的取值范围．23． （本题满分12分）在如图所示的几何体中，四边形ABCD 为矩形，直线⊥AF 平面ABCD ，AB EF //，12,2====EF AF AB AD ，点P 在棱DF 上.（1）求证：BF AD ⊥；（2）若P 是DF 的中点，求异面直线BE 与CP 所成角的余弦值； （3）若FD FP 31=，求二面角C AP D --的余弦值.24．已知点（1，）是函数f（x）=a x（a＞0且a≠1）的图象上一点，等比数列{a n}的前n项和为f（n）﹣c，数列{b n}（b n＞0）的首项为c，且前n项和S n满足S n﹣S n﹣1=+（n≥2）．记数列{}前n项和为T n，（1）求数列{a n}和{b n}的通项公式；（2）若对任意正整数n，当m∈[﹣1，1]时，不等式t2﹣2mt+＞T n恒成立，求实数t的取值范围（3）是否存在正整数m，n，且1＜m＜n，使得T1，T m，T n成等比数列？若存在，求出m，n的值，若不存在，说明理由．昌都市第四高级中学2018-2019学年高二上学期第二次月考试卷数学（参考答案） 一、选择题1． 【答案】A【解析】解：根据正弦定理有：=，代入已知等式得：﹣+1=0，即﹣1=，整理得：2sinAcosB ﹣cosBsinC=sinBcosC ， 即2sinAcosB=sinBcosC+cosBsinC=sin （B+C ）， 又∵A+B+C=180°， ∴sin （B+C ）=sinA ， 可得2sinAcosB=sinA ， ∵sinA ≠0，∴2cosB=1，即cosB=， 则B=60°． 故选：A ．【点评】此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．2． 【答案】A 【解析】解：∵a ＜b ＜0， ∴﹣a ＞﹣b ＞0，∴|a|＞|b|，a 2＞b 2，即，可知：B ，C ，D 都正确，因此A 不正确． 故选：A ．【点评】本题考查了不等式的基本性质，属于基础题．3． 【答案】C【解析】解析：本题考查等差数列的定义通项公式与“裂项法”求数列的前n 项和．由114n n n na a a a ++-=+得2214n n a a +-=，∴{}2n a 是等差数列，公差为4，首项为4，∴244(1)4n a n n =+-=，由0n a >得2na n=．111(1)2212n nn na a n n+==+-+++，∴数列11n na a+⎧⎫⎨⎬+⎩⎭的前n项和为1111(21)(32)(1)(11)52222n n n-+-+++-=+-=，∴120n=，选C．4．【答案】B【解析】解：已知抛物线y2=4x的焦点和双曲线的焦点重合，则双曲线的焦点坐标为（，0），即c=，又因为双曲线的渐近线方程为y=±x，则有a2+b2=c2=10和=，解得a=3，b=1．所以双曲线的方程为：﹣y2=1．故选B．【点评】本题主要考查的知识要点：双曲线方程的求法，渐近线的应用．属于基础题．5．【答案】A【解析】A． C． D．恰有11个零点，可得5π≤ω•＜6π，求得10≤ω＜12，故选：A．6．【答案】D【解析】考点：1、指数函数与三角函数的性质；2、真值表的应用.7．【答案】B【解析】解：因为复数a2﹣1+（a﹣1）i（i为虚数单位）是纯虚数，所以a2﹣1=0且a﹣1≠0，解得a=﹣1．故选B．【点评】本题考查复数的基本概念的应用，实部为0并且虚部不为0，是解题的关键．8． 【答案】C【解析】解：由于f （x ）在[3，6]上为增函数，f （x ）的最大值为f （6）=8，f （x ）的最小值为f （3）=﹣1，f （x ）为奇函数，故f （﹣3）=﹣f （3）=1，∴f （6）+f （﹣3）=8+1=9． 故选：C ．9． 【答案】【解析】解析：选B.设点P （m ，n ）是函数图象上任一点，P 关于（－1，2）的对称点为Q （－2－m ，4－n ），则⎩⎪⎨⎪⎧n ＝km ＋b m ＋14－n ＝k （－2－m ）＋b－1－m，恒成立．由方程组得4m ＋4＝2km ＋2k 恒成立， ∴4＝2k ，即k ＝2，∴f （x ）＝2x ＋b x ＋1，又f （－2）＝－4＋b －1＝3，∴b ＝1，故选B. 10．【答案】B 【解析】试题分析：若{}n a 为等差数列，()()111212nn n na S d a n nn -+==+-⨯，则n S n ⎧⎫⎨⎬⎩⎭为等差数列公差为2d ,2017171100,2000100,201717210S S d d ∴-=⨯==,故选B. 考点：1、等差数列的通项公式；2、等差数列的前项和公式.11．【答案】B 【解析】，，故或，解得或或，又根据集合元素的互异性，所以或。