浙江省温州地区2015年初中数学竞赛能力评估检测试卷

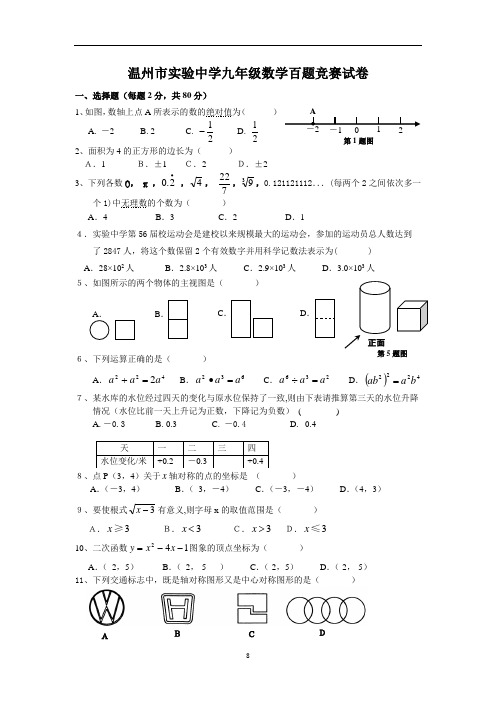
温州市实验中学九年级数学百题竞赛试卷一、选择题（每题2分，共80分）1、如图，数轴上点A所表示的数的绝对值为（）A.－2B. 2C.21- D.212、面积为4的正方形的边长为（）Ａ．1 Ｂ．±1 Ｃ．2 Ｄ．±23、下列各数0，π，•2.0，4，722，39，0.121121112．．．(每两个2之间依次多一个1)中无理数的个数为（）A．4 B．3 C．2 D．1４．实验中学第56届校运动会是建校以来规模最大的运动会，参加的运动员总人数达到了2847人，将这个数保留2个有效数字并用科学记数法表示为( )A．28×102人B．2.8×103人C．2.9×103人D．3.0×103人５、如图所示的两个物体的主视图是（）６、下列运算正确的是（）A．4222aaa=+B．632aaa=•C．236aaa=÷D．()4222baab=７、某水库的水位经过四天的变化与原水位保持了一致,则由下表请推算第三天的水位升降情况（水位比前一天上升记为正数，下降记为负数）( )A.－0.3B. 0.3C. －0.4D. 0.4８、点P（3，4）关于x轴对称的点的坐标是（）A．（－3，4）B．（3，－4）C．（－3，－4）D．（4，3）９、要使根式3-x有意义,则字母x的取值范围是（）Ａ．3x≥Ｂ．3x<Ｃ．3x>Ｄ．3x≤10、二次函数142--=xxy图象的顶点坐标为（）A．（2，5）B．（2，-5 ）C．（-2，5）D．（-2，-5）11、下列交通标志中，既是轴对称图形又是中心对称图形的是（）天一二三四水位变化/米+0.2 －0.3+0.4ＡＢＣＤ－1 0 1－2第1题图DB．C．正面题图12、反比例函数y=kx的图象经过点(-2,4)，则k 的值是( )A.-12B. 12C.-8D.8 13、如图，A 、B 、C 、是⊙O 上的三点，∠BAC=40°，则∠BOC 的大小是（ ） A ．80° B ．60° C ．45° D ．22.5°14、一个正方体的每一个面都写着一个汉字，其平面展开图如图所示， 那么在该正方体中，和“州”相对的字是 ( )A ．实B ．验C ．中D ．学 15、如图所示的是下列不等式组中（ ）的解集A ．⎩⎨⎧≤-<23x x B ．⎩⎨⎧≤-23x x ＞ C ． ⎩⎨⎧≥-23x x ＞ D ．⎩⎨⎧≥-23x x ＜16、如图, 在平行四边形ABCD 中, ∠B=600，AB=5cm ，则下面正确的是（ ）A ．BC=5cm ，∠D=600B ． ∠A=1200, AD=5cm. C ．AD=5cm, ∠A=600D ．∠C=1200, CD=5cm17、已知⎩⎨⎧==12y x 是方程x －k=y 的解,则k 的值为 ( )A. －1B. －3C. 1D. 318、已知圆锥的底面直径等于6，高等于4，则其侧面积为（ ） A ．π9 B ．π15 C ．π24 D ．π3019、若设下图中每支钢笔的价格为x 元，每本练习本的价格为y 元，根据 图示信息列出了下列方程组，其中正确的是（ ）A ．⎩⎨⎧=+=263y x yx B ．⎩⎨⎧=+=+263222y x y x C ．⎩⎨⎧=+=+2634422y x y x D ．⎩⎨⎧=+=+2624422y x y x20、 如图AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，如果 AB ＝10cm ，CD ＝8cm ，那么AE 的长是（ ）A ．4 B. 6 C. 7 D. 8x图1210-1-2-3第15题图ABC O第13题图 A BCD 第16题图验实 州 温 中 学 第14题图第20题图B ODA CE 第19题图共44元共26元第18题图21、已知在等腰△ABC 中，∠A=70°，AB=AC ，则∠B 为（ ）A ．70°B ．45°C ．55°D ．65° 22、在直角三角形ABC 中，∠C 为直角，sinA=1312,则cosB 的值为（ ） A ．1312 B ．135 C ．1213 D ． 12523、北京08奥运会吉祥物是“贝贝”、“晶晶”、“欢欢”、“迎迎”、“妮妮”。

温州地区2015年初中数学竞赛能力评估检测试卷（检测范围：初中数学竞赛大纲要求所有内容）一、单项选择题（本大题分2小题，每题5分，共10分）1. 关于x 的方程|x 2-2|=m -x 有3个互不相同的解，则m max 为( ).A 、29B 、43C 、49D 、27 2. 已知ABC ∆的两条中线的长分别为5、10.若第三条中线的长也是整数，则第三条中线长的最大值为( ).A 、7B 、8C 、14D 、15二、填空题（本大题分16小题，每空5分，共90分）3. 已知在平面直角坐标系xOy 中，O 为坐标原点，线段AB 的两个端点A (0,2)，B (1,0)分别在y 轴和x 轴的正半轴上，点C 为线段AB 的中点，现将线段BA 绕点B 按顺时针方向旋转90°得到线段BD ，抛物线y =ax 2+bx +c (a ≠0)经过点D .若该抛物线y =ax 2+bx +c (a ≠0)经过点E (1,1)，点Q 在抛物线上，且满足∠QOB 与∠BCD 互余，若符合条件的Q 点的个数是4个，则a 的取值范围为 .4. 圣诞老人有44个礼物，分别装在8个袋子中，袋子中礼物的个数各不相同，最多的有9个.现要从中选出一些袋子，将其中的所有礼物恰好平均分给8个同学(每个同学至少分得一个礼物)，那么共有 种不同的选择.5. 方程xyz+xy+xz+yz+x+y+z =2012的非负整数解有 组.6. 已知在平面直角坐标系中有如下36条直线：y =18x +17,y =17x +16,…,y =2x +1, y=x ,y =-x ,y =-2x +1,…,y =-17x +16,y =-18x +17，那么由这些直线相交所构成的交点有 .7. 如图，反比例函数xk y =的图象经过点(-1,22-)，点A 是该图象第一象限分支上的动点，连结AO 并延长交另一支于点B ，以AB 为斜边作等腰直角三角形ABC ，顶点C 在第四象限，AC 与x 轴交于点P ，连结BP .在点A 运动过程中，当BP 平分∠ABC 时，点C 的坐标是 . 8. 如图，抛物线)0(2≠+=a c ax y 与y 轴交于点A ，与x 轴交于点B ，C 两点(点C 在x 轴正半轴上)，ABC ∆为等腰直角三角形，且面积为4.现将抛物线沿BA 方向平移，平移后的抛物线经过点C 时，与x 轴的另一交点为E ，其顶点为F ，对称轴与x 轴的交点为H .现将一足够大的三角板的直角顶点Q 放在射线AF 或射线HF上，一直角边始终过点E ，另一直角边与y 轴相交于点P ，若存在这样的点Q ，使以点P ，Q ，E 为顶点的三角形与POE ∆全等，则点Q 的坐标为 .9. 在ABC ∆中，AB =10，AD 是BC 边上的高，已知AD=BD ，点H 、O 分别是ABC∆第7题第8题 第3题的垂心和外心，则HO 的最小长度为 .10. 方程x 3+Ax 2+Bx +C =0的系数A ,B ,C 为整数，|A |<10，|B |<10，|C |<10，且1是方程的根，那么这种方程总共有 个.11. 某同学用纸剪凸四边形，凸五边形，凸六边形，每种至少剪一个，剪出的多边形共有95条边，那么所剪的多边形中的内角是直角的个数最多是 个.12. 设a ,b 为实数，那么a 2+ab +b 2-a -b 的最小值是 .13. 已知a a 14501450-++，其中a 是正整数，那么所有使得x 为整数的a的取值之和为 .14. 摆出一个单位正方形，至少需要4根单位长的木棍，那么摆出18个单位正方形最少需要 根单位长的木棍.15. 已知正整数a ,b ,c 满足:1a b c <<<，111a b c ++=，2b ac =，则b = ．16. 三个正方体粘在一起构成的几何体如图所示，其中上面正方体的下底面正方形的四个顶点分别是下面正方体上底面正方形的三等分点.如果最下面正方体的棱长为9，那么这个几何体的表面积是 .17. 黑板上写有1,2,…,2013这2013个数，某人擦去黑板上的任意n 个数，要使得剩下的数中至少有两个数的和是2的幂次，则 n 最大是 .18. 设x ,y 是正实数，则x +y +xy y x 11-+-的最小值为 . 19. 今有2013个碗，排成一行.小明首先从左边开始, 在第一个碗里放入一枚硬币，接着每隔一个放入一枚；然后从右边开始，在第一个碗里放入一枚硬币，接着每隔2个放入一枚；最后再从左边开始，在第一个碗里放入一枚硬币，接着每隔4个放入一枚.那么从左向右数，有3枚硬币的碗，第一个是第 个，最后一个是第 个.20. 有n 个人在网上购物，n >2.已知，任意三个人中有两人买有同一种类的商品，没有三个人买有同一种类的商品.若他们中的甲和乙两人各买了四种商品，但没有买同一种类的商品，则n 的最大值是 .当n 最大时，这n 个人一共最少买了 种商品.三、分析解答题（本大题分5小题，分值依次为12分、10分、8分、10分、10分，共50分）21. (12分)全国初中数学竞赛共有14道题(5道选择题，5道填空题，4道解答题)，满分150分，其中选择题和填空题每题答对得7分，答错得0分，没有其他分值；解答题每题20分，步骤分只能是0、5、10、15、20分，没有其他分值，则所有可能得到的不同分值共有多少个？22. (10分)如图，在平行四边形ABCD 中，E 为对角线第7题 CA B EBD 上一点，且满足ECD ACB ∠=∠，AC 的延长线与ABD ∆的外接圆交于点F .证明：DFE AFB ∠=∠．23. (8分)在ABC ∆中，已知∠ABC =∠BAC =70°，P 为三角形内一点，∠P AB =40°，∠PBA =20°.证明：P A+PB=PC .24. (10分)某公司的工作人员每周都要工作5天连续休息2天，而公司要求每周从周一至周四，每天都有25人上班；从周五至周日，每天都有30人上班.那么该公司至少需要多少名工作人员？若最少n 个工作人员的工号1~n ，请按工号编出人员的排班表.25、(10分)设n 是整数，如果存在整数x ,y ,z 满足3333n x y z xyz =++-，则称n第22题具有性质P.在1,5,2013,2014这四个数中，哪些数具有性质P，哪些数不具有性质P？并说明理由.参 考 答 案一、单项选择题(本大题分2小题，每题5分，共10分) 题目 1 2答案 C C二、填空题(本大题分16小题，每空5分，共90分)3、415431+>-<a a 或 4、31 5、27 6、326 7、2-2， 8、），（2126（6,3）（10,12）），（146144±±9、5 10、270 11、90 12、31- 13、158 14、 45 15、 36 16、766 17、1003 18、2 19、21；2001 20、10；20三、分析解答题(本大题分5小题，分值依次为12分、10分、8分、10分，10分，共50分)21、(12分)【解】(4分+6分+2分=12分)22、(10分)【解】(2分+3分+2分+3分=10分)证明：由ABCD 是平行四边形及已知条件知ECD ACB DAF ∠=∠=∠(2分) 又A 、B 、F 、 D 四点共圆，∴BDC ABD AFD ∠=∠=∠，∴ECD ∆∽DAF ∆(5分)，∴ED CD AB DF AF AF==(7分)， 又EDF BDF BAF ∠=∠=∠，∴EDF ∆∽BAF ∆，故DFE AFB ∠=∠(10分)23、(8分)【解】(解法多种，酌情给分)24、(10分)【解】(暂无解答，征求答案)25、(10分)【解】取1x =，0y z ==，可得33311003100=++-⨯⨯⨯，所以1具有性质P .取2x y ==，1z =，可得33352213221=++-⨯⨯⨯，所以5具有性质P .(5分)为了一般地判断哪些数具有性质P ，记333(,,)3f x y z x y z xyz =++-，则33(,,)()3()3f x y z x y z xy x y xyz =++-+-3()3()()3()x y z x y z x y z xy x y z =++-+++-++＝3()3()()x y z x y z xy yz zx ++-++++222()()x y z x y z xy yz zx =++++--- 2221()[()()()]2x y z x y y z z x =++-+-+-. 即(,,)f x y z 2221()[()()()]2x y z x y y z z x =++-+-+- ①(4分) 不妨设x y z ≥≥，如果1,0,1x y y z x z -=-=-=，即1,x z y z =+=，则有(,,)31f x y z z =+；如果0,1,1x y y z x z -=-=-=，即1x y z ==+，则有(,,)32f x y z z =+；如果1,1,2x y y z x z -=-=-=，即2,1x z y z =+=+，则有(,,)9(1)f x y z z =+；由此可知，形如31k +或32k +或9k (k 为整数)的数都具有性质P .因此，1，5和2014都具有性质P . (8分)若2013具有性质P ，则存在整数,,x y z 使得32013()3()()x y z x y z xy yz zx =++-++++.注意到3|2013，从而可得33|()x y z ++，故3|()x y z ++，于是有39|()3()()x y z x y z xy yz zx ++-++++，即9|2013，但2013＝9×223＋6，矛盾，所以2013不具有性质P .(10分)。

G FE'C'E A DB C浙江省温州地区初中数学竞赛选拔试卷（检测范围：初中数学竞赛大纲要求所有内容）一、单项选择题（本大题分4小题，每题5分，共20分）1、设二次函数y 1=a (x -x 1)(x -x 2)(a ≠0,x 1≠x 2)的图象与一次函数y 2=dx +e (d ≠0)的图象交于点(x 1,0)，若函数y =y 2+y 1的图象与x 轴仅有一个交点，则( ). A ．a (x 1-x 2)=d B ．a (x 2-x 1)=d C ．a (x 1-x 2)2=d D ．a (x 1+x 2)2=d2、如图，ΔABC 、ΔEFG 均是边长为2的等边三角形，点D 是边BC 、EF 的中点，直线AG 、FC 相交于点M ．当ΔEFG 绕点D 旋转时，线段BM 长的最小值是( ). A ．32- B ．13+ C ．2 D ．13-3、一名模型赛车手遥控一辆赛车，先前进1m ，然后原地逆时针旋转α(0°<α<180°)，被称为一次操作．若5次操作后，发现赛车回到出发点，则α为( ). A ．72° B ．108° C ．144° D ．以上选项均不正确4、方程()y x y xy x +=++322的整数解有( ).A 、3组B 、4组C 、5组D 、6组 二、填空题（本大题分16小题，每题5分，共80分）5、如图，在矩形ABCD 中，AB =64，AD =10，连接BD ，DBC ∠的角平分线BE 交DC 于点E ，现把BCE ∆绕点B 逆时针旋转，记旋转后的BCE ∆为''E BC ∆，当射线'BE 和射线'BC 都与线段AD 相交时，设交点分别为F ，G ，若BFD ∆为等腰三角形，则线段DG 长为 .6、如图，在平面直角坐标系中，点M 是第一象限内一点，过M 的直线分别交x 轴，y 轴的正半轴于A 、B 两点，且M 是AB 的中点.以OM 为直径的⊙P 分别交x 轴，y 轴于C 、D 两点，交直线AB 于点E (位于点M 右下方)，连结DE 交OM 于点K .设x OBA =∠tan (0<x <1)，y MKOK=，则y 关于x 的函数解析式为 .7、如图，梯形ABCD 的面积为34cm 2，AE=BF ，CE 与DF 相交于O ，OCD ∆的面积为11cm 2，则阴影部分的面积为______cm 2．8、如图，四边形ABCD 为正方形，⊙O 过正方形的顶点第5题 第2题 第6题 第7题A 和对角线的交点P ，分别交AB 、AD 于点F 、E ．若⊙O 的半径为23，AB =2+1，则EDAE的值为 ． 9、已知一个正三角形的三个顶点在一个正方形的边上移动.如果这个内接三角形的最大面积是3.则该正方形的边长为 . 10、在四边形ABCD 中，边AB=x ，BC=CD =4，DA =5，它的对角线AC=y ，其中x ，y 都是整数，∠BAC =∠DAC ，那么x = ．11、如果满足 ||x 2-6x -16|-10| = a 的实数x 恰有6个，那么实数a 的值等于 ．12到三百多千米以外的乙站，已知每列货车的平均速度都相等，且记为v千米/小时．两列货车实在运行中的间隔不小于225v ⎛⎫⎪⎝⎭千米，这这批救灾物资全部运到目的地最快需要6小时，那么每隔 分钟从甲站向乙站发一趟货车才能使这批货物在6小时内运到.13、已知0≤a-b ≤1，1≤a+b ≤4，那么当a -2b 达到最大值时，8a +2015b 的值等于 .14、在边长为l 的正方形ABCD 中，点M 、N 、O 、P 分别在边AB 、BC 、CD 、DA 上．如果AM=BM ，DP =3AP ，则MN+NO+OP 的最小值是 .15、如图，在四边形纸片ABCD 中，AB=BC ，AD=CD ，∠A =∠C =90°，∠B =150°，将纸片先沿直线BD 对折，再将对折后的图形沿从一个顶点出发的直线裁剪，剪开后的图形打开铺平，若铺平后的图形中有一个是面积为2的平行四边形，则CD =______________. 16、从1,2,…,中选出总和为1009000的1004个数，并且这1004个数中的任意两数之和都不等于．则这1004个数的平方和为 ． 17、已知直角三角形ABC 中，斜边AB 长为2，∠ACB =90°，三角形内一个动点到三个顶点的距离之和的最小值为7，则这个直角三角形的两个锐角大小分别为 ， ． 18、若实数x 、y 满足：=+-13x x y y -+23，则若设p=x+y ，则p max = ，p min = ． 19、已知平面上有4个圆叠在一起形成10个区域，其中在外区域的三个圆每个圆有5个区域，在内区域的圆有7个区域．现将数字0,1,…,9分别放入10个区域，且使每个圆都有相同的数字和，则数字和S 的取值范围为 ．第8题 第10题第15题 第19题x 1x 2 x 3x 4 x 5 x 6x 7x 8 x 9x 1020、已知∠BAC =90°，四边形ADEF 是正方形且边长为1，则CABC AB 111++ 的最大值为 ，简述理由(可列式)： .三、分析解答题（本大题分5小题，分值依次为8分、10分、8分、14分、10分，共50分）21、(8分)牛顿和莱布尼茨于17世纪分别地创立了积分学.其中有一个重要的概念：定积分.我们规定把函数()x f 中区间[]b a ，(包括a ,b )与x 轴围成的面积记作：()⎰ba x x f d .(1).试证：()()x x f k x x kf babad d ⎰⎰=；(2)．对于任意实数c b a ，，其中(a ＜c ＜b ),是否都有：()()()⎰⎰⎰+=bccabax x f x x f x x f d d d .如没有请举出反例；如有，请证明之.22、(10分)在正方形ABCD 的AB 、AD 边各取点K 、N ，使得AK ·AN =2BK ·DN ，线段CK 、CN 交对角线BD 于点L 、M ，试证：∠BLK =∠DNC =∠BAM .第20题 ABD E C23、(8分)设AB ，CD 为圆O 的两直径，过B 作PB 垂直AB ，并与CD 延长线相交于点P ，过P 作直线PE ，与圆分别交于E ，F 两点，连AE ，AF 分别与CD 交于G ，H 两点(如图)，求证：OG=OH .24、(14分)如图，点A 和动点P 在直线l 上，点P 关于点A 的对称点为Q ，以AQ 为边作Rt ABQ ∆，使∠BAQ =90°，AQ ：AB =3：4，作ABQ ∆的外接圆O ．点C 在点P 右侧，PC =4，过点C 作直线m ⊥l ，过点O 作OD⊥m 于点D ，交AB 右侧的圆弧于点E ．在射线CD 上取点F ，使DF =23CD ，以DE ，DF 为邻边作矩形DEGF ．设AQ =3x ． (1)用关于x 的代数式表示BQ ，DF ．(2)当点P 在点A 右侧时，若矩形DEGF 的面积等于90，求AP 的长． (3)在点P 的整个运动过程中，①当AP 为何值时，矩形DEGF 是正方形？②作直线BG 交⊙O 于点N ，若BN 的弦心距为1，求AP 的长．第23题25、(10分)有A、B、C三个村庄，各村分别有适龄儿童a、b、c人.今要建立一所小学，使各村学生到校总里程最短.试问：若三村人数不一定相等时学校应建在哪里？初 中 数 学 竞 赛 选 拔 试 卷参 考 答 案一、单项选择题()题目 1 2 3 4 答案BDDD二、填空题(本大题分5、1798 6、212xy -= 7、12 8、222或 9、332+ 10、4或5 11、10 12、12 13、8 14、 48515、 432+或32+16、1351373940 17、30°,60° 18、2213921539++或 19、21≤S ≤25 20、221+；理由：求式=1+BC1，又EFC BDE ∆∆∽⇒BD ·CF =1，BC 2≥2+2BD ·CF +CF BD •4=8∴计算可得为221+三、分析解答题(本大题分5小题，分值依次为8分、10分、14分、10分，共50分)21、(8分)【解】(暂无解答，征求答案) 22、(10分)【解】连结KN 、KM ，将NDC ∆绕点C 顺时针旋转90°得EBC ∆.AB=AD ⇒AK+BK=AN+DN ⇒(AK-AN )2=(DN-BK )2⇒AK 2+AN 2-2AK ·AN =DN 2+BK 2-2ND ·BK (两边同加2AK ·AN )⇒AK 2+AN 2=(DN +BK )2(由AK ·AN =2BK ·DN 可知),结合图可知NK 2=KE 2 ∴EKC NKC ∆∆∽(SSS )∴∠DNC =∠KEC =∠KNC ，且∠KCN =45° ∴B 、C 、M 、K 四点共圆(∠KBN =45°) ∴KM ⊥CN ，∴A 、K 、M 、N 四点共圆 ∴∠KAM =∠KNM =∠DNC ，又∠MDN =45°=∠KCN ∴N 、L 、C 、D 四点共圆，∴∠DNC =∠DLC =∠KLB ∴∠DNC =∠KAM =∠KLB (即∠BLK =∠DNC =∠BAM )23、(8分)【解】23、第23题解24、(14分)【解】25、(10分)【解】(I)当三村人数相等时，分以下两种情形(如图)：(1)ABC∆中最大角大于120°，不妨令∠A≥120°，则学校应建在A村；(2)ABC∆中最大角小于120°，则学校应建在X点(此点到三边的张角相等，亦称ABC∆的费马点) (II)当三村人数不一定相等时，则学校所在地X，可通过物理学的模拟方法求出：在平面上，用三点A、B、C模拟三村，用重物a、b、c模拟相应各村人数，并用细线通过滑轮连接于X点.当出现平衡时，平衡点X就是学校该建的地方.由静力学势能原理可知：AX·a+BX·b+CX·c达最小值，即各村分别有适龄儿童到校总里程最短.当a=b=c时，AX、BX、CX三方向拉力ABC (1)XABC(2)相等且平衡.由对称关系，立得：∠AXB=∠BXC=∠CXA=90°.。

山东省临沂市2015年初中学生学业考试数学答案解析第Ⅰ卷【解析】如图：35=，故a a为：故选B。

故选D。

【考点】反比例函数与一次函数的交点问题第Ⅱ卷AB A⨯sin=4-AB BDAD BD=3721.【答案】（1）条形统计图如图：∵O切BC【考点】切线的性质，扇形面积的计算24.【答案】（1）303760(18)503600(923)x x y x x +⎧=⎨+⎩≤≤≤≤ （2）010560a 当＜＜时，方案二合算，当10560a ＞时，方案一合算 【解析】（1）当18x ≤≤时，每平方米的售价应为：4000(8)30303760y x x =--⨯=+（元/平方米）当923x ≤≤时，每平方米的售价应为：4000(8)50503600y x x =+-⨯=+（元/平方米）。

∴303760(18)503600(923)x x y x x +⎧=⎨+⎩≤≤≤≤。

（2）第十六层楼房的每平方米的价格为：501636004400⨯+=（元/平方米）， 按照方案一所交房款为：14400120(18%)485760W a a =⨯⨯--=-（元）， 按照方案二所交房款为：24400120(110%)475200W =⨯⨯-=（元），当12W W ＞时，即485760475200a -＞，解得：010560a ＜＜， 当12W W ＜时，即485760475200a -＜，解得：10560a ＞， ∴010560a 当＜＜时，方案二合算；当10560a ＞时，方案一合算。

【考点】利用一次函数解决问题25.【答案】（1）AF 与BE 的数量关系是：AF BE =，位置关系是：AF BE ⊥。

答案是：相等，互相垂直； （2）结论仍然成立。

理由是：∵正方形ABCD 中，AB AD CD ==，∴在ADE △和DCF △中，AE DF AD CD DE CF =⎧⎪=⎨⎪=⎩，∴ADE DCF △≌△， ∴DAE CDF ∠=∠，又∵正方形ABCD 中，90BAD ADC ∠=∠=︒， ∴BAE ADF ∠=∠，∴在ABE △和ADF △中，AB DA BAE ADF AE DF =⎧⎪∠=∠⎨⎪=⎩，∴ABE ADF △≌△ ，∴BE AF =，ABM DAF ∠=∠， 又∵90DAF BAM ∠+∠=︒， ∴90ABM BAM ∠+∠=︒，∴在ABM △中，180()90AMB ABM BAM ∠=︒-∠+∠=︒， ∴BE AF ⊥；（3）第（1）问中的结论都能成立.理由是：∵正方形ABCD 中，AB AD CD ==，∴在ADE △和DCF △中，AE DF AD CD DE CF =⎧⎪=⎨⎪=⎩，∴ADE DCF △≌△， ∴DAE CDF ∠=∠，又∵正方形ABCD 中，90BAD ADC ∠=∠=︒， ∴BAE ADF ∠=∠，∴在ABE △和ADF △中，AB DA BAE ADF AE DF =⎧⎪∠=∠⎨⎪=⎩，∴ABE ADF △≌△，∴BE AF =，ABM DAF ∠=∠， 又∵90DAF BAM ∠+∠=︒ ，90ABM BAM ∴∠+∠=︒，⊥。

温州市第三届初中数学学科知识竞赛试卷一 选择题〔每题5分，共30分〕1．平面上，在凸10边形的所有内角中，锐角的个数最多是〔 〕个. A .4 B .3 C .2 D .12.如图，A 、C 是函数的图象上的点，且A 、C 关于原点对称. AB ⊥x 轴，CD ⊥x 轴，垂足分别为B 、D ，如果四边形ABCD 的面积为S ，那么〔 〕A .S =1B .1＜S ＜2C ..S=2D .S ＞23．如图，直角梯形ABCD 中，A D ∥BC ，A B ⊥BC ，AB =7，AD =2，BC=3，如果在AB 边上取一点P ，使得以P 、A 、D 为顶点的三角形和以P 、B 、C 为顶点的三角形相似，那么这样的点P 能取到〔 〕个.A ．1B ．2C ．3D ．44．如图，直角梯形ABCD 中，A D ∥BC,A B ⊥BC ，AD=3，BC=5，将腰DC 绕点D 的逆时针方向旋转90°至DE ，连结AE ，那么△ADE 的面积是〔 〕A ．1B ．2C ．3D ．45．如图,甲、乙两人在斜坡AB 上作往返跑训练．：甲上坡的速度是a 米/分，下坡的速度是b 米/分，〔a ＜ b ；乙上坡的速度是12a 米/分，下坡的速度是2b 米/分．如果甲、乙二人同时从点A 出发，时间为t 〔分〕，离开点A 的路程为S 〔米〕．那么下面图象中，能大致表示甲、乙两人从点A 出发后的时间t 〔分〕及离开点A 的路程S 〔米〕之间的函数关系的是〔 〕 6．甲、乙两个茶杯中各装有200克盐水和糖水，盐水的含盐量及糖水的含糖量相等。

现将A CBD OBAAt 〔分〕S 〔米〕OBt 〔分〕 S 〔米〕Ct 〔分〕S 〔米〕Dt 〔分〕S 〔米〕ABCD〔第2题〕〔第3题〕〔第4题〕〔第5题〕市〔县〕 学 校 姓名 准考证号码 ………………………………………………………………… 密 …………………… 封 ……………………… 线 ……………………………………………甲杯中的盐水倒一局部到乙杯中，调匀后再倒回同量的混合液体那么〔 〕 A ．甲杯中液体的含盐量大于乙杯中液体的含糖量. B ．甲杯中液体的含盐量等于乙杯中液体的含糖量. C ．甲杯中液体的含盐量小于乙杯中液体的含糖量.D ．甲杯中液体的含盐量及乙杯中液体的含糖量谁多谁少不能确定.二 填空题〔每题6分，共30分〕7．如图，三个半圆依次相外切，它们的圆心都在x 轴的正半轴上，并都及直线y ＝33x 相切，设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1、r 2、r 3， 那么当r 1＝1时，r 3＝ _____. 8. 如图，B 是线段AC 的中点，过点C 的直线l 及AC 成60°的角，在直线l 上取一点P ，使∠APB=30°，那么符合条件的点P 共有 个9．记1231515,,253322y x y x y x =-+=+=-+，对每一个实数x ，都有唯一的一个值 y 1，y 2，y 3及之对应，取y 为三数之中的最小值，当x 取遍所有实数时，所有y 值中 的最大值为_________.222y x mx n =+-,假设图像经过点(1,1)，且记m ，n+4两数中的较大者为p ，那么p 的最小值为.11．△ABC 中，∠C=300，BM 是AC 边上的中线，AC=2a ，假设沿直线BM 将三角形对折起来，发现两个小三角形ABM 和BCM 重叠局部的面积恰好等于△ABC 面积的四分之一.那么△ABC 的面积是 .三、解答题〔五大题，共60分〕12.〔此题8分〕正数a,b 满足a 3b+ab 3-2a 2b+2ab 2=7ab-8，求a 2-b 213．〔此题10分〕一个长方体的香烟盒里，装满大小均匀的20支香烟．翻开烟盒的顶盖后，lAB C〔第7题〕〔第8题〕二十支香烟排列成三行，如下图．经测量，一支香烟的直径约为0.75 cm ，长约为8.4 cm ． (732.13≈，以下计算结果均保存4个有效数字) （1）求矩形ABCD 的面积；（2）制作这样一个封闭的长方体烟盒至少需要纸张面积是多少cm 2〔不考虑接缝〕？14.〔此题14分〕如图，Rt △ABC 中，∠C =90°，BC =6，AC =8．点P ，Q 都是斜边AB 上的动点，点P 从B 向A 运动〔不及点B 重合〕，点Q 从A 向B 运动，BP=AQ ．点D ，E 分别是点A ，B 以Q ，P 为对称中心的对称点， HQ ⊥AB 于Q ，交AC 于点H ．当点E 到达顶点A 时，P ，Q 同时停顿运动．设BP 的长为x ，△HDE 的面积为y ． 〔1〕求证：△DHQ ∽△ABC ；〔2〕当点D 在线段EQ 上时，求y 关于x 的函数解 析式，并求y 的最大值；〔3〕当x 为何值时，△HDE 为等腰三角形？15.〔此题14分〕设整数,,a b c 〔a b c ≥≥〕为三角形的三条边长，且满足22213a b c ab ac bc ++---=，求符合条件且周长不超过20的三角形的个数.〔第14题〕H………………16.〔此题14分〕如图，用水平线及竖直线将平面分成假设干个边长为1的小正方形格子,点O、A、B均在正方形格子的顶点〔称格点〕处，其中点O及点A在位于同一水平线上相距a 格，点O及点B位于同一竖直线上相距ｂ格.〔1〕假设a=5，b=4，那么△OAB中〔不包括三条边〕，共有多少个格点？〔2〕假设a、ｂ互质，那么在线段AB上〔不包括A、B两点〕是否有格点？证明你的结论.〔3〕假设a、ｂ互质，且a＞ｂ＞8，△OAB的值.温州市第三届初中数学学科知识竞赛参考答案及评分标准二、填空题〔每题6分，共30分〕7. 9 8. 2 9. 2 10. 2 11.或22a (第11题视情况给分)三、解答题〔五大题，共60分〕12.(此题8分)正数a,b 满足a 3b+ab 3-2a 2b+2ab 2=7ab-8，求a 2-b 2的值.[]()()).........(. (3)2112)( (020)1,)4(....................221)3(....................8821)(2)(872)(2)()2(....................872)(2)2()1(.....................87)(2)(872222222222222222222233８分（舍去）或者６分都是正数分分分分=-∴⎩⎨⎧-=-=⎩⎨⎧==∴⎩⎨⎧=-=--∴--=--∴-+-=+---∴-+-=---∴-+-=--+-∴-=--+∴-=+-+b a b a b a ab b a b a ab b a ab ab b a b a b a ab ab b a b a ab b a ab ab b a b a ab b ab a ab ab b a ab b a ab ab ab b a ab b a13.〔此题10分〕〔1〕解：如图，作321O O E O ⊥． ∵ 4375.0133221====O O O O O O ， ∴ ．∴ ，………………………(2分)〔cm 〕． ………………………(2分) ∴ 四边形ABCD 的面积是：)cm (76.1075725.10166336343334212≈=+=+⨯ ………………………(5分) 〔2〕制作一个烟盒至少需要纸张： ⎪⎪⎭⎫⎝⎛⨯+⨯+++4.84214.8433316633632)cm (1.144096.1442≈=．…………(10分)∴ 制作一个烟盒至少需要的纸张是144.1)cm (214.〔此题14分〕〔1〕∵A 、D 关于点Q 成中心对称，HQ ⊥AB ， ∴C HQD ∠=∠=90°，HD =HA ， ∴A HDQ ∠=∠，∴△DHQ ∽△ABC ．………………………(3分)〔2〕如图1 x x x x y 4152343)410(212+-=⨯-=． 当时，最大值．………………(6分) 〔3〕①如图1，当5.20≤<x 时，假设DE =DH ，∵DH =AH =， DE =x 410-，∴x 410-=x 45，． 显然ED =EH ，HD =HE 不可能；………………(10分) ②如图2，当55.2≤<x 时，假设DE =DH ，104-x =x 45，；假设HD =HE ，此时点D ，E 分别及点B ，A 重合，5=x ； 假设ED =EH ，那么△EDH ∽△HDA ， ∴，，．∴当x 的值为时，△HDE 是等腰三角形. ………………(14分)15. (此题14分) 设整数,,a b c 〔a b c ≥≥〕为三角形的三条边长，且满足 22213a b c ab ac bc ++---=，求符合条件且周长不超过20的三角形的个数. 解 由等式可得222()()()26a b b c a c -+-+-= ① ………… ………………(2分)令,a b m b c n -=-=，那么a c m n -=+，其中,m n 均为自然数. 于是，等式①变为222()26m n m n +++=，即2213m n mn ++= ② ………… ………………(4分)由于,m n 均为自然数，判断易知，使得等式②成立的,m n 只有两组： 和 …………………………………… ………………(6分)〔图1〕C〔图2〕〔1〕当3,1m n ==时，1b c =+，34a b c =+=+.又,,a b c 为三角形的三边长， 所以b c a +>，即(1)4c c c ++>+，解得3c >. ……… ………………(8分) 又因为三角形的周长不超过20，即20)1()4(≤++++=++c c c c b a ，解得5≤c .因此53≤<c ，所以c 可以取值4，5对应可得到2个符合条件的三角形. ………………(10分) 〔2〕当1,3m n ==时，3b c =+，14a b c =+=+.又,,a b c 为三角形的三边长， 所以b c a +>，即(3)4c c c ++>+，解得1c >. ………………(12分) 又因为三角形的周长不超过20，即20)3()4(≤++++=++c c c c b a ，解得.因此， 所以c 可以取值2，3，4对应可得到3个符合条件的三角形.综上所述，满足条件的三角形共有5个. …………………… ………………(14分)16.〔此题14分〕解：〔1〕根据题意，在△OAB 内〔不包括 三边上的点〕的格点数n 应满足， 当ａ=5、ｂ=4时，，〔这里n可认为是关于ａ、ｂ的二元函数。

2015学年第一学期九年级数学竞赛试卷(满分120分，时间120分钟)一、选择题：（每小题5分，共30分）1．已知三角形的每条边长是整数，且小于等于4，这样的互不全等的三角形有（ C ）A ．10个B ．12个C ．13个D ．14个4，4，4； 4，4，3； 4，4，2； 4，4，1； 4，3，3； 4，3，2； 3，3，3； 3，3，2； 3，3，1； 3，2，2； 2，2，2； 2，2，1； 1，1，1 2．已知,511b a b a +=+则ba ab +的值是（ C ） A ．5 B ．7 C ．3 D ．31222221155()533b a a b ab a b a b ab a ba b ab b a b a a b ab++=→=→+=++→+=+∴+== 3．如图，在Rt ABC 中，AC=4，BC=3，∠ACB=90°．四边形DEFG 、四边形GHIJ 均为正方形，点E 在AC 上、点I 在BC 上，J 为边DG 的中点．则GH 的长为（ C ） A ．1921 B ．1 C ．6077 D ．1802594．在ABC 中，已知AB=AC ，D 为边BC 的中点，BE ⊥AC 于点E ，BE 与AD 交于点P ．若BP=3，PE=1，则AE 等于（ B ）A ．62B ．2C ．3D ．6第3题图EPD CBA 第4题图5． 已知123,,y y y 分别表示二次函数、反比例函数和一次函数的三个函数值，它们的交点分别是A （1-，2-）、B （2，1）和C （32，3），规定M =｛123,,y y y 中最小的函数值｝ 则下列结论错误的是( B )A ．当1-<x 时，M =1yB ．当0≤x ≤2时，M 的最大值是1，无最小值C ．当01<<-x 时，231y y y <<D ．当x ≥2时，M 最大值是1，无最小值A 、由图象可知，当x ＜-1时，对于每一个x 的值，二次函数的图象都落在反比例函数和一次函数图象的下方，所以此时M=Y1，本选项正确，不符合题意；B 、由图象可知，当0≤x≤2时，M=Y3，最大值是1，最小值是-1，本选项错误，符合题意C 、由图象可知，当-1＜x ＜0时，Y2＜Y3＜Y1，本选项正确，不符合题意；D 、由图象可知，当x≥2时，M=Y1，最大值是1，无最小值，本选项正确，不符合题意； 6．如图，⊙O 的直径AB 与弦CD 交于点P ，交角为45°．若22PC PD +=8， 则⊙O 的半径为（ B ）A ．2B ．2C ．22D ．4 作OH 垂直于CD,垂足为H 则OH=HP ，CH=DH ， PC²+PD²=8 (CH+HP)²+(DH-HP)²=8 CH²+HP²=4， CH²+OH²=4， R²=4， R=2二、填空题：（每小题5分，共40分） 7．已知：12015,12015,22015a x b x c x =+=-=+，则多项式222a b c ab bc ca ++++-的值为 72222221()()()21(491)72a b c ab bc ca a b b c c a ⎡⎤++++-=++++-⎣⎦=++=第5题图第6题图8. 直角三角形斜边AB上的高CD=3，延长DC到P使得CP=2，过B作BF⊥AP交CD 于E，交AP于F，则DE =9/59. 以下四个命题：①每一条对角线都平分一组对角的平行四边形是菱形．②当m > 0时，y = –mx＋1与myx=两个函数都是y随着x的增大而减小．③已知正方形的对称中心在坐标原点，顶点A，B，C，D按逆时针依次排列，若A点坐标为（13）则D点坐标为（1，3-.④在一个不透明的袋子中装有标号为1，2，3，4的四个完全相同的小球，从袋中随机摸取一个然后放回，再从袋中随机地摸取一个，则两次取到的小球标号的和等于4的概率为18．其中正确的命题有①（只需填正确命题的序号）①每一条对角线都平分一组对角的平行四边形是菱形，故①正确．②当m＞0时，-m＜0，y=-mx+1是y随着x的增大而减小myx=，是在同一象限内y随着x的增大而减小，故②错误．③已知正方形的对称中心在坐标原点，顶点A，B，C，D按逆时针依次排列，若A点坐标为（1，3，则D点坐标为(3,1)-，故③错误．④在一个不透明的袋子中装有标号为1，2，3，4的四个完全相同的小球，从袋中随机摸取一个然后放回，再从袋中随机地摸取一个，则两次取到的小球标号的和等于4的概率为3 16，故④错误，DEFPC BA第8题图10.在一次剪纸活动中，小聪依次剪出6张正方形纸片 拼成如图所示的图形，若小聪所拼得的图形中正方形 ① 的面积为1，且正方形⑥与正方形③面积相等， 那么正方形⑤的面积为 36 设正方形②的边长是x ．结合图形，得x+1+1+1=x+1+x-1，解得x=3．则正方形⑤的边长是6，其面积是36． 11．已知A 为反比例函数4y x=图象上一点，点A 的横坐标为1，将一块三角板的直角顶点放在A 处旋转，保持两直角边始终与x轴交于D 、E 两点，(0,3)F -为y 轴上一点，连接DF 、EF ，则四边形ADFE 面积的最小值为 28要使四边形的面积最小，即DE 最小，DE 为直角三角形的斜边，其中点在x 轴上，由直角三角形斜边上的中线为斜边的一半，所以，中线等于4时，DE=8最小，此时S=2812．如图，已知PAB 、PCD 为圆O 的两条割线，PA=8，AB=10，CD=7，∠P=60°，则圆O 的半径为 73连接AC ，BC ，BD9PAC PDB PA PB PC PD PC ⇒=→=∵PB=2PC ，∠P=60°， ∴∠BCP=90°， ∴∠BCD=90°， ∵∠BCD=90°，∴BD 为直径，（第10题图）第11题图 ODCB A P 第12题图2224924329227373BD CD BC BD r ∴=+=+=→=→=13．如图，点G 是ABC 的重心（即三角形三条中线的交点），GA GB ⊥，AB=5， 则22AC BC +的值为 125延长AG 、BG 分别交BC 、AC 于F 、E2222222222222224()4()114()5()445125AC BC AE BF AG GE BG GF AG BG BG AG AG BG AB +=+=+++=+++=+==14．观察下图的三角形数阵，则第100行的最后一个数是 4951GCBA第13题图第14题图 FE三、解答题：（第15、16、17题各12分，第18题14分，共50分） 15．设,,a b c 均为实数，2212,24a b a b bc c +==-+，求,,a b c 的所有可取之值 解：由题意可得：22212242a b a b bc c +=⎧⎪⎨=-+⎪⎩ 于是，a 和2是关于方程22212402x bx b bc c -+-+=的两个根，-----------5分 222214(24)0(4)02b b bc c b c ∴=--+≥→--≥4b c ∴=---------------------------------------------------------------------------------8分 由222222242(42)88412242(1)012,4a c c c c c ab bc c c c a b +=⎧⎪⇒-=-+⎨=-+⎪⎩→-=→=∴==------------------10分--------------------------------------12分16．如图，已知ABCD 是圆O 的内接四边形，AB=BD ，BM ⊥AC 于M ，求证：AM=DC+CMB在AC 上取一点H ，使CM=HM ，连接BH-----2分BM AC BH BC BHC BCH⊥∴=∴∠=∠---------4分又∠BHC=∠BAH+∠ABH ∠BCH=∠BDA ∵BA=BD∴∠BAD=∠BDA=∠BAH+∠DAC ∴∠ABH=∠DAC =∠DBC∴△BA H ≌△BDC-----------------------------------10分 ∴AH=CD∴AM=AH+HM=CD+CM------------------------12分17．已知二次函数2y x bx c =++的图象与x 轴的两个交点的横坐标分别为12,x x ，一元二次方程22200x b x ++=的两实根为34,x x ，且23143x x x x -=-=，求二次函数的解析式，并写出顶点坐标 解：14123423363x x x x x x x x =+⎧⇒+=++⎨=+⎩-----------2分22126603,2b b b b b b ∴-=-+→--=→==-------------6分当2b =-时，2222004200x b x x x ++=→++=→无解--------8分当3b =时，2223420092004,5x b x x x x x ++=→++=→=-=-14233231x x x x =+=-⎧⎨=+=-⎩ 122x x c ∴==-----------10分二次函数的解析式为232y x x =++，顶点坐标为35(,)24----------12分H18．一个二次函数的图象上任一点的坐标(,)x y 满足方程298y =+（1）求此二次函数的解析式；（2）若此二次函数与x 轴的交点分别为A ，B （A 在B 的左边），与y 轴的交点为C ，在此二次函数的图象上与x 轴上分别找一点D 、E （点D 不同于点C ），使得以A 、D 、E 为顶点的三角形与ABC 相似，求出所有满足条件的点D 的坐标解：（1所以二次函数为2222y x x =------------------------5分（2）令21203401,4y x x x x =→--=→=-=即得(1,0),(4,0)A B -又令02(0,2)x y C =→=-→-2OC OA OB =∴ABC 是以∠ACB 为直角的直角三角形 DAE ∠不可能为直角由题意可得，DAE BAC ∠=∠或DAE ABC ∠=∠作DE x ⊥轴，E 为垂足，设00(,)D x y ，则00,1DE y AE x ==+ 若AE DEDAE BAC ACBAOC DEA OC OA∠=∠→→=00000001114211,3x y x x x x x +→=→+=++≠-∴=或5(3,2)(5,3)D D ∴-或--------------------------------------------11分同理，当DAE ABC ∠=∠时可得D （8，18）综上，D 点坐标为(3,2)(5,3)D D -或或（8，18）--------------14分。

2015年浙江省初中毕业生 学业考试(温州市卷)(满分:150分 时间:120分钟)第Ⅰ卷(选择题,共40分)一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)1.给出四个数0, ,,-1,其中最小的是( )A.0B.C.D.-12.将一个长方体内部挖去一个圆柱(如图所示),它的主视图是( )3.某校学生参加体育兴趣小组情况的统计图如图所示.若参加人数最少的小组有25人,则参加人数最多的小组有( )A.25人B.35人C.40人D.100人4.下列选项中的图形,不属于．．．中心对称图形的是( ) A.等边三角形 B.正方形 C.正六边形 D.圆5.如图,在△ABC 中,∠C=90°,AB=5,BC=3,则cos A 的值是( )A.B.C.D.6.若关于x 的一元二次方程4x 2-4x+c=0有两个相等实数根,则c 的值是( ) A.-1 B.1 C.-4 D.47.不等式组 ,- 的解是( )A.x<1B.x≥3C.1≤x<3D.1<x≤38.如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限.若反比例函数y=的图象经过点B,则k 的值是( )A.1B.2C.D.29.如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE.设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )A.y=x2B.y=x2C.y=2x2D.y=3x210.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG.DE,FG,,的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=18,则AB的长为( )A.9B.C.13D.16第Ⅱ卷(非选择题,共110分)二、填空题(本题有6小题,每小题5分,共30分)11.分解因式:a2-2a+1= .12.一个不透明的袋中只装有1个红球和2个蓝球,它们除颜色外其余均相同.现随机从袋中摸出两个球,颜色是一红一蓝的概率是.13.已知扇形的圆心角为120°,弧长为2π,则它的半径为.14.方程=的根是.15.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1 m宽的门.已知计划中的材料可建墙体(不包括门)总长为27 m,则能建成的饲养室总占地面积最大为m2.16.图甲是小明设计的带菱形图案的花边作品.该作品由形如图乙的矩形图案拼接而成(不重叠、无缝隙).图乙中,=,EF=4 cm,上下两个阴影三角形的面积之和为54 cm2,其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为cm.三、解答题(本题有8小题,共80分.解答需写出必要的文字说明、演算步骤或证明过程)17.(本题10分)(1)计算:2 0150++2×-;(2)化简:(2a+1)(2a-1)-4a(a-1).18.(本题8分)如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.(1)求证:AB=CD;(2)若AB=CF,∠B=30°,求∠D的度数.19.(本题8分)某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;(2)该公司规定:笔试、面试、体能得分分别不得低于80分、80分、70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.20.(本题8分)各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G.Pick,1859~1942年)证明了格点多边形的面积公式:S=a+b-1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图1,a=4,b=6,S=4+×6-1=6.(1)请在图2中画一个格点正方形,使它的内部只含有4个格点,并写出它的面积;(2)请在图3中画一个格点三角形,使它的面积为,且每条边上除顶点外无其他格点．．．．．.图1 图2 图321.(本题10分)如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E,DF切半圆于点F.已知∠AEF=135°.(1)求证:DF∥AB;(2)若OC=CE,BF=2,求DE的长.22.(本题10分)某农业观光园计划将一块面积为900 m2的园圃分成A,B,C三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲3株或乙6株或丙12株.已知B区域面积是A的2倍,设A区域面积为x(m2).(1)求该园圃栽种的花卉总株数y关于x的函数表达式;(2)若三种花卉共栽种6 600株,则A,B,C三个区域的面积分别是多少?(3)已知三种花卉的单价(都是整数)之和为45元,且差价均不超过10元.在(2)的前提下,全部栽种共需84 000元.请写出甲、乙、丙三种花卉中,种植面积最大的花卉总价.23.(本题12分)如图,抛物线y=-x2+6x交x轴正半轴于点A,顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.(1)求点A,M的坐标;(2)当BD为何值时,点F恰好落在该抛物线上?(3)当BD=1时,①求直线MF的解析式,并判断点A是否落在该直线上;②延长OE交FM于点G,取CF中点P,连结PG,△FPG,四边形DEGP,四边形OCDE的面积分别记为S1,S2,S3,则S1∶S2∶S3= .24.(本题14分)如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ∶AB=3∶4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m 于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.(1)用关于x的代数式表示BQ,DF;(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长;(3)在点P的整个运动过程中,①当AP为何值时,矩形DEGF是正方形?②作直线BG交☉O于另一点N,若BN的弦心距为1,求AP的长(直接写出答案).2015年浙江省初中毕业生学业考试(温州市卷)一、选择题1.D 根据正数大于0,0大于负数,知-1<0<<.故选D.2.A 根据从主视方向看得到的图形是主视图,可得主视图是长方形,且该长方形中有两条虚线.故选A.3.C 由题意知参加人数最少的小组有25人,占25%,∴参加体育兴趣小组的总人数为25÷25%=100(人).∴参加人数最多的小组有100×(1-25%-35%)=100×40%=40(人).故选C.4.A 根据中心对称图形的概念进行判断.5.D 在△ABC中,∠C=90°,AB=5,BC=3,根据勾股定理,得AC=4.∴cos A==.故选D.6.B ∵关于x的一元二次方程4x2-4x+c=0有两个相等实数根,∴Δ=(-4)2-4·4·c=0⇒c=1.故选B.7.D 由,-⇒ ,⇒1<x≤3.故选D.8.C 如图,过点B作BD⊥x轴于点D.∵点A的坐标是(2,0),△ABO是等边三角形,∴OB=OA=2,OD=1.由勾股定理得BD=.∵点B在第一象限,∴点B的坐标是(1,).∵反比例函数y=的图象经过点B,∴=⇒k=. 故选C.9.B ∵ON是Rt∠AOB的平分线,DE⊥OC,∴△ODE是等腰直角三角形.∵OC=x,∴DE=2x.∵∠DFE=120°,∴∠EDF=30°.∴CF=x.∴S△DEF=·2x·x=x2.在菱形FGMH中,∠GFH=120°,又FG=FE,∴S菱形FGMH=2S△DEF.∴y=3S△DEF=x2.故选B.10.C 如图,连结OP、OQ,∵DE,FG,,的中点分别是M,N,P,Q,∴O,P,M三点共线,O,Q,N三点共线.∵四边形ACDE,四边形BCFG是正方形,∴AE=CD=AC,BG=CF=BC.设AB=2r,则OM=MP+r,ON=NQ+r.∵点O,M分别是AB,ED的中点,∴OM是梯形ABDE的中位线.∴OM=(AE+BD)=(AE+CD+BC)=(2AC+BC),即MP+r=(2AC+BC).同理,得NQ+r=(2BC+AC).两式相加,得MP+NQ+2r=(AC+BC).∵MP+NQ=14,AC+BC=18,∴14+2r=×18⇒2r=13,即AB=13.故选C.二、填空题11.答案(a-1)2解析a2-2a+1=a2-2·a·1+12=(a-1)2.12.答案解析共有3种等可能的结果:(红球,蓝球1),(红球,蓝球2),(蓝球1,蓝球2),颜色是一红一蓝的情况有两种:(红球,蓝球1),(红球,蓝球2),∴随机从袋中摸出两个球,颜色是一红一蓝的概率是.13.答案 3解析由弧长公式得··=2π,解得r=3.14.答案x=2解析=⇒3x=2x+2⇒x=2.经检验,x=2是原方程的根.∴方程=的根是x=2.15.答案75解析设垂直于现有墙的一面墙长为x m,建成的饲养室总占地面积为y m2,则利用现有墙的长为(27+3-3x)m,∴y=x(30-3x)=-3x2+30x=-3(x-5)2+75.∵-3<0,∴当x=5时,y max=75,即能建成的饲养室总占地面积最大为75 m2.16答案解析如图,连结MN、PQ,设MN=2x cm,PQ=2y cm,∵=,∴可设AB=6k cm(k>0),则BC=7k cm.∵上下两个阴影三角形的面积之和为54 cm2,∴2··3k+54=6k·7k,即(2x+7k)·3k+54=42k2. ①易知四边形DENM、四边形AFMN是平行四边形,∴DE=AF=MN=2x cm.∵EF=4 cm,∴4x+4=7k,即2x=-. ②将②代入①得,-·3k+54=42k2,化简得7k2+4k-36=0.解得k1=2,k2=-(舍去).∴AB=12 cm,BC=14 cm,MN=5 cm,∴x=.易证△MCD∽△MPQ,∴=-,解得y=.∴PM===(cm).∴菱形MPNQ的周长为4×=(cm).评析本题主要考查平行四边形,菱形的性质以及相似三角形的性质.三、解答题17解析(1)原式=1+2-1=2.(2)原式=4a2-1-4a2+4a=4a-1.18.解析(1)证明:∵AB∥CD,∴∠B=∠C.∵AE=DF,∠A=∠D,∴△ABE≌△DCF,∴AB=CD.(2)∵AB=CF,AB=CD,∴CD=CF,∴∠D=∠CFD.∵∠B=∠C=30°,∴∠D=75°.19.解析(1)甲==84,乙==80,丙==81,∴甲>丙>乙,∴排名顺序为甲、丙、乙.(2)由题意可知,只有甲不符合规定.∵乙'=85×60%+80×30%+75×10%=82.5,丙'=80×60%+90×30%+73×10%=82.3,∴录用乙.20.解析(1)画法不唯一,如图①或图②.(2)画法不唯一,如图③,图④等.21.解析(1)证明:连结OF,∵DF切半圆O于点F,∴DF⊥OF.∵∠AEF=135°,四边形ABFE为圆内接四边形,∴∠B=45°.∴∠FOA=90°,∴AB⊥OF,∴DF∥AB.(2)连结OE,∵BF=2,∠FOB=90°,∴OB=OF=2.∵OC=CE,CE⊥AB,OE=OF=2,∴CE=.∵DC∥OF,DF∥AB,∴四边形OCDF是平行四边形,∴DC=OF=2.∴DE=DC-CE=2-.22.解析(1)y=3x+6·2x+12(900-3x),即y=-21x+10 800.(2)当y=6 600时,-21x+10 800=6 600,解得x=200.∴2x=400,900-3x=300.答:A的面积是200 m2,B的面积是400 m2,C的面积是300 m2.(3)种植面积最大的花卉总价为36 000元.23.解析(1)令y=0,则-x2+6x=0,解得x1=0,x2=6,∴A(6,0),∴对称轴是直线x=3,∴M(3,9).(2)∵OE∥CF,OC∥EF,C(2,0),∴EF=OC=2,∴BC=1.∴点F的横坐标为5.∵点F落在抛物线y=-x2+6x上,∴F(5,5),BE=5.∵==,∴DE=2BD,∴BE=3BD,∴BD=.(3)①当BD=1时,BE=3,∴F(5,3).设MF的解析式为y=kx+b,将M(3,9),F(5,3)代入,得,,解得-,,∴y=-3x+18.∵当x=6时,y=-3×6+18=0,∴点A落在直线MF上.②3∶4∶8.评析本题主要考查二次函数与几何问题的综合,主要涉及二次函数图象与坐标轴的交点坐标,点是否在抛物线上,函数与方程综合等知识点.24.解析(1)在Rt△ABQ中,∵AQ∶AB=3∶4,AQ=3x,∴AB=4x,∴BQ=5x.又∵OD⊥m,l⊥m,∴OD∥l.∵OB=OQ,∴AH=BH=AB=2x,∴CD=2x,∴FD=CD=3x.(2)∵AP=AQ=3x,PC=4,∴CQ=6x+4.作OM⊥AQ于点M(如图①),∴OM∥AB.图①∵☉O是△ABQ的外接圆,∠BAQ=90°,∴点O是BQ中点,∴QM=AM=x,∴OD=MC=x+4.∴OE=BQ=x,∴ED=2x+4,∴S矩形DEGF=DF·DE=3x(2x+4)=90,∴x1=-5(舍去),x2=3,∴AP=3x=9.(3)①若矩形DEGF是正方形,则ED=FD.Ⅰ.点P在点A的右侧时(如图①),∴2x+4=3x,解得x=4,∴AP=3x=12.Ⅱ.点P在点A的左侧时,i.当点C在点Q右侧,(i)0<x<时(如图②),图②∵ED=4-7x,FD=3x,∴4-7x=3x,解得x=,∴AP=.(ii)≤x<时(如图③),图③∵ED=7x-4,DF=3x,∴7x-4=3x,解得x=1(舍去).ii.当点C在点Q左侧或重合时,即x≥(如图④),图④DE=7x-4,DF=3x,∴7x-4=3x,解得x=1,∴AP=3.综上所述,当AP为12或或3时,矩形DEGF是正方形.②AP的长为6或.略解:连结NQ,由点O到BN的弦心距为1,得NQ=2.当点N在AB的左侧时(如图⑤),图⑤过点B作BK⊥EG于点K,∵GK=x,BK=x,∴∠GBK=45°.易知BK∥AQ,∴AI=AB=4x,∴IQ=x,∴NQ==2,∴x=2,∴AP=6.当点N在AB的右侧时(如图⑥),图⑥过点B作BJ⊥GE于点J,∵GJ=x,BJ=4x,∴tan∠GBJ=,∴AI=16x,∴QI=19x,∴NQ==2,∴x=,∴AP=.评析本题考查动点问题,主要涉及动点与图形运动.分类讨论是解决动点问题的必经过程,也是中考必考内容.难度比较大.。

温州市第三届初中数学学科知识竞赛试卷一 选择题（每小题5分，共30分）1．平面上，在凸10边形的所有内角中，锐角的个数最多是（ ）个. A .4 B .3 C .2 D .1 2.如图，A 、C 是函数xy 1=的图象上的点，且A 、C 关于原点对称. AB ⊥x 轴，CD ⊥x 轴，垂足分别为B 、D ，如果四边形ABCD 的面积为S ，那么（ ）A .S =1B .1＜S ＜2C ..S=2D .S ＞23．如图，直角梯形ABCD 中，A D ∥BC ，A B ⊥BC ，AB =7，AD =2，BC=3，如果在AB 边上取一点P ，使得以P 、A 、D 为顶点的三角形和以P 、B 、C 为顶点的三角形相似，那么这样的点P 能取到（ ）个.A ．1B ．2C ．3D ．44．如图，直角梯形ABCD 中，A D ∥BC,A B ⊥BC ，AD=3，BC=5，将腰DC 绕点D 的逆时针方向旋转90°至DE ，连结AE ，则△ADE 的面积是（ ）A ．1B ．2C ．3D ．45．如图,甲、乙两人在斜坡AB 上作往返跑训练．已知：甲上坡的速度是a 米/分，下坡的速度是b 米/分，（a ＜)b ；乙上坡的速度是12a 米/分，下坡的速度是2b 米/分．如果甲、乙二人同时从点A 出发，时间为t （分），离开点A 的路程为S （米）．那么下面图象中，能大致表示甲、乙两人从点A 出发后的时间t （分）与离开点A 的路程S （米）之间的函数关系的是（ ） A CBD OBAAt （分）S （米）Bt （分） S （米）Ct （分）S （米）Dt （分）S （米）ABCD（第2题）（第3题）（第4题）（第5题）市（县） 学 校 姓名 准考证号码 ………………………………………………………………… 密 …………………… 封 ……………………… 线 ……………………………………………6．甲、乙两个茶杯中各装有200克盐水和糖水，盐水的含盐量与糖水的含糖量相等。