应力疲劳S N曲线

金属的S-N曲线是指材料在循环载荷下的应力-应变曲线。

这个曲线可以用来描述材料在不同应力水平下的疲劳寿命。

金属的S-N曲线标准通常由国际标准化组织（ISO）或美国材料与试验协会（ASTM）等机构制定。

ISO标准中，金属的S-N曲线通常采用对数-对数坐标系绘制，横轴表示应力的对数值（log(σ))，纵轴表示相应的疲劳寿命对数值（log(N))。

在这个坐标系中，S-N曲线通常是一条过原点的直线，称为“主曲线”（master curve）。

主曲线是通过对大量试样进行疲劳试验得到的，可以反映出材料的疲劳性能和疲劳寿命的规律性。

除了主曲线，S-N曲线还包括一些辅助曲线，如“疲劳极限曲线”（fatigue limit curve）和“疲劳裂纹扩展曲线”（fatigue crack propagation curve）。

疲劳极限曲线是指材料能够承受的最大应力水平，当应力超过这个水平时，材料就会发生断裂；疲劳裂纹扩展曲线则是指材料在一定应力水平下，随着循环次数的增加，裂纹扩展的规律性。

总之，金属的S-N曲线标准是材料疲劳性能研究的基础，对于材料的设计和应用具有重要意义。

常用材料的s-n曲线
常用材料的S-N曲线因材料种类和测试条件的不同而有所差异。

一般来说，S-N曲线表示材料在循环应力作用下的疲劳寿命与应力之间的关系。

对于金属材料，S-N曲线通常呈现出一种幂函数的形式，即应力与寿命之间存在一定的指数关系。

这种关系可以通过实验获得，通过在不同应力水平下进行疲劳试验，记录材料的疲劳寿命，然后绘制出S-N曲线。

需要注意的是，S-N曲线受到多种因素的影响，如材料成分、微观结构、应力集中、环境条件等。

因此，不同材料或不同测试条件下的S-N曲线可能会有所不同。

如果您需要特定材料的S-N曲线，建议您查阅相关文献或咨询专业人士以获取准确的数据。

各种材料疲劳S—N曲线
材料的机械性能在结构设计和机械维修中发挥着重要作用，疲劳曲线是材料工程中重要的参数，其中SN曲线是最重要的曲线。

SN曲线，全称为可靠度曲线，也称为疲劳曲线，是表示疲劳寿命与应力水平间关系的曲线。

所谓可靠度，是指零件或系统在极限负荷下在规定时间不发生失效的概率。

通常，SN曲线由两条曲线组成，即极限负荷曲线和疲劳曲线。

极限负荷曲线是表示极限负荷与应力水平的关系，疲劳曲线则表示疲劳寿命与应力水平之间的关系。

SN曲线对于各种材料来说是不同的，材料的性质决定了其疲劳曲线的形状。

金属材料具有较高的强度，通常其SN曲线采用剪切受力模型，即弹性-强度-塑性变形模型。

一般情况下，SN曲线斜率越大，使用寿命越小，即SN曲线越陡峭，材料的耐疲劳性越差。

除金属材料外，塑料材料的疲劳曲线也有很大的不同。

塑料材料的强度较低，疲劳曲线可以采用力学模型，比如截面受力模型、动荷载循环模型和静荷载循环模型。

这些模型能够更准确地反应塑料材料的耐疲劳特性，并可以通过材料性质参数模拟塑料材料的疲劳寿命。

木材也可以用SN曲线分析，但它的SN曲线的形状与其他材料有很大的不同，主要受木材吸水率的影响。

随着吸水率的升高，木材的疲劳曲线也会发生变化，其疲劳曲线的幅度也会减小，即使在低应力水平下，木材耐疲劳性也不够好。

各种材料的SN曲线各有不同，对于任何材料，其SN曲线都是基于材料结构、性质和运动模式等分析出来的，因此，分析，加工和测
试各种材料的SN曲线是非常重要的。

只有通过准确分析各种材料的SN曲线，才能够准确预测材料的疲劳寿命，从而更好地指导材料的设计和使用过程。

材料的S-N曲线与基本术语一般情况下，材料所承受的循环载荷的应力幅越小，到发生疲劳破断时所经历的应力循环次数越长。

S-N曲线就是材料所承受的应力幅水平与该应力幅下发生疲劳破坏时所经历的应力循环次数的关系曲线。

S-N曲线一般是使用标准试样进行疲劳试验获得的。

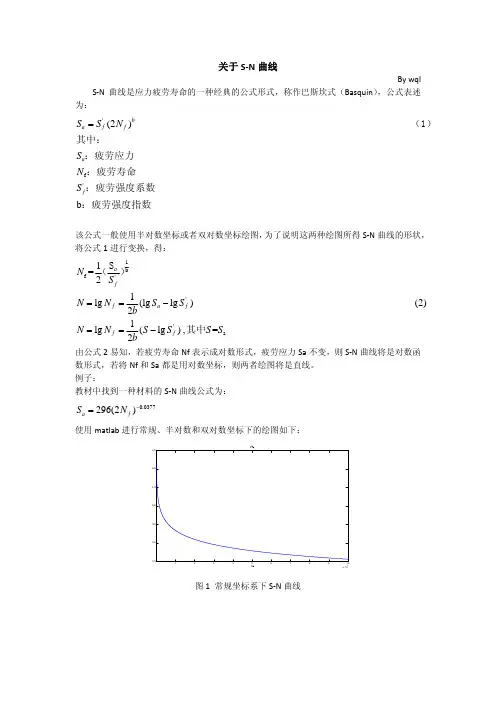
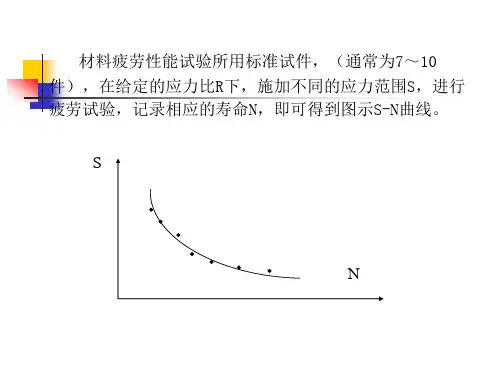
如图1所示，纵坐标表示试样承受的应力幅，有时也表示为最大应力，但二者一般都用σ表示；横坐标表示应力循环次数，常用Nf表示。

为使用方便，在双对数坐标系下S-N曲线被近似简化成两条直线。

但也有很多情况只对横坐标取对数，此时也常把S-N曲线近似简化成两条直线。

S-N曲线中的水平直线部分对应的应力水平就是材料的疲劳极限，其原意为材料经受无数次应力循环都不发生破坏的应力极限，对钢铁材料此“无限”的定义一般为107次应力循环。

但现代高速疲劳试验机的研究成果表明，即使应力循环次数超过107材料仍然有可能发生疲劳断裂。

不过107次的应力循环次数，对于实际的工程中的疲劳强度设计已经完全能够满足需要。

疲劳极限又称持久极限，对于无缺口的光滑试样，多用σw0表示，而应力比R=-1时的疲劳极限常用σ-1来表示。

某些不锈钢和有色金属的S-N中没有水平直线部分，此时的疲劳极限都一般定义为108次应力循环下对应的应力幅水平。

疲劳极限是材料抗疲劳能力的重要性能指标，也是进行疲劳强度的无限寿命设计的主要依据。

斜线部分给出了试样承受的应力幅水平与发生疲劳破断时所经历的应力循环次数之间的关系，多用如幂函数的形式表示。

式中σ为应力幅或最大应力，N为达到疲劳破断时的应力循环次数，m，C材料常数。

如果给定一个应力循环次数，便可由上式求出或由斜线量出材料在该条件下所能承受的最大应力幅水平。

反之，也可以由一定的工作应力幅求出对应的疲劳寿命。

因为此时试样或材料所能承受的应力幅水平是与给定的应力循环次数相关联的，所以称之为条件疲劳极限，或称为疲劳强度。

斜线部分是零部件疲劳强度的有限寿命设计或疲劳寿命计算的主要依据。

疲劳曲线和s-n曲线的区别《疲劳曲线与S-N曲线的区别》疲劳曲线和S-N曲线是研究材料疲劳寿命和疲劳性能的重要工具，两者在材料疲劳研究中起着不可替代的作用。

然而，疲劳曲线和S-N曲线有着不同的定义与用途。

疲劳曲线是研究材料在不同循环次数下的疲劳性能表现的曲线。

它描述了材料在应力变化循环作用下的疲劳寿命，通常以应力幅和循环次数为坐标轴。

疲劳曲线的形态取决于材料的性质和疲劳加载条件，常见的疲劳曲线有S-N曲线和Wöhler曲线。

疲劳曲线可用于预测材料疲劳寿命和评估其疲劳强度。

S-N曲线是研究材料在一定应力水平下的疲劳寿命的曲线，也被称为疲劳强度曲线。

S-N曲线的坐标轴一般为应力幅和循环次数，它展示了材料在不同应力水平下的疲劳寿命。

通过绘制S-N曲线，可以得到在给定应力水平下材料的疲劳强度、疲劳极限和疲劳寿命等信息。

S-N曲线常用于材料的疲劳强度设计和耐久性评价。

总的来说，疲劳曲线是研究材料在不同循环次数下的疲劳性能表现的曲线，而S-N曲线是研究材料在一定应力水平下的疲劳寿命的曲线。

两者的主要区别在于研究对象的不同：疲劳曲线是考察材料在不同循环次数下的性能变化，而S-N曲线则关注材料在各个应力水平下的寿命。

因此，疲劳曲线和S-N曲线在研究方法和实际应用中存在差异。

在材料设计和工程实践中，研究人员通常需要综合考虑疲劳曲线和S-N曲线两者的信息，以评估材料的疲劳性能和寿命。

通过综合分析两者的数据，可以更准确地预测材料在实际工作条件下的疲劳寿命，并采取相应的措施来提高材料的疲劳强度和耐久性。

综上所述，《疲劳曲线与S-N曲线的区别》主要在于研究对象的不同，前者考察材料在不同循环次数下的性能变化，后者则关注材料在一定应力水平下的疲劳寿命。

两者在材料疲劳研究中具有不可替代的作用，可以互相补充，为材料设计和工程实践提供有益的参考依据。

混凝土疲劳s-n曲线混凝土疲劳是混凝土材料经过长期的载荷循环作用下所出现的损伤现象，疲劳力学是模拟或者分析材料在振动载荷下的变形、应力、应变、损伤的科学领域，是材料疲劳现象的理论依据。

S-N曲线（即应力数-寿命曲线），是所长期以来广泛使用的疲劳测试方式。

它将应力与寿命联系在一起，显示出材料疲劳强度的变化规律。

S-N曲线一般包括下面几个部分：1. 断裂区随着应力数的增加，混凝土的寿命会不断缩短，直到最终破坏。

断裂区是指材料处于完全断裂之前的区域。

当混凝土受到高应力作用时，其断裂区域相对较小。

2. 逻辑区疲劳寿命在逻辑区内会变得不稳定，这是由于材料内部的微小裂纹形成，它们在应力作用下逐渐扩大，导致材料寿命逐渐缩短。

逻辑区位于应力数和寿命之间。

3. 弹性区此时材料的寿命取决于载荷大小以及振荡幅度。

如果在材料的弹性区中进行疲劳荷载测试，则可以通过增加载荷的大小来增加材料的寿命。

4. 压缩区压缩区是指在材料反向载荷作用下的区域，寿命主要取决于振幅大小。

混凝土疲劳S-N 曲线是一个将应力与寿命联系在一起的图表。

对于一个给定的载荷，S-N曲线会显示材料的不同应力下所需承受的寿命。

因此，S-N曲线可以用于推断材料的疲劳特性，进而用于制定更好的混凝土工程方案和结构设计。

要考虑如何在混凝土寿命测试中绘制S-N曲线。

首先，应该准备足够数量的混凝土样本，在不同的载荷水平下进行疲劳测试，通过测定疲劳寿命和载荷来制作数据点。

最后，将这些数据点绘制成与寿命S 相对于载荷N 的曲线，即S-N曲线。

总之，S-N曲线为我们提供了一种研究材料疲劳性质的有效工具，对于混凝土结构的持久性和可靠性有着重要的作用。

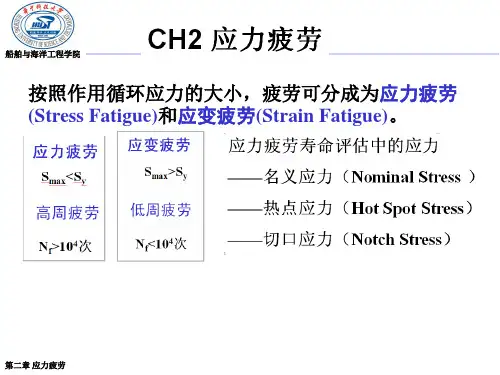
应力疲劳疲劳问题分类按循环应力作用的大小，疲劳可分为应力疲劳和应变疲劳应力疲劳：最大循环应力S max小于屈服应力S y寿命一般较高（>104），高周疲劳应变疲劳：最大循环应力S max大于屈服应力S y（材料屈服后应变变化较大而应力变化较小，故一般以应变为控制参量）寿命一般较低（<104），低周疲劳材料应力疲劳特性1．S-N曲线评价和估算疲劳寿命或强度需建立外荷载与寿命之间的关系。

反映外加应力S和疲劳寿命N之间关系的曲线称为S-N曲线。

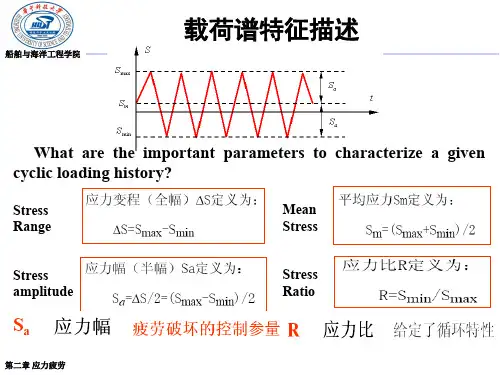
基本S-N曲线在最简单的荷载谱－恒幅循环应力作用下，R= -1时（对称恒幅荷载）实验给出的应力－寿命关系曲线2．S-N曲线的一般形状材料的S-N曲线一般由实验得到用一组标准试件在给定应力比和应力幅作用下，记录相应的寿命所得到的曲线。

典型S -N 曲线可分为 三段：低周疲劳区（LCF ），高周疲劳区（HCF ）和亚疲劳区（SF ）。

由S-N 曲线确定的对 应于寿命N 的应力称为寿命为N 次循环的疲劳强度S N 。

N = 1/4对应材料的静拉伸强度S b ，N = 106~7对应的疲劳强度为疲劳极限S f 。

特别地，R = -1的疲劳极限记为S -1。

在HCF 区，S -N 曲线在对数坐标系上近似为直线。

S -N 曲线的数学表达 1）指数函数式 C Ne S =αα和C 为材料常数。

两边取对数有 BS A N +=lgA = lg C 和B = -αlg e 为材料常数。

指数函数的S -N 关系在半对数坐标系上为直线。

2）幂函数式（最常用的形式）104106~7S bS fLCFHCFSFS maxNS NC N S =α两边取对数有：S B A N lg lg +=幂函数的S -N 关系在对数坐标系上为直线。

3）Weibull 公式C S S N f a =-α)(α和C 为材料常数，S af 为理论应力疲劳极限幅值。

Weibull 公式包含疲劳极限，即S 趋于S af 时N 趋于无穷大。

疲劳寿命sn曲线疲劳寿命S-N曲线是一个重要的工程概念，它描述了材料由正常状态到破坏性破裂发生的过程。

S-N曲线定量地描述了材料在某一指定的应力水平和应变水平下的疲劳承受能力。

它可以帮助工程师们进行设计分析和可靠性预测，以便确定系统操作的方式，预防材料失效。

因此，了解和掌握疲劳寿命S-N曲线的原理是非常重要的。

S-N曲线可以概括为两个主要组成部分：疲劳限和疲劳寿命。

S-N 曲线的垂直轴表示每次作用在材料上的一次疲劳应力，一般以MPa单位表示，它定义了材料受疲劳应力时的破坏限；而水平轴则表示该疲劳应力所能维持的周期数n，一般以次数表示。

简而言之，S-N曲线可以表明材料的可靠性，通过描述每次应力对材料寿命的影响。

S-N曲线可以根据应力参数类型的不同，归纳为多种类型。

其中，弯曲应力的S-N曲线如图1所示，由于材料受弯曲应力时比其他类型应力更容易破坏，因此相比其他类型S-N曲线，其破坏应力更为低，疲劳寿命也更短。

例如，对于不均匀曲线，其破坏应力约为200MPa，而对于均匀曲线，其破坏应力约为400MPa。

此外，还有其他多种类型的S-N曲线，如疲劳拉伸曲线、疲劳压缩曲线、拉伸拉断曲线、拉伸应变曲线等。

与弯曲曲线不同的是，这些类型的S-N曲线更稳定，受到应力的影响较弱，不但破坏应力更高，而且疲劳寿命更长。

另外，疲劳寿命S-N曲线还可以用来描述材料在不同温度下失效时的可靠性。

一般来说，随着环境温度的升高，材料的可靠性也会随之减小，同时破坏应力也会减小，即曲线的斜率变小。

因此，工程师们需要合理选择材料以满足特定的温度要求，同时要考虑疲劳寿命S-N曲线的影响，以保证系统的可靠性。

综上所述，疲劳寿命S-N曲线可以作为一种重要的参考，定量地描述材料在某一指定的应力水平和应变水平下的疲劳承受能力，并可以提供关于环境温度影响下材料破坏的重要信息。

因此，了解和掌握疲劳寿命S-N曲线的原理对于工程师们来说至关重要，可以帮助他们合理设计，提高系统的可靠性。

名义应力法修正s-n曲线
名义应力法修正S-N曲线是一种方法，用于将S-N曲线（即应力与疲劳寿命关系曲线）从研究中得到的基于应力振幅的数据转换为基于名义应力的数据。

该修正方法主要用于分析和预测疲劳寿命时，考虑到材料和构件的应力状态可能受到应力集中和多轴应力等因素的影响。

名义应力法修正S-N曲线的基本步骤如下：
1.获取基于应力振幅的S-N曲线：根据实验或试验数据，绘
制应力振幅与疲劳寿命的关系曲线。

2.估计应力集中因子：对于存在应力集中的部位或结构，通
过应力和应力集中的几何形状参数进行分析，估计应力集中因子。

3.计算名义应力：利用基于应力集中因子的分析结果，将应
力振幅转换为名义应力。

名义应力是一个等效应力，用于表示在应力集中部位的应力状态。

4.描绘名义应力S-N曲线：利用转换后的名义应力和相应的
疲劳寿命数据，绘制名义应力下的S-N曲线。

5.验证修正后的S-N曲线：将修正后的S-N曲线与实验数据
或现场应用中的观测结果相比较，评估修正方法的准确性和适用性。

名义应力法修正S-N曲线考虑了材料和结构的应力状态，尤其是对于存在应力集中的情况。

它提供了一种更准确的方法来估
计和预测材料和结构的疲劳寿命，以更好地评估其可靠性和安全性。

该方法在结构疲劳分析、工程设计和寿命预测等领域中得到广泛应用。

疲劳试验数据绘制n-s曲线是一种常用的方法，用于评估材料或结构的疲劳性能。

n-s曲线表示应力幅值（s）与循环次数（n）之间的关系。

通过绘制n-s曲线，可以观察到材料或结构在不同应力幅值下的疲劳寿命，从而判断其疲劳性能的好坏。

在绘制n-s曲线时，首先需要收集疲劳试验数据，包括应力幅值和对应的循环次数。

然后将这些数据整理成表格或图形形式，以便进行后续的分析和比较。

在绘制n-s曲线时，可以采用多种方法，如线性回归分析、指数回归分析等。

其中，线性回归分析是一种常用的方法，可以通过拟合直线来描述应力幅值与循环次数之间的关系。

指数回归分析则可以通过拟合指数函数来描述这种关系。

总之，绘制n-s曲线是评估材料或结构疲劳性能的重要手段之一。

通过分析n-s曲线，可以了解材料或结构在不同应力幅值下的疲劳寿命，从而为工程设计和应用提供重要的参考依据。

s—n（应力-等幅载荷数）曲线是材料的疲劳性能曲线，它是表征材料在不同应力下承受不同载荷循环次数的曲线。

疲劳寿命预测是工程实践中的重要问题，而s—n曲线则是对材料寿命进行预测的重要依据之一。

本文将从基本原理、测试方法和影响因素三个方面对s—n曲线进行详细介绍。

一、基本原理1.1 s—n曲线与疲劳寿命s—n曲线是一种以材料的应力（s）和载荷循环次数（n）作为坐标轴的曲线。

它反映了材料在不同应力水平下能承受的载荷循环次数，是一种经验公式。

根据s—n曲线所确定的载荷循环次数，可以对材料的疲劳寿命进行预测，为工程设计提供重要参考。

1.2 s—n曲线的特点s—n曲线通常呈现出两个阶段的特点。

最初的阶段是快速下降，这个阶段也称为疲劳寿命期。

随着载荷循环次数的增加，应力增加，材料的疲劳寿命将急剧下降。

其次是一个相对平坦的阶段，这个阶段称为长寿命区。

在这个阶段，随着载荷循环次数的增加，材料的寿命不再明显下降，也即已达到材料的疲劳极限。

二、测试方法2.1 旋转梁疲劳试验旋转梁疲劳试验是测定材料疲劳性能的一种常用方法。

其主要原理是通过将试件安装在旋转梁上，施加不同的应力载荷，通过记录试件的载荷循环次数和疲劳破坏情况，得到材料的s—n曲线。

2.2 拉伸-压缩疲劳试验拉伸-压缩疲劳试验是另一种常用的测试方法，其主要原理是通过在一定应力范围内施加拉伸-压缩载荷，测定试件的疲劳寿命。

通过不同的载荷循环次数和疲劳破坏情况，得到材料的s—n曲线。

2.3 影响因素（1）材料本身的性能，包括材料的强度、韧性、硬度等。

（2）试验条件，包括载荷类型、载荷大小、试验温度、环境湿度等。

（3）试件形状和尺寸，包括试件的几何形状、尺寸和表面处理情况。

三、影响因素3.1 材料性能材料的强度和韧性是影响s—n曲线的重要因素。

通常来说，强度高、韧性好的材料在低应力水平下也能承受较多的载荷循环次数，因此其s—n曲线相对平缓。

3.2 试验条件试验条件对材料的疲劳性能也有重要影响。

sn疲劳寿命曲线疲劳寿命曲线（SN曲线）是一种材料疲劳性能的描述方式，是用来衡量材料在受到交变载荷作用下所能承受的循环载荷次数的一种曲线。

这条曲线连接着材料的应力水平与循环次数，可以有效地评估材料的寿命。

疲劳是材料在受到交变载荷作用下的应力累积作用下发生的失效现象。

长期以来，疲劳失效一直是工程界的一个重要问题。

在现代工程中，大量的零件都会面临疲劳失效的威胁，因此了解材料的疲劳行为对工程设计和材料选择都非常重要。

疲劳寿命曲线是通过实验来获得的。

一般情况下，需要制备一系列的试样，在不同的应力水平下进行交变载荷的实验，记录下试样在不同循环次数下的失效情况，然后根据实验结果绘制出疲劳寿命曲线。

疲劳寿命曲线的形状通常可以分为三个阶段。

在曲线的起始阶段，也称为N阶段，试样的寿命很短，此时试样在较小的循环次数下就会发生失效。

在这个阶段，试样的强度是最高的，但由于强度不断下降，试样会很快失效。

随着循环次数的增加，试样进入到了曲线的第二个阶段，也称为S 阶段。

在这个阶段，试样在较小的应力水平下能够承受更多的循环次数，强度逐渐稳定。

这个阶段的特点是试样的寿命随着循环次数的增加而增加，但增加的速率逐渐减慢。

最后，试样进入到曲线的最后一个阶段，也称为W阶段。

在这个阶段，试样的强度已经下降到最低，试样的寿命会迅速减少，直至完全失效。

这个阶段的特点是试样的寿命随着循环次数的增加而减少，而减少的速率逐渐加快。

疲劳寿命曲线的形状与材料的特性密切相关。

不同材料的疲劳寿命曲线可能不同，甚至相同材料在不同的条件下也可能有差异。

材料的疲劳强度、硬度、塑性等特性都会影响到疲劳寿命曲线的形状。

疲劳寿命曲线的研究对于工程设计和材料选择都非常重要。

通过对材料进行疲劳试验，可以得到该材料在不同应力水平下的疲劳寿命曲线，从而可以评估材料的疲劳性能。

根据曲线的形状，可以预测材料在实际工程应用中的寿命，并且可以进行材料改进和工程设计的优化。

总之，疲劳寿命曲线是描述材料在受到交变载荷作用下所能承受的循环载荷次数的一种重要曲线。