电力系统元件的各序参数和等值电路共28页

对称分量法及元件的序模型与参数Symmetrical Components Method，Sequence ModelAnd Parameters第17讲问题1、计算电力系统三相不对称故障的总体思路？2、如何将相分量分解为正序、负序、零序分量之和？3、正常电力系统如何对正序、负序、零序三序解耦？4、发电机、线路的正序、负序、零序等值参数的定义及等值电路5、中性点上的阻抗对发电机或负荷的正序、负序、零序阻抗有什么影响？6、如何根据变压器的连接组别确定其零序等值电路？如何计算不对称短路故障？1、对于三相短路（对称短路），可用一相代表三相进行计算，采用相量分析方法，非常简单。

2、对于不对称故障，无法用一相代替三相，因而计算复杂，必须寻求新的方法。

单相短路无法用一相代替三相，如何求解？1、对称分量法(Symmetrical Components)•不对称故障后电力系统的特点•对称分量法•正序、负序、零序分量(Positive, Negative and Zero Sequence Components)等值2、各序分量对对称电力系统的作用•正常电力系统元件的对称性；三相参数完全相同三相参数循环(旋转)对称由这些元件连接成的电力系统是三相对称的。

•各序分量电量作用于对称系统的性质各序分量作用于对称系统的性质稳态分析中已有的结论：1、三相对称的网络注入三相正序电流，节点上只产生三相正序电压；三相正序电压施加在三相对称的网络只产生三相正序电流。

发电机正序电压加到电力网上，只产生正序电压与正序电流推测的结论：2、三相对称的网络注入三相负序电流，节点上只产生三相负序电压；三相负序电压施加在三相对称的网络只产生三相负序电流。

3、三相对称的网络注入三相零序电流，节点上只产生三相零序电压；三相零序电压施加在三相对称的网络只产生三相零序电流。

⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡222222222222222222222)()()(a s n ma m s n a n m s a s a n a m a m a s a n a n a m a s cb a s n mm s n n m s c b a I a Z a Z Z I a Z a Z Z I a Z a Z Z I a Z I a Z I Z I a Z I a Z I Z I a Z I a Z I Z I I I Z Z Z Z Z Z Z Z Z U U U 如对称矩阵加负序电流，产生的电压为所以ac a b U a U U a U ==,2负序电流产生的电压为负序电压！⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000000000000000)()()(a s n m a m s n a n m s a s a n a m a m a s a n a n a m a s c b a s n mm s n n m s c b a I Z Z Z I Z Z Z I Z Z Z I Z I Z I Z I Z I Z I Z I Z I Z I Z I I I Z Z Z Z Z Z Z Z Z U U U 对称矩阵加零序电流，产生的电压为所以ab c U U U ==零序电流产生的电压为零序电压！定理2正序量作用于对称系统后只产生正序量；负序量作用于对称系统后只产生负序量；零序量作用于对称系统后只产生零序量；三种分量对对称电力系统相互独立，互相解耦。

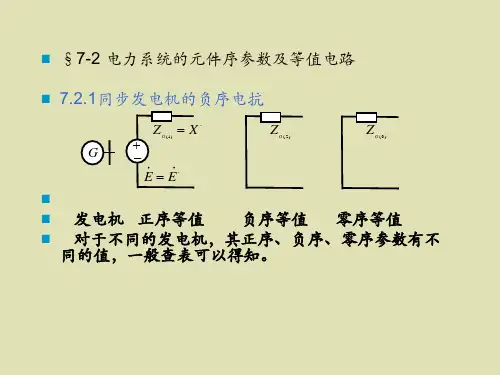
7.2 电力系统元件的序参数7.2.1 发电机的负序和零序电抗1.同步发电机的负序电抗当电力网络发生了不对称短路，不对称的三相基频短路电流可以分解为正、负、零序电流分量，这些电流分量将产生不同的磁场，其中负序电流产生的磁场将在定、转子绕组中产生许多高次谐波电流，其电磁过程十分复杂，使精确确定发电机的负序阻抗很困难。

在工程上通常忽略发电机定子绕组的电阻，对负序电抗定义为施加在发电机端点的负序电压同步频率分量与流入定子绕组负序电流同步频率分量的比值。

按这样的定义，当短路类型不同，同步发电机的负序电抗有不同的值，如表7-1所示。

表7-1 同步发电机的负序电抗表中，为同步发电机的零序电抗。

从表7-1可见，当，则负序电抗，即同步发电机的负序电抗与短路类型无关。

当同步发电机经外电抗短路时，表7-1中所有各电抗、都应以、代替，发电机转子不对称的影响被削弱。

实际的电力系统，短路大多是发生在输电线路上，所以在不对称短路电流计算中，可以近似认为同步发电机的负序电抗与短路类型无关，其具体的数值一般由制造厂提供，也可按下式估算。

对于汽轮发电机和有阻尼绕组的水轮发电机（7-13）对于无阻尼绕组的水轮发电机（7-14）2.同步发电机的零序电抗同步发电机的零序电抗定义为：施加在发电机端点的零序电压同步频率分量与流入定子绕组的零序电流同步频率分量的比值。

当三相定子绕组通以三相零序电流时，在三相定子绕组中产生大小相等、方向相同、空间相差120o的脉振磁场，它们在气隙中的合成磁场为零。

因此，同步发电机定子绕组中的零序电流只产生定子漏磁通，与此漏磁通相对应的电抗就是零序电抗。

但应注意，零序电流产生的漏磁通与正序电流产生的漏磁通往往不同，其差别和定子绕组的型式有关。

实际上，零序电流产生的漏磁通较正序的要小些，其数值范围大致为（7-15）表7-2列出了不同类型同步电机的和表7-2 国产同步电机的负序、零序电抗平均值序号元件名称1 无阻尼绕组的水轮发电机0.45 0.112 有阻尼绕组的水轮发电机0.215 0.0953 容量为50MW及以下的汽轮发电机0.175 0.0754 100MW及125MW汽轮发电机0.210 0.085 200MW汽轮发电机0.175 0.0856 300MW汽轮发电机0.198 0.0847 同步调相机0.165 0.0858 同步电动机0.160 0.0807.2.2 异步电动机的负序电抗和零序电抗异步电动机的等值电路在电机学已讲过，如图7-5(a)所示。

电力系统分析部分习题答案(参考) 稳态部分第四章复杂电力系统的潮流计算4-1-3解：（1）不考虑非标准变比时：（因为对称，所以只求上三角元素）所以：（2）当考虑非标准变比时，只有变压器两侧的节点的自导纳和这两个节点之间的互导纳有变化。

第五章电力系统的有功功率和频率调整5-1-2解：解得：均未超出发电厂的出力范围，为最优分配方案。

5-1-3解：（1）由耗量特性得到两台发电机的耗量为增率分别为：当负荷为40MW时两台发电机均按下限发电，各承担20MW负荷，相应微增率为因此负荷增加时机组1首先增加负荷，而机组2仍按下限发电，此时综合耗量微增率取决于发电机1。

负荷增加直到时发电机2才增加负荷。

当时此时当负荷大于55MW时才可以按照等耗量为增率准则最优分配负荷。

当负荷为250MW时两台发电机均满发电，此时即按等耗量为增率分配时发电机2就满发，在增加负荷时只有发电机1增加功率，综合耗量微增率仍表现为发电机1的耗量微增率。

时此时所以时按最优分配，综合特性为：得：（2）当负荷为150时按最优分配，代入综合特性为（3）最优分配时解得：平均分配时节省的燃料费用为：5-2-1解：（a）（b）5-2-2解：因为PG3满载，所以只有PG1和PG2能够参加调频（1）（此时PG1和PG2均未满载）（2）此时PG1已经超载，所以应该以发电机2和负荷的调节特性计算频率。

5-2-5解：所以设联络线的功率为Pab，则有解得：Pab=-230.77MW5-2-8解：第六章电力系统无功功率和电压调整6-2-3 思路见P230 6-36-3-2 注意升压变，符号的变化6-3-3 有一台降压变压器，其归算到高压侧的参数为，低压侧的最大、最小负荷表示于图中，高压侧电压波动范围是106.7～113.3kV，如果负荷允许的电压波动范围是6～6.6kV,是否可以选择变压器的分接头以满足电压水平的要求？若可以，试选择之。

若不能，试说明原因。

解：选择110-2×2.5%的分接头校验：最大负荷时：最小负荷时：求电压偏移：所以不能选出合适的变压器分接头满足调压要求6-3-8三串电容器组成，每串串3个，所以6-3-10：解：（1）选用调相机时：最大负荷时：即：最小负荷时解得：k=10.3312 高压侧电压=k*11=113.64kV 所以选择110+2.5%的抽头 k=10.25计算容量（2）当选用电容器时：依据最小负荷时选取变压器的抽头：k=10.75,所以选择电容器的容量为6-3-13：解：设补偿容量为则通过变压器的功率为：所以：所以6-3-17解：依题意，变电所的低压侧要求常调压。

第四章 对称分量法及元件的各序参数和等值电路第一节 对称分量法• 三个不对称相量可用三组对称相量来表示⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡•⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡)0()2()1(2211111a a a c b aF F F a a a a F F F S P F T F •= • 三个不对称相量可以分解为三组对称相量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡•⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡c b a a a a F F F a a a a F F F 111113122)0()2()1( P S F T F •=-1 特点1：对称分量具有明确的物理意义第二节 在不对称故障分析中的应用一.三相阻抗的对称分量三相静止对称元件：三相对称：scc bb aa z z z z ===，mac bc ab z z z z ===支路电压方程：缩写为： p p p I z U =∆ 作变换： p pp I T T z T U T 111---•=∆ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆∆∆c b a s mm m s m m m sc b a cc cb ca bc bb ba ac ab aa c b a I I Iz z z z z z z z z I I I z z z z z z z z z U U U得：s s p I z U =∆其中： ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--==-m s m s ms p s z z z z z z T z T z 20000001以序分量表示的支路电压方程为：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡•⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡•⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆∆∆)0()2()1()0()2()1()0()2()1()0()92)1(0000002000000a a a a a a m s m s ms a a a I I I z z z I I I z z z z z z U U U 三相对称系统对称分量变换为三个互不耦合的正、负、零序系统。

第七章电力系统各元件的序阻抗和等值电路7-1 对称分量法在不对称短路计算中的应用7.1.1 不对称三相量的分解在三相电路中，对于任意一组不对称的三相相量（电流或电压），可以分解为三组三相对称的相量。

当选择a相作为基准相时，三相相量与其对称分量之间的关系（以电流为例）可表示为：7.1.1 不对称三相量的分解a 、b 、c 三相各序分量之间的关系：正序：2(1)(1)(1)(1),b a c a I a I I a I ==i i i i负序：2(2)(2)(2)(2),b ac a I a I I a I ==iiii零序：(0)(0)(0)b c a I I I ==iii7.1.2 不对称三相量的序分量表示a 、b 、c 三相电流用a 相序分量可表示为：(1)(1)21(2)(2)2(0)(0)11111aa ab a ac a a I I I I a a I S I a aI I I −⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ii ii i i i i i7.1.3 序阻抗的概念序阻抗的概念：•各相自阻抗为：Zaa 、Zbb、Zcc•相间互阻抗为：Zab =Zba、Zbc=Zcb、Zac=Zca7.1.3 序阻抗的概念通过不对称电流时：a a aa ab ac b b ba bb bc c c ca cbcc Z Z Z V I V Z Z Z I V I Z Z Z ⎡⎤⎡⎤⎡⎤∆⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥∆=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥∆⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦iii i i i abc abcV ZI ∆=简记为：⇓abc abcS V SZI ∆=⇓1120120120abc sc V SZI SZS I Z I −∆===7.1.3 序阻抗的概念1sc Z SZS −=称为序阻抗矩阵aa bb cc s ab bc ca m Z Z Z Z Z Z Z Z ======当元件结构参数对称时： 令： (1)(2)(0)00000000020s m sc s ms m Z Z Z Z Z Z Z Z Z Z ⎡⎤−⎡⎤⎢⎥⎢⎥=−=⎢⎥⎢⎥⎢⎥⎢⎥+⎣⎦⎣⎦120120sc V Z I ∆=代入，并展开有7.1.3 序阻抗的概念(1)(1)(1)(2)(2)(2)(3)(3)(3)a a a a a a V z I V z I V z I ⎧∆=⎪⎪⎪∆=⎨⎪⎪∆=⎪⎩i ii i i i在三相参数对称的线性电路中，各序对称分量具有独立性。