高数上第六章-弧长
- 格式:ppt
- 大小:1.75 MB
- 文档页数:17



弧长公式高中数学
弧长公式是高中数学中用于计算圆或圆弧长度的重要公式。
具体来说,弧长公式有两种形式:
1. 弧长公式:L=n×π×r/180,其中n是圆心角度数,r是半径,L是圆心角弧长。
这个公式是基于角度制来计算的。
2. 弧长公式:L=α×r,其中α是圆心角度数(以弧度为单位),r是半径,L是圆心角弧长。
这个公式是基于弧度制来计算的。
需要注意的是,角度制和弧度制是两种不同的角度计量单位。
在角度制中,一个完整的圆被定义为360度;而在弧度制中,一个完整的圆被定义为2π弧度。
在实际应用中,需要根据具体情况选择合适的弧长公式来计算圆或圆弧的长度。


![6[1].2弧长大学数学高数一](https://uimg.taocdn.com/a298ac4afe4733687e21aa89.webp)



.习题621 求图621 中各画斜线部分的面积 (1)解 画斜线部分在x 轴上的投影区间为[0 1] 所求的面积为61]2132[)(1022310=-=-=⎰x x dx x x A . (2)解法一 画斜线部分在x 轴上的投影区间为[0 1] 所求的面积为 (1|)()(1010=-=-=⎰x x e ex dx e e A解法二 画斜线部分在y 轴上的投影区间为[1 e ] 所求的面积为1)1(|ln ln 111=--=-==⎰⎰e e dy y y ydy A ee e(3)解 画斜线部分在x 轴上的投影区间为[3 1] 所求的面积为332]2)3[(132=--=⎰-dx x x A(4)》解 画斜线部分在x 轴上的投影区间为[1 3] 所求的面积为332|)313()32(3132312=-+=-+=--⎰x x x dx x x A2. 求由下列各曲线所围成的图形的面积(1) 221x y =与x 2y28(两部分都要计算)解388282)218(220220*********--=--=--=⎰⎰⎰⎰dx x dx x dx x dx x x A34238cos 16402+=-=⎰ππtdt346)22(122-=-=ππS A—(2)xy 1=与直线yx 及x 2解所求的面积为 ⎰-=-=212ln 23)1(dx x x A(3) y e xy ex与直线x 1解所求的面积为⎰-+=-=-1021)(ee dx e e A x x\(4)y =ln x , y 轴与直线y =ln a , y =ln b (b >a >0). 解所求的面积为a b e dy e A ba y ba y -===⎰ln ln ln ln 3 求抛物线y x 24x 3及其在点(0 3)和(3 0)处的切线所围成的图形的面积解y 2 x 4~过点(0, 3)处的切线的斜率为4 切线方程为y 4(x 3) 过点(3, 0)处的切线的斜率为2 切线方程为y 2x 6 两切线的交点为)3 ,23( 所求的面积为49]34(62[)]34(34[23023232=-+--+-+-+---=⎰⎰dx x x x x x x A4 求抛物线y 2=2px 及其在点),2(p p 处的法线所围成的图形的面积解2y y 2p在点),2(p p处1),2(=='p p y p y 法线的斜率k 1$法线的方程为)2(px p y --=- 即y p x -=23求得法线与抛物线的两个交点为),2(p p 和)3,29(p p -法线与抛物线所围成的图形的面积为 233232316)612123()223(p y p y y p dy p y y p A p p pp =--=--=--⎰5 求由下列各曲线所围成的图形的面积(1)2a cos解所求的面积为 》⎰⎰==-2022222cos 4)cos 2(21πππθθθθd a d a A a 2(2)x a cos 3t , y a sin 3t ;解所求的面积为 ⎰⎰⎰===2042202330sin cos 34)cos ()sin (44ππtdt t a t a d t a ydx A a2206204283]sin sin [12a tdt tdt a πππ=-=⎰⎰。
微积分弧长公式微积分弧长公式,也称微分弧长公式,是在高等数学中,表示曲线上线段长度的一种数学公式。
由德国数学家威廉布哈里发现并完成,于17是其出名的作品内容之一,它为理解曲线概念,特别是计算曲线上某点的位置和连续性,提供了非常重要的依据。
通常,当我们所讨论的曲线是由某一关系式定义的二维曲线时,需要用到微积分弧长公式,其方程式如下:弧长公式:L =_{a}^{b}[1 + (f(x))^2]dx其中,L表示曲线上某段线段的长度,a和b分别表示线段两端点的横坐标,f(x)示函数 f(x)导数。
由于古希腊数学家赫拉克利特和欧几里得对数学提出的有限次微分与微积分原理可以很好的推广到几何的概念上,微积分弧长公式也经推广到三维空间中,其方程式如下:弧长公式:L =_{a}^{b}[1 + (f(x))^2 + (f(x))^2]dx其中,f(x) f(x)别表示函数 f(x)一阶和二阶导数。
微积分弧长公式已经成为数学研究和教学中最重要的基础公式之一,在微积分教学中经常使用,有助于清晰的表示曲线的特征,从而表示形式化和让学生能够理解。
由微积分弧长公式可以推出一些其它的公式,如牛顿二次曲线的弧长公式、椭圆的弧长公式和双曲线的弧长公式。
牛顿二次曲线的弧长公式可以用来计算圆弧的长度,如:L = 2√[R^2 - (R - x)^2]其中,L示圆弧长度,R示圆半径,x示圆弧上的点的横坐标。
此外,微积分弧长公式也可以用来计算曲线的内接圆半径,如: r =[1 + (f(x))^2]其中,r示曲线上点的内接圆半径,f(x)示函数 f(x)导数。
微积分弧长公式直接影响到各种学科上的计算,它在科学计算、机械工程、地理学等方面都起着很重要的作用。
例如,在地球物理学中,它可用来描述地球表面特征,从而评估地形地貌演变等。
此外,微积分弧长公式也可以用来计算机器人工作空间中路径曲线的弧长,以确定机器人的行驶范围和行驶路径的安全性。
总之,微积分弧长公式为高数学家们 (特别是曲线几何学家)供了重要的理解曲线的依据,帮助人们更清楚的描述曲线的概念,从而让人们更好的掌握和使用曲线知识,为很多科学计算提供了有效的方法,并对实际应用有着重要的意义。
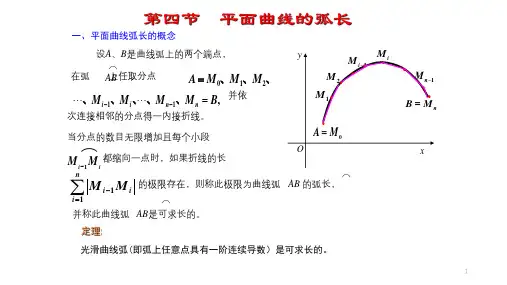
高数弧长ds的三种公式推导
在高等数学中,弧长是指曲线的一部分的长度。
以下是高数弧长的三种公式推导:
1. 直角坐标系下的弧长公式:
设曲线为函数y=f(x),曲线上两点A(x₁,y₁)和B(x₂,y₂)的弧长ds为两点之间的距离,即√((x₂-x₁)²+(y₂-y₁)²)。
由于y=f(x),则y₂=f(x₂)和y₁=f(x₁)。
将这些代入距离公式,得到弧长公式为:ds=√((dx)²+(dy)²)=√(1+(dy/dx)²)dx。
2. 参数方程下的弧长公式:
设曲线的参数方程为x=x(t),y=y(t),参数t的范围为[a,b]。
曲线上两点A和B的弧长ds为两点之间的距离,即√((x(t)₂-
x(t)₁)²+(y(t)₂-y(t)₁)²)。
将参数方程代入距离公式,并利用导数的链式法则,得到弧长公式为:ds=√((dx/dt)²+(dy/dt)²)dt。
3. 极坐标系下的弧长公式:
设曲线的极坐标方程为r=r(θ),θ的范围为[α,β]。
曲线上两点A和B的弧长ds为两点之间的距离,即√((r(θ)₂-r(θ)₁)²+(r(θ)₃-r(θ)₂)²)。
将极坐标方程代入距离公式,并利用极坐标导数的公式,得到弧长公式为:ds=√(r²+(dr/dθ)²)dθ。
这些是高数中常见的弧长公式推导,可以根据不同的曲线形式和坐标系选择适合的公式进行计算。