应用数理统计复习题(2014)

应⽤数理统计作业题及参考答案（第⼀章）第⼀章数理统计的基本概念P261.2 设总体X 的分布函数为()F x ，密度函数为()f x ，1X ，2X ，…，n X 为X 的⼦样，求最⼤顺序统计量()n X 与最⼩顺序统计量()1X 的分布函数与密度函数。

解：(){}{}()12nn i n F x P X x P X x X x X x F x =≤=≤≤≤= ，，，.()()()()1n n n f x F x n F x f x -'=??=.(){}{}1121i n F x P X x P X x X x X x =≤=->>> ，，，. {}{}{}121n P X x P X x P X x =->>>{}{}{}121111n P X x P X x P X x =-?-≤??-≤??-≤()11nF x =-?-()()()()1111n f x F x n F x f x -'=??=?-.1.3 设总体X 服从正态分布()124N ，，今抽取容量为5的⼦样1X ，2X ，…，5X ，试问：（i ）⼦样的平均值X ⼤于13的概率为多少？（ii ）⼦样的极⼩值（最⼩顺序统计量）⼩于10的概率为多少？（iii ）⼦样的极⼤值（最⼤顺序统计量）⼤于15的概率为多少？解：()~124X N ，，5n =，4~125X N ??∴ ??，. （i ）{}{}()13113111 1.1210.86860.1314P X P X P φφ>=-≤=-=-=-=-=. （ii ）令{}min 12345min X X X X X X =，，，，，{}max 12345max X X X X X X =，，，，.{}{}{}min min 125101*********P X P X P X X X <=->=->>> ，，，{}{}{}5551111011101110i i i i P X P X P X ===->=-?-()12~012X Y N -=，， {}{}121012*********X X P X P P P Y ---∴<=<=<-=<-{}()111110.84130.1587P Y φ=-<=-=-=.{}[]5min 10110.158710.42150.5785P X ∴<=--≈-=.（iii ）{}{}{}{}{}55max max 1251151151151515115115i i P X P X P X X X P X P X =>=-<=-<<<=-<=-? {}5max 1510.9331910.70770.2923P X ∴>=-≈-=.1.4 试证：（i ）()()()22211nni i i i x a x x n x a ==-=-+-∑∑对任意实数a 成⽴。

一 填空题 1设621,,,X X X 是总体)1,0(~N X 的一个样本，26542321)()(X X X X X X Y +++++=。

当常数C = 1/3 时，CY 服从2χ分布。

2 设统计量)(~n t X ，则~2X F(1,n) ，~12X F(n,1) 。

3 设n X X X ,,,21 是总体),(~2σu N X 的一个样本，当常数C = 1/2（n-1） 时，∑-=+-=11212)(n i i i X X C S 为2σ的无偏估计。

4 设)),0(~(2σεεβαN x y ++=，),,2,1)(,(n i y x i i =为观测数据。

对于固定的0x ，则0x βα+~ ()20201,x x N x n Lxx αβσ⎛⎫⎡⎤- ⎪⎢⎥++ ⎪⎢⎥ ⎪⎢⎥⎣⎦⎝⎭。

5．设总体X 服从参数为λ的泊松分布，，2，2，， 为样本，则λ的矩估计值为ˆλ＝ 。

6．设总体212~(,),,,...,n X N X X X μσ为样本，μ、σ2 未知，则σ2的置信度为1－α的置信区间为 ()()()()222212211,11n S n S n n ααχχ-⎡⎤--⎢⎥⎢⎥--⎢⎥⎣⎦。

7．设X 服从二维正态),(2∑μN 分布，其中⎪⎪⎭⎫ ⎝⎛=∑⎪⎪⎭⎫⎝⎛=8221,10μ令Y ＝X Y Y ⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛202121，则Y 的分布为 ()12,02TN A A A A μ⎛⎫= ⎪⎝⎭∑ 。

8．某试验的极差分析结果如下表（设指标越大越好）：表2 极差分析数据表则（1）较好工艺条件应为22121A B C D E 。

（2）方差分析中总离差平方和的自由度为 7 。

（3）上表中的第三列表示 A B ⨯交互作用 。

9．为了估计山上积雪溶化后对河流下游灌溉的影响，在山上建立观测站，测得连续10年的观测数据如下表（见表3）。

则y 关于x 的线性回归模型为 ()ˆ 2.356 1.813~0,1.611yx N εε=++ 10设总体12~(,1),,,...,n X U X X X θθ+为样本，则θ的矩估计量为 12x - ，极大似然估计量为 max{X 1,X 2,…,X n } 。

应用数理统计复习题一、填空题1.设总体212~(,),,,...,n X N X X X μσ为样本，样本均值及样本方差分别为，221111,()n n i i i i X X S X X n n ====-∑∑，设112,,...n n X X X X +与独立同分布，则统计量~Y =。

2.设21~(),~T t n T 则。

3.设总体X 的均值为μ，12,,...,n X X X 为样本，当a = 时，E 21()nii Xa =-∑达到最小值。

4. 设总体212~(,),,,...,n X N X X X μσ为样本，1||,()nii D XE D μ==-=∑则5.设总体X 的均值和方差分别为a , b , 样本均值及样本方差分别为221111,()n n i i i i X X S X X n n ====-∑∑，则 E (S 2 )= 。

6.在总体~(5,16)X N 中随机地抽取一个容量为36的样本，则均值 X 落在4与6之间的概率 =6. 设总体X 服从参数为λ的泊松分布，1.9，2，2，2.1， 2.5为样本，则λ的矩估计值为ˆλ＝ 。

7. 设总体212~(,),,,...,n X N X X X μσ为样本，12211ˆ()n i i i c XX σ-+==-∑，若2ˆσ为2σ的无偏估计，则 c = 。

8. 设总体12~(,1),,,...,n X U X X X θθ+为样本，则θ的矩估计量为 ，极大似然估计量为 。

9. 设总体212~(,),,,...,n X N X X X μσ为样本，μ未知，σ2已知，为使μ的置信度为1－α的置信区间长度不超过L ，则需抽取的样本的容量n 至少为 。

10. 设总体212~(,),,,...,n X N X X X μσ为样本，μ、σ2未知，则σ2的置信度为1－α的置信区间为 。

11设X 服从二维正态),(2∑μN 分布，其中⎪⎪⎭⎫⎝⎛=∑⎪⎪⎭⎫ ⎝⎛=8221,10μ令Y ＝X Y Y ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛202121，则Y 的分布为 (要求写出分布的参数) 12. 设总体X 在区间]1,[+θθ上服从均匀分布，则θ的矩估计=θˆ ；=)ˆ(θD 。

2014－2015 学年 第一学期期末试卷答案学号 姓名 成绩 考试日期： 2015年1月13日考试科目：《应用数理统计》（B 层）一、填空题（本题共16分，每小题4分）1．设122,,n x x x ，是来自正态总体2(,)N μσ的简单样本，则c =n mm- 时，统计量2221122211()()mkk k nk k k m xx cx x η-=-=+-=-∑∑服从F -分布。

2. 设12,,n x x x ，是来自正态总体2(0,)N σ的简单样本，用22211ˆ()ni i nx x n σ===∑估计2σ，则均方误差2222ˆ()E σσσ- 42σ 。

3．设总体X 的密度函数为22,[0,](;)0,[0,]x x p x x θθθθ⎧∈⎪=⎨⎪∉⎩，其中0θ>，12,,,n x x x 是来自总体X 简单样本，则2()q θθ=的矩估计ˆq = 294x 或212n i i x n =∑ 。

4．在双因素方差分析中，总离差平方和T S 的分解式为T A B A B e S S S S S ⨯=+++其中2111()p q re ijk ij i j k S x x ⋅====-∑∑∑，11rij ijk k x x r ⋅==∑，则e S 的自由度是 (1)pq r - 或n pq -，其中n pqr = 。

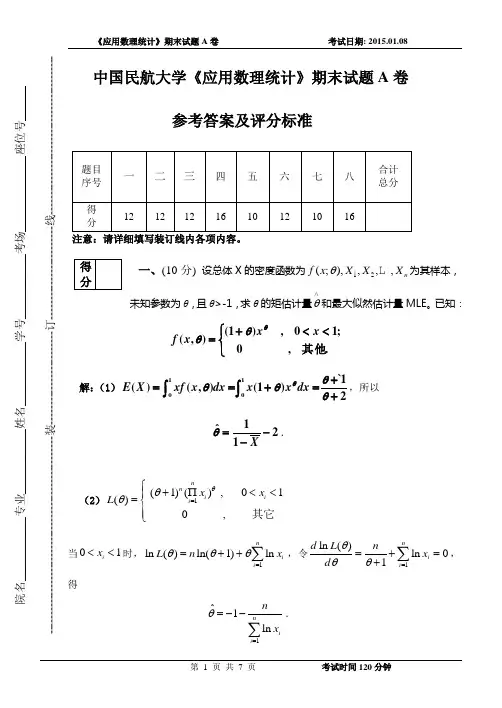
二、（本题12分）设总体X 的密度函数为111,(0,1)(;)0,(0,1)x x f x x θθθ-⎧∈⎪=⎨⎪∉⎩，其中0θ>，12,,,n x x x 是来自总体X 的简单样本。

（1）求θ的极大似然估计ˆθ；（2）求θ的一致最小方差无偏估计；（3）问θ的一致最小方差无偏估计是否为有效估计？证明你的结论。

解（1）似然函数为(1)()11{01}1211()()(,,,)n ni x x n ni L x I x x x θθθ-<≤<==∏对数似然函数为(1)(){01}1211ln ()ln (1)ln ln (,,,)n ni x x n i L n x I x x x θθθ<≤<==-+-+∑求导，有21ln ()1ln nii L n x θθθθ=∂=--∂∑令ln ()0L θθ∂=∂，可得θ的极大似然估计为11ˆln n i i x n θ==-∑。

山东科技大学2014—2015学年第一学期硕士研究生《应用统计》考试试卷班级 姓名 学号 一、填空题（每空3分，共36分）1．设某样本观测值为-1，1，2，2，-1，2，2，1，则对应的经验分布函数观测值为 .2．设总体X 的均值0EX =，方差2DX =，1210,,,X X X L 为其简单随机样本，5115i i X X ==∑，则DX = ；51016i j i j E X X ==⎡⎤⎛⎫⎛⎫=⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎝⎭⎣⎦∑∑ ； 521()i i E X X =⎡⎤-=⎢⎥⎣⎦∑ .3．设122,,,(0,1)n X X X iid N L ，则21nii X=∑服从 分布；22211nniji j n XX==+∑∑服从 分布.4．设1,,n X X L 为某总体X 的样本，X 为样本均值，若总体X 方差2σ的一个枢轴量221()nii XX σ-=-∑服从2(1)n χ-分布，则2σ的一个等尾双侧1α-置信区间为 ；2σ的一个单侧1α-置信下限为 .5．设μ为总体X 的均值，X 和2S 分别为样本均值和样本方差，检验00:0,:0H H μμ=≠的拒绝域形式为1C >；检验00:0,:0H H μμ≤>的拒绝域形式为2C >，已知0H(1)t n - ，则取显著性水平为α时，临界值1C = ；2C = .6．在样本量为29n =、水平数为5a =的单因子方差分析模型中，若总离差平方和231SS =，误差平方和126e SS =，则因素平方和A SS = ；F 检验统计量的值= .二、计算与证明（1、4小题每题18分，2、3小题每题14分，共64分）1．设总体X 服从参数为0λ>的泊松分布，即其概率分布为!(),1,2,kk P X k e k λλ-===L .（1）证明λ的矩估计量和极大似然估计量均为样本均值X ；（2）证明1ni ii a X=∑是λ的无偏估计，其中1,,n a a 为满足11nii a==∑的任意常实数；（3）证明在所有形如1ni ii a X=∑的线性无偏估计中，（1）中给出的估计X 最有效.2．对某市区2013年7月份地下水位进行调查，检测到20个采样点的地下水位数据如下：25.05, 25.30, 25.35, 25.81, 25.30, 25.16, 25.85, 25.10, 25.90, 25.18, 25.88, 25.22, 25.28, 25.35, 25.62, 25.28, 25.30, 25.22, 25.55, 25.30已知该市区2012年7月的地下水位平均为25.2米左右(指从地面到地下含水层的距离)，假设数据服从正态分布，在显著性水平0.05α=下，能否认为该市区2013年7月份的地下水位比往年同月份明显下降了?(已知0.95(19) 1.3277t =)3．为考察某种疾病是否与年龄有关，调查了200个对象，得列联表如下：(1) 给出该问题的假设和检验的拒绝域；(2) 对该问题做检验，并得出你的结论. (0.05α=,20.95(4)9.488χ=)4．为研究地层深度x 与某矿物元素含量y 的关系，采样数据如下：求 (1) y 关于x 的经验回归直线；(2) 检验回归方程的显著性（0.05α=）； (3) 求y 在200x =处的预测值和0.95的预测区间.(已知0.95(1,5) 6.61F =,0.975(5) 2.5706t =)。

应用数理统计复习题一、填空题1.设总体212~(,),,,...,n X N X X X μσ为样本，样本均值及样本方差分别为，221111,()n n i i i i X X S X X n n ====-∑∑，设112,,...n n X X X X +与独立同分布，则统计量~Y =。

2.设21~(),~T t n T 则。

3.设总体X 的均值为μ，12,,...,n X X X 为样本，当a = 时，E 21()nii Xa =-∑达到最小值。

4. 设总体212~(,),,,...,n X N X X X μσ为样本，1||,()nii D XE D μ==-=∑则5.设总体X 的均值和方差分别为a , b , 样本均值及样本方差分别为221111,()n n i i i i X X S X X n n ====-∑∑，则 E (S 2 )= 。

6.在总体~(5,16)X N 中随机地抽取一个容量为36的样本，则均值 X 落在4与6之间的概率 =6. 设总体X 服从参数为λ的泊松分布，1.9，2，2，2.1， 2.5为样本，则λ的矩估计值为ˆλ＝ 。

7. 设总体212~(,),,,...,n X N X X X μσ为样本，12211ˆ()n i i i c XX σ-+==-∑，若2ˆσ为2σ的无偏估计，则 c = 。

8. 设总体12~(,1),,,...,n X U X X X θθ+为样本，则θ的矩估计量为 ，极大似然估计量为 。

9. 设总体212~(,),,,...,n X N X X X μσ为样本，μ未知，σ2已知，为使μ的置信度为1－α的置信区间长度不超过L ，则需抽取的样本的容量n 至少为 。

10. 设总体212~(,),,,...,n X N X X X μσ为样本，μ、σ2未知，则σ2的置信度为1－α的置信区间为 。

11设X 服从二维正态),(2∑μN 分布，其中⎪⎪⎭⎫⎝⎛=∑⎪⎪⎭⎫ ⎝⎛=8221,10μ令Y ＝X Y Y ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛202121，则Y 的分布为 (要求写出分布的参数) 12. 设总体X 在区间]1,[+θθ上服从均匀分布，则θ的矩估计=θˆ ；=)ˆ(θD 。

一、填空题1．小概率原理是 .2．在数理统计学中，我们称研究对象的全体为总体母体，组成总体的每个单元为个体。

3．（12,,,n ξξξ ）是总体2~(3,5)N ξ的样本，则()(1,2,,)__________i E i n ξ== 3 4．如果总体ξ的样本（n ξξξ,,,21 ）满足下列条件：（1）n ξξξ,,,21 相互独立；（2）i ξ（1,2,,i n = ）与总体ξ 同分布 ，则称（n ξξξ,,,21 ）是总体的简单随机样本. 5．设0.05是假设检验中犯第一类错误的概率，H 0为原假设，则P {拒绝H 0｜H 0真}= __0.05__.6．评价估计量好坏的标准最常用的有________无偏性、有效性、一致性7．设总体ξ服从参数为λ（λ>0）的泊松分布，（12,,,n ξξξ ）为总体ξ的一个样本，其样本均值5ξ=，则λ的矩估计值λˆ=____5____ 8．由来自正态总体(,1)N μ容量为100的简单随机样本，算得样本均值为10，则未知参数μ的置信度为0.95的置信区间是_（9.804,10.196）_．(0.975 1.96u =)9．由来自正态总体(,1)N μ容量为100的简单随机样本，得样本均值为6，则未知参数μ的置信度为0.95的置信区间是_（5.804,6.196） . (0.975 1.96u =)10．设总体2~(,)N ξμσ，其中2σ未知，现由来自总体ξ的一个样本（129,,,ξξξ ）算得样本均值20ξ=，修正样本标准差S =3，并查得0.95(8) 1.86t =，则μ的置信度为0.9的置信区间是 （18.14,21.86） .11．设1234(,,,)ξξξξ为来自总体(0,1)N ξ 的样本，则统计量2212ξξ+ .12．设（1234,,,ξξξξ）为来自总体(0,1)N ξ 的样本，则统计量~22ξ .13．设（1234,,,ξξξξ）为来自总体(0,1)N ξ 的样本，则统计量22221234ξξξξ+++ . 14．设（123,,ξξξ）为来自总体(0,1)N ξ 的样本，则统计量222123ξξξ++ .15．已知一元线性回归方程为ˆˆ3ya x =+，且x =3，y =6，则ˆa = -3 . 16．已知一元线性回归方程为ˆˆ3ya x =+，且x =1，y =6，则ˆa = 3 . 17．已知一元线性回归方程为ˆˆ2ya x =+，且x =2，y =8，则ˆa = 4 . 18．设总体ξ的数学期望()E ξ存在，（123,,ξξξ）为总体ξ的样本，1231136Y k ξξξ=++，则当k =_______________时，Y 是()E ξ的无偏估计量.19．设总体ξ的数学期望()E ξ存在，（123,,ξξξ）为总体ξ的样本，1231155k ηξξξ=++，则当k =_______________时，η是()E ξ的无偏估计.20．设总体ξ的数学期望()E ξ存在，（123,,ξξξ）为总体ξ的样本，1231132k ηξξξ=++，则当k =_______________时，η是()E ξ的无偏估计量.21．12(,,,)n ξξξ 是总体)4,1(~2N ξ的样本，则__________)(1=ξD 1622．设(10)t ξ ，0.95(10)t 表示t 分布的下侧分位数，则{}0.95(10)P t ξ≤= 0.95 . 23．设(15)t ξ ，0.99(15)t 表示t 分布的下侧分位数，则{}0.99(15)P t ξ≤= 0.99 . 24．设2(8)ξχ ，20.95(8)χ表示χ分布的下侧分位数，则{}20.95(8)P ξχ≤= 0.95 .25．设(0,1)N ξ ，0.99μ表示正态分布的下侧分位数，则{}0.99P ξμ≤= 0.99 26．设（nξξξ,,,21 ）为总体ξ的一个样本，记11()nr r i i B n ξξ==-∑，则r B 叫做样本（n ξξξ,,,21 ）的r 阶 中心矩 . 设（12,,,n ξξξ ）为总体ξ的一个样本，记r A =11n ri i n ξ=∑，则r A 叫做样本（12,,,n ξξξ ）的r 阶 原点 .二、单项选择题1．设2(,)N ξμσ ，12(,,,)n ξξξ 为总体ξ的一个样本，记ξ=11ni i n ξ=∑，则下列选项中正确的是A ．2(,)N ξμσB ．(0,1)N ξ C．(N ξμ D ． 2(,)N nσξμ2．设（12100,,,ξξξ ）为来自总体2(0,5)N ξ 的一个样本，ξ表示样本均值，则ξ~A ．(0,5)NB ．(0,25)NC ．(0,0.05)ND ． (0,0.25)N3．设(1,1)N ξ ，（n ξξξ,,,21 ）为总体ξ的一个样本，记ξ=11ni i n ξ=∑，则下列选项中正确的是A ．(0,1)N ξB ．(1,1)N ξC ．1(1,)N n ξ D．N ξ 4．在假设检验问题中，犯第二类错误是指A ．在0H 不成立的条件下，经检验0H 被拒绝B ．在0H 不成立的条件下，经检验0H 被接受C ．在0H 成立的条件下，经检验0H 被拒绝D ．在0H 成立的条件下，经检验0H 被接受5．设总体2(,)N ξμσ ，12(,,,)n ξξξ 为总体ξ的一个样本,记2211()1nii Sn ξξ==--∑ , 则下列选项中正确的是A ．22(1)~(1)n Sn χ-- B ．222(1)~()n Sn χσ-C ．222(1)~(1)n Sn χσ--D ．222~(1)Sn χσ-6. 设总体ξ2(,)N μσ ，（12,,,n ξξξ ）为总体ξ的一个样本,记2211()1nii S n ξξ==--∑ ,则在下列各式中，正确的是A. 222(1)(1)n Sn χσ-- B.22(1)(1)n Sn χσ--C. 222(1)()n Sn χσ- D.22(1)()n Sn χσ-7．设总体ξ2(,)N μσ ，（12,,,n ξξξ ）为总体ξ的一个样本, 记2211()nii S nξξ==-∑,则下列选项中正确的是A ．22~(1)nS n χ- B ．222~(1)nS n χσ-C ．222(1)~(1)n S n χσ--D ．22(1)~(1)n S n χσ--8．设总体ξ2(,)N μσ ，（n ξξξ,,,21 ）为总体ξ的一个样本, 记2211()nii S nξξ==-∑,则下列选项中正确的是A ．22~()nS t n σ B ．22~(1)nS t n σ-C ．222~()nS n χσD ．222~(1)nS n χσ-9．(,)F m n α表示F 分布的下侧α分位数，则0.95(3,7)F =A ．0.95(7,3)FB ． 0.951(3,7)FC ．0.051(7,3)FD ．0.051(3,7)F10. (,)F m n α表示F 分布的下侧α分位数，则正确的是A. 11(,)(,)F n m F n m αα-=B. 111(,)(,)F n m F m n αα--=C. 1(,)(,)F n m F m n αα=D. ),(1),(1n m F m n F αα-=11．(,)F m n α表示F 分布的下侧α分位数，则0.975(10,7)F =A ．0.975(7,10)FB ．0.9751(10,7)FC ．0.0251(7,10)FD ．0.0251(10,7)F12．(,)F m n α表示F 分布的下侧α分位数，则0.91(1,2)F =A ．0.9(2,1)FB ．0.9(1,2)FC ．0.1(2,1)FD ．0.1(1,2)F13．设总体ξ2(,)N μσ ，2σ为已知，12(,,,)n ξξξ 为总体ξ的一个样本，ξ=11ni i n ξ=∑，2211()1nii Sn ξξ==--∑ ，欲检验假设0010:,:H H μμμμ=≠，则检验用的统计量是Aξ BξC ．22101()nii ξμσ=-∑D ．220(1)n Sσ-14．设总体ξ(0,1)N ，（126,,,ξξξ）为总体ξ(2)t ，则c =A ．1B ．2CD ．1215．设总体ξ(0,1)N ，（1234,,,ξξξξ）为总体ξ的一个样本，(3)t ，则k =A ．2B ．3CD16．设总体ξ(0,1)N ，（126,,,ξξξ）为总体ξ(5)t ，则k =A ．2B ．6CD17．设总体2(,)N ξμσ ，其中μ已知，2σ未知，123(,,)ξξξ是总体ξ的一个样本，则下列各式中不是统计量的是A ．3ξB ．122ξξ+C ．1233ξξξμ++-D ． 2221232ξξξσ++18．设（1234,,,ξξξξ）是总体ξ2(,)N μσ 的一个样本，其中μ未知，2σ已知，11ηξμ=-，1222ξξη+=，22212332ξξξησ++=，123444ξξξξμησ+++-=，则1234,,,ηηηη中统计量的个数是A.1B. 2C.3D. 419．设总体ξ2(,)N μσ ，其中μ和2σ均未知，（123,,ξξξ）是总体ξ的一个样本，则下列各式中是统计量的是A ．2221232ξξξσ++ B ．3ξC ．1233ξξξμ++-D ．1ξμ-20．设总体ξ2(,)N μσ ，其中μ已知，2σ未知，（n ξξξ,,,21 ）是总体ξ的一个样本，则下列各式中不是统计量的是A ．1ξB ．21ni i ξ=∑C ．22122ξξσ+ D ． {}12min ,,,n ξξξ21．设总体2(,)N ξμσ ，其中μ未知，1234(,,,)ξξξξ为来自总体ξ的一个样本，则以下关于μ的四个估计112341ˆ()4μξξξξ=+++，2123123ˆ555μξξξ=++，31211ˆ63μξξ=+，411ˆ7μξ=中，μ的无偏估计是A ．1ˆμB ．2ˆμC ．3ˆμD ．4ˆμ22．设（123,,ξξξ）是来自总体ξ的一个容量为3的样本，则下列关于()E ξ的无偏估计量中，最有效的估计量是A ．123212555ξξξ++B ．1231()3ξξξ++ C ．123111442ξξξ++D ．123124777ξξξ++23．设总体ξ2(,)N μσ ，其中μ未知，（12345,,,,ξξξξξ）为来自总体ξ的一个样本，11234511ˆ(),45μξξξξξ=++++22323ˆ,55μξξ=+31211ˆ,63μξξ=+41234512111ˆ77777μξξξξξ=++++，μ的无偏估计是A ．1ˆμB ．2ˆμC ．3ˆμD ．4ˆμ24．设随机变量~(0,1),~(0,1)N N ξη，且ξ与η相互独立，则22ξη服从的分布是A ．)2,0(NB ．)2(tC ．)2(2χD ．)1,1(F25．设ξ服从参数为λ的泊松分布()P λ，（12,,,n ξξξ ）为总体ξ的一个样本，ξ为样本均值，则λ的矩估计ˆλ= A ．ξ B ．2ξ C ．2ξ D ．1ξ26．设（1234,,,ξξξξ）是来自正态总体(0,1)N 的样本，则统计量22122234ξξξξ++服从A ．正态分布B ．F 分布C ．t 分布D ．2χ分布27．设总体ξ2(,)N μσ ，μ未知，（n ξξξ,,,21 ）为总体ξ的一个样本，ξ=11ni i n ξ=∑，2211()1nii Sn ξξ==--∑ ，欲检验假设22220010:,:H H σσσσ=≠，则检验用的统计量是 Aξ B ．220(1)n S σ-C ．22101()nii ξμσ=-∑ Dξ三、 计算题1. 若从自动车床加工的一批零件中随机抽取10件, 测得其尺寸与规定尺寸的偏差(单位: um)分别为: 2, 1, -2, 3, 2, 4, -2, 5, 3, 4, 零件尺寸的偏差设为ξ, 假 定2(,)N a ξσ ，试求置信度为0.9的a 的置信区间. （0.95(9) 1.8331t =）2.设总体ξ服从泊松分布()P λ, 即{},1,2,!k P k e k k λλξ-=== ，（1, 1, 1, 0）是总体ξ的一组样本观测值. 求λ的极大似然估计值.3.已知某班的应用数理统计的考试成绩服从正态分布2(,7)N a , 现从该班中抽取了9名同学, 测得成绩为: 75, 78, 80,81, 84, 86, 88, 90, 93. 求置信度为0.95的总体平均值a 的置信区间. )96.1(975.0=μ4．某台机床加工的产品的直径ξ服从正态分布2(,)N a σ, 今从该台机床加工的产品中随机抽取5件, 测得其直径(单位: 毫米)为: 20.1, 20.2, 20.3, 20.8, 21, 试在置信度0.95下, 求2σ的置信区间. )484.0)4(,143.11)4((025.02975.02==χχ5. 设罐头番茄汁中维生素C 含量服从正态分布. 按照规定, 维生素C 的平均含量约为21mg. 现从一批罐头中随机抽取16罐, 计算得23ξ= mg ，标准差 3.9S = mg. 问这批罐头的维生素C 含量是否合格？0.975(0.05,(15) 2.1315)t α==设各个工人的日产量都服从正态分布且方差相同, 试问在显著水平0.05=下, 操作工人之间的差异是否显著? )14.5)6,2((95.0=F（2）检验y 与x 的线性是否显著?0.95(0.05,(1,3)10.01)F α==。

和最大似然估计量MLE二、（12分）设总体X 服从指数分布，其密度函数为：10()00xe xf x x θθ-⎧>⎪=⎨⎪≤⎩X 1,X 2,…，X n 来自总体X 的简单样本，试问参数θ的极大似然估计θ∧是否为无偏估计？（2）求样本的Fisher 信息量；（3）问θ∧是否是θ的有效估计？由指数分布的总体满足正则条件可得222211()ln (;)I E f x E λλλλλ⎡⎤∂-⎛⎫=-=-= ⎪⎢⎥∂⎝⎭⎣⎦，1λ的的无偏估计方差的C-R 下界为 2221221[()]11()nI n n λλλλλ-⎡⎤⎢⎥'⎣⎦==． 另一方面()1E X =， 21V a r ()X n λ=， 即X 得方差达到C-R 下界，故X 是1λ的UMVUE ．三、（16分）设总体X~N(μ1,σ2)，Y~ N(μ2,σ2), 今随机抽取X 的样本X 1, X 2,…X 8；Y 的样本Y 1, Y 2,…Y 8；计算得：75.2,25.3,11.57,03.5422====Y X S S Y X1．试在水平α=0.01 下检验假设H 0：μ1=μ2，H 1：μ1>μ2 2．试求α=0.02 时，μ2-μ1的估计区间四、（12分）合格苹果的重量标准差应小于0.005公斤．在一批苹果中随机取9个苹果称重, 得其样本标准差为007.0=S 公斤, 试问：（1）在显著性水平05.0=α下,可否认为该批苹果重量标准差达到要求? （2）如果调整显著性水平0.025α=，结果会怎样？解：（1）()()2222021:0.005,~8n S H σχχσ-≤=，则应有： ()()2220.050.0580.005,(8)15.507P χχχ>=⇒=， 具体计算得：22280.00715.6815.507,0.005χ⨯==>所以拒绝假设0H ，即认为苹果重量标准差指标未达到要求．（2）新设 20:0.005,H σ≤ 由2220.025280.00717.535,15.6817.535,0.005χχ⨯=⇒==< 则接受假设，即可以认为苹果重量标准差指标达到要求．五、（10分）为了解一种节能灯的使用寿命，随机抽取了8只灯泡，测得其使用寿命（单位：小时）如下：3250 3500 2850 3700 3010 2910 2980 3420请用柯尔莫哥洛夫检验方法检验该种节能灯的使用寿命是否服从正态分布？(a=0.05)六、（12分）测定某肉鸡的生长过程，每两周记录一次鸡的重量，数据如下表：由经验知鸡的生长曲线为Logistic 曲线:且极限生长量为k=2.827，试求y 对x 的曲线回归方程并进行检验。