03三铰拱受力分析

第四章静定拱和悬索结构拱结构是一种主要承受轴向压力并由两端推力维持平衡的曲线或折线形构件。

拱结构的主要内力为压力，使构件摆脱了弯曲变形。

如采用抗压性能较好的材料（如砖石或混凝土），则能充分发挥材料性能。

悬索结构是由柔性受拉索及其边缘构件所形成的承重结构，它能充分利用高强材料的抗拉性能，可以做到跨度大、自重小、省材料、易施工。

本章主要针对这两种受力性能截然不同的结构，讲述其内力分析方法，并对受力特性进行讨论。

第一节概述和三铰拱的计算拱式结构是应用较广泛的工程结构形式之一，我国远在古代就在桥梁和房屋建筑中采用了拱式结构。

图4-1（a）所示为修建于公元606年前的河北赵州桥，跨径37.02m，桥高7.23m，宽9.6m，是当今世界上现存最早、保存最完整的古代单孔敞肩石拱桥，经历了多次水灾、战乱和地震，却安然屹于清水河上，被称为中国工程界一绝。

在近代土木工程中，拱式结构是桥梁、隧道及屋盖中的重要结构型式之一。

图4-1(b)为2003年建成的主跨跨径达550m的上海芦浦大桥，是当今世界跨度第二长的钢结构拱桥，也是世界上首座完全采用焊接工艺连接的大型拱桥。

（a）（b）图4-1 拱式结构工程实例(a)赵州桥(b) 上海芦浦大桥为了说明拱式结构和梁式结构的受力特点，可将图4-2(a)、图4-2(b)及图4-2(c) 所示三种情况做一对比，这三种情况下结构所受的荷载及跨度均相同。

图4-2(a)所示为简支梁，在竖向荷载作用下，梁内有弯矩和剪力。

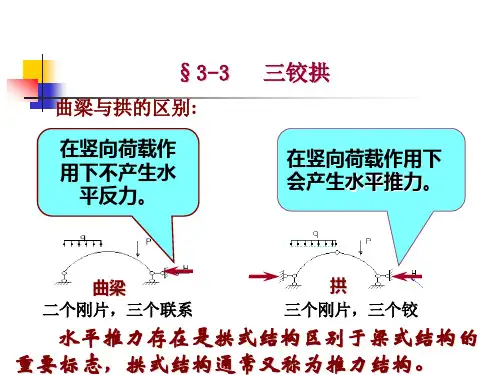
图4-2(b)所示结构，其杆轴虽为曲线，但在竖向荷载作用下支座并不产生水平支反力，它的弯矩图与图4-2(a)所示简支梁相同（剪力和轴力发生变化），故称为曲梁。

曲梁在竖向荷载作用下将在支座B处产生水平位移。

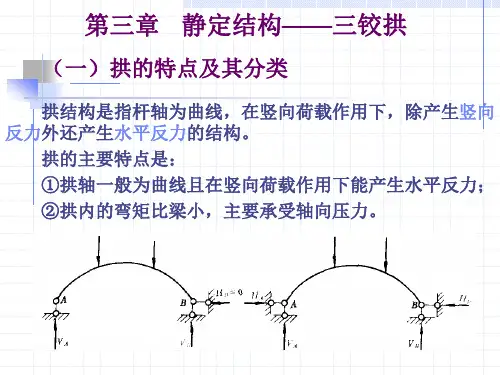
若用支承链杆约束该处的位移则变为图4-2(c)所示的情况，这种结构在竖向荷载作用下会产生水平推力，故属于拱式结构。

由此可见，水平推力的存在是拱式结构区别于梁式结构的一个重要标志，因此通常又将拱式结构称为有推力结构。

1 结构力学多媒体课件一、拱式结构的特征 1、拱与曲梁的区别拱式结构：指的是杆轴线是曲线，且在竖向荷载作用下会产生水平反力（推力）的结构。

FABH A ＝0 FABH A ＝0 三铰拱F PF P曲梁H≠0H≠0是否产生水平推力，是拱与梁的基本区别。

拱结构的应用：主要用于屋架结构、桥梁结构。

拱结构的应用：主要用于屋架结构、桥梁结构。

拱桥 （无铰拱）超静定拱 世界上最古老的铸铁拱桥（英国科尔布鲁克代尔桥) 万县长江大桥：世界上跨度最大的混凝土拱桥 灞陵桥是一座古典纯木结构伸臂曲拱型廊桥, 号称“渭水长虹”、“渭水第一桥” 主跨：40 米 建成时间：三峡工程对外交通专用公路下牢溪大桥（上承式钢管混凝土拱桥，主跨：160米 ，建成时间：1997）2、拱的类型三铰拱两铰拱无铰拱拉杆拱静 定 拱超 静 定 拱3、拱的优缺点a、在拱结构中，由于水平推力的存在，其各截面的弯矩要比相应简支梁或曲梁小得多，因此它的截面就可做得小一些，能节省材料、减小自重、加大跨度b、在拱结构中，主要内力是轴压力，因此可以用抗拉性能比较差而抗压性能比较好的材料来做。

c、由于拱结构会对下部支撑结构产生水平的推力，因此它需要更坚固的基础或下部结构。

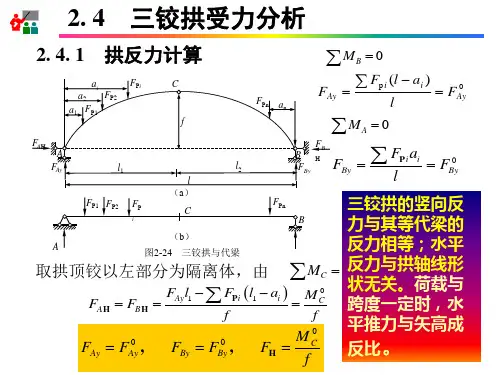
同时它的外形比较复杂，导致施工比较困难，模板费用也比较大4、拱的各部分名称lf 高跨比 BACf拱顶拱轴线拱高 f拱趾 起拱线跨度 l 平拱斜拱二、三铰拱的计算 1、支座反力的计算L 2L 1Lb 2a 2b 3a 3b 1a 1k y kx kCBAfF P1F P2F P3kCBAF P1F P2F P3B M =∑0Pi iYA YAFbF FL ==∑0A M =∑0Pi iYB YBF a F FL==∑取左半跨为隔离体：CM=∑()()01111212YA P P CH F L F L a F L a M F ff⨯----==F HF H1、支座反力的计算L 2L 1Lb 2a 2b 3a 3b 1a 1k y kx kCBA fF P1F P2F P3kCBAF P1F P2F P3在竖向荷载作用下，三铰拱的支座反力有如下特点： 1）支座反力与拱轴线形状无关，而与三个铰的位置有关。

第三节 三铰拱的合理轴线拱在荷载作用下，各截面上一般将产生三个内力，即弯矩、剪力和轴力。

其中，弯矩和剪力值较小，轴力较大，受力趋于合理。

若针对某种荷载作用下调整拱轴线的形状，使拱截面上弯矩为零（剪力也为零），则截面仅受轴力作用，拱处于均匀受压的状态。

从理论上来说，设计成这样的拱是最经济的。

将某种荷载作用下拱所有截面上弯矩为零时的拱轴线，称为合理拱轴线。

合理拱轴随荷载的变化而改变，荷载一定时，从理论上可求出其对应的合理拱轴线。

比如，对承受竖向荷载作用的三铰平拱，拱上任一x 截面处弯矩()M x 可表示为：0()()H M x M x F y =-当拱轴为合理拱轴时，根据合理拱轴的定义，有：0)()(0=-=y F x M x M H由此得：HF x M y )(0= (4-13) 式(4-13)即为竖向荷载作用下三铰平拱合理拱轴表达式。

由此可知，在竖向荷载作用下三铰平拱合理轴线的纵坐标y 与相应简支梁弯矩图的竖标0M 成比例。

当拱上所受荷载已知时，只需将相应简支梁的弯矩方程0()M x 除以推力H F 值，便可得到合理拱轴。

但应注意，合理拱轴线只是针对某一确定的固定荷载而言，当荷载布置改变时，合理拱轴形式亦会相应地改变。

下面讨论几种常见荷载作用下的合理拱轴线。

【例4-2】确定图4-9(a)所示三铰平拱在满跨竖向均布荷载q 作用下的合理轴线，已知拱跨度为l 。

图4-9 例4-2图（a ）三铰平拱承受满跨均布荷载作用 （b ）相应简支梁【解】建立如图4-9(a)所示的坐标系，与拱相应的简支梁如图4-9(b)所示。

求得支座反力如下：02AV AV ql F F ==，02BV BV ql F F == 028C AH BH H M ql F F F f f==== 相应简支梁中任一x 截面的弯矩方程为：2()22ql qx M x x =-根据式(4-13)，可得到拱的合理轴线方程为：0()HM x y F ==222422()8ql qx x f x l x ql l f-=- 由此可见，在竖向满跨均布荷载作用下，三铰平拱的合理轴线为二次抛物线。

第三章静定结构受力分析三铰拱三铰拱是指拱脚处设置了三个支座，可以在三个方向（横向、纵向和垂直）上无约束移动。

在受力分析中，三铰拱是一个非常重要的结构。

本文将对三铰拱的受力分析进行详细介绍。

三铰拱的受力分析首先需要了解其受力形式。

三铰拱受力主要包括水平向力和垂直向力。

水平向力主要来自于拱腹对拱脚的水平压力，而垂直向力主要来自于拱腹对拱脚的垂直压力。

在分析中，我们需要计算拱脚处的支座反力和弯矩大小。

首先，我们考虑横向受力平衡。

根据平衡条件，拱脚处的水平向力和法线向力之和为零。

即：∑Fx=0∑Fy=0其中，∑Fx表示水平向力的总和，∑Fy表示垂直向力的总和。

在接下来的分析中，我们假设拱脚处三个支座的反力分别为F1、F2和F3、由于三铰拱的支座可以自由移动，在计算反力时需要考虑拱腹对支座的约束力。

接下来，我们考虑拱腹对支座的约束力。

根据平衡条件，拱腹受到的约束力可以通过对整个拱腹的受力分析来得到。

我们将拱腹切割成多个小段，每个小段的受力可以看做静定问题。

对于每个小段，我们可以分别计算其水平向力和垂直向力。

在计算过程中需要注意，由于拱脚处的支座反力的未知，我们需要通过整个拱腹的受力平衡来解算这些未知。

最后，我们通过将每个小段的受力结果进行积分，得到拱脚处支座反力的大小和作用点位置。

在进行受力分析时，还需要考虑拱腹的几何特征，如拱的形状、拱腹曲线的方程等。

这些特征对于计算拱脚处的支座反力非常重要。

总的来说，三铰拱的受力分析是一个复杂而重要的过程。

通过考虑拱腹对支座的约束力，我们可以计算得到拱脚处支座反力的大小和作用点位置。

这些结果对于设计和分析三铰拱结构非常有帮助。