4.2 三铰拱的内力计算
- 格式:ppt
- 大小:994.00 KB
- 文档页数:18

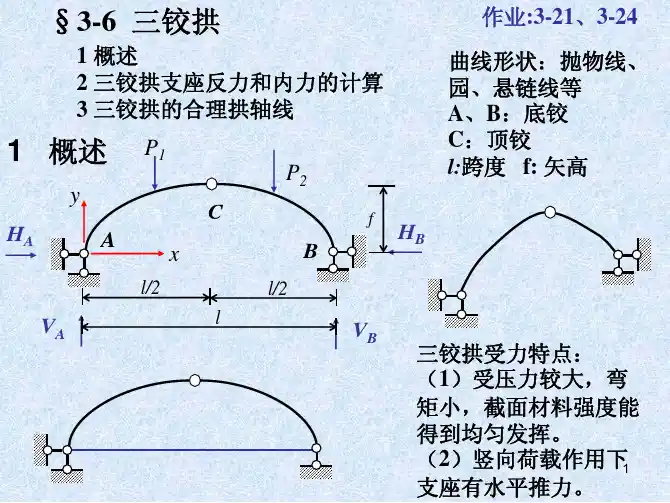
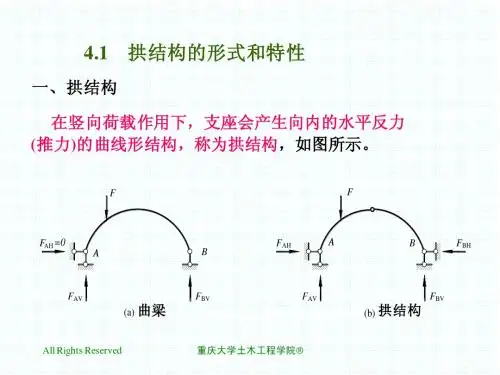

第4章 静定拱4.1 复习笔记【知识框架】【重点难点归纳】一、拱的基本概念及特点 ★★表4-1-1 拱的基本概念及特点表4-1-2 有拉杆和无拉杆三铰拱的区别与联系二、三铰拱的计算 ★★★★★1.支座反力的计算(见表4-1-3)表4-1-3 支座反力的计算2.内力的计算(见表4-1-4)表4-1-4 三铰拱的内力计算三、三铰拱的合理拱轴线(见表4-1-5) ★★★表4-1-5 三铰拱的合理拱轴线4.2 课后习题详解复习思考题1.拱的受力情况和内力计算与梁和刚架有何异同?答:(1)拱与梁的受力情况和内力计算的区别①约束反力方面,拱在竖向荷载作用下会产生水平反力(推力),而梁在竖向荷载作用下不会产生水平反力(推力);②内力分布方面,由于水平推力的存在,拱的弯矩常比跨度、荷载相同的梁的弯矩小得多,使得拱截面上的应力分布较为均匀;③内力分析方法方面,若只有竖向荷载时,梁只需进行简单的整体分析即可求解,而拱由于水平力的存在,需要整体分析与局部分析相结合。
(2)拱与刚架的受力情况和内力计算的异同①内力分析方法方面,拱与刚架的受力情况和内力计算的特点和所应用方法基本一致,例如三铰刚架也属于拱式结构;②拱的轴线是曲线,刚架杆的轴线是直线,在应用平衡条件计算内力时,拱仍然取投2.在非竖向荷载作用下怎样计算三铰拱的反力和内力?能否使用式(4-1)和(4-2)?答:(1)对于三铰拱承受非竖向荷载的情况,可将非竖向荷载分解为水平荷载和竖向荷载。
(2)仍然可以应用式(4-1)和(4-2),将水平反力加上非竖向荷载水平方向上的分量一起代入公式中进行求解。
(4-1)o AV AV o BV BV o c H F F F F M F f ⎫⎪=⎪⎪=⎬⎪⎪=⎪⎭cos sin (4-2)sin cos o H o S S H o N S H M M F y F F F F F F ϕϕϕϕ⎫=-⎪⎪=-⎬⎪=+⎪⎭3.什么是合理拱轴线?试绘出图4-2-1各荷载作用下三铰拱的合理拱轴线形状。


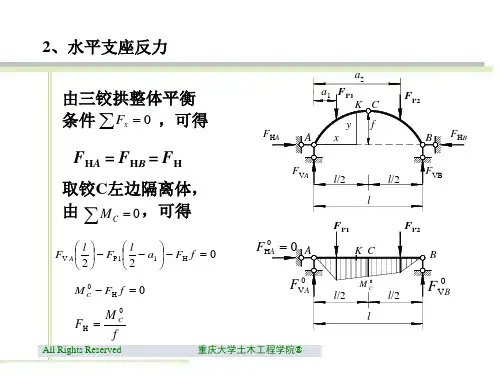


指定三铰拱内力计算及简图姓名:刘风喜班级:土木5班学号:1123310529 一、三铰拱参数及受力三铰拱的轴线方程是:Y=0.1X(20-X),即跨度为20m,矢高为10m受均布荷载q=20KN/m,在X=5,10,15m处受集中荷载F=10KN。
二、计算简图当0<X<5 时,M=215X-0.5qX2-110Y,Fy=215-20X,Fx=110当 5<X<10时,M=215X-0.5qX2-110Y-10(X-5),Fy=215-20X-10,Fx=110当10<X<15时,M=215X-0.5qX2-110Y-10(X-5)-10(X-10),Fy=215-20X-20,Fx=110当15<X<20时,M=215X-0.5qX2-110Y-10(X-5)-10(X-10)-10(X-15),Fy=215-20X-30,F x =110F x=F HF y=F Q0M=M0-F H yF Q=F y cosθ-F x sinθFN=-(Fysinθ+Fxcosθ)F ay=215 F ax=110三、计算表四、内力图五、讨论在相同荷载下,不同拱轴线所对应的内力分布也不同。
特别的,由F y=F Q0说明F y和拱轴线方程(拱的形状,高度)无关,由F x=F H=M c0/f 说明F x只与矢高有关,由M=M0-F H y 说明M只与矢高有关其和形状无关,而F Q , F N 都是θ(tanθ=Y X’)的函数。
所以在相同荷载下,不同拱轴线所对应的内力分布也不同。


第二节 拱内力图的绘制以上是按照三铰平拱承受竖向荷载作用的情况进行推导的,所导出的公式也适用于带拉杆的三铰平拱,拉杆拉力即为水平推力H F ,其支座反力和内力和的计算公式不变。
如图4-6(a)所示三铰斜拱在竖向荷载作用下,同样可根据三个整体平衡条件,以及半拱对拱顶铰C 的平衡条件0CM=∑,联立求解这四个平衡方程即可求出两个水平向支反力(AH F 、BH F )和两个竖向支反力(AV F 、BV F )。
有时为了避免求解联立方程组,也可先将斜拱支座反力分别沿竖直方向及拱趾连线方向分解为两个互相斜交的分力,即'AV F 、'AH F 和'BV F 、'BH F ,如图4-6(b)所示。
图4-6(c)所示为与斜拱相应的简支梁,其竖向支座反力记为0AV F 、0BV F 。
首先,分别对斜拱(图4-6(b))及相应简支梁(图4-6(c)),由整体平衡条件0BM=∑及0AM=∑可得:图4-6 三铰斜拱的计算(a)斜拱计算简图 (b)斜拱支反力沿斜向分解 (c)相应简支梁0'AV AVF F =, 0'BV BV F F = (4-9) 再由半拱的平衡条件0C M =∑,有:0'''CAHBHHM FFF h === (4-10)式中,h 为斜拱中拱顶铰C 至拱趾连线的垂直距离,0C M 为相应水平简支梁中相应C 截面的弯矩值。
式(4-9)和式(4-10)表明,三铰斜拱在竖向荷载作用下,若将两支座的反力沿竖向和起拱线方向分解为相互斜交的分力,其求解方法与三铰平拱在竖向荷载作用下支座反力的求解公式相同,只是求起拱线方向支反力分量时采用h 值,而不是f 值。
将图4-6(b)中斜向支座反力('AH F 和'BH F )沿水平方向和竖直方向进行分解,从而可求出斜拱在竖直方向和水平方向的支座反力分别为:00'cos cos C c H HM M F F h f αα===0''00sin sin tan C AV AVAHAVAV H M F FFFF F hααα=+=+=+ (4-11) 0''00sin sin tan C BVBVBHBVBV H M F F F F F F h ααα=-=-=-式(4-11)中,α为起拱线与水平线之间的夹角,f 为拱顶铰C 至拱趾连线的竖向距离。