考研高数总复习Laplace变换(讲义)
- 格式:pptx
- 大小:705.44 KB
- 文档页数:32










Laplace变换法讲义讲授人:郭蕴华、李格升武汉理工大学能源与动力工程学院 热能工程系第1节用Laplace变换法求解非稳态导热问题例1 图1所示的是一个双容系统,一个导热系数很大的薄壁容器,其中盛满某种液体,且液体被强烈搅拌为保持大致均匀的温度,于是容器和液体就组成了一个双容系统。
如果双容系统的初温为t i,τ > 0时,把它放置于温度为t f的环境中(设t f> t i),则容器和液体从环境吸热而升温。
设容器与环境之间的表面传热系数为h1,容器与内部液体之间的表面传热系数为h2,容器的容积与内、外表面积分别为V1、A2和A1,物性为ρ1、c1,液体的容积为V2,物性为ρ2、c2,求容器及液体的温度响应。
图1 双容系统非稳态导热设用t1(τ)表示容器的温度响应,t2(τ)表示液体的温度响应。
由能量守恒方程可以导出液体和容器的能量方程:(1)(2)且在时,有。
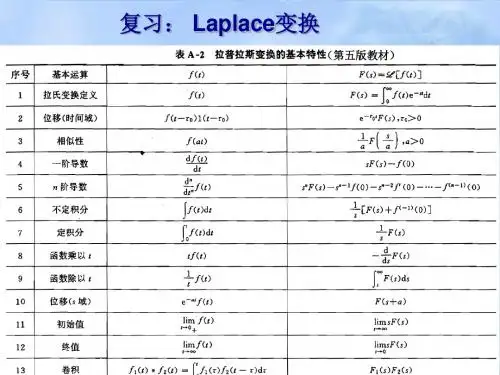
令,则式(1)和式(2)化为:(3)(4)对式(3)和式(4)进行Laplace变换,有(5)(6)第2节 Laplace变换回顾2.1 Laplace变换的定义函数f(τ)的Laplace变换定义为(2-1)其中,f(τ)称之为原函数,F(s)称之为象函数。
Laplace反变换定义为(2-2) 2.2几个常见函数的Laplace变换2.2.1) 单位阶跃函数的1(τ)的Laplace变换(2-3) 2.2.2) 指数函数exp(aτ)的Laplace变换(2-4) 2.2.3) 正弦函数和余弦函数的Laplace变换(2-5)(2-6) 2.2.4) 幂函数的Laplace变换(2-7) 2.3 Laplace变换的性质2.3.1) 线性定理若,,则有(2-8)证明:2.3.2) 微分定理(2-9)证明:推论1:(2-10)推论2:在零初值条件下,有(2-11) 2.3.3) 积分定理(2-12)证明:2.3.4) 衰减定理(2-13) 2.3.5) 延时定理(2-14) 2.3.6) 相似定理(2-15) 2.3.7) 象函数微分定理(2-16)证明:同理,可以得出推论:(2-17) 2.3.8) 象函数积分定理(2-18)证明:2.3.9) 卷积定理定义卷积:(2-19)则有卷积定理:(2-20) 2.3.10) 初值定理(2-21) 2.3.11) 终值定理(2-22) 2.4 Laplace反变换的定义Laplace反变换的公式为:(2-23)例2-1) 求的Laplace反变换。