点都绕原点O按逆时针方向旋转1800

2021中考数学一轮知识点系统复习之图形的平移、旋转与轴对称能力达标测试题（附答案详解）1．在平行四边形ABCD 中，AB=6，AD=8，∠B 是锐角，将△ACD 沿对角线AC 折叠，点D 落在△ABC 所在平面内的点E 处．如果AE 过BC 的中点，则平行四边形ABCD 的面积等于（ ）A ．48 B ．106 C ．127 D ．242 2．如图，在直角坐标系中，△OBC 的顶点O （0，0），B （﹣6，0），且∠OCB=90°，OC=BC ，则点C 关于y 轴对称的点的坐标是（ ）A ．（3，3）B ．（﹣3，3）C ．（﹣3，﹣3）D ．（32，32） 3．下列各组图形，可以经过平移变换由一个图形得到另一个图形的是( )．A ．B ．C ．D ． 4．如图，COD 是AOB 绕点O 顺时针方向旋转38后所得的图形，点C 恰好在AB 上，AOD 90∠=，那么BOC ∠的度数为（ ）A ．12°B ．14°C ．24°D ．30°5．点P （﹣4，﹣3）关于原点对称的点的坐标是（ ）A ．（4，3）B ．（﹣4，3）C ．（﹣4，﹣3）D ．（4，﹣3）6．如图，将∠BAC 沿DE 向∠BAC 内折叠，使AD 与A′D 重合，A′E 与AE 重合，若∠A=30°，则∠1+∠2=（ ）A ．50°B ．60°C ．45°D ．以上都不对 7．图中由“○”和“□”组成轴对称图形，该图形的对称轴是直线（ ）8．下面的图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．9．下列分子结构模型平面图中，只有一条对称轴的是（）A．B．C．D．10．如图，ABCD和DCGH是两块全等的正方形铁皮，要使它们重合，则存在的旋转中心有（）A．1个B．2个C．3个D．4个11．如图，点P在等边△ABC的内部，且PC=6，PA=8，PB=10，将线段PC绕点C顺时针旋转60°得到P'C，连接AP'，则sin∠PAP'的值为________．12．如图，正方形ABCD的边长为4，E是边BC上的一点且BE＝1，P为对角线AC上的一动点，连接PB，PE，当点P在AC上运动时，△PBE周长的最小值是____．13．如图，把△ABC经过一定的变换得到△A′B′C′，如果图中△ABC上的点P的坐标为（a，b），那么它的对应点P′的坐标为________．14．如图，将△ABE向右平移3cm得到△DCF，如果△ABE的周长是12cm，那么四边形ABFD的周长是_____cm．15．将点P（﹣1，3）绕原点顺时针旋转180°后坐标变为_____．16．已知平面直角坐标系内点P的坐标为（-1,3），如果将平面直角坐标系．．．．．．．向左平移3个单位,再向下平移2个单位,那么平移后点P的坐标为___________17．在平面直角坐标系中，已知点P0的坐标为(1，0)，将P0绕原点O按逆时针方向旋转30°得点P1，延长OP1到P2，使OP2＝2OP1，再将点P2绕原点O按逆时针方向转动30°得到点P3，延长OP3到P4，使OP4＝2OP3，…，如果继续下去，点P2016的坐标为_________.18．如图，△ABC中，AC＝10，AB＝12，△ABC的面积为48，AD平分∠BAC，F，E分别为AC，AD上两动点，连接CE，EF，则CE+EF的最小值为______．19．在等腰三角形ABC中，∠C=90°，BC=2cm．如果以AC的中点O为旋转中心，将这个三角形旋转180°，点B落在点B′处，那么点B′与点B的原来位置相距_____cm．20．如图①，在平面直角坐标系中，等边△ABC的顶点A，B的坐标分别为（5，0），（9，0），点D是x轴正半轴上一个动点，连接CD，将△ACD绕点C逆时针旋转60°得到△BCE，连接DE．（1）直接写出点C的坐标，并判断△CDE的形状，说明理由；（2）如图②，当点D在线段AB上运动时，△BDE的周长是否存在最小值？若存在，求出△BDE的最小周长及此时点D的坐标；若不存在，说明理由；（3）当△BDE是直角三角形时，求点D的坐标．（直接写出结果即可）21．三角形右边的是由左边的怎样平移得到的？22．如图，已知在△ABC中，AB=AC，AD⊥BC于D，且AD=BC=4，若将三角形沿AD剪开成为两个三角形，在平面上把这两个三角形拼成一个四边形，你能拼出所有的不同形状的四边形吗？画出所拼四边形的示意图（标出图中的直角），并分别写出所拼四边形的对角线的长．（只需写出结果即可）23．如图，正方形ABCD和正方形A1B1C1D1的对角线(正方形相对顶点之间所连的线段)BD，B1D1都在x轴上，O，O1分别为正方形ABCD和正方形A1B1C1D1的中心(正方形对角线的交点称为正方形的中心)，O为平面直角坐标系的原点．OD＝3，O1D1＝2.(1)如果O1在x轴上平移时，正方形A1B1C1D1也随之平移，其形状、大小没有改变，当中心O1在x轴上平移到两个正方形只有一个公共点时，求此时正方形A1B1C1D1各顶点的坐标；(2)如果O在x轴上平移时，正方形ABCD也随之平移，其形状、大小没有改变，当中心O在x轴上平移到两个正方形公共部分的面积为2个平方单位时，求此时正方形ABCD 各顶点的坐标．24．如图，正方形网格中的△ABC，若小方格边长为1，格点三角形（顶点是网格线交点的三角形）ABC的顶点A，C的坐标分别为（﹣1，1），（0，﹣2），请你根据所学的知识．（1）在如图所示的网格平面内作出平面直角坐标系；（2）作出三角形ABC关于y轴对称的三角形A1B1C1；（3）判断△ABC的形状，并求出△ABC的面积．25．在平面直角坐标系中，△ABC的三个顶点坐标分别为A（2，﹣1），B（3，﹣3），C（0，﹣4）（1）画出△ABC关于原点O成中心对称的△A1B1C1；（2）画出△A1B1C1关于y轴对称的△A2B2C2．26．如图，在正方形网格中，每个小正方形的边长为1，格点△ABC（顶点在网格线的交点上）的顶点A、C的坐标分别为A（﹣3，4）C（0，2）（1）请在网格所在的平面内建立平面直角坐标系，并写出点B的坐标；（2）画出△ABC关于原点对称的图形△A1B1C1；（3）求△ABC的面积；（4）在x轴上存在一点P，使PA+PB的值最小，请直接写出点P的坐标．27．已知：如图，在△ABC中，∠BAC=120°，以BC为边向形外作等边三角形BCD，把△ABD绕着点D按顺时针方向旋转60°后得到△ECD，若AB=5，AC=3，求∠BAD 的度数与AD的长．28．将△ABC的∠C折起，翻折后角的顶点位置记作C′，当C′落在AC上时（如图1），易证：∠1=2∠2．当C′点落在CA和CB之间（如图2）时，或当C′落在CB、CA的同旁（如图3）时，∠1、∠2、∠3关系又如何，请写出你的猜想，并就其中一种情况给出证明．图1 图2 图329．已知，△AOB中，AB=BC=2,∠ABC=90°，点O是线段AC的中点，连接OB，将△AOB 绕点A逆时针旋转α度得到△ANM，连接CM，点P是线段CM的中点，连接PN、PB．（1）如图1，当α=180°时，直接写出线段PN和PB之间的位置关系和数量关系；（2）如图2，当α=90°时，探究线段PN和PB之间的位置关系和数量关系，并给出完整的证明过程；（3）如图3，直接写出当△AOB在绕点A逆时针旋转的过程中，线段PN的最大值和最小值．参考答案1．C【解析】设AE 与BC 交于O 点，O 点是BC 的中点．∵四边形ABCD 是平行四边形，∴∠B =∠D ．AB ∥CD ，又由折叠的性质推知∠D =∠E ，CE =CD∴∠B =∠E ．CE =AB∴△ABO 和△ECO 中 ，所以△ABO ≌△CEO （AAS ），所以AO =CO =4，OE =OB =4．∴AE =AD =8．∴△AED 为等腰三角形，又C 为底边中点，故三线合一可知∠ACE =90°，从而由勾股定理求得AC =． 平行四边形ABCD 的面积=AC ×CD =12．故选：C ．2．A【解析】试题解析：已知90,OCB OC BC ∠=︒=，∴OBC 为等腰直角三角形，又因为顶点()()00,60,O B -，， 过点C 作CD OB ⊥于点D ，则 3.OD DC ==所以C 点坐标为()33-，，点C 关于y 轴对称的点的坐标是()33.， 故选A ．点睛：关于y轴对称的点的坐标特征：纵坐标不变，横坐标互为相反数. 3．A【解析】试题分析：根据平移的性质，结合图形对选项进行一一分析，选出正确答案．解：A、图形的形状和大小没有变化，符合平移的性质，属于平移得到；B、图形的大小发生变化，不符合平移的性质，不属于平移得到；C、图形的方向发生变化，不符合平移的性质，不属于平移得到；D、图形由轴对称得到，不属于平移得到．故选A．考点：生活中的平移现象．4．B【解析】【分析】直接利用旋转的性质得出∠AOC=∠BOD=38°，进而得出∠BOC的度数．【详解】∵△COD是△AOB绕点O顺时针方向旋转38°后所得的图形，∴∠AOC=∠BOD=38°，∵∠AOD=90°，∴∠BOC=90°-38°-38°=14°．故选：B．【点睛】此题主要考查了旋转的性质，正确得出∠AOC=∠BOD是解题关键．5．A【解析】解：点P(-4，-3)关于原点对称的点的坐标是（4，3）．故选A．6．B【解析】试题解析：∵∠1=180﹣2∠ADE；∠2=180﹣2∠AED．∴∠1+∠2=360°﹣2（∠ADE+∠AED）=360°﹣2（180°﹣30°）=60°．故选B．7．C【解析】【分析】根据轴对称图形的定义进行判断即可得到对称轴.【详解】解:观察可知沿l1折叠时，直线两旁的部分不能够完全重合，故l1不是对称轴；沿l2折叠时，直线两旁的部分不能够完全重合，故l2不是对称轴；沿l3折叠时，直线两旁的部分能够完全重合，故l3是对称轴，所以该图形的对称轴是直线l3，故选C．【点睛】本题主要考查了轴对称图形，关键是掌握轴对称图形的定义．根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴．8．B【解析】分析：根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．详解：A．该图形是是轴对称图形不是中心对称图形，故本选项错误；B．该图形既是轴对称图形，又是中心对称图形，故本选项正确；C．该图形不是轴对称图形，是中心对称图形，故本选项错误；D．该图形是是轴对称图形，不是中心对称图形，故本选项错误．故选B．点睛：本题主要考查了中心对称图形与轴对称的定义，根据定义得出图形形状是解决问题的关键．9．A【解析】根据图形可得：选项A有1条对称轴，选项B、C各有2条对称轴，选项D有6条对称轴，故选A.【点睛】本题主要考查了轴对称图形的定义，关键是正确找出每个图形的对称轴．10．C【解析】分析：旋转中心即是对应点连线的垂直平分线的交点.详解：根据旋转中心即是对应点连线的垂直平分线的交点，可得要使正方形ABCD和DCGH重合，有3种方法，可以分别绕D，C或CD的中点旋转，即旋转中心有3个．故选C．点睛：本题考查了旋转的性质旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等，旋转中心即是对应点连线的垂直平分线的交点.11．35．【解析】解：连接PP′．如图，∵线段PC绕点C顺时针旋转60°得到P'C，∴CP=CP′=6，∠PCP′=60°，∴△CPP′为等边三角形，∴PP′=PC=6．∵△ABC为等边三角形，∴CB=CA，∠ACB=60°，∴∠PCB=∠P′CA．在△PCB和△P′CA中，∵PC=P′C，∠PCB=∠P′CA，CB=CA，∴△PCB≌△P′CA，∴PB=P′A=10．∵62+82=102，∴PP′2+AP2=P′A2，∴△APP′为直角三角形，∠APP′=90°，∴sin∠P AP′='6'10PPP A=35．故答案为35．12．6【解析】连接DE于AC交于点P′，连接BP′，则此时△BP′E的周长就是△PBE周长的最小值，∵BE=1，BC=CD=4，∴CE=3，DE=5，∴BP′+P′E=DE=5，∴△PBE周长的最小值是5+1=6，故答案为6．13．（﹣a﹣2，﹣b）【解析】由图可知，△ABC关于点（﹣1，0）对称变换得到△A′B′C′，∵△ABC上的点P的坐标为（a，b），∴它的对应点P′的坐标为（﹣a﹣2，﹣b），故答案为：（﹣a﹣2，﹣b）．14．18．【解析】【分析】根据平移的性质可得DF=AE，然后判断出四边形ABFD的周长=△ABE的周长+AD+EF，然后代入数据计算即可得解．【详解】∵△ABE向右平移3cm得到△DCF，∴DF=AE，∴四边形ABFD的周长=AB+BE+DF+AD+EF，=AB+BE+AE+AD+EF，=△ABE的周长+AD+EF，∵平移距离为3cm，∴AD=EF=3cm，∵△ABE的周长是12cm，∴四边形ABFD的周长=12+3+3=18cm.故答案为18cm.【点睛】本题考查了平移的性质，解题的关键是熟练的掌握平移的性质.15．（1，﹣3）【解析】【分析】画出平面直角坐标系，然后作出点P绕原点O顺时针旋转180°的点P′的位置，再根据平面直角坐标系写出坐标即可．【详解】如图所示：点P（-1，3）绕原点O顺时针旋转180°后的对应点P′的坐标为（1，-3）．故答案是：（1，-3）．【点睛】考查了坐标与图形变化-旋转，作出图形，利用数形结合的思想求解更简便，形象直观．16．（2,5）【解析】【分析】平面直角坐标系．．．．．．．向左平移3个单位,再向下平移2个单位,相当于将点(-1,3)向右平移3个单位,再向上平移2个单位.应用点的平移与坐标关系便可得出答案.【详解】因为将平面直角坐标系．．．．．．．向左平移3个单位,再向下平移2个单位,相当于将点(-1,3)向右平移3个单位,再向上平移2个单位，此时得到对应点的坐标是(-1+3,3+2),即(2,5).故正确答案为: (2,5).【点睛】此题考核知识点：点的平移和坐标.关键要弄清点移动的方向和距离，特别要注意此题是移动平面直角坐标系．．．．．．．.17．(21008,0)【解析】∵点P0的坐标为(1,0)，∴OP0=1，∴OP2=2OP1=2，OP3=OP2=2，OP4=2OP3=2×2=22，…，OP2016=21008，∵2016÷24=84，∴点P2016是第84循环组的最后一个点，在x轴正半轴，∴点P2016的坐标为(21008,0).故答案为：(21008,0).点睛：本田考查了坐标与图形的变化-旋转，点的坐标变化规律，读懂题目信息，理解点的规律变化是解题的关键.18．8【解析】【分析】根据题意画出符合条件的图形，作F关于AD的对称点为M，作AB边上的高CP，求出EM+EC=MC，根据垂线段最短得出EM+EC=MC≥PC，求出PC即可得出CE+EF的最小值．【详解】试题分析：作F关于AD的对称点为M，作AB边上的高CP，∵AD平分∠CAB，△ABC为锐角三角形，∴M必在AC上，∵F关于AD的对称点为M，∴ME＝EF，∴EF＋EC＝EM＋EC，即EM＋EC＝MC≥PC（垂线段最短），∵△ABC的面积是48，AB＝12，∴12×12×PC＝48，∴PC＝8，即CE＋EF的最小值为8．故答案为8．点睛：本题考查了最短路线问题，关键是画出符合条件的图形，题目具有一定的代表性，是一道比较好的题目．19．．【解析】分析：由中心对称的性质得OA＝OC，OB＝OB′，用勾股定理求出OB即可.详解：根据中心对称的性质得，OB＝OB′，OC＝1，又BC＝2，由勾股定理得BO BB′＝2OB＝故答案为点睛：中心对称的性质有：①关于中心对称的两个图形是全等形；②关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分；③关于中心对称的两个图形，对应线段平行(或在同一直线上)且相等.20．（Ⅰ）C(7，△CDE是等边三角形；（Ⅱ）存在；4 ；D（7，0）；（Ⅲ）D（1，0）或（13，0）．【解析】分析：（1）如图1，过点C作CH⊥x轴于点H，由△ABC是等边三角形易得AH=12AB=2，结合AC=AB=4、OA=5，可得CH=OH=7，由此即可得到点C的坐标；由旋转的性质可知CE=CD，结合旋转角∠DCE=60°可知△CDE是等边三角形；（2）如图2，由（1）可知△CDE是等边三角形，由此可得DE=CD，由△CDE是由△CAD绕点C旋转得到的，由此可得BE=AD，从而可得△BDE的周长=BD+BE+DE=BD+AD+CD=AB+CD=4+CD，由此可知，当CD⊥AB时，CD最小，此时△BDE 的周长最小，由（1）可知，此时CD=23，OD=7，即当点D的坐标为（7，0）时，△BDE 的周长最小，最小值为423+；（3）如图3，由∠CBE=∠CAD=120°可得∠ABC=60°，由此可得∠DBE=60°≠90°，结合△BDE是直角三角形，可知：存在①∠BED=90°；②∠BDE=90°（如图3，∠BD'E'=90°）两种情况，分两种情况画出符合要求的图形，并结合已知条件进行分析计算即可.详解：（Ⅰ）如图1，过点C作CH⊥AB于H，∵△ABC是等边三角形，CH⊥AB于点H，∴∠AHC=90°，AH=12AB=12（9﹣5）=2，∴OH=OA+AH=7，∵AC=AB=4，∴在Rt△ACH中，224223-=∴ C(723)，；∵△CBE是由△CAD绕点C逆时针旋转60°得到的，∴∠DCE=60°，DC=EC，∴△CDE是等边三角形；（Ⅱ）存在，理由如下：如图2，由（Ⅰ）知，△CDE是等边三角形，∴DE=CD，由旋转知，BE=AD，∴C△DBE=BE+DB+DE=AB+DE=4+DE=4+CD，由垂线段最短可知，CD⊥AB于D时，△BDE的周长最小，此时，由（1）可知CD=23，OD=7，∴△BDE的周长最小值为4+23，点D（7，0）；（Ⅲ）如图3，∵由旋转知，∠CBE=∠CAD=120°，∵∠ABC=60°，∴∠DBE=60°≠90°，∵△BDE是直角三角形，∴存在∠BED=90°或∠BDE=90°（如图3，∠BD'E'=90°）两种情况，①当∠BED=90°时，∵△CDE是等边三角形，∴∠CED=60°，∴∠BEC=30°，∵∠CBE=∠CAD=120°，∴∠BCE=30°，∴BE=BC=AB=4，在Rt△BDE中，∠DBE=∠CBE﹣∠ABC=60°，∴BD=2BE=8，∵OB=9，∴OD=OB﹣BD=1，∴D（1，0），②当∠BD'E'=90°时，∵△CD'E'是等边三角形，∴∠CD'E'=60°，∴∠BD'C=30°，∵∠ABC=60°，∴∠BCD'=30°=∠BD'E，∴BD'=BC=6，∵OB=9，∴OD'=OB+BD'=13，∴D'（13，0），即：存在点D使△BDE是直角三角形，此时点D的坐标分别为：（1，0）或（13，0）．点睛：（1）解第1小题的关键是：作出如图1所示的辅助线，利用等边三角形的性质和直角三角形的性质求得AH和CH的长；（2）解第2小题的关键是：利用旋转的性质得到BE=AD，从而把△BDE的周长转化为为：(4+CD)来表达，这样当CD⊥x轴时，CD最短，则△BDE 的周长就最小，由此即可使问题得到解决；（3）解第3小题的要点是：根据已知条件分析存在∠BED=90°或∠BDE=90°两种情况，然后画出符合题意的图形，再进行分析计算即可得到所求结果.21．向右平移7个单位.【解析】试题分析:观察图形中对应点的变化，即可得出图形的变化规律.试题解析：找出对应点来后会发现右边的图形是由左边的向右平移7个单位长度得到的.22．略【解析】可让两斜边重合，得到一个矩形和一个一般的四边形，根据勾股定理和三角形的面积公式可求得对角线长；让两长直角边重合或两短直角边重合，可得到一个平行四边形，利用勾股定理求得一对角线的长．图1是矩形，两条对角线长相等，均为2；图2是平行四边形，两条对角线长4和4；图3是平行四边形，两条对角线长2和2；图4是一般的四边形，两条对角线长2和．23．（1）A1(5，2)，B1(3，0)，C1(5，－2)，D1(7，0)；（2）A(11，3)，B(8，0)，C(11，－3)，D(14，0)．【解析】【分析】（1）两个正方形只有一个公共点时，分D和B1为公共点，B和D1为公共点两种情况，结合平移的性质写出各点的坐标；（2）根据两个正方形的位置可知公共部分肯定是个正方形，面积是2，可以算出它的对角线长为2，所以有两种情况：点D和O1重合，点B和O1重合，据此解答.【详解】解：(1)当点B1与点D重合时，两个正方形只有一个公共点，此时A1(5，2)，B1(3，0)，C1(5，－2)，D1(7，0)；当点B与D1重合时，两个正方形只有一个公共点，此时A1(－5，2)，B1(－7，0)，C1(－5，－2)，D1(－3，0)．(2)当点D与O1重合时，两个正方形公共部分的面积为2个平方单位，此时A(5，3)，B(2，0)，C (5，－3)，D (8，0)；当点B 与O 1重合时，两个正方形公共部分的面积为2个平方单位，此时A (11，3)，B (8，0)，C (11，－3)，D (14，0)．【点睛】本题考查了坐标与图形变化-平移，解题的关键是熟练的掌握平移的相关知识点. 24．（1）见解析；（2）见解析；（3）直角三角形，2．【解析】【分析】（1）根据点A 和点C 的坐标即可作出坐标系；（2）分别作出三角形的三顶点关于y 轴的对称点，顺次连接可得；（3）根据勾股定理的逆定理可得．【详解】解：（1）如图所示：（2）如图所示，△A 1B 1C 1即为所求；（3）∵正方形小方格边长为1，∴AB 2211+2，BC 2222+2，AC 2213+10，∴AB 2+BC 2=AC 2，∴网格中的△ABC 是直角三角形．△ABC 的面积为122×2=2． 【点睛】本题考查的是作图﹣轴对称变换，熟知关于y 轴对称的点的坐标特点是解答此题的关键． 25．（1）答案见解析；（2）答案见解析．【解析】试题分析：（1）根据网格结构找出点A 、B 、C 关于原点对称的点A 1、B 1、C 1的位置，然后顺次连接即可；（2）根据网格结构找出点A1、B1、C1关于y轴对称的点A2、B2、C2的位置，然后顺次连接即可．试题解析：（1）△A1B1C1如图所示；（2）△A2B2C2如图所示．考点：（1）作图-旋转变换；（2）作图-轴对称变换26．（1）坐标系详见解析，点B的坐标（﹣2，0）；（2）详见解析；（3）5；（4）点P 的坐标（﹣2，0）．【解析】【分析】（1）根据A、C点坐标，作出的平面直角坐标系即可，根据作出的平面直角坐标系写出B 点的坐标即可；（2）根据原点对称的特点画出图形即可；（3）利用矩形面积减去周围三角形面积得出即可；（4）根据轴对称的性质解答即可．【详解】解：（1）如图所示：点B的坐标（-2，0）；（2）如图所示，△A1B1C1即为所求；（3）△ABC的面积111 34222314222=⨯-⨯⨯-⨯⨯-⨯⨯=5；（4）点P的坐标（-2，0）．【点睛】本题考查的知识点是平移变换以及三角形面积求法和坐标轴确定方法，解题关键是正确平移顶点．27．∠BAD=60°，AD=8．【解析】【分析】根据旋转的性质先证明△ADE是等边三角形，由相似三角形的性质可得∠EAD=60°，AD=AE，即可得到∠BAD=∠BAC﹣∠CAD=60°，AD=AE=AC+CE=AC+AB=3+5=8．【详解】∵△ABD≌△ECD，∴AD=DE，∠BDA=∠DCE，∴∠BDC=∠ADE=60°，∠ABD=∠ECD，∵∠BAC=120°，∠BDC=60°，∴∠BAC+∠BDC=180°，∴∠ABD+∠ACD=180°，∴∠ACD+∠ECD=180°，∴A、C、E共线，∴△ADE是等边三角形，∴∠EAD=60°，AD=AE，∴∠BAD=∠BAC﹣∠CAD=60°，∴AD=AE=AC+CE=AC+AB=3+5=8．【点睛】本题考查了旋转的性质、等边三角形的判定与性质，证明△AED是等边三角形是解决问题的关键．28．∠1－∠3=2∠2，证明见解析．【解析】【分析】利用轴对称的知识找出等解即可进行推理判断．【详解】解：当C′点落在CA和CB之间（如图2）时，∠1+∠3=2∠2；当C′落在CB、CA的同旁（如图3）时，∠1－∠3=2∠2；对于图2证明如下：连结CC’，如图4所示，∵⊿EC’D是由⊿ECD翻折得到的，∴⊿EC’D≌⊿ECD，由此得EC=EC’，DC=DC’，∠EC’D=∠ECD，∴∠EC’C=∠ECC；∠DC’C=∠DCC，∵∠1=∠DC’C+∠DCC’ ，∠3=∠EC’C+∠ECC’ ，∴∠1+∠3=∠DC’C+∠DCC’ +∠EC’C+∠ECC’=2∠D C’C+2∠ EC’C =2(∠DC’C+∠EC’C)= 2∠2；∴∠1+∠3=2∠2；对于图3证明如下：设AC与DC’在⊿ABC内部所夹角为∠4，如图5所示，则有∠1=∠C +∠4，∠4=∠3+∠2，又由翻折得：∠2=∠C ，∴∠1=∠2+∠3+∠2=∠3+2∠2，∴∠1－∠3=2∠2．【点睛】本题主要考查了轴对称的性质.找准对称轴是解题的关键．29．(1)PN=PB ，PN⊥PB；(2)略；221-【解析】（1）由旋转的性质可得△ABC ≌△ANM ,再由直角三角形斜边的中线等于斜边的一半，得到PN 和PB 之间的位置关系和数量关系；（2）结论一样，证明的方法与（1）一样；（3）连接OP ，利用勾股定理可得出线段PN 的最大值和最小值.解：（1）PN PB ⊥，PN PB =．（2）连接PO ，∵90α=︒，∴90MAB ∠=︒．∵90ABC ∠=︒，∴//AM BC ． ∵AMN ≌ABO ，∴AB AM =，OB MN =，∴//AM BC ，=AM BC ,又∵90ABC ∠=︒,∴四边形ABCM 为正方形．∵P 为CM 中点，O 为AC 中点，∴12OP AM ， ∴OP PM =，45POC MAC ∠=∠=︒， ∴135BOP BOC POC ∠=∠+∠=︒． ∵9045135PMN ∠=︒+︒=︒， ∴PMN POB ∠=∠． PMN ≌POB ， ∴PN PB =，MPN OPB ∠=∠． ∵90MPO ∠=︒， ∴90NPB ∠=︒， ∴PN PB ⊥．（3）连接OP ． ∵P ，O 为AC ，MC 中点， ∴11122OP AM AB ===． 在Rt AOB 中， ∵OA OB =，2AB =，∴OB =PO OP PB BO PO -≤≤+． ∵PB PN =，11PN ≤≤．PN ∴11．。

授课设计教师学生科目数学上课时间课次 1授课内容中考中的格点图形问题授课重难点解题方法授课设计：近来几年来，有关格点问题已成为中考的亮点，这类问题题型多样，形式爽朗，主要观察同学们的直觉推理能力和问题研究能力．格点问题操作性强、兴趣性浓，表现了新课标的“在‘玩’中学，在学中思，在思中得”的崭新理念．下面就中考中的几类格点问题归纳以下，望能对学习有所帮助．一、格点中的对称问题例 1 （绍兴市）如图 1，在网格中有两个全等的图形 (阴影部分 )，用这两个图形拼成轴对称图形，试分别在图(1) 、(2) 中画出两种不同样的拼法．图1图2二、格点中的画图问题例 2 （黑龙江鸡西市）如图3，在网格中有一个四边形图案．（1）请你画出此图案绕点 O 顺时针方向旋转 900， 1800，2700的图案，你会获取一个美丽的图案，千万不要将阴影地址涂错；图 3图4（2）若网格中每个小正方形的边长为l ，旋转后点 A 的对应点依次为 A1、 A2、A3，求四边形 AA1A2A3的面积；(3)这个美丽图案可以说明一个出名结论的正确性，请写出这个结论．三、格点中的坐标问题例3 （苏州市）如图 5．围棋盘的左下角表现的是一局围棋比赛中的几手棋．为记录棋谱方便，横线用数字表示．纵线用英文字母表示，这样，黑棋①的地址可记为(C，4)，白棋②的地址可记为( E， 3) 则白棋⑨的地址应记为＿＿＿．图 5四、格点中的相似问题例 4 （福州市罗源平潭）如图成的相似三角形有（）A ． 4 对B ． 3 对C． 2 对6，在 7×12 的正方形网格中有一只可爱的小狐狸，算算看画面中由实线组DD ．1 对A C F析解：本题是一道以网格为背景的结论研究性问题， B E J H在正方形网格中画了一只可爱的小狐狸，增强了题目G I R L的兴趣性．由网格的特色结合勾股定理，可以获取三角图6形三边的长，从而利用“三边对应成比率，两三角形相似”的判断来求解．．五、格点中的位似问题例5 （广东省）如图 7，图中的小方格都是边长为 1 的正方形，△ ABC 与△ A′B′C′是关于点 O 为位似中心的位似图形，它们的极点都在小正方形的极点上．（1）画出位似中心点 O；（2）求出△ ABC 与△ A/B/C/的位似比；（ 3）以点 O 为位似中心，再画一个△A1B1C1，使它与△ ABC的位似比等于．C/ C/C1B/ C B/ CA/BA/B1 BA A1 A O 图 7 图 8六、格点中的面积问题例 6 （浙江湖州市）一青蛙在如图8×8 的正方形（每个小正方形的边长为 1）网格的格点（小正方形的极点）上跳跃，青蛙每次所跳的最远距离为 5 ，青蛙从点A开始连续跳六次正好跳回到点 A，则所组成的封闭图形的面积的最大值是_______．图 9析解：本题以青蛙这一幽默且有益的动物为背景设计题目，增加了题目的兴趣性．解题时涉及无理数、勾股定理的应用、图形面积的计算等知识．只要正确画出图形，再运用割补法即可求得面积为 12．七、格点中等腰三角形问题例 7 （重庆市）以下列图，A、 B 是 4×5 网络中的格点，网格中的每个小正方形的边长为晰标出使以Ａ、B、C 为极点的三角形是等腰三角形的所有格点 C 的地址．1，请在图中清A AB B图10 图11析解：依照网格的特色及等腰三角形的有关知识易得，AB 只能为一腰，且AB= 13 ，由勾股定理即可知点C1、 C2、 C3吻合要求（如图11）．八、格点中的拼图问题例 8 （北京市）请阅读以下资料：问题：现有 5 个边长为画出切割线并在正方形网格图1 的正方形，排列形式如图①，请把它们切割后拼接成一个新的正方形．(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形．要求：小东同学的做法是：设新正方形的边长为x(x＞ 0)．依题意，割补前后图形的面积相等，有x2=5 ，解得x= 5 ．由此可知新正方形得边长等于两个小正方形组成得矩形对角线得长．于是，画出如图②所示的分割线，拼出如图③ 所示的新正方形．图①图②图③图④图⑤图12请你参照小东同学的做法，解决以下问题：现有 10 个边长为 1 的正方形，排列形式如图④，请把它们切割后拼接成一个新的正方形．要求：在图④中画出切割线，并在图⑤的正方形网格图 (图中每个小正方形的边长均为 1)中用实线画出拼接成的新正方形．说明：直接画出图形，不要求写解析过程．析解：本题是一道综合型网格作图试题，涉及到无理数、勾股定理等知识，主要观察同学们的计算能力、着手操作能力．类比小东的作法，可设新正方形的边长为x(x>0)，便有 x2=10 ，解得 x=10 ．由此可知，新正方形得边长等于两个小正方形组成得矩形对角线得长．于是，画出如图②所示的切割线，拼出如图③所示的新正方形．图 13图14温州历年中考中的格点问题19．（ 2009?温州） ( 本题 8 分 ) 在所给的 9×9方格中，每个小正方形的边长都是1．按要求画平行四边形，使它的四个极点以及对角线交点都在方格的极点上．(1) 在图甲中画一个平行四边形，使它的周长是整数； (2) 在图乙中画一个平行四边形，使它的周长不是整数． ( 注：图甲、图乙在答题纸上 )19、（ 2011?温州）（本题8 分）七巧板是我们祖先的一项优异创立，用它可以拼出多种图形，请你用七巧板中标号为○1 ○2 ○3的三块板（如图1）经过平移、旋转拼成图形。

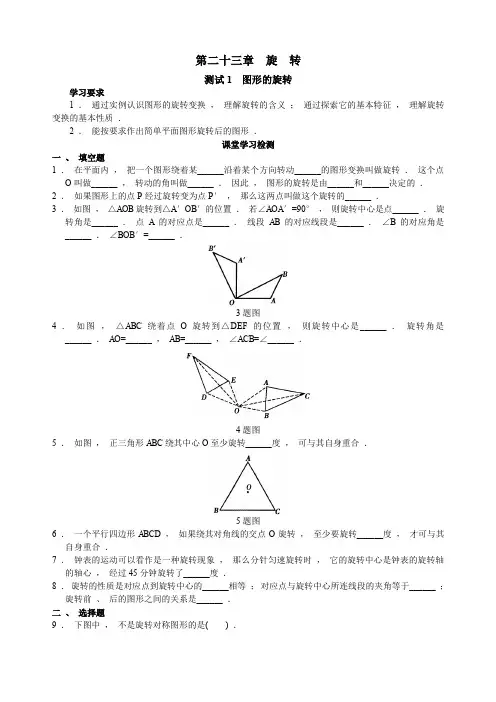
第二十三章旋转测试1 图形的旋转学习要求1 ．通过实例认识图形的旋转变换，理解旋转的含义；通过探索它的基本特征，理解旋转变换的基本性质．2 ．能按要求作出简单平面图形旋转后的图形．课堂学习检测一、填空题1 ．在平面内，把一个图形绕着某______沿着某个方向转动______的图形变换叫做旋转．这个点O叫做______ ，转动的角叫做______ ．因此，图形的旋转是由______和______决定的．2 ．如果图形上的点P经过旋转变为点P′，那么这两点叫做这个旋转的______ ．3 ．如图，△AOB旋转到△A′OB′的位置．若∠AOA′=90°，则旋转中心是点______ ．旋转角是______ ．点A的对应点是______ ．线段AB的对应线段是______ ．∠B的对应角是______ ．∠BOB′=______ ．3题图4 ．如图，△ABC绕着点O旋转到△DEF的位置，则旋转中心是______ ．旋转角是______ ．AO=______ ，AB=______ ，∠ACB=∠______ ．4题图5 ．如图，正三角形ABC绕其中心O至少旋转______度，可与其自身重合．5题图6 ．一个平行四边形ABCD，如果绕其对角线的交点O旋转，至少要旋转______度，才可与其自身重合．7 ．钟表的运动可以看作是一种旋转现象，那么分针匀速旋转时，它的旋转中心是钟表的旋转轴的轴心，经过45分钟旋转了______度．8 ．旋转的性质是对应点到旋转中心的______相等；对应点与旋转中心所连线段的夹角等于______ ；旋转前、后的图形之间的关系是______ ．二、选择题9 ．下图中，不是旋转对称图形的是( ) ．10 ．有下列四个说法，其中正确说法的个数是( ) ．①图形旋转时，位置保持不变的点只有旋转中心；②图形旋转时，图形上的每一个点都绕着旋转中心旋转了相同的角度；③图形旋转时，对应点与旋转中心的距离相等；④图形旋转时，对应线段相等，对应角相等，图形的形状和大小都没有发生变化A ．1个B ．2个C ．3个D ．4个11 ．如图，把菱形ABOC绕点O顺时针旋转得到菱形DFOE，则下列角中不是旋转角的为( ) ．A ．∠BOFB ．∠AODC ．∠COED ．∠COF12 ．如图，若正方形DCEF旋转后能与正方形ABCD重合，则图形所在平面内可作为旋转中心的点共有( )个．A ．1B ．2C ．3D ．413 ．下面各图中，哪些绕一点旋转180°后能与原来的图形重合？( ) ．A ．①、④、⑤B ．①、③、⑤C ．②、③、⑤D ．②、④、⑤综合、运用、诊断14 ．如图，六角星可看作是由什么“基本图形”通过怎样的旋转而得到的？15 ．如图，五角星可看作是由什么“基本图形”通过怎样的旋转而得到的？16 ．已知：如图，四边形ABCD及一点P．求作：四边形A′B′C′D′，使得它是由四边形ABCD绕P点顺时针旋转150°得到的．17 ．如图，已知有两个同心圆，半径OA、OB成30°角，OB与小圆交于C点，若把△ABC每次绕O点逆时针旋转30°，试画出所得的图形．拓广、探究、思考18 ．已知：如图，当半径为30cm的转动轮按顺时针方向转过120°角时，传送带上的物体A向哪个方向移动？移动的距离是多少？19 ．已知：如图，F是正方形ABCD中BC边上一点，延长AB到E，使得BE=BF，试用旋转的性质说明：AF=CE且AF⊥CE．20 ．已知：如图，若线段CD是由线段AB经过旋转变换得到的．求作：旋转中心O点．21 ．已知：如图，P为等边△ABC内一点，∠APB=113°，∠APC=123°，试说明：以AP、BP、CP为边长可以构成一个三角形，并确定所构成三角形的各内角的度数．测试2 中心对称学习要求1 ．理解两个图形关于某一点中心对称的概念及其性质，能作一个图形关于某一个点的中心对称图形．2 ．理解中心对称图形．3 ．能熟练掌握关于原点对称的点的坐标．4 ．能综合运用平移、轴对称、旋转等变换解决图形变换问题．课堂学习检测一、填空题1 ．把一个图形绕着某一个点旋转______ ，如果它能够与另一个图形______ ，那么称这两个图形关于这个点对称或中心对称，这个点叫做______ ，这两个图形中的对应点叫做关于中心的______ ．2 ．关于中心对称的两个图形的性质是：(1)关于中心对称的两个图形，对称点所连______都经过______ ，而且被对称中心所______ ．(2)关于中心对称的两个图形是______ ．3 ．把一个图形绕着某一个点旋转______ ，如果旋转后的图形能够与原来的图形______ ，那么这个图形叫做中心对称图形，这个点就是它的______ ．4 ．线段不仅是轴对称图形，而且是______图形，它的对称中心是______ ．5 ．平行四边形是______图形，它的对称中心是____________ ．6 ．圆不仅是轴对称图形，而且是______图形，它的对称中心是______ ．7 ．若线段AB、CD关于点P成中心对称，则线段AB、CD的关系是______ ．8 ．如图，若四边形ABCD与四边形CEFG成中心对称，则它们的对称中心是______ ，点A的对称点是______ ，E的对称点是______ ．BD∥______且BD=______ ．连结A，F的线段经过______ ，且被C点______ ，△ABD≌______ ．8题图9 ．若O点是□ABCD对角线AC、BD的交点，过O点作直线l交AD于E，交BC于F．则线段OF与OE的关系是______ ，梯形ABFE与梯形CDEF是______图形．二、选择题10 ．下列图形中，不是．．中心对称图形的是( ) ．A ．圆B ．菱形C ．矩形D ．等边三角形11 ．以下四个图形中，既是轴对称图形又是中心对称图形的有( ) ．A ．4个B ．3个C ．2个D ．1个12 ．下列图形中，是中心对称图形的有( ) ．A ．1个B ．2个C ．3个D ．4个13 ．下列图形中，是轴对称图形而不是中心对称图形的是( ) ．综合、运用、诊断14 ．如图，已知四边形ABCD及点O．求作：四边形A′B′C′D′，使得四边形A′B′C′D′与四边形ABCD关于O点中心对称．15 ．已知：如图，四边形ABCD与四边形EFGH成中心对称，试画出它们的对称中心，并简要说明理由．16 ．如下图，图(1)和图(2)是中心对称图形，仿照(1)和(2) ，完成(3) ，(4) ，(5) ，(6)的中心对称图形．17 ．如图，有一块长方形钢板，工人师傅想把它分成面积相等的两部分，请你在图中画出作图痕迹．18 ．已知：三点A(－1 ，1) ，B(－3 ，2) ，C(－4 ，－1) ．(1)作出与△ABC关于原点对称的△A1B1C1，并写出各顶点的坐标；(2)作出与△ABC关于P(1 ，－2)点对称的△A2B2C2，并写出各顶点的坐标．拓广、探究、思考19 ．(1)到目前为止，已研究的图形变换有哪几种？这些变换的共同性质有哪些？(2)如图，O是正六边形ABCDEF的中心，图中可由△OBC旋转得到的三角形有a个，可由△OBC平移得到的三角形有b个，可由△OBC轴对称得到的三角形有c个，试求(a＋b＋c)a ＋b－c的值．20 ．已知：直线l的解析式为y=2x＋3 ，若先作直线l关于原点的对称直线l1，再作直线l1关于y轴的对称直线l2，最后将直线l2沿y轴向上平移4个单位长度得到直线l3，试求l3的解析式．21 ．如图，将给出的4张扑克牌摆成第一行的样子，然后将其中的1张牌旋转180°成第二行的样子，你能判断出被旋转过的1张牌是哪一张吗？为什么？科学家名言对称性原理在探索自然奥秘中所起的作用，无论怎么强调也不会过分的．因为物理学家发现，一个对称规律打破后，会出现更高一级的对称．——杨振宁测试3 旋转的综合训练一、填空题1 ．如图，用等腰直角三角板画∠AOB=45°，并将三角板沿OB方向平移到如图所示的虚线处后绕点M按逆时针方向旋转22°，则三角板的斜边与射线OA的夹角α为______°．1题图2 ．如图，把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形A′B′C′D′，则它们的公共部分的面积等于______ ．2题图3 ．在平面直角坐标系中，已知点P0的坐标为(1 ，0) ，将点P0绕着原点O按逆时针方向旋转60°得到P1，延长OP1到点P2，使OP2=2OP1，再将点P2绕着原点O按逆时针方向旋转60°，得点P3，则P3的坐标是______ ．4 ．如图，已知梯形ABCD中，AD∥BC，∠B=90°，AD=3 ，BC=5 ，AB=1 ，把线段CD绕点D逆时针旋转90°到DE位置，连结AE，则AE的长为______ ．4题图5 ．如图，以等腰直角三角形ABC的斜边AB为边作等边△ABD，连结DC，以DC为边作等边△DCE，B，E在C，D的同侧．若,2AB则BE=______ ．=5题图6 ．如图，已知D，E分别是正三角形的边BC和CA上的点，且AE=CD，AD与BE交于P，则∠BPD______°．6题图二、选择题7 ．下列图形中，既是中心对称图形又是轴对称图形的是( ) ．A ．等边三角形B ．菱形C ．等腰梯形D ．平行四边形8 ．数学课上，老师让同学们观察如图所示的图形，问：它绕着圆心O旋转多少度后和它自身重合？甲同学说：45°；乙同学说：60°；丙同学说：90°；丁同学说：135°．以上四位同学的回答中，错误的是( ) ．8题图A ．甲B ．乙C ．丙D ．丁9 ．如图，在平面直角坐标系中，△ABC和△DEF为等边三角形，AB=DE，点B，C，D在x轴上，点A，E，F在y轴上，下面判断正确的是( ) ．A ．△DEF是△ABC绕点O顺时针旋转90°得到的B ．△DEF是△ABC绕点O逆时针旋转90°得到的C ．△DEF是△ABC绕点O顺时针旋转60°得到的D ．△DEF是△ABC绕点O顺时针旋转120°得到的10 ．以下图的边缘所在直线为轴将该图案向右翻折后，再绕中心旋转180°，所得到的图形是( ) ．三 、 解答题11 ． 已知 ： 如图 ， 四边形ABCD 中 ， ∠D =60° ， ∠B =30° ， AD =CD ．求证 ： BD 2=AB 2＋BC 2 ．12 ． 已知 ： 如图 ， E 是正方形ABCD 的边CD 上任意一点 ， F 是边AD 上的点 ， 且FB 平分∠ABE ．求证 ： BE =AF ＋CE ．13 ． 已知 ： 如图 ， 在四边形ABCD 中 ， ∠B ＋∠D =180° ， AB =AD ， E ， F 分别是线段BC ， CD 上的点 ， 且BE ＋FD =EF ．求证 ： .21BAD EAF ∠=∠14 ． 已知 ： 如图 ， Rt △ABC 中 ， ∠ACB =90° ， D 为AB 中点 ， DE 、 DF 分别交AC 于E ，交BC 于F ， 且DE ⊥DF ．(1)如果CA =CB ， 求证 ： AE 2＋BF 2=EF 2 ；(2)如果CA ＜CB ， (1)中的结论还成立吗 ？ 若成立 ， 请证明 ； 若不成立 ， 请说明理由 ．答案与提示第二十三章旋转测试11 ．一点O，一个角度，旋转中心，旋转角，旋转中心，旋转角．2 ．对应点．3 ．O，90°，A'点，A'B'，∠B'，∠AO A'＝90°．4 ．O点，∠DOA或∠FOC或∠EOB，DO，DE，∠DFE．5 ．120 ．6 ．180 ．7 ．270 ．8 ．距离，旋转角，全等．9 ．B ．10 ．D ．11 ．D ．12 ．C ．13 ．A ．14 ．答案不唯一，如可看成正△ACE绕其中心旋转60°得到的．15 ．可看成四边形AFOJ绕O点每次旋转72°，共旋转了四次得到的．16 ．略．17 ．略．18 ．物体A向右平移，移动的距离是20πcm ．19 ．△CBE可看成由△ABF按顺时针旋转90°得到的，所以△CBE≌△ABF，并且CE＝AF，AF⊥CE．20 ．分两类：(1)A与C是对应点．(2)B与C是对应点，对(1)的作法：(1)连结AC，作线段AC的垂直平分线l1；(2)连结BD，作线段BD的垂直平分线l2，与l1交于O点，则O点为所求．同理可作出(2)的O′选点．21 ．提示：如图1 ，以C为旋转中心，将△APC绕C点逆时针旋转60°得到△BDC，易证△PCD为等边三角形，△PBD是以BP，AP(＝BD) ，CP(＝PD)为三边的三角形．∠PBD ＝53°，∠BPD＝64°，∠PDB＝63°．图1测试21 ．180°，重合，对称中心，对称点．2 ．(1)线段，对称中心，平分；(2)全等图形．3 ．180°，重合，对称中心．4 ．中心对称，它的中点．5 ．中心对称，它的两条对角线的交点．6 ．中心对称，它的圆心．7 ．AB＝CD且AB∥CD或AB与CD共线．8 ．C点，点F，D点，EG，EG，C点，平分，△FGE．9 ． OF ＝OE ， 全等 ．10 ． D ． 11 ． B ． 12 ． C ． 13 ． C ．14 ． 略 ．15 ． 作法 ： 分别连结CG 、 BF ， 则它们的交点O 为两四边形的对称中心 ． 其理由是关于中心对称的两个图形 ， 对称点所连线段都经过对称中心 ， 而CG 、 BF 两线段不共线 ， 所以它们的交点即为对称中心 ．16 ． 略 ．17 ．18 ． (1)A 1(1 ， －1) 、 B 1(3 ， －2) 、 C 1(4 ， 1) ．(2)A 2(3 ， －5) 、 B 2(5 ， －6) 、 C 2(6 ， －3) ．19 ． (1)平移变换 、 轴对称变换 、 旋转变换 ． 一个图形经过平移 、 轴对称 、 旋转变换 ， 它的形状和大小都不会改变 ． 即所得的图形与原图形全等 ．(2)a ＝5 ， b ＝2 ， c ＝5 ， (a ＋b ＋c )a ＋b －c ＝122＝144 ．20 ． l 1∶y ＝2x －3 ， l 2∶y ＝－2x －3 ， l 3∶y ＝－2x ＋1 ．21 ． 第2张 ， 是中心对称图形 ．测试31 ． 22 ． 2 ． ⋅33 3 ． ⋅-)3,1(4 ． .525 ． 16 ． 60 ．7 ． B ． 8 ． B ． 9 ． A ． 10 ． A ．11 ． 提示 ： 如图 ， 以BC 为边向形外作等边△BCE ， 连结AC ， AE ． 可证△BCD ≌△ECA ，AE ＝BD ， ∠ABE ＝90° ， 在Rt △ABE 中 ， 有AB 2＋BE 2＝AE 2 ， 即AB 2＋BC 2＝BD 2 ．11题图12 ． 提示 ： 如图 ， 延长EC 到M ， 使CM ＝AF ， 连结BM ． 易证△AFB ≌△CMB ， ∠4＝∠M ． 又AD ∥BC ，∴4＝∠2＋∠5＝∠1＋∠5＝∠3＋∠5 ．∴∠M ＝∠EBM ．∴BE ＝EM ＝AF ＋CE ．12题图13 ． 提示 ： 延长FD 到H ， 使DH ＝BE ， 易证△ABE ≌△ADH ． 再证△AEF ≌△AHF ．21=∠=∠∴FAH EAF .21BAD EAH ∠=∠ 14 ． 提示 ： 如图 ，(1)连结CD ， 证△CDE ≌△BDF ． CE ＝BF ．∵CA ＝CB ， ∴ AE ＝CF ．在Rt △CEF 中 ， CE 2＋CF 2＝EF 2 ， ∴AE 2＋BF 2＝EF 2 ．(2)延长FD 到M ， 使DM ＝DF ， 连结AM 、 EM ， 先证△BFD ≌△AMD ． ∴AM ＝BF ， ∠DAM ＝∠B ， 再证EM ＝EF ．14题图第二十三章 旋转全章测试一 、 填空题1 ． 如图 ， 正方形ABCD 和正方形CEFG 中 ， BC ⊥EC ， 它们的边长为10cm ．1题图(1)正方形ABCD 可看成是由正方形CEFG 向______平移______cm 得到的 ．(2)正方形ABCD 又可看成是由正方形CEFG 绕______点 ， 旋转______角得到的 ， 并且它们成______对称 ， 对称中心是______ ．2 ． 图形的旋转是由______和______决定的 ， 图形在旋转过程中 ， 它的______和______都不会发生变化 ．3 ． 如图 ， 若△ABD 绕A 点逆时针方向旋转60°得到△ACE ， 则旋转中心是______ ， 旋转角度是______ ， △ABC 和△ADE 都是______ ．3题图4 ．如图，若O是正方形ABCD的中心，直角∠MON绕O点旋转，则∠MON与正方形围成的四边形的面积是正方形ABCD面积的______ ．4题图5 ．如图，当△AED绕正方形ABCD的顶点D旋转到与△DCF重合时，∠DEF的度数为______ ．5题图6 ．若点A(2m－1 ，2n＋3)与B(2－m，2－n)关于原点O对称，则m＝______且n＝______ ．二、选择题7 ．如图，四边形ABCD是中心对称图形，对称中心为点O，过点O的直线与AD，BC分别交于E，F，则图中相等的线段有( ) ．A ．3对B ．4对C ．5对D ．6对8 ．下列关于旋转的说法不正确的是( ) ．A ．旋转中心在旋转过程中保持不动B ．旋转中心可以是图形上的一点，也可以是图形外的一点C ．旋转由旋转中心、旋转方向和旋转角度所决定D ．旋转由旋转中心所决定9 ．下列说法正确的是( ) ．A ．中心对称图形是旋转对称图形B ．旋转对称图形是中心对称图形C ．轴对称图形是旋转对称图形D ． 轴对称图形是中心对称图形10 ． 下列图形中 ， 既是轴对称图形又是中心对称图形的是( )三 、 解答题11 ． 如图 ， 把一个直角三角尺ACB 绕着30°角的顶点B 顺时针旋转 ， 使得点A 与CB 的延长线上的点E 重合 ．(1)三角尺旋转了多少度 ？(2)连结CD ， 试判断△CBD 的形状 ；(3)求∠BDC 的度数 ．12 ． 已知 ： 两点A (－2 ， 1) ， B (－3 ， 0) ．(1)把△ABO 绕O 点顺时针旋转90° ， 得到△A 1B 1O ， 求A 1 ， B 1点的坐标 ；(2)把△A 1B 1O 沿x 轴向右平移2个单位长度 ， 得到△A 2B 2C ， 求A 2 ， B 2 ， C 点的坐标 ；(3)作△A 2B 2C 关于原点O 的对称图形 ， 得到△A 3B 3D ， 求A 3 ， B 3 ， D 点的坐标 ．13 ． 已知 ： 反比例函数⋅-=xy 6 (1)若将反比例函数xy 6-=的图象绕原点O 旋转90° ， 求所得到的双曲线C 的解析式并画图 ； (2)双曲线C 上是否存在到原点O 距离为13的点P ， 若存在 ， 求出点P 的坐标 ．14 ． 已知 ： 如图 ， P 是正方形ABCD 内一点 ， ∠.7,1,135===AP BP APB求PC 的长 ．答案与提示第二十三章 旋转全章测试1 ． (1)左 ， .210 (2)C ， 180° ， 中心 ， C 点 ．2 ． 旋转中心 ， 旋转角 ， 形状 、 大小 ．3 ． A 点 ， 60° ， 正三角形 ．4 ． ⋅41 5 ． 45° ． 6 ． －1 ， －5 ． 7 ． C ． 8 ． D ． 9 ． A ． 10 ． B ．11 ． (1)150° ； (2)等腰三角形 ； (3)15° ．12 ． (1)A 1(1 ， 2) ， B 1(0 ， 3) ；(2)A 2(3 ， 2) ， B 2(2 ， 3) ， C (2 ， 0) ；(3)A 3(－3 ， －2) ， B 2(－2 ， －3) ， D (－2 ， 0) ．13 ． (1);6xy = (2)P 1(2 ， 3) ， P 2(3 ， 2) ， P 3(－2 ， －3) ， P 4(－3 ， －2) ．14 ． PC ＝3 ． 提示 ： 将△ABP 绕B 点顺时针旋转90° ， 这时A 点与C 点重合 ， P 点的对应点是P ' ， 连结PP ′ ， 则△ABP ≌△CBP ′ ， △PBP ′为等腰直角三角形 ， ∠PP ′C ＝90° ， .3)7()2(''2222=+=+=C P PP PC。

九年级数学上册第二十三章旋转经典大题例题单选题1、如图，AB是⊙O的直径，OD垂直于弦AC于点D，DO的延长线交⊙O于点E．若AC=4√2，DE=4，则BC的长是（）A．1B．√2C．2D．4答案：C分析：根据垂径定理求出OD的长，再根据中位线求出BC=2OD即可．设OD=x，则OE=OA=DE-OD=4-x．∵AB是⊙O的直径，OD垂直于弦AC于点，AC=4√2∴AD=DC=1AC=2√22∴OD是△ABC的中位线∴BC=2OD∵OA2=OD2+AD2∴(4−x)2=x2+(2√2)2，解得x=1∴BC=2OD=2x=2故选：C小提示：本题考查垂径定理、中位线的性质，根据垂径定理结合勾股定理求出OD的长是解题的关键．2、如图，有①～⑤5个条形方格图，每个小方格的边长均为1，则②～⑤中由实线围成的图形与①中由实线围成的图形全等的有（）A．②③④B．③④⑤C．②④⑤D．②③⑤答案：C分析：根据旋转变换及全等图形的定义对应边相等，对应角相等的图形是全等图形对个图进行一一分析判断即可解：②以右下角顶点为定点顺时针旋转90°后，两个实线图形刚好重合，③中为平行四边形，而①中为梯形，所以不能和①中图形完全重合，④可上下反转成②的情况，然后旋转可和①中图形完全重合，⑤可旋转180°后可和①中图形完全重合，∴与①中由实线围成的图形全等的有②④⑤．故选择C．小提示：本题考查多边形全等的判定，掌握全等图形的定义，关键是会通过图形的旋转使它们全等．3、在平面直角坐标系中，点（a+2，2）关于原点的对称点为（4，﹣b），则ab的值为（）A．﹣4B．4C．12D．﹣12答案：D分析：首先根据关于原点对称的点的坐标特点可得a+2+4=0,2−b=0，可得a，b的值，再代入求解即可得到答案．解：∵点（a+2，2）关于原点的对称点为（4，﹣b），∴a+2+4=0,2−b=0，解得：a=−6,b=2,∴ab=−12,故选D小提示：本题主要考查了关于原点对称的点的坐标特点：两个点关于原点对称时，它们的横纵坐标都互为相反数．4、如图，△OAB中，∠AOB=60°，OA=4，点B的坐标为（6，0），将△OAB绕点A逆时针旋转得到△CAD，当点O的对应点C落在OB上时，点D的坐标为（）A．（7，3√3）B．（7，5）C．（5√3，5）D．（5√3，3√3）答案：A分析：如图，过点D作DE⊥x轴于点E．证明△AOC是等边三角形，解直角三角形求出DE，CE，可得结论．解：如图，过点D作DE⊥x轴于点E．∵B（6，0），∴OB=6，由旋转的性质可知AO=AC=4，OB=CD=6，∠ACD=∠AOB=60°，∵∠AOC=60°，∴△AOC是等边三角形，∴OC=OA=4，∠ACO=60°，∴∠DCE=60°，∴CE=1CD=3，DE=√CD2−CE2=3√3，2∴OE=OC+CE=4+3=7，∴D（7，3√3），故选：A．小提示：本题考查了旋转变换，含30度角的直角三角形的性质，勾股定理，等边三角形的判定和性质等知识，解题的关键是掌握旋转变换的性质．5、如图，在由小正方形组成的网格图中再涂黑一个小正方形，使它与原来涂黑的小正方形组成的新图案为轴对称图形，则涂法有（）A．1种B．2种C．3种D．4种答案：C分析：根据轴对称图形的概念，找到对称轴即可得答案．解：如下图，∵图形是轴对称图形，对称轴是直线AB，∴把1、2、3三个正方形涂黑，与原来涂黑的小正方形组成的新图案仍然是轴对称图形，故选：C．小提示：本题考查了轴对称图形的概念，解题的关键是找到对称轴．6、连接正八边形的三个顶点，得到如图所示的图形，下列说法不正确的是（）A．四边形ABCH与四边形EFGH的周长相等B．连接HD，则HD平分∠CHEC．整个图形不是中心对称图形D．△CEH是等边三角形答案：D分析：根据正八边形和圆的性质进行解答即可．解：A．∵根据正八边形的性质，四边形ABCH与四边形EFGH能够完全重合，即四边形ABCH与四边形EFGH 全等∴四边形ABCH与四边形EFGH的周长相等，故选项正确，不符合题意；B．连接DH，如图1，∵正八边形是轴对称图形，直线HD是对称轴，∴HD平分∠CHE故选项正确，不符合题意；C．整个图形是轴对称图形，但不是中心对称图形，故选项正确，不符合题意；D．∵八边形ABCDEFGH是正八边形，∴B＝BC＝CD＝DE＝EF＝FG＝GH，CH＝EH，设正八边形的中心是O，连接EO、DH，如图2，∠DOE＝360°=45°8∵OE＝OH∠DOE＝22.5°∴∠OEH＝∠OHE＝12∴∠CHE＝2∠OHE＝45°∴∠HCE＝∠HEC＝1（180°－∠CHE）＝67.5°2∴△CEH不是等边三角形，故选项错误，符合题意．故选：D．小提示：本题考查了正多边形和圆，熟记正八边形与等腰三角形的性质是解题的关键．7、平面直角坐标系中，O为坐标原点，点A的坐标为(−5,1)，将OA绕原点按逆时针方向旋转90°得OB，则点B 的坐标为（）A．(−5,1)B．(−1,−5)C．(−5,−1)D．(−1,5)答案：B分析：根据题意证得△AOC≌△OBD，可得结论．解：如图，根据题意得∶∠AOB=90°，∠ACO=∠BDO=90°，OA=OB，∴∠AOC+∠BOD=90°，∠AOC+∠OAC=90°，∴∠BOD=∠OAC，∴△AOC≌△OBD，∴BD=OC，OD=AC，∵点A的坐标为(−5,1)，∴BD=OC=1，OD=AC=5，∴B(−1,−5)．故选：B．小提示：本题考查坐标与图形变化−旋转，解题的关键是熟练掌握旋转的性质，属于中考常考题型．8、如图，正方形OABC的边长为√2，将正方形OABC绕原点O顺时针旋转45°，则点B的对应点B1的坐标为（）A．(−√2,0)B．(−√2,0)C．(0,√2)D．(0,2)答案：D分析：连接OB，由正方形ABCD绕原点O顺时针旋转45°，推出∠A1OB1=45°，得到△A1OB1为等腰直角三角形，点B1在y轴上，利用勾股定理求出O B1即可．解：连接OB，∵正方形ABCD绕原点O顺时针旋转45°，∴∠AOA1=45°，∠AOB=45°，∴∠A1OB1=45°，∴△A1OB1为等腰直角三角形，点B1在y轴上，∵∠B1A1O=90°,A1B1=OA1=√2，∴OB1=√A1B12+OA12=√2+2=2，∴B1（0，2），故选：D．小提示：本题考查了正方形的性质，旋转的性质，特殊三角形的性质．关键是根据旋转角证明点B1在y轴上．9、在平面直角坐标系中，点(3,2)关于原点对称的点的坐标是（）A．(2,3)B．(−3,2)C．(−3,−2)D．(−2,−3)答案：C分析：根据坐标系中对称点与原点的关系判断即可．关于原点对称的一组坐标横纵坐标互为相反数,所以(3,2)关于原点对称的点是(-3,-2),故选C．小提示：本题考查原点对称的性质,关键在于牢记基础知识．10、已知两点M1(x1,y1),M2(x2,y2)，若x1+x2=0,y1+y2=0，则点M1与M2（）A．关于y轴对称B．关于x轴对称C．关于原点对称D．以上均不对答案：C分析：首先利用等式求出x1=−x2,y1=−y2,然后可以根据横纵坐标的关系得出结果．∵x1+x2=0,y1+y2=0，∴x1=−x2,y1=−y2,∵两点M1(x1,y1),M2(x2,y2)，∴点M1与M2关于原点对称，故选：C．小提示：本题主要考查平面直角坐标系中关于原点对称的点，属于基础题，利用等式找到点M1与M2横纵坐标的关系是解题关键．填空题11、如图，在四边形ABCD中，∠ABC=30°，将△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE，AB=5，BC=9，则BD=______．答案：√106分析：连接BE，如图，根据旋转的性质得∠BCE=60°，CB=CE，BD=AE，再判断△BCE为等边三角形得到BE=BC=9，∠CBE=60°，从而有∠ABE=90°，然后利用勾股定理计算出AE即可．解：连接BE，如图，∵△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE，∴∠BCE=60°，CB=CE，BD=AE，∴△BCE为等边三角形，∴BE=BC=9，∠CBE=60°，∵∠ABC=30°，∴∠ABE=90°，在Rt△ABE中，AE=√52+92=√106．所以答案是：√106．小提示：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．12、以原点为中心，把M(3,4)逆时针旋转90°得到点N，则点N的坐标为______．答案：(−4,3)分析：建立平面直角坐标系，根据旋转的性质得出N点坐标，由此即可得出答案．解：如图：由旋转的性质可得：M点横坐标等于N点纵坐标的值，M点纵坐标的值等于N点横坐标的绝对值，又∵M（3，4），∴N（-4，3），所以答案是：（-4，3）．小提示：此题考查有关点的坐标旋转的性质，结合坐标轴和旋转的特点确定坐标即可．13、如图，在平面直角坐标系xOy中，点A的坐标为（0，4），P是x轴上一动点，把线段PA绕点P顺时针旋转60°得到线段PF，连接OF，则线段OF长的最小值是__________．答案：2分析：点F 运动所形成的图象是一条直线，当OF ⊥F 1F 2时，垂线段OF 最短，当点F 1在x 轴上时，由勾股定理得：P 1O =F 1O =4√33，进而得P 1A =P 1F 1=AF 1=8√33，求得点F 1的坐标为(4√33,0)，当点F 2在y 轴上时，求得点F 2的坐标为（0，-4），最后根据待定系数法，求得直线F 1F 2的解析式为y =√3x -4，再由线段中垂线性质得出F 1F 2=AF 1=8√33，在Rt △OF 1F 2中，设点O 到F 1F 2的距离为h ，则根据面积法得12×OF 1×OF 2=12×F 1F 2×ℎ，即12×4√33×4=12×8√33×ℎ，解得h =2，根据垂线段最短，即可得到线段OF 的最小值为2．解：∵将线段PA 绕点P 顺时针旋转60°得到线段PF ，∴∠APF =60°，PF =PA ，∴△APF 是等边三角形，∴AP =AF ，如图，当点F 1在x 轴上时，△P 1AF 1为等边三角形，则P 1A =P 1F 1=AF 1，∠AP 1F 1=60°，∵AO ⊥P 1F 1，∴P 1O =F 1O ，∠AOP 1=90°，∴∠P 1AO =30°，且AO =4，由勾股定理得：P 1O =F 1O =4√33， ∴P 1A =P 1F 1=AF 1=8√33， ∴点F 1的坐标为(4√33,0)， 如图，当点F 2在y 轴上时，∵△P 2AF 2为等边三角形，AO ⊥P 2O ，∴AO =F 2O =4，∴点F 2的坐标为（0，-4），∵tan∠OF 1F 2=OF 2OF 1=4√33=√3，∴∠OF 1F 2=60°，∴点F 运动所形成的图象是一条直线，∴当OF ⊥F 1F 2时，线段OF 最短，设直线F 1F 2的解析式为y =kx +b ， 则{4√33k +b =0b =−4，解得{k =√3b =−4， ∴直线F 1F 2的解析式为y =√3x -4，∵AO =F 2O =4，AO ⊥P 1F 1，∴F 1F 2=AF 1=8√33， 在Rt △OF 1F 2中，OF ⊥F 1F 2，设点O 到F 1F 2的距离为h ，则12×OF 1×OF 2=12×F 1F 2×ℎ，∴12×4√33×4=12×8√33×ℎ，解得h =2，即线段OF的最小值为2，故答案为2．小提示：本题属于三角形的综合题，主要考查了旋转的性质，勾股定理的应用，等边三角形的性质以及待定系数法的运用等，解决问题的关键是作辅助线构造等边三角形以及面积法求最短距离，解题时注意勾股定理、等边三角形三线合一以及方程思想的灵活运用．14、已知点P(m−2,m)关于原点对称的点在第三象限，则m的取值范围是_______．答案：m>2分析：根据关于原点对称的点的性质可得点P在第一象限，进而得出不等式组，再解不等式组即可．解：∵点P（m−2，m）关于原点对称的点在第三象限，∴点P（m−2，m）在第一象限，∴{m−2>0，m>0解得：m＞2，所以答案是：m＞2．小提示：此题主要考查了关于原点对称的点的坐标特点，解一元一次不等式组，关键是掌握各象限内点的坐标符号．15、如图，在△AOB中，∠AOB=90°，AO=3cm，BO=4cm，将△AOB绕顶点O，按顺时针方向旋转到△AB，则线段B1D的长度为______．A1OB1处，此时线段OB1与AB的交点D恰好为AB的中点，OD=12答案：1.5cm##3cm2分析：先在直角△AOB中利用勾股定理求出AB＝5cm，再利用直角三角形斜边上的中线等于斜边的一半得出ODAB＝2.5cm．然后根据旋转的性质得到OB1＝OB＝4cm，则问题得解．＝12∵在△AOB中，∠AOB＝90°，AO＝3cm，BO＝4cm，∴AB＝√OA2+OB2＝5cm，∴OD＝1AB＝2.5cm，2∵将△AOB绕顶点O，按顺时针方向旋转到△A1OB1处，∴OB1＝OB＝4cm，∴B1D＝OB1-OD＝1.5cm．所以答案是：1.5cm．小提示：本题主要考查勾股定理和直角三角形的性质以及图形旋转的性质，掌握勾股定理是解题的关键．解答题16、如图，在平面直角坐标系中，线段AB的两个端点的坐标分别是A（﹣1，4），B（﹣3，1）．（1）画出线段AB向右平移4个单位后的线段A1B1；（2）画出线段AB绕原点O旋转180°后的线段A2B2．答案：（1）画图见解析，（2）画图见解析分析：（1）分别确定A,B向右平移4个单位后的对应点A1,B1，再连接A1B1即可；（2）分别确定A,B绕原点O旋转180°后的对应点A2,B2，再连接A2B2即可.解：（1）如图，线段A1B1即为所求作的线段，（2）如图，线段A2B2即为所求作的线段，小提示：本题考查的是平移的作图，中心对称的作图，掌握平移的性质与中心对称的性质是解题的关键. 17、如图，点O为平面直角坐标系的原点，点A在x轴上，△OAB是边长为2的等边三角形．(1)写出△OAB各顶点的坐标；(2)以点O为旋转中心，将△OAB按顺时针方向旋转60°，得到△OA′B′，写出A′，B′的坐标．答案：(1)A（-2，0），B（-1，√3），C（0，0）(2)A′（−1,√3），B′（1,√3）分析：（1）作高线BC，根据等边三角形的性质和勾股定理求OC和BC的长，写出三点的坐标，注意象限的符号问题；（2）如图2，由旋转可知：A′与B重合，B与B′关于y轴对称，可得：A′，B′的坐标．（1）解：如图1，过B作BC⊥OA于C，∵△AOB是等边三角形，且OA=2，OA=1，∴OC=12由勾股定理得：BC=√22−12=√3，∴A(−2，0)，B(−1，√3)，O(0，0)；（2）解：如图2，∵∠AOB=60°，OA=OB，∴A′与B重合，∴A′(−1，√3)，由旋转得：∠BOB′=60°，OB=OB′，∵∠AOD=90°，∴∠BOD=30°，∴∠DOB′=30°，∴BB′⊥OD，DB=DB′，∴B′(1，√3)．小提示：本题考查了坐标与图形变换、等边三角形的性质、旋转的性质，熟练掌握旋转和等边三角形的性质是关键，并注意点所在象限的符号问题．18、如图，一伞状图形，已知∠AOB=120°，点P是∠AOB角平分线上一点，且OP=2，∠MPN=60°，PM与OB交于点F，PN与OA交于点E．(1)如图一，当PN与PO重合时，探索PE，PF的数量关系(2)如图二，将∠MPN在(1)的情形下绕点P逆时针旋转α度(0<α<60°)，继续探索PE，PF的数量关系，并求四边形OEPF的面积．答案：（1）PE＝PF，证明详见解析；（2）PE＝PF，√3分析：（1）根据角平分线定义得到∠POF=60°，推出△PEF是等边三角形，得到PE=PF；（2）过点P作PQ⊥OA，PH⊥OB，根据角平分线的性质得到PQ=PH，∠PQO=∠PHO=90°，根据全等三角形的性质得到PE=PF，S四边形OEPF=S四边形OQPH，求得OQ=1，QP=√3，根据三角形的面积公式即可得到结论．解：（1）∵∠AOB＝120°，OP平分∠AOB，∴∠POF＝60°，∵∠MPN＝60°，∴∠MPN＝∠FOP＝60°，∴ΔPEF是等边三角形，∴PE＝PF；（2）过点P作PQ⊥OA，PH⊥OB，∵OP平分∠AOB，∴PQ＝PH，∠PQO＝∠PHO＝90°，∵∠AOB＝120°，∴∠QPH＝60°，∴∠QPE+∠FPH+∠EPH，∴∠QPE＝∠EPF，在ΔQPE与ΔHPF中{∠EQP=∠FHP ∠QPE=∠HPFPQ=PH，∴ΔQPE≌ΔHPF（AAS），∴PE＝PF，S四边形OEPF ＝S四边形OQPH，∵PQ⊥OA，PH⊥OB，OP平分∠AOB，∴∠QPO＝30°，∴OQ＝1，QP＝√22−12＝√3，∴SΔOPQ＝12×1×√3＝√32，∴四边形OEPF的面积＝2SΔOPQ＝√3小提示：本题考查了旋转的性质，角平分线的性质，全等三角形的判定和性质，三角形的面积，正确的作出辅助线是解题的关键．。

旋转练习题集锦（含答案）一、作图题1、如图，在每个小正方形的边长均为1个单位长度的方格纸中，有一个和一点O，的顶点和点O均与小正方形的顶点重合．（1）在方格纸中，将△ABC向下平移5个单位长度得到，请画出；（2）在方格纸中，将△ABC绕点O旋转180°得到，请画出。

二、简答题2、如图，已知的三个顶点的坐标分别为、、．（1）请直接写出点关于轴对称的点的坐标；（2）将绕坐标原点逆时针旋转90°．画出图形，直接写出点的对应点的坐标；（3）请直接写出：以为顶点的平行四边形的第四个顶点的坐标．三、选择题3、如图所示，在平面直角坐标系中，点A、B的坐标分别为（2，0）和（2，0）.月牙①绕点B顺时针旋转900得到月牙②，则点A的对应点A’的坐标为【】（A）（2，2）（B）（2，4）(C)（4，2） (D)（1，2）4、将图按顺时针方向旋转90°后得到的是( )5、在方格纸（每个小方格都是边长为1个单位长度的正方形）中，我们把每个小正方形的顶点称为格点，以格点为顶点的图形称为格点图形．如上图中的△ABC称为格点△ABC．现将图中△ABC绕点A顺时针旋转，并将其边长扩大为原来的2倍，则变形后点B的对应点所在的位置是（）A．甲 B．乙C．丙 D．丁6、下图是一个旋转对称图形，以O为旋转中心，以下列哪一个角为旋转角旋转，能使旋转后的图形与原图形重合（）A．60° B．90° C．120°D．180°7、在下图右侧的四个三角形中，不能由△ABC经过旋转或平移得到的是 ( )8、下面四个图案中，是旋转对称图形的是（）Ａ．Ｂ．Ｃ．Ｄ．9、下列运动是属于旋转的是( )A．电梯的上下运动 B．火车的运动C．钟表中分针的运动 D．升国旗时，国旗的徐徐运动10、如图所示，将其中的图甲变成图乙，可经过的变换是( )A．旋转、平移 B．平移、对称 C．旋转、对称 D．不能确定11、如图，该图形围绕自己的旋转中心，按下列角度旋转后，不能与其自身重合的是（）A．72° B．108° C．144° D．216°12、如图，D是等腰Rt△ABC内一点，BC是斜边，如果将△ABD绕点A逆时针方向旋转到△ACD’的位置，则∠ADD’的度数是( )A．25° B．30° C．35°D．45°13、如图可以看作是一个等腰直角三角形旋转若干次而成的，则每次旋转的度数最小是( )A．90° B．60° C．45°D．30°14、如图，经过平移或旋转不可能将图甲变为图乙的是（）15、下列图形中，既是中心对称图形，又是轴对称图形的是（）A．菱形B．等边三角形 C．等腰三角形D．平行四边形16、如图所示，可由一个“基本图案”旋转l80°而形成的是（）A B CD17、已知，将点A1（6，1）向左平移4个单位到达点A2的位置，再向上平移3个单位到达点A3的位置，△A1A2A3绕点A2逆时针方向旋转900，则旋转湖A3的坐标为（）A．（－2，1） B．（1，1） C．（－1，1） D．（5，1）18、下图是一张边被裁直的白纸，把一边折叠后，BC、BD为折痕，、、B在同一直线上，则∠CBD的度数（）A．不能确定B．大于C．小于 D．等于四、计算题19、将一张透明的平行四边形胶片沿对角线剪开，得到图①中的两张三角形胶片和．将这两张三角形胶片的顶点与顶点重合，把绕点顺时针方向旋转，这时与相交于点．（1）当旋转至如图②位置，点，在同一直线上时，与的数量关系是．（2）当继续旋转至如图③位置时，（1）中的结论还成立吗？请说明理由．（3）在图③中，连接，探索与之间有怎样的位置关系，并证明．20、如图所示，左边方格纸中每个正方形的边长均为a，右边方格纸中每个正方形的边长均为b，将左边方格纸中的图形顺时针旋转90°，并按b:a的比例画在右边方格纸中．21、点B．C．E在同一直线上，点A．D在直线CE的同侧，AB＝AC，EC＝ED，∠BAC＝∠CED，直线AE、BD交于点F。

用坐标表示旋转考点分析在坐标平面内，某一点绕原点旋转前后坐标的变化规律如下：1. 点A（a，b）绕原点旋转180°得点A'（－a，－b），即点A（a，b）关于原点对称的点的坐标是A'（－a，－b）.2. 点A（a，b）绕原点旋转90°所得点A'的坐标是（－b，a）.方法归纳：坐标系中的旋转问题通常构造全等三角形加以解决，而且一般是直角三角形.因为图形的旋转问题都可以归结为点的旋转问题，而点的坐标可以表示某点到坐标的距离.所以解决坐标系的旋转问题时经常过图形的顶点向坐标轴作垂线段，构造直角三角形来解决问题.总结：1. 通过具体实例认识直角坐标系中图形的旋转变换，加深理解旋转变换的概念和基本性质，并能按要求作出简单平面图形绕坐标原点旋转90度、180度后的图形.2. 通过多角度地认识旋转图形的形成过程，培养学生的发散思维能力.解题技巧例题1在如图所示的单位正方形网格中，△ABC经过平移后得到△A1B1C1，已知在AC 上一点P（2.4，2）平移后的对应点为P1，点P1绕点O逆时针旋转180°，得到对应点P2，则P2点的坐标为（）A. （1.4，－1）B. （1.5，2）C. （1.6，1）D. （2.4，1）解析：根据平移的性质得出，△ABC的平移方向以及平移距离，即可得出P1的坐标，进而利用中心对称图形的性质得出P2点的坐标.答案：∵A 点坐标为：（2，4），A 1（－2，1），∴点P （2.4，2）平移后的对应点P 1为（－1.6，－1），∵点P 1绕点O 逆时针旋转180°，得到对应点P 2，∴P 2点的坐标为（1.6，1）.故选C .点拨：此题主要考查了旋转的性质以及平移的性质，根据已知得出平移距离是解题关键.例题2 在如图所示的直角坐标系中，将△OAB 绕点O 顺时针旋转90°得△OA 1B 1，则线段A 1B 1所在直线l 的函数解析式为（ ）A. y ＝32x －2B. y ＝－32x ＋2C. y ＝－32x －2D. y ＝32x ＋2解析：根据旋转方向及角度画出旋转后的三角形，求出对应点坐标，设直线的解析式为y ＝kx ＋b ，将点的坐标代入，用待定系数法确定其解析式.答案：如图，根据旋转可得A 1（0，－2），B 1（－2，1），设直线的解析式为y ＝kx ＋b ，由题意得：⎩⎨⎧－2＝b1＝－2k ＋b ，解之得：⎩⎪⎨⎪⎧k ＝－32b ＝－2，所以直线的解析式为：y ＝－32x －2.故选C .点拨：本题考查图形的旋转及一次函数的解析式，关键是能够根据图形的旋转找出点的坐标，然后根据点的坐标来确定直线的解析式，求函数解析式，常用方法是待定系数法，把点的坐标代入解析式，然后组成关于k 与b 的方程组求解.总结提升平面直角坐标系中的旋转问题，若旋转角是180°，则可按中心对称图形问题来解决.有些题目的旋转角为90°，和少量的旋转角为30°,45°,60°,120°,150°等的问题，解答这类问题时除了要构造旋转本身形成的全等三角形外，一般还要通过向坐标轴作垂线来构造含有特殊角的直角三角形，利用特殊角的边角关系和勾股定理求解.例题如图，△ABO中，AB⊥OB，OB＝3，AB＝1，把△ABO绕点O旋转150°后得到△A1B1O，则点A1的坐标为（）A. （－1，－3）B. （－1，－3）或（－2，0）C. （－3，－1）或（0，－2）D. （－3，－1）解：∵△ABO中，AB⊥OB，OB＝3，AB＝1，∴OA＝2，∴∠AOB＝30°.如图1，当△ABO 绕点O顺时针旋转150°后得到△A1B1O，则∠A1OC＝150°－∠AOB－∠BOC＝150°－30°－90°＝30°，则易求A1（－1，－3）；如图2，当△ABO绕点O逆时针旋转150°后得到△A1B1O，则易求A1（0，－2）.综上所述，点A1的坐标为（－1，－3）或（－2，0），故选B.解析：本题考查了坐标与图形的变化——旋转，解题时注意两点，一是未指明旋转方向的问题需分类讨论，以防错解；二是图形中一些特殊角往往和旋转角交织在一起，解题时需正确区分它们.巩固训练一、选择题1. 在方格纸上建立如图所示的平面直角坐标系，将△ABO绕点O按顺时针方向旋转90°，得△A’B’O，则点A的对应点A’的坐标及AA’的长分别为（）A. （2，3），26B. （2，3），6C. （－3，2），26D. （－3，2），6*2. 如图，直线y ＝－43x ＋4与x 轴、y 轴分别交于A ,B 两点，把△AOB 绕点A 顺时针旋转90°后得到△AO 'B '，则点B '的坐标是（ ）A. （3，4）B. （7，3）C. （7，4）D. （4，5）*3. 将等腰直角三角形AOB 按如图所示放置，然后绕点O 逆时针旋转90至△A 'OB '的位置，点B 的横坐标为2，则点A '的坐标为（ ）xyOAB A'B'A. （1，1）B. （2， 2）C. （－1，1）D. （－2，2）**4. 如图所示，在平面直角坐标系xOy 中，等腰梯形ABCD 的顶点坐标分别为A （1，1），B （2，－1），C （－2，－1），D （－1，1）.y 轴上一点P （0，2）绕点A 旋转180°得点P 1，点P 1绕点B 旋转180°得点P 2，点P 2绕点C 旋转180°得点P 3，点P 3绕点D 旋转180°得点P 4，…，重复操作依次得到点P 1,P 2,…，则点P 2012的坐标是（ ）xy ABCDPA. （2010，2）B. （2010，－2） C . （2012，2） D. （2012，－2）二、填空题5. 如图，在平面直角坐标系中，将线段AB绕点A按逆时针方向旋转90°后，得到线段AB′，则点B′的坐标为__________.6. 如图，在直角坐标系中，△ABC各顶点的坐标分别为A（0，3）、B（－1，0）、C（1，0），若△DEF各顶点的坐标分别为D（3，0）,E（0，1）,F（0，－1），则△DEF由△ABC 绕O点顺时针旋转__________度得到.7. 如图，在方格纸上建立的平面直角坐标系中，A,B是格点，若△A′B′O与△ABO关于点O成中心对称，则AA′的距离为__________.**8. 如图，矩形ABCD的四个顶点的坐标分别为A（1，0），B（5，0），C（5，3），D（1，3），边CD上有一点E（4，3），过点E的直线与AB交于点F，若直线EF平分矩形的面积，则点F的坐标为__________.三、解答题9. 如图，在平面直角坐标系中，△ABC 的三个顶点都在格点上，点A 的坐标为（2，4），请解答下列问题：（1）画出△ABC 关于x 轴对称的△A 1B 1C 1，并写出点A 1的坐标.（2）画出△A 1B 1C 1绕原点O 旋转180°后得到的△A 2B 2C 2，并写出点A 2的坐标. *10. 如图，已知A （—3，—3），B （—2，—1），C （—1，—2）是直角坐标平面上的三点.y x-1-2-3-4-55432112345-1-2-3-4-5OAB C（1）请画出ΔABC 关于原点O 对称的ΔA 1B 1C 1，（2）请写出点B 关于y 轴对称的点B 2的坐标，若将点B 2向上平移h 个单位，使其落在ΔA 1B 1C 1内部，指出h 的取值范围.11. 在平面直角坐标系中，四边形ABCD 的位置如图所示，解答下列问题：（1）将四边形ABCD 先向左平移4个单位，再向下平移6个单位，得到四边形A 1B 1C 1D 1，画出平移后的四边形A 1B 1C 1D 1；（2）将四边形A 1B 1C 1D 1绕点A 1逆时针旋转90°，得到四边形A 1B 2C 2D 2，画出旋转后的四边形A 1B 2C 2D 2，并写出点C 2的坐标.*12. △ABC 在平面直角坐标系xOy 中的位置如图所示.y x-1-2-35432112345-1-2O67ABC（1）作△ABC 关于点C 成中心对称的△A 1B 1C 1.（2）将△A 1B 1C 1向右平移5个单位，作出平移后的△A 2B 2C 2.（3）在x 轴上求作一点P ，使P A 1＋PC 2的值最小，并写出点P 的坐标（不写解答过程，直接写出结果）.参考答案一、选择题1. A 解析：将△ABO 绕点O 按顺时针方向旋转90°得△A ’B ’O ，如下图：所以A ’（2，3），AA ’＝52＋12＝26.*2. B 解析：令y ＝0，则y ＝－43x ＋4＝0，解得x ＝3，即点A 的坐标为（3，0）.令x ＝0，则y ＝4，即点B 的坐标为（0，4），∴OB ＝4＝O 'B '，OA ＝3＝O 'A ，点B '的横坐标为：3＋4＝7，纵坐标为3，∴点B '的坐标是（7，3）.*3. C 解析：在Rt △AOB 中，OB ＝2，由勾股定理可得OA ＝2，所以OA '＝2，过A '作A 'C ⊥y 轴于点C ，在Rt △A 'OC 中，∠A 'OC ＝45°，由勾股定理可得A 'C ＝1，OC ＝1，且点A '在第二象限，所以点A '的坐标为（－1，1）.**4. C 解析：由题意可知，点P 1（2，0），P 2（2，－2），P 3（－6，0），P 4（4，2），P 5（－2，0），P 6（6，－2），P 7（－10，0），P 8（8，2）；….规律如下：像点P 1，P 5，…这样的点横坐标逐个减4，纵坐标都是0；像点P 2、P 6，…这样的点横坐标逐个加4，纵坐标都是－2；像P 3,P 7，…这样的点横坐标逐个减4，纵坐标都是0；像P 4,P 8，…这样的点横坐标逐个加4，纵坐标都是2.因为2012÷4＝503，观察P 4（4，2），P 8（8，2），…，得P 2012的坐标是（2012，2），故选C.PP 1P 2P 3P 4xy P 5P 6P 7P 8二、填空题5. （4，2） 解析：可利用旋转的性质，结合全等三角形求解.6. 90 解析：∵△ABC 各个顶点的坐标分别为A （0，3）、B （－1，0）、C （1，0）；△DEF 各顶点的坐标分别为D （3，0）,E （0，1）,F （0，－1），∴旋转对应点为A 和D ， B 和E ，C 和F ，∴△DEF 由△ABC 绕O 点顺时针旋转90°得到.7. 210 解析：因为△A ′B ′O 与△ABO 关于点O 成中心对称，所以A ′的坐标为（3，－1），AO ＝32＋12＝10，由中心对称图形的特征可知AA ′＝210.**8. （2，0） 解析：∵EF 平分矩形ABCD 的面积，∴EF 过矩形ABCD 的对称中心，点E 、F 是对应点，∴CE ＝AF .∵A （1，0），B （5，0），C （5，3），D （1，3），E （4，3），∴点F 的坐标为（2，0）.三、解答题9. 解：（1）如图所示：点A 1的坐标为（2，－4）；（2）如图所示，点A 2的坐标为（－2，4）.*10. 解：（1）作图如下：（2）点B 2的坐标为（2，－1），h 的取值范围是2＜h ＜3.5.y x-1-2-3-4-55432112345-1-2-3-4-5OAB CA 1B 1C 111. 解：（1）四边形A 1B 1C 1D 1如图所示；（2）四边形A 1B 2C 2D 2如图所示，C 2（1，－2）.*12. 解：（1）如图所示：（2）如图所示：（3）如图所示：作出A 1关于x 轴的对称点A ′，连接A ′C 2，交x 轴于点P ，可得P 点坐标为：（3，0）.y x-1-2-35432112345-1-2O67ABCA 1B 1C 1A 2B 2C 2A'P。

2012年安徽高考数学试题及答案第I卷（选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．复数x满足 (x-i)(2-i)＝5，则x=A．-2-2iB．-2+2iC．2-2iD．2+2i2．下列函数中，不满足f（2x）等于2f(x)的是A．f(x)=|x|B．f (x)=x-|x|C．f(x)=x+1D．f(x)=-x3．如图所示，程序框图（算法流程图）的输出结果是A．3B．4C．5D．84．公比为2的等比数列{a n}的各项都是正数，且a3a11=16，则log2a16=A．4B．5C．6D．75．甲、乙两人在一次射击比赛中各射靶5次，两人成绩的条形统计图如图所示，则A．甲的成绩的平均数小于乙的成绩的平均数B．甲的成绩的中位数等于乙的成绩的中位数C．甲的成绩的方差小于乙的成绩的方差D．甲的成绩的极差小于乙的成绩的极差6．设平面α与平面β相交于直线m，直线a在平面α内，直线b在平面β内，且b⊥m，则“α⊥β”是“a⊥b”的A．充分不必要条件B．必要不充分条件C．既不充分也不必要条件D．既不充分也不必要条件7．的展开式的常数项是A．-3B．-2C．2D．38．在平面直角坐标系中，点O（0,0），P（6,8），将向量绕点O逆时针方向旋转后得向量,则Q点的坐标是A．（-7，-）B．（-7，）C．（-4，-2）D．（-4，2）9．过抛物线y2=4x的焦点F的直线交该抛物线于A，B两点，O为坐标原点。

若|AF|=3，则△AOB的面积为10．6位同学在毕业聚会活动中进行纪念品的交换，任意两位同学之间最多交换一次，进行交换的两位同学互赠一份纪念品。

已知6位同学之间共进行了13次交换，则收到4份纪念品的同学人数为A．1或3B．1或4C．2或3D．2或4二、填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卡的相应位置。

（11）若x，y满足约束条件则x-y的取值范围是______。

第01讲图形的旋转1.掌握旋转的概念，探索它的基本性质，理解对应点到旋转中心的距离相等，对应点与旋转中心连线所成的角彼此相等的性质。

2.能够按要求作出简单平面满图形旋转后的图形，并能利用旋转的性质进行规律的探究，利用旋转进行简单的图案设计。

知识点1：旋转的概念把一个平面图形绕着平面内某一点O转动一个角度，叫做图形的旋转，点O叫做旋转中心，转动的角叫做旋转角（如下图中的∠BOF），如果图形上的点B经过旋转变为点F，那么这两个点叫做对应点.注意 :（1）图形的旋转就是一个图形围绕一点旋转一定的角度，因而旋转一定有旋转中心和旋转角，且旋转前后图形能够重合，这是判断旋转的关键。

（2）旋转中心是点而不是线，旋转必须指出旋转方向。

（3）旋转的范围是平面内的旋转，否则有可能旋转成立体图形，因而要注意此点。

知识点2 ：旋转的性质旋转的性质：（1）对应点到旋转中心的距离相等。

（2）对应点与旋转中心所连线段的夹角等于旋转角。

（3）旋转前、后的图形全等。

注意：（1）旋转中心、旋转方向、旋转角度是确定旋转的关键.（2）性质是通过学生操作验证得出的结论，性质（1）和（2）是旋转作图的关键，整个性质是旋转这部分内容的核心，是解决有关旋转问题的基础.（3）要正确理解旋转中的变与不变，寻找等量关系，解决问题。

知识点3：旋转作图（1）旋转图形的作法：根据旋转的性质可知，对应角都相等，都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形。

（2）旋转作图有自己独特的特点，决定图形位置的因素较多，旋转角、旋转方向、旋转中心，其中任一元素不同，位置就不同，但得到的图形全等.【题型1 生活中的旋转现象】【典例1】（2022秋•新丰县期末）下列现象：①地下水位逐年下降，②传送带的移动，③方向盘的转动，④水龙头的转动；其中属于旋转的有（）A．4个B．3个C．2个D．1个【变式11】（2023春•沭阳县月考）下列运动属于数学上的旋转的有（）A．钟表上的时针运动B．城市环路公共汽车C．地球绕太阳转动D．将等腰三角形沿着底边上的高对折【变式12】（2022秋•隆安县期中）下列运动形式属于旋转的是（）A．飞驰的动车B．匀速转动的摩天轮C．运动员投掷标枪D．乘坐升降电梯【变式13】（2023春•洛宁县期末）如图，在新型俄罗斯方块游戏中（出现的图案可进行顺时针、逆时针旋转；向左、向右平移），已拼好的图案如图所示，现又出现一个形如的方块正向下运动，你必须进行以下哪项操作，才能拼成一个完整的图形（）A．顺时针旋转90°，向右平移B．逆时针旋转90°，向右平移C．顺时针旋转90°，向左平移D．逆时针旋转90°，向左平移【题型2 利用旋转的性质求角度】【典例2】（2023春•新邵县期末）如图，将△ABC绕点A按逆时针方向旋转100°得到△AB'C'，点B的对应点是点B′，点C的对应点是点C′，连接BB'，若AC'∥BB'，∠CAB'＝60°，则∠AB′B的度数为（）A．20°B．30°C．40°D．60°【变式21】（2023春•肃州区校级期中）如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，将△ABC绕点C顺时针旋转至△AB'C使得点A恰好落在AB 上，则旋转角度为（）A．30°B．60°C．90°D．150°【变式22】（2023春•曹县期末）如图，△ABC绕点A顺时针旋转50°，得到△ADE，点E落在BC边上，连接BD，当BD⊥BC时，∠ABC的度数为（）A．20°B．25°C．30°D．35°【变式23】（2023春•顺德区期末）如图，将△ABC绕点A逆时针旋转90°得到△ADE，连接BD，则∠ABD的度数为（）A．30°B．45°C．55°D．60°【变式24】（2023春•德化县期末）如图，△AED是由△ABC点A顺时针旋转得到的，若点C恰好在DE的延长线上，且∠BCD＝50°，则∠EAB等于（）A．120°B．125°C．130°D．135°【题型3 利用旋转的性质求线段长度】【典例3】（2023春•沙坪坝区校级期中）如图，在边长为4的正方形ABCD中，M为边AB上一点，且，将CM绕着点M顺时针旋转使得点C落在AB延长线上的点E处，连接CE，则点M到直线CE的距离是（）A．2B．C．5D．【变式31】（2023•和田市校级二模）如图，将△ABC绕点C逆时针旋转一定的角度得到△A′B′C′，此点A在边B′C上，若BC＝5，AC＝3，则AB′的长为（）A．5B．4C．3D．2【变式32】（2023•扎兰屯市一模）如图，P为正方形ABCD内一点，PC＝1，将△CDP绕点C逆时针旋转得到△CBE，则PE的长是（）A．1B．C．2D．2【变式33】（2023春•沈河区期末）如图，在Rt△ABC中，∠ACB＝90°，∠A ＝60°，AC＝2，将△ABC绕点C按逆时针方向旋转得到△A'B'C，此时点A'恰好在边AB上，则点B'与点B之间的距离为（）A．4B．2C．3D．【题型4 旋转中的坐标与图形变换】【典例4】（2023春•越城区期中）在平面直角坐标系中，点A的坐标是（1，3），将坐标原点O绕点A顺时针旋转90°得到点O'，则点O'的坐标是（）A．（3，1）B．（﹣3，﹣1）C．（﹣4，2）D．（﹣2，4）【变式41】（2023•南海区校级三模）如图，A（2，0），C（0，4），将线段AC绕点A顺时针旋转90°到AB，则B点坐标为（）A．（6，2）B．（2，6）C．（2，4）D．（4，2）【变式42】（2023•商丘模拟）如图，在平面直角坐标系中，点A的坐标为（0，3），点B的坐标为（4，0），连接AB，若将△ABO绕点B顺时针旋转90°，得到△A′BO′，则点A′的坐标为（）A．（6，4）B．（4，3）C．（7，4）D．（8，6）【题型5 作图旋转变换】【典例5】（2023春•温江区校级期末）如图，方格纸中的每个小方格都是边长为1的正方形，建立平面直角坐标系后，△ABC的顶点都在格点上．（1）画出△ABC关于y轴对称的△A1B1C1；（2）画出△ABC关于原点对称的△A2B2C2；（3）△ABC绕点B顺时针旋转90°后的△A3BC3的点C3的坐标为．（4）△ABC的面积为．【变式51】（2023春•锡山区期末）如图，在平面直角坐标系中，已知△ABC 的三个顶点的坐标分别为A（﹣2，3）、B（﹣6，0）、C（﹣1，0）．（1）已知△A′B′C′与△ABC关于坐标原点O成中心对称，则点A的对应点A′的坐标为；（2）将△ABC绕坐标原点O逆时针旋转90°得到△A″B″C″，画出△A″B″C″；（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．【变式52】（2023•合肥模拟）如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点），直线l也经过格点．（1）画出△ABC关于直线l对称的△A′B′C′；（2）将线段AB绕点A′顺时针旋转90°得到线段DE，画出线段DE．【变式53】（2023春•崂山区期末）在平面直角坐标系中，△ABC的位置如图，网格中小正方形边长为1，点A坐标为（1，2），请解答下列问题：（1）作出△ABC绕点O的逆时针旋转90°得到的△A1B1C1；（2）计算△A1B1C1的面积．【题型6 旋转对称图形】【典例6】（2023春•青羊区期末）下列正多边形，绕其中心旋转72°后，能和自身重合的是（）A．B．C．D．【变式61】（2023•东城区模拟）以下图形绕点O旋转一定角度后都能与原图形重合，其中旋转角最小的是（）A．B．C．D．【变式62】（2023•吉林模拟）如图，要使此图形旋转后与自身重合，至少应将它绕中心旋转的度数为（）A．30°B．60°C．120°D．180°【题型7 旋转中周期性问题】【典例7】（2023•中牟县二模）如图，在平面直角坐标系中，已知点A（2，0），∠OAB＝120°，AB＝AO＝2，且点B在第一象限内，将△AOB绕点O顺时针旋转，每次旋转60°，则第2023次旋转后，点B的坐标是（）A．B．C．D．【变式71】（2023春•忠县期末）已知平面直角坐标系中质点从点A0（1，0）出发，第1次向上移动1个单位后往逆时针转90°方向作第2次移动，第n （n为正整数）次移动n个单位后往逆时针转90°方向作第n+1次移动．设质点第n次移动后到达点A n，则点A2023为（）A．（1013，1013）B．（1013，﹣1012）C．（﹣1011，﹣1012）D．（﹣1011，1011）【变式72】（2023•渠县校级模拟）如图，正方形OABC的顶点A，C在坐标轴上，将正方形绕点O第1次逆时针旋转45°得到正方形OA1B1C1，依此方式，连续旋转至第2023次得到正方形OA2023B2023C2023．若点A的坐标为（1，0），则点B2023的坐标为（）A．（1，﹣1）B．C．D．（﹣1，1）【变式73】（2023春•中原区校级期中）如图，Rt△AOB中，∠AOB＝90°，OA＝3，OB＝4，将△AOB沿x轴依次以三角形三个顶点为旋转中心顺时针旋转，分别得图②，图③，则旋转到图⑩时直角顶点的坐标是（）A．（28，4）B．（36，0）C．（39，0）D．（，）1．（2023•无锡）如图，△ABC中，∠BAC＝55°，将△ABC逆时针旋转α（0°＜α＜55°），得到△ADE，DE交AC于F．当α＝40°时，点D恰好落在BC上，此时∠AFE等于（）A．80°B．85°C．90°D．95°2．（2023•天津）如图，把△ABC以点A为中心逆时针旋转得到△ADE，点B，C的对应点分别是点D，E，且点E在BC的延长线上，连接BD，则下列结论一定正确的是（）A．∠CAE＝∠BED B．AB＝AE C．∠ACE＝∠ADE D．CE＝BD 3．（2022•益阳）如图，已知△ABC中，∠CAB＝20°，∠ABC＝30°，将△ABC 绕A点逆时针旋转50°得到△AB′C′，以下结论：①BC＝B′C′，②AC ∥C′B′，③C′B′⊥BB′，④∠ABB′＝∠ACC′，正确的有（）A．①②③B．①②④C．①③④D．②③④4．（2022•聊城）如图，在直角坐标系中，线段A1B1是将△ABC绕着点P（3，2）逆时针旋转一定角度后得到的△A1B1C1的一部分，则点C的对应点C1的坐标是（）A．（﹣2，3）B．（﹣3，2）C．（﹣2，4）D．（﹣3，3）5．（2023•张家界）如图，AO为∠BAC的平分线，且∠BAC＝50°，将四边形ABOC绕点A逆时针方向旋转后，得到四边形AB′O′C′，且∠OAC′＝100°，则四边形ABOC旋转的角度是．6．（2023•枣庄）银杏是著名的活化石植物，其叶有细长的叶柄，呈扇形．如图是一片银杏叶标本，叶片上两点B，C的标分别为（﹣3，2），（4，3），将银杏叶绕原点顺时针旋转90°后，叶柄上点A对应点的坐标为．7．（2023•金华）在直角坐标系中，点（4，5）绕原点O逆时针方向旋转90°，得到的点的坐标．1．（2023•肇东市校级一模）如图，在△ABC中，∠BAC＝55°，∠C＝20°，将△ABC绕点A逆时针旋转α角度（0＜α＜180°）得到△ADE，若DE∥AB，则α的值为（）A．65°B．75°C．85°D．130°2．（2023•顺庆区校级二模）下列图形中，旋转120°后能与原图形重合的是（）A．等边三角形B．正方形C．正五边形D．正八边形3．（2023•衡水模拟）如图1是一副创意卡通圆规，图2是其平面示意图，OA 是支撑臂，OB是旋转臂，已知OA＝OB＝8cm．使用时，以点A为支撑点，铅笔芯端点B可绕点A旋转作出圆，则圆的半径AB不可能是（）A．10cm B．13cm C．15cm D．17cm 4．（2022秋•遵义期末）如图，在正方形网格中，△EFG绕某一点旋转某一角度得到△RPQ．则旋转中心可能是（）A．点A B．点B C．点C D．点D 5．（2023•市北区一模）如图，在方格纸上建立的平面直角坐标系中，将△ABO 绕点O按顺时针方向旋转90°，得△A′B′O′，则点A′的坐标为（）A．（3，1）B．（3，2）C．（2，3）D．（1，3）6．（2022秋•南宁期末）以原点为中心，把点A（3，0）逆时针旋转90°得到点B，则点B的坐标为（）A．（0，3）B．（﹣3，0）C．（3，3）D．（0，﹣3）7．（2023•三亚一模）如图，在平面直角坐标系中，Rt△ABO的顶点B在x轴的正半轴上，∠ABO＝90°，点A的坐标为，将△ABO绕点O逆时针旋转，使点B的对应点B′落在边OA上，连接A、A′，则线段AA′的长度是（）A．1B．2C．D．2 8．（2022秋•大足区期末）如图，在△ABC中，∠BAC＝135°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD．当点A，D，E在同一条直线上时，下列结论不正确的是（）A．△ABC≌△DEC B．∠ADC＝45°C．AD＝AC D．AE＝AB+CD 9．（2023•繁昌县校级模拟）小明把一副三角板按如图所示叠放在一起，固定三角板ABC，将另一块三角板DEF绕公共顶点B顺时针旋转（旋转角度不超过180°）．若两块三角板有一边平行，则三角板DEF旋转的度数可能是（）A．15°或45°B．15°或45°或90°C．45°或90°或135°D．15°或45°或90°或135°10．（2023春•巴州区期中）如图，△ABC三个顶点的坐标分别为A（2，4），B（1，1），C（4，3）．（1）请画出△ABC关于原点对称的△A1B1C1；（2）请画出△ABC绕点B逆时针旋转90°后的△A2B2C2，并写出A2的坐标．11．（2023春•遂平县期末）如图，四边形ABCD是正方形，△ADE旋转后能与△ABF重合．（1）判断△AEF的形状，试说明理由；（2）若CF＝7，CE＝3，求四边形AECF的面积．12．（2023春•惠来县期末）如图，在Rt△ABC中，∠B＝90°，将△ABC绕点A逆时针旋转得到△ADE，点B的对应点D刚好落在AC边上，连接EC．（1）若∠BAC＝50°，求∠BCE的度数；（2）若AB＝3，BC＝4，求四边形ABCE的面积．。

九年级上册数学《旋转》单元测试卷(满分120分,考试用时120分钟)一、选择题1.时钟上的分针匀速旋转一周需要 60min,则经过 5min,分针旋转了( )A . 10°B . 20°C . 30°D . 60°2.如图,在△A B C 中,∠C A B =65°,将△A B C 在平面内绕点A 旋转到△A B 'C '的位置.若∠C A B '=25°则∠AC C ''的度数为()A . 25°B . 40°C . 65°D . 70°3.如图,香港特别行政区区徽中的紫荆花图案,该图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( )A . 45°B . 60°C . 72°D . 108°4.如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1,△A B C 经过平移后得到△A 1B 1C 1,若A C 上一点P(1.2,1.4)平移后对应点为P1,点P1绕原点顺时针旋转180°,对应点为P2,则点P2的坐标为( )A . (2.8,3.6)B . (﹣2.8,﹣3.6)C . (3.8,2.6)D . (﹣3.8,﹣2.6)5.已知下列命题,其中正确的个数是( )(1)关于中心对称的两个图形一定不全等；(2)关于中心对称的两个图形是全等形；(3)两个全等的图形一定关于中心对称．A . 0个B . l个C . 2个D . 3个6.在下列图案中,既是轴对称又是中心对称图形的是( )A .B .C .D .7.已知点A (1,2),点A 关于原点的对称点是A 1,则点A 1的坐标是( )A . (-1,-2)B . (-2,1)C . (2,-1)D . (-1,2)8.如图,若将直角坐标系中“鱼“形图案的每个“顶点”的纵坐标保持不变,横坐标都乘以﹣1,得到一组新的点,再依次连接这些点,所得图案与原图案的关系为( )A . 重合B . 关于x轴对称C . 关于y轴对称D . 宽度不变,高度变为原来的一半9.观察下面图案,在(A )(B )(C )(D )四幅图案中,能通过图案(1)平移得到的是( )A .B .C .D .10.将绕点旋转得到,则下列作图正确的是( )A .B .C .D .二、填空题11.如图,已知△A B C ,D 是A B 上一点,E是B C 延长线上一点,将△A B C 绕点C 顺时针方向旋转,恰好能与△ED C 重合．若∠A =33°,则旋转角为_____°．12.在平面直角坐标系中,已知点P0的坐标为(2,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是_____．13.若点A (1,2)与点B (m,﹣2)关于原点对称,则m＝_____．14.若点P(﹣m,3﹣m)关于原点的对称点在第四象限,则m满足_____．15.如图,在的正方形格纸中,有一个以格点为顶点的,请你找出格纸中所有与成轴对称且也以格点为顶点的三角形,这样的三角形共有个．16.如图,已知∠MON=30°,B 为OM上一点,B A ⊥ON于A ,四边形A B C D 为正方形,P为射线B M上一动点,连结C P,将C P绕点C 顺时针方向旋转90°得C E,连结B E,若A B =4,则B E的最小值为_____．17.如图,▱A B C D 绕点A 逆时针旋转32°,得到▱A B ′C ′D ′,若点B ′与点B 是对应点,若点B ′恰好落在B C 边上,则∠C =_____．18.如图,正方形A EFG与正方形A B C D 的边长都为1,正方形A EFG绕正方形A B C D 的顶点A 旋转一周,在此旋转过程中,线段D F的长取值范围为_____．三、解答题19.如图,将△A B C 绕顶点C 逆时针旋转得到△A ′B ′C ,且点B 刚好落在A ′B ′上,若∠A ＝25°,∠BC A ′＝45°,求∠A ′B A 的度数．20.如图所示：已知∠A B C ＝120°,作等边△A C D ,将△A C D 旋转60°,得到△C D E,A B ＝3,B C ＝2,求B D 和∠A B D ．21.有一块方角形钢板如图所示,如何用一条直线将其分为面积相等的两部分．22.(1)指出下列旋转对称图形的最小旋转角,并在图中标明它的旋转中心O．(2)在上述几个图形中有没有中心对称图形？具体指明是哪几个？解：图形A 的最小旋转角是度,它中心对称图形．图形B 的最小旋转角是度,它中心对称图形．图形C 的最小旋转角是度,它中心对称图形．图形D 的最小旋转角是度,它中心对称图形．图形E的最小旋转角是度,它中心对称图形．23.如图,将△OA B 绕点O逆时针旋转80°得到△OC D ,点A 与点C 是对应点．(1)画出△OA B 关于点O对称的图形(保留画图痕迹,不写画法)；(2)若∠A =110°,∠D =40°,求∠A OD 的度数．24.在Rt△A B C 中,∠A C B =90°,A C =B C =3,点D 是斜边A B 上一动点(点D 与点A 、B 不重合),连接CD ,将C D 绕点C 顺时针旋转90°得到C E,连接A E,D E．(1)求△A D E的周长的最小值；(2)若C D =4,求A E的长度．25.如图,Rt△A B C 中,∠C = 90°,把Rt△A B C 绕着B 点逆时针旋转,得到Rt△D B E,点E在A B 上．(1)若∠B D A = 70°,求∠B A C 的度数．(2)若B C = 8,A C = 6,求△A B D 中A D 边上的高．参考答案一、选择题1.时钟上的分针匀速旋转一周需要 60min,则经过 5min,分针旋转了( )A . 10°B . 20°C . 30°D . 60°[答案]C[解析][分析]钟表的分针匀速旋转一周需要60分,分针旋转了360°；求经过6分,分针的旋转度数,列出算式,解答出即可．[详解]根据题意知,分针旋转一周(360°)需要60min,则分针每分钟旋转=6°,∴经过5min,分针旋转了5×6=30°,故选：C ．[点睛]本题考查了生活中的旋转现象,明确分针旋转一周,分针旋转了360°是解答本题的关键．2.如图,在△A B C 中,∠C A B =65°,将△A B C 在平面内绕点A 旋转到△A B 'C '的位置.若∠C A B '=25°则∠AC C ''的度数为()A . 25°B . 40°C . 65°D . 70°[答案]D[解析]分析：由旋转的性质结合已知易得∠C A C ′=∠B A B ′=∠C A B -∠C A B ′=65°-25°=40°,A C =A C ′,由此可得∠A C C ′=∠A C ′C =70°.详解：∵△A B ′C ′是由△A B C 绕点A 旋转得到的,∴∠C A C ′=∠B A B ′,A C =A C ′,∵∠B A B ′=∠B A C -∠C A B ′=65°-25°=40°,∴∠C A C ′=40°,∴∠A C C ′=∠A C ′C =(180°-40°)=70°.故选D .点睛：熟悉“旋转的性质,并能结合已知条件得到A C =A C ′,∠C A C ′=∠B A B ′=40°”是解答本题的关键.3.如图,香港特别行政区区徽中的紫荆花图案,该图案绕中心旋转n°后能与原来的图案互相重合,则n的最小值为( )A . 45°B . 60°C . 72°D . 108°[答案]C[解析]由题意得360º÷5=72º.故选C .4.如图,将正方形网格放置在平面直角坐标系中,其中每个小正方形的边长均为1,△A B C 经过平移后得到△A 1B 1C 1,若A C 上一点P(1.2,1.4)平移后对应点为P1,点P1绕原点顺时针旋转180°,对应点为P2,则点P2的坐标为( )A . (2.8,3.6)B . (﹣2.8,﹣3.6)C . (3.8,2.6)D . (﹣3.8,﹣2.6)[解析][分析]根据平移的性质得出,△A B C 的平移方向以及平移距离,即可得出P1坐标,进而利用中心对称图形的性质得出P2点的坐标．[详解]∵A 点坐标为：(1,1),A 1(-3,-4),∴△A B C 向左平移了4个单位,向下平移了5个单位,∴点P(1.2,1.4)平移后的对应点P1为：(-2.8,-3.6),∵点P1绕点O逆时针旋转180°,得到对应点P2,∴P2点的坐标为：(2.8,3.6)．故选A ．[点睛]此题主要考查了旋转的性质以及平移的性质,根据已知得出平移的方式是解题关键．关于原点对称的两个点横纵坐标均为互为相反数的关系.5.已知下列命题,其中正确的个数是( )(1)关于中心对称的两个图形一定不全等；(2)关于中心对称的两个图形是全等形；(3)两个全等的图形一定关于中心对称．A . 0个B . l个C . 2个D . 3个[答案]B[解析]试题解析：关于中心对称的两个图形一定是全等形,所以(1)错误,(2)正确；(3)两个全等的图形位置可以是任意的,不一定是中心对称的,所以真命题只有一个．故选B .6.在下列图案中,既是轴对称又是中心对称图形的是( )A .B .C .D .[答案]C[解析]根据中心对称图形和轴对称图形的概念对各选项分析判断即可得解．[详解]A 、既不是轴对称图形又不是中心对称图形,故不符合题意；B 、是轴对称图形,不是中心对称图形,故不符合题意；C 、既是轴对称图形又是中心对称图形,符合题意；D 、是中心对称图形,不是轴对称图形,故不符合题意,故选C ．[点睛]本题考查了中心对称图形与轴对称图形的概念．熟练掌握相关定义是解题的关键.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合．7.已知点A (1,2),点A 关于原点的对称点是A 1,则点A 1的坐标是( )A . (-1,-2)B . (-2,1)C . (2,-1)D . (-1,2)[答案]A[解析]根据关于原点的对称点,横坐标互为相反数、纵坐标互为相反数,知点 A (1, 2)关于原点对称点的坐标是(−1,-2),故选A .8.如图,若将直角坐标系中“鱼“形图案的每个“顶点”的纵坐标保持不变,横坐标都乘以﹣1,得到一组新的点,再依次连接这些点,所得图案与原图案的关系为( )A . 重合B . 关于x轴对称C . 关于y轴对称D . 宽度不变,高度变为原来的一半[答案]C[解析]根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答．[详解]解：图案的每个“顶点”的纵坐标保持不变,横坐标分别乘-1,则对应点的横坐标互为相反数,纵坐标相同,所以,所得图案与原图案关于y轴对称．故选：C ．[点睛]本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律．9.观察下面图案,在(A )(B )(C )(D )四幅图案中,能通过图案(1)平移得到的是( )A .B .C .D .[答案]C[解析][分析]把一个图形整体沿某一直线方向移动,得到的新图形与原图形的形状和大小完全相同．[详解]解：因为平移不改变图形的形状和大小,只改变图形的位置,所以在(A )(B )(C )(D )四幅图案中,能通过图案(1)平移得到的是C 选项的图案.故选：C ．[点睛]本题考查平移的性质,把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同．10.将绕点旋转得到,则下列作图正确的是( )A .B .C .D .[答案]D[解析][分析]把一个图形绕某一点O转动一个角度的图形变换叫做旋转.[详解]解：观察选项中的图形,只有D 选项为△A B O绕O点旋转了180°.[点睛]本题考察了旋转的定义.二、填空题11.如图,已知△A B C ,D 是A B 上一点,E是B C 延长线上一点,将△A B C 绕点C 顺时针方向旋转,恰好能与△ED C 重合．若∠A =33°,则旋转角为_____°．[答案]82°[解析][分析]设∠B =x,根据旋转的旋转得C B =C D ,∠C D E=∠B =x,∠A =∠E=33°,∠B C D 的度数等于旋转角的度数,再利用三角形外角性质得∠B C D =x+33°,接着证明∠C D B =∠B =x,则利用三角形内角和得到x+x+33°+x=180°,然后求出x后计算x+33°即可得到旋转角的度数．[详解]解：设∠B =x,∵△A B C 绕点C 顺时针方向旋转,恰好能与△ED C 重合,∴C B =C D ,∠C D E=∠B =x,∠A =∠E=33°,∠B C D 的度数等于旋转角的度数,∴∠B C D =∠C D E+∠E=x+33°,在△B C D 中,∵C B =C D ,∴∠C D B =x,∴x+x+33°+x=180°,解得x=49°,∴旋转角的度数为49°+33°=82°．故答案为82°．[点睛]本题考查旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．12.在平面直角坐标系中,已知点P0的坐标为(2,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是_____．[答案](﹣2,2)．[解析][分析]利用旋转的性质得到OP2=2OP1=OP3=4,∠xOP2=∠P2OP3=60°,作P3H⊥x轴于H,利用含30度的直角三角形求出OH、P3H,从而得到P3点坐标．[详解]解：如图,∵点P0的坐标为(2,0),∴OP0=OP1=2,∵将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O 按逆时针方向旋转60°得点P3,∴OP2=2OP1=OP3=4,∠xOP2=∠P2OP3=60°,作P3H⊥x轴于H,OH=OP3=2,P3H=OH=2,∴P3(-2,2)．故答案为(-2,2)．[点睛]本题考查了坐标与图形变化：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°,45°,60°,90°,180°．13.若点A (1,2)与点B (m,﹣2)关于原点对称,则m＝_____．[答案]-1[解析][分析]根据关于原点对称的点的横坐标与纵坐标都互为相反数解答．[详解]根据关于原点对称的点的横坐标与纵坐标都互为相反数解答．[解答]∵点A (1,2)与点B (m,-2)关于原点对称,∴m=-1.故答案为：-1.[点睛]本题考查的是关于原点对称,熟练掌握关于原点对称的点的坐标是解题的关键.14.若点P(﹣m,3﹣m)关于原点的对称点在第四象限,则m满足_____．[答案]0＜m＜3[解析][分析]根据题意判断出点P在第二象限,再根据第二象限内点的坐标特点可得关于m的不等式组,再解不等式组即可．[详解]解：∵点P(﹣m,3﹣m)关于原点的对称点在第四象限,∴点P在第二象限,∴,解得：0＜m＜3,故答案为：0＜m＜3．[点睛]本题考查关于原点对称的点的坐标,以及平面直角坐标系中各象限内点的坐标符号,关键是掌握四个象限内点的坐标符号．15.如图,在的正方形格纸中,有一个以格点为顶点的,请你找出格纸中所有与成轴对称且也以格点为顶点的三角形,这样的三角形共有个．[答案]5[解析]与△A B C 成轴对称且也以格点为顶点的三角形有5个,分别为△B C D ,△B FH,△A D C ,△A EF,△C GH．16.如图,已知∠MON=30°,B 为OM上一点,B A ⊥ON于A ,四边形A B C D 为正方形,P为射线B M上一动点,连结C P,将C P绕点C 顺时针方向旋转90°得C E,连结B E,若A B =4,则B E的最小值为_____．[答案]2+2[解析]如图所示,将B C 绕着点C 顺时针旋转90°得FC ,作直线FE交OM于H,则∠B C F=90°,B C =FC , ∵将C P绕点C 按顺时针方向旋转90°得C E,∴∠PC E=90°,PC =EC ,∴∠B C P=∠FC E,在△B C P和△FC E中,B C =FC ,∠B C P=∠FC E,PC =EC ,∴△B C P≌△FC E(SA S),∴∠C B P=∠C FE,又∵∠B C F=90°,∴∠B HF=90°,∴点E在直线FH上,即点E的轨迹为直线FH,∵B H⊥EF,∴当点E与点H重合时,B E=B H最短,∵当C P⊥OM时,Rt△B C P中,∠C B P=30°,∴C P=B C =2,B P= C P=2,又∵∠PC E=∠C PH=∠PHE=90°,C P=C E,∴正方形C PHE中,PH=C P=2,∴B H=B H+PH=2+2,即B E的最小值为2+2,故答案为：2+2.点睛：本题主要考查了正方形的性质,勾股定理,全等三角形的判定与性质以及垂线段最短的综合运用,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应边相等以及垂线段最短进行判断.17.如图,▱A B C D 绕点A 逆时针旋转32°,得到▱A B ′C ′D ′,若点B ′与点B 是对应点,若点B ′恰好落在B C 边上,则∠C =_____．[答案]106°[解析][分析]根据旋转的性质得出A B =A B ′,∠B A B ′=32°,进而得出∠B 的度数,再利用平行四边形的性质得出∠C 的度数.[详解]解：∵平行四边形A B C D 绕点A 逆时针旋转30°,得到平行四边形A B ′C ′D ′(点B ′与点B 是对应点,点C ′与点C 是对应点,点D ′与点D 是对应点),∴A B =A B ′,∠B A B ′=32°,∴∠B =∠A B ′B =(180°﹣32°)÷2=74°,∴∠C =180°﹣74°=106°．故答案为：106°．[点睛]本题考查旋转的性质以及平行四边形的性质,根据已知得出∠B =∠A B ′B =74°是解题关键．18.如图,正方形A EFG与正方形A B C D 的边长都为1,正方形A EFG绕正方形A B C D 的顶点A 旋转一周,在此旋转过程中,线段D F的长取值范围为_____．[答案]≤D F≤+1[解析][分析]由题意可求A F=,且点F是以A 为圆心,为半径的圆上一点,即可求D F的取值范围．[详解]解：∵正方形A EFG与正方形A B C D 的边长都为1∴A F=∴点F是以A 为圆心,为半径的圆上一点∴当F,D ,A 三点共线且D 在线段A F之间时,D F最短为﹣1当F,D ,A 三点共线且A 在线段D F之间时,D F最长为+1∴-1≤D F≤+1故答案为-1≤D F≤+1[点睛]本题考查旋转的性质,正方形的性质,解题关键是利用点F的轨迹求D F的取值范围．三、解答题19.如图,将△A B C 绕顶点C 逆时针旋转得到△A ′B ′C ,且点B 刚好落在A ′B ′上,若∠A ＝25°,∠BC A ′＝45°,求∠A ′B A 的度数．[答案]40°[解析][分析]先利用旋转的性质得∠A ′＝∠A ＝25°,∠A B C ＝∠B ′,C B ＝C B ′,再利用等腰三角形的性质得∠B ′＝∠C B B ′,则根据三角形外角性质得∠C B B ′＝70°,所以∠B ′＝∠A B C ＝70°,然后利用平角定义计算∠A ′B A 的度数．[详解]∵△A B C 绕顶点C 逆时针旋转得到△A ′B ′C ,且点B 刚好落在A ′B ′上,∴∠A ′＝∠A ＝25°,∠A B C ＝∠B ′,C B ＝C B ′,∴∠B ′＝∠C B B ′,∵∠C B B ′＝∠A ′+∠B C A ′＝25°+45°＝70°,∴∠B ′＝70°,∴∠A B C ＝70°,∴∠A ′B A ＝180°﹣70°﹣70°＝40°．[点睛]本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．20.如图所示：已知∠A B C ＝120°,作等边△A C D ,将△A C D 旋转60°,得到△C D E,A B ＝3,B C ＝2,求B D 和∠A B D ．[答案]B D ＝5．∠B A D ＝60°[解析][分析]先根据等边三角形的性质得∠A D C ＝∠A C D ＝60°,由于∠A B C ＝120°,根据四边形内角和得到∠B A D +∠B C D ＝180°,则∠B A D +∠B C A ＝120°,再根据旋转的性质得∠B A D ＝∠EC D ,D B ＝D E,∠B D E＝60°,A B ＝C E,于是有∠B C A +∠EC D +∠A C D ＝180°,得到B 、C 、E在同一条直线上,接着证明△B D E为等边三角形得到∠D B E＝60°,所以∠B A D ＝∠A B C ﹣∠D B E＝60°,B D ＝B E＝B C +C E＝B C +A B ＝5．[详解]∵△A C D 是等边三角形,∴∠A D C ＝∠A C D ＝60°,∵∠A B C ＝120°,∴∠B A D +∠B C D ＝180°,∴∠B A D +∠B C A ＝120°,∵△A B D 绕点D 按顺时针方向旋转60°后到△EC D 的位置,∴∠B A D ＝∠EC D ,D B ＝D E,∠B D E＝60°,A B ＝C E,∴∠B C A +∠EC D ＝120°,∴∠B C A +∠EC D +∠A C D ＝180°,∴B 、C 、E在同一条直线上．∵D B ＝D E,∠B D E＝60°,∴△B D E为等边三角形,∴∠D B E＝60°,∴∠B A D ＝∠A B C ﹣∠D B E＝60°,∴B D ＝B E＝B C +C E＝B C +A B ＝3+2＝5．[点睛]本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等边三角形的判定与性质．21.有一块方角形钢板如图所示,如何用一条直线将其分为面积相等的两部分．[答案]答案见解析[解析][分析]思路1：先将图形分割成两个矩形,找出各自的对称中心,过两个对称中心做直线即可；思路2：先将图形补充成一个大矩形,分别找出图中两个矩形各自的对称中心,过两个对称中心做直线即可．[详解]如图所示,有三种思路：[点睛]本题需利用矩形的中心对称性解决问题．22.(1)指出下列旋转对称图形的最小旋转角,并在图中标明它的旋转中心O．(2)在上述几个图形中有没有中心对称图形？具体指明是哪几个？解：图形A 的最小旋转角是度,它中心对称图形．图形B 的最小旋转角是度,它中心对称图形．图形C 的最小旋转角是度,它中心对称图形．图形D 的最小旋转角是度,它中心对称图形．图形E的最小旋转角是度,它中心对称图形．[答案](1)详见解析；(2)60,是；72,不是；72,不是；120,不是；90,是．[解析][分析](1)一个图形围绕某一点旋转一定的角度(小于360°)后能与原图形重合,那么这个图形就叫做旋转对称图形．(2)一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心．[详解]解：(1)如图所示,(2)图形A 的最小旋转角是60°,它是中心对称图形．图形B 的最小旋转角是72°,它不是中心对称图形．图形C 的最小旋转角是72°,它不是中心对称图形．图形D 的最小旋转角是120°,它不是中心对称图形．图形E的最小旋转角是90°,它是中心对称图形．故答案为：60,是；72,不是；72,不是；120,不是；90,是．[点睛]本题考查中心对称图形以及旋转对称图形,常见的中心对称图形有平行四边形、圆形、正方形、长方形等等．23.如图,将△OA B 绕点O逆时针旋转80°得到△OC D ,点A 与点C 是对应点．(1)画出△OA B 关于点O对称的图形(保留画图痕迹,不写画法)；(2)若∠A =110°,∠D =40°,求∠A OD 的度数．[答案](1)详见解析；(2)50°[解析][分析](1)延长A O到A ′,使OA ′=O A ,延长B O到B ′,使OB ′=O B ,则△OA ′B ′满足条件；(2)根据旋转的性质得∠A OC =80°,∠C =∠A =110°,再利用三角形内角和计算出∠C OD ,然后计算∠A OC ﹣∠C OD 即可．[详解]解：(1)如图,△OA ′B ′为所作．(2)∵△OA B 绕点O逆时针旋转80°得到△OC D ,∴∠A OC =80°,∠C =∠A =110°,∴∠C OD =180°﹣110°﹣40°=30°,∴∠A OD =∠A OC ﹣∠C OD =80°﹣30°=50°．[点睛]本题考查作图﹣旋转变换：根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形．24.在Rt△A B C 中,∠A C B =90°,A C =B C =3,点D 是斜边A B 上一动点(点D 与点A 、B 不重合),连接CD ,将C D 绕点C 顺时针旋转90°得到C E,连接A E,D E．(1)求△A D E的周长的最小值；(2)若C D =4,求A E的长度．[答案](1)6+；(2)3﹣或3+[解析][分析](1)根据勾股定理得到A B = A C =6,根据全等三角形的性质得到A E=B D ,当D E最小时,△A D E的周长最小,过点C 作C F⊥A B 于点F,于是得到结论；(2)当点D 在C F的右侧,当点D 在C F的左侧,根据勾股定理即可得到结论[详解]解：(1)∵在Rt△A B C 中,∠A C B =90°,A C =B C =3∴A B = A C =6,∵∠EC D =∠A C B =90°,∴∠A C E=∠B C D ,在△A C E与△B C D 中,,∴△A C E≌△B C D (SA S),∴A E=B D ,∴△A D E的周长=A E+A D +D E=A B +D E,∴当D E最小时,△A D E的周长最小,过点C 作C F⊥A B 于点F,当C D ⊥A B 时,C D 最短,等于3,此时D E=3,∴△A D E的周长的最小值是6+3；(2)当点D 在C F的右侧,∵C F=A B =3,C D =4,∴D F=,∴A E=B D =B F﹣D F=3﹣；当点D 在C F的左侧,同理可得A E=B D =3+,综上所述：A E的长度为3﹣或3+．[点睛]本题考查旋转的性质,全等三角形的判定与性质,勾股定理,解题的关键是熟练运用旋转的性质以及全等三角形的判定与性质．25.如图,Rt△A B C 中,∠C = 90°,把Rt△A B C 绕着B 点逆时针旋转,得到Rt△D B E,点E在A B 上．(1)若∠B D A = 70°,求∠B A C 的度数．(2)若B C = 8,A C = 6,求△A B D 中A D 边上的高．[答案](1)∠B A C =50°；(2)[解析]解：(1) 由旋转得△A C B ≌△D EB∴B D = B A∴∠B A D =∠B D A =∴∠A B D =∴∠A B C =∠A B D =∵∠C =∴∠B A C =·········································································· 5分(2) ∵B C = 8,A C = 6,∠C =∴∵∠D EB =∠C =且B E=B C = 8,D E ="A C " = 6∴A E =" A B " – B E = 2在Rt△D EA 中,设A D 边上的高为h∴∴······················································· 10分。

第五章《平面直角坐标系》基础训练一一、选择题1.一只小虫从点(2,1)A -出发，先向右跳4个单位长度，再向下跳3个单位长度，到达点B 处，则点B 的坐标是( )A. (5,5)-B. (2,2)-C. (1,5)D. (2,2) 2.如桌点(3,24)P m m ++在y 轴上，那么点P 的坐标为( )A. (2,0)-B. (0,2)-C. (1,0)D. (0,1) 3. 在平面直角坐标系中，若点A 与点B 关于y 轴对称，点A 的坐标是(2,8)-，则点B 的坐标是( )A. (2,8)--B. (2,8)C. (2,8)-D. (8,2) 4. 如图，在平面直角坐标系中，ABC ∆位于第二象限，点A 的坐标是(2,3)-，先把ABC ∆向右平移4个单位长度得到111A B C ∆，再作与111A B C ∆关于x 轴对称的222A B C ∆，则点A 的对应点2A 的坐标是( )A. (3,2)-B. (2,3)-C. (1,2)-D. (1,2)-5.若点(,)N x y 在x 轴下方，y 轴左侧，且30x -=，240y -=，则点N 的坐标为( )A. (3,2)--B. (3,2)-C. (3,2)-D. (3,2) 二、填空题6.若点(3,)P m 到x 轴的距离是4，则m 的值是 .7.若(,5)A a -，(2,)B b 两点关于x 轴对称，则32a b -的值是 .8.如图，在长方形ABCD 中，(4,1)A ，(0,1)B ，(0,3)C ，则点D 的坐标是 .9.如图，在平面直角坐标系中，已知点(1,0)A ，(0,2)B .如果将线段AB 绕点B 顺时针旋转90º至线段CB ，那么点C 的坐标是 .10.阅读材料:设11(,)a x y =，22(,)b x y =，若//a b ，则1221x y x y =.根据该材料填空:已知(2,3)a =，(4,)b m =，且//a b ，则m 的值为 . 三、解答题11．如图所示，△ABC 在直角坐标系中． (1)请写出△ABC 各顶点的坐标；(2)若把△ABC 向上平移2个单位长度，再向左平移1个单位长度得到△A ′B ′C ′，写出点A ′，B ′，C ′的坐标； (3)求出△ABC 的面积．12．在平面直角坐标系中，点A (1，2a ＋3) 在第一象限． (1) 若点A 到x 轴的距离与到y 轴的距离相等，求a 的值； (2) 若点A 到x 轴的距离小于到y 轴的距离，求a 的取值范围．13．已知点M (3，2) 与点N (x，y) 在同一条平行于x轴的直线上，且点N到y 轴的距离为5，试求点N的坐标．14．在同一平面直角坐标系中分别描出点A（－3，0），B(2，0)，C(1，3)，再用线段将这三点首尾依次连接起来，求△ABC的面积与周长．15.在平面直角坐标系xOy中，已知A（－1，5），B（4，2），C（－1，0）三点。

新高考数学大一轮复习专题：第1讲 平面向量[考情分析] 1.平面向量是高考的热点和重点，命题突出向量的基本运算与工具性，在解答题中常与三角函数、直线和圆锥曲线的位置关系问题相结合，主要以条件的形式出现，涉及向量共线、数量积等.2.常以选择题、填空题形式考查平面向量的基本运算，中低等难度；平面向量在解答题中一般为中等难度． 考点一 平面向量的线性运算 核心提炼1．平面向量加减法求解的关键是：对平面向量加法抓住“共起点”或“首尾相连”．对平面向量减法应抓住“共起点，连两终点，指向被减向量的终点”，再观察图形对向量进行等价转化，即可快速得到结果．2．在一般向量的线性运算中，只要把其中的向量当作一个字母看待即可，其运算方法类似于代数中合并同类项的运算，在计算时可以进行类比．例1 (1)如图所示，AD 是△ABC 的中线，O 是AD 的中点，若CO →＝λAB →＋μAC →，其中λ，μ∈R ，则λ＋μ的值为( )A ．－12B.12 C ．－14D.14答案 A解析 由题意知，CO →＝12(CD →＋CA →)＝12×⎝ ⎛⎭⎪⎫12CB →＋CA →＝14(AB →－AC →)＋12CA →＝14AB →－34AC →， 则λ＝14，μ＝－34，故λ＋μ＝－12.(2)已知e 1，e 2是不共线向量，a ＝m e 1＋2e 2，b ＝n e 1－e 2，且mn ≠0.若a ∥b ，则m n＝________. 答案 －2解析 ∵a ∥b ，∴m ×(－1)＝2×n ，∴m n＝－2.(3)A ，B ，C 是圆O 上不同的三点，线段CO 与线段AB 交于点D ，若OC →＝λOA →＋μOB →(λ∈R ，μ∈R )，则λ＋μ的取值范围是________．答案 (1，＋∞)解析 由题意可得，OD →＝kOC →＝kλOA →＋kμOB →(0<k <1)，又A ，D ，B 三点共线，所以kλ＋kμ＝1，则λ＋μ＝1k>1，即λ＋μ的取值范围是(1，＋∞)．易错提醒 在平面向量的化简或运算中，要根据平面向量基本定理恰当地选取基底，变形要有方向，不能盲目转化．跟踪演练1 (1)如图，在平行四边形ABCD 中，E ，F 分别为边AB ，BC 的中点，连接CE ，DF ，交于点G .若CG →＝λCD →＋μCB →(λ，μ∈R )，则λμ＝________.答案 12解析 由题意可设CG →＝xCE →(0<x <1)， 则CG →＝x (CB →＋BE →)＝x ⎝ ⎛⎭⎪⎫CB →＋12CD →＝x 2CD →＋xCB →.因为CG →＝λCD →＋μCB →，CD →与CB →不共线，所以λ＝x 2，μ＝x ，所以λμ＝12.(2)如图，在扇形OAB 中，∠AOB ＝π3，C 为弧AB 上的一个动点，若OC →＝xOA →＋yOB →，则x ＋3y的取值范围是________．答案 [1,3]解析 设扇形的半径为1，以OB 所在直线为x 轴，O 为坐标原点建立平面直角坐标系(图略)， 则B (1,0)，A ⎝ ⎛⎭⎪⎫12，32，C (cos θ，sin θ)⎝ ⎛⎭⎪⎫其中∠BOC ＝θ，0≤θ≤π3.则OC →＝(cos θ，sin θ)＝x ⎝ ⎛⎭⎪⎫12，32＋y (1,0)，即⎩⎪⎨⎪⎧x 2＋y ＝cos θ，32x ＝sin θ，解得x ＝23sin θ3，y ＝cos θ－3sin θ3，故x ＋3y ＝23sin θ3＋3cos θ－3sin θ＝3cos θ－33sin θ，0≤θ≤π3. 令g (θ)＝3cos θ－33sin θ， 易知g (θ)＝3cos θ－33sin θ在⎣⎢⎡⎦⎥⎤0，π3上单调递减，故当θ＝0时，g (θ)取得最大值为3， 当θ＝π3时，g (θ)取得最小值为1，故x ＋3y 的取值范围为[1,3]．考点二 平面向量的数量积 核心提炼1．若a ＝(x ，y )，则|a |＝a ·a ＝x 2＋y 2. 2．若A (x 1，y 1)，B (x 2，y 2)，则|AB →|＝x 2－x 12＋y 2－y 12.3．若a ＝(x 1，y 1)，b ＝(x 2，y 2)，θ为a 与b 的夹角， 则cos θ＝a ·b |a ||b |＝x 1x 2＋y 1y 2x 21＋y 21x 22＋y 22. 例2 (1)(2020·全国Ⅲ)已知向量a ，b 满足|a |＝5，|b |＝6，a ·b ＝－6，则cos 〈a ，a ＋b 〉等于( )A ．－3135B ．－1935C.1735D.1935答案 D解析 ∵|a ＋b |2＝(a ＋b )2＝a 2＋2a ·b ＋b 2＝25－12＋36＝49， ∴|a ＋b |＝7，∴cos〈a ，a ＋b 〉＝a ·a ＋b |a ||a ＋b |＝a 2＋a ·b|a ||a ＋b |＝25－65×7＝1935. (2)已知扇形OAB 的半径为2，圆心角为2π3，点C 是弧AB 的中点，OD →＝－12OB →，则CD →·AB →的值为( )A ．3B ．4C ．－3D ．－4 答案 C解析 如图，连接CO ，∵点C 是弧AB 的中点， ∴CO ⊥AB ，又∵OA ＝OB ＝2，OD →＝－12OB →，∠AOB ＝2π3，∴CD →·AB →＝(OD →－OC →)·AB →＝－12OB →·AB →＝－12OB →·(OB →－OA →)＝12OA →·OB →－12OB →2＝12×2×2×⎝ ⎛⎭⎪⎫－12－12×4＝－3. (3)已知在直角梯形ABCD 中，AB ＝AD ＝2CD ＝2，∠ADC ＝90°，若点M 在线段AC 上，则|MB →＋MD →|的取值范围为________________．答案 ⎣⎢⎡⎦⎥⎤255，22 解析 以A 为坐标原点，AB ，AD 所在直线分别为x 轴，y 轴， 建立如图所示的平面直角坐标系，则A (0,0)，B (2,0)，C (1,2)，D (0,2)，设AM →＝λAC →(0≤λ≤1)，则M (λ，2λ)， 故MD →＝(－λ，2－2λ)，MB →＝(2－λ，－2λ)， 则MB →＋MD →＝(2－2λ，2－4λ)， ∴|MB →＋MD →|＝2－2λ2＋2－4λ2＝20⎝⎛⎭⎪⎫λ－352＋45，0≤λ≤1， 当λ＝0时，|MB →＋MD →|取得最大值为22， 当λ＝35时，|MB →＋MD →|取得最小值为255，∴|MB →＋MD →|∈⎣⎢⎡⎦⎥⎤255，22.易错提醒 两个向量的夹角的范围是[0，π]，在使用平面向量解决问题时要特别注意两个向量的夹角可能是0或π的情况，如已知两个向量的夹角为钝角时，不仅要求其数量积小于零，还要求不能反向共线．跟踪演练2 (1)(2019·全国Ⅰ)已知非零向量a ，b 满足|a |＝2|b |，且(a －b )⊥b ，则a 与b 的夹角为( )A.π6B.π3C.2π3D.5π6 答案 B解析 方法一 设a 与b 的夹角为θ，因为(a －b )⊥b ，所以(a －b )·b ＝a ·b －|b |2＝0， 又因为|a |＝2|b |，所以2|b |2cos θ－|b |2＝0， 即cos θ＝12，又θ∈[0，π]，所以θ＝π3，故选B. 方法二 如图，令OA →＝a ，OB →＝b ，则BA →＝OA →－OB →＝a －b .因为(a －b )⊥b ，所以∠OBA ＝π2，又|a |＝2|b |，所以∠AOB ＝π3，即a 与b 的夹角为π3，故选B.(2)(2020·新高考全国Ⅰ)已知P 是边长为2的正六边形ABCDEF 内的一点，则AP →·AB →的取值范围是( ) A ．(－2,6) B ．(－6,2) C ．(－2,4) D ．(－4,6)答案 A解析 如图，取A 为坐标原点，AB 所在直线为x 轴建立平面直角坐标系，则A (0,0)，B (2,0)，C (3，3)，F (－1，3)． 设P (x ，y )，则AP →＝(x ，y )，AB →＝(2,0)，且－1<x <3. 所以AP →·AB →＝(x ，y )·(2,0)＝2x ∈(－2,6)．(3)设A ，B ，C 是半径为1的圆O 上的三点，且OA →⊥OB →，则(OC →－OA →)·(OC →－OB →)的最大值是( ) A ．1＋ 2 B ．1－ 2 C.2－1 D ．1答案 A解析 如图，作出OD →，使得OA →＋OB →＝OD →.则(OC →－OA →)·(OC →－OB →)＝OC →2－OA →·OC →－OB →·OC →＋OA →·OB →＝1－(OA →＋OB →)·OC →＝1－OD →·OC →，由图可知，当点C 在OD 的反向延长线与圆O 的交点处时，OD →·OC →取得最小值，最小值为－2，此时(OC →－OA →)·(OC →－OB →)取得最大值，最大值为1＋ 2.故选A.专题强化练一、单项选择题1．已知四边形ABCD 是平行四边形，点E 为边CD 的中点，则BE →等于( )A ．－12AB →＋AD →B.12AB →－AD →C.AB →＋12AD →D.AB →－12AD →答案 A解析 由题意可知，BE →＝BC →＋CE →＝－12AB →＋AD →.2．(2020·广州模拟)加强体育锻炼是青少年生活学习中非常重要的组成部分，某学生做引体向上运动，处于如图所示的平衡状态时，若两只胳膊的夹角为π3，每只胳膊的拉力大小均为400 N ，则该学生的体重(单位：kg)约为(参考数据：取重力加速度大小为g ＝10 m/s 2，3≈1.732)( )A ．63B ．69C ．75D ．81 答案 B解析 设该学生的体重为m ，重力为G ，两臂的合力为F ′，则|G |＝|F ′|，由余弦定理得|F ′|2＝4002＋4002－2×400×400×cos 2π3＝3×4002，∴|F ′|＝4003，∴|G |＝mg ＝4003，m ＝403≈69kg.3．已知向量a ＝(1,2)，b ＝(2，－2)，c ＝(λ，－1)，若c ∥(2a ＋b )，则λ等于( ) A ．－2B ．－1C ．－12D.12答案 A解析 ∵a ＝(1,2)，b ＝(2，－2)，∴2a ＋b ＝(4,2)，又c ＝(λ，－1)，c ∥(2a ＋b )，∴2λ＋4＝0，解得λ＝－2，故选A.4．(2020·潍坊模拟)在平面直角坐标系xOy 中，点P (3，1)，将向量OP →绕点O 按逆时针方向旋转π2后得到向量OQ →，则点Q 的坐标是( )A ．(－2，1)B ．(－1，2)C ．(－3，1)D ．(－1，3) 答案 D解析 由P (3，1)，得P ⎝⎛⎭⎪⎫2cos π6，2sin π6，∵将向量OP →绕点O 按逆时针方向旋转π2后得到向量OQ →，∴Q ⎝ ⎛⎭⎪⎫2cos ⎝ ⎛⎭⎪⎫π6＋π2，2sin ⎝ ⎛⎭⎪⎫π6＋π2， 又cos ⎝⎛⎭⎪⎫π6＋π2＝－sin π6＝－12，sin ⎝ ⎛⎭⎪⎫π6＋π2＝cos π6＝32，∴Q (－1，3)．5．(2020·泰安模拟)如图，在△ABC 中，点O 是BC 的中点，过点O 的直线分别交直线AB ，AC 于不同的两点M ，N ，若AB →＝mAM →，AC →＝nAN →，则m ＋n 等于( )A ．0B ．1C ．2D ．3 答案 C解析 如图，连接AO ，由O 为BC 的中点可得，AO →＝12(AB →＋AC →)＝m 2AM →＋n 2AN →， ∵M ，O ，N 三点共线， ∴m 2＋n2＝1. ∴m ＋n ＝2.6．在同一平面中，AD →＝DC →，BE →＝2ED →.若AE →＝mAB →＋nAC →(m ，n ∈R )，则m ＋n 等于( ) A.23B.34C.56D ．1 答案 A解析 由题意得，AD →＝12AC →，DE →＝13DB →，故AE →＝AD →＋DE →＝12AC →＋13DB →＝12AC →＋13(AB →－AD →)＝12AC →＋13⎝ ⎛⎭⎪⎫AB →－12AC →＝13AB →＋13AC →，所以m ＝13，n ＝13，故m ＋n ＝23.7．若P 为△ABC 所在平面内一点，且|PA →－PB →|＝|PA →＋PB →－2PC →|，则△ABC 的形状为( ) A ．等边三角形 B ．等腰三角形 C ．直角三角形 D ．等腰直角三角形答案 C解析 ∵|PA →－PB →|＝|PA →＋PB →－2PC →|，∴|BA →|＝|(PA →－PC →)＋(PB →－PC →)|＝|CA →＋CB →|，即|CA →－CB →|＝|CA →＋CB →|，两边平方整理得，CA →·CB →＝0，∴CA →⊥CB →，∴△ABC 为直角三角形．故选C. 8．已知P 是边长为3的等边三角形ABC 外接圆上的动点，则||PA →＋PB →＋2PC →的最大值为( )A ．23B ．33C ．43D ．5 3 答案 D解析 设△ABC 的外接圆的圆心为O ， 则圆的半径为332×12＝3，OA →＋OB →＋OC →＝0， 故PA →＋PB →＋2PC →＝4PO →＋OC →.又||4PO →＋OC→2＝51＋8PO →·OC →≤51＋24＝75， 故||PA →＋PB →＋2PC →≤53， 当PO →，OC →同向共线时取最大值．9．如图，圆O 是边长为23的等边三角形ABC 的内切圆，其与BC 边相切于点D ，点M 为圆上任意一点，BM →＝xBA →＋yBD →(x ，y ∈R )，则2x ＋y 的最大值为( )A.2B.3C ．2D ．2 2 答案 C解析 方法一 如图，连接DA ，以D 点为原点，BC 所在直线为x 轴，DA 所在直线为y 轴，建立如图所示的平面直角坐标系．设内切圆的半径为r ，则圆心为坐标(0，r )，根据三角形面积公式，得12×l △ABC ×r ＝12×AB ×AC ×sin60°(l △ABC 为△ABC 的周长)，解得r ＝1.易得B (－3，0)，C (3，0)，A (0,3)，D (0,0)， 设M (cos θ，1＋sin θ)，θ∈[0,2π)，则BM →＝(cos θ＋3，1＋sin θ)，BA →＝(3，3)，BD →＝(3，0)， 故BM →＝(cos θ＋3，1＋sin θ)＝(3x ＋3y ,3x )，故⎩⎨⎧cos θ＝3x ＋3y －3，sin θ＝3x －1，则⎩⎪⎨⎪⎧x ＝1＋sin θ3，y ＝3cos θ3－sin θ3＋23，所以2x ＋y ＝3cos θ3＋sin θ3＋43＝23sin ⎝⎛⎭⎪⎫θ＋π3＋43≤2.当θ＝π6时等号成立．故2x ＋y 的最大值为2.方法二 因为BM →＝xBA →＋yBD →，所以|BM →|2＝3(4x 2＋2xy ＋y 2)＝3[(2x ＋y )2－2xy ]． 由题意知，x ≥0，y ≥0， |BM →|的最大值为232－32＝3，又2x ＋y 24≥2xy ，即－2x ＋y 24≤－2xy ，所以3×34(2x ＋y )2≤9，得2x ＋y ≤2，当且仅当2x ＝y ＝1时取等号． 二、多项选择题10．(2020·长沙模拟)已知a ，b 是单位向量，且a ＋b ＝(1，－1)，则( ) A ．|a ＋b |＝2 B ．a 与b 垂直C ．a 与a －b 的夹角为π4D ．|a －b |＝1 答案 BC解析 |a ＋b |＝12＋－12＝2，故A 错误；因为a ，b 是单位向量，所以|a |2＋|b |2＋2a ·b ＝1＋1＋2a ·b ＝2，得a ·b ＝0，a 与b 垂直，故B 正确；|a －b |2＝a 2＋b 2－2a ·b ＝2，|a －b |＝2，故D 错误；cos 〈a ，a －b 〉＝a ·a －b |a ||a －b |＝a 2－a ·b 1×2＝22，所以a 与a －b 的夹角为π4，故C 正确． 11．设向量a ＝(k,2)，b ＝(1，－1)，则下列叙述错误的是( )A ．若k <－2，则a 与b 的夹角为钝角B ．|a |的最小值为2C ．与b 共线的单位向量只有一个为⎝ ⎛⎭⎪⎫22，－22 D ．若|a |＝2|b |，则k ＝22或－2 2 答案 CD解析 对于A 选项，若a 与b 的夹角为钝角，则a ·b <0且a 与b 不共线，则k －2<0且k ≠－2，解得k <2且k ≠－2，A 选项正确；对于B 选项，|a |＝k 2＋4≥4＝2，当且仅当k ＝0时等号成立，B 选项正确；对于C 选项，|b |＝2，与b 共线的单位向量为±b |b |，即与b 共线的单位向量为⎝⎛⎭⎪⎫22，－22或⎝ ⎛⎭⎪⎫－22，22，C 选项错误；对于D 选项，∵|a |＝2|b |＝22，∴k 2＋4＝22，解得k ＝±2，D 选项错误．12．已知△ABC 是边长为2的等边三角形，D ，E 分别是AC ，AB 上的两点，且AE →＝EB →，AD →＝2DC →，BD 与CE 交于点O ，则下列说法正确的是( )A.AB →·CE →＝－1B.OE →＋OC →＝0C ．|OA →＋OB →＋OC →|＝32D.ED →在BC →方向上的投影为76答案 BCD解析 因为AE →＝EB →，△ABC 是等边三角形，所以CE ⊥AB ，所以AB →·CE →＝0，选项A 错误；以E 为坐标原点，EA →，EC →的方向分别为x 轴，y 轴正方向建立平面直角坐标系，如图所示，所以E (0,0)，A (1,0)，B (－1,0)，C (0，3)，D ⎝ ⎛⎭⎪⎫13，233， 设O (0，y )，y ∈(0，3)，则BO →＝(1，y )，DO →＝⎝ ⎛⎭⎪⎫－13，y －233， 又BO →∥DO →，所以y －233＝－13y ，解得y ＝32， 即O 是CE 的中点，OE →＋OC →＝0，所以选项B 正确；|OA →＋OB →＋OC →|＝|2OE →＋OC →|＝|OE →|＝32， 所以选项C 正确；ED →＝⎝ ⎛⎭⎪⎫13，233，BC →＝(1，3)，ED →在BC →方向上的投影为ED →·BC →|BC →|＝13＋22＝76，所以选项D 正确． 三、填空题13．(2020·全国Ⅱ)已知单位向量a ，b 的夹角为45°，k a －b 与a 垂直，则k ＝________. 答案 22解析 由题意知(k a －b )·a ＝0，即k a 2－b ·a ＝0.因为a ，b 为单位向量，且夹角为45°，所以k ×12－1×1×22＝0，解得k ＝22. 14．在△ABC 中，AB ＝1，∠ABC ＝60°，AC →·AB →＝－1，若O 是△ABC 的重心，则BO →·AC →＝________.答案 5解析 如图所示，以B 为坐标原点，BC 所在直线为x 轴，建立平面直角坐标系．∵AB ＝1，∠ABC ＝60°，∴A ⎝ ⎛⎭⎪⎫12，32.设C (a,0)． ∵AC →·AB →＝－1，∴⎝ ⎛⎭⎪⎫a －12，－32·⎝ ⎛⎭⎪⎫－12，－32 ＝－12⎝ ⎛⎭⎪⎫a －12＋34＝－1，解得a ＝4. ∵O 是△ABC 的重心，延长BO 交AC 于点D ，∴BO →＝23BD →＝23×12()BA →＋BC → ＝13⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫12，32＋4，0＝⎝ ⎛⎭⎪⎫32，36. ∴BO →·AC →＝⎝ ⎛⎭⎪⎫32，36·⎝ ⎛⎭⎪⎫72，－32＝5. 15．(2020·石家庄模拟)在锐角三角形ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，点O为△ABC 的外接圆的圆心，A ＝π3，且AO →＝λAB →＋μAC →，则λμ的最大值为________． 答案 19解析 ∵△ABC 是锐角三角形，∴O 在△ABC 的内部，∴0<λ<1,0<μ<1.由AO →＝λ(OB →－OA →)＋μ(OC →－OA →)， 得(1－λ－μ)AO →＝λOB →＋μOC →，两边平方后得，(1－λ－μ)2AO →2＝(λOB →＋μOC →)2＝λ2OB →2＋μ2OC →2＋2λμOB →·OC →，∵A ＝π3，∴∠BOC ＝2π3，又|AO →|＝|BO →|＝|CO →|. ∴(1－λ－μ)2＝λ2＋μ2－λμ，∴1＋3λμ＝2(λ＋μ)，∵0<λ<1,0<μ<1，∴1＋3λμ≥4λμ，设λμ＝t ，∴3t 2－4t ＋1≥0，解得t ≥1(舍)或t ≤13， 即λμ≤13⇒λμ≤19，∴λμ的最大值是19.16．(2020·浙江)已知平面单位向量e 1，e 2满足|2e 1－e 2|≤2，设a ＝e 1＋e 2，b ＝3e 1＋e 2，向量a ，b 的夹角为θ，则cos 2θ的最小值是________． 答案 2829解析 设e 1＝(1,0)，e 2＝(x ，y )，则a ＝(x ＋1，y )，b ＝(x ＋3，y )．由2e 1－e 2＝(2－x ，－y )，故|2e 1－e 2|＝2－x 2＋y 2≤2，得(x －2)2＋y 2≤2.又有x 2＋y 2＝1，得(x －2)2＋1－x 2≤2，化简，得4x ≥3，即x ≥34，因此34≤x ≤1.cos 2θ＝⎝ ⎛⎭⎪⎫a ·b|a |·|b |2＝⎣⎢⎡⎦⎥⎤x ＋1x ＋3＋y 2x ＋12＋y 2x ＋32＋y 22＝⎝ ⎛⎭⎪⎫4x ＋42x ＋26x ＋102＝4x ＋12x ＋13x ＋5＝4x ＋13x ＋5＝433x ＋5－833x ＋5＝43－833x ＋5，。

浙教版九年级数学上册期末综合检测试卷一、单选题（共10题；共30分）1.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为，和，另一个三角形的最短边长为2.5 cm，则它的最长边为（）A. 3cmB. 4cmC. 4.5cmD. 5cm2.如图，点D在△ABC的边AC上，要判定△ADB与△ABC相似，添加一个条件，不正确的是（）A. ∠ABD=∠CB. ∠ADB=∠ABCC.D.3.抛物线y=3x2，y=-3x2，y= x2+3共有的性质是（）A. 开口向上B. 对称轴是y轴C. 都有最高点D. y随x值的增大而增大4.已知二次函数y=kx2-7x-7的图象与x轴有两个交点，则k的取值范围为（）A. k＞-B. k＞- 且k≠0C. k≥-D. k≥- 且k≠05.小刚身高1.7m，测得他站立在阳光下的影子长为0.85m，紧接着他把手臂竖直举起，测得影子长为1.1m，那么小刚举起的手臂超出头顶（）A. 0.5mB. 0.55mC. 0.6mD. 2.2m6.如图，在△ABC中，点D、E、F分别在边AB、AC、BC上，且DE∥BC，EF∥AB，若AD=2BD，则的值为（）A. B. C. D.7.平面直角坐标系中，O为坐标原点，点A的坐标为(，1)，将OA绕原点按逆时针方向旋转30°得OB，则点B的坐标为( )A. (1，)B. ( －1，)C. (0，2)D. (2，0)8.如图，A、B、C是⊙O上的点，若∠AOB=70°，则∠ACB的度数为（）A. 70°B. 50°C. 40°D. 35°9.两个相似三角形的相似比为2：3，它们的面积之差为25cm2，则较大三角形的面积是（）A. 75cm2B. 65cm2C. 50cm2D. 45cm210.如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，下面四个结论：①CF=2AF；②tan∠CAD=；③DF=DC；④△AEF∽△CAB；⑤ S四边形CDEF=S△ABF ,其中正确的结论有（）A. 2个B. 3个C. 4个D. 5个二、填空题（共10题；共30分）11.如图，锐角三角形ABC的边AB和AC上的高线CE和BF相交于点D．请写出图中的一对相似三角形，如________．12. 如图24-1-4-5，OB、OC是⊙O的半径，A是⊙O上一点，若已知∠B=20°，∠C=30°，则∠A=________.13.如图，△AOB三个顶点的坐标分别为A（8，0），O（0，0），B（8，﹣6），点M为OB的中点．以点O为位似中心，把△AOB缩小为原来的，得到△A′O′B′，点M′为O′B′的中点，则MM′的长为________．14.已知二次函数y＝ax2＋bx＋c的部分图像如图所示，则关于x的方程ax2＋bx＋c＝0的两个根的和等于________．15.如图，点G是△ABC的重心，连结AG并延长交BC于点D，过点G作EF∥AB交BC于E，交AC于F．若AB=12，那么EF=________．16.某种商品每件的进价为30元，在某段时间内若以每件x元出售，可卖出（100﹣x）件，则将每件的销售价定为________ 元时，可获得最大利润．17.如图，抛物线y=ax2+bx+c（a，b，c是常数，a≠0）与x轴交于A，B两点，顶点P（m，n）．给出下列结论：①2a+c＜0；②若（﹣，y1），（﹣，y2），（，y3）在抛物线上，则y1＞y2＞y3；③关于x的方程ax2+bx+k=0有实数解，则k＞c﹣n；④当n=﹣时，△ABP为等腰直角三角形．其中正确结论是________（填写序号）．18.如果2+ 是方程的一个根，那么c的值是________.19.如图，在直角坐标系中，点Ａ在y轴上，△OAB是等腰直角三角形，斜边OA=2，将△OAB绕点O逆时针旋转90°得△′′，则点′的坐标为________20.如图，△ABC中，已知∠C=90°，∠B=55°，点D在边BC上，BD=2CD．把△ABC绕着点D逆时针旋转m （0＜m＜180）度后，如果点B恰好落在初始Rt△ABC的边上，那么m=________ ．三、解答题（共8题；共60分）21.如图，已知△ABC三个顶点的坐标分别是A（-2,3），B（-3，-1），C（-1,1）（1）画出△ABC绕点O逆时针旋转90°后的△A1B1C1，并写出点A1的坐标；（2）画出△ABC绕点O逆时针旋转180°后的△A2B2C2，并写出点A2的坐标；（3）直接回答：∠AOB与∠A2OB2有什么关系？22.已知：如图所示，AD=BC。

人教版数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________ 一．选择题(共10小题)1.12-的相反数是( )A. B. 2 C.12- D.122. 中国是一个干旱缺水严重的国家，淡水资源总量约为28000亿立方米，约占全球水资源的6%．将28000用科学记数法表示为()A. 28×103B. 2.8×104C. 2.8×105D. 0.28×1063. 下列各运算中，计算正确的是()A. 4a2﹣2a2=2B. (a2)3=a5C. a3•a6=a9D. (3a)2=6a24.下列四个图形中，既是轴对称图形又是中心对称图形的是( )A. B. C. D.5. 如图所示的图形是由7个完全相同的小正方体组成的立体图形，则下面四个平面图形中不是这个立体图形的三视图的是( )A. B. C. D.6.下面是扬帆中学九年八班43名同学家庭人口统计表：这43个家庭人口的众数和中位数分别是( )家庭人口数(人) 2 3 4 5 6学生人数(人) 3 15 10 8 7A. 5，6B. 3，4C. 3，5D. 4，67.如图，直线a与直线b交于点A，与直线c交于点B，∠1=120°，∠2=45°，若使直线b与直线c平行，则可将直线b 绕点A 逆时针旋转( )A. 15°B. 30°C. 45°D. 60°8. 圆心角为120°，弧长为12π的扇形半径为( )A 6 B. 9 C. 18 D. 369.在同一直角坐标系中，函数y ＝kx +1与y ＝﹣k x(k ≠0)的图象大致是( ) A. B.C. D.10.如图，在ABC 中，点D E F 、、分别在AB AC BC 、、边上，连接DE EF 、，若//,//DE BC EF AB ，则下列结论错误的是( )A. AE BF EC FC =B. AD AB BF BC =C. EF DE AB BC =D. CE EA CF BF= 二．填空题(共10小题)11.计算：6826)＝_____．12.在函数y＝34xx--中，自变量x取值范围是___________．13.在平面直角坐标系中，已知一次函数y＝2x+1图象经过P1(x1，y1)、P2(x2，y2)两点，若x1＜x2，则y1_____y2．(填”＞”“＜”或”＝”)14.小明把如图所示的矩形纸板挂在墙上，玩飞镖游戏(每次飞镖均落在纸板上)，则飞镖落在阴影区域的概率是．15.分式方程12x xx x-=+的解为x=_______．16.如图，AB是⊙O的直径，AB＝6，BD、CD分别是过⊙O上点B、C的切线，且∠BDC＝120°，连接AC，则AC＝_____．17.如图，在平面直角坐标系xOy中，已知点M0的坐标为(1，0)，将线段OM0绕原点O逆时针方向旋转45°，再将其延长到M1，使得M1M0⊥OM0，得到线段OM1;又将线段OM1绕原点O逆时针方向旋转45°，再将其延长到M2，使得M2M1⊥OM1，得到线段OM2;如此下去，得到线段OM3，OM4，OM5，…根据以上规律，请直接写出OM2014的长度为_______．18.如图，正方形ABCD的边长为3cm，E为CD边上一点，∠DAE＝30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q．若PQ＝AE，则AP等于_____cm．19.如图，矩形ABCD中，点E，F分别在AD，BC上，且AE＝DE，BC＝3BF，连接EF，将矩形ABCD沿EF折叠，点A恰好落在BC边上的点G处，则cos∠EGF的值为_____．20.如图，在Rt△ABC中，∠ACB＝90°，点D在AC上，DE⊥AB于点E，且CD＝DE．点F在BC上，连接EF，AF，若∠CEF＝45°，∠B＝2∠CAF，BF＝2，则AB的长为_____．三．解答题(共7小题)21.先化简，再求代数式(1﹣25 4a-)223aa a+⋅-的值，其中a＝2tan45°﹣cos60°．22.如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABC的三个顶点A、B、C都在格点上，将△ABC绕点A按顺时针方向旋转90°得到△AB'C'．(1)在正方形网格中，画出△AB'C';(2)计算线段AB在旋转过程中所扫过的面积．23.某中学开展以”我最喜欢的职业”为主题的调查活动，通过对学生的随机抽样调查得到一组数据，如图是根据这组数据绘制成的不完整统计图．(1)把折线统计图补充完整;(2)求出扇形统计图中，公务员部分对应的圆心角的度数;(3)若从被调查的学生中任意抽取一名，求取出的这名学生最喜欢的职业是”教师”的概率．24.如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，连接AD，E为AD的中点，过A作AF∥BC交BE 延长线于F，连接CF．(1)求证：四边形ADCF是菱形;(2)在不添加任何辅助线的情况下，请直接写出与△ACD面积相等的三角形(不包含△ACD)．25.某水果商贩用600元购进了一批水果，上市后销售非常好，商贩又用1400元购进第二批这种水果，所购水果数量是第一批购进数量的2倍，但每箱进价多了5元．(1)求该商贩第一批购进水果每箱多少元;(2)由于储存不当，第二批购进的水果中有10%腐坏，不能售卖，该商贩将两批水果按同一价格全部销售完毕后获利不低于800元，求每箱水果的售价至少是多少元?26.已知：点A，B，C都在⊙O上，连接AB，AC，点D，E分别在AC，AB上，连接CE并延长交⊙O于点F，连接BD，BF，∠BDC﹣∠BFC＝2∠ABF．(1)如图1，求证：∠ABD＝2∠ACF;(2)如图2，CE交BD于点G，过点G作GM⊥AC于点M，若AM＝MD，求证：AE＝GD;(3)如图3，在(2)的条件下，当AE：BE＝8：7时，连接DE，且∠ADE＝30°．延长BD交⊙O于点H，连接AH，AH＝83，求⊙O的半径．27.如图，在平面直角坐标系中，点O为坐标原点，直线y＝﹣x+b交y轴于点A，交x轴于点B，S△AOB＝81 2．(1)求b的值;(2)点C以每秒1个单位长度速度从O点出发沿x轴向点B运动，点D以每秒2个单位长度的速度从A点出发沿y轴向点O运动，C，D两点同时出发，当点D运动到点O时，C，D两点同时停止运动．连接CD，设点C的运动时间为t秒，△CDO的面积为S，求S与t的函数关系式(不要求写出自变量t的取值范围);(3)在(2)条件下，过点C作CE⊥CD交AB于点E，过点D作DF∥x轴交AB于点F，过点F作FH⊥CE，垂足为H．在CH上取点M，使得MH：HE＝8：33，连接FM，若∠FMH＝32∠FEH，求t的值．答案与解析一．选择题(共10小题)1.12-的相反数是( )A. B. 2 C.12- D.12【答案】D 【解析】【详解】因为-12+12＝0，所以-12的相反数是12.故选D.2. 中国是一个干旱缺水严重的国家，淡水资源总量约为28000亿立方米，约占全球水资源的6%．将28000用科学记数法表示为()A. 28×103B. 2.8×104C. 2.8×105D. 0.28×106【答案】B【解析】【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数;当原数的绝对值＜1时，n是负数．【详解】解：28000=2.8×104，故选B．考点：科学记数法——表示较大的数.3. 下列各运算中，计算正确的是( )A. 4a2﹣2a2=2B. (a2)3=a5C. a3•a6=a9D. (3a)2=6a2【答案】C【解析】【详解】试题分析：A、合并同类项，系数相加字母部分不变，故A错误;B、幂的乘方，底数不变指数相乘，故B错误;C、同底数幂相乘，底数不变指数相加，故C正确;D、3的平方是9，故D错误;故选C．考点：1、幂的乘方与积的乘方;2、合并同类项;3、同底数幂的乘法．4.下列四个图形中，既是轴对称图形又是中心对称图形的是( )A. B. C. D.【答案】C【解析】【分析】根据轴对称图形与中心对称图形的概念求解．【详解】A选项：不是轴对称图形，是中心对称图形，故错误;B选项：不是轴对称图形，是中心对称图形．故错误;C选项：是轴对称图形，也是中心对称图形．故正确;D选项：不是轴对称图形，是中心对称图形．故错误;故选C.【点睛】考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．5. 如图所示的图形是由7个完全相同的小正方体组成的立体图形，则下面四个平面图形中不是这个立体图形的三视图的是( )A. B. C. D.【答案】B【解析】【详解】试题分析：根据立方体的组成，结合三视图的观察角度，可得出：A、是几何体的左视图，故此选项错误;B、不是几何体的三视图，故此选项正确;C、是几何体的主视图，故此选项错误;D、是几何体的俯视图，故此选项错误．故选B．考点：简单组合体的三视图．6.下面是扬帆中学九年八班43名同学家庭人口的统计表：这43个家庭人口的众数和中位数分别是( ) 家庭人口数(人) 2 3 4 5 6学生人数(人) 3 15 10 8 7A. 5，6B. 3，4C. 3，5D. 4，6【答案】B【解析】【分析】根据众数和中位数的概念求解可得．【详解】解：这43个家庭人口的众数3，将家庭人口数从小到大排列后,第22个数为4,即中位数为4，故选：B．【点睛】此题考查的是求众数和中位数，掌握众数和中位数的概念是解决此题的关键．7.如图，直线a与直线b交于点A，与直线c交于点B，∠1=120°，∠2=45°，若使直线b与直线c平行，则可将直线b绕点A逆时针旋转( )A. 15°B. 30°C. 45°D. 60°【答案】A【解析】试题分析：先根据邻补角的定义得到∠3=60°，根据平行线的判定当b与a的夹角为45°时，b∥c，由此得到直线b绕点A逆时针旋转60°﹣45°=15°．解：∵∠1=120°，∴∠3=60°，∵∠2=45°，∴当∠3=∠2=45°时，b ∥c ，∴直线b 绕点A 逆时针旋转60°﹣45°=15°．故选A ．点评：本题考查了平行线的判定：同位角相等，两直线平行;内错角相等，两直线平行;同旁内角互补，两直线平行;两条直线都和第三条直线平行，那么这两条直线平行．8. 圆心角为120°，弧长为12π的扇形半径为( )A. 6B. 9C. 18D. 36 【答案】C【解析】 试题分析：直接根据弧长的公式180n r l π=列式求解： 设该扇形的半径是r ， ∵n=120°，l=12π，∴1201218180r r ππ=⇒= ．故选C ．考点：弧长的计算．9.在同一直角坐标系中，函数y ＝kx +1与y ＝﹣k x(k ≠0)的图象大致是( ) A. B.C. D.【答案】D【解析】【分析】先根据一次函数图象与系数的关系得到k 的范围，然后根据k 的范围判断反比例函数图象的位置，逐一判断即可．【详解】解：A 、对于y ＝kx +1经过第一、三象限，则k ＞0，﹣k ＜0，所以反比例函数图象应该分布在第二、四象限，所以A 选项错误;B 、一次函数y ＝kx +1与y 轴的交点在x 轴上方，所以B 选项错误;C 、对于y ＝kx +1经过第二、四象限，则k ＜0，﹣k ＞0，所以反比例函数图象应该分布在第一、三象限，所以C 选项错误;D 、对于y ＝kx +1经过第二、四象限，则k ＜0，﹣k ＞0，所以反比例函数图象应该分布在第一、三象限，所以D 选项正确．故选：D ．【点睛】此题考查的是反比例函数和一次函数的综合题型，掌握一次函数的图象及性质和反比例函数的图象及性质是解决此题的关键．10.如图，在ABC 中，点D E F 、、分别在AB AC BC 、、边上，连接DE EF 、，若//,//DE BC EF AB ，则下列结论错误的是( )A. AE BF EC FC =B. AD AB BF BC =C. EF DE AB BC =D. CE EA CF BF= 【答案】C【解析】【分析】根据平行线分线段成比例定理分别对每一项进行判断即可．【详解】解：A ．∵EF ∥AB ，∴AE BF EC FC=，故本选项正确; B ．∵DE ∥BC ，∴AD DE AB BC=，∵EF∥AB，∴四边形BDEF是平行四边形，∴DE＝BF，∴AD BF AB BC=，∴AD ABBF BC=，故本选项正确;C．∵EF∥AB，∴EF CF AB BC=，∵CF和DE的大小关系不能确定，∴EF DEAB BC≠，故本选项错误;D．∵EF∥AB，∴CE CF EA BF=，∴CE EACF BF=，故本选项正确，故选：C．【点睛】此题主要考查平行线分线段成比例定理，关键是根据平行线分线段成比例定理列出比例式并能进行灵活变形．二．填空题(共10小题)11.计算：)＝_____．【答案】-2【解析】【分析】利用平方差公式和二次根式的乘法公式计算．【详解】解：原式＝﹣2)＝6﹣8＝﹣2．故答案为﹣2．【点睛】此题考查的是二次根式的运算，掌握平方差公式和二次根式的乘法公式是解决此题的关键．12.在函数y＝34xx--中，自变量x的取值范围是___________．【答案】x≥3且x≠4．【解析】【详解】试题解析：根据题意知：30 {40 xx-≥-≠解得：x≥3且x≠4故答案为：x≥3且x≠4．【点睛】本题考查了函数自变量的取值范围，函数自变量的范围一般从三个方面考虑：当函数表达式是整式时，自变量可取全体实数;当函数表达式是分式时，考虑分式的分母不能为0;当函数表达式是二次根式时，被开方数非负．13.在平面直角坐标系中，已知一次函数y＝2x+1的图象经过P1(x1，y1)、P2(x2，y2)两点，若x1＜x2，则y1_____y2．(填”＞”“＜”或”＝”)【答案】＜【解析】【分析】根据一次函数的性质，当k＞0时，y随x的增大而增大，然后根据横坐标的大小关系即可求出结论．【详解】解：∵一次函数y＝2x+1中k＝2＞0，∴y随x的增大而增大，∵x1＜x2，∴y1＜y2．故答案为：＜．【点睛】此题考查的是一次函数增减性的应用，掌握一次函数增减性与k的符号关系是解决此题的关键．14.小明把如图所示的矩形纸板挂在墙上，玩飞镖游戏(每次飞镖均落在纸板上)，则飞镖落在阴影区域的概率是．【答案】14．【解析】分析】根据概率的求法，找准两点：①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率．【详解】如图，根据矩形的性质易证矩形的对角线把矩形分成的四个三角形均为同底等高的三角形，故其面积相等，根据平行线的性质易证S1=S2，故阴影部分的面积占一份，故针头扎在阴影区域的概率为14．15.分式方程12x xx x-=+的解为x=_______．【答案】2．【解析】【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【详解】解：去分母得：x2=x2﹣x+2x﹣2，解得：x=2，经检验x=2是分式方程的解．故答案为：2．【点睛】本题考查解分式方程．16.如图，AB是⊙O的直径，AB＝6，BD、CD分别是过⊙O上点B、C的切线，且∠BDC＝120°，连接AC，则AC＝_____．【答案】3【解析】【分析】连接OC，BC．只要证明∠A＝30°，根据AC＝AB•cos30°计算即可．【详解】解：连接OC，BC．∵BD，CD分别是过⊙O上点B，C的切线，∴OC⊥CD，OB⊥BD，∴∠OCD＝∠OBD＝90°，∵∠BDC＝120°，∴∠BOC＝360°﹣∠OCD﹣∠BDC﹣∠OBD＝60°，∴∠A＝12∠BOC＝30°，∵AB是直径，∴∠ACB＝90°，∴AC＝AB•cos30°＝33故答案为：33．【点睛】此题考查的是切线的性质、四边形的内角和、圆周角定理及推论和锐角三角函数，掌握是切线的性质、四边形的内角和、圆周角定理及推论和锐角三角函数是解决此题的关键．17.如图，在平面直角坐标系xOy中，已知点M0的坐标为(1，0)，将线段OM0绕原点O逆时针方向旋转45°，再将其延长到M1，使得M1M0⊥OM0，得到线段OM1;又将线段OM1绕原点O逆时针方向旋转45°，再将其延长到M2，使得M2M1⊥OM1，得到线段OM2;如此下去，得到线段OM3，OM4，OM5，…根据以上规律，请直接写出OM2014的长度为_______．【答案】21007．【解析】【分析】根据点M0的坐标求出OM0，然后判断出△OM0M1是等腰直角三角形，然后根据等腰直角三角形的性质求出OM1，同理求出OM2，OM3，然后根据规律写出OM2014即可．【详解】解：∵点M0的坐标为(1，0)，∴OM0=1．∵线段OM0绕原点O逆时针方向旋转45°，M1M0⊥OM0，∴△OM0M1是等腰直角三角形．∴OM1=2OM0=2，同理，OM2=2OM1=(2)2，OM3=2OM2=(2)3，…，OM2014=2OM2013=(2)2014=21007．故答案为：21007．【点睛】本题考查探索规律题(图形的变化类);点的坐标;旋转的性质;等腰直角三角形的判定和性质．18.如图，正方形ABCD的边长为3cm，E为CD边上一点，∠DAE＝30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q．若PQ＝AE，则AP等于_____cm．【答案】1或2．【解析】【详解】解：根据题意画出图形，过P作PN⊥BC，交BC于点N，∵四边形ABCD为正方形，∴AD=DC=PN，在Rt△ADE中，∠DAE=30°，AD=3cm，∴tan30°=DEAD，即3cm，根据勾股定理得：223(3)23cm，∵M为AE的中点，∴3cm在Rt△ADE和Rt△PNQ中，AD=PN，AE=PQ，∴Rt△ADE≌Rt△PNQ(HL)，∴DE=NQ，∠DAE=∠NPQ=30°，∵PN∥DC，∴∠PFA=∠DEA=60°，∴∠PMF=90°，即PM⊥AF，在Rt△AMP中，∠MAP=30°，cos30°=AM AP，∴AP=2cm;由对称性得到AP′=DP=AD-AP=3-2=1cm，综上，AP等于1cm或2cm．故答案为：1或2【点睛】本题考查全等三角形的判定与性质;正方形的性质;锐角三角函数．19.如图，矩形ABCD中，点E，F分别在AD，BC上，且AE＝DE，BC＝3BF，连接EF，将矩形ABCD沿EF折叠，点A恰好落在BC边上的点G处，则cos∠EGF的值为_____．【答案】2 3【解析】【分析】连接AF，由矩形的性质得AD∥BC，AD＝BC，由平行线的性质得∠AEF＝∠GFE，由折叠的性质得∠AFE ＝∠GFE，AF＝FG，推出∠AEF＝∠AFE，则AF＝AE，AE＝FG，得出四边形AFGE是菱形，则AF∥EG，得出∠EGF＝∠AFB，设BF＝2x，则AD＝BC＝6x，AF＝AE＝FG＝3x，在Rt△ABF中，cos∠AFB＝BF AF＝23，即可得出结果．【详解】解：连接AF，如图所示：∵四边形ABCD为矩形，∴AD∥BC，AD＝BC，∴∠AEF＝∠GFE，由折叠的性质可知：∠AFE＝∠GFE，AF＝FG，∴∠AEF＝∠AFE，∴AF＝AE，∴AE＝FG，∴四边形AFGE是菱形，∴AF∥EG，∴∠EGF＝∠AFB，设BF＝2x，则AD＝BC＝6x，AF＝AE＝FG＝3x，在Rt△ABF中，cos∠AFB＝BFAF＝23xx＝23，∴cos∠EGF＝23，故答案为：23．【点睛】此题考查的是矩形与折叠问题、菱形的判定及性质、等腰三角形的性质和锐角三角函数，掌握矩形的性质、折叠的性质、菱形的判定及性质、等角对等边和等角的锐角三角函数值相等是解决此题的关键．20.如图，在Rt△ABC中，∠ACB＝90°，点D在AC上，DE⊥AB于点E，且CD＝DE．点F在BC上，连接EF，AF，若∠CEF＝45°，∠B＝2∠CAF，BF＝2，则AB的长为_____．【答案】10【解析】分析】以AC为轴将△ACF翻至△ACK，在AB边上截取BL＝BF＝2，设CF＝x，则EL＝CK＝x，分别用含x的式子表示出Rt△ABC中的三边长，根据勾股定理列方程，解得x值，则可得答案．【详解】解：如图，以AC为轴将△ACF翻至△ACK，在AB边上截取BL＝BF＝2∵∠ACB＝90°，DE⊥AB∴∠BCE+∠DCE＝90°，∠BEC+∠DEC＝90°∵CD＝DE∴∠DCE＝∠DEC∴∠BCE＝∠BEC∴BC＝BE∵BF=BL=2∴EL=CF设CF＝x，则EL＝CK＝x∴BK＝2x+2，BC＝BE＝x+2设∠B＝2∠CAF＝2α则∠CAK＝α，∠K＝90°﹣α∴∠KAB＝180°﹣2α﹣(90°﹣α)＝90°﹣α∴∠K＝∠KAB∴BA＝BK＝2x+2在△CBL和△EBF中CB EB B B BL BF =⎧⎪∠=∠⎨⎪=⎩∴△CBL ≌△EBF (SAS )∴∠BCL ＝∠BEF又∵∠CEF ＝45°，∠BCE ＝∠BEC∴∠ECL ＝∠CEF ＝45°∴∠ALC ＝180°﹣45°﹣45°﹣∠BEF ＝90°﹣∠BEF∵∠ACL ＝90°﹣∠BCL ，∠BCL ＝∠BEF∴∠ALC ＝∠ACL∴AC ＝AL ＝2x在Rt △ABC 中，由勾股定理得：(x +2)2+(2x )2＝(2x +2)2解得x ＝4或x ＝0(舍)∴AB ＝10故答案为：10．【点睛】此题考查的是等腰三角形的判定及性质、全等三角形的判定及性质和勾股定理，掌握等角对等边、等边对等角、全等三角形的判定及性质和勾股定理是解决此题的关键．三．解答题(共7小题)21.先化简，再求代数式(1﹣254a -)223a a a+⋅-的值，其中a ＝2tan45°﹣cos60°． 【答案】3(2)a a a +-，-6 【解析】【分析】 根据特殊角的锐角三角函数值求出a 的值，然后根据分式的运算法则化简，代入即可求出答案．【详解】解：a ＝2×1﹣12＝32∴原式＝22924(3)-+•--a a a a a ＝(3)(3)2(2)(2)(3)+-+•-+-a a a a a a a＝3 (2) aa a+-将32a=代入，得原式＝33233222+⎛⎫⨯-⎪⎝⎭＝﹣6．【点睛】此题考查的是分式的化简求值题和特殊角的锐角三角函数值，掌握分式的各个运算法则和特殊角的锐角三角函数值是解决此题的关键．22.如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ABC的三个顶点A、B、C都在格点上，将△ABC绕点A按顺时针方向旋转90°得到△AB'C'．(1)在正方形网格中，画出△AB'C';(2)计算线段AB在旋转过程中所扫过的面积．【答案】(1)画图见解析;(2)面积为254π．【解析】试题分析：(1)根据旋转性质得出对应点旋转后位置进而得出答案;(2)利用勾股定理得出AB=5，再利用扇形面积公式求出即可．解：(1)如图所示：△AB′C′即为所求;(2)∵AB==5，∴线段AB在变换到AB′的过程中扫过区域的面积为：=π．考点：作图-旋转变换;扇形面积的计算．23.某中学开展以”我最喜欢的职业”为主题的调查活动，通过对学生的随机抽样调查得到一组数据，如图是根据这组数据绘制成的不完整统计图．(1)把折线统计图补充完整;(2)求出扇形统计图中，公务员部分对应的圆心角的度数;(3)若从被调查的学生中任意抽取一名，求取出的这名学生最喜欢的职业是”教师”的概率．【答案】(1)见解析;(2)72°;(3)1 5【解析】【分析】(1)根据军人的人数与所占的百分比求出调查总人数，再分别求出教师、医生的人数，补全统计图即可;(2)根据公务员的人数占总人数的比例再乘360°即可得出结论;(3)根据教师的人数占总人数的比例即可得出结论．【详解】解：(1)∵军人的人数为20，百分比为10%，∴学生总人数为20÷10%＝200(人);∵医生的人数占15%，∴医生的人数为：200×15%＝30(人)，∴教师的人数为：200﹣30﹣40﹣20﹣70＝40(人)，∴折线统计图如图所示;(2)∵由扇形统计图可知，公务员占20%，∴20%×360°＝72°;(3)∵最喜欢的职业是”教师”的人数是40人，∴从被调查的学生中任意抽取一名，求抽取的这名学生最喜欢的职业是”教师”的概率＝40200＝15．【点睛】此题考查的是折线统计图、扇形统计图和求概率问题，结合折线统计图、扇形统计图得出有用信息和掌握概率公式是解决此题的关键．24.如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，连接AD，E为AD的中点，过A作AF∥BC交BE 延长线于F，连接CF．(1)求证：四边形ADCF是菱形;(2)在不添加任何辅助线的情况下，请直接写出与△ACD面积相等的三角形(不包含△ACD)．【答案】(1)见解析;(2)与△ACD面积相等的三角形有：△ABD，△ACF，△AFB【解析】【分析】(1)首先由E是AD的中点，AF∥BC，易证得△AFE≌△DBE，即可得AF＝BD，又由在Rt△ABC中，∠BAC ＝90°，D是BC的中点，可得AD＝BD＝CD＝AF，证得四边形ADCF是平行四边形，继而判定四边形ADCF 是菱形;(2)根据平行线之间的距离处处相等、等高模型和菱形的性质即可解决问题;【详解】(1)证明：如图，∵AF∥BC，∴∠AFE＝∠DBE，∵E 是AD 的中点，AD 是BC 边上的中线，∴AE ＝DE ，BD ＝CD ，在△AFE 和△DBE 中，AFE DBE FEA BED AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AFE ≌△DBE (AAS );∴AF ＝DB ．∵DB ＝DC ，∴AF ＝CD ，∴四边形ADCF 是平行四边形，∵∠BAC ＝90°，D 是BC 的中点，∴AD ＝DC ＝12BC ， ∴四边形ADCF 是菱形;(2)∵BD=CD ，而△ABD 的边BD 上的高即为△ACD 的边CD 上的高∴S △ACD =S △ABD ;∵四边形ADCF 是菱形∴S △ACD =S △ACF ;∵AF ∥CD∴△ACD 的边CD 上的高等于△BAF 的边AF 上的高∵AF=CD∴S △ACD =S △AFB综上：与△ACD 面积相等的三角形有：△ABD ，△ACF ，△AFB ．【点睛】此题考查的是全等三角形的判定及性质、菱形的判定及性质、直角三角形的性质和三角形的面积，掌握全等三角形的判定及性质、菱形的判定及性质、直角三角形斜边上的中线等于斜边的一半和平行线之间的距离处处相等是解决此题的关键．25.某水果商贩用600元购进了一批水果，上市后销售非常好，商贩又用1400元购进第二批这种水果，所购水果数量是第一批购进数量的2倍，但每箱进价多了5元．(1)求该商贩第一批购进水果每箱多少元;(2)由于储存不当，第二批购进的水果中有10%腐坏，不能售卖，该商贩将两批水果按同一价格全部销售完毕后获利不低于800元，求每箱水果的售价至少是多少元?【答案】(1)每箱30元;(2)至少为50元【解析】【分析】(1)设该商场第一批购进了这种水果x箱，则第二批购进这种水果2x箱，根据关键语句”每个进价多了5元”可得方程140060052-=x x，解方程即可;(2)设水果的售价为y元，根据题意可得不等关系：水果的总售价﹣成本﹣损耗≥利润，由不等关系列出不等式即可．【详解】解：(1)设该商场第一批购进了这种水果x箱，则第二批购进这种水果2x箱，可得：14006005 2-=x x，解得：x＝20，经检验：x＝20是原分式方程的解，6003020=元，答：该商贩第一批购进水果每箱30元;(2)这两批水果共有20＋2×20=60箱设水果的售价为y元，根据题意得：60y﹣(600+1400)﹣2×20×10%y≥800，解得：y≥50，则水果的售价为50元．答：水果的售价至少为50元．【点睛】此题考查的是分式方程的应用和一元一次不等式的应用，掌握实际问题中的等量关系和不等关系是解决此题的关键．26.已知：点A，B，C都在⊙O上，连接AB，AC，点D，E分别在AC，AB上，连接CE并延长交⊙O于点F，连接BD，BF，∠BDC﹣∠BFC＝2∠ABF．(1)如图1，求证：∠ABD＝2∠ACF;(2)如图2，CE交BD于点G，过点G作GM⊥AC于点M，若AM＝MD，求证：AE＝GD;(3)如图3，在(2)的条件下，当AE：BE＝8：7时，连接DE，且∠ADE＝30°．延长BD交⊙O于点H，连接AH，AH＝3，求⊙O的半径．【答案】(1)见解析;(2)见解析;(3)13【解析】【分析】(1)注意到同弧所对的圆周角相等以及∠BDC是△ABD的外角，结合题中所告诉的角度等式进行代换变形即可得结论;(2)连接AG，设∠CGD＝∠BGE＝β，∠ACF＝α，然后推出∠AEG＝∠AGE，再根据等角对等边即可证出结论;(3)首先注意到特殊角∠ADE＝30°，于是作AP⊥DE于P，由HL定理可得△AEP≌△AGM，进而推出△AEG 是等边三角形，设AE＝8k，BE＝7k，作GN⊥AE于N，解△BGN可得sin∠ABG的值，而∠ABG是圆周角且所对的弦为AH，于是连接AO并延长交圆O于Q，连接HQ，sin∠AQH＝sin∠ABG＝AHAQ，而AH已知，从而求出直径AQ，半径也就自然知道了．【详解】解：(1)∵∠BDC＝∠ABD+∠BAC，∠BDC﹣∠BFC＝2∠ABF，∴∠ABD+∠BAC﹣∠BFC＝2∠ABF，∵∠ABF＝∠ACF，∠BFC＝∠BAC，∴∠ABD+∠BFC﹣∠BFC＝2∠ACF，∴∠ABD＝2∠ACF．(2)如图2，连接AG．设∠CGD＝∠BGE＝β，∠ACF＝α，则∠ABD＝2α，∠AEG＝∠ABD+∠BGE＝2α+β，∠GDA＝∠CGD+∠ACF＝α+β，∵GM⊥AD于M且AM＝DM，∴AG＝DG，∴∠GAD＝∠GDA＝α+β，∴∠AGE＝∠GAD+∠ACF＝α+β+α＝2α+β，∴∠AGE＝∠AEG，∴AE＝AG＝GD．(3)如图3，连接AG，作AP⊥DE于P，∵∠ADE＝30°，∴∠P AD＝60°，AP＝12 AD，∵GM⊥AD，∴∠AMG＝∠APE＝90°，∵AM＝MD，∴AM＝12AD＝AP，由(2)可知AE ＝AG ，在Rt △AEP 和Rt △AGM 中：AE AG AP AM=⎧⎨=⎩ ∴Rt △AEP ≌Rt △AGM (HL )，∴∠EAP ＝∠GAM ，∵∠GAM +∠P AG ＝∠P AD ＝60°，∴∠EAP +∠P AG ＝∠EAG ＝60°，∴△AEG 是等边三角形，∴EG ＝AE ＝AG ＝DG ，∵AE ：BE ＝8：7，∴设AE ＝8k ，BE ＝7k ，作GN ⊥AE 于N ，AN ＝EN ＝4k ，NG ＝，∴BN ＝BE +EN ＝11k ，∴BG 13k ，∴sin ∠ABG ＝NG BG ＝13， 连接AO 并延长交圆O 于Q ，连接HQ ，则AQ 直径，∠AHQ ＝90°，∴sin ∠AQH ＝AH AQ，∵∠AQH ＝∠ABG ，AH ＝∴AQ ＝26，∴AO ＝12A Q ＝13， 即⊙O 的半径为13．【点睛】此题考查的是圆周角定理及推论、三角形外角的性质、垂直平分线的性质、等腰三角形的判定及性质、直角三角形的性质、全等三角形的判定及性质和锐角三角函数，此题难度较大，掌握是圆周角定理及推论、三角形外角的性质、垂直平分线的性质、等腰三角形的判定及性质、直角三角形的性质、全等三角形的判定及性质和锐角三角函数是解决此题的关键．27.如图，在平面直角坐标系中，点O为坐标原点，直线y＝﹣x+b交y轴于点A，交x轴于点B，S△AOB＝81 2．(1)求b的值;(2)点C以每秒1个单位长度的速度从O点出发沿x轴向点B运动，点D以每秒2个单位长度的速度从A 点出发沿y轴向点O运动，C，D两点同时出发，当点D运动到点O时，C，D两点同时停止运动．连接CD，设点C的运动时间为t秒，△CDO的面积为S，求S与t的函数关系式(不要求写出自变量t的取值范围);(3)在(2)条件下，过点C作CE⊥CD交AB于点E，过点D作DF∥x轴交AB于点F，过点F作FH⊥CE，垂足为H．在CH上取点M，使得MH：HE＝8：33，连接FM，若∠FMH＝32∠FEH，求t的值．【答案】(1)b＝9;(2)S＝﹣t2+92t;(3)t＝1【解析】【分析】(1)由直线解析式可得A、B两点坐标，根据△AOB的面积列方程解出b的值．(2)分别用t表示OC和OD的长即可得到S与t的表达式．(3)首先根据题意画出示意图，然后根据所给定的线段等量关系与角度等量关系推导出∠FEM的正切值，过点E作GP⊥OB于P交DF的延长线于点G，可以推证∠DEG＝∠FEM，于是利用∠DEG的正切值列出比例方程，最后解出t的值．【详解】解：(1)如图1，∵直线y＝﹣x+b交y轴于点A，交x轴于点B，∴A (0，b )，B (b ，0)∴OA ＝OB ＝b ，∴S △AOB ＝212b ＝812． ∴b ＝9或-9(不符合与y 轴的交点，舍去负值)．(2)如图2，由题意知OC ＝t ，AD ＝2t ，则OD ＝OA ﹣AD ＝9﹣2t ， ∴S ＝12OD •OC ＝12t (9﹣2t )＝﹣t 2+92t ． (3)∵MH HE ＝833， ∴设MH ＝8k ，HE ＝33k ，如图3，在HE 上截取HN ＝MH ＝8k ，连接FN ，则EN ＝EH ﹣HN ＝25k ，∵FH ⊥CE 于H ，∴FM ＝FN ，∠FME ＝∠FNM ，∵∠FME ＝32∠FEM ， ∴设∠FEM ＝2α，∠FME ＝3α，∴∠FNM＝3α，∵∠FNM＝∠NFE+∠FEN，∴∠NFE＝∠FNM﹣∠FEM＝3α﹣2α＝α，在FE上取一点Q，连接NQ，使NQ＝NE＝25k，则∠NQE＝∠FEM＝2α，∵∠NQE＝∠NFE+∠QNF＝α+∠QNF，∴∠QNF＝α＝∠NFE，∴FQ＝NQ＝25k，作NR⊥QE于R，则QR＝RE＝n，∴FE＝FQ+QE＝25k+2n，∵cos∠FEH＝cos2α＝HEFE＝REEN，∴33252+kk n＝25nk，解得n＝15k，∴QR＝RE＝15k，∴NR20k，∴tan2α＝NRRE＝43．过点E作GP⊥OB于P交DF的延长线于点G，∴∠CPE＝∠BPE＝90°，∵OA＝OB＝9，∴∠OAB＝∠OBA＝45°，∴∠PEB＝45°，∴BP＝PE，∵DF∥OB，∴∠ODF＝∠ADF＝90°，∴四边形DOPG为矩形，∴GP＝OD，DG＝OP，作CT⊥OB交AB于T，交DF于K，连接DT，则ODKC 为矩形，△CTB 为等腰直角三角形，∴DK ＝OC ＝t ，CK ＝OD ，CT ＝CB ，∵∠FDA ＝90°，∠F AF ＝45°，∴△ADF 为等腰直角三角形，∴DF ＝AD ＝2OC ＝2t ，∴KDF 中点，∴T 为AF 中点，∴△DTF 为等腰直角三角形，∴∠DTK ＝∠FTK ＝45°，∵DC ⊥CE ，∴∠DCT +∠TCE ＝∠TCE +∠BCE ＝90°，∴∠DCT ＝∠ECB ，在△DCT 和△ECB 中：DTC EBC CT CBDCT ECB ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△DCT ≌△ECB (ASA )，∴CD ＝CE ，∴△DCE 为等腰直角三角形，∴∠CED ＝45°，∵∠DCO +∠ECP ＝∠DCO +∠ODC ＝90°，∴∠ODC ＝∠ECP ，在△DOC 和△CPE 中：DOC CPE ODC PCE DC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DOC ≌△CPE (AAS )，∴BP ＝PE ＝OC ＝t ，∴DG ＝OP ＝OB ﹣PB ＝9﹣t ，∴FG ＝DG ﹣DF ＝9﹣3t ，∵∠GFE ＝∠AFD ＝45°，∠GEF ＝∠BEP ＝45°，。

7.3 复数的三角表示（精讲）考法一复数的三角表示【例1-1】（2020·全国高一课时练习）把下列复数的代数形式化成三角形式.（1）3-；（2.【答案】（1）11113cos isin 66ππ+⎫-=⎪⎭（277cos isin 244ππ⎛⎫=⎝+⎪⎭【解析】（1）r ==因为与3-对应的点在第四象限，所以()11arg 36π=，所以11113cos isin 66ππ+⎫-=⎪⎭.（2）2r ==.对应的点在第四象限，所以)7arg 4π=，77cosisin 244ππ⎛⎫= ⎝+⎪⎭. 【例1-2】．（2020·全国高一课时练习）把下列复数的三角形式化成代数形式.（1）4cos isin 33ππ⎛⎫+ ⎪⎝⎭；（2）553cosisin 44ππ⎛⎫+ ⎪⎝⎭.【答案】（1）2+（2）22--【解析】（1）4cos isin 4cos 4sin i 3333ππππ⎛⎫⎛⎫+==+ ⎪ ⎪⎝⎭⎝⎭144i 22⎛=⨯+=+ ⎝⎭.（2）55553cos isin 3cos 3sin i 33i 4444ππππ⎛⎛⎛⎫⎛⎫+=+=⨯+⨯= ⎪⎪ ⎝⎭⎝⎭⎝⎭⎝⎭.【一隅三反】1．（2020·全国高一课时练习）画出下列复数对应的向量，并把这些复数表示成三角形式：（1）122i +； （2）1i -.【答案】（1）作图见解析;1cos sin 233i ππ+=+（2）作图见解析;771cos sin 44i i ππ⎫-=+⎪⎭【解析】（1）复数12+对应的向量如图所示，则11,cos 2r θ===.因为与122+对应的点在第一象限，所以1arg 223π⎛⎫+=⎪⎝⎭.于是1cos sin 2233i ππ+=+.（2）复数1i -对应的向量如图所示，则2r θ====. 因为与1i -对应的点在第四象限，所以7arg(1)4i π-=.于是771cos sin 44i i ππ⎫-=+⎪⎭.当然，把一个复数表示成三角形式时，辐角θ不一定取主值.cos sin 44i ππ⎤⎛⎫⎛⎫-+- ⎪ ⎪⎥⎝⎭⎝⎭⎦也是1i -的三角形式.2．（2020·全国高一课时练习）将下列各复数的三角形式转化为代数形式：（1）sin )i ππ+； （2）11116cossin 66i ππ⎛⎫+ ⎪⎝⎭；（3）44cos sin 33i ππ⎫+⎪⎭；（4）338cossin 22i ππ⎛⎫+ ⎪⎝⎭.【答案】（1）-2）3i -（3）（4）8i -【解析】（1）sin )10)i i ππ+=-+⋅=-（2）111116cos sin 636622i i i ππ⎛⎫⎛⎫+=-= ⎪ ⎪⎝⎭⎝⎭.（3）441cos sin 332222i ππ⎫⎫+=--=--⎪⎪⎭⎭. （4）338cossin 8(0)822i i i ππ⎛⎫+=-=- ⎪⎝⎭. 3．（2020·全国高一课时练习）将下列各复数转化为三角形式（辐角取辐角主值）：（1）2i -； （2）-2i ；（3）1；（4）【答案】（1）11114cossin 66i ππ⎛⎫+ ⎪⎝⎭；（2）332cos sin 22i ππ⎛⎫+⎪⎝⎭；（3）552cos sin 33i ππ⎛⎫+⎪⎝⎭；（4）sin )i ππ+【解析】（1）∵4r ==，cos θ=，1sin 2θ=-，又[0,2)θπ∈，∴116πθ=，∴111124cos sin 66i i ππ⎛⎫=+ ⎪⎝⎭. （2）∵2r，cos 0θ=，sin 1θ=-，又[0,2)θπ∈，∴32πθ=， ∴3322cossin 22i i ππ⎛⎫-=+ ⎪⎝⎭.（3）∵2r ==，1cos 2θ=，sin 2θ=-， 又[0,2)θπ∈，∴53πθ=，∴5512cos sin 33i ππ⎛⎫-=+ ⎪⎝⎭.（4）∵r =cos 1θ=-，sin 0θ=，又[0,2)θπ∈，∴θπ=.∴sin )i ππ=+.考法二 复数的辅角【例2】（2020·全国高一课时练习）复数55sin cos 1818z i ππ=-+的辐角主值为（ ） A ．518πB ．169πC ．29π D ．79π 【答案】D 【解析】5577sincos cos sin 181899z i i ππππ=-+=+,故复数z 的辐角主值为79π.故选：D【一隅三反】1.（2020·全国）复数11z =，2z 由向量1OZ 绕原点O 逆时针方向旋转3π而得到.则21arg()2z z -的值为（ ） A ．6π B ．3πC ．23π D ．43π 【答案】C【解析】11z =,1cos 0sin 0z i ∴=+,121(cossin )332Z i O OZ ππ=+=+2111()2222z z i --∴=+所以复数在第二象限，设幅角为θ，tan θ=23πθ∴=故选：C 2．（2020·全国高一课时练习）若复数1z =--（i 为虚数单位），则arg z 为（ ） A ．120︒- B ．120°C ．240°D ．210°【答案】C【解析】由1z =-，得复数z 对应的点在第三象限，且1cos 2θ=-，所以arg 240z ︒=. 故选：C.3．（2020·辽宁辽师大附中高一期末）把复数z 1与z 2对应的向量OA OB ，分别按逆时针方向旋转4π和53π后，重合于向量OM且模相等，已知21z =-，则复数1z 的代数式和它的辐角主值分别是（ ） A ．22i --，34π B ．322,4i π-+ C ．22,4i π--D ．22,4i π-+【答案】B【解析】由题可知1255cossincos sin 4433z i z i ππππ⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭， 则()1112222z ⎛⎫⎛⎫+=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭， )()()11111i z i i i ---∴====++-，可知1z 对应的坐标为(，则它的辐角主值为34π.故选：B. 考法三 复数的乘、除运算的三角表示及及其几何意义【例3】（2020·全国高一课时练习）计算下列各式：（122cossincos sin 3333i i ππππ⎫⎫+⨯+⎪⎪⎭⎭； （2）()112cos15sin1522i ︒︒⎛⎫+⨯-+ ⎪⎝⎭；（3）)552cos sin cos135sin13533i i ππ︒︒⎛⎫⎤+÷+⎪⎦⎝⎭；（4）1cos sin 233i ππ⎛⎫⎤⎫÷+ ⎪⎪⎥ ⎪⎭⎦⎝⎭.【答案】（1）6-；（2）2i ；（3）；（4）4-【解析】（122cossincos sin 3333i i ππππ⎫⎫+⨯+⎪⎪⎭⎭226cos isin 6(cos sin )63333i ππππππ⎡⎤⎛⎫⎛⎫=+++=+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.（2）()112cos15sin1522i i ︒︒⎛⎫+⨯-+ ⎪⎝⎭332cos sin cos sin 1212244i i ππππ⎛⎫⎫=+⨯+ ⎪⎪⎝⎭⎝⎭33cos isin 124124ππππ⎤⎛⎫⎛⎫=+++ ⎪ ⎪⎥⎝⎭⎝⎭⎦551cos sin6622i i ππ⎛⎫⎫=+=-+ ⎪⎪ ⎪⎭⎝⎭22=-+.（3）)552cossin cos135sin13533i i ππ︒︒⎛⎫⎤+÷+ ⎪⎦⎝⎭55332cos sincos sin 3344i i ππππ⎤⎛⎫⎫=+÷+ ⎪⎪⎥⎝⎭⎭⎦5353cos sin3434i ππππ⎤⎛⎫⎛⎫=-+- ⎪ ⎪⎥⎝⎭⎝⎭⎦1111cos sin1212i ππ⎫=+⎪⎭cos sin 1212i ππ⎛⎫=-+ ⎪⎝⎭44⎛⎫-=-+ ⎪ ⎪⎝⎭1122i +-=-+.（4）1cos sin 2233i ππ⎛⎫⎤⎫-÷+ ⎪⎪⎥ ⎪⎭⎦⎝⎭ 55cos sincos sin 3333i i ππππ⎤⎛⎫⎫=+÷+ ⎪⎪⎥⎝⎭⎭⎦55cos isin3333ππππ⎤⎛⎫⎛⎫=-+- ⎪ ⎪⎥⎝⎭⎝⎭⎦44cos sin 233i ππ⎫=+⎪⎝⎭1222⎛⎫=⨯-- ⎪ ⎪⎝⎭44=--. 【一隅三反】1．（2020·全国高一课时练习）cosisin3cos isin 2266ππππ⎛⎫⎛⎫+⨯+= ⎪ ⎪⎝⎭⎝⎭（ ）A ．32 B ．32 C ．32-D ．32-- 【答案】C【解析】cosisin3cos isin 3cos isin 22662626ππππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+⨯+==+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦2233cos isini 3322ππ⎛⎫=+=-+ ⎪⎝⎭.故选：C 2．（2020·全国高一课时练习）()()9cos3isin33cos2isin 2ππππ+÷+=（ ）A ．3B ．3-CD ．【答案】B【解析】()()9cos3isin33cos2isin 2933ππππ+÷+=-÷=-.故选：B 3．（2020·全国高一课时练习）()()()1cos30sin 302cos60sin 603cos 45sin 452i i i ︒+︒⨯︒+︒⨯︒+︒=（ ）A B C ． D ． 【答案】C 【解析】()()1cos30sin 302cos60sin 602i i ︒+︒⨯︒+︒⨯()3cos45sin 45i ︒+︒ ()()123cos 306045sin 3060452i =⨯⨯︒+︒+︒+︒+︒+︒⎡⎤⎣⎦ ()3cos135sin135i =︒+︒3⎛⎫= ⎪ ⎪⎝⎭=+. 故选：C.4．（2020·全国高一课时练习）计算下列各式，并作出几何解释：（122cossin cos sin 3333i i ππππ⎫⎫+⨯+⎪⎪⎭⎭（2）()112cos 75sin 7522i i ︒︒⎛⎫+⨯-⎪⎝⎭（3）()334cos300sin300cossin 44i i ππ︒︒⎤⎫+÷+⎪⎥⎭⎦（4）12cos sin 233i ππ⎛⎫⎡⎤⎛⎫-+÷+ ⎪ ⎪⎢⎥ ⎪⎝⎭⎣⎦⎝⎭.【答案】（1）-4，几何解释见解析 （22i +，几何解释见解析 （3）1)1)i -++-，几何解释见解析 （4）14+，几何解释见解析【解析】（1）原式(cos sin )4(10)4i ππ=+=⨯-+=-.几何解释：设1222cos sin,cos sin 3333z i z i ππππ⎫⎫=+=+⎪⎪⎭⎭，作与12,z z 对应的向量12,OZ OZ ，然后把向量1OZ 绕原点O 按逆时针方向旋转3π，再将其长度伸长为原来的4,辐角为π的 向量OZ ，则OZ 即为积124z z ⋅=-所对应的向量.（2）原式()2cos 75sin 75222i ︒︒⎛⎫=+⨯- ⎪ ⎪⎝⎭()()2cos 75sin 75cos315sin 3152︒︒︒︒=+⨯+)1cos390sin 3902i i ︒︒⎫=+==⎪⎪⎝⎭.几何解释：设())12112cos 75sin 75,cos315sin 31522z i z i ︒︒︒︒=+=-=+， 作与12,z z 对应的向量12,OZ OZ ，然后把向量1OZ 绕原点O 按逆时针方向旋转315°，再将其长度缩短、辐角为6π 的向量OZ，则OZ即为积1222z z i⋅=+所对应的向量.（3）原式5533 4cos sin cos sin3344i iππππ⎤⎛⎫⎫=+÷+⎪⎪⎥⎝⎭⎭⎦1111cos sin cos sin12121212i iππππ⎫⎛⎫=+=-+⎪ ⎪⎭⎝⎭1)1)i⎛⎫==-+⎪⎪⎝⎭.几何解释：设()1554cos300sin3004cos sin33z i iππ︒︒⎛⎫=+=+⎪⎝⎭，233cos sin44z iππ⎫=+⎪⎭作与12,z z对应的向量12,OZ OZ，然后把向量1OZ绕原点0按顺时针方向旋转34π，再将其长度，辐角为1112π的向量OZ，则OZ即为121)1)ziz=-+所对应的向量.（4）原式22cos sin2cos sin3333i iππππ⎡⎤⎛⎫⎛⎫=+÷+⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦1111cos sin233224iππ⎛⎫⎛⎫=+=⨯=+⎪⎪ ⎪⎝⎭⎝⎭.几何解释：设1122cos sin,2cos sin223333z i z iππππ⎛⎫=-+=+=+⎪⎝⎭，作与12,z z对应的向量12,OZ OZ，然后把向量1OZ绕原点0按顺时针方向旋转3π，再将其长度缩短为原来的12，得到一个长度为12，辐角为3π的向量OZ，则OZ即为1214zz=所对应的向量.11/ 11。

人教版九年级数学上册第二十三章旋转章节测试考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、下列所述图形中，既是轴对称图形又是中心对称图形的是（ ）A ．等腰三角形B ．等边三角形C ．菱形D ．平行四边形2、如图，将△ABC 绕点A 逆时针旋转70°得到△ADE ，点B 、C 的对应点分别为D 、E ，当点B 、C 、D 、P 在同一条直线上时，则∠PDE 的度数为（ ）A ．55°B ．70°C ．80°D ．110°3、如图，将ABC 绕点A 逆时针旋转55︒得到ADE ，若70E ∠=︒且AD BC ⊥于点F ，则BAC ∠的度数为（ ）A ．65︒B ．70︒C ．75︒D ．80︒4、如图，将Rt△ABC 绕直角顶点C 顺时针旋转90°，得到△A 'B 'C ，连接AA '，若∠1=25°，则∠BAA '的度数是（ ）A ．70°B ．65°C ．60°D ．55°5、已知四边形ABCD 的对角线相交于点O ，且OA=OB=OC=OD ，那么这个四边形是（ ）A ．是中心对称图形，但不是轴对称图形B ．是轴对称图形，但不是中心对称图形C ．既是中心对称图形，又是轴对称图形D ．既不是中心对称图形，又不是轴对称图形6、如图，由4个小正方形组成的田字格，ABC 的顶点都是小正方形的顶点，在田字格上能画出与ABC 成轴对称，且顶点都在小正方形顶点上的三角形的个数共有（ ）A ．2个B ．3个C ．4个D ．5个7、如图，在方格纸上建立的平面直角坐标系中，将ABO 绕点O 按顺时针方向旋转90°，得到A B O ''△，则点B '的坐标为（ ）．A ．(2,1)B ．(1,2)C ．(2,1)-D ．(2,0)8、如图，将ABC ∆绕点C 顺时针旋转得到DEC ∆，使点A 的对应点D 恰好落在边AB 上，点B 的对应点为E ，连接BE ．下列结论一定正确的是（ ）A ．AC AD =B ．AB EB ⊥C ．BC DE =D ．A EBC ∠=∠9、如图，已知点O （0，0），P （1，2），将线段PO 绕点P 按顺时针方向以每秒90°的速度旋转，则第19秒时，点O 的对应点坐标为（ ）A ．（0，0）B ．（3，1）C ．（﹣1，3）D ．（2，4）10、将OBA △按如图方式放在平面直角坐标系中，其中90OBA ∠=︒，30A ∠=︒，顶点A 的坐标为(，将OBA △绕原点逆时针旋转，每次旋转60°，则第2023次旋转结束时，点A 对应点的坐标为（ ）A ．(-B ．()C ．⎛⎫ ⎪ ⎪⎝⎭D ．⎛- ⎝⎭第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，在Rt △ABC ，∠B ＝90°，∠ACB ＝50°．将Rt △ABC 在平面内绕点A 逆时针旋转到△AB ′C ′的位置，连接CC ′．若AB ∥CC ′，则旋转角的度数为_____°．2、将点(5,3)A 绕原点O 顺时针旋转90︒得到点A '，则点A '落在第____________象限．3、如图，在△ABC 中，∠CAB ＝65°，在同一平面内，将△ABC 绕点A 逆时针旋转到AB C ''△的位置，使得CC AB '∥，则B AB ∠'等于_____．4、在4×4的方格中有五个同样大小的正方形如图摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有__种．5、如图，P 是正方形ABCD 内一点，将ABP △绕点B 顺时针方向旋转,能与1CBP 重合，若5PB =，则1PP =______．三、解答题（5小题，每小题10分，共计50分）1、如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC 的顶点均为格点（网格线的交点）．(1)将△ABC 向上平移6个单位，再向右平移2个单位，得到111A B C △，请画出111A B C △﹔(2)以边AC 的中点O 为旋转中心，将△ABC 按逆时针方向旋转180°，得到222A B C △，请画出222A B C △．2、在ABC 中，90ACB ∠=︒，AC BC =，直线MN 经过点C 且AD MN ⊥于D ，BE MN ⊥于E ．(1)当直线MN绕点C旋转到图1的位置时，求证：△；①ADC≌CEB②DE AD BE=+；(2)当直线MN烧点C旋转到图2的位置时，求证：DE AD BE=-；(3)当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．3、如图1，已知正方形ABCD的边CD在正方形DEFG的边DE上，连接AE、GC．（1）试猜想AE与GC的数量关系与位置关系；（2）将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和GC．你认为（1）中的结论是否还成立？若成立，给出证明；若不成立，请说明理由．4、ABC为等边三角形，AB＝8，AD⊥BC于点D，E为线段AD上一点，AE=AE为边在直线AD右侧构造等边三角形AEF，连接CE，N为CE的中点．(1)如图1，EF 与AC 交于点G ，连接NG ，BE ，直接写出NG 与BE 的数量关系；(2)如图2，将AEF 绕点A 逆时针旋转，旋转角为α，M 为线段EF 的中点，连接DN ，MN ．当30120α︒<<︒时，猜想∠DNM 的大小是否为定值，如果是定值，请写出∠DNM 的度数并证明，如果不是，请说明理由；(3)连接BN ，在AEF 绕点A 逆时针旋转过程中，请直接写出线段BN 的最大值．5、在Rt△ABC 中，∠BAC ＝90°，AB ＝AC ，动点D 在直线BC 上（不与点B ，C 重合），连接AD ，把AD 绕点A 逆时针旋转90°得到AE ，连接DE ，F ，G 分别是DE ，CD 的中点，连接FG ．【特例感知】（1）如图1，当点D 是BC 的中点时，FG 与BD 的数量关系是 ，FG 与直线BC 的位置关系是 ；【猜想论证】（2）当点D 在线段BC 上且不是BC 的中点时，（1）中的结论是否仍然成立？ ①请在图2中补全图形；②若成立，请给出证明；若不成立，请说明理由．【拓展应用】（3）若AB ＝AC ，其他条件不变，连接BF 、CF ．当△ACF 是等边三角形时，请直接写出△BDF 的面积．-参考答案-一、单选题1、C【解析】【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．【详解】解：A 、等腰三角形是轴对称图形，不是中心对称图形，故本选项错误；B 、等边三角形是轴对称图形，不是中心对称图形，故本选项错误；C 、菱形既是轴对称图形，又是中心对称图形，故本选项正确；D 、平行四边形不是轴对称图形，是中心对称图形，故本选项错误．故选C ．【考点】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．2、B【解析】【分析】首先根据旋转的性质可得=70BAD ∠︒，=ABC ADE ∠∠，AB =AD ，据此即可求得===55ABC ADE ADB ∠∠∠︒，据此即可求得．【详解】 解：将△ABC 绕点A 逆时针旋转70°得到△ADE ，=70BAD ∴∠︒，=ABC ADE ∠∠，AB =AD ，()()11==180=18070=5522ABC ADB BAD ∴∠∠︒-∠⨯︒-︒︒， ===55ABC ADE ADB ∴∠∠∠︒， 又点B 、C 、D 、P 在同一条直线上，=180=1805555=70PDE ADE ADB ∴∠︒-∠-∠︒-︒-︒︒，故选：B ．【考点】本题考查了旋转的性质，等边对等角的应用，三角形内角和定理，熟练掌握和运用旋转的性质是解决本题的关键．3、C【解析】【分析】由旋转的性质可得∠BAD =55°，∠E =∠ACB =70°，由直角三角形的性质可得∠DAC =20°，即可求解．【详解】解：∵将△ABC 绕点A 逆时针旋转55°得△ADE ，∴∠BAD =55°，∠E =∠ACB =70°，∵AD ⊥BC ，∴∠DAC =20°，∴∠BAC =∠BAD +∠DAC =75°．故选C ．【考点】本题考查了旋转的性质，掌握旋转的性质是本题的关键．4、B【解析】【分析】根据旋转的性质可得AC=A′C，然后判断出△ACA′是等腰直角三角形，根据等腰直角三角形的性质可得∠CAA′=45°，再根据三角形的内角和定理可得结果．【详解】∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C，∴AC=A′C，∴△ACA′是等腰直角三角形，∴∠CA′A=45°，∠CA′B′=20°=∠BAC∴∠BAA′=180°-70°-45°=65°，故选：B．【考点】本题考查了旋转的性质，等腰直角三角形的判定与性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质并准确识图是解题的关键．5、C【解析】【分析】先根据已知条件OA=OB=OC=OD，可知四边形ABCD的对角线相等且互相平分，得出四边形ABCD是矩形，然后根据矩形的对称性，得出结果．【详解】解：如图所示：∵四边形ABCD的对角线相交于点O且OA=OB=OC=OD，∴OA=OC，OB=OD；AC=BD，∴四边形ABCD是矩形，∴四边形ABCD既是轴对称图形，又是中心对称图形．故选：C．【考点】本题主要考查了矩形的判定及矩形的对称性．对角线相等且互相平分的四边形是矩形，矩形既是轴对称图形，又是中心对称图形．6、C【解析】【分析】因为顶点都在小正方形上，故可分别以大正方形的两条对角线AB、EF及MN、CH为对称轴进行寻找．【详解】分别以大正方形的两条对角线AB、EF及MN、CH为对称轴，作轴对称图形：则△ABM、△ANB、△EHF、△EFC都是符合题意的三角形.故选：C.【考点】考查了利用轴对称涉及图案的知识,关键是根据要求顶点在格点上寻找对称轴,有一定难度,不要漏解.7、A【解析】【分析】根据网格结构作出旋转后的图形，然后根据平面直角坐标系写出点B′的坐标即可．【详解】△A′B′O如图所示，点B′（2，1）．故选A．【考点】本题考查了坐标与图形变化，熟练掌握网格结构，作出图形是解题的关键．8、D【解析】【分析】利用旋转的性质得AC=CD，BC=EC，∠ACD=∠BCE，所以选项A、C不一定正确∠=∠，所以选项D正确；再根据∠EBC再根据等腰三角形的性质即可得出A EBC=∠EBC+∠ABC=∠A+∠ABC=0180-∠ACB判断选项B不一定正确即可．【详解】解：∵ABC ∆绕点C 顺时针旋转得到DEC ∆，∴AC=CD，BC=EC ，∠ACD=∠BCE， ∴∠A=∠CDA=180ACD 2∠︒-；∠EBC=∠BEC=180BCE 2∠︒-， ∴选项A 、C 不一定正确，∴∠A =∠EBC，∴选项D 正确．∵∠EBC=∠EBC+∠ABC=∠A+∠ABC=0180-∠ACB 不一定等于090，∴选项B 不一定正确；故选D ．【考点】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了等腰三角形的性质．9、B【解析】【分析】依据线段PO 绕点P 按顺时针方向以每秒90°的速度旋转，即可得到19秒后点O 旋转到点O '的位置，再根据全等三角形的对应边相等，即可得到点O 的对应点O '的坐标．【详解】解：如图所示，∵线段PO 绕点P 按顺时针方向以每秒90°的速度旋转，每4秒一个循环，19＝4×4+3，∴3×90°＝270°，∴19秒后点O 旋转到点O '的位置，∠OPO '＝90°，如图所示，过P 作MN ⊥y 轴于点M ，过O '作O 'N ⊥MN 于点N ，则∠OMP ＝∠PNO '＝90°，∠POM ＝∠O 'PN ，OP ＝PO '，在△OPM 和△PO 'N 中，'''OMP PNO POM O PN OP PO ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△OPM ≌△PO 'N （AAS ），∴O 'N ＝PM ＝1，PN ＝OM ＝2，∴MN ＝1+2＝3，点O '离x 轴的距离为2-1＝1，∴点O '的坐标为（3，1），故选：B ．【考点】本题主要考查了坐标与图形变化，图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．10、A【解析】【分析】根据旋转性质，可知6次旋转为1个循环，故先需要求出前6次循环对应的A 点坐标即可，利用全等三角形性质求出第一次旋转对应的A 点坐标，之后第2次旋转，根据图形位置以及OA 长，即可求出，第3、4、5次分别利用关于原点中心对称，即可求出，最后一次和A 点重合，再判断第2023次属于循环中的第1次，最后即可得出答案．【详解】解：由题意可知：6次旋转为1个循环，故只需要求出前6次循环对应的A 点坐标即可第一次旋转时：过点'A 作x 轴的垂线，垂足为C ，如下图所示：由A的坐标为(可知：1OB =，AB =在Rt AOB ∆中，9060AOB A ∠=︒-∠=︒，2OA =由旋转性质可知：''AOB AOB ∆∆≌， ''60AOB AOB ∴∠=∠=︒，'=OA OA ，'''18060AOC AOB AOB ∴∠=︒-∠-∠=︒，在'AOC ∆与AOB ∆中：6090A OC AOB A CO ABO OA OA ∠=∠=︒⎧⎪∠='''∠=︒⎨='⎪⎩''()AOC AOC AAS ∴∆∆≌，1∴==OC OB，'AC AB ==∴此时点A对应坐标为(-，当第二次旋转时，如下图所示：此时A 点对应点的坐标为(20)-，．当第3次旋转时，第3次的点A 对应点与A 点中心对称，故坐标为(1--，．当第4次旋转时，第4次的点A 对应点与第1次旋转的A 点对应点中心对称，故坐标为(1-，．当第5次旋转时，第5次的点A 对应点与第2次旋转的A 点对应点中心对称，故坐标为(2)0，． 第6次旋转时，与A 点重合．故前6次旋转，点A 对应点的坐标分别为：(-、(20)-，、(1--，、(1-，、(2)0，、(．由于20236=3371÷⋅⋅⋅⋅⋅⋅，故第2023次旋转时，A 点的对应点为(-．故选：A ．【考点】本题主要是考查了旋转性质、中心对称求点坐标、三角形全等以及点的坐标特征，熟练利用条件证明全等三角形，；通过旋转和中心对称求解对应点坐标，是求解该题的关键．二、填空题1、100【解析】【分析】由AB CC '∥，可得ACC CAB '∠=∠，90CAB ACB ∠=︒-∠，由旋转的性质可得AC AC '=，AC A C C C ∠='∠'，由三角形内角和定理得180CAC ACC AC C '''∠=︒-∠-∠，计算求解即可．【详解】解：∵AB CC '∥∴ACC CAB '∠=∠∴9040CAB ACB ∠=︒-∠=︒由旋转的性质可得AC AC '=∴40AC A C C C ∠=∠=''︒∴180100CA AC A C C C C '''∠=︒-∠-∠=︒故答案为：100．【考点】本题考查了平行的性质，旋转的性质，旋转角，等边对等角，三角形的内角和定理等知识．解题的关键在于找出旋转角．2、四【解析】【分析】画出图形，利用图象解决问题即可．【详解】解：如图35(,)A '-，所以在第四象限，故答案为：四．【考点】本题考查坐标与图形变化—旋转，解题的关键是正确画出图形，属于中考常考题型．3、50°【解析】【分析】由平行线的性质可求得C CA '∠的度数，然后由旋转的性质得到AC AC '=，然后依据三角形的性质可知AC C '∠的度数，依据三角形的内角和定理可求得CAC '∠的度数，从而得到BAB '∠的度数.【详解】解：∵CC AB '∥∴65C CA CAB '∠=∠=︒∵由旋转的性质可知：AC AC '=∴65ACC AC C ''∠=∠=︒∴180656550CAC '∠=︒-︒-︒=︒∴50BAB '∠=︒故答案为：50︒.4、13【解析】【分析】根据轴对称图形的性质，分别移动一个正方形，即可得出符合要求的答案．【详解】如图所示：故一共有13画法.5、【解析】【分析】根据旋转角相等可得1PBP ∠90ABC =∠=︒，进而勾股定理求解即可【详解】 解：四边形ABCD 是正方形90ABC ∴∠=︒将ABP △绕点B 顺时针方向旋转,能与1CBP 重合，∴1PBP ∠90ABC =∠=︒，15PB PB==1PP ∴==故答案为：【考点】本题考查了旋转的性质，勾股定理，求得旋转角相等且等于90°是解题的关键．三、解答题1、 (1)见解析(2)见解析【解析】【分析】（1）根据平移的方式确定出点A 1，B 1，C 1的位置，再顺次连接即可得到111A B C △；（2）根据旋转可得出确定出点A 2，B 2，C 2的位置，再顺次连接即可得到222A B C △．(1)如图，111A B C △即为所作；(2)如图，222A B C △即为所作；【考点】本题考查作图-旋转变换与平移变换，解题的关键是理解题意，灵活运用所学知识解决问题．2、 (1)①证明见解析；②证明见解析(2)证明见解析(3)DE BE AD =-（或者对其恒等变形得到AD BE DE =-，BE AD DE =+），证明见解析【解析】【分析】（1）①根据AD MN ⊥，BE MN ⊥，90ACB ∠=︒，得出CAD BCE ∠=∠，再根据AAS 即可判定ADC CEB ∆≅∆；②根据全等三角形的对应边相等，即可得出CE AD =，CD BE =，进而得到DE CE CD AD BE =+=+；（2）先根据AD MN ⊥，BE MN ⊥，得到90ADC CEB ACB ∠=∠=∠=︒，进而得出CAD BCE ∠=∠，再根据AAS 即可判定ADC CEB ∆≅∆，进而得到CE AD =，CD BE =，最后得出DE CE CD AD BE =-=-；（3）运用（2）中的方法即可得出DE ，AD ，BE 之间的等量关系是：DE BE AD =-或恒等变形的其他形式．(1)解：①AD MN ⊥，BE MN ⊥，90ADC ACB CEB ∴∠=∠=︒=∠，90CAD ACD ∴∠+∠=︒，90BCE ACD ∠+∠=︒，CAD BCE ∴∠=∠，在ADC ∆和CEB ∆中，CAD BCE ADC CEB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩()ADC CEB AAS ∴∆≅∆；②ADC CEB ∆≅∆，CE AD ∴=，CD BE =，DE CE CD AD BE ∴=+=+；(2)证明：AD MN ⊥，BE MN ⊥，90ADC CEB ACB ∴∠=∠=∠=︒，CAD BCE ∴∠=∠，在ADC ∆和CEB ∆中，CAD BCE ADC CEB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩()ADC CEB AAS ∴∆≅∆；CE AD ∴=，CD BE =，DE CE CD AD BE ∴=-=-；(3)证明：当MN 旋转到题图（3）的位置时，AD ，DE ，BE 所满足的等量关系是：DE BE AD =-或AD BE DE =+或BE AD DE =+．理由如下：AD MN ⊥，BE MN ⊥，90ADC CEB ACB ∴∠=∠=∠=︒，CAD BCE ∴∠=∠，在ADC ∆和CEB ∆中，CAD BCE ADC CEB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩()ADC CEB AAS ∴∆≅∆，CE AD ∴=，CD BE =，DE CD CE BE AD ∴=-=-（或者对其恒等变形得到AD BE DE =+或BE AD DE =+）．【考点】本题属于三角形综合题，主要考查了全等三角形的判定与性质的综合应用，解题时注意：全等三角形的对应边相等，同角的余角相等，解决问题的关键是根据线段的和差关系进行推导，得出结论．3、（1）AE =GC ，AE ⊥GC ；（2）成立，见解析【解析】【分析】（1）观察图形，AE 、CG 的位置关系可能是垂直，下面着手证明．由于四边形ABCD 、DEFG 都是正方形，易证得ADE CDG ∆≅∆，则12∠=∠，AE CG =，由于2∠、3∠互余，所以1∠、3∠互余，由此可得AE GC ⊥．（2）题（1）的结论仍然成立，参照（1）题的解题方法，可证ADE CDG ∆≅∆，得54∠=∠，AE CG =，由于4∠、7∠互余，而5∠、6∠互余，那么67∠=∠；由图知906AEB CEH ∠=∠=︒-∠，即790CEH ∠+∠=︒，由此得证．【详解】解：（1）答：AE GC ⊥；证明：如图1中，延长GC 交AE 于点H ．在正方形ABCD 与正方形DEFG 中，AD DC =，90ADE CDG ∠=∠=︒DE DG =，ADE CDG ∴∆≅∆，12∠∠∴=，AE GC =，2390∠+∠=︒，1390∴∠+∠=︒，(180********)0AHG ∴∠=︒-∠+∠=︒-︒=︒，AE GC ∴⊥．故答案为AE GC ⊥，AE GC =．（2）答：成立；证明：如图2中，延长AE 和GC 相交于点H ．在正方形ABCD 和正方形DEFG 中，AD DC =，DE DG =，90ADC DCB B BAD EDG ∠=∠=∠=∠=∠=︒，12903∴∠=∠=︒-∠；ADE CDG ∴∆≅∆，54∴∠=∠，AE CG =，又5690∠+∠=︒，471801809090DCE ∠+∠=︒-∠=︒-︒=︒，67∴∠=∠，又690AEB ∠+∠=︒，AEB CEH ∠=∠，790CEH ∴∠+∠=︒，90EHC ∴∠=︒，AE GC ∴⊥．【考点】本题主要考查旋转的性质以及全等三角形的判定和性质，解题的关键是需要注意的是：旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．4、 (1)2BE NG =(2)∠DNM 的大小是定值，为120°(3)【解析】【分析】（1）连接CF ．由等边三角形的性质易证△BAE ≌△CAF (SAS)，即得出CF BE =．再根据三角形中位线定理即可求出2BE NG =；（2）连接BE ，CF ．利用全等三角形的性质证明∠EBC +∠BCF =120°，再利用三角形的中位线定理，三角形的外角的性质证明∠DNM =∠EBC +∠BCF 即可；（3）取AC 的中点J ，连接BJ ，结合三角形的中位线定理可求出BJ ，JN ．最后根据三角形三边关系即可得出结论．(1)解：如图，连接CF ．∵△ABC 是等边三角形，AD ⊥BC ，∴AB =BC =AC ，∠BAD =∠CAD =30°．∵△AEF 是等边三角形，∴∠EAF =60°，G 为EF 中点，∴∠EAG =∠GAF =30°．即在△BAE 和△CAF 中，=30=AB AC BAE CAF AE AF =⎧⎪∠=∠︒⎨⎪⎩，∴△BAE ≌△CAF (SAS)，∴CF BE =，∵N 为CE 的中点，G 为EF 中点， ∴12GN CF =，∴2BE NG =；(2)∠DNM =120°是定值，证明如下，如图，连接BE ，CF ．同（1）可证△BAE ≌△CAF （SAS ），∴∠ABE =∠ACF ．∵∠ABC +∠ACB =60°+60°=120°，∴∠EBC +∠BCF =∠ABC -∠ABE +∠ACB +∠ACF =120°．∵EN =NC ，EM =MF ，∴MN ∥CF ，∴∠ENM =∠ECF ，∵BD =DC ，EN =NC ，∴DN∥BE，∴∠CDN=∠EBC，∵∠END=∠NDC+∠NCD，∴∠DNM=∠DNE+∠ENM=∠NDC+∠ACB+∠ACN+∠ECF=∠EBC+∠ACB+∠ACF=∠EBC+∠BCF=120°．综上可知∠DNM的大小是定值，为120°；(3)如图，取AC的中点J，连接BJ，BN．∵AJ=CJ，EN=NC，AE∴JN=1∵BJ=AD=∴BN≤BJ+JN，即BN≤故线段BN的最大值为【考点】本题属于几何变换综合题，考查了等边三角形的性质，全等三角形的判定和性质，三角形的中位线定理，三角形三边关系的应用．解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．5、（1）FG=12BD，FG⊥BC；（2）①补全图形见解析；②结论仍然成立，理由见解析；（3）△BDF的面积为1或【解析】【分析】（1）根据等腰直角三角形的性质以及中位线定理可得结果；（2）①根据题意画出图形即可；②根据旋转的性质证明△ABD≌△ACE，结合中位线定理证明结论；（3）分两种情况进行讨论：当点D在点B的左侧时；当点D在点C的右侧时，分别画出图形结合等边三角形的性质解答．【详解】（1）∵∠BAC＝90°，AB＝AC，点D是BC的中点，∴AD⊥BC，AD＝BD＝CD，∠ABC＝∠ACB＝45°，∵F，G分别是DE，CD的中点，∴FG12=AD，FG∥AD，∴FG12=BD，FG⊥BC，故答案为：FG12=BD，FG⊥BC；（2）①补全图形如图所示；②结论仍然成立，理由如下：如图2，连接CE，∵把AD 绕点A 逆时针旋转90°得到AE ， ∴∠BAC ＝∠DAE ＝90°，AD ＝AE ， ∴∠BAD ＝∠CAE ，又∵AB ＝AC ，∴△ABD ≌△ACE （SAS ）， ∴CE ＝BD ，∠ACE ＝∠B ＝∠ACB ＝45°， ∴∠DCE ＝90°，∵F ，G 分别是DE ，CD 的中点，∴FG 12=CE 12=BD ，FG ∥CE ， ∴FG ⊥BC ；（3）当点D 在点B 的左侧时，如图3﹣1中，作AM ⊥BC 于M ，连接FG ，∵∠BAC ＝90°，AB ＝AC =AM ⊥BC ， ∴BC ＝2，BM ＝CM ＝AM 12=BC ＝1，∠BAM ＝∠CAM ＝45°， ∵AD ＝AE ，∠DAE ＝90°，点F 是DE 中点， ∴∠EAF ＝∠CAM ＝45°，AF ＝FD ＝EF ， ∵△AFC 是等边三角形，∴AF ＝AC ＝FC =FAC ＝∠AFC ＝∠ACF ＝60°， ∴∠CAE ＝15°＝∠BAD ，∴DM =∴BD ＝DM ﹣BM 1，由（2）的结论可得：FG ⊥BC ，FG 12=BD =∴△BDF 的面积11)12=⨯= 当点D 在点C 的右侧时，如图3﹣2中，作AM ⊥BC 于M ，连接FG ，∵∠BAC ＝90°，AB ＝AC =AM ⊥BC ，∴BC ＝2，BM ＝CM ＝AM 12=BC ＝1，∠BAM ＝∠CAM ＝45°， ∵AD ＝AE ，∠DAE ＝90°，点F 是DE 中点，∴∠EAF ＝∠CAM ＝45°，AF ＝FD ＝EF ，∠DAF ＝45°，∵△AFC 是等边三角形，∴AF ＝AC ＝FC =FAC ＝∠AFC ＝∠ACF ＝60°，∴∠CAD ＝∠CAF ﹣∠DAF ＝15°，∴DM=BD＝DM+BM=1，由（2）的结论可得：FG⊥BC，FG1=BD=2∴△BDF的面积11)1=⨯=2综上所述：△BDF的面积为1或1．【考点】本题考查了等腰三角形的性质，旋转的性质，等边三角形的性质以及全等三角形的判定与性质，熟练掌握以上性质定理是解本题的关键．。