基准特征
- 格式:ppt
- 大小:413.50 KB
- 文档页数:22

solidworks的特征Solidworks的特征可以帮助工程师和设计师更有效地进行3D建模和设计。
以下是一些常见的Solidworks特征及其功能。
1. 父子特征:通过父子特征,用户可以将多个特征组合在一起,以便更好地控制模型的属性。
例如,用户可以创建一个螺纹孔特征,然后将其用作父特征,并在其上添加其他特征,如圆形特征或方形特征。
这些特征将成为父特征的子特征,并且将共享相同的位置和属性。
2. 基准特征:基准特征是Solidworks中最常用的特征之一。
它允许用户确定模型的位置和方向。
例如,用户可以使用基准特征来确定一个零件的底部表面,然后在该表面上添加其他特征,如孔或凸台。
3. 倒角特征:倒角特征可用于将模型的边缘或拐角变得更加平滑。
倒角特征可以应用于直线边缘、弧形边缘和多边形边缘。
例如,用户可以使用倒角特征来为轴承孔的边缘添加圆角,以便使轴承更容易安装和拆卸。
4. 分离面特征:分离面特征可用于将模型分解为多个部分。
用户可以使用分离面特征来切割模型,并将其分为两个或多个零件。
例如,用户可以使用分离面特征来切割一个圆柱体,将其分成一个顶部和一个底部。
5. 镜像特征:镜像特征可用于复制模型的一部分,并将其镜像到另一侧。
例如,用户可以使用镜像特征来创建一个对称零件,如镜像的齿轮或镜像的支架。
6. 模式特征:模式特征可用于在模型中创建重复的几何形状。
例如,用户可以使用模式特征来创建一个六边形螺钉孔的阵列,或一排相同大小的圆孔。
7. 草绘特征:草绘特征可用于创建几何形状的基础。
Solidworks提供了各种草绘工具,包括线条、弧线、圆形和椭圆形工具。
用户可以使用这些工具来创建各种形状,包括直线、曲线和复杂的几何形状。
8. 塑性特征:塑性特征可用于在模型中创建具有弯曲和扭曲形状的几何形状。
例如,用户可以使用塑性特征来创建一个弯曲的管道或一个弯曲的板材。
9. 壁厚特征:壁厚特征可用于调整模型的壁厚。
例如,用户可以使用壁厚特征来增加或减少零件的壁厚,以适应不同的应用需求。



基准特征符号及含义
基准特征符号是一种在统计学和数据分析中常用的工具,用于表示数据集中的中心趋势和离散程度。
基准特征符号包括平均值、中位数、众数和标准差等。
平均值是指将所有数据值相加后除以数据的总个数得到的结果。
它是衡量数据集中心趋势的一种常用指标。
平均值可以帮助了解数据的总体水平。
中位数是将数据集按照大小顺序排列后位于中间位置的数值。
它刻画了数据集的中心位置,并且对异常值不敏感,适合用于描述偏态分布的数据。
众数是指在数据集中出现频率最高的数值。
它可以用来描述数据集的典型值和集中程度。
对于离散型数据,众数是一个有意义的统计指标。
标准差是一种用来衡量数据的离散程度的指标。
它表示数据离平均值的平均距离。
标准差越大,表示数据的分散程度越大。
除了上述基准特征符号,还有其他一些常用的特征符号,如最小值、最大值、四分位数等。
最小值表示数据集中的最小数值,最大值表示数据集中的最大数值,四分位数是将数据集分成四个等分的数值。
这些基准特征符号可以帮助我们对数据集进行描述和分析。
通过对数据的中心趋势和离散程度的了解,我们可以更好地理解数据的特点,并做出相应的决策和推断。
在实际应用中,我们可以根据具体的数据类型和分析目的选择适当的特征符号进行分析。
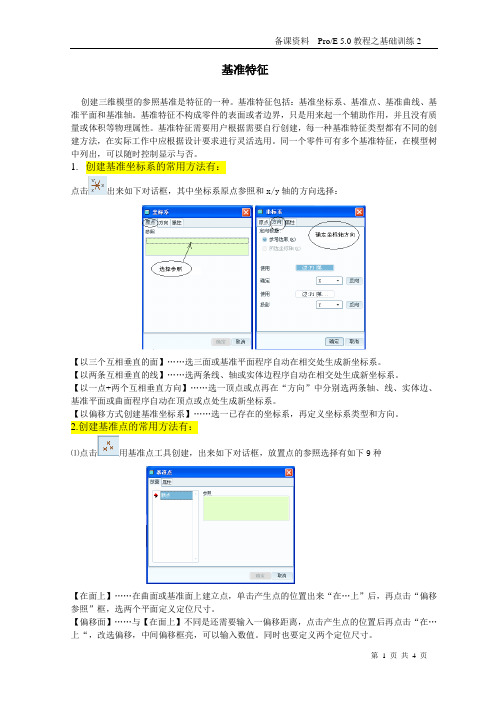
基准特征创建三维模型的参照基准是特征的一种。
基准特征包括:基准坐标系、基准点、基准曲线、基准平面和基准轴。
基准特征不构成零件的表面或者边界,只是用来起一个辅助作用,并且没有质量或体积等物理属性。
基准特征需要用户根据需要自行创建,每一种基准特征类型都有不同的创建方法,在实际工作中应根据设计要求进行灵活选用。
同一个零件可有多个基准特征,在模型树中列出,可以随时控制显示与否。
1.创建基准坐标系的常用方法有:点击出来如下对话框,其中坐标系原点参照和x/y轴的方向选择:【以三个互相垂直的面】……选三面或基准平面程序自动在相交处生成新坐标系。
【以两条互相垂直的线】……选两条线、轴或实体边程序自动在相交处生成新坐标系。
【以一点+两个互相垂直方向】……选一顶点或点再在“方向”中分别选两条轴、线、实体边、基准平面或曲面程序自动在顶点或点处生成新坐标系。
【以偏移方式创建基准坐标系】……选一已存在的坐标系,再定义坐标系类型和方向。
2.创建基准点的常用方法有:⑴点击用基准点工具创建,出来如下对话框,放置点的参照选择有如下9种【在面上】……在曲面或基准面上建立点,单击产生点的位置出来“在…上”后,再点击“偏移参照”框,选两个平面定义定位尺寸。
【偏移面】……与【在面上】不同是还需要输入一偏移距离,点击产生点的位置后再点击“在…上“,改选偏移,中间偏移框亮,可以输入数值。
同时也要定义两个定位尺寸。
【曲线+曲面】……选一曲线和曲面,建立一条曲线与曲面的所交点。
【在顶点】……可在实体、曲面或曲线的端点处建立点。
【三面求交】……选三个曲面求交点。
【在圆或圆弧的中心】……在一曲线圆弧或圆的中心点。
选好一圆弧曲线或圆后点开“在…上”,选居中。
【在曲线上】……在实体边或曲线上产生点。
选好一边或曲线后,在对话框里有三中定义方法:①偏移参照选“参照”则选一平面参照并输入数值,②偏移参照选“曲线末端”偏移值按比率(曲线长度比例)数值输入,③偏移参照选“曲线末端”偏移值按实数(曲线实际长度)数值输入。

基准特征符号及含义
基准特征符号是指在统计学中用来表示特定数据集的中心趋势
和离散程度的指标。
这些符号可以帮助我们更好地理解和分析数据,从而推断出关于总体的特征。
常用的基准特征符号包括平均数、中位数、众数和四分位数等。
1. 平均数(Mean):平均数是一组数据的总和除以数据的个数。
它是最常用的基准特征符号之一,能够反映数据的总体趋势。
2. 中位数(Median):中位数是一组数据按大小排列后位于中间位置的数值。
它不受异常值的影响,能够更准确地表示数据的中心位置。
3. 众数(Mode):众数是一组数据中出现次数最多的数值。
它可以反映数据的集中趋势,特别适用于描述离散型数据。
4. 四分位数(Quartiles):四分位数把一组数据按大小排列后分成四等份,这四个等份的位置分别是第1/4、第2/4(即中位数)、第
3/4处。
它能够提供关于数据分布的更详细信息。
除了上述基准特征符号外,还有其他一些常见的符号用于表示数据的离散程度。
例如:
1. 方差(Variance):方差衡量数据与其平均数之间的差异。
方差越大,数据的离散程度越大。
2. 标准差(Standard Deviation):标准差是方差的平方根,它衡量数据的离散程度。
标准差越大,数据分布越分散。
3. 极差(Range):极差是一组数据的最大值和最小值之间的差异,它能够提供数据的范围信息。
综上所述,基准特征符号是统计学中用来表示数据集中心趋势和离散程度的符号。
通过计算和分析这些符号,我们可以更好地理解和解释数据集的特征,从而做出相关的推断和决策。