安徽省淮北一中、合肥六中、合肥一中、阜阳一中、滁州中学2018-2019学年高一上学期期末考试数学试题

2019-2020学年安徽省合肥一中，八中、六中高一（上）期末数学试卷一、选择题：本大题共12小题，每小题5分共60分.每小题只有一个选项符合题意，答案填涂到答题卡上.1．（5分）设集合{1A =，2，4}，2{|40}B x x x m =-+=．若{1}A B =I ，则(B = ) A ．{1，3}- B ．{1，5} C ．{1，0} D ．{1，3}2．（5分）函数()f x =的定义域为( )A ．1(0,)2B ．(2,)+∞C ．(0，1)(22⋃，)+∞D ．(0，1][22U ，)+∞3．（5分）已知角θ的顶点与坐标原点重合，始边与x 轴的非负半轴重合，终边落在直线3y x =上，则cos2(θ= ) A ．34B ．23 C ．35D ．45-4．（5分）《九章算术》是我国古代内容极为丰富的数学名著，卷一《方田》[三三]：“今有宛田，下周六步，径四步问为田几何？”译成现代汉语其意思为：有一块扇形的田，弧长6步，其所在圆的直径是4步，问这块田的面积是( )平方步？ A ．6B ．3C ．12D ．95．（5分）若[0,]4πθ∈，sin 2θ=sin (θ= )A ．35BC ．45D ．346．（5分）已知函数1()()44x x f x =-，则()(f x )A ．是奇函数，且在R 上是增函数B ．是偶函数，且在R 上是增函数C ．是奇函数，且在R 上是减函数D ．是偶函数，且在R 上是减函数7．（5分）要得到函数4sin(3)3y x π=-的图象，只需要将函数4sin3y x =的图象( )A ．向左平移9π个单位 B ．向右平移9π个单位 C ．向左平移3π个单位D ．向右平移3π个单位8．（5分）函数2()x xe ef x x --=的图象大致为( )A ．B ．C ．D ．9．（5分）设函数2()cos cos f x x b x c =++，则()f x 的最小正周期( ) A ．与b 有关，但与c 无关 B ．与b 有关，且与c 有关C ．与b 无关，且与c 无关D ．与b 无关，但与c 有关10．（5分）已知函数23,0()(1),0x x x f x ln x x ⎧-+<=⎨+⎩…，若|()|f x ax …，则a 的取值范围是( )A ．(-∞，0]B ．(-∞，1]C ．[3-，0]D ．[3-，1] 11．（5分）已知函数()()f x x R ∈满足()4()f x f x -=-，若函数21x y x+=与()y f x =图象的交点为1(x ，1)y ，2(x ，2)y ，⋯，(m x ，)m y ，则1()(mi i i x y =+=∑ )A ．0B ．mC ．2mD ．4m12．（5分）关于函数()sin |||sin |f x x x =+有下述四个结论： ①()f x 是偶函数②()f x 的最大值为2③()f x 在[π-，]π有4个零点④()f x 在区间(,)2ππ单调递减其中所有正确结论的编号是( ) A ．①②④B ．②③④C ．①③④D ．①②③二、填空题：本大题共4小题，每小题5分，共20分.请将答案填写在答题卡相应位置上. 13．（5分）已知函数2()(142)2f x ln x x =++，则1(5)()5f lg f lg += ．14．（5分）已知sin(5)cos(8)tan()()3sin()cos()22f αππααπαππαα----=-+，其中α是第三象限角，且31cos()25πα-=，则()f α= ． 15．（5分）若04πα<<，04πβ-<<，1cos()43πα+=，cos()43πβ-=，则cos()3βα+= ． 16．（5分）设函数()()f x x R ∈满足()()f x f x -=，()(2)f x f x =-，且当[0x ∈，1]时，3()f x x =又函数()|cos()|g x x x π=，则函数13()()()[,]22h x g x f x =--上的零点个数为 ．三、解答题：本大题共6小题共70分.解答应写出文字说明，演算步骤或证明过程.解答写在答题卡上的指定区域内. 17．已知(,)2παπ∈，sin α=（1）求sin()6πα+的值；（2）求5cos(2)3πα-的值． 18．已知函数22()sin cos cos ()f x x x x x x R =-+∈． （Ⅰ）求()3f π的值；（Ⅱ）求()f x 的最小正周期及单调递增区间．19．若函数()y f x =是周期为2的偶函数，当[1x ∈，2]时，()3f x x =-+．在()y f x =的图象上有两点A 、B ，它们的纵坐标相等，横坐标都在区间[1，3]上． （1）求当[2x ∈，3]时()f x 的解析式；（2）定点C 的坐标为(0,3)，求ABC ∆面积的最大值．20．如图，一个半圆和长方形组成的木块，长方形的边CD 为半圆的直径，O 为半圆的圆心，2AB =，1AD =，现要将此木块锯出一个等腰三角形EFG ，其底边EF AB ⊥，点E 在半圆上．（1）设6EOC π∠=，求三角形木块EFG 面积；（2）设EOC θ∠=，试用θ表示三角形木块EFG 的面积S ，并求S 的最大值．21．对于函数()f x ，若在定义域内存在实数x ，满足()2()f x f x -=-，则称“局部中心函数”．（1）已知二次函数2()241()f x ax x a a R =+-+∈，试判断()f x 是否为“局部中心函数”，并说明理由；（2）若12()423x x f x m m +=-+-g 是定义域为R 上的“局部中心函数”，求实数m 的取值范围．22．已知a R ∈，函数21()log ()f x a x=+．（1）当9a =时，解不等式()0f x >；（2）若关于x 的方程2()log [(3)24]0f x a x a --+-=的解集中恰好有一个元素，求a 的取值范围；（3）设0a >，若对任意1[,1]2t ∈，函数()f x 在区间[t ，1]t +上的最大值与最小值的差不超过1，求a 的取值范围．2019-2020学年安徽省合肥一中，八中、六中高一（上）期末数学试卷参考答案与试题解析一、选择题：本大题共12小题，每小题5分共60分.每小题只有一个选项符合题意，答案填涂到答题卡上.1．（5分）设集合{1A =，2，4}，2{|40}B x x x m =-+=．若{1}A B =I ，则(B = ) A ．{1，3}-B ．{1，5}C ．{1，0}D ．{1，3}【解答】解：集合{1A =，2，4}，2{|40}B x x x m =-+=． 若{1}A B =I ，则1A ∈且1B ∈， 可得140m -+=，解得3m =， 即有2{|430}{1B x x x =-+==，3}． 故选：D ．2．（5分）函数()f x =的定义域为( )A ．1(0,)2B ．(2,)+∞C ．(0，1)(22⋃，)+∞D ．(0，1][22U ，)+∞【解答】解：要使函数有意义，则22()10log x ->， 即2log 1x >或2log 1x <-， 解得2x >或102x <<， 即函数的定义域为(0，1)(22⋃，)+∞，故选：C ．3．（5分）已知角θ的顶点与坐标原点重合，始边与x 轴的非负半轴重合，终边落在直线3y x =上，则cos2(θ= ) A ．34B ．23 C ．35D ．45-【解答】解：由题意知：直线的斜率tan 3k θ==，2222222214cos2cos sin 15cos sin tan cos sin tan θθθθθθθθθ--∴=-===-++， 故选：D ．4．（5分）《九章算术》是我国古代内容极为丰富的数学名著，卷一《方田》[三三]：“今有宛田，下周六步，径四步问为田几何？”译成现代汉语其意思为：有一块扇形的田，弧长6步，其所在圆的直径是4步，问这块田的面积是( )平方步？ A ．6B ．3C ．12D ．9【解答】解：Q 弧长6步，其所在圆的直径是4步，∴由题意可得：12662S =⨯⨯=（平方步）， 故选：A ．5．（5分）若[0,]4πθ∈，sin 2θ=sin (θ= )A ．35B C ．45D ．34【解答】解：sin 2θ=又[0,]4πθ∈，cos sin 0θθ∴>>，则sin cos θθ+===，sin cos θθ-==2sin θ∴==则sin θ=． 故选：B ．6．（5分）已知函数1()()44x x f x =-，则()(f x )A ．是奇函数，且在R 上是增函数B ．是偶函数，且在R 上是增函数C ．是奇函数，且在R 上是减函数D ．是偶函数，且在R 上是减函数【解答】解：1()4x y =为减函数，4x y =为增函数，故函数()f x 为减函数，又()44x x f x -=-，则()44(44)()x x x x f x f x ---=-=--=-，则函数()f x 为奇函数，故选：C ．7．（5分）要得到函数4sin(3)3y x π=-的图象，只需要将函数4sin3y x =的图象( )A ．向左平移9π个单位 B ．向右平移9π个单位 C ．向左平移3π个单位D ．向右平移3π个单位【解答】解：由于4sin(3)4sin3()39y x x ππ=-=-，故只需要将函数4sin3y x =的图象向右平移9π个单位． 故选：B ．8．（5分）函数2()x xe ef x x --=的图象大致为( )A ．B ．C ．D ．【解答】解：函数的定义域为{|0}x x ≠，2()()x xe ef x f x x ---==-，则函数()f x 是奇函数，图象关于原点对称，排除A ，当x →+∞，()f x →+∞排除C ，D ， 故选：B ．9．（5分）设函数2()cos cos f x x b x c =++，则()f x 的最小正周期( ) A ．与b 有关，但与c 无关 B ．与b 有关，且与c 有关C ．与b 无关，且与c 无关D ．与b 无关，但与c 有关【解答】解2cos2111()cos cos cos cos2cos 222x f x x b x c b x c x b x c +=++=++=+++Q ； 0b =时，11()cos222f x x c =++的最小正周期为π；0b ≠时，显然有()()f x f x π+≠，(2)()x f x π+=其最小正周期为2π；而c 不影响周期()f x ∴的最小正周期与b 有关，但与c 无关；故选：A ．10．（5分）已知函数23,0()(1),0x x x f x ln x x ⎧-+<=⎨+⎩…，若|()|f x ax …，则a 的取值范围是( )A ．(-∞，0]B ．(-∞，1]C ．[3-，0]D ．[3-，1]【解答】解：当0x >时，根据(1)0ln x +>恒成立，则此时0a „．当0x „时，根据23x x -+的取值为(-∞，0]，2|()|3f x x x ax =-…， 0x =时 左边=右边，a 取任意值．0x <时，有3a x -…，即3a -…． 综上可得，a 的取值为[3-，0]， 故选：C ．11．（5分）已知函数()()f x x R ∈满足()4()f x f x -=-，若函数21x y x+=与()y f x =图象的交点为1(x ，1)y ，2(x ，2)y ，⋯，(m x ，)m y ，则1()(mi i i x y =+=∑ )A ．0B ．mC ．2mD ．4m【解答】()4()f x f x -=-Q ，()()4f x f x -+=， ()f x ∴的图象关于点(0,2)对称， 2112x y x x+==+Q ，y ∴关于点(0,2)对称， 1230m x x x x ∴+++⋯+=，123422m my y y y m +++⋯+=⨯=， ∴1()2mi i i x y m =+=∑．故选：C ．12．（5分）关于函数()sin |||sin |f x x x =+有下述四个结论： ①()f x 是偶函数②()f x 的最大值为2③()f x 在[π-，]π有4个零点④()f x 在区间(,)2ππ单调递减其中所有正确结论的编号是( ) A ．①②④B ．②③④C ．①③④D ．①②③【解答】解：关于函数()sin |||sin |f x x x =+有下述四个结论： 对于①：由于()()f x f x -=，所以函数()f x 是偶函数．故正确． 对于②：当0x >时，当2x π=时，函数()f x 的最大值为2，故正确．对于③()f x 在[π-，]π有3个零点，故错误．对于④根据函数的图象())sin |||sin |f x x x =+在区间(,)2ππ都单调递减，所以函数在区间(,)2ππ单调递减．故正确． 故选：A ．二、填空题：本大题共4小题，每小题5分，共20分.请将答案填写在答题卡相应位置上. 13．（5分）已知函数()2)2f x ln x =+，则1(5)()5f lg f lg += 4 ．【解答】解：根据题意，函数()2)2f x ln x =+，其定义域为R ，()2)2f x ln x -=+，则()()2)2)44f x f x ln x ln x +-=++=， 则1(5)()(5)(5)45f lg f lg f lg f lg +=+-=；故答案为：4．14．（5分）已知sin(5)cos(8)tan()()3sin()cos()22f αππααπαππαα----=-+，其中α是第三象限角，且31cos()25πα-=，则()f α=． 【解答】解：Q sin(5)cos(8)tan()(sin )cos (tan )()tan 3(cos )sin sin()cos()22f αππααπαααααππαααα------====---+，又Q 31cos()25πα-=， 1sin 5α∴=-，αQ 是第三象限角，cos α∴=sin ()tan cos f αααα∴=-=-=故答案为：．15．（5分）若04πα<<，04πβ-<<，1cos()43πα+=，cos()43πβ-=，则cos()3βα+=． 【解答】解：Q 04πα<<，∴442πππα<+<，且1cos()43πα+=，∴sin()4πα+ Q 04πβ-<<，∴4433ππβπ<-<，且cos()43πβ-=，∴sin()43πβ-， ∴cos()cos[()()]3443βππβαα+=+-- cos()cos()sin()sin()443443ππβππβαα=+-++-13=+=16．（5分）设函数()()f x x R ∈满足()()f x f x -=，()(2)f x f x =-，且当[0x ∈，1]时，3()f x x =又函数()|cos()|g x x x π=，则函数13()()()[,]22h x g x f x =--上的零点个数为 6 ．【解答】解：因为当[0x ∈，1]时，3()f x x =，所以， 当[1x ∈，2]时，2[0x -∈，1]，3()(2)(2)f x f x x =-=-．当[0x ∈，1]2时，()cos()g x x x π=；当1[2x ∈，3]2时，()cos g x x x π=-．注意到函数()f x 、()g x 都是偶函数，且(0)(0)f g =，f （1）g =（1）1=，13()()022g g ==，作出函数()f x 、()g x 的草图，函数()h x 除了0、1这两个零点之外， 分别在区间1[2-，0]，[0，1]2，1[2，1]，[1，3]2上各有一个零点．共有6个零点， 故答案为 6．三、解答题：本大题共6小题共70分.解答应写出文字说明，演算步骤或证明过程.解答写在答题卡上的指定区域内. 17．已知(,)2παπ∈，5sin α=（1）求sin()6πα+的值；（2）求5cos(2)3πα-的值． 【解答】解：（1）Q 5(,),sin 2παπα∈=，∴25cos α= ∴sin()sincos cos sin 666πππααα+=+ 12535(2=⨯155=（2）5254sin 22sin cos 2(5ααα===-，213cos2121255sin αα=-=-⨯=， ∴555cos(2)cos cos2sin sin 2333πππααα-=-g1334()()255=⨯-⨯- 343-=． 18．已知函数22()sin cos 3cos ()f x x x x x x R =-+∈． （Ⅰ）求()3f π的值；（Ⅱ）求()f x 的最小正周期及单调递增区间．【解答】解：函数22()sin cos 23cos ff x x x x x =-+．化简可得：()3sin 2cos22sin(2)6f x x x x π=-=-（Ⅰ）()2sin(2)2sin 23362f ππππ=⨯-==；（Ⅱ）()f x 的最小正周期22T ππ==． 由222262k x k πππππ--+剟，得：63k x k ππππ-+剟()f x ∴的单调递增区间为[6k ππ-，]3k ππ+．k Z ∈． 19．若函数()y f x =是周期为2的偶函数，当[1x ∈，2]时，()3f x x =-+．在()y f x =的图象上有两点A 、B ，它们的纵坐标相等，横坐标都在区间[1，3]上． （1）求当[2x ∈，3]时()f x 的解析式；（2）定点C 的坐标为(0,3)，求ABC ∆面积的最大值． 【解答】解：（1）Q 函数()y f x =是周期为2的偶函数，当[1x ∈，2]时，()3f x x =-+，[2x ∈-，1]-时，()()3f x f x x =-=+，∴当[0x ∈，1]时，2[2x -∈-，1]-，()(2)1f x f x x ∴=-=+，当[2x ∈，3]时，2[0x -∈，1]，()(2)(2)11f x f x x x =-=-+=-（2）在()y f x =的图象上有两点A 、B ，它们的纵坐标相等，横坐标都在区间[1，3]上． 如图A 、B 的横坐标的差的最大值为2，(0,1)A ，(2,1)B 时， ABC ∆的面积为12222S =⨯⨯=．20．如图，一个半圆和长方形组成的木块，长方形的边CD 为半圆的直径，O 为半圆的圆心，2AB =，1AD =，现要将此木块锯出一个等腰三角形EFG ，其底边EF AB ⊥，点E 在半圆上．（1）设6EOC π∠=，求三角形木块EFG 面积；（2）设EOC θ∠=，试用θ表示三角形木块EFG 的面积S ，并求S 的最大值．【解答】解：（1）设EF 交CD 交于Q 点，因为6EOC π∠=，所以12EG =，3OQ =，1133633(1)222EFG S EF DQ ∆+==⨯⨯+=g g ； （2）设EOQ θ∠=，所以[0θ∈，]2π，sin EQ θ=，cos OQ θ=所以11(1sin )(1cos )22EFG S EF AQ θθ∆=⨯=++g1(1sin cos sin cos )2θθθθ=+++ 令sin cos [1t θθ+=∈，2]， 所以2211(1)(1)224EFG t t S t ∆-+=++=， 所以4πθ=，当2t =，EFG S ∆的最大值为322+．21．对于函数()f x ，若在定义域内存在实数x ，满足()2()f x f x -=-，则称“局部中心函数”．（1）已知二次函数2()241()f x ax x a a R =+-+∈，试判断()f x 是否为“局部中心函数”，并说明理由；（2）若12()423x x f x m m +=-+-g 是定义域为R 上的“局部中心函数”，求实数m 的取值范围．【解答】解：（1）由()()2f x f x -+=可得22282(4)0ax a a x -=-=显然有解2x =或2x =-， 故()f x 为“局部中心函数，（2）若()f x 为局部中心函数，则()()2f x f x -+=有解， 得12124234232x x x x m m m m +--+-+-+-+-=g g ， 令222x x t -+=…，从而22()22100g t t mt m =-+-=在[2，)+∞有解．①当g （2）0„时，2222100t mt m -+-=在[2，)+∞有解，由g （2）0„，即22460m m --„，解得13m -剟； ②当g （2）0>时，2222100t mt m -+-=在[2，)+∞有解等价于2224040(2)2(23)0m m g m m >⎧⎪=-⎨⎪=-->⎩V …，解得3m <„综上，所求实数m的取值范围为1m -<„ 22．已知a R ∈，函数21()log ()f x a x=+．（1）当9a =时，解不等式()0f x >；（2）若关于x 的方程2()log [(3)24]0f x a x a --+-=的解集中恰好有一个元素，求a 的取值范围；（3）设0a >，若对任意1[,1]2t ∈，函数()f x 在区间[t ，1]t +上的最大值与最小值的差不超过1，求a 的取值范围．【解答】解：（1）当9a =时，令21()(9)0f x log x =+>，则1901910x xx ⎧+>⎪⎪⎪+>⎨⎪≠⎪⎪⎩，解得18x <-或0x >，∴所求不等式的解集为1(,)(0,)8-∞-+∞U ；（2）方程2()log [(3)24]0f x a x a --+-=即1(3)24a a x a x +=-+-，亦即1(3)4a x a x=-+-， 设1(),()(3)4g x h x a x a x==-+-，则依题意，函数()g x 与函数()h x 在第一象限有且仅有一个交点，而函数()g x 为反比例函数，函数()h x 为恒过定点(1,1)--的一条直线，易知，要使函数()g x 与函数()h x 在第一象限有且仅有一个交点，只需30a ->即可，解得3a >．∴所求实数a 的取值范围为(3,)+∞；（3）由复合函数的单调性可知，函数21()log ()f x a x =+在[t ，1]t +上为减函数，其中1[,1]2t ∈， 依题意，22110()()11log a log a t t <+-++„，即112()1a a t t +++„，亦即121a t t -+…， 设1212(1)212121()22,[,1]111121t t t q t t t t t t t t t t +-=-=-=+-=+-∈++++， 设1[1,2]m t =∈，令22()213,[1,2]11p m m m m m m =+-=++-∈++，由双勾函数的性质可知，函数()p m 在[1，2]上单调递增，故2()(2)3max p m p ==， ∴实数m 的取值范围为2[,)3+∞．。

合肥一中 芜湖一中 安师大附中 蚌埠二中 安庆一中 淮北一中安徽省六校2015级高一新生入学素质测试数 学一、选择题（每题3分，共30分）1．下列各式中，正确的是（ ）A ．632a a a =⋅B ．9312=⎪⎭⎫ ⎝⎛-C ．()63293a a -=-D ．()ππ-=-2222．下列说法中正确的是（ ）A ．若0a <，则20a <B ．x 是实数，且2x a =，则0a > C ．x -有意义时，0x ≤ D ．0.1的平方根是0.01±3．某公司员工分别住在A 、B 、C 三个住宅区，A 区有30人，B 区有15人，C 区有10人．三个区在一条直线上，位置如图所示．公司的接送打算在此间只设一个停靠点，要使所有员工步行到停靠点的路程总和最少，那么停靠点的位置应在（ ）A ．A 区B ． B 区C ． C 区D ． 不确定4．若某几何体的正视图与侧视图均为边长是1的正方形，且其体积为，则该几何体的俯视图可以是（ ）A ． B. C ． D ．5．甲、乙两人完成一项工作，甲先做了3天，然后乙加入合作，完成剩下的工作，设工作总量为1，工作进度如下表：天数累计到第3天 累计到第5天 工作进度 14 12则完成这项工作共需（ ）A ．9天B ．10天C ．11天D ．12天6．东东准备给南南打电话，由于保管不善，电话本上的南南手机号码中，有两个数字已模糊不清．如果用x ，y 表示这两个看不清的数字，那么南南的手机号码为139x370y580，东东记得这11个数字之和是20的整数倍．则东东一次拨对南南手机号码的概率是（ ）A ．B ．C ．D ． 7．如图，△ABC 中，∠A=30°，3tan B =，AC=，则AB 的长为（ ）A ．B ．C ． 5D ．8．有两个一元二次方程：M ：20ax bx c ++= N ：20cx bx a ++=，其中0,ac a c ≠≠，下列四个结论中，错误的是（ ）A ．如果方程M 有两个不相等的实数根，那么方程N 也有两个不相等的实数根；B ．如果方程M 有两根符号相同，那么方程N 的两根符号也相同；C ．如果5是方程M 的一个根，那么15是方程N 的一个根；D ．如果方程M 和方程N 有一个相同的根，那么这个根必是1x =9．已知二次函数()=-+-211≤≤1y x bx b ，当b 从-1逐渐变化到1的过程中，它所对应的抛物线位置也随之变动．下列关于抛物线的移动方向的描述中，正确的是（ ）A ．先往左上方移动，再往左下方移动B ．先往左下方移动，再往左上方移动C ．先往右下方移动，再往右上方移动D ．先往右上方移动，再往右下方移动10． 如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形。

合肥六中、淮北一中、阜阳一中、滁州中学、合肥一中2018-2019学年第一学期高二年级期末考试生物试卷参考答案
分值100分；时长90分钟
命题人：王攀审题人：夏书敏
参考答案
一．选择题（共60分，1-15每题2分，16-25每题3分）
1-5CDAAD6-10BAACC
11-15BDDCD16-20CAADB
21-25DDBCA
二．非选择题（共40分）
31.（共10分，除标注外，每空1分）
和有机物（2分）（2）适当提高温度；适当增加光照（1）类囊体薄膜上；C
5
（3）D
溶液浓度过高，使叶肉细胞失水而导致代谢水平下降（2分）
（4）因为NaHCO
3
；层析液
（5）CaCO
3
32.（共10分，每空2分）
（1）含GLUT的囊泡;GLUT（2）突触小泡释放神经递质
（3）抑制炎症因子释放导致的神经细胞变性、坏死（4）低
33.（共10分，每空2分）
（1）1/2n-12n-2/2n(2)大于（3）0≤x≤64%（4）DNA解旋酶和RNA聚合酶34.（共10分，每空2分）
果蝇的眼色及性别（2）1/4
Ⅰ（1）F
2
Ⅱ21表现型和比例。

安徽省合肥市第六中学2018-2019学年高二上学期开学质量检测数学试题一、选择题（本大题共12小题，共60.0分）1.）161820222.函数的定义域为（）A. B. C. D.3.已知函数f（x）与g（x）的图象在R上不间断，由下表知方程f（x）=g（x）有实数解的区间是（）4.已知偶函数f（x）在区间[0，+∞）单调递增，则满足f（2x-1）＜f（）的x取值范围是（）A. B. C. D.5.已知角α的终边经过一点P（x，x2+1）（x＞0），则tanα的最小值为（）A. 1B. 2C.D.已知各项不为0的等差数列{a n}满足a3-a72+a11=0，数列{b n}是等比数列，且b7=a7，则b5•b7•b9等于（）A. 1B. 2C. 4D. 87.已知O，N，P在△ABC所在平面内，且|=，且，则点O，N，P依次是△ABC的（）A. 重心外心垂心B. 重心外心内心C. 外心重心垂心D. 外心重心内心将函数y=cos x+sin x（x∈R）的图象向左平移m（m＞0）个单位长度后，所得到的图象关于y 轴对称，则m的最小值是（）A. B. C. D.9.已知数列{a n}，{b n}满足a1=1，=，a n b n=1，则使b n＞101的最小的n为（）A. 4B. 5C. 6D. 710.△ABC中，角A，B，C的对边分别为a，b，c，已知，，则S△ABC的最大值为（）A. B. C. D.设函数，若关于x的方程[f（x）]2-af（x）=0恰有三个不同的实数解，则实数a的取值范围为（）A. B. C. D.12.已知ω＞0，函数f（x）=sin（ωx+）在区间[，π]上单调递减，则实数ω的取值范围是（）A. B. C. D.二、填空题（本大题共4小题，共20.0分）若以连续掷两次骰子分别得到的点数m、n作为点P的横、纵坐标，则点P（m，n）落在直线x+y=4下方的概率为______14.已知=（-2，-1），=（λ，1），若和的夹角为钝角，则λ的取值范围是______．已知函数f（x）=log a x（a＞0且a≠1）和函数g（x）=sin x，若f（x）与g（x）的图象有且只有3个交点，则a的取值范围是______．在等腰梯形ABCD中，已知AB∥DC，AB=2，BC=1，∠ABC=60°．动点E和F分别在线段BC和DC上，且=λ，=，则•的最小值为______．三、解答题（本大题共6小题，共70.0分）已知向量=（cosωx-sinωx，sinωx），=（-cosωx-sinωx，2cosωx），设函数f（x）=•+λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（，1）（1）求函数f（x）的最小正周期；（2）若y=f（x）的图象经过点（，0）求函数f（x）在区间[0，]上的取值范围．设△ABC的内角A、B、C的对边长分别为a、b、c．设S为△ABC的面积，满足S=（a2+c2-b2）．（Ⅰ）求B；（Ⅱ）若b=，求（-1）a+2c的最大值．某港口有一个泊位，现统计了某月100艘轮船在该泊位停靠的时间（单位：小时），如果停靠时间不足半小时按半小时计时，超过半小时不足1小时按1小时计时，依此类推，统计结果如表：（Ⅰ）设该月100艘轮船在该泊位的平均停靠时间为a小时，求a的值；（Ⅱ）假定某天只有甲、乙两艘轮船需要在该泊位停靠a小时，且在一昼夜的时间段中随机到达，求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率．已知指数函数y=g（x）满足：g（2）=4，定义域为R的函数f（x）=是奇函数．（1）确定y=g（x）的解析式；（2）求m，n的值；（3）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求实数k的取值范围．已知关于x的二次方程x2+2mx+2m+1=0．（Ⅰ）若方程有两根，其中一根在区间（-1，0）内，另一根在区间（1，2）内，求m的取值范围．（Ⅱ）若方程两根均在区间（0，1）内，求m的取值范围．设等差数列{a n}的前n项和为S n，且a2=2，S5=15，数列{b n}的前n项和为T n，且，2nb n+1=（n+1）b n（n∈N*）．（1）求数列{a n}的通项公式a n及前n项和S n；（2）求数列{b n}的通项公式b n及前n项和为T n；（3）记集合，若集合A中有且仅有5个元素，求实数λ的取值范围．答案和解析1. B【解析】解：由表中数据知，样本中心点的横坐标为：=×（2+3+4+5+6）=4，由回归直线经过样本中心点，得=4×4-4=12，即=×（3+7+11+a+21）=12，解得a=18．故选：B．由表中数据计算样本中心点的横坐标，根据回归直线经过样本中心点求出的值，从而求出a的值．本题考查了回归直线过样本中心点的应用问题，是基础题目．2.【答案】C【解析】解：由题意知，函数的定义域为，解得-1＜x＜1，故选：C．由题意知，解得-1＜x＜1，由此能求出函数的定义域．本题考查对数函数的定义域，解题时要注意不等式组的解法．3.【答案】B【解析】解：构造函数F（x）=f（x）-g（x），则由题意，F（0）=3.011-3.451＜0，F（1）=5.432-5.241＞0，∴函数F（x）=f（x）-g（x）有零点的区间是（0，1），∴方程f（x）=g（x）有实数解的区间是（0，1），故选：B．构造函数F（x）=f（x）-g（x），则由题意，F（0）=3.011-3.451＜0，F（1）=5.432-5.241＞0，即可得出结论．本题考查方程f（x）=g（x）有实数解的区间，考查函数的零点，考查学生的计算能力，属于基础题．4.【答案】A【解析】解：∵f（x）是偶函数，∴f（x）=f（|x|），∴不等式等价为f（|2x-1|），∵f（x）在区间[0，+∞）单调递增，∴，解得．故选：A．根据函数奇偶性和单调性的性质，将不等式进行转化求解即可．本题主要考查不等式的求解，根据函数奇偶性和单调性的关系将不等式进行转化是解决本题的关键．5.【答案】B【解析】解：∵已知角α的终边经过一点P（x，x2+1）（x＞0），则tanα==x+≥2=2，当且仅当x=1时，取等号，故tanα的最小值为2，故选：B．由题意利用任意角的三角函数的定义，基本不等式，求得tanα的最小值．本题主要考查任意角的三角函数的定义，基本不等式的应用，属于基础题．6.【答案】D【解析】解：在等差数列{a n}中，由a3-a72+a11=0，得，∵a n≠0，∴a7=2．∴b7=a7=2，在等比数列{b n}中，有b5•b7•b9 =．故选：D．由已知a3-a72+a11=0结合等差数列的性质求得a7，得到b7，再由等比数列的性质求得a5•b7•b9 ．本题考查等差数列的通项公式，考查了等比数列的性质，是基础题．7.【答案】C【解析】解：∵||=||=||，∴O到三角形三个顶点的距离相等，∴O是三角形的外心，根据所给的四个选项，第一个判断为外心的只有C，D两个选项，∴只要判断第三个条件可以得到三角形的内心或垂心就可以，∵，∴（）=0，=0，∴，同理得到另外两个向量都与边垂直，得到P是三角形的垂心，故选：C．据O到三角形三个顶点的距离相等，得到O 是三角形的外心，根据所给的四个选项，第一个判断为外心的只有③④两个选项，只要判断第三个条件可以得到三角形的什么心就可以，移项相减，得到垂直，即得到P是三角形的垂心．本小题主要考查向量的数量积的运算法则、三角形五心等基础知识，考查运算求解能力，考查化归与转化思想，本题是一个考查的向量的知识点比较全面的题目，把几种三角形的心总结的比较全面，解题时注意向量的有关定律的应用．8.【答案】C【解析】解：将函数y=cosx+sinx=2sin（x+）（x∈R）的图象向左平移m（m＞0）个单位长度后得到y=2sin（x+m+），所得到的图象关于y轴对称，则m+=kπ+，k∈Z，即m=kπ+，故m的最小值为；故选：C．利用函数y=Asin（ωx+φ）的图象变换规律，三角函数的图象的对称性，求得m的最小值本题主要考查函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，属于基础题9.【答案】C【解析】解：由=，得3a n+1a n+2a n+1=a n，两边同除a n+1a n得，=+3，设+k=2（+k），则=+k，即k=3，∴=2，由a1=1得=4，∴数列{+3}是以2为公比、4为首项的等比数列，则+3=4•2n-1=2n+1，∴=2n+1-3，由a n b n=1得b n==2n+1-3，∴b n＞101为2n+1-3＞101，即2n+1＞104，∵26=64，27=128，∴使b n＞101的最小的n为6．故选：C．先化简已知的等式，利用待定系数法和构造法得到数列{+3}是等比数列，由条件和等比数列的通项公式求出，代入a n b n=1求出b n，化简使b n＞101即可求出最小的n．本题考查数列递推公式的化简，待定系数法和构造法求数列的通项公式，是中档题．10.【答案】D【解析】解：由正弦定理知：，即，故，所以，又，由余弦定理得b2=a2+c2-2accosB=a2+c2+ac≥3ac，∴，故，故选：D．由正弦定理化简已知等式可求，进而可求B，由余弦定理，基本不等式可求，进而利用三角形面积公式即可得解．本题主要考查了正弦定理，余弦定理，基本不等式，三角形面积公式在解三角形中的应用，考查了转化思想，属于基础题．11.【答案】A【解析】解：作出函数的图象如图，令t=f（x），要使方程[f（x）]2-af（x）=0恰有三个不同的实数解，则方程t2-at=0一个根为0，另一根a∈（0，1]．故选：A．画出函数，令t=f（x），则要使方程[f（x）]2-af（x）=0恰有三个不同的实数解，可得方程t2-at=0一个根为0，另一根a∈（0，1]．本题考查根的存在性及根的个数判断，考查数形结合的解题思想方法，是中档题．12.【答案】A【解析】解：法一：令：不合题意排除（D）合题意排除（B）（C）法二：，得：．故选：A．法一：通过特殊值ω=2、ω=1，验证三角函数的角的范围，排除选项，得到结果．法二：可以通过角的范围，直接推导ω的范围即可．本题考查三角函数的单调性的应用，函数的解析式的求法，考查计算能力．13.【答案】【解析】解：以连续掷两次骰子分别得到的点数m、n作为点P的横、纵坐标，基本事件总数N=6×6=36，点P（m，n）落在直线x+y=4下方包含的基本事件有：（1，1），（1，2），（2，1），共3个，则点P（m，n）落在直线x+y=4下方的概率为p=．故答案为：．基本事件总数N=6×6=36，利用列举法求出点P（m，n）落在直线x+y=4下方包含的基本事件有3个，由此能求出点P（m，n）落在直线x+y=4下方的概率．本题考查概率的求法，考查古典概型、列举法等基础知识，考查运算求解能力，是基础题．14.【答案】λ＞-且λ≠2【解析】解：∵与的夹角为钝角，∴cos＜，＞＜0．且与不共线∴•＜0．且-λ+2≠0∴-2λ-1＜0．且λ≠2∴λ＞-且λ≠2．故答案为：λ＞-且λ≠2根据两个向量的夹角是钝角，则两个向量的夹角的余弦小于零，从而得到两个向量的数量积小于零，用坐标形式表示向量的数量积，解不等式，得到变量的范围．两个向量的数量积是一个数量，它的值是两个向量的模与两向量夹角余弦的乘积，结果可正、可负、可以为零，其符号由夹角的余弦值确定．15.【答案】（，）∪（5，9）【解析】解：作图分析，y=sin x，与y=log a x（a＞0，a≠1），要使得原方程恰有三个不相等的实数根，转会为两函数图象有三个不同的交点．当a∈（0，1）时，y=log a3＞-1，y=log a7＜-1，得：a∈（，）当a∈（1，+∞）时，y=loga5＜1，y=loga9＞1，得：a∈（5，9）故答案为：（，）∪（5，9）．画出两个函数的图象，结合图象列出不等式，求出a的范围．本题用到的基本方法是数形结合法和分类讨论法，这两种方法都是高考重点考查的方法，对高中学生来讲，务必掌握．16.【答案】【解析】解：由题意，得到AD=BC=CD=1，所以•=（）•（）=（）•（）==2×1×cos60°+λ1×1×cos60°+×2×1+×1×1×cos120°=1++-≥+=（当且仅当时等号成立）；故答案为：．利用等腰梯形的性质结合向量的数量积公式将所求表示为关于λ的代数式，根据具体的形式求最值．本题考查了等腰梯形的性质以及向量的数量积公式的运用、基本不等式求最值；关键是正确表示所求，利用基本不等式求最小值．17.【答案】解：（1）∵f（x）=•+λ=（cosωx-sinωx）×（-cosωx-sinωx）+sinωx×2cosωx+λ=-（cos2ωx-sin2ωx）+sin2ωx+λ=sin2ωx-cos2ωx+λ=2sin（2ωx-）+λ∵图象关于直线x=π对称，∴2πω-=+kπ，k∈z∴ω=+，又ω∈（，1）∴k=1时，ω=∴函数f（x）的最小正周期为=（2）∵f（）=0∴2sin（2××-）+λ=0∴λ=-∴f（x）=2sin （x-）-由x∈[0，]∴x-∈[-，]∴sin（x-）∈[-，1]∴2sin（x-）-=f（x）∈[-1-，2-]故函数f（x）在区间[0，]上的取值范围为[-1-，2-]【解析】（1）先利用向量数量积运算性质，求函数f（x）的解析式，再利用二倍角公式和两角差的余弦公式将函数f（x）化为y=Asin（ωx+φ）+k型函数，最后利用函数的对称性和ω的范围，计算ω的值，从而得函数的最小正周期；（2）先将已知点的坐标代入函数解析式，求得λ的值，再求内层函数的值域，最后将内层函数看做整体，利用正弦函数的图象和性质即可求得函数f（x）的值域．本题主要考查了y=Asin （ωx+φ）+k型函数的图象和性质，向量数量积运算性质，复合函数值域的求法，整体代入的思想方法，属基础题18.【答案】解：（Ⅰ）∵S=ac sin B，cos B=即a2+c2-b2=2ac cos B，∴S=（a2+c2-b2）变形得：ac sin B=×2ac cos B，整理得：tan B=，又0＜B＜π，∴B=，（Ⅱ）∵A+B+C=π，∴0＜A＜，由正弦定理知a===2sin A，c==2sin （-A），∴（-1）a+2c=2（-1）sin A+4sin（-A）=2sin A+2cos A=2sin（A+）≤2，当且仅当A=时取最大值，故（-1）a+2c的最大值为2．【解析】（Ⅰ）利用三角形的面积公式表示出S，利用余弦定理表示出cosB，代入已知等式求出tanB的值，即可求出B，（Ⅱ）先求出A的范围，再根据正弦定理表示出a，c，根据两角和差的正弦公式，正弦函数的图象和性质即可求出最大值本题考查三角形面积公式正弦定理、余弦定理和三角函数的化简，正弦函数的图象和性质，属于中档题．19.【答案】解：（Ⅰ）a=（2.5×12+3×12+3.5×17+4×20+4.5×15+5×13+5.5×8+6×3）=4，（Ⅱ）设甲船到达的时间为x，乙船到达的时间为y，则若这两艘轮船在停靠该泊位时至少有一艘船需要等待，则|y-x|＜4，所以必须等待的概率为P=1-=，答：这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率为．【解析】（Ⅰ）根据平均数的定义即可求出，（Ⅱ）设出甲、乙到达的时刻，列出所有基本事件的约束条件同时列出这两艘船中至少有一艘在停靠泊位时必须等待约束条件，利用线性规划作出平面区域，利用几何概型概率公式求出概率．本题主要考查建模、解模能力；解答关键是利用线性规划作出事件对应的平面区域，再利用几何概型概率公式求出事件的概率．20.【答案】解：（1）∵指数函数y=g（x）满足：g（2）=4，∴g（x）=2x；（2）由（1）知：f （x）=是奇函数．因为f（x）是奇函数，所以f（0）=0，即，∴n=1；∴f（x）=，又由f（1）=-f （-1）知，∴m=2；（3）由（2）知f（x）=，易知f（x）在（-∞，+∞）上为减函数．又因f（x）是奇函数，从而不等式：f（t2-2t）+f（2t2-k）＜0等价于f（t2-2t）＜-f（2t2-k）=f（k-2t2），因f （x）为减函数，由上式推得：t2-2t＞k-2t2，即对一切t∈R有：3t2-2t-k＞0，从而判别式△=4+12k＜0，解得：k＜．【解析】（1）根据指数函数y=g（x）满足：g（2）=4，即可求出y=g（x）的解析式；（2）由题意知f （0）=0，f（1）=-f（-1），解方程组即可求出m，n的值；（3）由已知易知函数f（x）在定义域f（x）在（-∞，+∞）上为减函数．我们可将f（t2-2t）+f（2t2-k）＜0转化为一个关于实数t的不等式组，解不等式组，即可得到实数t的取值范围．本题考查的知识点：待定系数法求指数函数的解析式，函数的奇偶性和函数单调性的性质，其中根据函数的单调性将f（t2-2t）+f（2t2-k）＜0转化为一个关于实数t的不等式组是解答本题的关键，体现了转化的思想，考查了运算能力和灵活应用知识分析解决问题的能力，属中档题．21.【答案】解：（Ⅰ）设f（x）=x2+2mx+2m+1，问题转化为抛物线f（x）=x2+2mx+2m+1与x 轴的交点分别在区间（-1，0）和（1，2）内，则，可得．解得，∴m的取值范围为．（Ⅱ）若抛物线与x轴交点均落在区间（0，1）内，则有，即，解得，故m的取值范围为．【解析】（Ⅰ）把问题转化为抛物线f（x）=x2+2mx+2m+1与x轴的交点分别在区间（-1，0）和（1，2）内，解不等式组求出m的取值范．（Ⅱ）若抛物线与x轴交点均落在区间（0，1）内，则有，由此求得m的取值范围．本题主要考查一元二次方程根的分布与系数的关系，体现了转化的数学思想，属于中档题．22.【答案】解：（1）由等差数列性质可知，S5=5a3=15，即a3=3，由d=a3-a2=1，∴a n=a2+（n-2）d=n，…（2分）∴．…（4分）（2）由得，∴当n≥2时，，即，当n=1时，，适合上式，∴．…（6分），①，②①-②得，，∴．…（10分）（3）∵=…（11分）由上面得，令，∵，∴当n≥3时，f（n+1）-f（n）＜0，即f（n+1）＜f（n）…（12分）又f（1）=1，，，，，…（14分）∵集合A中有且仅有5个元素，∴，n∈N*解的个数为5，∴．…（16分）【解析】（1）由等差数列的性质S5=5a3=15，求得a3=3，由d=a3-a2=1，a n=a2+（n-2）d=n，根据等差数列前n项和公式即可求得S n；（2），采用“累乘法”即可求得，“错位相减法”即可求得前n项和为T n；（3）由集合A可知：A=，令，利用函数的单调性建立不等进行求解，实数λ的取值范围．本题考查等差数列的性质，等差数列前n项和公式，考查“累乘法”及“错位相减法”的应用，考查数列与不等式相结合，考查计算能力，属于难题．。

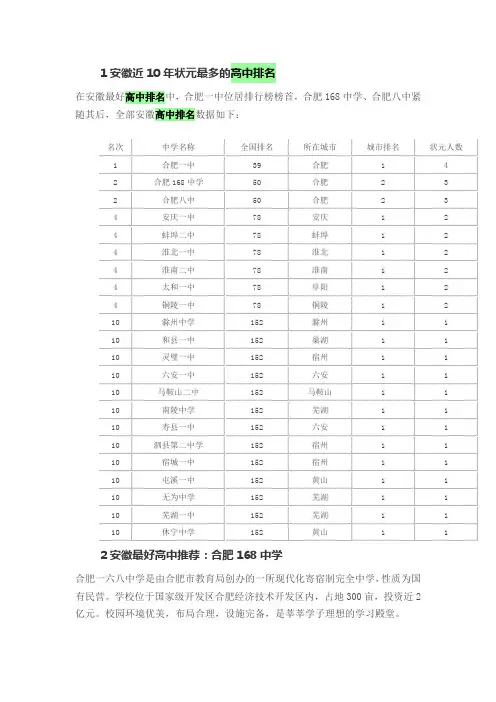
1安徽近10年状元最多的高中排名
在安徽最好高中排名中，合肥一中位居排行榜榜首，合肥168中学、合肥八中紧随其后，全部安徽高中排名数据如下：
2安徽最好高中推荐：合肥168中学
合肥一六八中学是由合肥市教育局创办的一所现代化寄宿制完全中学，性质为国有民营。

学校位于国家级开发区合肥经济技术开发区内，占地300亩，投资近2亿元。

校园环境优美，布局合理，设施完备，是莘莘学子理想的学习殿堂。

学校名称所在地区学校类型合肥168中学安徽省非示范中学3安徽最好高中推荐：合肥八中
合肥市第八中学，创办于1956年，时为初级中学，1970年开始招收第一届高中
学生，成为一所完全中学。

1998年高初中分离，成为一所高级中学。

1999年被
评为合肥市示范高中，2002年被评为安徽省示范高中。

创建时间学校类型隶属单位
1956年公立高中合肥市教育局
最好的高中排名数据仅是依据近10年高考状元而定，不能代表安徽高中学校的
整体水平，所以学生和家长们在择校时还要根据自身情况选择适合的学校，不能
盲目跟风，最后希望安徽最新高中排行榜能给大家做参考。

安徽省淮北一中、合肥六中、阜阳一中、滁州中学2025届高三第一次调研测试数学试卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置． 3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效． 5．如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若集合{}(2)0A x x x =->，{}10B x x =->，则A B =A ．{}10x x x ><或B ．{}12x x <<C ．{|2}x x >D ．{}1x x >2．如果直线1ax by +=与圆22:1C x y +=相交，则点(),M a b 与圆C 的位置关系是（ ） A ．点M 在圆C 上 B ．点M 在圆C 外 C ．点M 在圆C 内D ．上述三种情况都有可能3．已知双曲线C 的两条渐近线的夹角为60°，则双曲线C 的方程不可能为（ ）A ．221155x y -=B ．221515x y -=C ．221312y x -=D ．221217y x -=4．设x ∈R ，则“327x <”是“||3x <”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件5．如图，在四边形ABCD 中，1AB =，3BC =，120ABC ∠=︒，90ACD ∠=︒，60CDA ∠=︒，则BD 的长度为（ ）A 53B ．3C ．33D ．336．已知m ，n 为异面直线，m ⊥平面α，n ⊥平面β，直线l 满足l ⊥m ，l ⊥n ，,l α⊄,l β⊄则（ ）A ．α∥β且l ∥αB ．α⊥β且l ⊥βC ．α与β相交，且交线垂直于lD ．α与β相交，且交线平行于l7．近年来，随着4G 网络的普及和智能手机的更新换代，各种方便的app 相继出世，其功能也是五花八门.某大学为了调查在校大学生使用app 的主要用途，随机抽取了56290名大学生进行调查，各主要用途与对应人数的结果统计如图所示，现有如下说法：①可以估计使用app 主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数； ②可以估计不足10%的大学生使用app 主要玩游戏； ③可以估计使用app 主要找人聊天的大学生超过总数的14. 其中正确的个数为（ ）A ．0B ．1C ．2D ．38．如图，在中，点M 是边的中点，将沿着AM 翻折成，且点不在平面内，点是线段上一点.若二面角与二面角的平面角相等，则直线经过的（ ）A ．重心B ．垂心C ．内心D ．外心9．由曲线y ＝x 2与曲线y 2＝x 所围成的平面图形的面积为( ) A ．1B ．13C ．23D ．4310．已知a ＞b ＞0，c ＞1，则下列各式成立的是（ ） A ．sin a ＞sin bB ．c a ＞c bC ．a c ＜b cD ．11c c b a--＜ 11．函数()()sin f x A x ωϕ=+（0A >，0>ω， 2πϕ<）的部分图象如图所示，则,ωϕ的值分别为（ ）A ．2，0B ．2，4π C ．2， 3π-D ．2，6π 12．i 是虚数单位，21iz i=-则||z =（ ） A ．1 B ．2C ．2D ．22二、填空题：本题共4小题，每小题5分，共20分。

安徽省合肥六中、合肥八中、阜阳一中、淮北一中四校2025届高三六校第一次联考语文试卷注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

1、阅读下面的文字,完成下面小题阅读的目的与诉求不同，方式与结果自然也不一样。

有的阅读是为了消遣取乐，或者满足个人趣味，这样的阅读强调个体的兴会和悦纳，自由度大，个体差异也大。

思辨性阅读则不同。

它是为了获取真知，或者为了解决问题，个人的好恶与体验都要退居其次，阅读的准确性、明断性与合理性，则成了判断阅读效果的首要标准。

这就要求读者的思维始终处在“思辨”的理性状态，自觉地分析与论证，审慎地权衡与判断。

文本是思辨性阅读的根基，尊重文本，知易行难。

文本似迷宫,其意蕴与逻辑并不会直接呈現在我们面前，而是隐藏在文本之中，等着读者去挖掘。

迷宫里歧路纵横，浮云蔽日，走着走着，恐怕连自己都会走丢。

干扰我们的因素很多，语言自身就是其中之一。

语言是桥梁，是工具，这个道理人所共知；但语言又常常成为沟通与理解的障碍，成为横亘在我们与文本之间的一堵墙。

譬如《廉颇蔺相如列传》中的“秦王”，如果对他一无所知，对他的理解就会走向脸谱化。

就“完璧归赵”一节看，这个秦王看起来倒有点虚弱与怯懦，至少表面如此。

你看，蔺相如在朝堂上斥责秦王倨傲轻慢,要求他举行一个隆重仪式来交换和氏璧。

面对咄咄逼人的蔺相如，秦王没有暴跳如雷，而是满口答应。

等到秦王布置好了场面，蔺相如却派人把和氏璧送回了赵国，还公然指责秦王祖宗八辈都是背信弃义之徒。

设身处地站在秦王的角度想一想，他能不恼火吗？但秦王的反应也只是“与群臣相视而嘻”，不仅没杀蔺相如，还好生款待他，很多人由此断言秦王“外强中干”。

其实，教科书对秦王的介绍也大多如此，但历史上的秦昭襄王并非如此粗鄙与虚弱。