西南大学信号与系统作业答案
- 格式:docx
- 大小:306.49 KB
- 文档页数:14

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
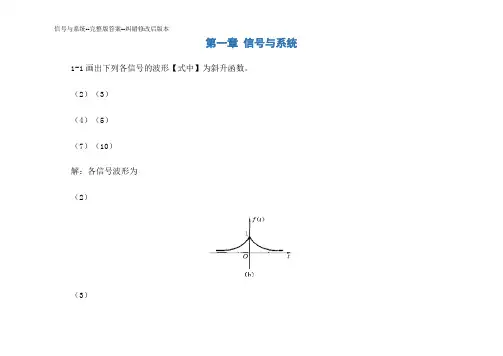
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
![18春西南大学[1073]《信号与系统》机考随机答案](https://uimg.taocdn.com/b6d257395901020207409c29.webp)
t 西南大学网络与继续教育学院课程考试一、计算题(本大题共1小题,每道题20.0分,共20.0分)1.二、判断题(本大题共10小题,每道题4.0分,共40.0分)正确的打√错误的打×1.抽取与内插意味着抽样率的转换。
对错2.系统函数可由比值形式定义,故与输入信号的形式有关。
对错3.实序列的频谱,其幅值偶对称,相位奇对称。
对错4.线性相位,指的是系统的相频特性与频率成正比。
对错5.系统为因果系统的充要条件是冲激响应是因果的信号。
对错6.一个域离散,对应另一个域的周期延拓。
对错7.冲激响应只适用于LTI系统。
对错8.连续时间LTI系统稳定的充要条件是所有极点的实部小于等于零。
对错9.任意普通信号可分解为冲激函数的叠加,可用卷积形式来描述。
对错10.离散系统原点处的零极点,不影响频率特性幅值,只影响相位。
对错三、单项选择题(本大题共10小题,每道题4.0分,共40.0分) 1.A.4B.-2C.2D.-42.A.B.C.D.3.A.因果不稳定B.非因果稳定C.因果稳定D.非因果不稳定4.关于三个变换之间的关系,下列叙述错误的是()。
A.s域的左半平面映射到z域的单位圆内部B.从s域到z域的映射是单值映射C.若原信号收敛,虚轴上的拉氏变换就是傅里叶变换D.s域的右半平面映射到z域的单位圆外部5.下列系统中,属于线性时不变系统的是()。
A.B.C.D.6.对离散系统系统频率响应仿真,调用的函数是()。
A.impulseB.freqsC.stepD.freqz7.关于稳定性的描述,下列叙述中错误的是()。
A.线性时不变系统的稳定性理论上与输入信号无关B.稳定性指的是系统克服扰动恢复到平衡态的能力C.稳定的充要条件是有界输入产生有界输出,简称BIBOD.冲激响应可以表征系统的稳定性8.A.B.C.D.9.A.中心频率点为±ω0,幅值为原信号频谱幅值的一半B.中心频率点为ω0,幅值为原信号频谱的幅值C.中心频率点为ω0,幅值为原信号频谱幅值的一半D.中心频率点为±ω0,幅值为原信号频谱的幅值10.关于信号的分解,下列叙述正确的是()A.任意普通信号可分解为冲激函数的叠加,可用卷积形式来描述B.信号能分解为实分量和虚部分量,故可对信号进行滤波C.傅里叶级数是一致性意义下的正交分解D.由于信号的可分解性,故在时域中可用冲激响应来表征系统。
![[1073]信号与系统 西南大学网络与继续教育学院课程考试试题卷](https://uimg.taocdn.com/00175178b84ae45c3b358c1d.webp)
西南大学网络与继续教育学院课程考试试题卷类别:网教 专业:电气工程及其自动化 2016 年12 月 课程名称【编号】:信号与系统【1073】 A 卷 大作业 满分:100 分一、简答题(每小题20分,共40分)1. 简述信号带宽的概念。
2. 利用公式描述时域理想冲激抽样的过程,说明抽样信号的频谱及无混叠的条件。
二、计算题(每小题20分,共60分)1. 计算序列[]{1,0,0,1},[]{1,1,2}x k h k == 的卷积。
2. 求z 反变换。
2()||1(1)(0.5)z X z z z z =>--3. 已知二阶系统的差分方程为121[][1][2][1]y k a y k a y k b x k =-+-+- 21240a a +<试求:(1)系统的系统函数; (2)频率响应;(3)绘制幅频特性曲线。
一、简答题1. 简述信号带宽的概念。
答:实际信号的频谱往往是无限延伸的。
为了便于分析与设计实现,信号的带宽指所需要考虑的有效频率分量,一般可用频谱包络线第一次的过零点作为信号的带宽。
2. 利用公式描述时域理想冲激抽样的过程,说明抽样信号的频谱及无混叠的条件。
答:时域的理想冲激抽样可表示为两边同时取傅里叶变换,得信号经时域离散化后,频域会产生周期延拓,幅值会加权1/T 。
如果要从采样信号的频谱得到原信号的频谱,在周期延拓过程中就不能有混叠产生。
从而有抽样定理采样的角频率,应比信号的最高频率大2倍以上。
二、 计算题1.计算序列[]{1,0,0,1},[]{1,1,2}x k h k == 的卷积。
2.求z 反变换。
2()||1(1)(0.5)z X z z z z =>--3.已知二阶系统的差分方程为121[][1][2][1]y k a y k a y k b x k =-+-+- 21240a a +<试求:(1)系统的系统函数; (2)频率响应;(3)绘制幅频特性曲线。

⼤学信号与系统习题答案§ 1.1 信号与系统信号(signal)消息(Message):在通信系统中,⼀般将语⾔、⽂字、图像或数据统称为消息。
信号(Signal):指消息的表现形式与传送载体。
信息(Information):⼀般指消息中赋予⼈们的新知识、新概念,定义⽅法复杂,将在后续课程中研究。
信号是消息的表现形式与传送载体,消息是信号的传送内容。
如电信号传送声⾳、图像、⽂字等。
电信号是应⽤最⼴泛的物理量,如电压、电流、电荷、磁通等。
系统(system)系统(system):由若⼲相互作⽤和相互依赖的事物组合⽽成的,具有稳定功能的整体。
如太阳系、通信系统【-----为传送消息⽽装设的全套技术设备(包括传输信道),其⽅框如下图所⽰:消息信号】、控制系统、经济系统、⽣态系统等。
系统可以看作是变换器、处理器。
电系统具有特殊的重要地位,某个电路的输⼊、输出是完成某种功能,如微分、积分、放⼤,也可以称系统。
在电⼦技术领域中,“系统”、“电路”、“⽹络”三个名词在⼀般情况下可以通⽤。
信号理论与系统理论信号理论信号分析:研究信号的基本性能,如信号的描述、性质等。
信号传输:通信的⽬的是为了实现消息的传输。
原始的光通信系统——古代利⽤烽⽕传送边疆警报;声⾳信号的传输——击⿎鸣⾦。
利⽤电信号传送消息。
1837年,莫尔斯(F.B.Morse)发明电报;1876年,贝尔(A.G.Bell)发明电话利⽤电磁波传送⽆线电信号。
1901年,马可尼(G.Marconi)成功地实现了横渡⼤西洋的⽆线电通信;全球定位系统GPS(Global Positioning System);个⼈通信具有美好的发展前景光纤通信带来了更加宽⼴的带宽。
信号的传输离不开信号的交换。
信号处理:对信号进⾏某种加⼯或变换。
其⽬的是:消除信号中的多余内容;滤除混杂的噪声和⼲扰;将信号变换成容易分析与识别的形式,便于估计和选择它的特征参量。
信号处理的应⽤已遍及许多科学技术领域。

附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦:e e sh 2x xx --=双曲余弦:e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =,C 为常数(下同)d()d d u v u v ±=±,u 、v 为t 的函数(下同) d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式(1)等比数列123,,,,N a a a a 的通项为11n n a a q -=,q 为公比,前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑(2)等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-,d 为公差,前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰, 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰,1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭,B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰,0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑,0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑,0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤,附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤,B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1(a)确定信号、连续时间信号、非周期信号、能量信号、非因果信号。
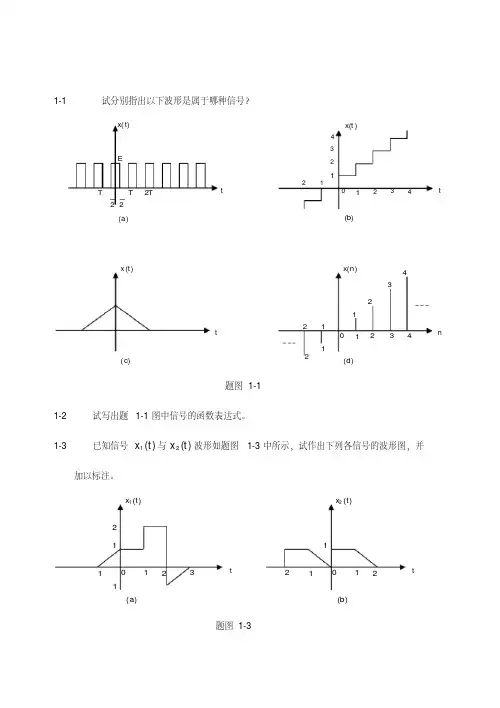
1-1试分别指出以下波形是属于哪种信号?题图1-11-2 试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3t)(2t x )(b 12112t)(1t x )(a 121123122T T2TEt)(t x )(a t)(t x )(b 13124023412t)(t x )(c n)(n x )(d 2213012112344⑴)2(1t x ⑵)1(1t x ⑶)22(1t x ⑷)3(2tx ⑸)22(2t x ⑹)21(2t x ⑺)(1t x )(2t x ⑻)1(1t x )1(2tx ⑼)22(1t x )4(2tx 1-4 已知信号)(1n x 与)(2n x 波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴)12(1n x ⑵)4(1n x ⑶)2(1n x ⑷)2(2n x ⑸)2(2n x ⑹)1()2(22n x n x ⑺)2(1nx )21(2n x ⑻)1(1n x )4(2nx ⑼)1(1nx )3(2nx 1-5 已知信号)25(t x 的波形如题图1-5所示,试作出信号)(t x 的波形图,并加以标注。
题图1-5t)25(t x 110232523n)(2n x )(b 2213121124n)(1n x )(a 22131142134212321231-6 试画出下列信号的波形图:⑴)8sin()sin()(t t t x ⑵)8sin()]sin(211[)(t t t x ⑶)8sin()]sin(1[)(t t t x ⑷)2sin(1)(t tt x 1-7 试画出下列信号的波形图:⑴)(1)(t u e t x t⑵)]2()1([10cos )(t u t u t e t x t⑶)()2()(t u e t x t⑷)()()1(t u et x t ⑸)9()(2tu t x ⑹)4()(2tt x 1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。

信号与系统一、单项选择题(本大题共46分,共 10 小题,每小题 4.599999 分)1. 若一因果系统的系统函数为则有如下结论——————————() A. 若,则系统稳定 B. 若H(s)的所有极点均在左半s平面,则系统稳定 C. 若H(s)的所有极点均在s平面的单位圆内,则系统稳定。
2. 连续信号,该信号的拉普拉斯变换收敛域为()。
A.B.C.D.3. 连续信号与的乘积,即*=( )A.B.C.D.4. 已知f(t),为求f(t0−at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A. f(-at)左移t0 B. f(-at) 右移tC. f(at) 左移D. f(at)右移5. 已知 f(t),为求f(t0-at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A.B. f(at) 右移t0 C. f(at) 左移t/a D. f(-at) 右移t/a6. 系统函数H(s)与激励信号X(s)之间——() A. 是反比关系; B. 无关系; C. 线性关系; D. 不确定。
7. 下列论断正确的为()。
A. 两个周期信号之和必为周期信号; B. 非周期信号一定是能量信号; C. 能量信号一定是非周期信号; D. 两个功率信号之和仍为功率信号。
8. 的拉氏反变换为()A.B.C.D.9. 系统结构框图如下,该系统单位冲激响应h(t)的表达式为()A.B.C.D.10. 已知,可以求得—————()A.B.C.D.二、多项选择题(本大题共18分,共 3 小题,每小题 6 分)1. 线性系统响应满足以下规律————————————() A. 若起始状态为零,则零输入响应为零。
B. 若起始状态为零,则零状态响应为零。
C. 若系统的零状态响应为零,则强迫响应也为零。
D. 若激励信号为零,零输入响应就是自由响应。
2. 1.之间满足如下关系———————()A.B.C.D.3. 一线性时不变因果系统的系统函数为H(s),系统稳定的条件是——()A. H(s)的极点在s平面的单位圆内B. H(s)的极点的模值小于1C. H (s)的极点全部在s平面的左半平面D. H(s)为有理多项式。

1.27a) y (t )=x (t −2)+x(2−t)1) 记忆的,系统输出取决于过去和未来时刻的输入;2) 时变的,令y 1(t 0)=x 1(t 0−2)+x 1(2−t 0),假设x 2(t )=x 1(t 0−2),则y 2(t )=x 1(t 0−4)+x 1(4−t 0),而y 1(t 0−2)=x 1(t 0−4)+x 1(2−t 0−2)=x 1(t 0−4)+x 1(−t 0),显然,y 2(t )≠y 1(t 0−2).因此,这是时变系统;3) 线性的,y=x(t-2)和y=x(2-t)均是线性的,两者的线性组合仍旧是线性的;4) 非因果的,当前输出取决于过去和未来时刻的输入;5) 稳定的,输入有界,输出也有界。
b) y (t )=[cos (3t )]x(t)1) 无记忆的,输出只取决于当前输入值;2) 时变的,从概念上理解,就是系统属性cos(3t)随时间在发生改变; 3) 线性的,例如:令x 3(t )=ax 1(t )+bx 2(t ),, x 1(t)→y 1(t ),x 2(t)→y 2(t),则y 3(t )=[cos (3t )][ax 1(t )+bx 2(t )]=ay 1(t )+by 2(t) ;4) 因果的,系统输出只取决于当前输入;5) 稳定的,系统输入有界,输出也有界。
c) y (t )=∫x (τ)dτ2t −∞1) 记忆的,系统输出不只取决于当前时刻输入;2) 时变的,令y 1(t 0)=∫x 1(τ)dτ2t 0−∞ ,x 2(t )=x 1(t 0−a ),则y 2(t )=∫x 1(τ−a )dτ2t −∞,而y 1(t 0−a )=∫x 1(τ−a )dτ2t0−∞。
显然,y 2(t )≠y 1(t 0−a ),因此此系统是时变的;3) 线性的,这是一个一阶线性常系数积分方程满足叠加定理;4) 非因果的,在此积分方程里,τ取得的最大值为2t,当t>0时,2t 是未来时刻的输入;5) 不稳定的,令x (τ)≡1,则∫x (τ)dτ2t−∞=2t +(+∞)=+∞,因此输出是无界的。

西南大学信号与系统作业答案西南大学网络与继续教育学院课程代码: 1073 学年学季:20172单项选择题1、连续系统的结构图如图所示,系统的系统函数为()。
1.H1(s) H2(s) - H3(s)2.h1(t) *h2(t)+h3(t)3.H1(s) H2(s) + H3(s)4.h1(t) *h2(t)-h3(t)2、1.h1(k)+h2(k)2.h1(k)*h2(k)3.h1(k)*h2(k)+14.h1(k)*h2(k)+δ(k)3、1. 32.3. 14. 24、LTI的含义是()1.线性因果2.线性稳定3.因果稳定4.线性时不变5、若数字滤波器在两点处的幅值为(1,1),则该滤波器为()1. A. lp2.bp3.bs4.hp6、利用Matlab求取系统的冲激响应,调用的函数是()1.step2.impulse3.initial4.lism7、关于序列的插值,下列叙述错误的是()1.插值过程可分为两步,先补零,再经过低通滤波器2.插值意味着抽样率的转换3.样点之间补零,意味着零阶插值4.零插值后的序列,频谱会被压缩并产生基带映像频谱8、已知,设抽样频率为100Hz,则所得序列的数字频率为( )1. E.2.3.4.9、已知周期序列,其周期为 ( )1.92. 63.124. 310、设,则 ( )1. 22. 13.04.-311、共轭对称的信号,其幅值与相位分别为()1. C. 偶、偶函数2.奇、偶函数3.偶、奇函数4.奇、奇函数12、()1. B. -12.03. 24. 113、( )1.f'(t)2.13.f(0)4.f(t)14、序列,其周期为()1.72. 23.不是周期序列4.1415、对信号进行采样,最大采样间隔为 ( )1.2.3.4.16、1.因果稳定2.因果不稳定3.非因果稳定4.非因果不稳定17、对离散系统系统频率响应仿真,调用的函数是()。
1.step2.impulse3.freqs4.freqz18、下列系统中,属于线性时不变系统的是()。
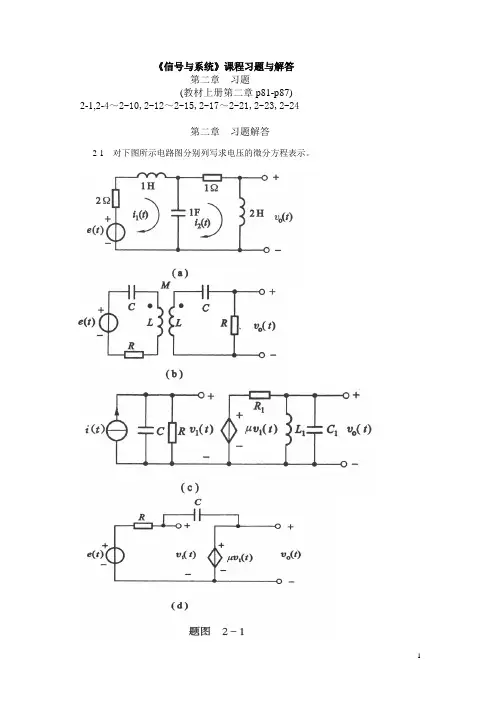
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
单项选择题1、下列不是傅里叶变换对关系的是()A. 冲激函数与常数B. 矩形与抽样函数C. 三角脉冲与抽样函数的平方D. 阶跃信号与符号函数单项选择题2、利用Matlab建立系统的多项式模型,调用的函数是()A. tfB. zpkC. ssD. fdatool单项选择题3、设是信号的傅里叶变换,的波形如图所示,则等于()。
A. 6piB. 4piC. 2piD. 0单项选择题4、完整表示对理想滤波器的逼近,可以采用()A. 通带内最大误差B. 阻带最小衰减C. 误差容限图D. 对模拟与数字滤波器要区别对待单项选择题5、等于()A. 0B. 1C. e^-1D. e^-5单项选择题6、()A. f(0)B. f(1)C. f(-1)D. 0单项选择题7、已知,则等于()A. 2piB. 1C. 0D. 1/2单项选择题8、周期信号的波形如图所示,则其傅里叶级数中含有()。
A. 正弦分量与余弦分量B. 奇次谐波分量C. 直流分量与正弦分量D. 直流分量与余弦分量判断题9、抽样函数可简写为Sa(t)=sin(t)/t,是偶对称的函数。
A.√B.×判断题10、连续信号的移位、翻转、尺度等运算,都是针对独立变量t而言。
A.√B.×判断题11、线性时不变的系统,其响应可分解为零输入响应与零状态响应的和。
A.√B.×判断题12、由欧拉公式,可以有。
A.√判断题13、各种形式的傅里叶变换是本课程的核心基础。
A.√B.×判断题14、可以用迭代法求离散系统的差分方程,但可能得不到闭合形式的解。
A.√B.×判断题15、若 y(t)=x(1-t) ,则系统是时不变的系统。
A.√B.×判断题16、A.√B.×判断题17、周期冲激串的傅里叶变换仍然是周期冲激串。
A.√B.×判断题18、无论连续还是离散系统,其性能主要是由极点决定的。
A.√B.×判断题19、通过信号的分解,可以考察基本信号经过系统的响应,从而建立相关的系统数学模型。
第二章第二章 课后题答案课后题答案2-1.1.图题2-1所示电路,求响应u 2(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图题2.1(b )所示,故对节点①,②可列出算子形式的KCL 方程为= +++−=−+0)(111)(1)()(1)(1312121t u p p t u p t f t u p t u p即()=+++−=−+0)(1)()()()(13122121t u p p t u t pf t u t u p联解得)()()(443)(22t f p H t f p p t u =++=故得转移算子为443)()()22++==p p t f t u p H (u 2(t)对f(t)的微分方程为())()(t f t u p p 34422=++即)(t f t u t u dt d t u dt d 3)(4)(4)(22222=++2-2图题2-2所示电路,求响应i(t)对激励f(t)的转移算子H(p)及微分方程。
解 其对应的算子电路模型如图2.2(b)所示。
故得)()(t f p p p p pp t f t i 3011101022221.01)(2+++=+×++=故得转移算子为30111010)()()(2+++==p p p t f t i p Hi(t)对f(t)的微分方程为)()1010()()3011(2t f p t i p p +=++即)(10)(10)(30)(11)(22t f t f dt d t i t i dt d t i dt d +=++2-3图题2-3所示电路,已知u C (0-)=1 V, i(0-)=2 A。
求t>0时的零输入响应i(t)和u C (t)。
解 其对应的算子电路模型如图题2.3(b)所示。
故对节点N 可列写出算子形式的KCL 方程为0)(2312= ++t u p p C又有uc(t)=pi(t),代入上式化简,即得电路的微分方程为=====++−+−+1)0()0(2)0()0(0)()23(2c cu u i i t i p p电路的特征方程为0232=++p p故得特征根(即电路的自然频率)为p 1=-1,p 2=-2。
04-05A一、填空(每空2 分,共20分)(1) LTI 表示 线性是不变系统 。
(2)⎰∞∞-=-dt t t t f )()(0δ f(t 0) 。
(3) 无失真传输的频域条件为 。
(4) )]([)(t u et u at-*= 。
(5) 设)(0t f 是周期脉冲序列)(t f (周期为T 1)中截取的主值区间,其傅里叶变换为)(0w F ,n F 是)(t f 傅里叶级数的系数。
则n F = 。
(6) 设)3)(2(6)(+++=s s s s H ,=+)0(h 1 。
(7) 设)(t f 是带限信号,πω2=m rad/s ,则对)12(-t f 进行均匀采样的奈奎斯特采样间隔为 0.5s 。
(8) 某连续系统的系统函数jw jw H -=)(,则输入为tj et f 2)(=时系统的零状态响应=)(t r zs 。
(9) 周期序列)873cos()(ππ-=n A n x ,其周期为 14 。
(10) 信号)(t f 的频谱如图如示,则其带宽为 w1 。
二、选择题(将正确的答案的标号填在括号内,每小题2分,共20分)1) 能正确反映)()(n u n 与δ关系的表达式是( C )。
A. ∑∞=-=0)()(k k n n u δ B. ∑∞=-=1)()(k k n n u δC. ∑∞==)()(k k n u δ D. )1()()(+--=n u n u n δ2) 下列叙述正确的是( A )。
A. 各种离散信号都是数字信号B. 数字信号的幅度只能取0或1C. 将模拟信号采样直接可得数字信号D. 采样信号经滤波可得模拟信号3) 下列系统中,属于线性时不变系统的是( C )A. )1()(t e t r -=B. ∑∞-∞==m m x n y )()(C. ⎰∞-=td e t r 5)()(ττ D. )443sin()()(ππ+=n n x n y 4) 关于因果系统稳定性的描述或判定,错误的是( D )A. 系统稳定的充要条件是所有的特征根都必须具有负实部。
《信号与系统》习题参考答案(1)2—1(1) 01()()()()(1)()ta at x t h t x u t d e d e u t aτττττ∞---∞*=⋅-==-⎰⎰ (2) 00()()(cos sin )()x t h t t d ωτωτδττ∞-∞*=+⋅-⎰0000(cos sin )()cos sin t t t d t t ωωδττωω∞-∞=+⋅-=+⎰(3) 当0t <时 ()()0x t h t *=当01t ≤<时 20()()(1)2tt x t h t d t ττ*=+=+⎰当12t ≤<时 13()()(1)2x t h t d ττ*=+=⎰ 当23t ≤<时 12213()()(1)22t x t h t d t t ττ-*=+=-++⎰ 当3t ≥时 ()()0x t h t *= (4) 当0t <时 ()()0x t h t *=当0t ≥时 01()()sin 2(1cos 2)2tx t h t d t ττ*==-⎰ (5) 22222(2)2(4)241()()(2)2t t t t t t t x t h t e d e d e ee ττττ-----*=-=-+⎰⎰ (6)()x t at b =+11212()()()()()(2)3363tt x t h t a b d a tb t a t a bττδ-*=+++*--=++⎰2—2(1) [][][][2](2)[2]x n h n nu n n n u n δ*=*-=--(2) 10[][](2)[](21)[]nin i x n h n u n u n +=*==-∑(3) 当0n ≥时 1111[][]2()()232i n in i x n h n --=-∞*==∑ 当0n <时 111[][]2()223n i n i n i x n h n --=-∞*==⋅∑ (4) 当0n <时 [][]0x n h n *=当0n ≥时 110[][]()[]n n nin ii x n h n u n βααββα++-=-*==-∑(5) 当07n ≤≤时 071[][](1)[1(1)]2in i n x n h n -=-*=-=--∑ 当70n -≤≤时 71[][](1)[(1)1]2ni n i x n h n -=-*=-=--∑ 2—3(1) 12()()[(1)(1)][(5)(5)]x t x t u t u t t t δδ*=+--*++- (6)(4)(4)(6)u t u t u t u t =++--+-- (2) 123()()()x t x t x t **{[(6)(4)][(4)(6)]}*[u t u t u t u t =+-++---11()()]22t t δδ++- ( 6.5)( 4.5)( 5.5)( 3.5)( 3.5)( 5.5)u t u t u t u t u t u t =+-+++-++--- ( 4.5)( 6.5)u t u t +---(3) 1311()()[(1)(1)][()()]22x t x t u t u t t t δδ*=+--*++- ( 1.5)(0.5)(0.5)( 1.5)u t u t u t u t =+--++-- 2—4 0(3)331()(3)1t k k t tk k y t eu t k e e e e∞-----=-∞=-∞=-=⋅=-∑∑311A e-=- 2—5(1) 当2t ≥时 ()()0x t h t *= 当20t -<<时 11()()2t x t h t d t τ+-*==+⎰当02t <<时 11()()2t x t h t d t τ-*==-⎰(2) 当01t <<时 1()()22(1)tx t h t d t τ*==-⎰ 当10t -<<时 01()()22(1)2t tx t h t d d t t t ττ+*=+=-++=+⎰⎰当21t -<<-时 11()()2t x t h t d t τ+-*==+⎰当 1t ≥ 或 2t <-时 ()()0x t h t *=此题也可利用性质,先对()x t 积分,对()h t 微分,'()()()y t x t dt h t =*⎰(3) 当0t <时 (1)1()()1t x t h t e dt +∞--*==⎰当0t ≥时 1(1)(1)11()()22t t t t t x t h t e dt e dt e ++∞-----+*=+=-⎰⎰(4) 当t π< 或 5t π>时 ()()0x t h t *= 当3t ππ<<时 0()()sin 1cos t x t h t d t πττ-*==+⎰当35t ππ<<时 23()()sin 1cos t x t h t d t ππττ-*==--⎰(5) 当01t <<时 2211()()222()22x t h t t t t *=-=--当12t <≤时 2231()()264[2()]22x t h t t t t *=-+-=---()()x t h t *是以2为周期的周期函数 2—7(1) 111[][1]()[]()[1]22nn h n Ah n u n A u n ---=--111()[()()][1]()22nn n A u n n δδ-=+--=12A =(2) 111[][][][1][][]h n h n Ah n h n h n n δ---*-*-=*11[][][1]2h n n n δδ-∴=-- (3) 11[][][]2[[][1]][]nx n h n h n u n u n h n --**=--* 2[]2[[][4]]2[[1][5]]nn x n u n u n u n u n -∴=------2—8(1) 0()3()y t y t =(2) 00()()(2)y t y t y t =-- (3) 0()(1)y t y t =- (4) 0()()y t y t =-(5) 0()()dy t y t dt=(6) 202()()d y t y t dt =2—9 12111[][]()[]()[1]222n n x n h n u n u n -*=-+--1()([][1])[]2nu n u n n δ=---=1221[][][][]([][])*[]y n x n h n h n x n h n h n =**=* []*([][])[][]n n n n n u n u n u n u n δαβαβ=+=+ 2—10(1) 341201[][]((0.5))[3]2(1())[3]2n nn n x n x n u n u n ++=*=+=-+∑ (2) 4123[][][]2(1(0.5))[3]([][1])n x n x n x n u n n n δδ+**=-+*-- 43312(1(0.5))[3]2(1(0.5))[2]()[3]2n n n u n u n u n +++=-+--+=+ (3) 23[][][3]([][1])[3][2][3]x n x n u n n n u n u n n δδδ*=+*--=+-+=+ 2—11(1) 12345[][]([][][])[]h n h n h n h n h n h n =*-*+ (2) 34[][][1]h n h n nu n *=- 234[][][](1)[][1][]h n h n h nn u n n u n u n -*=+--= 12345[][]([][][])[]h n h n h n h n h n h n =*-*+514()([][3])*[][]2nu n u n u n hn =--+ 4[]6[1]7[2][]4[3]5[]6[1]7[2]4[3]n n u n n n n n u n n δδδδδδδ=+-+-++-=+-+---(1)'()()(2)(2)()(2)tt y t e x d x t y t x t τττ---∞=--+-=-+-⎰(2)()(2)t h t eu t --=- (2)当1t ≤时 ()0y t =当14t <≤时 1(2)(1)2()1t t y t e d e ττ+----==-⎰当4t >时 1(2)(4)(1)2()t t t t y t e d e e ττ+-------==-⎰2—13(1)213()()()()(1)[()](1)[()](1)h t h t h t u t t t u t t u t δδδ**=*-*-=-*-=-- 1213()()()()()()(1)h t h t h t h t h t u t u t =+**=--(2)1(10)1(02)()3(23)0t t t y t t t +-<<⎧⎪<<⎪=⎨-<<⎪⎪⎩其余2—14(1)因果、稳定 (2)非因果、非稳定 (3)非因果、稳定 (4)非因果、稳定 (5)非因果、稳定 (6)因果、稳定 (7)因果、非稳定 2—15(1)因果、稳定 (2)非因果、稳定 (3)非因果、非稳定 (4)非因果、稳定 (5)因果、非稳定 (6)非因果、稳定 (7)因果、稳定 2—16(1)对 (2)对()h t dt ∞-∞=+∞⎰(3)错 例如单位冲激响应(1)t δ-是因果的,但LTI 系统的逆系统(1)t δ+不是因果的。
判断题1、应用DFT分析无限长信号的频谱时,必然会产生误差。
1. A.√2. B.×2、离散周期信号的DFS中,频域的周期N对应数字频率为2π。
1. A.√2. B.×3、实数序列的DFT为共轭对称的序列。
1. A.√2. B.×4、一个域的周期性,对应另一域的离散性。
1. A.√2. B.×5、信号的最高频率为3π/5,则最大程度减小数据量的I/D值为3/5 。
1. A.√2. B.×6、单位圆上的零点,对应幅频特性的零值。
1. A.√2. B.×7、LP表示的滤波器类型是低通滤波器。
1. A.√2. B.×8、通带最平坦的滤波器是巴特沃思滤波器。
1. A.√2. B.×9、陷波器必然有零点位于单位圆上。
1. A.√2. B.×10、圆周卷积和线卷积相等的条件是圆周卷积的点数不小于线性卷积的长度。
1. A.√2. B.×11、按照最大误差最小准则设计的滤波器,具有等波纹的特点。
1. A.√2. B.×12、单位脉冲序列的DTFT结果为1。
1. A.√2. B.×13、x(n)与h(n)的卷积的Z变换为X(Z)H(Z)。
1. A.√2. B.×14、所谓全通系统,就是其频率响应的幅度在任意需要考虑的频率点处均为常数。
1. A.√2. B.×15、FIR滤波器由于无原点外的极点,故相比IIR阶次更高。
1. A.√2. B.×16、对连续信号作频谱分析,设信号的采样频率为10KHz,频域的分辨能力为不大于10Hz,则对应DFS点数为1000 点。
1. A.√2. B.×17、靠近单位圆上的极点,对应幅频特性的极大值。
1. A.√2. B.×18、线性相位可分为第一类与第二类线性相位两种情况。
1. A.√2. B.×19、为满足线性相位要求,窗函数本身也应满足相应的对称性。
单项选择题1、连续系统的结构图如图所示,系统的系统函数为()。
1.H1(s) H2(s) - H3(s)2.h1(t) *h2(t)+h3(t)3.H1(s) H2(s) + H3(s)4.h1(t) *h2(t)-h3(t)2、1.h1(k)+h2(k)2.h1(k)*h2(k)3.h1(k)*h2(k)+14.h1(k)*h2(k)+δ(k)3、1. 32.0.53. 14. 24、LTI的含义是()1.线性因果2.线性稳定3.因果稳定4.线性时不变5、若数字滤波器在两点处的幅值为(1,1),则该滤波器为()1. A. lp2.bp3.bs4.hp6、利用Matlab求取系统的冲激响应,调用的函数是()1.step2.impulse3.initial4.lism7、关于序列的插值,下列叙述错误的是()1.插值过程可分为两步,先补零,再经过低通滤波器2.插值意味着抽样率的转换3.样点之间补零,意味着零阶插值4.零插值后的序列,频谱会被压缩并产生基带映像频谱8、已知,设抽样频率为100Hz,则所得序列的数字频率为( )1. E. 0.4pi2.0.3pi3.0.2pi4.0.1pi9、已知周期序列,其周期为 ( )1.92. 63.124. 310、设,则 ( )1. 22. 13.04.-311、共轭对称的信号,其幅值与相位分别为()1. C. 偶、偶函数2.奇、偶函数3.偶、奇函数4.奇、奇函数12、()1. B. -12.03. 24. 113、( )1.f'(t)2.13.f(0)4.f(t)14、序列,其周期为()1.72. 23.不是周期序列4.1415、对信号进行采样,最大采样间隔为 ( )1.0.0012.0.0053.0.054.0.0116、1.因果稳定2.因果不稳定3.非因果稳定4.非因果不稳定17、对离散系统系统频率响应仿真,调用的函数是()。
1.step2.impulse3.freqs4.freqz18、下列系统中,属于线性时不变系统的是()。
19、关于稳定性的描述,下列叙述中错误的是()。
1.稳定的充要条件是有界输入产生有界输出,简称BIBO2.线性时不变系统的稳定性理论上与输入信号无关3.稳定性指的是系统克服扰动恢复到平衡态的能力4.冲激响应可以表征系统的稳定性20、21、1. 22. 43.-24.-422、关于信号的分解,下列叙述正确的是()1.傅里叶级数是一致性意义下的正交分解2.任意普通信号可分解为冲激函数的叠加,可用卷积形式来描述3.信号能分解为实分量和虚部分量,故可对信号进行滤波4.由于信号的可分解性,故在时域中可用冲激响应来表征系统23、关于三个变换之间的关系,下列叙述错误的是()。
1.若原信号收敛,虚轴上的拉氏变换就是傅里叶变换2.s域的左半平面映射到z域的单位圆内部3.从s域到z域的映射是单值映射4.s域的右半平面映射到z域的单位圆外部24、25、26、1. 12.无法确定27、下列系统中,不属于线性系统的是()。
28、下列叙述正确的是()。
1.各种离散信号都是数字信号2.数字信号的幅度只能取0或13.将模拟信号采样直接可得数字信号4.采样信号经保持、滤波后可得模拟信号29、1.02. 13.无穷大4.不存在30、1.LP2.HP3.BP4.BS31、关于无失真传输的充要条件,下列叙述中正确的是()。
1.系统的幅频特性为常数2.系统的相频特性与频率成正比32、设系统输入输出关系为y(t)=x(t)cos(t) ,则系统为()。
1.因果稳定2.非因果稳定3.因果不稳定4.非因果不稳定33、下列信号中属于数字信号的是()。
34、已知序列,则()1.122.93. 34. 635、设是带限信号,rad/s,则对进行均匀采样的最大间隔为( )1.0.2s2.0.5s3.0.1s4.0.3s36、( )1. D. x(t)2.-x(t)3.x(0)4.-x(0)判断题37、当周期趋于无穷大时,周期信号的频谱就由离散谱变为了连续谱。
1. A.√2. B.×38、离散因果LTI系统稳定的充要条件是所有极点的模值小于1。
1. A.√2. B.×39、1. A.√2. B.×40、竖式乘法可用来求有限长序列的卷积和。
1. A.√2. B.×41、正弦信号是功率信号。
1. A.√2. B.×42、数字域中,带限信号的意思是指最高频率小于等于2π。
1. A.√2. B.×43、若群延迟为常数,则数字滤滤器具有线性相位。
1. A.√2. B.×44、周期信号的单边谱与双边谱中,直流分量的幅值相同。
1. A.√2. B.×45、一个共轭对称的实信号,必为偶函数。
1. A.√2. B.×46、信号间断点处的微分,存在有冲激函数。
1. A.√2. B.×47、离散因果LTI系统,特征根模值小于1时,响应分量收敛。
1. A.√2. B.×48、可选择频谱包络线第一次的过零点作为信号的带宽。
1. A.√2. B.×49、利用几何作图的方法,可以由零极点的分布绘制频率响应曲线。
1. A.√2. B.×50、单位圆上的DTFT对应序列的z变换。
1. A.√2. B.×51、原信号收敛时,虚轴上的拉氏变换就是信号的傅里叶变换。
1. A.√2. B.×52、理想模拟滤波器都是物理上不可实现的滤波器。
1. A.√2. B.×53、对于DFS,时域与频域的周期都是N。
1. A.√2. B.×54、周期信号谐波分量的频率,都是基频的整数倍。
1. A.√2. B.×55、线性常系数的微分方程表示的系统是LTI系统。
1. A.√2. B.×56、冲激信号是偶函数。
1. A.√2. B.×57、抽取与内插意味着抽样率的转换。
1. A.√2. B.×58、系统函数可由比值形式定义,故与输入信号的形式有关。
1. A.√2. B.×59、离散系统原点处的零极点,不影响频率特性幅值,只影响相位。
1. A.√2. B.×60、线性相位,指的是系统的相频特性与频率成正比。
1. A.√2. B.×61、实序列的频谱,其幅值偶对称,相位奇对称。
1. A.√2. B.×62、系统为因果系统的充要条件是冲激响应是因果的信号。
1. A.√2. B.×63、任意普通信号可分解为冲激函数的叠加,可用卷积形式来描述。
1. A.√2. B.×64、一个域离散,对应另一个域的周期延拓。
1. A.√2. B.×65、连续时间LTI系统稳定的充要条件是所有极点的实部小于等于零。
1. A.√2. B.×66、冲激响应只适用于LTI系统。
1. A.√2. B.×67、从s域到z域映射,s平面虚轴与z平面单位圆,必须对应。
1. A.√2. B.×68、系统函数可由比值形式定义,故与输入信号的形式有关。
1. A.√2. B.×69、频率响应反映了对输入频谱的加权作用。
1. A.√2. B.×70、非周期序列的频谱,是周期连续的频谱。
1. A.√2. B.×71、实际周期信号的频谱具有离散谐波性与收敛性。
1. A.√2. B.×72、无论连续还是离散的LTI系统,响应都可以分解为零输入与零状态响应之和。
1. A.√2. B.×73、冲激响应是冲激函数作用下的零状态响应。
1. A.√2. B.×74、任意序列可看作单位脉冲序列移位加权的和。
1. A.√2. B.×75、因果信号是稳定的信号。
1. A.√2. B.×76、本课程中,信号一般指电信号。
1. A.√2. B.×。