热量衡算

物料衡算和热量衡算1. 引言物料衡算和热量衡算是在工程设计和过程优化中常用的方法和工具。

物料衡算是指通过对物料的进出量、质量和组成等参数的分析，计算出物料的平衡以及物料流动过程中的相关参数。

热量衡算是指通过对热量的进出量、热平衡等参数的分析，计算出热量在系统中的平衡和流动情况。

本文将介绍物料衡算和热量衡算的基本概念、方法和应用。

2. 物料衡算2.1 物料平衡物料平衡是对物料流动系统中物料的进出量进行分析和计算的过程。

物料平衡的基本原理是质量守恒定律，即在封闭系统中，物料的质量不会发生净变化。

物料平衡可用于分析物料的流动路径、损耗情况以及优化物料的使用和回收。

2.2 物料衡算的方法常用的物料衡算的方法包括输入-输出法和组分衡算法。

- 输入-输出法：通过记录系统中物料的进出量，计算出物料的平衡情况。

该方法适用于物料流动较简单且没有复杂反应的系统。

具体步骤包括确定进料和产出物料的量和质量，计算进出物料的差值，并检查误差，使其趋近于零。

- 组分衡算法：通过对物料组分的平衡进行计算，得到物料的进出量。

该方法适用于需要考虑物料成分变化的系统。

具体步骤包括确定进料和产出物料的组分及其相对含量，计算进出物料组分的差值，并检查误差。

2.3 物料衡算的应用物料衡算在化工、冶金、环境工程等领域有广泛的应用，例如： - 在化工生产中，物料衡算可以用于优化原料的使用和能源的消耗，减少产品的损耗和废物的排放。

- 在冶金过程中，物料衡算可以用于优化矿石的选矿和冶炼过程，提高生产效率和产品质量。

- 在环境工程中，物料衡算可以用于分析和优化废物处理和排放过程，减少对环境的污染。

3. 热量衡算3.1 热量平衡热量平衡是对热量在系统中的分布和流动进行分析和计算的过程。

热量平衡的基本原理是热力学第一定律，即能量守恒定律。

热量衡算可以用于分析热量的传递、损失和利用情况，以及优化热能的使用和节约。

3.2 热量衡算的方法常用的热量衡算的方法包括输入-输出法和能量平衡法。

化工原理物料衡算和热量衡算引言化工工程涉及许多物料的处理和转化过程，同时也需要考虑热量的平衡。

物料衡算和热量衡算是化工原理的重要内容，对于工程实践和过程优化具有重要的意义。

本文将介绍化工原理中的物料衡算和热量衡算的基本原理和计算方法。

物料衡算物料衡算是指对于化工工程中物料流动和转化过程的计算和分析。

在化工工程中，物料的流动和转化是实现各种反应和分离操作的基础，因此正确的物料衡算是保证工程设计和操作的关键。

在物料衡算中，我们通常需要考虑以下几个方面： 1. 物料的质量衡算：即对物料的质量输入和输出进行计算和分析。

对于物料的质量衡算，我们需要注意物料流动的平衡原则，即质量的输入必须等于输出。

2. 物料的能量衡算：即对物料的能量输入和输出进行计算和分析。

能量的输入和输出会影响物料的温度和相变过程，因此在能量衡算中需要考虑物料的热力学性质。

3. 物料的流动速度衡算：即对物料流动速度进行计算和分析。

物料的流动速度决定了反应和分离操作的效率，因此在物料衡算中需要合理地确定流量和速度的关系。

4. 物料的浓度衡算：即对物料中组分浓度的计算和分析。

物料的浓度会影响其反应和分离的速率和效果，因此在物料衡算中需要考虑不同组分浓度的变化规律。

物料衡算通常使用质量守恒和能量守恒等基本原理进行计算。

同时，还可以利用化学反应平衡的原理和质量流动的平衡原则进行衡算过程中的参数确定。

热量衡算热量衡算是化工工程中热力学过程的计算和分析。

在化工工程中，热量的平衡是保证反应和分离操作能够正常进行的基础。

热量衡算需要考虑以下几个方面： 1. 热量的输入和输出：即对于热量的输入和输出进行计算和分析。

在化工工程中，我们通常需要对热量的输入和输出进行平衡，以保证工程操作的稳定性。

2. 热量的传递和转化：即对于热量的传递和转化过程进行计算和分析。

热量的传递可以通过传导、对流和辐射等方式进行，因此在热量衡算中需要考虑传热方式的影响。

3. 热平衡的计算：即对于反应和分离过程中热量平衡的计算和分析。

热量衡算1计算方法与原则1.1热量衡算的目的及意义热量衡算的主要目的是为了确定设备的热负荷。

根据设备热负荷的大小、所处理物料的性质及工艺要求再选择传热面的形式、计算传热面积、确定设备的主要工艺尺寸。

传热所需的加热剂或冷却剂的用量也是以热负荷的大小为依据而进行计算的。

1.2热量衡算的依据及必要条件热量衡算的主要依据是能量守恒定律，其数学表达式为Q1+ Q2+Q3=Q4+Q5+Q6 式1其中：Q1——物料带入到设备的热量，kJQ2——加热剂或冷却剂传给设备和所处理物料的热量，kJQ3——过程热效应，kJQ4——物料离开设备所消耗的热量，kJQ5——加热或冷却设备所消耗的热量，kJQ6——设备向环境散失的热量，kJQ1（Q4）=Σ mC P(t2- t0) kJ式2m——输入或输出设备的物料质量，kgC P——物料的平均比热容，kJ/(kg•℃)t2——物料的温度，℃t0——基准温度，℃Q5=Σ C P M (t2-t1) kJ式3M——设备各部件的质量，kgC P——设备各部件的比热容，kJ/(kg•℃)t1——设备各部件的初始温度，℃t——设备各部件的最终温度，℃2Q5+Q6=10%Q总式4热量衡算是在车间物料衡算的结果基础上而进行的，因此，车间物料衡算表是进行车间热量衡算的首要条件。

其次还必须收集有关物质的热力学数据，例如比热容，相变热，反应热等。

本设计还将涉及到的所有物料的热力学数据汇总成表4，以便于后期的计算。

1.3热量衡算基准因为物料衡算计算的是各个岗位的天处理量，所以热量衡算计算的也是某个设备天换热介质消耗量，同时温度基准采用的是0℃做基准。

当然，进行传热面积校核时，是根据批处理量计算。

2全车间物料热力学数据的估算2.1所用纯化合物比热的推算0i i pMc n C ∑=式 5式中M ——化合物分子量；n i ——分子中同种元素原子数； c i ——元素的原子比热容，kJ/(kg•℃)查《制药工程工艺设计》P111，得到原子的摩尔热容相关数据，见表1表1 元素原子的摩尔热容单位：kcal/( kmol•℃)(当物质为固体时，各原子的C a 取值近似值）原子 C a 原子 C a 原子 C a 碳C 2.8 氧O 6.0 氮N 2.6 氢H4.3硫S7.4其他8.0(当物质为液体时，各原子的C a 取值近似值）而在实际生产的过程中遇到的物质大多是混合物，极少数的混合物有实验测定的热容数据，一般都是根据混合物内各种物质的热容和组成进行推算的，其中杂质的含量极少，热效应可以忽略不计。

热量衡算主要依据是能量平衡方程ΣQ in=ΣQ out +ΣQ其中ΣQ in输入设备流量ΣQ out +输出设备流量ΣQ为损失流量对于连续系统：Q+W=ΣH out +ΣH其中。

Q为设备热负荷W为输入系统的机械能ΣH out 离开设备的各物料焓之和ΣH进入设备的各物料焓之和在进入全厂能量横算时，是以单位设备为基本单位，考虑由机械能转换、化学反应释放和单纯的物理变化带来的能量变化，最终对全工艺段进行系统级的能量平衡计算，进而用于指导节能降耗设计工作。

热量衡算任务1、确定加热剂和冷却剂的用量2、计算有设备传递的热量，为设备设计提供依据3、提高热量应用水平4、最终确定总需求能量和能量费用各工段其热量衡算如下萃取精馏段：第一萃取精馏塔物流焓变一览表流股名反应前物流反应后物流温度（℃）60/6044/110压力（Kg/sqcm）7.767/6.118 5.099/6.099质量流量（Kg/hr）41600/2710017320/295280焓值（KW）-2575.31068.09热负荷一览表Q热负荷（Kw）—8296.9热量平衡一览表Q IN OUT Error -8296.9 -2575.3 1068.09 -1.241汽提塔物流焓变一览表流股名反应前物流反应后物流温度（℃）118.1/110.1/135.0108.4/134.4压力（Kg/sqcm）7.000/6.099/5.166 5.166/5.167质量流量（Kg/hr）37970.026/295280.000/7.04087E+623999.999/7.35012E+6焓值（KW）14050311412557热负荷一览表Q热负荷（Kw）—9789.0065热量平衡一览表Q IN OUT Error -9789.0065 1405031 1412557 -0.00533闪蒸塔物流焓变一览表流股名反应前物流反应后物流压力（Kg/sqcm） 5.167 5.166/5.166质量流量（Kg/hr）7.35012E+6202622.872/7.04087E+6焓值（KW）1407162.091435001.24热负荷一览表Q热负荷（Kw）46985.4228热量平衡一览表Q IN OUT Error 46985.4228 1407162.09 1435001.24 -0.0194第二萃取精馏塔物流焓变一览表流股名反应前物流反应后物流压力（Kg/sqcm） 5.000/5.160 3.071/3.059质量流量（Kg/hr）36000.000/23999.99937970.026/22030.029焓值（KW）3895.678174103.97348热负荷一览表Q热负荷（Kw）-4281.0457热量平衡一览表Q IN OUT Error -4281.0457 3895.67817 4103.97348 -0.0507545第一精馏塔物流焓变一览表流股名反应前物流反应后物流温度（℃）92.241.6/55.8压力（Kg/ sqcm） 3.059 5.099/5.099质量流量（Kg/hr）22030.029990.029/21040.000焓值（KW）12503.739251.09429热负荷一览表Q热负荷（Kw）-516.35568热量平衡一览表Q IN OUT Error -516.35568 12503.73 9251.09429 0.26013323第二精馏塔物流焓变一览表流股名反应前物流反应后物流(顶/釜)温度（℃）70.143.1/55.4压力（atm） 5.92 4.74/5.42质量流量（Kg/hr）19758.483419087.1667/671.3167焓值（KW）11111.0668 8876.86583热负荷一览表（KW）Q热负荷-9642.5248热量平衡一览表（KW）Q IN OUT Error -9642.524811111.06688876.86583-0.201079。

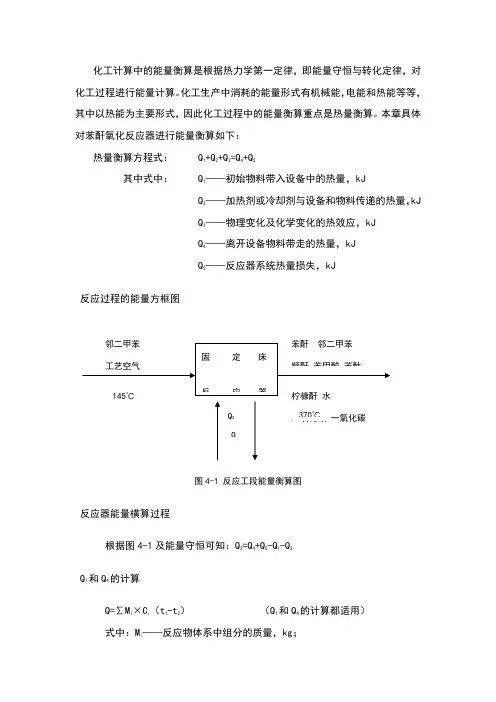
化工计算中的能量衡算是根据热力学第一定律，即能量守恒与转化定律，对化工过程进行能量计算。

化工生产中消耗的能量形式有机械能，电能和热能等等，其中以热能为主要形式，因此化工过程中的能量衡算重点是热量衡算。

本章具体对苯酐氧化反应器进行能量衡算如下：热量衡算方程式： Q1+Q2+Q3=Q4+Q5其中式中： Q1——初始物料带入设备中的热量，kJQ2——加热剂或冷却剂与设备和物料传递的热量，kJQ3——物理变化及化学变化的热效应，kJQ4——离开设备物料带走的热量，kJQ5——反应器系统热量损失，kJ反应过程的能量方框图图4-1 反应工段能量衡算图反应器能量横算过程根据图4-1及能量守恒可知：Q2=Q4+Q5-Q1-Q3Q1和Q4的计算Q=∑Mi×Ci（t1-t2）（Q1和Q4的计算都适用）式中：Mi——反应物体系中组分的质量，kg；C i ——组分i 在0-T℃时的平均比热容，KJ/； t 1，t 2——反应物系在反应前后的温度，℃。

物料进入设备时的温度为145℃，热量衡算的基准为145℃，△T=0,则： Q 1=0查得各物项平均比热容数据： （kJ/kg.℃）表4-1 各物相平均比热容所以： ()21i i 4t C M Q t -=∑=××(370-145)+××225+××225+××225+××225+××225+××225+××225+××225+××225+××225=.4kJ 过程Q 3的计算过程热效率可以分为两类：一类是化学过程的热效率即化学反应速率；另一类是物理过程热效率。

物料化学变化过程，除化学反应外，往往伴随着物料状态变化热效率，但本工艺流程中物理过程热效率较低，可以忽略不计，该过程皆为放热反应，则过程热效率可以由下式计算：主反应：C 8H 10+3O 2→C 8H 4O 3+3H 2O + Q 3-1=×103×=×103kJ/h副反应：CH 3C 6H 4CH 3+→C 4H 2O 3（顺酐）+4CO 2+4H 2O + Q 3-2=×103×=×103kJ/hCH 3C 6H 4CH 3+3O 2→C 6H 5COOH （苯甲酸）+CO 2+2H 2O +Q3-3=×103×=×103kJ/hCH3C6H4CH3+2O2→C8H6O2（苯酞）+2H2O +Q3-4=×103×=×103kJ/hCH3C6H4CH3+→C5H5O3（柠槺酐）+3CO+3H2O +Q3-5=×103×=×103kJ/hCH3C6H4CH3+→8CO+5H2O +Q3-6=×103×=×103kJ/hCH3C6H4CH3+→8CO2+5H2O +Q3-7=×103×=×103kJ/h 继而得到：Q 3 = Q3-1+Q3-2+Q3-3+Q3-4+Q3-5+Q3-6+Q3-7 =×103kJ/hQ5的计算该反应中的热损失按5%计算，即：Q 5=5%×（Q1+Q3）=5%×（0+×103）=×103kJ/hQ2的计算Q2为熔岩移出反应器的热量，由反应器热量守恒可知：Q 2=Q4+Q5-Q1-Q3=.8kJ/h反应器能量衡算表根据以上计算列出氧化反应工段能量衡算表格如下：表4-2 反应工段能量衡算表（吸收热量为“+”，释放热量为“-”）。

物料衡算和热量衡算物料衡算根据质量守恒定律，以生产过程或生产单元设备为研究对象，对其进出口处进行定量计算，称为物料衡算。

通过物料衡算可以计算原料与产品间的定量转变关系，以及计算各种原料的消耗量，各种中间产品、副产品的产量、损耗量及组成。

物料衡算的基础物料衡算的基础是物质的质量守恒定律，即进入一个系统的全部物料量必等于离开系统的全部物料量，再加上过程中的损失量和在系统中的积累量。

∑G1=∑G2+∑G3+∑G4∑G2：——输人物料量总和；∑G3：——输出物料量总和；∑G4：——物料损失量总和；∑G5：——物料积累量总和。

当系统内物料积累量为零时，上式可以写成：∑G1=∑G2+∑G3物料衡算是所有工艺计算的基础，通过物料衡算可确定设备容积、台数、主要尺寸，同时可进行热量衡算、管路尺寸计算等。

物料衡算的基准(1)对于间歇式操作的过程，常采用一批原料为基准进行计算。

(2)对于连续式操作的过程，可以采用单位时间产品数量或原料量为基准进行计算。

物料衡算的结果应列成原材料消耗定额及消耗量表。

消耗定额是指每吨产品或以一定量的产品(如每千克针剂、每万片药片等)所消耗的原材料量；而消耗量是指以每年或每日等时间所消耗的原材料量。

制剂车间的消耗定额及消耗量计算时应把原料、辅料及主要包装材料一起算入。

热量衡算制药生产过程中包含有化学过程和物理过程，往往伴随着能量变化，因此必须进行能量衡算。

又因生产中一般无轴功存在或轴功相对来讲影响较小，因此能量衡算实质上是热量衡算。

生产过程中产生的热量或冷量会使物料温度上升或下降，为了保证生产过程在一定温度下进行，则外界须对生产系统有热量的加入或排除。

通过热量衡算，对需加热或冷却设备进行热量计算，可以确定加热或冷却介质的用量，以及设备所需传递的热量。

热量衡算的基础热量衡算按能量守恒定律“在无轴功条件下，进入系统的热量与离开热量应该平衡”，在实际中对传热设备的衡算可由下式表示Q1+Q2+Q3=Q4+Q5+Q6（1—1）式中：Q1—所处理的物料带入设备总的热量，KJ;Q2—加热剂或冷却剂与设备和物料传递的热量（符号规定加热剂加入热量为“+”，冷却剂吸收热量为“-”），KJ;Q3—过程的热效率，（符号规定过程放热为“+”；过程吸热为“-”）Q4—反应终了时物料的焓（输出反应器的物料的焓）Q5—设备部件所消耗的热量，KJ;Q6—设备向四周散失的热量，又称热损失,KJ;热量衡算的基准可与物料衡算相同，即对间歇生产可以以每日或每批处理物料基准。

第二章 能量衡算2.1 能量衡算概述物料衡算完成后，对于没有传热要求的设备，可以由物料处理量，物料的性质及工艺要求进行设备的工艺设计，以确定设备的型式，台数，容积以及重要尺寸。

对于有传热要求的设备则必须通过能量衡算，才能确定设备的主要工艺尺寸。

无论进行物理过程的设备或是化学过程的设备，多数伴有能量传递过程，所以必须进行能量衡算。

2.2 能量衡算目的对于新设计的生产车间，能量衡算的主要目的是为了确定设备的热负荷。

根据设备热负荷的大小，所处理物料的性质及工艺要求在选择传热面的型式，计算传热面积，确定设备的主要尺寸。

传热所需要的加热剂或冷却剂的用量也是以热负荷的大小为依据而进行计算的。

对于有些伴有热效应的过程，其物料衡算也要通过与能量衡算的联合求解才能得出最后的结果。

2.3 能量衡算依据能量衡算的主要依据是能量守恒定律。

能量守恒定律是以车间物料衡算的结果为基础而进行的。

2.4 能量衡算过程 2.4.1 反应釜的热量衡算反应工段的热量衡算主要体现在反应釜和夹套。

对于有传热要求的的设备，其热量衡算为：654321Q Q Q Q Q Q ++=++；式中 1Q —物料带入到设备的热量kJ ； 2Q —加热剂传给设备的热量kJ ； 3Q —物理变化及化学反应的热效应kJ ； 4Q —物料离开设备所带走的热量kJ ； 5Q —消耗于提高设备本身温度的热量kJ ； 6Q —设备向环境散失的热量kJ 。

物料热量衡算以天为单位。

1Q 与4Q 的计算1Q 与4Q 均可按照下式计算：()tkJ mc Q Q p ∑=41式中m —输入或输出设备的物料量，kgp c —物料的平均比热容，()C kg kJ ︒⋅/t —物料的温度，℃。

该式的计算标准是标准状态，即Pa C 3101013.10⨯︒及为计算标准。

固体和液体的比热容可以采用下式计算：Mn c c p∑⋅=α184.4； []1式中：αc —元素的原子比热容，()C kg kJ ︒⋅/ ；n —分子中同一原子的原子数；M —化合物的分子量，kmol kg /。

热量衡算一、2#氨塔水冷器进口温度 t=115℃，压力 P=29.0 MPa 入塔气NH3含量 Z1=3.6 %出塔气NH3含量 Z2=14.2 %氨产量 G=10000 Kg/h进塔气量 V进= G(1+Z2)/(Z2-Z1)=[10000*(1+14.2%)]/[17*(14.2%-3.6%)]=6337.4 kmol/h=141957.8 Nm3/h出塔气量 V出=V进-G/17=6337.4-10000/17=5749.2 kmol/h=128781.3 Nm3/h 取 Cp=7.85 kcal/kmol.℃带入水冷器热量 Q入=V出.Cp.t=5749.2*7.85*115=5190090.3 kcal/h=519009.03 kcal/t.NH3二、3#氨塔水冷器进口温度t=145℃入塔气NH3含量Z1=3.5 %出塔气NH3含量Z2=15.0 %氨产量 G=10500 Kg/h进塔气量 V进=G(1+Z2)/(Z2-Z1)=[10500*(1+15%)]/[17*(15%-3.5%)]=6176.5 kmol/h=138352.9 Nm3/h出塔气量 V出=V进-G/17=6176.5-10500/17=5558.8 kmol/h=124517.6 Nm3/h取 Cp=7.85 kcal/kmol.℃带入水冷器热量 Q入=V出.Cp.t=5558.8*7.85*145=6327304 kcal/h=602600 kcal/t.NH3三、甲醇塔1、1#甲醇塔（后期）气体流量 G=20000 Ｎm3/h塔出口温度200℃进塔co%含量Z1=6.5%出塔co%含量Z2=2.3%甲醇塔转化率α=（6.5-2.3)/6.5*100%=64.6%塔出口气量V出=V进-2*V进.Z.α=20000-20000*6.5%*64.6%*2 =18320 Nm3/h=817.9 kmol/h取Cp=7.1 kcal/kmol.℃带入水冷器热量Q入=V出.Cp.t=817.9*7.1*200=1161382 kcal/h2、2#甲醇塔入塔气量40000 Nm3/h气体出塔温度145℃进塔气co%含量5.5%出塔气co%含量1.5%co转化率α=(5.5-1.5)/5.5*100%=72.7%塔出口气体量V出=V进-2*V进.Z1.α=40000-2*40000*5.5%*72.7% =36801 Nm3/h=1642.9 kmol/h取Cp=7.1 kcal/kmol.℃带入水冷器热量Ｑ入=Ｖ出.Cp.t=1642.9*7.1*145=1691377 kcal/h3、3#甲醇塔入塔气量23000Nm3/h入塔气co%含量6.0%出塔气co%含量2.0%气体出塔温度150℃co转化率α=(6.0-2.0)/6.0*100%=66.7%塔出口气体量V出=V进-2*V进*Z1*α=23000-2*23000*6.0%*66.7% =21159 Nm3/h=944.6 kmol/h取Cp=7.1 kcal/kmol.℃带入水冷器热量Q入=V出.Cp.t=944.6*7.1*150=1006001 kcal/h氨塔、甲醇塔气体带入水冷器热量如下：如果部分热能回收利用，则需在水冷器前增加一个换热器，换热器出口气体温度能降至80℃，以3#氨塔为例，回收热能为Q回=5558.8*7.85*(145-80)=2836377 kcal/h如果用25℃的水回收，每小时用70吨水，则水升高的温度为：△t=2836377/(1000*70)≈40℃即水可加热到65℃左右。

热量衡算三、衡算方法和步骤1，明确衡算目的 确定热负荷、加热剂或冷却剂的消耗量 2，明确衡算对象 划定衡算范围，绘出热量衡算示意图 3，收集与热量衡算有关的计算数据 定压比热、相变热、反应热 4，选定衡算基准 5，列出热量衡算方程式6，根据热量衡算结果，编制物料平衡表 过程热效应物理变化热1，相变热 蒸发、冷凝、熔融、结晶、升华、凝华 恒温恒压 潜热蒸发、熔融、升华 吸热过程 (相变热为负) 冷凝、结晶、凝华 放热过程 （相变热为正） 相变热可从手册文献中查出，要注意正负号和单位 物理变化热2，浓度变化热 恒温恒压 浓度改变产生热效应积分溶解热：恒温恒压下，将1mol 溶质溶解在nmol 溶剂中，该过程所产生的热效应即为积分溶解热。

123456Q Q Q Q Q Q ++=++123456Q Q Q Q Q Q ++=++可从手册文献中查出 通过回归经验方程计算 硫酸积分溶解热计算经验式：m 为硫酸质量分率；T 为操作温度 硝酸积分溶解热计算经验式：n 为溶解1mol 硝酸的水的摩尔数；T 为操作温度 盐酸积分溶解热计算经验式：n 为溶解1mol 盐酸的水的摩尔数；T 为操作温度积分稀释热 恒温恒压下，将一定量的溶剂加入到含1mol 溶质的溶液中，形成较稀的溶液时，所产生的热效应即积分稀释热。

两种不同浓度下的积分溶解热之差 四．热量衡算举例例7-1 根据物料衡算数据表(书P110) ，已知加入甲苯和浓硫酸的温度均为30℃，脱水器的排水温度为65 ℃，磺化液的出料温度为140 ℃，甲苯与硫酸的标准化学反应热为117.2kJ/mol （放热），设备2111 2.989(15)110.20130.062s T H m mm m-∆=+--++37.571.757sn H n ∆=+50.15822.51s nH n∆=++（包括磺化釜、回流冷凝器和脱水器，下同）升温所需的热量为1.3×105kJ，设备表面向周围环境散失的热量为6.2×104kJ，回流冷凝器中冷却水移走的热量为9.8×105kJ.试对甲苯磺化过程进行热量衡算。