单筋矩形截面受弯构件正截面承载力计算教学讲义
- 格式:ppt
- 大小:1.25 MB
- 文档页数:44

基本构件计算:单筋矩形梁正截面承载力计算一、计算简图二、基本公式1.公式法的三个基本公式:单筋矩形梁正截面受弯承载力计算的三个基本公式:s y c A f bx f =1α⎪⎭⎫ ⎝⎛-=≤201x h bx f M M c u α⎪⎭⎫ ⎝⎛-=≤20x h A f M M s y u式中 M —— 弯矩设计值;M u —— 受弯承载力设计值,即破坏弯矩设计值;c f 1α—— 混凝土等效矩形应力图的应力值; y f —— 钢筋抗拉强度设计值; s A —— 受拉钢筋截面面积; b —— 梁截面宽度; x —— 混凝土受压区高度;h 0 —— 截面有效高度,即截面受压边缘到受拉钢筋合力点的距离,h 0=h-a ; a —— 受拉钢筋合力点到梁受拉边缘的距离,当受拉钢筋为一排时,a =c+d/2; c —— 混凝土保护层厚度; d —— 受拉钢筋直径。
2.系数法的基本公式(1)系数的公式).(s ξ-ξ=α501(4-21)s αξ211--= (4-25)ξ-=α-+=γ5012211.ss (4-26)(2)基本公式 201201)5.01(bh f bh f M c s c ααξξα=-=0h A f M s s y γ=三、基本公式的适用条件1)防止超筋破坏b ξξ≤ 或 b ρρ≤ 或 0h x b ξ≤2)防止少筋破坏bh A A s s min min ,ρ=≥四、计算方法1.截面选择(设计题)按已知的荷载设计值作用下的弯矩M 设计截面时,常遇到下列两种情形: 情形1 : 已知:M 、混凝土强度等级及钢筋等级;构件截面尺寸b 及h 。
求:所需的受拉钢筋截面面积A s 。
[解](1)确定基本数据c f ;y f ;a h h -=0(2)计算有关系数21bh f Mc s αα=s αξ211--=ξ-=α-+=γ5012211.ss(3)计算受拉钢筋 0h f MA s y s γ=或 01bh f f A ycs αξ=(4)根据求得的受拉钢筋A s ,按照有关构造要求从附表20中选用钢筋直径和根数 (5)验算适用条件1)适用条件:b ξ≤ξ;2)若b ξ>ξ:需加大截面,或提高混凝土强度等级,或改用双筋矩形截面 3)验算bh A A min min ,s s ρ=≥。




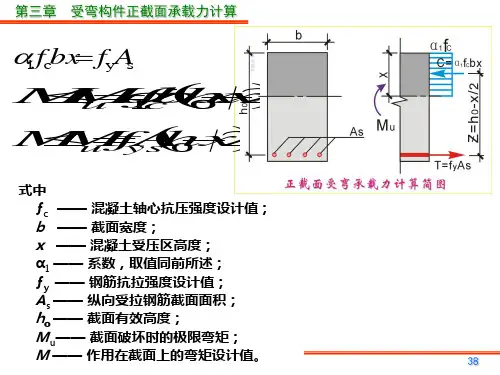

单筋矩形截面受弯构件承载力计算一、计算简图二、基本公式与适用条件1.基本公式由截面上水平方向内力之和为零,得到 g g a A R bx R =由截面上对受拉钢筋合力T 作用点的力矩之和等于零,可得⎪⎭⎫ ⎝⎛-=≤20x h bx R M M c au j γ 对压区混凝土合力C 作用点取力矩,可得 ⎪⎭⎫ ⎝⎛-=≤20x h A R M M g sgu j γ式中:M j ——考虑了荷载安全系数后计算截面上的荷载效应(计算弯矩);M u ——受弯构件计算截面的承载能力(抗力); R a ——混凝土轴心抗压设计强度; R g ——钢筋抗拉设计强度;x ——按等效矩形应力图的计算受压区高度;b ——截面宽度;h 0——截面有效高度;h 0=h -a (a 为钢筋截面中心至截面受拉边缘距离)γc ,γS ——分别为混凝土和钢筋的材料安全系数。
25.1==S c γγ2.系数法公式)5.01(0ξξ-=A )0211A --=ξξγ5.010-=;)211(5.000A -+=γ则可得0201A bh R M a cu γ=001γγh A R M g g Su =3.适用条件(1)为防止出现超筋梁情况,计算受压区高度x 应满足 0h x ig ξ≤或gaigR R ξμμ=≤max 混凝土受压区界限高度系数(2)为防止出现少筋梁的情况,计算的配筋率μ应满足min μμ≥纵向受拉钢筋最小配筋率(%)注:受压区有翼缘的T 形截面构件,表中配筋率系指钢筋截面面积与构件腹板宽乘以有效高度的截面面积之比。
三、计算方法及计算步骤1. 截面设计已知:计算弯矩M j ,混凝土和钢筋材料级别,截面尺寸b 及h求:钢筋截面面积A g 解:(1)假设钢筋截面积的重心至截面受拉边缘距离为a 。
对于绑扎钢筋骨架的梁,可设a ≈40mm (布置一层钢筋时)或65mm (布置两层钢筋时)。
对于板,一般可根据板厚假设a 为25mm 或35mm 。

受弯构件正截面承载力计算与截面设计系列总结之单筋矩形截面相关计算1 承载力计算:截面尺寸(b 、h 、h 0)、配筋(A s )和材料强度(f c ,f t 、f y )等条件已知情况下,求M u ,其计算步骤如下:1.1 计算配筋率:s A bh ρ=或s 0A bh ρ= 1.2若min ρρ<,则2u crA 0.292(1 2.5)t M M f bh α==+,其中s A E 2A bh αα= ;s E cE E α= 1.3若min max ρρρ<≤,按适筋梁进行计算,由1c y s f bx f A α=求x ,再将x 代入u 1c 0y s 0()()22x x M f bx h f A h α=−=−,其中1c max b y f f αρξ=;t min max y (0.2%,45%)f f ρ= 1.4若max ρρ>,按超筋梁进行计算,先将s y b 0.80.8f ξσξ−=−代入1c s s f bx A ασ=求x 或ξ,再将x 或ξ及s y b 0.80.8f ξσξ−=−代入u 1c 0s s 0()()22x x M f bx h A h ασ=−=− 说明:上述式中0h 按如下取值:单排配筋时, 02d h h c =−−;双排配筋时,()0max 25,22d h h c d =−−+,其中,c 为混凝土的保护层厚度,d 为钢筋的 直径,c 为混凝土保护层厚度。
2 截面设计:截面尺寸(b 、h 、h 0)、材料强度(f c ,f t 、f y )和M 等条件已知情况下,求配筋A s ,为保证所设计的截面在给定弯矩作用下不发生破坏,应要求截面的弯矩承载力不低于其所受弯矩,即:M u ≥ M ,其计算步骤如下:2.1 按22u,max 1c 0b b s,max 1c 0(10.5)M f bh f bh αξξαα=−=,其中s,max b b (10.5)αξξ=−求u,max M ,若u,max M M >则需加大截面重新计算;若u,max M M ≤则进行下一步2.2 由u 1c 0y s 0()()22x x M f bx h f A h α=−=−和1c y s f bx f A α=求s A2.3 计算配筋率:s A bhρ= 2.4 若min ρρ≥,计算结束2.5 若min ρρ<,取s min A bh ρ=说明:设计时钢筋直径未知,故上述式中0h 按如下取值:对钢筋混凝土梁,单排配筋时, 035h h =−(mm );双排配筋时,060h h =−(mm ),对钢筋混凝土板,020h h =−(mm )。
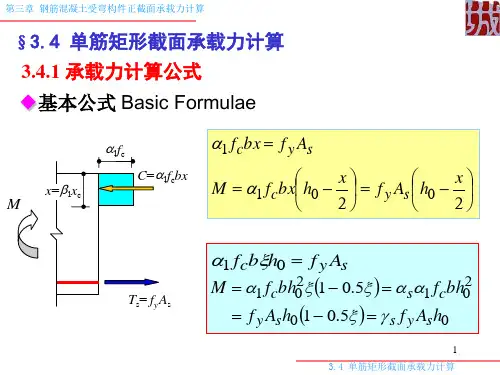

4. 3 正截面受弯承载力计算原理 一、 基本假定试验梁破坏特征→正截面承载力的四个基本假定:1. 截面应变保持平面 平截面假定:指梁在荷载作用下,正截面变形规律 符合“平均应变平截面假定” 。
实验表明:砼和钢筋纵向应变呈直线变化钢筋混凝土梁的应变2. 不考虑混凝土的抗拉强度 1) 砼的抗拉强度很 小;2)其合力作用点 离中和轴较近,抗弯 力矩的力臂很小 → 忽略受拉区砼的 抗拉作用3. 砼受压的应力-应变 关系曲线1) 当εc≤ε0时, εc n σ c = f c [1 − (1 − ) ] ε0式中 1 n = 2 − ( f cu , k − 50) ≤ 2.0 60 ε 0 = 0.002 + 0.5( f cu ,k − 50) × 10−5 ≥ 0.002f c --砼轴心抗压强度设计值ε 0 − − 相应于峰值应力的应变2) 当ε0≤εc≤εcu时, 式中σ c = fcεcu = 0.0033 − ( fcu,k − 50) ×10−5 ≤ 0.0033 εcu −− 砼的极限压应变《规范》混凝土应力-应变曲线参数 ≤C50 2 0.002 0.0033 C60 1.83 0.00205 0.0032 C70 1.67 0.0021 0.0031 C80 1.5 0.00215 0.003f cu,k nε0 εu4. 钢筋的应力-应变关系方程σ s = Es ⋅ ε s ≤ f y纵向钢筋的极限拉应变取为 0.01 纵向钢筋的极限拉应变二、 基本方程1. 受压区砼压 应力合力及作用点 假定:1. 承载力极限状态, 受压区边缘砼极限压应变 ε cu 2. 截面受压区高度 x c单 筋 矩 形 截 面xch0Asε cuy 处纤维的压应变:ε = ε y c cu xc受拉钢筋的 应变:ε s = ε cuh0 − xc xcyεcεsεc n σ c = f c [1 − (1 − ) ] ε0则,压应力 的合力 C: 力的平衡条件: C=T 截面的弯矩,即 截面受弯承载 力 Mu:y ε c = ε cu xcfCzT = f y As 受压区砼的应力图C = ∫ σ c bdy0xc∫xc0σ c bdy = f y Asxc 0M u = Cz = ∫ σ cb(h0 − xc + y )dyz--C与T之间的距离 ,内力臂2. 等效矩形应力图公式复杂,可取等效矩形应力图 形来代替受压区砼应力图形两个图形满足的等效条件: 1) 受压区砼压应力合力C 的大小相等 2) 两图形中受压区合力C的作用点不变fcxcx = β1 xcα1 fcC = α1 fcbxzT = f y AszT = f y As等效矩形应力图fcxcx = β1 xcα1 f cC = α1 f cbxzT = f y AszT = f y As 等效矩形应力图αα 1 β1β1 --等效矩形应力图的受压区高度与平截面假 定的中和轴高度的比值--无量纲参数,用来确定等效矩形应力图 1 --等效矩形应力图的强度与受压区砼最大应力的比值α 1 β1β1 = x xc--取值见 P.65.采用等效矩形应力图受弯承 载力的计算公式α1 fcC = α 1 f c bxx⎞ ⎛ M u = α1 f c bx ⎜ h0 − ⎟ 2⎠ ⎝ 令 ξ = x h0相对受压区高度x = β 1 xCzT = f y As等效矩形应力图M u = α1 f cbh ξ (1 − 0.5ξ )2 0三、适筋梁与超筋梁的界限及界限配筋率适筋梁与超筋梁的 界限破坏条件: 受拉纵筋屈服:ε cuε y = f y ES 砼发生受压破坏:ε c = ε cu 设:界限破坏时中和轴高度 xcb界限受压区高度x β1 = xcxcb εcu = h0 εcu + ε yxb = β1 xcbxbεs = ε yxb ε cu = β1h0 ε cu + ε yxb --界限相对受压区高度 设 ξb = h0ξb =β11+fy Es ⋅ ε cub相对界限受压区高度 ξ取值α1 f c bxb = f y AsAs ρb = bh0最大配筋率比较 与 ξ 的大小, b 判定是否是超筋梁 1. ξ > ξ 超筋梁 b 适筋梁 2. ξ ≤ξb 界限梁 ξ =ξb 纵向受拉钢筋的配 ρb 筋率为界限配筋率 力的平衡条件:ξα 1 f c ε cuC = α 1 f c bxx = β 1 xCzεs = ε yT = f y Asρb =α1 f c bxbbh0 f y等效矩形应力图ρ maxfc = ρb = α1ξ b fyf c xb fc = α1 = α1ξ b f y h0 fy四、适筋梁与少筋梁的界限及最小配筋率少筋破坏的特点:一产生裂缝就破坏 要避免少筋破坏发生,必须确定构件的最小配筋率 ρ min 最小配筋率是少筋梁和适筋梁的界限。