基本构件计算单筋矩形截面受弯构件承载力计算

3.2 正截面承载力计算钢筋混凝土受弯构件通常承受弯矩和剪力共同作用，其破坏有两种可能：一种是由弯矩引起的，破坏截面与构件的纵轴线垂直，称为沿正截面破坏；另一种是由弯矩和剪力共同作用引起的，破坏截面是倾斜的，称为沿斜截面破坏。

所以，设计受弯构件时，需进行正截面承载力和斜截面承载力计算。

一、单筋矩形截面1.单筋截面受弯构件沿正截面的破坏特征钢筋混凝土受弯构件正截面的破坏形式与钢筋和混凝土的强度以及纵向受拉钢筋配筋率ρ有关。

ρ用纵向受拉钢筋的截面面积与正截面的有效面积的比值来表示，即ρ＝As/(bh0)，其中A s为受拉钢筋截面面积；b为梁的截面宽度；h0为梁的截面有效高度。

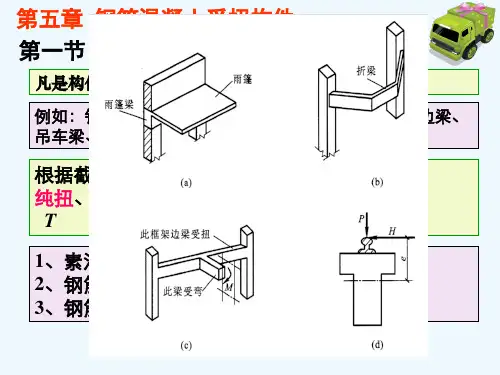
根据梁纵向钢筋配筋率的不同，钢筋混凝土梁可分为适筋梁、超筋梁和少筋梁三种类型，不同类型梁的具有不同破坏特征。

①适筋梁配置适量纵向受力钢筋的梁称为适筋梁。

适筋梁从开始加载到完全破坏，其应力变化经历了三个阶段，如图3.2.1。

第I阶段（弹性工作阶段）：荷载很小时，混凝土的压应力及拉应力都很小，应力和应变几乎成直线关系，如图3.2.1a。

当弯矩增大时，受拉区混凝土表现出明显的塑性特征，应力和应变不再呈直线关系，应力分布呈曲线。

当受拉边缘纤维的应变达到混凝土的极限拉应变εtu时，截面处于将裂未裂的极限状态，即第Ⅰ阶段末，用Ⅰa表示，此时截面所能承担的弯矩称抗裂弯矩M cr，如图3.2.1b。

Ⅰa阶段的应力状态是抗裂验算的依据。

第Ⅱ阶段（带裂缝工作阶段）：当弯矩继续增加时，受拉区混凝土的拉应变超过其极限拉应变εtu，受拉区出现裂缝，截面即进入第Ⅱ阶段。

裂缝出现后，在裂缝截面处，受拉区混凝土大部分退出工作，拉力几乎全部由受拉钢筋承担。

随着弯矩的不断增加，裂缝逐渐向上扩展，中和轴逐渐上移，受压区混凝土呈现出一定的塑性特征，应力图形呈曲线形，如图3.2.1c。

第Ⅱ阶段的应力状态是裂缝宽度和变形验算的依据。

当弯矩继续增加，钢筋应力达到屈服强度f y，这时截面所能承担的弯矩称为屈服弯矩M y。

因此得出
b

1
1
fy
cu E s
第四章 受弯构件正截面承载力计算
由平衡条件: 1 fcbxb= fyAs
可得出 1fcbbh0fyAs,max ---（4-15）
可推出适筋受弯构件最大配筋率max与 b
的表达式
maxAbs,m 0 hax b
1fc fy
---（4-16）
fy h0
360 465
0.2% h 0.2% 500 0.215%,可以。
h0
465
例题2
第四章 受弯构件正截面承载力计算
已知一单跨简支板，计算跨L0=2.34m，承受均 布荷载qk=3kN/m2（不包括板自重）；混凝土 强度等级为C30；钢筋采用HPB235级钢筋。可
最小配筋率ρmin
第四章 受弯构件正截面承载力计算
4.2.2适筋受弯构件截面受力的几个阶段
第一阶段 —— 截面开裂前阶段。
第二阶段 —— 从截面开裂到纵向受拉钢筋屈服前阶段。
第三阶段 —— 钢筋屈服到破坏阶段。
第四章 受弯构件正截面承载力计算
各阶段和各特征点的截面应力 — 应变分析：
第四章 受弯构件正截面承载力计算
由式（4-16）可知，当构件按最大配筋率配筋时，由式
M1fcb(xh02 x) (4-9a)
可以求出适筋受弯构件所能承受的最大弯矩为
M m a1 x fc b 0 2b h ( 1 0 .5 b )sb b 0 2h 1 fc
其中， sb ----截面最大的抵抗矩系数，可查表。
坏。
第四章 受弯构件正截面承载力计算
受弯构件的配筋形式
P
P

钢筋代换计算公式一、抗弯承载力（强度）验算：单筋矩形截面受弯构件正截面受弯承载力计算基本公式为：M≤Mu=fyAs(ho-fyAs/2a1fcb)当砼强度等级超过C50，a1取1.0.钢筋代换后的截面强度：fy2As2(ho2-fy2As2/2fcb)≥fy1As1(ho1-fy1As1/2fcb)fy2---拟代换钢筋的抗拉强度设计值fy1---原设计钢筋的抗拉强度设计值As2---拟代换钢筋的截面面积As1---原设计钢筋的截面面积ho2---拟代换钢筋合力作用点至构件截面受压边缘的距离ho1---原设计钢筋合力作用点至构件截面受压边缘的距离fc---砼抗压强度设计值b---构件截面宽度二、钢筋代换抗剪承载力（强度）验算：钢筋砼受弯构件，当配有箍筋和弯起钢筋时，其：斜截面受剪承载力的计算公式为：v≤0.7ftbho+1.25fyvAsvho/s+0.8fyAstysinαs,αs---斜截面上弯起钢筋与构件纵向轴向的夹角，一般取αs=45°，当梁截面较高时取αs=60°即钢筋砼受弯斜截面所承受的剪力主要由三部分组成：1.砼承担的剪力；2、箍筋承担的剪力；3、弯起钢筋承担的剪力。

其中：箍筋所承担的剪力为：vsv=1.25fyvAsvho/s, 所以，（1）、箍筋代换应满足：fyv2Asv2/s2≥fyv1Asv1/s1fyv2---拟代箍筋换的抗拉强度设计值fyv1---原设计箍筋的抗拉强度设计值Asv2---拟代换箍筋截面积Asv1---原设计箍筋截面积s2---拟代换箍筋沿构件长度方向上的距离s1---原设计箍筋沿构件长度方向上的距离弯起钢筋所能承载的剪力为：vsb=0.8fyAsbsinαs，所以，（2）、弯起钢筋代换后应满足：fy2Asb2≥fy1Asb1fy2---拟代换弯起钢筋的抗拉强度设计值fy1---原设计弯起钢筋的抗拉强度设计值Asb2---同一弯起平面内拟代换弯起钢筋的截面积Asb1---同一弯起平面内原设计弯起钢筋的截面积当fy2Asb2＜fy1Asb1时，即拟代换弯起钢筋抗力小于原设计弯起钢筋的抗力时，可通过适当增强箍筋的方法补强。

桥梁工程系－杨 剑
3.3.1 线弹性梁截面正应力计算原理
一.基本假定
1. 平截面假定成立－变形前的平截面在变形后保持平截面 不变，即截面上的正应变沿截面高度呈线形分布－给出 了截面变形的几何条件或变形协调条件。
2. 材料的应力－应变关系符合Hook定律，即应力应变之间 呈线性关系－给出了材料的物理关系。
有三种基本形式
延性破坏：配筋合适的构件，具有较高的承载力，同时破 坏时具有一定的延性，钢筋的抗拉强度和混凝土的抗压强度 都得到发挥，如适筋梁。 受拉脆性破坏：承载力很小，取决于混凝土的抗拉强度，混 凝土的抗压强度未能发挥，破坏特征与素混凝土构件类似。 虽然由于配筋使构件在破坏阶段表现出很长的破坏过程，但 这种破坏是在混凝土一开裂就产生，没有预兆，如少筋梁。 受压脆性破坏：具有较高的承载力，取决于混凝土抗压强度， 其延性能力取决于混凝土的受压塑性，因而较差，钢筋的受 拉强度没有发挥，如超筋梁 。
正常使用阶段的裂缝宽度和挠度变形验算；
绘制施工图。
桥梁工程系－杨 剑
3.2 试验研究
桥梁工程系－杨 剑
3.2.1 配筋率对正截面破坏形态的影响
一.两个名词
As’
as'
as'
h0 h
AS b
as
桥梁工程系－杨 剑
1.截面的有效高度h0及有效面积 bh0
截面的有效高度h0－截面内纵向受拉钢筋重心至 截面受压边缘的距离；
M/Mu
1.0 Mu 0.8 My
0.6
0.4
Mcr
0
fcr
fy
fu f
桥梁工程系－杨 剑
(a) (b) (c)
(d)
(e) (f) ε cu

第五章 钢筋混凝土受扭构件
第二节 矩形截面纯扭构件承载力计算
T形截面或I形截面----配筋构造
第五章 钢筋混凝土受扭构件 第三节 矩形截面弯剪扭构件承载力计算
2、矩形截面剪扭构件承载力计算
剪力的存在会使混凝土构件的受扭承载力降低，降低系数 为βt，同时，扭矩的存在也会使混凝土的受剪承载力降低， 降低系数为（1.5-βt）
素混凝土构件的受扭承载力=开裂扭矩
Tcr=0.7ftWt
ft―混凝土抗拉强度设计值； Wt―受扭构件的截面抗扭塑性抵抗矩。 矩形截面Wt=b2(3h - b) / 6。
第五章 钢筋混凝土受扭构件 第一节 受力特点与配筋构造
2、钢筋混凝土纯扭构件
扭矩在匀质弹性材料构件中引起的主拉应力方向与构件轴线 成45°。 最合理的配筋方式 为45°螺旋形配筋 ，但不便于施工。
t10 .5 V 1 .5 tW /T0 b ， h0 .5 且 1 .0
第五章 钢筋混凝土受扭构件 第三节 矩形截面弯剪扭构件承载力计算
2、矩形截面剪扭构件承载力计算
集中荷载为主的剪扭构件受剪承载力公式：
V u1 .7 1 (1 5 .5 t)b0fh t 1 .2fy 5v A s sv h 0
u c o 2 ( r b c o h c r ) ， or b c 一 o b r 5 m 般 0 ， h c m o h r 取 5 m 0
第五章 钢筋混凝土受扭构件 第二节 矩形截面纯扭构件承载力计算
1、承载力计算公式
Tu0.35 ftW t 1.2 •fysv A t s1t Acor
在实际工程中，采用构件表面设置的横向箍筋和构件周边均 匀对称设置纵向钢筋，共同形成抗扭钢筋骨架。
第五章 钢筋混凝土受扭构件 第一节 受力特点与配筋构造

为保证钢筋混凝土结构的耐久性、防火性以及钢
筋与混凝土的粘结性能，钢筋的混凝土保护层厚
５度、一配般筋不率小于2A 5msm% ； ....4...2()
bh0
用下述公式表示
As bh0
%
公式中各符号含义：
As为受拉钢筋截面面积； b为梁宽；h0为梁的有效 高度，h0=h-as；as为所有受拉钢筋重心到梁底面 的距离，单排钢筋as= 35mm ，双排钢筋as= 55~60mm 。
M/ M u
Mu
1.0
0.8 My
0.6
II
0.4
III III a II a
M cr I a
I
0
f cr
fy
fu f
加载过程中弯矩－曲率关系
说明：
对于配筋合适的梁，在III
阶段，其承载力基本保持不 变而变形可以很大，在完全
M/ M u
Mu
1.0
破坏以前具有很好的变形能 力，破坏预兆明显，我们把
0.8 My
通常采用两点对称集中加荷，加载点位于梁跨度 的1/3处，如下图所示。这样，在两个对称集中荷载间 的区段(称“纯弯段”)上，不仅可以基本上排除剪力的 影响(忽略自重)，同时也有利于在这一较长的区段上(L ／3)布置仪表，以观察粱受荷后变形和裂缝出现与开 展的情况。在“纯弯段”内，沿梁高两侧布置多排测 点，用仪表量测梁的纵向变形。
梁破坏时的极限弯矩Mu小于在正常情况下的开
裂弯矩Mcr。梁配筋率越小， Mcr -Mu的差值越大； 越大(但仍在少筋梁范围内)， Mcr -Mu的差值越小。
当Mcr -Mu =0时，它就是少筋梁与适筋梁的界限。这
时的配筋率就是适筋梁最小配筋率的理论值min。

破坏特征：一裂即坏
无明显预兆，脆性破坏，避免采用
目录
4.1
4.2
(a)适筋
4.3
梁
4.4
4.5
(b) 超筋 梁
4.6
4.7
(c) 少筋 梁
钢筋混凝土梁正截面破坏形态
Back
目录
4.4 受弯构件正截面承载力计算基本规定 4.1 4.2
4.4.1 基 本 假
4.3
定
4.4
• 1. 平截面假定
4.5
图4.4 并筋
Back
目录
4.3 受弯构件正截面受力性能
4.1
4.2
4.3
4.3.1试验研究
4.4
4.5
4.6
4.7
(b) (a)
(a) 试验梁测点布置
(b) 截面及应变分 布
图4.5 钢筋混凝土简支梁受弯试验
目录
1 适筋梁受力过程的三个阶段 4.1 4.2 4.3 4.4 4.5 4.6 4.7
• (5) 梁最外层钢筋（从箍筋外皮算起）至混凝土表面的最小距 目录
离为钢筋的混凝土保护层厚度c，其值应满足《规范》规定的最 4.1
小保护层厚度中规定（见附表14），且不小于受力钢筋的直径d。
截面有效高度h0=h-c-dv-d/2，其中dv是箍筋直径。
4.2
(6) 钢筋的净间距:
4.3
• 水平方向的净间距:梁上部钢筋水平方向的净间距不应小于 4.4
目录 4.1 4.2 4.3 4.4 4.5 4.6 4.7
目录
4.1
例4.2 某钢筋混凝土矩形截面梁，混凝 4.2
土保护层厚为25mm(二a类环境)，b=250mm， 4.3
h=500mm ， 承 受 弯 矩 设 计 值 M=160 ， 采 用 4.4

（3）弯起钢筋
在跨中承受正弯矩产生的拉力，在靠近支座的 弯起段则用来承受弯矩和剪力共同产生的主拉应 力，弯起后的水平段可用于承受支座端的负弯矩。
a.弯起钢筋的数量 通过斜截面承载能力计算得到， 一般由受力钢筋弯起而成，如受力钢筋数量不足 可单独设置。 b.弯起钢筋的弯起角度 当梁高小于等于800mm时 采用450，当梁高大于800mm时采用600
图4.2
梁钢筋净距、保护层及有效高度
（2）箍筋 ：用以承受梁的剪力，固定纵 向受力钢筋,并和其它钢筋一起形成钢筋骨 架。 a.箍筋的数量 箍筋的数量应通过计算确定。 如计算不需要时，当截面高度大于300mm时 应全梁按构造布置；当截面高度在150～ 300mm时，应在梁的端部1/4跨度内布置箍筋 但如果在梁的中部1/2的范围内有集中荷载的 作用时，应全梁设置；截面高度小于150mm 的梁可不设置箍筋。
环境类别
一类： 室内正常环境、无侵蚀性静水浸没环境
二类a：室内潮湿环境：非严寒和非寒冷地区的露天环境，与 无侵蚀性的水或土壤直接接触的环境，严寒和寒冷地区的冰冻 线以下与无侵蚀性的水或土壤直接接触的环境 二类b：干湿交替的环境，水位频繁变动环境，严寒和寒冷地 区的露天环境，与无侵蚀性的水或土壤直接接触的环境
（5）梁侧构造钢筋 当梁的腹板高度hw≥450mm时，在梁的 两个侧面应沿高度配置纵向构造钢筋， 每侧纵向构造钢筋（不包括上、下部受 力钢筋及架立钢筋）的截面面积不应小 于腹板截面面积的0.1％，且间距不宜 大于200 mm。其作用是承受温度变化、 混凝土收缩在梁侧面引起的拉应力，防 止产生裂缝。梁两侧的纵向构造钢筋用 拉筋联系。拉筋直径与箍筋直径相同， 其间距常为箍筋间距的两倍 。
梁的截面高度一般根据刚度条件 和设计经验确定，工程结构中梁的 截面高度可参照表4-1选用

fy
(3)
相对受压区高度ξ不仅反映了钢筋与混凝土的面积比（配筋率 ρ），也反映了钢筋与混凝土的材料强度比，是反映构件中两种材 料配比本质的参数。
桥梁工程系－杨 剑
界限相对受压区高度ξb
ecu
x>xb’ Xb ’ x<xb’
ρ<ρmax
ρ=ρmax ρ>ρmax
ey
桥梁工程系－杨 剑
h0
有明显屈服点钢筋：
2
(5) (5a)
桥梁工程系－杨 剑
三. 适用条件
1. b x b h0
或
max b
a fc
f sd
2 0
M M u ,max a s ,max a f cbh
a s a s ,max b (1 - 0.5b )
防止所设计的梁为超筋梁
桥梁工程系－杨 剑
4
受弯构件强度和变形计算 ——混凝土结构规范部分
本章按照混凝土结构设计规范对钢筋砼受弯 构件进行分析
桥梁工程系－杨 剑
本章主要内容
4-1 受弯构件的应力阶段及破坏状态
4-2 受弯构件正截面承载力计算 4-3 单筋矩形截面受弯构件正截面承载力计算 4-4 双筋矩形截面受弯构件正截面承载力计算
4-5 T形截面受弯构件正截面承载力计算
b =(1/3~1/4)h － T形截面，焊接骨架；
简支板可取h = (1/30 ~ 1/35)L
桥梁工程系－杨 剑
给定M时 ● 截面尺寸b、h(h0)越大，所需的As就越少， 越小，但 混凝土用量和模板费用增加，并影响使用净空高度； ● 反之，b、h(h0)越小，所需的As就越大， 增大。
b as

矩形截面偏心受压构件正截面承载力的计算一、基本公式1． 计算图式2． 基本公式由0=∑x N 得：)](11[g g g gsa cb u j A A R bx R N N σγγγ-''+=≤ 由0=∑gA M 得：)](1)2(1[00g g g sa cb u j a h A R x h bx R M e N '-''+-=≤γγγ由0=∑'gA M 得：)](1)2(1[0g g g sg a c b u j a h A a x bx R M e N '-+'--=≤'σγγγ 混凝土受压区高度由下式确定：e A R e A xh e bx R g gg g a '''-=+-σ)2(0（对偏心作用力点取矩） e e '、－分别为偏心压力j N 作用点至钢筋g A 合力作用点和钢筋g A '合力作用点的距离，按下式计算：η=e g a h e -+20；η='e g a h e '+-203．公式的注意事项（1）钢筋g A 的应力g σ取值当jg h x ξξ≤=0时，构件属于大偏心受压构件，这时取g g R =σ（受拉钢筋屈服）；当jg h x ξξ>=0时，构件属于小偏心受压构件，这时g σ按下式计算，但不大于g R 值：)19.0(003.0-=ξσg g E ，式中g E 为受拉钢筋的弹性模量。

（2）为保证构件破坏时，大偏心受压构件截面上的受压钢筋能达到抗压设计强度gR '，必须满足g a x '≥2，否则受压钢筋的应力可能达不到g R '。

与双筋截面受弯构件类似，这时可近似取g a x '=2，由截面受力平衡条件（0=∑'g A M ）可得：)(0gg g s bu j a h A R M e N '-=≤'γγ 上式计算的正截面承载力u M 比不考虑受压钢筋gA '更小时，计算中不考虑受压钢筋g A '的影响。

二、实用计算方法
1. 截面设计
已知: •
b×h、 fc、 fy、 M
求: As 用基本公式计算步骤：
(1) 查表1-7得混凝土保护层最小厚度c
(2) 假定 as
梁 as = c + 10mm （梁内两层钢筋时as =
60mm）
板 as = c + 5mm (3) h0 = h - as
a s 的确定
布置：近梁端第一根箍筋应设置在距端面一个混凝土保护 层距离处。梁与梁或梁与柱的交接范围内可不设箍筋；靠 近交接面的一根箍筋，其与交接面的距离不宜大于50mm。
形式：开口、闭口，单肢、双肢。
a双肢、开口 b双肢、闭口 c四肢、闭口
4）架立钢筋
直径：10~14mm，一般采用大值。
布置：梁上部两角。
5）纵向水平钢筋
(a) p
p
第三节钢筋混凝土受弯构件承载力极限状态计算 的一般问题
一、基本假设
（1）构件变形符合平面假设，即砼和钢筋的应变沿 截面高度符合线性分布；
（2）截面受压混凝土的应力图简化为矩形，其压力 强度值取混凝土的轴心抗压强度设计值fcd，不考虑 截面受拉混凝土的抗拉强度。
（3）极限状态时,受拉钢筋应力取其抗拉强度设计值 fsd，受压区取其抗压强度设计值f'sd。
直径：6~8mm。
间距：在受拉区不大于腹板宽度，且不大于200mm，在受 压区不大于300mm。在支点附近和预应力锚固区段，纵向钢 筋间距宜为100～150mm。
布置：骨架的侧面，下密上疏。
数量：每腹板内钢筋截面面积为(0.001～0.002)bh，其中 b为腹板宽度，h为梁的高度。
第二节 钢筋混凝土梁正截面破坏特征
受拉钢筋应力保持不变，应变持续增长。

第5章 受弯构件正截面承载力计算
Flexure Strength of RC Beams
第5章
受弯构件
如何进行一个实际工程中的梁设计？
梁的截面形式 为什么要有不同的截面形式？ 配筋基本要求 简化计算方法 如何保证所设计的是一个适筋梁？ 最大配筋率和最小配筋率 当不能满足配筋限制要求时，如何解决问题？
h/3 h/4
Mcr=Mu
h⎛h h⎞ 7 2 M cr = f tk b ⎜ + ⎟ = f tk bh 2 ⎝ 4 3 ⎠ 24
◆ 矩形截面梁高宽比h/b=2.0~3.5
c≥cmin
d
c≥cmin
d
1.5d
d=10~32mm(常用)
h0=h-as
单排 a= 35mm 双排 a= 55~60mm
T形截面梁高宽比h/b=2.5~4.0。 To ensure lateral stability
5.1 概述
第5章
受弯构件
≥30mm
5.1 概述
第5章
受弯构件
≥30mm
1.5d
c≥cmin
d
◆ 梁上部无受压钢筋时，需配置2根架
立筋(Hanger Bars)，以便与箍筋和 梁底部纵筋形成钢筋骨架，直径一 般不小于10mm；
≥cmin
h0
◆ 梁高度h0>450mm时，要求在梁两侧
a
≥cmin
1.5d
沿高度每隔200设置一根纵向构造钢 筋(Skin Reinforcement)，以减小梁 腹部的裂缝宽度，直径≥10mm；
C70 0.96 0.76
C75 0.95 0.73
C80 0.94 0.74
α fc
x=β xn C=α fcbx

b 净距30mm
钢筋直径d
净距25mm 钢筋直径d
h b
2 ~ 2.5
3.5(矩形截面) ~ 4.0(T形截面)
二、梁正截面受弯性能的试验分析
1、适筋粱的工作阶段（试验）
试验 梁
荷载分 配梁 P
外加荷 载
应变 计
位移
L/3
计
L/3
L
As
bh0
数据采集 系统
h0 h
As b
2. 受弯阶段正截面各阶段应力状态
nb
xnb h0
cu cu y
y
超筋破坏
xb 矩形应力图形的界限受压区高度
b 矩形应力图形的界限受压区相对高度
b
xb h0
1xb
h0
1 cu cu y
1
1
y
1
1 fy
cu
Es cu
界限受压区高度
fcu 50Mpa时：
b
1
0.8 fy
0.0033 Es
b即n nb
b即n nb
c c Ec
t t Ec
c xn sAs
s s Es
2. 基本公式及适用条件
压区混凝土等效矩形应力图形（极限状态下）
cu
xn=nh
xn=nh0
0
C
A
h0 h
s
Mu
s
sAs
b
xn=nh
0
Mu
1 fc
yc C
x=1xn
sAs
xn=nh
0
Mu
fc yc
C
sAs
引入参数1、1进行简 化
原则：C的大小和作用点 位置不变
1

3.2 例题例4-1: 一钢筋砼矩形截面简支梁，计算跨度l 0=6.0m ，截面尺寸： b ×h =250mm×600mm ，承受均布荷截标准值g k =15kN/m(不含自重)，均布活截标准值q k =18KN/m ，一类环境，试确定该梁的配筋并给出配筋图。

解:1.选择材料,确定计算参数选用 C25级砼： f C =11.9N/mm 2 α1=1.0钢筋：HRB335级 f y =300N/mm 2 取C=25 ξb =0.55 a s =35 h 0=600-35=5652.确定荷载设计值，据《荷载规范》 取：γG =1.2 γQ =1.4恒载设计值：G =γG （g k +b ×h ×γ）=1.2(15+0.25×0.6×25)=22.5KN/m活载设计值：Q =γQ ×q k =1.4×18=25.2kN/m 3.确定梁跨中截面弯矩设计值 M =()228181lQ G ql+=mKN .65.2140.67.47812=⨯⨯=4.确定构件重要性系数0γ 据《规范》：一般构件0γ=1.05.求受压区高度x由∑x=0 f y A s =1αf c bx∑M=0 M=α1f c bx(h o －2x ) 联立求解可得：mmbf Mh h x C 76.1462509.110.11065.2140.1256556526210200=⨯⨯⨯⨯⨯--=--=αγ6.求受拉钢筋的面积A s A s =2137.145530076.1462509.110.1mmf bxf yC =⨯⨯⨯=α5.求截面抵抗矩系数αs226.05652509.110.11065.2142621=⨯⨯⨯⨯==bh f MC sαα6.求ξ, A sξ＝260.0226.0211211=⨯--=--s α 或查表： αｓ＝0.26 → ξ=0.260 γs =0.87A s =26145687.0.5653001065.214mmr h f Mso y =⨯⨯=7.选择钢筋据《规范》附录B ，选用22,As=1520mm 2 钢筋净距: s =25373224252250>=⨯-⨯-8.验算适用条件,据《规范7.2.1》 x =147.76<75.31056555.00=⨯=h bξ或55.026.0=<=b ξξ据《规范9.5.1》, A s =1520 > ρmin bh 0=0.002×250×600=300 ρmin =45f t /f y =45×1.27/300=0.0019=0.19% 均满足要求。